Improved approximation algorithms for two-stage flexible flow shop scheduling

Abstract

A two-stage flexible flow shop scheduling is a manufacturing infrastructure designed to process a set of jobs, in which a single machine is available at the first stage and m parallel machines are available at the second stage. At the second stage, each task can be processed by multiple parallel machines. The objective is to minimize the maximum job completion time, i.e., the makespan. Sun et al. (J Softw 25:298–313, 2014) presented an $O(n\log n)$-time 3-approximation algorithm for $F2(1, Pm)~|~size_i~|~C_{\max }$ under some special conditions. Zhang et al. (J Comb Optim 39:1–14, 2020) presented a 2.5-approximation algorithm for $F2(1, P2)~|~line_i~|~C_{\max }$ and a 2.67-approximation algorithm for $F2(1, P3)~|~line_i~|~C_{\max }$, which both run in linear time. In this paper, we achieved following improved results: for $F2(1, P2)~|~line_i~|~C_{\max }$, we present an $O(n\log n)$-time 2.25-approximation algorithm, for $F2(1, P3)~|~line_i~|~C_{\max }$, we present an $O(n\log n)$-time 7/3-approximation algorithm, for $F2(1, Pm)~|~size_i~|~C_{\max }$ with the assumption $\mathop {\min }_{1 \le i \le n} \left\{ {{p_{1i}}} \right\} \ge \mathop {\max }_{1 \le i \le n} \left\{ {{p_{2i}}} \right\}$, we present a linear time optimal algorithm.

1 Introduction

We study the following two-stage flexible flow shop scheduling problem, denoted as $F2(1,Pm)~|~size_i~|~C_{\max }$ or $F2(1,Pm)~|~line_i~|~C_{\max }$ in the three field notation (Graham et al. 1979). Given a job set $\mathcal {J}=\{J_1,J_2,\ldots ,J_n\}$ and a two-stage flow shop where there are a single machine at the first stage and m parallel machines at the second stage. Each job has to be processed non-preemptively on the only one machine of the first stage. After it has been finished in the first stage, it has to be processed non-preemptively on one or multiple parallel machines of the second stage. Each job $J_i$ can be charactered as $(p_{1i}, p_{2i}, size_i/line_i)$, where $p_{1i}$ means the processing time at the first stage, $p_{2i}$ means the processing time at the second stage and $size_i$ or $line_i$ means the number of required parallel machines at the second stage, particularly, $line_i$ represents the contiguous machine assignments at the second stage. The objective is to minimize the maximum job completion time, i.e., the makespan. The scheduling constraint is as usual, that is at every time point, a job can be processed by at most one machine and a machine can process at most one job.

Flexible flow shop scheduling problems have many real-life applications: many discrete manufacturing industries have a flow shop architecture where there is a multi-stage production process with the property that all tasks have to be proceed through the stages in the same order. Flexible flow shop scheduling problems have been studied since the 1970’s (Arthanari and Ramamurthy 1971; Salvador 1973) and attract more and more attention from all over the world. For the two-stage flexible flow shop under the condition that each task requires only one machine, and multiple parallel machines are available at every stage, Lee and Vairaktarakis (1994) developed a $2 - \frac{1}{\max \{m_1, m_2\}}$ approximation algorithm, where $m_1$ and $m_2$ are the numbers of machines at the first and the second stage. Gupta et al. (2002) studied a generalization of the permutation flow shop problem that combines the scheduling function with planning stage. They presented iterative algorithms based on local search and constructive algorithms based on job insertion techniques. Alisantoso et al. (2003) studied the scheduling of a flexible flow shop for PCB (printed circuit board) manufacturing. They first presented an overview of the flexible flow shop problem and the basic notions of an immune algorithm. And then, they presented an immune algorithm in detail and implemented it to compare with the well know evolutionary algorithms-genetic algorithms, which showed that immune algorithm outperformed genetic algorithms. Lin and Liao (2003) considered a two-stage hybrid flow shop with characteristics of sequence dependent setup time at first stage, dedicated machines at the second stage, and two due dates. They presented a heuristic algorithm to find the near-optimal schedule for the problem. He et al. (2008) considered the two-stage flexible flow shop scheduling problem with m identical parallel machines in stage 1 and only one batch machine in stage 2. They showed the problem is NP-hard in general and proposed corresponding approximation algorithm. Moseley et al. (2011) presented a 12-approximation algorithm for two-stage parallel machine scheduling problem and used it to solve the popular Map-Reduce frame of big data circumstance. Almeder and Hartl (2013) considered a scheduling problem of a real-world production process in the metal-working industry which can be described as an offline stochastic flexible flow-shop problem with limited buffers. They first studied a simplified model and proposed a variable neighbourhood search based solution approach. And then, they applied the solution approach to a real-world case using a detailed discrete-event simulation to evaluate the production plans. Choi and Lee (2013) proposed approximation algorithms for the two-stage flexible flow shop problem with the condition that the processing times of each job are identical at both stages and with a single machine at one stage and m identical machines at the other stage. For $m=2$, they presented a 5/4-approximation algorithm, and for $m \ge 3$, they presented a $\frac{\sqrt{1+m^2}+1+m}{2m}$-approximation algorithm. Sun et al. (2014) considered the two-stage scheduling problem with multiple parallel machines at the executing stage, which can be used to solve the transporting and executing stage of massively parallel load tasks on GPU. Especially, they proposed an $O(n\log n)$-time 3-approximation algorithm for $F2(1, Pm)~|~size_i~|~C_{\max }$ with the assumptions that $\sum _{{J_i} \in \mathcal {J} } {{p_{1i}}} > \sum _{{J _i} \in \mathcal {J} } {\left\{ {siz{e_i} \times {p_{2i}}} \right\} }$ and $\mathop {\min }_{1 \le i \le n} \left\{ {{p_{1i}}} \right\} \ge \mathop {\max }_{1 \le i \le n} \left\{ {{p_{2i}}} \right\}$. Recently, Zhang et al. (2020) studied the two-stage flexible flow shop scheduling problem with m identical parallel machines at one stage and a single machine at the other stage. They first presented a $(2+\epsilon )$-approximation algorithm for $F2(1,Pm)~|~size_i~|~C_{\max }$ and a $(2.5+\epsilon )$-approximation algorithm for $F2(1,Pm)~|~line_i~|~C_{\max }$. Then, they presented a 2.5-approximation algorithm for $F2(1, P2)~|~line_i~|~C_{\max }$ and a 2.67-approximation algorithm for $F2(1, P3)~|~line_i~|~C_{\max }$, which both run in linear time.

In this paper, we consider the two-stage flow shop where there are a single machine at the first stage and m parallel machines at the second stage. For $F2(1, P2)~|~line_i~|~C_{\max }$, we present an $O(n\log n)$-time 2.25-approximation algorithm, for $F2(1, P3)~|~line_i~|~C_{\max }$, we present an $O(n\log n)$-time 7/3-approximation algorithm, which improved the approximation results presented in Zhang et al. (2020). For $F2(1, Pm)~|~size_i~|~C_{\max }$ with the assumption that $\mathop {\min }_{1 \le i \le n} \left\{ {{p_{1i}}} \right\} \ge \mathop {\max }_{1 \le i \le n} \left\{ {{p_{2i}}} \right\}$, we present a linear time optimal algorithm, which improved the result presented in Sun et al. (2014).

The rest of the paper is organized as follows. In Sect. 2, we present an $O(n\log n)$-time 2.25-approximation algorithm for $F2(1, P2)~|~line_i~|~C_{\max }$. We present in Sect. 3 an $O(n\log n)$-time 7/3-approximation algorithm for $F2(1, P3)~|~line_i~|~C_{\max }$. Section 4 contains a linear time optimal algorithm for $F2(1, Pm)~|~size_i~|~C_{\max }$ with the assumption that $\mathop {\min }_{1 \le i \le n} \left\{ {{p_{1i}}} \right\} \ge \mathop {\max }_{1 \le i \le n} \left\{ {{p_{2i}}} \right\}$. We conclude the paper with some remarks in Sect. 5.

2 A 2.25-approximation algorithm for $F2(1, P2)~|~line_i~|~C_{\max }$

In this section, we consider $F2(1, P2)~|~line_i~|~C_{\max }$: the two-stage flexible flow shop scheduling problem with a machine at the first stage and two machines at the second stage, the objective is to minimize the makespan. It is easy to see that the bounds of $line_i$ case are also hold for the $size_i$ case. Hence, the algorithm we present in this section are applicable for $F2(1, P2)~|~size_i~|~C_{\max }$.

Now, we are ready to present an approximation algorithm for $F2(1, P2)~|~line_i~|~C_{\max }$.

In the first stage, we arrange all the jobs on the machine one by one in random order non-preemptively.

In the second stage, we first group the jobs into two subsets: $\mathcal {J}_1$ denote the set of jobs that requiring only one machine at the second stage and $\mathcal {J}_2$ denote the set of jobs that requiring two machines at the second stage. Secondly, we sort the jobs in $\mathcal {J}_1$ in non-increasing order according to $p_{2i}$. At last, we first arrange the jobs in $\mathcal {J}_2$ on the two parallel machines one by one non-preemptively, and then arrange the jobs in $\mathcal {J}_1$ according to list scheduling rule where the order of the jobs is priority.

A high-level description of the approximation algorithm is showed in Algorithm 1.

Theorem 1

The Algorithm 1 is an $O(n\log n)$-time 2.25-approximation algorithm for ${F2}\left( {1,{P2}} \right) |lin{e_i}|{C_{\max }}$.

Proof

Without loss of generality, we assume that the job set $\mathcal {J}_1 = \{ J_1, J_2, \ldots , J_k \}$ satisfies $p_{21} \ge p_{22} \ge \cdots \ge p_{2k}$.

Let us consider the following two cases:

Case 1: $p_{21} \ge \sum \limits _{i = 2}^{k}p_{2i}.$

From the feature of ${F2}\left( {1,{P2}} \right) |lin{e_i}|{C_{\max }}$,we have

$$\begin{aligned} C_{\max }^{*}\ge & {} \sum _{J _i \in \mathcal {J} }p_{1i}, \end{aligned}$$

(1)

$$\begin{aligned} C_{\max }^{*}\ge & {} \sum _{J _i \in \mathcal {J} _2 }p_{2i}+p_{21}, \end{aligned}$$

(2)

where $C_{\max }^{*}$ denote the optimal value for ${F2}\left( {1,{P2}} \right) |lin{e_i}|{C_{\max }}$.

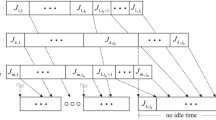
According to the Algorithm 1 we have (an illustration is showed in Fig. 1)

$$\begin{aligned} C_{\max }\left( L \right) =\sum \limits _{J _i \in \mathcal {J} }p_{1i}+\sum _{J _i \in \mathcal {J} _2 }p_{2i}+p_{21}. \end{aligned}$$

(3)

Fig. 1

An illustration of the schedule produced by Algorithm 1 under case 1, where $s_1$ is the processing time of jobs in ${\mathcal {J}}$ on the first stage, $s_2$ is the processing time of jobs in ${\mathcal {J}_2}$ on the second stage, $s_3$ is the processing time of job $J_1$ on the second stage

Put (1), (2) and (3) together, we have

$$\begin{aligned} C_{\max }\left( L \right) \le 2 C_{\max }^{*} . \end{aligned}$$

Case 2: $p_{21} < \sum \limits _{i = 2}^{k}p_{2i}.$

In this case, (1) is also hold.

From the feature of ${F2}\left( {1,{P2}} \right) |lin{e_i}|{C_{\max }}$,we have

$$\begin{aligned} C_{\max }^{*} \ge \sum _{J _i \in \mathcal {J} _2 }p_{2i}+\frac{1}{2} \sum _{J _i \in \mathcal {J} _1 }p_{2i}. \end{aligned}$$

(4)

There are at least three jobs $J_1, J_2, J_3$ in the job set $\mathcal {J}_1$ since $p_{21} < \sum \limits _{i = 2}^{k}p_{2i}.$ Hence we have

$$\begin{aligned} C_{\max }^{*} \ge p_{22} +p_{23}. \end{aligned}$$

(5)

According to the Algorithm 1 we have (an illustration is showed in Fig. 2)

$$\begin{aligned} C_{\max }\left( L \right) \le \sum \limits _{J _i \in \mathcal {J} }p_{1i}+\sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}+\frac{1}{2}\sum \limits _{J _i \in \mathcal {J} _1 }p_{2i}+\frac{1}{2}p_{23}. \end{aligned}$$

(6)

Fig. 2

An illustration of the schedule produced by Algorithm 1 under case 2, where $s_1$ is the processing time of jobs in ${\mathcal {J}}$ on the first stage, $s_2$ is the processing time of jobs in ${\mathcal {J}_2}$ on the second stage, $s_3$ is the average processing time of jobs in ${\mathcal {J}_1}$ on the second stage, $s_4$ is $C_{\max }\left( L \right) -s_1-s_2-s_3$, and it’s easy to know that $s_4 \le \frac{1}{2}p_{2k} \le \frac{1}{2}p_{23}$

Put (1), (4), (5) and (6) together, we have

$$\begin{aligned} \begin{array}{rcl} &{} &{}C_{\max }\left( L \right) \le 2C_{\max }^{*} + \frac{1}{2} \times \frac{1}{2}\left( {p_{22} +p_{23}} \right) \\ &{} &{}\qquad \qquad \qquad \le 2.25C_{\max }^{*}. \end{array} \end{aligned}$$

Combining cases 1 and 2, we have showed the approximation ratio of Algorithm 1 is 2.25.

At last, the time complexity of the Algorithm 1 is $O(n\log n)$ which is obviously from the algorithm. $\square$

3 A 7/3-approximation algorithm for $F2(1, P3)~|~line_i~|~C_{\max }$

In this section, we consider $F2(1, P3)~|~line_i~|~C_{\max }$: the two-stage flexible flow shop scheduling problem with a machine at the first stage and three machines ($m_1$, $m_2$ and $m_3$) at the second stage, the objective is to minimize the makespan. It is easy to see that the bounds of $line_i$ case are also hold for the $size_i$ case. Hence, the algorithm we present in this section are applicable for $F2(1, P3)~|~size_i~|~C_{\max }$.

Now, we are ready to present an approximation algorithm for $F2(1, P3)~|~line_i~|~C_{\max }$.

In the first stage, we arrange all the jobs on the machine one by one in random order non-preemptively.

In the second stage, we first group the jobs into three subsets: $\mathcal {J}_1$ denote the set of jobs that requiring only one machine at the second stage, $\mathcal {J}_2$ denote the set of jobs that requiring two machines at the second stage, and $\mathcal {J}_3$ denote the set of jobs that requiring three machines at the second stage. Secondly, we sort the jobs in $\mathcal {J}_1$ in non-increasing order according to $p_{2i}$. At last, we first arrange the jobs in $\mathcal {J}_3$ on the three parallel machines one by one non-preemptively, and then arrange the jobs in $\mathcal {J}_2$ on machine $m_1$ and machine $m_2$, arrange the jobs in $\mathcal {J}_1$ on machine $m_3$. Here we discuss the following two cases:

Case 1: $\sum _{{J _i} \in {\mathcal {J} _2}} {{p_{2i}}} \ge \sum _{{J _i} \in {\mathcal {J} _1}} {p_{2i}}$, i.e., machine ${m_3}$ is idle after processing the jobs in ${\mathcal {J} _1}$. In this case, we continue processing the jobs in ${\mathcal {J} _2}$ on machine ${m_1}$ and machine ${m_2}$.

Case 2: $\sum _{{J _i} \in {\mathcal {J} _2}} {{p_{2i}}} < \sum _{{J _i} \in {\mathcal {J} _1}} {p_{2i}}$. In this case, after processing all the jobs in ${\mathcal {J}_2}$ on machine ${m_1}$ and machine ${m_2}$, we process the remaining jobs of ${\mathcal {J} _1}$ on machine ${m_1}$, machine ${m_2}$ and machine ${m_3}$ according to list scheduling rule.

A high-level description of the approximation algorithm is showed in Algorithm 2.

Theorem 2

The Algorithm 2 is an $O(n\log n)$-time 7/3-approximation algorithm ${F2}\left( {1,{P3}} \right) |lin{e_i}|{C_{\max }}$.

Proof

Without loss of generality, we assume that the job set $\mathcal {J}_1 =\{J_1, J_2, \ldots , J_k\}$ satisfies $p_{21} \ge p_{22} \ge \cdots \ge p_{2k}$.

Let us consider the following three cases.

Case 1: $\sum \limits _{{J _i} \in {\mathcal {J} _2}} {{p_{2i}}} \ge \sum \limits _{{J _i} \in {\mathcal {J} _1}} {p_{2i}}$.

From the feature of ${F2}\left( {1,{P3}} \right) |lin{e_i}|{C_{\max }}$, we have

$$\begin{aligned} C_{\max }^{*}\ge & {} \sum _{J _i \in \mathcal {J} }p_{1i}, \end{aligned}$$

(7)

$$\begin{aligned} C_{\max }^{*}\ge & {} \sum _{J _i \in \mathcal {J} _3 }p_{2i}+\sum _{J _i \in \mathcal {J} _2 }p_{2i}. \end{aligned}$$

(8)

According to the Algorithm 2, we have (an illustration is showed in Fig. 3)

$$\begin{aligned} C_{\max }\left( L \right) =\sum \limits _{J _i \in \mathcal {J} }p_{1i}+\sum \limits _{J _i \in \mathcal {J} _3 }p_{2i}+\sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}. \end{aligned}$$

(9)

Fig. 3

An illustration of the schedule produced by Algorithm 2 under case 1, where $s_1$ is the processing time of jobs in ${\mathcal {J}}$ on the first stage, $s_2$ is the processing time of jobs in ${\mathcal {J}_3}$ on the second stage, $s_3$ is the processing time of jobs in ${\mathcal {J}_2}$ on the second stage

Put (7), (8) and (9) together, we have

$$\begin{aligned} C_{\max }\left( L \right) \le 2 C_{\max }^{*}. \end{aligned}$$

Case 2: $\sum \limits _{{J _i} \in {\mathcal {J} _2}} {{p_{2i}}} < \sum \limits _{{J _i} \in {\mathcal {J} _1}} {p_{2i}}$ and $p_{21} \le \sum \limits _{{J _i} \in {\mathcal {J} _2}} {{p_{2i}}}$.

In this case, (7) is also hold.

From the feature of ${F2}\left( {1,{P3}} \right) |lin{e_i}|{C_{\max }}$, we have

$$\begin{aligned} C_{\max }^{*} \ge \sum _{J _i \in \mathcal {J} _3 }p_{2i}+ \frac{2}{3} \sum _{J _i \in \mathcal {J} _2 }p_{2i}+ \frac{1}{3} \sum _{J _i \in \mathcal {J} _1 }p_{2i}. \end{aligned}$$

(10)

There are at least two jobs in $\mathcal {J}_1$ since $\sum \limits _{{J _i} \in {\mathcal {J} _2}} {{p_{2i}}} < \sum \limits _{{J _i} \in {\mathcal {J} _1}} {p_{2i}}$ and $p_{21} \le \sum \limits _{{J _i} \in {\mathcal {J} _2}} {{p_{2i}}}$. Hence, we have

$$\begin{aligned} C_{\max }^{*} \ge p_{21} +p_{22}. \end{aligned}$$

(11)

According to the Algorithm 2, we have (an illustration is showed in Fig. 4)

$$\begin{aligned} C_{\max }\left( L \right)\le & {} \sum \limits _{J _i \in \mathcal {J} }p_{1i}+\sum \limits _{J _i \in \mathcal {J} _3 }p_{2i}+\sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}\nonumber \\&+\frac{1}{3}\left( \sum \limits _{{J _i} \in {\mathcal {J} _1}} {p_{2i}}-\sum \limits _{{J _i} \in {\mathcal {J} _2}} {{p_{2i}}}\right) +\frac{2}{3}p_{22}. \end{aligned}$$

(12)

Fig. 4

An illustration of the schedule produced by Algorithm 2 under case 2, where $s_1$ is the processing time of jobs in ${\mathcal {J}}$ on the first stage, $s_2$ is the processing time of jobs in ${\mathcal {J}_3}$ on the second stage, $s_3$ is the processing time of jobs in ${\mathcal {J}_2}$ on the second stage, $s_4$ is the average processing time of the processing time of jobs in ${\mathcal {J}_1}$ subtract the processing time of jobs in ${\mathcal {J}_2}$ on the second stage, $s_5$ is $C_{\max }\left( L \right) -s_1-s_2-s_3-s_4$, and it’s easy to know that $s_5 \le \frac{2}{3}p_{2k} \le \frac{2}{3}p_{22}$

Put (7), (10), (11) and (12) together, we have

$$\begin{aligned} \begin{array}{rcl} &{} &{} C_{\max }\left( L \right) \le 2C_{\max }^{*} + \frac{2}{3} \times \frac{1}{2}\left( p_{21} +p_{22} \right) \\ &{} &{}\qquad \qquad \qquad \le \frac{7}{3}C_{\max }^{*}. \end{array} \end{aligned}$$

Case 3: $p_{21} > \sum \limits _{{J _i} \in {\mathcal {J} _2}} {{p_{2i}}}$.

In this case, (7) and (10) are also hold.

If the number of the jobs in $\mathcal {J}_1$ satisfies $k < 4$, then from the feature of ${F2}\left( {1,{P3}} \right) |lin{e_i}|{C_{\max }}$,we have

$$\begin{aligned} C_{\max }^{*} \ge \max \left\{ {\sum \limits _{J _i \in \mathcal {J} _3 }p_{2i}+p_{21}, \sum \limits _{J _i \in \mathcal {J} _3 }p_{2i}+\sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}+p_{22}} \right\} . \end{aligned}$$

(13)

According to the Algorithm 2, we have (an illustration is showed in Fig. 5)

$$\begin{aligned} C_{\max }\left( L \right) = \sum \limits _{J _i \in \mathcal {J} }p_{1i}+\max \left\{ \sum \limits _{J _i \in \mathcal {J} _3 }p_{2i}+p_{21}, \sum \limits _{J _i \in \mathcal {J} _3 }p_{2i}+\sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}+p_{22} \right\} . \end{aligned}$$

(14)

Fig. 5

An illustration of the schedule produced by Algorithm 2 under case 3 with $k < 3$, where $s_1$ is the processing time of jobs in ${\mathcal {J}}$ on the first stage, $s_2$ is the processing time of jobs in ${\mathcal {J}_3}$ on the second stage, $s_3$ is $C_{\max }\left( L \right) -s_1-s_2$, $C_1$ is the case that $p_{21} \ge \sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}+p_{22}$, $C_2$ is the case that $p_{21} < \sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}+p_{22}$

Put (7), (13) and (14) together, we have

$$\begin{aligned} C_{\max }\left( L \right) \le 2C_{\max }^{*}. \end{aligned}$$

Otherwise, the number of the jobs in $\mathcal {J}_1$ satisfies $k \ge 4$, i.e., there exists at least four jobs $J _1$, $J _2$, $J _3$ and $J _4$ in $\mathcal {J}_1$, which means one of the machines at the second stage must process at least two jobs of $\{ J _1, J _2, J _3, J _4 \}$ since there are only three machines. Hence, we have

$$\begin{aligned} C_{\max }^{*} \ge p_{23} +p_{24}. \end{aligned}$$

(15)

From the feature of ${F2}\left( {1,{P3}} \right) |lin{e_i}|{C_{\max }}$, we have

$$\begin{aligned} C_{\max }^{*}\ge & {} \sum \limits _{J _i \in \mathcal {J} _3 }p_{2i}+p_{21}, \end{aligned}$$

(16)

$$\begin{aligned} C_{\max }^{*}\ge & {} \sum \limits _{J _i \in \mathcal {J} _3 }p_{2i}+\sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}+p_{22}. \end{aligned}$$

(17)

According to the Algorithm 2, we know that at the second stage, the job $J _1$ is processed on the machine $m_3$, the job $J _2$ is processed on the machine $m_1$, the job $J _3$ is processed on the machine $m_2$.

Let us consider the following two subcases.

Case 3.1: $p_{21}<\sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}+p_{22}$.

According to the Algorithm 2, we first process the remaining jobs in $\mathcal {J} _1$ on machines $m_2$ and $m_3$.

If machines $m_2$ and $m_3$ are idle after finish processing the remaining jobs in $\mathcal {J} _1$ when the job $J _2$ are still processed on machine $m_1$, then, according to the Algorithm 2, we have (an illustration is showed in Fig. 6)

$$\begin{aligned} C_{\max }\left( L \right) =\sum \limits _{J _i \in \mathcal {J} }p_{1i}+\sum \limits _{J _i \in \mathcal {J} _3 }p_{2i}+\sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}+p_{22}. \end{aligned}$$

(18)

Put (7), (17) and (18) together, we have

$$\begin{aligned} C_{\max }\left( L \right) \le 2C_{\max }^{*}. \end{aligned}$$

Otherwise, the job $J _2$ is finished first on machine $m_1$, then we process the remaining jobs in $\mathcal {J} _1$ on machines $m_1$, $m_2$ and $m_3$ according to list scheduling rule, so we have (an illustration is showed in Fig. 7)

$$\begin{aligned} C_{\max }\left( L \right)\le & {} \sum \limits _{J _i \in \mathcal {J} }p_{1i}+\sum \limits _{J _i \in \mathcal {J} _3 }p_{2i}+\sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}\nonumber \\&+\frac{1}{3}\left( \sum \limits _{{J _i} \in {\mathcal {J} _1}} {p_{2i}}-\sum \limits _{{J _i} \in {\mathcal {J} _2}} {{p_{2i}}}\right) +\frac{2}{3}p_{24}. \end{aligned}$$

(19)

Fig. 6

An illustration of the schedule produced by Algorithm 2 under case 3.1 with machines $m_2$ and $m_3$ are idle after finish processing the remaining jobs in $\mathcal {J} _1$ when the job $J _2$ are still processed on machine $m_1$, where $s_1$ is the processing time of jobs in ${\mathcal {J}}$ on the first stage, $s_2$ is the processing time of jobs in ${\mathcal {J}_3}$ on the second stage, $s_3$ is the processing time of jobs in ${\mathcal {J}_2}$ on the second stage, $s_4$ is the processing time of job ${J_2}$ on the second stage

Put (7), (10), (15) and (19) together, we have

$$\begin{aligned} C_{\max }\left( L \right) \le 2C_{\max }^{*} + \frac{2}{3} \times \frac{1}{2}\left( {p_{23} +p_{24}} \right) \le \frac{7}{3}C_{\max }^{*}. \end{aligned}$$

Case 3.2: $p_{21} \ge \sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}+p_{22}$.

According to the Algorithm 2, we first process the remaining jobs in $\mathcal {J} _1$ on machines $m_1$ and $m_2$.

If machines $m_1$ and $m_2$ are idle after finishing all the jobs in $\mathcal {J} _1$ when the job $J _1$ is still processed on machine $m_3$, then, according to the Algorithm 2, we have (an illustration is showed in Fig. 8)

$$\begin{aligned} C_{\max }\left( L \right) =\sum \limits _{J _i \in \mathcal {J} }p_{1i}+\sum \limits _{J _i \in \mathcal {J} _3 }p_{2i}+p_{21}. \end{aligned}$$

(20)

Fig. 7

An illustration of the schedule produced by Algorithm 2 under case 3.1 with the job $J _2$ is finished first on machine $m_1$, where $s_1$ is the processing time of jobs in ${\mathcal {J}}$ on the first stage, $s_2$ is the processing time of jobs in ${\mathcal {J}_3}$ on the second stage, $s_3$ is the processing time of jobs in ${\mathcal {J}_2}$ on the second stage, $s_4$ is the average processing time of the processing time of jobs in ${\mathcal {J}_1}$ subtract the processing time of jobs in ${\mathcal {J}_2}$ on the second stage, $s_5$ is $C_{\max }\left( L \right) -s_1-s_2-s_3-s_4$, and it’s easy to know that $s_5 \le \frac{2}{3}p_{2k} \le \frac{2}{3}p_{24}$

Put (7), (16) and (20) together, we have

$$\begin{aligned} C_{\max }\left( L \right) \le 2C_{\max }^{*}. \end{aligned}$$

Otherwise, the job $J _1$ is finished first on machine $m_3$, then we process the remaining jobs in $\mathcal {J} _1$ on machines $m_1$, $m_2$ and $m_3$ according to list scheduling rule, so we have (an illustration is showed in Fig. 9)

$$\begin{aligned} C_{\max }\left( L \right)\le & {} \sum \limits _{J _i \in \mathcal {J} }p_{1i}+\sum \limits _{J _i \in \mathcal {J} _3 }p_{2i}+\sum \limits _{J _i \in \mathcal {J} _2 }p_{2i}\nonumber \\&+\frac{1}{3}\left( \sum \limits _{{J _i} \in {\mathcal {J} _1}} {p_{2i}}-\sum \limits _{{J _i} \in {\mathcal {J} _2}} {{p_{2i}}}\right) +\frac{2}{3}p_{24}. \end{aligned}$$

(21)

Fig. 8

An illustration of the schedule produced by Algorithm 2 under case 3.2 with machines $m_1$ and $m_2$ are idle after finishing all the jobs in $\mathcal {J} _1$ when the job $J _1$ is still processed on machine $m_3$, where $s_1$ is the processing time of jobs in ${\mathcal {J}}$ on the first stage, $s_2$ is the processing time of jobs in ${\mathcal {J}_3}$ on the second stage, $s_3$ is the processing time of job ${J_1}$ on the second stage

Fig. 9

An illustration of the schedule produced by Algorithm 2 under case 3.2 with the job $J _1$ is finished first on machine $m_3$, where $s_1$ is the processing time of jobs in ${\mathcal {J}}$ on the first stage, $s_2$ is the processing time of jobs in ${\mathcal {J}_3}$ on the second stage, $s_3$ is the processing time of jobs in ${\mathcal {J}_2}$ on the second stage, $s_4$ is the average processing time of the processing time of jobs in ${\mathcal {J}_1}$ subtract the processing time of jobs in ${\mathcal {J}_2}$ on the second stage, $s_5$ is $C_{\max }\left( L \right) -s_1-s_2-s_3-s_4$, and it’s easy to know that $s_5 \le \frac{2}{3}p_{2k} \le \frac{2}{3}p_{24}$

Put (7), (10), (15) and (21) together, we have

$$\begin{aligned} \begin{array}{rcl} &{} &{}C_{\max }\left( L \right) \le 2C_{\max }^{*} + \frac{2}{3} \times \frac{1}{2}\left( {p_{23} +p_{24}} \right) \\ &{} &{}\qquad \qquad \le \frac{7}{3}C_{\max }^{*}. \end{array} \end{aligned}$$

Hence, the approximation ratio of the Algorithm 2 is 7/3.

At last, it is easy to know that the time complexity of the Algorithm 2 is $O(n\log n)$. $\square$

4 An optimal algorithm for $F2(1, Pm)~|~size_i~|~C_{\max }$ under some special conditions

In this section, we consider $F2(1, Pm)~|~size_i~|~C_{\max }$ under some special conditions: the two-stage flexible flow shop scheduling problem with a machine at the first stage and m machines at the second stage, the processing time of the jobs satisfies: $\mathop {\min }_{1 \le i \le n} \left\{ {{p_{1i}}} \right\} \ge \mathop {\max }_{1 \le i \le n} \left\{ {{p_{2i}}} \right\}$, the objective is to minimize the makespan.

Now, we are ready to present an optimal algorithm for the problem.

Firstly, for the given job set $\mathcal {J} = \{ J_1, J_2, \ldots , J_n \}$, find out the job with the smallest processing time on the second stage, if there are more than one job with the smallest processing time on the second stage, then arbitrarily choose one of them. Without loss of generality, we assume $J_n$ is the job with the smallest processing time on the second stage, i.e., $p_{2n} = \mathop {\min }\limits _{1 \le i \le n} \left\{ {{p_{2i}}} \right\}$.

Secondly, process the jobs with the order $\{ J_1, J_2, \ldots , J_n \}$ non-preemptively in the first stage.

Lastly, for each job $J_i$, process it in the second stage immediately when it has been finished in the first stage.

A high-level description of the algorithm is showed in Algorithm 3.

Theorem 3

The Algorithm 3 is a linear time optimal algorithm for $F2(1, Pm)~|~size_i~| C_{\max }$ with the assumption that $\mathop {\min }_{1 \le i \le n} \left\{ {{p_{1i}}} \right\} \ge \mathop {\max }_{1 \le i \le n} \left\{ {{p_{2i}}} \right\}$.

Proof

From the feature of $F2(1, Pm)~|~size_i~|~C_{\max }$ with the assumption that $\mathop {\min }_{1 \le i \le n} \left\{ {{p_{1i}}} \right\} \ge \mathop {\max }_{1 \le i \le n} \left\{ {{p_{2i}}} \right\}$, we have

$$\begin{aligned} C_{\max }^{*} \ge \sum \limits _{J _i \in \mathcal {J}}p_{1i}+\mathop {\min }\limits _{1 \le i \le n} \left\{ {{p_{2i}}} \right\} . \end{aligned}$$

(22)

According to Algorithm 3 with the assumption that $\mathop {\min }_{1 \le i \le n} \left\{ {{p_{1i}}} \right\} \ge \mathop {\max }_{1 \le i \le n} \left\{ {{p_{2i}}} \right\}$, we have (an illustration is showed in Fig. 10)

$$\begin{aligned} C_{max}(L) = \sum \limits _{J _i \in \mathcal {J}}p_{1i} + p_{2n} = \sum \limits _{J _i \in \mathcal {J}}p_{1i} + \mathop {\min }\limits _{1 \le i \le n} \left\{ {{p_{2i}}} \right\} . \end{aligned}$$

(23)

Fig. 10

An illustration of the schedule produced by Algorithm 3, where $s_1$ is the processing time of jobs in ${\mathcal {J}}$ on the first stage, $s_2$ is the minimal processing time of jobs in ${\mathcal {J}}$ on the second stage, $P_1$ is the first stage, $P_2$ is the second stage

Put (22) and (23) together, we have

$$\begin{aligned} C_{max}(L) \le C_{\max }^{*}. \end{aligned}$$

Combining with the fact that $C_{\max }^{*}$ is the optimal value, we have

$$\begin{aligned} C_{max}(L) = C_{\max }^{*}. \end{aligned}$$

Hence, the Algorithm 3 is an optimal algorithm for $F2(1, Pm)~|~size_i~|~C_{\max }$ with the assumption that $\mathop {\min }_{1 \le i \le n} \left\{ {{p_{1i}}} \right\} \ge \mathop {\max }_{1 \le i \le n} \left\{ {{p_{2i}}} \right\}$.

At last, it is easy to know that the Algorithm 3 can be finished in linear time. $\square$

5 Concluding remarks

In this paper, we studied the two-stage flexible flow shop scheduling problems. We first presented an $O(n\log n)$-time 2.25-approximation algorithm for $F2(1, P2)~|~line_i~|~C_{\max }$, and then proposed an $O(n\log n)$-time 7/3-approximation algorithm for $F2(1, P3)~|~line_i~|~C_{\max }$. Lastly we proposed a linear time optimal algorithm for $F2(1, Pm)~|~size_i~|~C_{\max }$ with the assumption that $\mathop {\min }_{1 \le i \le n} \left\{ {{p_{1i}}} \right\} \ge \mathop {\max }_{1 \le i \le n} \left\{ {{p_{2i}}} \right\}$.

As a future research topic, firstly, it will be meaningful to consider the more efficient approximation algorithms for the problem discussed in this paper. Secondly, design optimal algorithms or approximation algorithms for other type of two-stage flexible flow shop scheduling problems are also very interesting.