1 Introduction

Generalized minimum spanning tree (GMST) was employed to support various problems in the field of graph optimization and has received much attention over the past 30 years (Dror and Haouari 2000). In a clustered graph, GMST aims to find a minimum spanning tree in which every node belongs to only one cluster. Although GMST and the minimum spanning tree (MST) have similar behavior, when the problem is solved by well-known polynomial algorithms of Prim and Kruskal (Golden et al. 2005), the inclusion of the concept of clustering and the selection of a node from each cluster, turns GMST into an NP-hard problem (Myung and Lee 1995). A weighted, undirected graph G in principle can be represented as G(V, E) where V is a set of nodes and E is a set of edges connecting node pairs in V.

Fig. 1
figure 1

A clustered graph with 20 nodes

Full size image
Fig. 2
figure 2

An array of selected node numbers

Full size image
Fig. 3
figure 3

A generalized spanning tree

Full size image

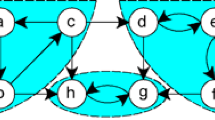
In a ’weighted graph’, each edge includes additional information called weights and the Euclidean distance between two nodes can be considered as the weight of the corresponding edge. Let R be an equivalence relation partitioning the node-set V into M equivalent classes called clusters. Figure 1 shows a clustered graph with 20 nodes. After clustering, one node is selected from each cluster (Fig. 2). Next, a spanning tree is constructed over the chosen nodes (Fig. 3). Such a tree is called generalized spanning tree (GST), and the total weight of the GST is equal to the sum of all edges’ weight constructing this tree. There might be several GSTs possible. A GMST would be one with the lowest total weight.

In the literature, some exact algorithms have been exposed in an attempt to find an optimum solution for GMST (Pop et al. 2006). These methods are based on various formulations of integer linear programming such as branch and bound, Lagrangian relaxation, and network flow (Haouari and Chaouachi 2006; Pop et al. 2006). However, such approaches are limited by the size of the graph. Consequently, metaheuristic algorithms have been explored to overcome this problem. These are typically problem-independent techniques; therefore, they can be used as black boxes (BoussaïD et al. 2013). In the last 10 years, some metaheuristic methods have been developed to solve the GMST problem.

Specifically, the common drawbacks in these methods are their high execution time and complex parameter tuning. This problem is important in real-time environments. One aspect of environments relevant to GMST problems is cluster head selection in mobile ad-hoc networks (MANETS) (Park et al. 2017; Mukherjee et al. 2018; Dua et al. 2018). An ad-hoc network consists of mobile nodes communicating with each other using wireless links, in the absence of a fixed infrastructure. In the network, the cluster-based topology can be used to reduce the overall network energy consumption (Reddy and Babu 2019; Rao et al. 2017; Prabaharan and Jayashri 2019; Sengottuvelan and Prasath 2017; Farman et al. 2018). In the topology, sensor nodes are grouped into clusters and one node is selected as a cluster head (CH). The selection of an appropriate CH is an optimization problem. This problem can be converted into a GMST problem on a graph when data transmission between clusters is based on a minimum spanning tree algorithm (Tang et al. 2011).

Despite recent researches, solving GMST in a time-sensitive environment is still a major challenge. Therefore, in this paper, a rapid LA-based method is presented to solve GMST.

The proposed algorithm assigns an LA to every cluster, and the number of actions is the same as that of the nodes in the corresponding cluster. At each iteration, each LA selects one node from its cluster. Then, the spanning tree of the selected nodes is constructed. Such a tree is called generalized spanning tree (GST). The total weight of GST is used as a criterion for rewarding or penalizing the selected actions.

Owing to the simple computational complexity of LA and the small number of required parameters, the proposed LA-based method can be applied to time-sensitive environments. The remaining of the paper is outlined as follows: In Sect. 2, some previous metaheuristic-based algorithms are discussed to solve GMST problems. Then, some preliminary materials are defined in Sect. 3. Next, Sect. 4 outlines the fundamentals of the proposed algorithm. Afterward, the experimental results are described in Sect. 5. Finally, Sect. 6 contains conclusions from these experiments.

2 Related work

Myung et al. (Myung and Lee 1995) first introduced the GMST problem, proving that GMST is an NP-hard problem. The problem has been approached by exact methods called integer programming, leading to several mathematical formulations (Pop et al. 2006). Since GMST is an NP-hard problem, it is impossible to solve large instances optimally by exact algorithms. Hence, various metaheuristics have been proposed for this problem.

Golden et al. (Golden et al. 2005) utilized a new genetic algorithm hybridized with a local search using a new operator called tree separation. Their results indicated that both local search and genetic algorithms rapidly generated near-optimal solutions for the GMST problem.

Oncan et al. (Öncan et al. 2008) proposed an efficient tabu search (TS) based method employing innovative neighborhood techniques. Additionally, they developed a new and large data set for the GMST problem called Extended TSPLIB. Their study results demonstrated that the TS-based algorithm yielded the best solutions. Although the performance of the technique compared to a genetic-based algorithm (Golden et al. 2005) is better, it requires long-term memory during execution and high computational time owing to the use of a local search approach.

In Hu’s study (Hu et al. 2008), a general variable neighborhood search (VNS) algorithm was proposed to solve the GMST problem by employing three different neighborhood types. Based on their study results, the VNS methodology produced a significantly better solution for the GMST problem and improved other previously proposed metaheuristic algorithms. Furthermore, the algorithm must be investigated to scale up to large problems.

To achieve solutions better than the existing algorithms, Ferreira (Ferreira et al. 2012) proposed a greedy randomized adaptive search procedure (GRASP)-based algorithm, including constructive heuristics and improvement techniques such as path-relinking and iterated local search.

Contreras-Bolton et al. (Contreras-Bolton et al. 2016) introduced a new evolutionary algorithm inspired by the genetic algorithm, named multi-operator genetic algorithm (MOGA) in which two crossover and five mutation operators were utilized for the optimization phase of GMST. MOGA outperforms a mono-operator genetic algorithm. Thus, the use of multi-operators enhances the diversification of the algorithm and allows MOGA to avoid being trapped easily into a local minimum. Although MOGA was an innovative method, it did not scale owing to the high required computational time. The results demonstrate that MOGA outperforms GRASP-based and TS-based algorithms.

Table 1 presents the features of some metaheuristic-based algorithms introduced to solve GMST.

Table 1 A comparison among some features of previously proposed algorithms for solving GMSTP
Full size table

3 Preliminaries

In this section, the useful preliminaries about the GMST problem and LA will be described.

3.1 Problem definition

Definition 1

(Graph) A graph can be regarded as a 3-tuple \(G=(V(G),E(G),I(G))\) where \(V(G)\ne \emptyset \), \(V(G)\cap E(G)=\emptyset \), and I(G) is a function which maps an unordered pair (identical or distinct) of V(G) to every member of E(G). The members of V(G) and E(G) are called vertices and edges, respectively. When there is \(I_{G}(e)=\lbrace u,v \rbrace \) for each \(e \in E(G)\), denoted by \(I_{G}=uv\) , said to be u and v are the endpoints of edge e.

Definition 2

(Subgraph) A subgraph of a graph G, H, is a graph when \(V(H) \subseteq V(G)\) , \(E(H) \subseteq E(G)\), and I(H) has the same restrictions of I(G) on E(G).

Definition 3

(Vertex-Induced Subgraph) A subgraph of a graph G, H, is called a vertex-induced subgraph if any edge of G whose endpoints are in V(H), is also an edge in H. The induced subgraph of G with the set of vertices \(S \subseteq V(G)\) is called the induced subgraph of G by S; it is denoted by G[S] .

Definition 4

(Edge-Induced Subgraph) Let \(\acute{E}\) and S be a subset of E and V, respectively; let S consist of all endpoints in set \(\acute{E}\). Then, the subgraph \((S,\acute{E}, I_G(\acute{e})\vert \acute{e} \in \acute{E})\) is induced by the set of edges \(\acute{E}\) from G; it is denoted by \(G[\acute{E}]\).

Definition 5

(Graph with Weighted Edges) If W is a function that assigns a non-negative integer W(e) to every edge \(e \in E\), then the resulting graph is called a graph with weighted edges. Let H be a subgraph of G, W(H) denotes the weight of H and equal to the total weights of the edges in this set (Nettleton 2013).

Definition 6

(Generalized Spanning Tree) Let R be an equivalence relation partitioning the vertex set R into m equivalent classes called clusters, where \(k={1,2,...,m}\) is the set of cluster indices. Then, \(V= \bigcup \limits _{i=1}^m V_i \) and \(\forall _{i \ne f \in k}: V_i \cap V_f=\emptyset \). It is assumed that the edges are defined between pairs of nodes belonging to different clusters. In other words, \(\lbrace e_{ij} \in E | i \in V_t , j \in V_s, t \ne s \rbrace \) . A tree spanning all clusters and containing a node from each cluster is called a GST. The total weight of the GST(\(\tau \)) is denoted by \(W(\tau )=\sum \limits _ {e_{ij}\in \tau } w(i,j)\).

Definition 7

(Generalized Minimum Spanning Tree) Let \(T_G=\lbrace \tau _1, \tau _2,...,\tau _r \rbrace \) be the set of all GSTs of G and \(W(\tau _i)\) be the weight of \(\tau _i\). Then, the GMST of G is defined by \(\tau ^*=arg min_{\tau _i} W(\tau _i)\) .

In other words, GMST is the generalized spanning tree having the lowest weight among all GSTs. The GMST problem consists of finding a subset of nodes including one node from each cluster. Therefore, the minimum spanning tree of the vertex-induced subgraph G[S] has the lowest weight among all vertex-induced subgraphs.

3.2 Learning automata

Learning automata have long been regarded as a field of artificial intelligence and have been studied extensively in the computer science and engineering problems (Jiang et al. 2016; Di et al. 2019). For example, covering problem (Rezvanian and Meybodi 2015), wireless network (Mostafaei 2015; Shojafar et al. 2015; Mostafaei et al. 2017; Mostafaei and Meybodi 2013), task offloading in mobile cloud (Krishna et al. 2016), image segmentation (Sang et al. 2016), fuzzy recommender system (Ghavipour and Meybodi 2016), social networks (Ghavipour and Meybodi 2018; Daliri Khomami et al. 2018; Moradabadi and Meybodi 2018; Rezvanian and Meybodi 2017; Moradabadi and Meybodi 2017), spectrum management problem (Fahimi and Ghasemi 2017), autonomous unmanned vehicle (Misra et al. 2017), cloud computing (Ranjbari and Akbari Torkestani 2018; Misra et al. 2014), MST problem (Akbari Torkestani and Meybodi 2011), Cyber-physical system(Ren et al. 2018), clustering (Hasanzadeh-Mofrad and Rezvanian 2018),Wireless mobile Ad-hoc networks (Akbari Torkestani and Meybodi 2010b, a), and vehicular sensor networks (Kumar et al. 2015) are a wide range of research areas for learning automata.

Stochastic learning automata (SLA) as a reinforcement learning method includes a finite set of available actions which is obtained through repeated interactions with a random environment. Therefore, it called adaptive decision-making unit. In this method, how to select an optimal action has an important role in improving the performance of SLA.

At each instant, the automaton chooses an action from its available actions based on a probability distribution over the action set. Indeed, the input to the random environment is the selected action. The environment replies to the action with a reinforcement signal. Therefore, the probability vector of the action is updated by a learning algorithm with the objective of minimizing the average penalty received from the environment. On the other hand, SLA consists of two parts:

  1. 1.

    A stochastic automaton with a limited number of actions and a random environment associated with it.

  2. 2.

    The learning algorithm used by the automata to learn the optimal action.

Fig. 4
figure 4

Relationship between LA and the random environment (Mollakhalili Meybodi and Meybodi 2014)

Full size image

SLA can be divided into fixed structure SLA (FSLA) and variable structure SLA (VSLA). In the former case, the probability vector of the actions is constant, while in the latter case, the probability vector is updated in each iteration. Figure 4 shows, the relation between VSLA and the random environment. VSLA can be defined by a quadric \(\lbrace {\varvec{\alpha }}, {\varvec{\beta }}, \mathbf {P}, T, \mathbf {c} \rbrace \) where:

\(\varvec{\alpha } \equiv \lbrace \alpha _1, \alpha _2, ... , \alpha _r \rbrace \) is a set of actions of the automation/inputs of the environment and \(\varvec{\beta } \equiv \lbrace \beta _1, \beta _2, ... , \beta _r \rbrace \) represents a set of inputs of the automation/outputs of the environment; \(\mathbf {P} \equiv \lbrace p_1, p_2, ... , p_r \rbrace \) is the probability vector of actions and \(T \equiv \mathbf {P} \rightarrow \varvec{\alpha } \) is a learning automata algorithm; \(\mathbf {P} \) is the internal state of VSLA which can be considered by the probability vector. A set of penalized probabilities, \(\mathbf {c}\equiv \lbrace c_1, c_2, ... , c_r \rbrace \), represents the environment (Mollakhalili Meybodi and Meybodi 2014).

The role of the learning algorithm is to modify the probability vector of the actions in VSLA. The algorithm, which has a significant impact on the performance of VSLA, is explained as follows:

  1. 1.

    If VSLA selects an action \(\alpha _i(t)\) from the action set \(\mathbf {\alpha }\) in time t and receives a desired response, then the probability vector of the action \(p_i(t)\) is increased and the probability vector of other actions is decreased.

  2. 2.

    If VSLA selects an action \(\alpha _i(t)\) and receives an undesired response, then the probability vector of the action \(p_i(t)\) is decreased and, the probability vector of other actions is increased. Therefore, the probabilities change as follows:

$$\begin{aligned} {p_{j=1,...,r}}\left( {t + 1} \right)= & {} \left\{ {\begin{array}{*{20}{l}} {\left( {1 - a} \right) {p_j}\left( t \right) + a } &{} j = i\\ {\left( {1 - a} \right) {p_j}\left( t \right) } &{} \forall j \ne i \end{array}} \right. \end{aligned}$$
(1)
$$\begin{aligned} {p_{j=1,...,r}}\left( {t + 1} \right)= & {} \left\{ \begin{array}{*{20}{l}} \left( {1 - b} \right) {p_j}\left( t \right) &{} j = i\\ \left( {1 - b} \right) {p_j}\left( t \right) + \dfrac{b}{r - 1} &{} \forall j \ne i \end{array} \right. \end{aligned}$$
(2)

Where a is a reward parameter, b is a penalty parameter, and r is the number of actions that can be taken by VSLA. Learning algorithms can be divided into three classes based on the relative values of the learning parameters (namely a and b ):

  • linear reward-penalty method(\(L_{R-P}\)): \(a=b\).

  • linear reward-penalty method(\(L_{R-{\epsilon P}}\)):\(a\gg b\).

  • linear reward-inaction(\(L_{R-I}\) ): \(b=0\). This strategy means the probability vector remains unchanged when the taken action is penalized by the environment.

4 Proposed algorithm

In all cases of the GMST problem, there is a preprocessing phase in which the graph is partitioned into a set of meaningful sub-classes called clusters. In the proposed algorithm, the partitional clustering (Tarabalka et al. 2009) method is considered for the clustering phase, including center clustering and grid clustering, which commonly exist in GMST (Golden et al. 2005; Öncan et al. 2008; Contreras-Bolton et al. 2016). Algorithm 1 and  2 outline both approaches, respectively.

figure a
figure b
Fig. 5
figure 5

An example of a grid clustering method

Full size image

Figure 5 illustrates an example of a grid clustering approach. After the clustering procedure, the optimization phase must be performed to solve the GMST problem. In this article, we propose a novel strategy based on LA to obtain a near-optimal GMST in a graph. Algorithm 3 presents the pseudo-code of the LA-based proposed algorithm.

figure c

Each iteration of the proposed algorithm embodies three steps. The following parts describes the steps of one iteration.

  • Step1. After associating an LA with each cluster, one action is selected from the action sets of the corresponding cluster. Every LA and its corresponding cluster have the same number of members. The applied selection mechanism is similar to the roulette wheel selection depending on the probability vector of LA. In Line 13, the notation \(\alpha _{Rnd}^i\) means that action with index Rnd is selected from \(i^{th}\) cluster. The chosen actions determine a subset of nodes, each node of which is picked only from one cluster \(\{S|S\subset V\}\) (Lines 16,17). Figure 6, represents this subset.

  • Step2. A spanning tree is derived on the vertex-induced subgraph \(G_s\) called GST. Then, a MST is constructed by a greedy algorithm like Kruskal (Golden et al. 2005). Next, the weight of MST, which is equal to the total weight of edges of this tree, is computed (Lines 18,19).

  • Step3. The weight of the pre-constructed MST is considered a criterion for the reward or penalty of the actions taken by the automata. Let \(w_k\) denote the weight of MST in the \(k^{th}\) iteration of the algorithm. If \(w_k\) is less than a defined threshold, the subset of chosen vertices is rewarded in the first step, otherwise it is penalized (Lines 20–24).

Fig. 6
figure 6

An example of the vertex-induced subgraph

Full size image

Afterward, the threshold value is updated based on the weight of the resulting MST in the previous step. Let \(TH_k\) represent the threshold value in the \(k^{th}\) iteration of the algorithm (Line 25). Then, \(TH_k\) is updated according to the following formula:

$$\begin{aligned} \begin{aligned} TH_k&=\dfrac{(k-1)TH_{k-1}+w_k}{k}\\&=TH_{k-1}+\dfrac{w_k-TH_{k-1}}{k} \end{aligned} \end{aligned}$$
(3)

Finally, the LA-GMST algorithm performs the above steps until a specified number of iterations is exceeded, or alternatively the probability vector of the selected GMST reaches a predefined value (near to one). After stopping the algorithm, the last MST is introduced as GMST (Line 27).

5 Experimental result and discussion

This section aims to analyze the behavior of LA-GMST experimentally. In the LA-GMST algorithm, for stopping criteria, the number of iterations and the threshold of probability are set 10, 000 and 0.95, respectively. The results of the LA-GMST algorithm are compared to those of two famous metaheuristic-based algorithms, including MOGA (Contreras-Bolton et al. 2016) and TS (Öncan et al. 2008). These algorithms have been tested on a standard benchmark instance-sets (extended TSPLIB ) including the twenty large-scale instances described in (Öncan et al. 2008). Each of the instances is solved by any of LA-GMST, MOGA and TS for 35 times. The Euclidean distance among nodes has been used as the weight of edges. However, comparison of the running times among various metaheuristics is difficult owning to different computing environments. Therefore, to ensure a fair comparison to other algorithms, the same platform is employed. The LA-GMST algorithm and the compared metaheuristics are implemented in MATLAB2016a, and the computational platform is based on PC running on a 2.70 GHz Intel Ci5 processor and 8 GB RAM.

  • Experiment 1. In the proposed LA-based algorithm, the parameter a (namely learning rate) should be chosen correctly. Depending on the type of problem, a tuning stage might be needed for this parameter. In this experiment, the learning rate decreases linearly from 0.1 to 0.008.

    Table 2 presents the results of the proposed algorithm using four different learning rates. The first column consists of two parts, namely the graph name from TSPLIB benchmarks and the number of nodes. Moreover, the second column denotes the number of clusters. For each learning rate, two columns are considered as Avg.w and Avg.t. The columns denote the average weight of the obtained GMST (based on Euclidean distance) and the average CPU time( in seconds), respectively. Meanwhile, the best results are shown in bold. As Table 2 shows, the learning rates 0.1 and 0.06 converge faster than the other two in all of the graph instances. Thereby, the algorithm falls into the trap of the local minimum. It seems that the learning rate of 0.01 and 0.008 have similar performance in some instances. To evaluate the results above, a statistical analysis of the proposed algorithm is investigated for four learning rates.

    Table 3 compares the ranking of the learning rates in multi problems. The rankings are obtained based on a non-parametric test (namely Friedman’s test). Owning to the dissimilarities in the results and the small size of the analyzed sample, the parametric test may result in unpredictable conclusions (García et al. 2009). As Table 3 shows, it can be observed that the average rank of \(a=0.01\) is smaller than other learning rates.

    The p value (0.000) obtained from Friedman’s test indicates the existence of a significant difference among results. For this reason, a two-tailed Wilcoxon rank-sum test for the learning rates compared is conducted. The results confirm that the performance of the proposed algorithm with the learning rate 0.01 is statistically better than learning rates 0.1 (\(p=0.000\)), 0.06 (\(p=0.000\)), and 0.008 (\(p=0.049\)), since the p values were all zero at the \(\alpha = 0.05\) level. Thus, \(a=0.01\) is used in all experiments reported in the remainder of this section.

Table 2 Performance comparison of different learning rates
Full size table
Table 3 The ranking of comparing different learning rates
Full size table
Table 4 Computational results for the proposed method, TS, and MOGA for TSPLIB instances with center clustering
Full size table
Table 5 Computational results for the proposed method, TS, and MOGA for TSPLIB instances with the grid clustering \(\mu =3\)
Full size table
Table 6 Computational results for the proposed method, TS, and MOGA for TSPLIB instances with the grid clustering \(\mu =5\)
Full size table
Table 7 Computational results for the proposed method, TS, and MOGA for TSPLIB instances with the grid clustering \(\mu =7\)
Full size table
Table 8 Computational results for the proposed method, TS, and MOGA for TSPLIB instances with the grid clustering \(\mu =10\)
Full size table

  • Experiment 2. After tuning the parameters, the effects of clustering on the LA-GMST algorithm are assessed with the selected learning rate and some performance measures. As previously mentioned, two ways of clustering exist for the GMST problem. One possibility is to select k center nodes to be located with each other as far as possible. Another possibility is to determine the \(g \times g\) grids in which clusters are constructed based on these grids, and a parameter called \(\mu \). Similar to the kinds of literature on GMST, it takes their values in \(\lbrace 3,5,7,10 \rbrace \) in grid clustering. To make an accurate comparison, the best available weight of GMST in the unlimited computational time was recorded.

    Tables 4, 5, 6, 7 and 8 present the results of running the proposed method and other metaheuristics for different clustering modes. Results are averaged over 35 runs. In these tables, for all algorithms, two columns need to be considered including the average weight of the obtained GMST (Ave.weight), and the average CPU time value in seconds (CPU Time).

    As Table 4 shows, in all cases, the performance of the LA-GMST algorithm is better than that of TS. Compared to MOGA, LA-GMST outperforms for 16 instances of 20 instances, which are shown in bold. For the average computation time, the proposed algorithm is faster than others.

    The TS-based algorithm fails to achieve the best results for different values of \(\mu \). When LA-GMST and the MOGA algorithms are compared to each other in terms of the best weights of GMST, \(LA-GMST_{\mu =3}\) finds 9 best values, \(LA-GMST_{\mu =5}\) finds 10, \(LA-GMST_{\mu =7}\) finds 13, and \(LA-GMST_{\mu =10}\) obtains 13. As the results report, it appears that the performance of the proposed algorithm with MOGA is competitive. However, it is worth mentioning that the running time of LA-GMST is considerably shorter than that of MOGA.

    To identify statistical differences among compared algorithms, the two-tailed Wilcoxon rank-sum test is conducted at a significant level of \(\alpha =0.05\). Table 9 summarizes the results of the pairwise comparisons of algorithms. The p values indicate that there is either no difference between the weight of the GMST obtained by the first algorithm and the weight of the GMST obtained by the second algorithm (null hypothesis \(H_0\)) or the weight of the GMST obtained by the first algorithm better than the weight of the GMST obtained by the second algorithm (alternative hypothesis \(H_1\)). Table 9 confirms that the difference between the LA-GMST algorithm and the TS-based algorithm is statistically significant since the p values were all zero at the \(\alpha = 0.05\) level. When the proposed and MOGA algorithms are compared to each other in terms of the p values, LA-GMST significantly yielded better results than MOGA did for instances in generating in the center clustering and grid clustering with \(\mu =10\). While for the grid clustering with \(\mu =3\), \(\mu =5\), and \(\mu =7\), there is no difference between the weight of the GMST obtained by the proposed algorithm and the weight of the GMST obtained by the MOGA algorithm, since the p values were higher than the \(\alpha = 0.05\) level. Therefore, the performance of the algorithms is similar in terms of the quality of the solution.

    As the statistical results in Table 10 show, it can be concluded that the performance of the proposed algorithm is remarkable in terms of running time.

Table 9 The result of the Wilcoxon test based on the solution quality
Full size table
Table 10 The result of the Wilcoxon test based on the running time
Full size table

6 Conclusions

In this paper, an algorithm based on the learning automata is introduced to solve the GMST problem, which is denoted as LA-GMST. In the proposed algorithm, an LA is considered for each cluster. The number of LA actions is the same as the number of nodes in the corresponding cluster. All LAs select an action from their action-sets. The selected actions are used to determine one node from each cluster. Then, a MST is constructed on the selected nodes and its weight is taken into account for a reinforcement signal to LAs. This process continues until the desired GMST is obtained. The selection of a proper learning rate plays a crucial role in the efficiency of the algorithm. Therefore, its influence on the algorithm result is investigated. The results indicate that a high value for the learning rate conduces to a few repetitions to explore the best actions. It is worth mentioning that low value results in focusing on a few regions of the search space and will miss other potential regions. To evaluate the quality of the results returned by the proposed algorithm, it was compared to the two best existing algorithms, the TS-based and MOGA algorithm. The numerical experiments are performed on a large set of extended TSPLIB. The results indicate that the proposed algorithm performs better than the TS-based algorithm both in terms of both solution quality and running time. Although in terms of solution quality, the performance of the proposed and MOGA algorithms is highly competitive, the proposed algorithm dominates the compared algorithm regarding the running time. The difference between the running time of our algorithm and other algorithms becomes much more remarkable in a time-sensitive environment like cluster head selection in ad-hoc networks.