On the minimum routing cost clustered tree problem

Abstract

For an edge-weighted graph $G=(V,E,w)$, in which the vertices are partitioned into k clusters $\mathcal {R}=\{R_1,R_2,\ldots ,R_k\}$, a spanning tree T of G is a clustered spanning tree if T can be cut into k subtrees by removing $k-1$ edges such that each subtree is a spanning tree for one cluster. In this paper, we show the inapproximability of finding a clustered spanning tree with minimum routing cost, where the routing cost is the total distance summed over all pairs of vertices. We present a 2-approximation for the case that the input is a complete weighted graph whose edge weights obey the triangle inequality. We also study a variant in which the objective function is the total distance summed over all pairs of vertices of different clusters. We show that the problem is polynomial-time solvable when the number of clusters k is 2 and NP-hard for $k=3$. Finally, we propose a polynomial-time 2-approximation algorithm for the case of three clusters.

1 Introduction

Finding a minimum cost spanning tree of an edge-weighted graph is one of the most well-studied problems in applied mathematics and theoretical computer science, and it can be applied in many areas such as telecommunications and logistics. Several problems with different cost functions and requirements have been extensively studied in the literature, for example, minimum spanning trees, Steiner minimum trees, shortest-path trees, and minimum routing cost spanning trees (Wu and Chao 2004). In some network applications, terminals may be grouped into clusters such that the communications between terminals of the same cluster should be routed “locally” for the sake of efficiency and safety. In such cases, we look for a spanning tree in which vertices of each cluster should be clustered together. More precisely speaking, the subtree spanning the vertices of a cluster should not contain any vertex from a different cluster.

Let $G=(V,E,w)$ be a graph with nonnegative edge length function w. For any spanning tree T of G, the routing cost between two vertices is defined as their distance on T, i.e., the sum of the costs of the edges of the unique tree path between them. The routing cost of T is the total distance summed over all pairs of vertices in T, i.e., $c(T)=\sum _{u,v\in V(T)}d_{T}(u,v)$, where $d_{T}(u,v)$ is the distance between u and v on T. A minimum routing cost spanning tree (MRCT) is a spanning tree with minimum routing cost among all possible spanning trees. For a clustered tree problem, in addition to a graph $G=(V,E,w)$, we are also given a partition $\mathcal {R}=\{R_1,R_2,\ldots ,R_k\}$ of V. A tree T is a clustered spanning tree if all the vertices in the same cluster ($R_i$) are clustered together in T. That is, T can be cut into k subtrees by removing $k-1$ edges such that each subtree is a spanning tree for one cluster $R_i$. The complexity and approximability of the following problem will be discussed in the first part of this paper.

Minimum Routing Cost Clustered Tree problem (CluMRCT)

Instance::

A graph $G=(V,E,w)$ and a partition $\mathcal {R}=\{R_1,R_2, \dots , R_k\}$ of V.

Goal::

Find a clustered spanning tree for $\mathcal {R}$ such that the routing cost is as small as possible.

Since the communication cost between vertices of different clusters may be more important in some applications, we study the minimum inter-cluster routing cost clustered tree problem (InterCluMRCT), in which the goal is to find a clustered spanning tree such that the sum of the inter-cluster distances is as small as possible. That is, we want to find a tree T minimizing $c_{I}(T)=\sum _{i=1}^k\sum _{j\ne i}d_T(R_i,R_j)$, where $d_T(R_i,R_j)=\sum _{u\in R_i}\sum _{v\in R_j}d_T(u,v)$. For an integer $k>1$, let k-InterCluMRCT denote the variant of InterCluMRCT such that the number of clusters is k.

The minimum routing cost spanning tree problem is NP-hard (Garey and Johnson 1979) and the first approximation algorithm appeared in Wong (1980) with ratio two. The approximation ratio was improved to $(4/3+\varepsilon )$ for any fixed $\varepsilon >0$ in Wu et al. (2000) and furthermore a polynomial time approximation scheme (PTAS) was presented in Wu et al. (2000). Applications of MRCT problem arise in the fields of network design, computational biology and transportation. There are also several variants and extensions in the literature, such as on special graphs (Dahlhaus et al. 2004; Fischetti et al. 2002) with multiple sources (Wu 2002; Chen et al. 2006) finding a swapping edge (Bilò et al. 2014; Wu et al. 2008) building a network instead of a tree (Wu et al. 2002). For more variants and their approximation algorithms, we refer to Wu and Chao (2004). An experimental study can also be found in the literature (Tan and Due 2013). There are also distributed algorithms (Hochuli et al. 2014) and algorithms using the bio-computing approach (Singh and Sundar 2011). Some extensions to more complicated objective functions were still developed recently (Ravelo and Ferreira 2015a, b).

In Wu (2006), another similar problem was studied, which looks for a spanning tree with minimum average inter-cluster distance, and a 2-approximation algorithm was proposed. Different from InterCluMRCT, in Wu (2006) the solution could be any spanning tree, rather than a clustered spanning tree.

The concept of finding clustered solutions also appeared as variants of the traveling salesperson problem (TSP) and the Steiner tree problem. For clustered TSP problem, the goal is to find a minimum cost Hamiltonian path such that the vertices of each cluster are visited consecutively (Bao and Liu 2012; Chisman 1975; Guttmann-beck et al. 2000). For the clustered Steiner tree problem, the required vertices are partitioned into clusters, and the goal is to find a clustered spanning tree of minimum total edge cost (Wu and Lin 2015). In the literature, there are some other problems in which the feasibility conditions are also expressed in terms of the clusters but different from the definition in this paper. In the review paper by Feremans et al. (2003), such generalized versions of the minimum spanning tree problem, the travelling salesperson problem and the shortest path problem are surveyed. Three variants of the problems are discussed in their paper such that a feasible solution must contain exactly one, at least one, or at most one vertex from each cluster, respectively.

In this paper, we study the complexities and approximabilities of CluMRCT and InterCluMRCT and show the following results.

• Unless NP = P, CluMRCT cannot be approximated with any polynomial factor in polynomial time. As an intermediate problem, we show the inapproximability of the shortest clustered st-path problem, which asks for a shortest clustered path between two specified vertices. The problem is also interesting in itself.

• A metric graph is a complete graph with edge lengths satisfying the triangle inequality. We design a 2-approximation algorithm with time complexity $O(n^2)$ for CluMRCT on metric graphs, where n is the number of vertices of input graph.

• When there are only two clusters, 2-InterCluMRCT can be solved in $O(mn+n^2\log n)$ time, where m and n are numbers of edges and vertices, respectively.

• k-InterCluMRCT is NP-hard for any fixed $k>2$, and we present a 2-approximation algorithm for 3-InterCluMRCT.

The rest of the paper is organized as follows. In Sect. 2, we give some notation and definitions. In Sect. 3, we study the shortest clustered st-path problem and show the inapproximability result of CluMRCT. In Sect. 4, we show the 2-approximation algorithm for CluMRCT on metric graphs. The results for InterCluMRCT are in Sect. 5. Concluding remarks are in the last section.

2 Notation and definitions

In this paper, a graph is a simple, connected and undirected graph. For a graph $G=(V,E,w)$, V and E are the vertex and the edge sets, respectively, and w is the nonnegative edge length function. Let $n=|V|$ and $m=|E|$. An edge between vertices u and v is denoted by (u, v), and its weight is denoted by w(u, v). For a graph G, V(G) and E(G) denote the vertex and the edge sets, respectively. For a vertex subset U, the subgraph of G induced by U is denoted by G[U]. For a vertex set V, a collection $\mathcal {R}=\{R_i\mid 1\le i\le k\}$ of subsets of V is a partition of V if the subsets are mutually disjoint and their union is exactly V. A path of G is simple if no vertex appears more than once on the path. In this paper we consider only simple paths.

Definition 1

For a tree T spanning S, i.e., $S\subseteq V(T)$, the local tree of S on T is the subtree of T induced by T[S].

Definition 2

Let $\mathcal {R}=\{R_i\mid 1\le i\le k\}$ be a partition of V. A spanning tree T is a clustered spanning tree for $\mathcal {R}$ if the local trees of all $R_i\in \mathcal {R}$ are mutually disjoint, i.e., there exists a cut set $C\subseteq E(T)$ with $|C|=k-1$ such that each component of $T-C$ is a spanning tree $T_i$ for $R_i$ for all $1\le i\le k$. The edges in the cut set C are called inter-cluster edges.

Fig. 1

An example of the clustered spanning tree. There are three inter-cluster edges and each circle is a local tree for one cluster

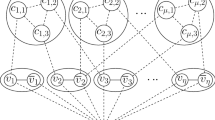
Figure 1 illustrates a clustered spanning tree. It can be partitioned into four local trees by removing three inter-cluster edges. For an arbitrary vertex partition of a graph, it is possible that there does not exist any clustered spanning tree. The following sufficient and necessary condition can be easily shown. In the remaining paper we shall assume that the input always satisfies the condition.

Proposition 1

For a connected graph G and vertex partition $\mathcal {R}$, there exists a clustered spanning tree for $\mathcal {R}$ iff $G[R_i]$ is a connected subgraph for each i.

For a subgraph H of $G=(V,E,w)$ and $u,v\in V$, let $d_H(u,v)$ denote the shortest path length between u and v on H. Let $d_H(v,U)=\sum _{u\in U}d_H(v,u)$ for a vertex v and a vertex subset U. For vertex subsets $U_1$ and $U_2$, let $d_H(U_1,U_2)=\sum _{u\in U_1}d_H(u,U_2)$.

Definition 3

Let $G=(V,E,w)$ be a graph and $\mathcal {R}=\{R_1,R_2,\ldots ,R_k\}$ be a partition of V. For a clustered spanning tree T for $\mathcal {R}$, the inter-cluster distance between clusters $R_i$ and $R_j$ on T is $d_T(R_i,R_j)$. The inter-cluster distance (cost) of T is $c_{I}(T)=\sum _{i=1}^k\sum _{j\ne i}d_T(R_i,R_j)$.

An st-path is a path with endpoints s and t. Let $P=(v_0,v_1,\ldots ,v_p)$ be a $v_0v_p$-path passing through $v_1$,$v_2$,$\ldots ,v_{p-1}$ in this order. For $0\le i\le j\le p$, the subpath between $v_i$ and $v_j$ of P is denoted by $P[v_i,v_j]$. An edge (x, y) is also thought of as a path. For an xy-path $P_1$ and a yz-path $P_2$, let $P_1\circ P_2$ denote the concatenation of the two paths.

3 Shortest clustered st-path problem

In this section, we first give the formal definition of the shortest clustered st-path problem (Shortest CluPath) and show its NP-hardness. Then, we show the inapproximability of CluMRCT in general graphs.

Definition 4

Given a graph $G=(V,E,w)$, where vertices are partitioned into clusters $\mathcal {R}=\{R_1,R_2,\ldots ,R_k\}$, a path $P=(v_0,...,v_p)$ is a clustered path if the vertices from the same cluster appear consecutively, that is, if $\{v_i,v_j\}\subseteq R_h$ then $V(P[v_i,v_j])\subseteq R_h$ for any $0\le i< j\le p$.

In other words, a clustered path P can be partitioned into $P=P_1\circ P_2\circ \ldots \circ P_r$, such that each $P_i$ consists of vertices from the same cluster and for $i\ne j$, $V(P_i)$ and $V(P_j)$ are from different clusters. We define the problem Shortest st -CluPath as follows.

Shortest Clustered st-path Problem (Shortest st -CluPath)

Instance::

An undirected graph $G=(V,E,w)$, a partition $\mathcal {R}$ of V, and two specific vertices s and t.

Goal::

Find a shortest clustered st-path in G.

Shortest st -CluPath coincides with the shortest path problem when all clusters are singletons or the number of clusters k is one. Consider the following problem in which we only need to determine the existence of any clustered st-path.

Clustered st-path Problem ( st -CluPath)

Instance::

An undirected graph $G=(V,E,w)$, a partition $\mathcal {R}$ of V, and two specific vertices s and t.

Question::

Whether there is a clustered st-path in G.

We shall show that st -CluPath is NP-complete by a transformation from the undirected version of “path with forbidden pairs” (FP) problem. The directed FP problem is a well known NP-complete problem (Garey and Johnson 1979). The undirected version has also been shown to be NP-complete (Hajiaghayi et al. 2012). Let $G=(V,E)$ be an undirected graph with two specific vertices $s,t\in V$ and let $\mathcal {F}=\{\{a_1,b_1\},\ldots ,\{a_r,b_r\}\}$ be a set of forbidden pairs of vertices. An st-path in G is called $\mathcal {F}$-path if it contains at most one vertex from each pair in $\mathcal {F}$. The problem Undirected FP is to determine whether there is an $\mathcal {F}$-path. The following result appeared in Hajiaghayi et al. (2012).

Theorem 1

(Hajiaghayi et al. 2012) Unless $P\,=\,NP$, Undirected FP admits no $(1-\rho )\cdot n$ approximation ratio, where n is the number of vertices and $\rho >0$ is a universal constant. The same holds for directed acyclic graphs.

We shall show the NP-completeness of the Disjoint Undirected FP problem, which is a variant of Undirected FP such that the forbidden problem pairs are mutually disjoint. Let $\delta (v)$ be the degree of vertex v, i.e., the number of edges incident to v.

Lemma 1

Disjoint Undirected FP is NP-complete.

Proof

Let $G=(V,E)$, $\mathcal {F}$ and s, t be an instance of Undirected FP. We want to construct a new instance $G'=(V',E')$ and $\mathcal {F'}$ in polynomial time such that each vertex appears in at most one forbidden pair. For each vertex u we subdivide all the edges incident to u by inserting degree-2 vertices as follows:

Let $\{u,v_1\},...,\{u,v_h\}$ be the forbidden pairs containing u. Let $(u,w_j)$ be the edges incident to u, where $1\le j\le \delta (v)$. Let $q=\delta (v_1)+\delta (v_2) + \cdots + \delta (v_h)$. We subdivide each of the edge $(u,w_j)$ by q new vertices.

Note that the above gadget is applied to all vertices, and therefore for $1\le i\le h$, there is a group of $\delta (u)$ degree-2 vertices corresponding to u at each of the edge incident to $v_i$, as well as possibly some other groups if $v_i$ is in more than one forbidden pair.

Fig. 2

An example of the edge gadgets. The new added vertices are drawn by white circles. a Subdivisions of the edges incident to u. b Subdivisions of the edges incident to x. c Subdivisions of the edges incident to y

An example is illustrated in Fig. 2, where $\{u,x\}$ and $\{u,y\}$ are the two forbidden pairs containing u. Suppose that $\delta (u)=3$, $\delta (x)=2$, and $\delta (y)=3$. We subdivide the first edge of u by inserting five new vertices $u^{x}_{1,1}$,$u^{x}_{1,2}$,$u^{y}_{1,1}$,$u^{y}_{1,2}$, and $u^{y}_{1,3}$. Similarly, we subdivide the second and third edges of u by new obtained 5 vertices. The resulting gadget is shown in Fig. 2a. Likewise, the subdivisions of edges incident to x and y are shown in Fig. 2b, c, respectively. Then, we replace the forbidden pair $\{u,x\}$ by the following six pairs: $\{u^{x}_{1,1},x^{u}_{1,1}\}$,$\{u^{x}_{2,1},x^{u}_{1,2}\}$, $\{u^{x}_{3,1},x^{u}_{1,3}\}$,$\{u^{x}_{1,2},x^{u}_{2,1}\}$, $\{u^{x}_{2,2},x^{u}_{2,2}\}$, and $\{u^{x}_{3,2},x^{u}_{2,3}\}$. The similar transformation is applied on $\{u,y\}$. At this point each vertex appears in at most one forbidden pair. Furthermore, after the above transformation, if $\{u,v\}$ is an original forbidden pair, then there is a forbidden pair for every edge incident to u and every edge incident to v. Thus, the solution does not change.

For each forbidden pair, we construct $O(n^2)$ forbidden pairs, and then the total number of new forbidden pairs is bounded by $O(n^2|\mathcal {F}|)$. As a result, the transformation can be done in polynomial time, and this completes the proof. $\square$

Theorem 2

Shortest st -CluPath is NP-hard and cannot be approximated with a factor of any polynomial time computable function, unless $NP\,=\,P$.

Proof

We reduce Disjoint Undirected FP to st -CluPath. Let an instance of Disjoint Undirected FP consist of $G=(V,E)$, two specified vertices $s,t\in V$ and a set $\mathcal {F}=\{\{a_i,b_i\}\mid 1\le i\le r\}$ of pairs of disjoint vertices. We transform the instance into an instance of st -CluPath as follows. First, we construct a weighted graph $G'$ from G by inserting a “long” edge $(a_i,b_i)$ for $1\le i\le r$. The weight of each long edge is $\alpha (n)$ and all the other edges have unit length, where $\alpha (n)\ge n$ is any polynomial computable function. Next, there is a cluster $C_i=\{a_i,b_i\}$ for $1\le i\le r$ and each vertex not appearing in any forbidden pair is itself a singleton cluster. To complete the proof, we claim that

• 1. if there is an $\mathcal {F}$-path P in G, then there is a clustered st-path $P'$ of length at most $n-1$ in $G'$; and

• 2. if there is no $\mathcal {F}$-path P in G, then the length of any clustered st-path in $G'$ is at least $\alpha (n)$.

Since the gap between the two cases can be any polynomial time computable function, the inapproximability result follows.

If there exists an $\mathcal {F}$-path P in G from s to t, then it contains at most one vertex from each pair in $\mathcal {F}$. Since P contains at most one vertex from each cluster, it must be a clustered path by definition. The length of the path is at most $n-1$ since it passes through at most $n-2$ vertices and no any long edge.

Conversely, if $P'$ is a clustered path in $G'$, then either each pair $\{a_i,b_i\}$ successively appears on $P'$ or at most one vertex from each pair $\{a_i,b_i\}$ is on $P'$. If the length of $P'$ is less than $\alpha (n)$, the clustered path won’t traverse through such a long edge between $a_i$ and $b_i$. Therefore, we can find a path P that contains at most one vertex from each pair in $\mathcal {F}$. $\square$

Since Shortest st -CluPath is NP-hard, this implies the inapproximability result for CluMRCT.

Corollary 1

CluMRCT cannot be approximated within any polynomial factor in polynomial time, unless NP $=$ P.

Proof

Let q(n) be a polynomial. Let $G'$ be the instance of Shortest st -CluPath in the proof of Theorem 2. We construct a graph $G''$ from $G'$ by adding $q(n)-1$ new leaves adjacent to both s and t with zero-weight edges. Let S be the set containing s and the new leaves adjacent to s. Similarly let T the set containing t and the new leaves adjacent to t.

If there is an $\mathcal {F}$-path P for the Disjoint Undirected FP problem, then we can find a clustered spanning tree Y containing P. For any $u\in S$ and $v\in T$, $d_Y(u,v)<n$. We have $d_Y(S,T)=d_Y(T,S)<|S||T|\cdot n=q^2(n)\cdot n$. For any other pair of vertices, the distance is less than $n\cdot \alpha (n)$. Thus, the routing cost of Y is less than $2q^2(n)\cdot n+(2q(n)+n)n\cdot n\cdot \alpha (n)$. On the other hand, if there is no $\mathcal {F}$-path P for the Disjoint Undirected FP problem, then on any clustered spanning tree, the distance between s and t is at least $\alpha (n)$, and therefore the routing cost of any clustered spanning tree is larger than $2q^2(n)\cdot \alpha (n)$. The cost ratio of the two cases is asymptomatically $q(n)/n^2$ when $\alpha (n) \gg q(n) \gg n$.

Thus, if there is a polynomial-time algorithm approximating CluMRCT with a polynomial factor, then we can solve Disjoint Undirected FP in polynomial time. $\square$

4 CluMRCT on metric graphs

In this section we investigate CluMRCT on metric graphs. A metric graph is a complete graph with edge lengths satisfying the triangle inequality, i.e., $w(x,y)\le w(x,z)+w(z,y)$ for all $x,y,z\in V$.

Metric CluMRCT Problem

Instance::

A metric graph $G=(V,E,w)$ and a partition $\mathcal {R}=\{R_1,R_2, \dots , R_k\}$ of V.

Goal::

Find a clustered spanning tree for $\mathcal {R}$ such that the routing cost is as small as possible.

We design a 2-approximation algorithm for metric CluMRCT by constructing a two-level star-like graph. A star is a tree with at most one internal vertex which is called “center” of the star. For a star with at least three vertices, there must be exactly one internal vertex. For simplicity, a tree with one or two vertices is also thought of as a star, and in this case any vertex is a center. For a tree T with n vertices, a vertex v is a centroid if each subgraph after removing v from T has at most n / 2 vertices. A tree has one or two centroids (Wu and Chao 2004). We shall assume that $G=(V,E,w)$ is the input metric graph in this section.

Definition 5

Let $G=(V,E,w)$ be a metric graph and $\mathcal {R}=\{R_1,R_2,\ldots ,R_k\}$ a partition of V. An $\mathcal {R}$-star is a spanning tree of G such that the inter-cluster edges induce a star and each local tree is also a star. By definition, the center of the inter-cluster star must be also the center of a local star. W.l.o.g. we shall assume that the center of the inter-cluster star belongs to $R_1$.

Fig. 3

An $\mathcal {R}$-star Y. Each circle is for one local star. The topmost vertex is the center of both the inter-cluster star (bold lines) and its local star

Figure 3 depicts an $\mathcal {R}$-star, the uppermost vertex is the center of both the inter-cluster star and its local star. In other words, all local trees as well as the inter-cluster tree are stars, which will be called local stars and inter-cluster star, respectively. Note that an $\mathcal {R}$-star must be a clustered spanning tree. The routing cost of an $\mathcal {R}$-star can be computed according to the following lemma.

Lemma 2

For an $\mathcal {R}$-star Y, where $r_i$ is the center of the local tree of $R_i$, $c(Y)=2(n-1)\sum _{1\le i\le k}\sum _{v\in R_i} w(v,r_i)+ \sum _{2\le i\le k}2|R_i|(n-|R_i|) w(r_i,r_1)$.

Proof

Recall that, for a spanning tree T of G, the routing cost of T is defined by $c(T)=\sum _{u,v\in V(T)}d_{T}(u,v)$. The routing load on edge e is defined by $l(T,e)=2|V(X)|\times |V(Y)|$, where X and Y are the two subgraphs obtained from T by removing e. As shown in Wu and Chao (2004), the routing cost of T can be computed by the following formula:

$$\begin{aligned} c(T)=\sum _{e\in E(T)}l(T,e)w(e) \end{aligned}$$

(1)

The result directly follows from Eq. (1) and the definition of an $\mathcal {R}$-star Y. $\square$

Our 2-approximation algorithm is based on the following two properties, which will be shown in the remaining paragraphs of this section.

• There exists an $\mathcal {R}$-star whose routing cost is at most twice of the optimal cost.

• An $\mathcal {R}$-star with minimum routing cost can be computed in $O(n^2)$ time.

Lemma 3

There exists an $\mathcal {R}$-star Y such that $c(Y)\le 2c(T)$, where T is an optimal solution of the metric CluMRCT problem.

Proof

We show how to construct an $\mathcal {R}$-star Y such that $c(Y)\le 2c(T)$. Root T at its centroid. By definition, each branch contains no more than n / 2 vertices. W.l.o.g. assume that the centroid, named $r_1$, is in $R_1$. For each $2\le i\le k$, there must be a vertex $r_i\in R_i$ such that the parent of $r_i$ is not in $R_i$. Since by definition there are exactly $k-1$ inter-cluster edges, the inter-cluster edges must be the edges between $r_i$ and their parents for all $2\le i\le k$. We construct an $\mathcal {R}$-star Y with the following edges.

• For $2\le i\le k$, there is an edge $(r_1,r_i)$.

• For $1\le i\le k$ and $v\in R_i\setminus \{r_i\}$, there is an edge $(r_i,v)$.

It is clear Y is an $\mathcal {R}$-star. An example for the construction of Y is presented in Fig. 4.

Fig. 4

An example illustrates the construction of an $\mathcal {R}$-star Y (below) from an optimal solution T (above)

We shall show that the cost of Y is at most twice of c(T). First, we give a lower bound of the optimal routing cost. Let T be rooted at the centroid $r_1$. For any vertex v in T, there are at least n / 2 vertices not in the same branch of $r_1$ as v, i.e., the path from v to any of these vertices passes through $r_1$. Since the path from u to v and the path from v to u are both counted, $d_{T}(v,r_1)$ will be counted at least n times. Thus, we have

$$\begin{aligned} c(T)\ge n\sum _{v\in V}d_T(v,r_1) \end{aligned}$$

For $v\in R_i$, since $r_i$ must be on the path between v and $r_1$, we have $d_T(v,r_1)\ge w(v,r_i)+w(r_i,r_1)$ by the triangle inequality. Hence, we obtain

$$\begin{aligned} c(T)\ge & {} n\sum _{v\in V}d_T(v,r_1)\nonumber \\\ge & {} n\sum _{1\le i\le k}\sum _{v\in R_i}(w(v,r_i)+w(r_i,r_1))\nonumber \\= & {} n\sum _{1\le i\le k}\sum _{v\in R_i}w(v,r_i)+n|R_i|\sum _{2\le i\le k}w(r_i,r_1) \end{aligned}$$

(2)

By Lemma 2, we have

$$\begin{aligned} c(Y)= & {} \sum _{1\le i\le k}\sum _{v\in R_i}2(n-1)w(v,r_i)+\sum _{2\le i\le k}2|R_i|(n-|R_i|) w(r_i,r_1)\nonumber \\< & {} 2n\sum _{1\le i\le k}\sum _{v\in R_i} w(v,r_i)+2n|R_i|\sum _{1\le i\le k}w(r_i,r_1) \end{aligned}$$

(3)

By Eqs. (2) and (3), we have that $c(Y)\le 2c(T)$. $\square$

Lemma 4

In $O(n^2)$ time, one can construct an $\mathcal {R}$-star with minimum routing cost.

Proof

We consider each vertex as the centroid $r_1$. For a fixed $r_1$, we need to determine the center of the local star of $R_i$ for each $2\le i\le k$. By Lemma 2, it is equivalent to find $u\in R_i$ minimizing

$$\begin{aligned} 2(n-1)\sum _{v\in R_i} w(v,u)+2|R_i|(n-|R_i|) w(u,r_1). \end{aligned}$$

(4)

For each $u\in R_i$, if we compute $\sum _{v\in R_i}w(v,u)$ in a preprocessing stage, then the center of $R_i$ can be determined in $O(|R_i|)$ time, and therefore for each possible $r_1$ the time complexity is $O(\sum _{i=2}^{k} |R_i|)= O(n)$. Since we try each vertex as $r_1$, the total time complexity except for the preprocessing is $O(n^2)$. For the preprocessing stage, it takes $O(|R_i|^2)$ time by a brute force method for each cluster $R_i$, and therefore the time complexity of the preprocessing is $O(\sum _{i=1}^{k} |R_i|^2)= O(n^2)$. $\square$

Theorem 3

Metric CluMRCT can be 2-approximated in $O(n^2)$ time, where n is the number of vertices.

Proof

By Lemmas 3 and 4. $\square$

5 InterCluMRCT

In this section we investigate the problem of finding a clustered tree with minimum inter-cluster cost. For a clustered spanning tree T for $\mathcal {R}$, the inter-cluster cost between clusters $R_i$ and $R_j$ on T is $d_T(R_i,R_j)$. The inter-cluster cost of T is defined by $c_{I}(T)=\sum _{i=1}^k\sum _{j\ne i}d_T(R_i,R_j)$.

Min Inter-cluster Cost Clustered Tree Problem (InterCluMRCT)

Instance::

A graph $G=(V,E,w)$ and a partition $\mathcal {R}=\{R_1,R_2,\ldots ,R_k\}$ of V, where w is a nonnegative edge weight function.

Goal::

Find a clustered spanning tree for $\mathcal {R}$ such that the inter-cluster cost is as small as possible.

When the number of clusters is restricted to a fixed integer k, the problem is called k-InterCluMRCT. We denote by $E_i$ the edges with both endpoints in $R_i$, and similarly let $E_{i,j}=\{(u,v)\in E\mid u\in R_i, v\in R_j\}$ for $i\ne j$. For a cluster $R_i$ and $r\in R_i$, a shortest-path tree of $R_i$ rooted at r is a spanning tree T of $R_i$ such that $d_T(r,v)=d_G(r,v)$ for each $v\in R_i$. Let $n_i=|R_i|$ and $m_i=\{(u,v)\in E\mid u,v\in R_i\}$ for $1\le i\le k$. By the assumption on the input, $G[R_i]$ must be connected for each i and therefore a shortest-path tree always exists. We shall first show that 2-InterCluMRCT is solvable in polynomial time, and then give a 2-approximation algorithm for 3-InterCluMRCT.

We call a local tree terminal local tree if it is connected to only one inter-cluster edge. The port of a terminal local tree is the vertex adjacent to a vertex not in the cluster. Figure 5 contains an example illustrating these definitions. The next property can be easily derived from the definition of the cost function.

Fig. 5

An example of 2-InterCluMRCT. Each triangle represent a terminal local tree. The inter-cluster edge (s, t) connects the two ports of the terminal local trees

Lemma 5

If $T_i$ is a terminal local tree of an optimal solution of InterCluMRCT, then $T_i$ is a shortest-path tree of $R_i$ rooted at the port of $T_i$.

Proof

By definition, $c_{I}(T)=\sum _{i=1}^k\sum _{j\ne i}d_T(R_i,R_j)$. Since $T_i$ is a terminal tree, a shortest-path tree of $R_i$ rooted at the port of $T_i$ minimizes $c_{I}(T)$. $\square$

Theorem 4

The 2-InterCluMRCT problem can be solved in $O(mn+n^2\log n)$ time.

Proof

When $k=2$, there is exactly one inter-cluster edge in any feasible clustered spanning tree, and both local trees are terminal local trees. Let $f(v)=\sum _{u\in R_i}d_G(v,u)$, where $v\in R_i$. For any $(s,t)\in E_{1,2}$ such that $s\in R_1$ and $t\in R_2$, by Lemma 5, the optimal tree with (s, t) as the inter-cluster edge consists of shortest-path trees of $R_1$ and $R_2$ rooted at s and t, respectively. That is, the optimal inter-cluster cost is

$$\begin{aligned} \min _{(s,t)\in E_{1,2}} \left( n_2f(s)+n_1f(t)+n_1n_2w(s,t)\right) , \end{aligned}$$

which can be easily computed in $O(|E_{1,2}|)$ time after f(v) for every v is known. By using Dijkstra algorithm (Cormen et al. 2001; Dijkstra 1959) computing f(v) for all v takes $O(n_1^2\log n_1+n_1m_1+n_2^2\log n_2+n_2m_2)= O(mn+n^2\log n)$, and the total time complexity is $O(mn+n^2\log n+|E_{1,2}|)=O(mn+n^2\log n)$. $\square$

Next, we show that 3-InterCluMRCT is NP-hard and present a 2-approximation algorithm. We show that 3-InterCluMRCT is NP-hard by a transformation from the 2-MRCT problem, which is an NP-hard problem and admits a PTAS (Wu 2002). The 2-MRCT problem can be formalized as follows.

2-MRCT Problem

Instance::

A graph $G=(V,E,w)$ and $s,t\in V$, where w is a nonnegative edge weight function.

Goal::

Find a spanning tree T such that the 2-source routing cost of T, defined by $c_2(T)=\sum _{v\in V}(d_T(s,v)+d_T(t,v))$, is minimized.

Theorem 5

The 3-InterCluMRCT problem is NP-hard.

Proof

Let $G=(V,E,w)$ and $s,t\in V$ be an instance of the 2-MRCT problem. We construct an instance $(G',\mathcal {R}=\{R_1,R_2,R_3\})$ of 3-InterCluMRCT as follows. First, for each $v\in V$ we add a new vertex $v'$ and a zero-weight edge $(v',v)$, i.e., all $v'$ are new vertices with degree one. In addition, we add vertices $s''$ and $t''$, as well as zero-weight edges $(s',s'')$ and $(t',t'')$. Next, let $R_1=\{s',s''\}$, $R_2=\{t',t''\}$, and $R_3=V'\setminus (R_1\cup R_2)$, where $V'$ is the vertex set of $G'$. The proof is completed by showing the next claim. $\square$

Claim 1

There exists a spanning tree T of G with $c_2(T)=C$ iff there exists a clustered spanning tree $T'$ for $\mathcal {R}$ of $G'$ with $c_I(T')=8C$.

For a spanning tree T of G, we can construct a clustered tree $T'$ by adding edges $(s'',s')$, $(t'',t')$, and $(v,v')$ for all $v\in V$ to T. Conversely, we can easily obtain the spanning tree T of G by removing these new vertices on any spanning tree $T'$ of $G'$. The transformation of an instance of the 2-MRCT problem to an instance of 3-InterCluMRCT is given in Fig. 6. To prove the above claim, it is sufficient to show the relation of the costs of the two trees.

Fig. 6

The transformation of an instance of the 2-MRCT problem to an instance of 3-InterCluMRCT. Dotted lines represent the zero-weighted edges. The triangular pattern represents an instance of the 2-MRCT problem

Since $d_{T'}(s',v)=d_{T'}(s'',v)=d_{T'}(s,v)$ and $d_{T'}(t',v)=d_{T'}(t'',v)=d_{T'}(t,v)$ for any v, by definition,

$$\begin{aligned} c_I(T')= & {} 4\sum _{v\in R_3}d_{T'}(s,v)+8d_{T'}(s,t)+4\sum _{v\in R_3}d_{T'}(t,v)\\= & {} 4\left( 2\sum _{v\in V}d_{T}(s,v)-d_T(s,t)\right) +8d_{T}(s,t)\\&+\,4\left( 2\sum _{v\in V}d_{T}(t,v)-d_T(s,t)\right) \\= & {} 8\sum _{v\in V}d_{T}(s,v)+8\sum _{v\in V}d_{T}(t,v)\\= & {} 8c_2(T). \end{aligned}$$

Next, we present a 2-approximation algorithm for 3-InterCluMRCT. First, we consider the weighted version of the 2-MRCT problem. In the weighted 2-MRCT problem, the goal is to minimize $\sum _{v\in V}(\lambda _1 d_T(s,v)+\lambda _2 d_T(t,v))$, where $\lambda _1$ and $\lambda _2$ are given positive real numbers. Let $h(v,T)=\lambda _1d_T(s,v)+\lambda _2d_T(t,v)$ for each vertex v. To derive a 2-approximation algorithm of the weighted 2-MRCT, the following result was shown in Wu (2002), Sect. 5.

Lemma 6

(Wu 2002) With the same time complexity as computing a shortest-path tree, one can construct a spanning tree T such that (1) $d_T(s,t)=d_G(s,t)$; and (2) for each vertex $v\in V$, $h(v,T)\le 2h(v,Y)$ for any spanning tree Y.

Fig. 7

An example of 3-InterCluMRCT. There are two terminal local trees connected by inter-cluster edges $(r_1,s_1)$ and $(r_2,s_2)$, respectively

A clustered tree with three clusters has exactly two terminal local trees and two inter-cluster edges. The other local tree is called the center local tree. Figure 7 contains an example of 3-InterCluMRCT. To approximate the 3-InterCluMRCT, we consider each possible combination of two inter-cluster edges. Suppose that $(s_1,r_1)$ and $(s_2,r_2)$ are the two inter-cluster edges, where $s_1,s_2\in R_3$, $r_1\in R_1$ and $r_2\in R_2$, i.e., the local tree of $R_3$ is the center local tree.

Theorem 6

The 3-InterCluMRCT problem admits a 2-approximation algorithm with time complexity $O(m^2n\log n+m^3)$.

Proof

Let $T_1$ and $T_2$ be shortest-path trees of $R_1$ and $R_2$ rooted at $r_1$ and $r_2$, respectively. By Lemma 5, an optimal 3-InterCluMRCT consists of $T_1$ and $T_2$ as the local trees. The question is the other local tree of $R_3$. Let $T_3$ be a spanning tree of $R_3$ and T consist of $\bigcup _{1\le i\le 3}T_i$, as well as the two inter-cluster edges $(s_1,r_1)$ and $(s_2,r_2)$. We have that

$$\begin{aligned} d_T(R_1,R_2)\nonumber= & {} \sum _{u\in R_1}\sum _{v\in R_2}\left( d(u,r_1)+d(r_2,v)\right) \nonumber \\&+\,\sum _{u\in R_1}\sum _{v\in R_2}(w(r_2,s_2)+w(r_1,s_1)+d_T(s_1,s_2)) \nonumber \\= & {} n_2d(r_1,R_1)+n_1d(r_2,R_2)\nonumber \\&+\,n_1n_2(w(r_1,s_1)+w(r_2,s_2)+d_T(s_1,s_2)) \end{aligned}$$

(5)

and for $i=1$ and 2,

$$\begin{aligned} d_T(R_i,R_3)\nonumber \\= & {} \sum _{u\in R_i}\sum _{v\in R_3}(d(u,r_i)+w(r_i,s_i)+d_T(s_i,v)) \nonumber \\= & {} n_3d(r_i,R_i)+n_in_3w(r_i,s_i)+n_id_T(s_i,R_3). \end{aligned}$$

(6)

By definition,

$$\begin{aligned} c_{I}(T)/2= & {} d_T(R_1,R_2)+d_T(R_1,R_3)+d_T(R_2,R_3)\nonumber \\= & {} (n_2+n_3)d(r_1,R_1)+(n_1+n_3)d(r_2,R_2)\nonumber \\&+\,n_1(n_2+n_3)w(r_1,s_1)+n_2(n_1+n_3)w(r_2,s_2)\nonumber \\&+\,n_1n_2d_T(s_1,s_2)+n_1d_T(s_1,R_3)+n_2d_T(s_2,R_3). \end{aligned}$$

(7)

For fixed $(r_1,s_1)$ and $(r_2,s_2)$, our goal is to compute a spanning tree $T_3$ of $R_3$ minimizing

$$\begin{aligned} n_1n_2d_{T_3}(s_1,s_2)+n_1d_{T_3}(s_1,R_3)+n_2d_{T_3}(s_2,R_3) \end{aligned}$$

since the other terms in (7) are fixed. By Lemma 6, the optimal cost can be 2-approximated with $n_1$ and $n_3$ as the weights in the weighted 2-MRCT problem. Since this takes $O(m+n\log n)$ time for each possible pair of the inter-cluster edges, the total time complexity is $O(m^{2}n\log n+m^3)$. $\square$

6 Concluding remarks

In Sect. 3, we showed the inapproximability of Shortest st -CluPath. It is not hard to show that the problem is fixed-parameter tractable with the number of clusters as the parameter. The reason is that given a sequence of clusters a path passes through, the shortest path or determining there is no such path can be computed in polynomial time.

For CluMRCT on metric graphs, we show a 2-approximation algorithm on metric graphs. Our future work includes improving the approximation ratio. Also, it would be interesting to extend the approximation algorithm for 3-InterCluMRCT to the case of more than three clusters.