More bounds for the Grundy number of graphs

Abstract

A coloring of a graph $G=(V,E)$ is a partition $\{V_1, V_2, \ldots , V_k\}$ of V into independent sets or color classes. A vertex $v\in V_i$ is a Grundy vertex if it is adjacent to at least one vertex in each color class $V_j$ for every $j<i$. A coloring is a Grundy coloring if every vertex is a Grundy vertex, and the Grundy number $\Gamma (G)$ of a graph G is the maximum number of colors in a Grundy coloring. We provide two new upper bounds on Grundy number of a graph and a stronger version of the well-known Nordhaus-Gaddum theorem. In addition, we give a new characterization for a $\{P_{4}, C_4\}$-free graph by supporting a conjecture of Zaker, which says that $\Gamma (G)\ge \delta (G)+1$ for any $C_4$-free graph G.

1 Introduction

All graphs considered in this paper are finite and simple. Let $G=(V,E)$ be a finite simple graph with vertex set V and edge set E, |V| and |E| are its order and size, respectively. As usual, $\delta (G)$ and $\Delta (G)$ denote the minimum degree and the maximum degree of G, respectively. A set $S\subseteq V$ is called a clique of G if any two vertices of S are adjacent in G. Moreover, S is maximal if there exists no clique properly contain it. The clique number of G, denoted by $\omega (G)$, is the cardinality of a maximum clique of G. Conversely, S is called an independent set of G if no two vertices of S are adjacent in G. The independence number of G, denoted by $\alpha (G)$, is the cardinality of a maximum independent set of G. The induced subgraph of G induced by S, denoted by G[S], is subgraph of G whose vertex set is S and whose edge set consists of all edges of G which have both ends in S.

Let C be a set of k colors. A k -coloring of G is a mapping $c: V\rightarrow C$, such that $c(u)\ne c(v)$ for any adjacent vertices u and v in G. The chromatic number of G, denoted by $\chi (G)$, is the minimum integer k for which G has a k-coloring. Alternately, a k-coloring may be viewed as a partition $\{V_1, \ldots , V_k\}$ of V into independent sets, where $V_i$ is the set of vertices assigned color i. The sets $V_i$ are called the color classes of the coloring.

The coloring number col(G) of a graph G is the least integer k such that G has a vertex ordering in which each vertex is preceded by fewer than k of its neighbors. The degeneracy of G, denoted by deg(G), is defined as $deg(G)=max\{\delta (H): H\subseteq G\}$. It is well known (see Page 8 in Jensen and Toft 1995) that for any graph G,

$$\begin{aligned} col(G)=deg(G)+1. \end{aligned}$$

(1)

It is clear that for a graph G,

$$\begin{aligned} \omega (G)\le \chi (G)\le col(G)\le \Delta (G)+1. \end{aligned}$$

(2)

Let c be a k-coloring of G with the color classes $\{V_1, \ldots , V_k\}$. A vertex $v\in V_i$ is called a Grundy vertex if it has a neighbor in each $V_j$ with $j<i$. Moreover, c is called a Grundy k -coloring of G if each vertex v of G is a Grundy vertex. The Grundy number $\Gamma (G)$ is the largest integer k, for which there exists a Grundy k-coloring for G. It is clear that for any graph G,

$$\begin{aligned} \chi (G)\le \Gamma (G)\le \Delta (G)+1. \end{aligned}$$

(3)

A stronger upper bound for Grundy number in terms of vertex degree was obtained in Zaker (2008) as follows. For any graph G and $u\in V(G)$ we denote $\{v\in V(G): uv \in E(G), d(v) \le d(u)\}$ by $N_{\le }(u)$, where d(v) is the degree of v. We define $\Delta _2(G) = \max _{u\in V(G)} \max _{v\in N_{\le }(u)} d(v)$. It was proved in Zaker (2008) that $\Gamma (G)\le \Delta _2(G)+1$. Since $\Delta _2(G)\le \Delta (G)$, we have

$$\begin{aligned} \Gamma (G)\le \Delta _2(G)+1\le \Delta (G)+1. \end{aligned}$$

(4)

The study of Grundy number dates back to 1930s when Grundy (1939) used it to study kernels of directed graphs. The Grundy number was first named and studied by Christen and Selkow (1979). Zaker (2005) proved that determining the Grundy number of the complement of a bipartite graph is NP-hard.

A complete k-coloring c of a graph G is a k-coloring of the graph such that for each pair of different colors there are adjacent vertices with these colors. The achromaic number of G, denoted by $\psi (G)$, is the maximum number k for which the graph has a complete k-coloring. It is trivial to see that for any graph G,

$$\begin{aligned} \Gamma (G)\le \psi (G). \end{aligned}$$

(5)

Note that col(G) and $\Gamma (G)$ (or $\psi (G)$) is not comparable for a general graph G. For instacne, $col (C_{4})=3$, $\Gamma (C_{4})=2=\psi (C_4)$, while $col(P_{4})=2$, $\Gamma (P_{4})=3=\psi (P_4)$. Grundy number was also studied under the name of first-fit chromatic number, see Kierstead et al. (1995) for instance.

2 New bounds on Grundy number

In this section, we give two upper bounds on the Grundy number of a graph in terms of its Randić index, and the order and clique number, respectively.

2.1 Randić index

The Randić index R(G) of a (molecular) graph G was introduced by Randić (1975) as the sum of $\frac{1}{\sqrt{d(u)d(v)}}$ over all edges uv of G, where d(u) denotes the degree of a vertex u in G, i.e, $R(G)=\sum \limits _{uv\in E(G)}1/{\sqrt{d(u)d(v)}}$. This index is quite useful in mathematical chemistry and has been extensively studied, see Li and Gutman (2006). For some recent results on Randić index, we refer to Divnić and Pavlović (2013), Li and Shi (2010), Liu et al. (2011, 2013).

Theorem 2.1

(Bollobás and Erdős 1998) For a graph G of size m,

$$\begin{aligned} R(G)\ge \frac{\sqrt{8m+1}+1}{4}, \end{aligned}$$

with equality if and only if G is consists of a complete graph and some isolated vertices.

Theorem 2.2

For a connected graph G of order $n\ge 2$, $\psi (G)\le 2R(G)$, with equality if and only if $G\cong K_n$.

Proof

Let $\psi (G)=k$. Then $m=e(G)\ge \frac{k(k-1)}{2}$. By Theorem 2.1,

$$\begin{aligned}&R(G)\ge \frac{\sqrt{8m+1}+1}{4} \ge \frac{\sqrt{4k(k-1)+1}+1}{4}\\&\quad =\frac{\sqrt{(2k-1)^{2}}+1}{4} =\frac{2k-1+1}{4} =\frac{k}{2}. \end{aligned}$$

This shows that $\psi (G)\le 2R(G).$ If $k=2R(G)$, then $m= \frac{k(k-1)}{2}$ and the equality is satisfied. Since G is connected, by Theorem 2.1, $G=K_k=K_n$.

If $G=K_n$, then $\psi (G)=n=2R(G)$. $\square$

Corollary 2.3

For a connected graph G of order n, $\Gamma (G)\le 2R(G)$, with equality if and only if $G\cong K_n$.

Theorem 2.4

(Wu et al. 2014) If G is a connected graph of order $n\ge 2$, then $col(G)\le 2R(G)$, with equality if and only if $G\cong K_n$

So, combining the above two results, we have

Corollary 2.5

For a connected graph G of order $n\ge 2$, $\max \{\psi (G), col(G)\}\le 2R(G)$, with equality if and only if $G\cong K_n$.

2.2 Clique number

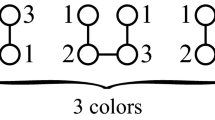
Zaker (2006) showed that for a graph G, $\Gamma (G)=2$ if and only if G is a complete bipartite (see also the page 351 in Chartrand and Zhang 2008). Zaker and Soltani (2015) showed that for any integer $k\ge 2$, the smallest triangle-free graph of Grundy number k has $2k-2$ vertices. Let $B_k$ be the graph obtained from $K_{k-1,k-1}$ by deleting a matching of cardinality $k-2$, see $B_k$ for an illustration in Fig. 1. The authors showed that $\Gamma (B_k)=k$.

Fig. 1

The graph $B_k$ for $k\ge 2$

One may formulate the above result of Zaker and Soltani: $\Gamma (G)\le \frac{n+2}{2}$ for any triangle-free graph G of order n.

Theorem 2.6

• (i) For a graph G of order $n\ge 1$, $\Gamma (G)\le \frac{n+\omega (G)}{2}.$

• (ii) Let k and n be any two integers such that $k+n$ is even and $k\le n$. Then there exists a graph $G_{k,n}$ on n vertices such that $\omega (G_{k,n})=k$ and $\Gamma (G_{k,n})=\frac{n+k}{2}$.

• (iii) In particular, if G is a connected triangle-free graph of order $n\ge 2$, then $\Gamma (G)=\frac{n+2}{2}$ if and only if $G\cong B_{\frac{n+2}{2}}$.

Proof

We prove part (i) of the assertion by induction on $\Gamma (G)$. Let $k=\Gamma (G)$. If $k=1$, then $G=\overline{K_n}$. The result is trivially true. Next we assume that $k\ge 2$.

Let $V_{1}, V_{2}, \ldots , V_{k}$ be the color classes of a Grundy coloring of G. Set $H=G\setminus V_{1}$. Then $\Gamma (H)=k-1$. By the induction hypothesis, $\Gamma (H)\le \frac{n-|V_{1}|+\omega (H)}{2}$. Hence,

$$\begin{aligned} \Gamma (G)=\Gamma (H)+1\le \frac{n-|V_{1}|+\omega (H)}{2}+1=\frac{n+\omega (H)+2-|V_{1}|}{2}. \end{aligned}$$

We consider two cases. If $|V_{1}|\ge 2$, then

$$\begin{aligned} \Gamma (G)\le \frac{n+\omega (H)+2-|V_{1}|}{2}\le \frac{n+\omega (G)+2-2}{2}=\frac{n+\omega (G)}{2}. \end{aligned}$$

Now assume that $|V_{1}|=1$. Since $V_1$ is a maximal independent set of G, every vertex in H is adjacent to the vertex in $V_1$, and thus $\omega (H)=\omega (G)-1$. So,

$$\begin{aligned} \Gamma (G)=\frac{n+\omega (G)+1-|V_{1}|}{2}=\frac{n+\omega (G)}{2}. \end{aligned}$$

To prove part (ii), we construct $G_{k,n}$ as follows. First consider a complete graph on k vertices and partition its vertex set into two subsets A and B such that $||A|-|B||\le 1$. Let t be an integer such that $t=\frac{n-k}{2}$. Let also $H_t$ be the graph obtained from $K_{t,t}$ by deleting a perfect matching of size t. It is easily observed that $\Gamma (H_t)=t$, where any Grundy coloring with t colors consists of t color classes $C_1, \ldots , C_t$ such that for each i, $|C_i|=2$. Let $C_i=\{a_i, b_i\}$. Now for each $i\in \{1, \ldots , t\}$, join all vertices of A to $a_i$ and join all vertices of B to $b_i$. We denote the resulting graph by $G_{k,n}$. We note by our construction that $\omega (G_{k,n})=k$ and $\Gamma (G_{k,n})\ge k+t$. Also, clearly $\Delta (G_{k,n})=t+k-1$. Then $\Gamma (G_{k,n}) = k+t = (n+k)/2$. This completes the proof of part (ii).

Now we show part (iii) of the statement. It is straightforward to check that $\Gamma (B_k)=k$. Next, we assume that G is connected triangle-free graph of order $n\ge 2$ with $\Gamma (G)=\frac{n+2}{2}$. Let $k=\frac{n+2}{2}$. To show $G\cong B_k$, let $V_1, \ldots , V_k$ be a Grundy coloring of G.

Claim 1

(a) $|V_k|=1$; (b) $|V_{k-1}|=1$; (c) $|V_i|=2$ for each $i\le k-2$.

Since G is triangle-free, there are at most two color classes with cardinality 1 among $V_1, \ldots , V_k$. Since

$$\begin{aligned} 2k-2=|V_1|+\cdots +|V_k|\ge 1+1+2+\cdots +2=2(k-1), \end{aligned}$$

there are exactly two color classes with cardinality 1, and all others have cardinality two. Let u and v the two vertices lying the color classes of cardinality 1. Observe that u and v are adjacent.

We show (a) by contradiction. Suppose that $|V_k|=2$, and let $V_k=\{u_k, v_k\}$. Since u is adjacent to v and both $u_k$ and $v_k$ are adjacent to u and v, we have a contradiction with the fact that G is triangle-free. This shows $|V_k|=1$.

To complete the proof of the claim, it suffices to show (b). Toward a contradiction, suppose $|V_{k-1}|=2$, and let $V_{k-1}=\{u_{k-1}, v_{k-1}\}$. By (a), let $|V_i|=1$ for an integer $i<k-1$. Without loss of generality, let $V_i=\{u\}$ and $V_k=\{v\}$. Since $u_{k-1}u\in E(G)$, $v_{k-1}u\in E(G)$, and at least one of $u_{k-1}$ and $v_{k-1}$ is adjacent to v, it follows that there must be a triangle in G, a contradiction.

So, the proof of the claim is completed.

Note that $uv\in E(G)$. Let $V_i=\{u_i, v_i\}$ for each $i\in \{1, \ldots , k-2\}$. Since G is triangle-free, exactly one of $u_i$ and $v_i$ is adjacent to u and the other one is adjacent to v. Without loss of generality, let $u_iv\in E(G)$ and $v_iu\in E(G)$ for each i. Since G is triangle-free, both $\{u_1, \ldots , u_{k-1}, u\}$ and $\{v_1, \ldots , v_{k-1}, v\}$ are independent sets of G, implying that G is a bipartite graph.

To complete the proof for $G\cong B_k$, it remains to show that $u_iv_j\in E(G)$ for any i and j with $i\ne j$. Without loss of generality, let $i<j$. Since $v_iv_j\notin E(G)$, $u_iv_j\in E(G)$.

So, the proof is completed. $\square$

Since for any graph G of order n, $\chi (\overline{G})\omega (G)=\chi (\overline{G})\alpha (\overline{G})\ge n$, by Theorem 2.6, the following result is immediate.

Corollary 2.7

(Zaker 2007) For any graph G of order n, $\Gamma (G)\le \frac{\chi (\overline{G})+1}{2} \omega (G)$.

Corollary 2.8

(Zaker 2005) Let G be the complement of a bipartite graph. Then $\Gamma (G)\le \frac{3\omega (G)}{2}$.

Proof

Let n be the order of G and (X, Y) be the bipartition of $V(\overline{G})$. Since X and Y are cliques of G, $\max \{|X|, |Y|\}\le \omega (G)$. By Theorem 2.6,

$$\begin{aligned} \Gamma (G)\le \frac{n+\omega (G)}{2}= \frac{|X|+|Y|+\omega (G)}{2} \le \frac{3\omega (G)}{2}. \end{aligned}$$

$\square$

The following result is immediate from by the inequality (2) and Theorem 2.6.

Corollary 2.9

For any graph G of order n, $\Gamma (G)\le \frac{n+ \chi (G)}{2}\le \frac{n+ col(G)}{2}$.

Chang and Hsu (2012) proved that $\Gamma (G)\le log_{\frac{col(G)}{col(G)-1}}n +2$ for a nonempty graph G of order n. Note that this bound is not comparable to that given in the above corollary.

3 Nordhaus-Gaddum type inequality

Nordhaus and Gaddum (1956) proved that for any graph G of order n,

$$\begin{aligned} \chi (G)+\chi (\overline{G})\le n+1. \end{aligned}$$

Since then, relations of a similar type have been proposed for many other graph invariants, in several hundred papers, see the survey paper of Aouchiche and Hansen (2013). Cockayne and Thomason (1982) proved that

$$\begin{aligned} \Gamma (G)+\Gamma (\overline{G})\le \lfloor \frac{5n+2}{4}\rfloor \end{aligned}$$

for a graph G of order $n\ge 10$, and this is sharp. Füredi et al. (2008) rediscovered the above theorem. Harary and Hedetniemi (1970) established that $\psi (G)+\chi (\overline{G})\le n+1$ for any graph G of order n extending the Nordhaus-Gaddum theorem.

Next, we give a theorem, which is stronger than the Nordhaus-Gaddum theorem, but is weaker than Harary-Hedetniemi’s theorem. Our proof is turned out to be much simpler than that of Harary-Hedetniemi’s theorem.

It is well known that $\chi (G-S)\ge \chi (G)-|S|$ for a set $S\subseteq V(G)$ of a graph G. The following result assures that a stronger assertion holds when S is a maximal clique of a graph G.

Lemma 3.1

Let G be a graph of order at least two which is not a complete graph. For a maximal clique S of G, $\chi (G-S)\ge \chi (G)-|S|+1$.

Proof

Let $V_1, V_2, \ldots , V_k$ be the color classes of a k-coloring of $G-S$, where $k=\chi (G-S)$. Since S is a maximal clique of G, for each vertex $v\in V(G)\setminus S$, there exists a vertex $v'$ which is not adjacent to v. Hence $G[S\cup V_k]$ is s-colorable, where $s=|S|$. Let $U_1, \ldots , U_s$ be the color classes of an s-coloring of $G[S\cup V_k]$. Thus, we can obtain a $(k+s-1)$-coloring of G with the color classes $V_1, V_2, \ldots , V_{k-1}, U_1, \ldots , U_s$. So,

$$\begin{aligned} \chi (G)\le k+s-1=\chi (G-S)+|S|-1. \end{aligned}$$

$\square$

Theorem 3.2

For a graph G of order n, $\Gamma (G)+\chi (\overline{G})\le n+1$, and this is sharp.

Proof

We prove by induction on $\Gamma (G)$. If $\Gamma (G)=1$, then $G=\overline{K_n}$. The result is trivially holds, because $\Gamma (G)=1$ and $\chi (\overline{G})=n$. The result also clearly true when $G=K_n$.

Now assume that G is not a complete graph and $\Gamma (G)\ge 2$. Let $V_{1},V_{2},\ldots ,V_{k}$ be a Grundy coloring of G. Set $H=G\setminus V_{1}$. Then $\Gamma (H)=\Gamma (G)-1$. By the induction hypothesis,

$$\begin{aligned} \Gamma (H)+\chi (\overline{H})\le n-|V_{1}|+1. \end{aligned}$$

Since $V_{1}$ is a maximal independent set of G, it is a maximal clique of $\overline{G}$. By Lemma 3.1, we have

$$\begin{aligned} \chi (\overline{H})\ge \chi (\overline{G})-|V_1|+1. \end{aligned}$$

Therefore

$$\begin{aligned} \Gamma (G)+\chi (\overline{G})\le & {} \ (\Gamma (H)+1)+( \chi (\overline{H})+|V_1|-1)\\\le & {} \ (\Gamma (H)+\chi (\overline{H}))+|V_1| \\\le & {} \ n-|V_1|+1+|V_1| \\= & {} \ n+1. \end{aligned}$$

To see the sharpness of the bound, let us consider $G_{n,k}$, which is the graph obtained from the joining each vertex of $K_k$ to all vertices of $\overline{K_{n-k}}$, where $1\le k\le n-1$. It can be checked that $\Gamma (G_{n,k})=k+1$ and $\chi (\overline{G_{n,k}})=n-k$. So $\Gamma (G_{n,k})+\chi (\overline{G_{n,k}})=n+1$. The proof is completed. $\square$

Finck (1966) characterized all graphs G of order n such that $\chi (G)+\chi (\overline{G})=n+1$. It is an interesting problem to characterize all graphs G attaining the bound in Theorem 3.2. Since $\alpha (G)=\omega (\overline{G})\le \chi (\overline{G})$ for any graph G, the following corollary is a direct consequence of Theorem 3.2.

Corollary 3.3

(Effantin and Kheddouci 2007) For a graph G of order n,

$$\begin{aligned} \Gamma (G)+\alpha (G) \le n+1. \end{aligned}$$

4 Perfectness

Let $\mathcal {H}$ be a family of graphs. A graph G is called $\mathcal {H}$ -free if no induced subgraph of G is isomorphic to any $H\in \mathcal {H}$. In particular, we simply write H-free instead of $\{H\}$-free if $\mathcal {H}=\{H\}$. A graph G is called perfect, if $\chi (H)=\omega (H)$ for each induced subgraph H of G. It is well known that every $P_4$-free graph is perfect.

A chordal graph is a simple graph which contains no induced cycle of length four or more. Berge (1961) showed that every chordal graph is perfect. A simplicial vertex of a graph is vertex whose neighbors induce a clique.

Theorem 4.1

(Dirac 1961) Every chordal graph has a simplicial vertex.

Corollary 4.2

If G is a chordal graph, then $\delta (G)\le \omega (G)-1$.

Proof

Let v be a simplicial vertex. By Theorem 4.1, N(v) is a clique, and thus $d(v)\le \omega (G)-1$. $\square$

Markossian et al. (1996) remarked that for a chordal graph G, $col(H)=\omega (H)$ for any induced subgraph H of G. Indeed, its converse is also true. For convenience, we give the proof here.

Theorem 4.3

A graph G is chordal if and only if $col(H)=\omega (H)$ for any induced subgraph H of G.

Proof

The sufficiency is immediate from the fact that any cycle $C_k$ with $k\ge 4$, $col(C_k)=3\ne 2=\omega (C_k)$.

Since every induced subgraph of a chordal graph is still a chordal graph, to prove the necessity of the theorem, it suffices to show that $col(G)=\omega (G)$. Recall that $col(G)=deg(G)+1$ and $deg(G)=\max \{\delta (H): H\subseteq G\}$. Observe that

$$\begin{aligned} \max \{\delta (H): H\subseteq G\}=\max \{\delta (H): H \text { is an induced subgraph of}\ G\}. \end{aligned}$$

Since $\omega (G)-1\le \max \{\delta (H): H\subseteq G\}$ and $\delta (H)\le \omega (H)-1$ for any induced subgraph H of G, $\max \{\delta (H): H \text { is an induced subgraph of}\ G\}\le \omega (G)-1,$ we have $deg(G)=\max \{\delta (H): H\subseteq G\}=\omega (G)-1$. Thus, $col(G)=\omega (G)$. $\square$

Let $\alpha , \beta \in \{\omega , \chi , \Gamma , \psi \}$. A graph G is called $\alpha \beta$ -perfect if for each induced subgraph H of G, $\alpha (H)=\beta (H)$. Among other things, Christen and Selkow proved that

Theorem 4.4

(Christen and Selkow 1979) For any graph G, the following statements are equivalent:

• (1) G is $\Gamma \omega$-perfect.

• (2) G is $\Gamma \chi$-perfect.

• (3) G is $P_4$-free.

For a graph G, m(G) denotes the number of of maximal cliques of G. Clearly, $\alpha (G)\le m(G)$. A graph G is called trivially perfect if for every induced subgraph H of G, $\alpha (H)=m(H)$. A partially order set $(V, <)$ is an arborescence order if for all $x\in V$, $\{y:\ y<x\}$ is a totally ordered set.

Theorem 4.5

(Wolks 1962; Golumbic 1978) Let G be a graph. The following conditions are equivalent:

• (i) G is the comparability graph of an arborescence order.

• (ii) G is $\{P_4, C_4\}$-free.

• (iii) G is trivially perfect.

Next we provide another characterization of $\{P_{4}, C_4\}$-free graphs.

Theorem 4.6

Let G be a graph. Then G is $\{P_{4}, C_4\}$-free if and only if $\Gamma (H)=col(H)$ for any induced subgraph H of G.

Proof

To show its sufficiency, we assume that $\Gamma (H)=col(H)$ for any induced subgraph H of G. Since $col (C_{4})=3$ while $\Gamma (C_{4})=2$, and $col(P_{4})=2$ while $\Gamma (P_{4})=3$, it follows that G is $C_{4}$-free and $P_{4}$-free.

To show its necessity, let G be a $\{P_{4}, C_{4}\}$-free graph. Let H be an induced subgraph of G. Since G is $P_4$-free, by Theorem 4.4, $\Gamma (H)=\omega (H)$. On the other hand, by Theorem 4.3, $col(H)=\omega (H)$. The result then follows. $\square$

Gastineau et al. (2014) posed the following conjecture.

Conjecture 1

(Gastineau et al. 2014). For any integer $r\ge 1$ , every $C_4$ -free r -regular graph has Grundy number $r+1$.

So, Theorem 4.6 asserts that the above conjecture is true for every regular $\{P_{4}, C_{4}\}$ -free graph. However, it is not hard to show that a regular graph is $\{P_{4}, C_{4}\}$ -free if and only if it is a complete graph. Indeed, Zaker (2011) made the following beautiful conjecture, which implies Conjecture 1.

Conjecture 2

(Zaker 2011) If G is $C_4$ -free graph, then $\Gamma (G)\ge \delta (G)+1$.

Note that Theorem 4.6 shows that Conjecture 2 is valid for all $\{P_{4}, C_{4}\}$-free graphs.