Problem dependent optimization (PDO)

Abstract

A metaheuristic is generally a procedure designed to find a good solution to a difficult optimization problem. Known optimization search metaheuristics heavily rely on parameters, which are usually introduced so that the metaheuristic follows some supposedly related to the optimization problem natural process (simulated annealing, swarm optimization, genetic algorithms). Adjusting the parameters so that the metaheuristic performs successfully in the problem at hand could be quite tricky and time consuming task which often requires intimate knowledge of the problem and a lot of experimenting to achieve the needed level of performance. In this article I present a metaheuristic with parameters depending only on the problem at hand, which virtually eliminates the preliminary work on adjusting the parameters. Moreover, the parameters are frequently updated during the process, based on the increasing amount of information about the solution space collected during the run. The metaheuristic has been successfully applied in several different searches for discrete objects such as designs, packings, coverings and partitions.

1 Discrete optimization problems (DOPs)

In this type of problems we define a set $S$ of discrete objects called solutions; the set $S$ is the solution space. Every solution $i\in S$ possesses a number of properties. The question is to find a solution having an additional property, called optimality.

Optimality is defined by introducing a function $c:S\rightarrow R$ from the set of solutions to the real numbers, called the cost function. In the applications we dealt with, the cost function was defined as

$$\begin{aligned} c:S\rightarrow Z^+\cup \{0\}. \end{aligned}$$

In what follows we will assume a cost function of the above type.

An optimal solution is a solution $i^*\in S$ such that $c(i^*)\le c(i)$ for all $i\in S$. We can always define the cost function in such a way that $c(i^*)=0$.

We can define a DOP as the problem of finding an optimal solution assuming the pair $(S,c)$ is defined. In some applications finding an optimal solution is not feasible (or we do not know the cost of an optimal solution; we might have defined the cost function in a way such that a zero cost solution seems feasible, but in reality, it might happen that an optimal solution has cost higher than zero), so we might be just interested in finding a “good enough solution”. The usual approach to solve a DOP is by moving from one solution to another and try to find solutions of lower and lower cost, until either an optimal solution is found or the process is terminated with the best solution found so far recorded.

A move is defined to be a function $d:S(d)\rightarrow S$, where $S(d)\subseteq S$ is the domain of $d$. A move $d$ has an inverse, denoted $d^{-1}$, if $s=d^{-1}(d(s))=s$ for every $s\in S(d)$. In all of the applications we were dealing with, we used invertible moves.

Let $D$ be the set of all moves of a DOP. We require that the union of the domains of all the moves in $D$ is the solution set, that is,

$$\begin{aligned} \bigcup _{d\in D} S(d) =S \end{aligned}$$

(so that for every solution $s\in S$ there is at least one $d\in D$ so that $d(s)\in S$).

A solution $s'$ is a neighbor of the solution $s$, if $s^{\prime }=d(s)$ for some $d\in D$.

The neighborhood $N(s)$ of a solution $s$ is the union of all neighbors of $s$:

$$\begin{aligned} N(s)=\bigcup _{\{ d\in D|s\in S(d)\}}d(s). \end{aligned}$$

Conventions: Solutions having the same cost will be referred to as solutions having the same level. Given a solution $s$, a very good neighbour of $s$ is any solution $s^{\prime }\in N(s)$ with $c(s^{\prime })< c(s)$, and just a good neighbour $s^{\prime }$ is one with $c(s^{\prime })\le c(s)$. A bad neighbour is one with $c(s^{\prime })> c(s)$.

A move from a solution $s$ to a new solution $s'$ such that $c(s^{\prime })=c(s)$ is called a sideway move.

2 Problems with the known heuristics

In known optimization metaheuristics, the strategy of moving from one solution to another is based on a prespecified function, usually borrowed from some natural phenomenon (simulated annealing, great deluge, etc.) There are not too many good reasons why the best strategy for attacking discrete problems by optimization should be based on that kind of phenomena.

In the best known optimization metaheuristics, the good performance is due to the ability of the metaheuristic to avoid getting stuck in a local minimum. However, there are some issues that are not really well addressed. In trying to avoid getting stuck in a local minimum, the metaheuristic might be missing global minima too often. There are no ways to know whether the metaheuristic is close to a global minimum and switch to a complete search. On the other hand, if the metaheuristic has mechanisms to avoid missing a global minimum (say, performing a complete search when the cost of the current solution is under fixed level), then it might be spending too much time on that.

In the known metaheuristics, it is usually possible that the process “freezes” in the neighbourhood of a local solution, which requires a restart (or restarts) if the freezing is somehow recognized.

Known optimization search metaheuristics heavily rely on parameters. Adjusting these parameters so that the metaheuristic performs successfully in the problem at hand could be quite tricky and time consuming task which often requires intimate knowledge of the problem and a lot of experimenting to achieve the needed level of performance.

3 Objects in a DOP

• Set of solutions (huge size; known)

• Neighborhood of a solution (size known; constant)

• Set of very good neighbors of a solution (size variable; unknown)

• Set of optimal solutions (size unknown)

4 Introducing problem dependent optimization (PDO)

The new metaheuristic suggested here addresses many of the problems with the known metaheuristics and resolves them in a natural way.

In PDO, the strategy of moving from one solution to another is based on a function which only depends on the solution space of the particular $DOP$; we call it the jump-down function (JDF). We will define it shortly, but we first discuss the relevance of the definition to follow.

Let $\mathcal C$ be the set of all possible costs. Let $S_c\subseteq S$ be the set of all solutions of cost $c$ (we assume there is at least one solution of cost $c$, for each cost $c\in \mathcal C$). Let $G(B)$ be the set of all very good neighbours of the solution $B$. (Note that $G(B)=\emptyset$ is possible.) Then

$$\begin{aligned} \frac{\sum _{B\in S_c}\frac{|G(B)|}{|N(B)|}}{|S_c|} \end{aligned}$$

is the average probability of choosing a move from a solution $B$ (residing at level $c$) to a very good neighbour of $B$. We denote this probability by $p_{c}$. Then $p^{-1}_c$ is the average number of moves which have to be tried in order to find a cost-decreasing solution from a solution $B$ at level $c$.

The jump down function is a function $f$ from the set $\mathcal C$ to $Z^+$, such that for every $c\in \mathcal C$, at every moment of the run of the heuristic, $f(c)$ is an approximation to the average number of moves needed to find a cost-decreasing solution at level $c$ under the conditions of the heuristic. It is difficult to imagine what the precise value of this average number is for a particular cost $c$. At this point, it looks like $f(c)$ could be an approximation to $p^{-1}_c$, and this will indeed be the case if the heuristic stays at one solution and examines solutions from the neighbourhood of the current one until it finds a cost decreasing one and moves to it. But that is not exactly how the new heuristic works... (It would be stuck at any solution which does not have a very good neighbour, if it did work that way.)

In fact, PDO always accepts sideways moves, and these moves and the subsequent moves to investigate the neighbourhoods of the accepted solutions at the same level during one loop are also counted within the count of moves needed to find a cost decreasing solution at that level. Hence $f(c)$ is not related to $p^{-1}_c$ in any observable way.

The precise value of the average number of moves used in the definition of $f(c)$ is somewhat tricky to define; technically, it is over all possible runs of the heuristic which includes runs with infinite number of moves (say if the heuristic does not converge to an optimal solution), and so there are infinitely many runs possible. We can define it in a feasible manner by observing that there is a finite number of possible runs with any prespecified number $M$ of moves (there is a finite number of choices for a starting solution, and a finite number of moves from each solution visited, so the number of all possible runs for any particular $M$ is finite), and then let $M$ go to infinity.

At the start of the heuristic, we can assign the values of $f(c)$ quite arbitrarily; we can even use the same constant for the values of $f$ for all $c$, for example, if $N$ is the constant size of a neighborhood, we can use $f(c)=kN$ for some $k$, say $k=10$. The heuristic will steadily improve on the values of $f(c)$ to almost a constant state, optimal for the solution space of the particular DOP we solve.

The improving of the jump-down function comes from frequent updates of its values based on the increasing amount of data collected during the run of the heuristic. It is done as follows: Suppose the heuristic has already visited $n$ times the level $c$. Let $s_j$, $j=1,2,...,n$, be the number of moves the heuristic tried in order to find a cost-decreasing solution during its $j$-th visit to level $c$. Then the average number of moves tried in finding a cost-decreasing solution, immediately after finding the last one is $\frac{\sum _{j=1}^{n}s_j}{n}$.

Therefore, we can set a value of the jump-down function at $c$ to be

$$\begin{aligned} f(c)=\left\lceil \frac{\sum _{j=1}^{n}s_j}{n} \right\rceil \, \end{aligned}$$

for the $(n+1)$-th visit of level $c$. This value will remain the same until the next jump-down from that level happens; then it will be updated again, etc.

It is possible to keep all of the the information about how many moves the heuristic tried before a jump-down from level $c$ (that is, to keep all of the numbers $s_j$, $j=1,2,...,n$ in memory); that was done in earlier stages of testing the heuristic. In the version we present here, we choose to save memory and update the jump-down function as follows: After the $(n+1)$-st jump-down from level $c$, we just need $s_{n+1}$ and the current value of the jump-down function, $f(c)$. The new value of the jump-down function is set to

$$\begin{aligned} f(c):=\left\lceil \frac{nf(c)+s_{n+1}}{n+1}\right\rceil \, . \end{aligned}$$

Clearly, the expression on the right is sufficiently close to

$$\begin{aligned} \left\lceil \frac{\sum _{j=1}^{n+1}s_j}{n+1}\right\rceil \, , \end{aligned}$$

as evident from the next lemma.

Lemma

Let

$$\begin{aligned} S_n=\frac{a_1+a_2+\cdots +a_n}{n}\, . \end{aligned}$$

Then

$$\begin{aligned} \left\lceil S_{n+1}\right\rceil =\left\lceil \frac{n\left\lceil S_n\right\rceil +a_{n+1}}{n+1}\right\rceil -\epsilon , \end{aligned}$$

where $\epsilon =0$ or 1.

Proof

We have

$$\begin{aligned} \frac{n\left\lceil S_n\right\rceil +a_{n+1}}{n+1}\ge \frac{n S_n+a_{n+1}}{n+1}=S_{n+1}\, , \end{aligned}$$

so that

$$\begin{aligned} \left\lceil \frac{n\left\lceil S_n\right\rceil +a_{n+1}}{n+1}\right\rceil \ge \left\lceil S_{n+1}\right\rceil \, . \end{aligned}$$

Equality is attained only if $S_n=\left\lceil S_n\right\rceil$, that is, if $S_n$ is an integer. On the other hand,

$$\begin{aligned} \frac{n\left\lceil S_n\right\rceil +a_{n+1}}{n+1}&< \frac{n\left( S_n+1 \right) +a_{n+1}}{n+1}\\&= \frac{n\left( \frac{a_1+a_2+\cdots +a_n}{n} +1 \right) +a_{n+1}}{n+1}\\&= \frac{a_1+a_2+\cdots +a_{n+1}+n}{n+1}\\&= \frac{a_1+a_2+\cdots +a_{n+1}}{n+1}+\frac{n}{n+1}\\&< S_{n+1}+1\, , \end{aligned}$$

so that

$$\begin{aligned} \left\lceil \frac{n\left\lceil S_n\right\rceil +a_{n+1}}{n+1}\right\rceil \le \left\lceil S_{n+1}+1\right\rceil =\left\lceil S_{n+1}\right\rceil +1\, . \end{aligned}$$

Thus

$$\begin{aligned} \left\lceil S_{n+1}\right\rceil \le \left\lceil \frac{n\left\lceil S_n\right\rceil +a_{n+1}}{n+1}\right\rceil \le \left\lceil S_{n+1}\right\rceil +1\, , \end{aligned}$$

which completes the proof. $\square$

Suppose we knew the precise value of $f(c)$ for any cost $c\ge 1$ (we do not, but as the heuristic progresses we get better and better idea about it). Then we would not want to try way more than $f(c)$ moves in an attempt to find a cost decreasing solution while being at level $c$, because that would be waste of time; in particular, this would lead to spending too much time in the neighborhood of each local minimum encountered, and slow convergence, if at all, as a result. We would not want to try much less than $f(c)$ moves either, because we would be missing cost decreasing solutions often, thereby making it difficult to reach low cost levels, which again will lead to slow convergence, if at all. Testing more (but not much more) than $f(c)$ neighbours of the current solution before accepting a cost-increasing solution yields fairly good convergence of the optimization process. The reason for that will be further clarified after we present the new metaheuristic.

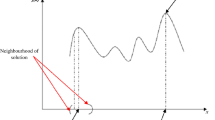
The above picture illustrates a part of the solution space of a DOP and possible moves. Each plane corresponds to a fixed cost (level). We can associate a graph with each DOP as follows: The vertices are the solutions, and there is an edge between two solutions $B_i$ and $B_j$ if there is a move $d$ such that $d(B_i)=B_j$ (then $d^{-1}(B_j)=B_i$). The solutions residing in the same plane have the same cost. The heuristic jumps between levels trying to reach the lowest one (which corresponds to cost 0).

Generally, there are edges between vertices in the same level (corresponding to sideways moves) and edges between vertices residing in adjacent levels or edges crossing several levels (both corresponding to cost-increasing and cost-decreasing moves). Note that the graph of a DOP is $N$-regular; where $N$ is the (constant) size of a neighbourhood.

5 Description of PDO

• 1. Set values for $f(c)$ for all $c\ge 1$. (A rough approximation will do; for example, if the size of a neighborhood is $N$, then $f(c)=kN$ for all $c\ge 1$ would be OK; $k=10$ worked pretty well in all of the applications we tried.)

• 2. Set $jdc(c):=1$ for all $c$. ($jdc(c)$ counts the number of jump-downs from level $c$.)

• 3. Start with any solution $B$.

• 4. Set $counter:=0$.

• 5. Perform a single move to obtain a new solution $B^{\prime }=d(B)\in N(B)$, and set $counter:= counter+1$.

• (a) If $c(B^{\prime })=0$ then stop ($B'$ is an optimal solution.)

• (b) If $c(B^{\prime })<c(B)$, then

  $$\begin{aligned} f(c(B)):=\left\lceil \frac{jdc(c(B)).f(c(B))+counter}{jdc(c(B))+1}\right\rceil , \end{aligned}$$

  (1)

  set $jdc(c(B)):=jdc(c(B))+1$, set $B:= B^{\prime }$, and go to 4 (jump-down happened).

• (c) If $c(B^{\prime })=c(B)$, then set $B:= B^{\prime }$, and go to 5.

• (d) If [$c(B^{\prime })>c(B)$ and $counter > mf(c(B)$], then set $B:= B^{\prime }$, and go to 4. (Accept a cost-increasing solution and continue the process. Setting $m=2$ works well, although $m\in (a,2)$, with $a>1$ and not too close to 1, or $m\in (2,3]$ provide similar performance.)

• (e) If [$c(B^{\prime })>c(B)$ and $counter \le mf(c(B))$], then go to 5.

Notes:

• The counter counter counts the number of moves tried in order to find a cost decreasing solution while at the level of the current solution (the sideway moves and the moves from the accepted solutions are also counted).

• $f(c)$ is (approximately) the average number of moves needed to jump-down from level $c$ after all of the jump-downs from that level so far.

• In other words: At level $c$, try up to $mf(c)$ moves in order to find a cost-decreasing solution ($m$ is real, $m>1$. We experimented with $m\in (1,3]$ with $m=2$ being universal). If such is found, accept it and continue the process at the level of the accepted solution. If no cost-decreasing solution is found after $mf(c)$ moves, then accept a cost-increasing solution and continue the process. Accept sideway moves all the time.

• The reason we use $mf(c)$ rather than just $f(c)$ is to allow the heuristic to gradually improve on the values of $f(c)$. If we only try up to $f(c)$ moves, the values of $f(c)$ will gradually decrease and this will diminish the ability of the heuristic to reach very low levels, eventually bringing it to an almost non-convergent state.

• Technically, the initial values of $jdc(c)$ (in 2.) should be set to 0, because, initially, no level has been visited. However, setting $jdc(c)=1$ for all $c$ works slightly better. This avoids the possible assigning of too small values for $f(c)$ during the first application of step 5.(b), and then wasting time to improve them (although, technically the heuristic will gradually improve on the values of $f(c)$ even if the initial assignment is $f(c)=0$ for all $c$).

$$\begin{aligned} \textsc {Pseudo \,Code \,Description \,of \,PDO} \end{aligned}$$

Below is a description of the PDO heuristic in pseudo code. Pseudo language elements used:

6 Advantages of PDO

• Clearly, the entire procedure is a self-improving optimization process, where the jump-down function is constantly updated, based on the gradually increasing information about the solution space; thus during the run of the metaheuristic, more and more data about the solution space is examined and more precise values of the jump-down function are obtained.

• The metaheuristic can be applied in any $DOP$, including ones where we are interested in finding a global minimum. A justification for the good performance of PDO comes from the fact that it uses a self-adjusting and problem-dependent jump-down function instead of a prespecified jump-down function as in some known good metaheuristics, such as simulated annealing, in particular.

Based on the description of PDO and on the author’s experience, PDO overperforms the known metaheuristics in some aspects. In support to this statement, we next list a number of advantages of PDO. (Some of these, but not all, are present in other metaheuristics.) The first three items on this list are what separates the new metaheuristic from the known ones.

• Self-improving, self-adjusting.

• No need of assigning values of parameters at the start; no need of adjusting the parameters later or after a restart.

• No need of restart.

• Space-efficient (only one solution is kept in memory at any time) which allows to speed the search by running several copies of the software in one computer. Generally, many copies can be ran on each of many computers for speeding up the search.

• Accepts cost increasing solutions often enough to avoid getting stuck in a neighborhood of a local minimum.

• Comparatively easy to program; generally, one does not need too deep specialized knowledge on the objects of interest (although some knowledge on the structure of the objects might help in achieving more efficient search, say, by reducing the solution space, and/or introducing more refined cost function).

PDO has been successfully employed in finding cyclic designs (Abel et al. 2001, 2002, 2004a, b); super-simple designs (Bluskov and Heinrich 2001); coverings (Abel et al. 2006, 2007, Bertolo et al. 2004, Bluskov 2007, Bluskov and Greig 2006); packings (Abel et al. 2010); large sets of cyclic designs (Bluskov and Magliveras 2001); constant weight codes [Bluskov (in press)], and covering by coverings (in progress).