Magnetism in Simple Metal and 4d Transition Metal Clusters

Abstract

In this review article I discuss two aspects of magnetism in small metal clusters. The first question discussed is whether simple metal clusters, that obey electronic shell models and mimic properties of elemental atoms, also obey Hund’s rule of maximum spin multiplicity. The second question is whether small clusters of 4d transition metal atoms, that are non-magnetic in the bulk, have magnetic ground states. The question arises because calculations showed that small V clusters are magnetic although the bulk metal is not. We discuss known results on Rh clusters in detail to show that small clusters are generally magnetic, but it is difficult to unequivocally identify the ground state due to the presence of many isomers and spin states that are very close in energy.

Introduction

Magnetism remains one of the most intriguing aspects of physical reality we are familiar with. Being as fascinating as it is in bulk materials, magnetism in finite size systems, such as atomic clusters and quantum dots, poses further conceptual challenge to our understanding of how nature works. In this article I wish to review some of the attempts to understand magnetic properties of materials at very small length scales, in atomic clusters composed of a few atoms. I approach the question of magnetism in small atomic clusters from two different perspectives. The first approach is in the context of simple metal clusters such as group IA, IIA, group III, and the coinage metals, particularly Cu and Ag. The second approach is in the context of 4d transition metal (TM) elements. I elaborate these below.

By now a rich literature exists which establishes that properties of the simple metal clusters (as defined above) can be understood in terms of the electronic shell models. Since review articles [1] and book chapters [2] have discussed this issue at great lengths, I will only mention the essential points here. The first point is to assume that just as in bulk metals, the properties of the clusters can essentially be understood in terms of their valence electrons. The simplest model for the valence electrons in a bulk metal is the free-electron theory. One can similarly take a free electron model for the simple metal clusters. The crucial difference between the bulk metals and clusters is that the latter are finite objects, and hence the electrons are confined in space. Theoretically, one has to solve the problem of free electrons confined to a finite region by an appropriate confining potential rather than applying periodic boundary conditions on a cubic box, as is typically done in case of bulk metals. The simplest assumption one makes for the shape of the confining potential is that it is spherically symmetric. Quantum confinement leads to discrete one-electron energy levels. Spherical symmetry of the confining potential ensures that the energy eigenstates are simultaneously eigenstates of the angular momentum operator. The energy levels thus occur in bunches, called electronic shells. The exact values of the energies, of course, depend on the detailed functional form of the confining potential. For electrons confined in a spherical box, for example, the energy levels are ordered in increasing energy as 1S, 1P, 1D, 2S, 1F, 2P, 1H…. S, P, D,… denote eigenstates with the angular momentum quantum number $l= 0, 1, 2, \ldots$. Here we have used capital letters S, P, D etc. to distinguish these shell orbitals from the atomic orbitals with the same angular momentum quantum numbers.

The next step of the argument is that as atoms with filled electronic shells are less reactive and more stable, the same should be the case with metal clusters. Noting that S, P, D… orbitals can accommodate maximum of 2, 6, 10,… electrons, clusters with 2, 8, 18, 20, 34, 40, 58,… valence electrons will have filled electronic shells, and hence will be more stable than their neighbors. This was in fact demonstrated for the first time in, what has by now become a cult paper in the area of cluster science, by Knight et al. [3]. Na _n clusters at sizes 8, 18, 20, 40, 58 and 92 were found to be more stable than the neighboring sizes. Analogy of the simple metal clusters was taken a step further when it was experimentally shown that clusters with one electron less than shell filling have large electron affinities (EA), like halogen atoms [4–7], and those with one electron more than shell filling have small ionization potentials (IP), like alkali atoms [8–12]. From these it became clear that some simple metal clusters mimic properties of elemental atoms. Clusters that mimic properties of atoms, or have other useful properties and retain their structures in chemical assemblies were termed ‘superatoms’. Pioneering works by Khanna, Jena, Rao and Castleman have firmly established the conceptual foundations of superatoms, and have demonstrated their existence in experiments [13–17]. More recently, the idea of superatoms has been extended to include magnetic species called ‘magnetic superatoms’. Some of the fundamental ideas about designing magnetic superatoms may be found in these references [2, 18–20].

Here I will discuss a different aspect of the analogy of simple metal clusters with elemental atoms. This has to do with Hund’s rule of maximum spin multiplicity. Based on experimental spectroscopic data, Hund proposed that of all possible electron configurations for an atom, the state that has the maximum value of total spin S has the lowest energy. Since electrons in simple metal clusters occupy shells similar to atomic orbitals, and these clusters mimic certain properties of elemental atoms, a natural question is whether Hund’s rule of maximum spin is valid in these as well. In that case, one would have an interesting situation where small clusters of elements, that are non-magnetic in the bulk, have finite magnetic moments. As a concrete example, the Na₄ cluster has an electron configuration 1S²1P². If Hund’s rule is obeyed, the ground state will be a triplet. On the other hand, if Hund’s rule is not obeyed, a singlet state will result. Similar questions can be asked about all clusters that do not lead to filled electronic shells in the sense discussed above. I will review what is known about possible magnetism in small alkali and aluminum clusters containing a few atoms, and will briefly mention some results on clusters containing a few tens ($\sim$50–70) of atoms.

A clarification is in order here. Although I started the discussion on simple metal clusters with spherical shell models, not all clusters are ‘spherical’. Only when high-symmetry structures happen to be ground states, either due to filled electronic shells or complete geometric shells, the clusters are found to be spherical as measured by the so-called Hill-Wheeler parameter [1, 21, 22]. Clusters having partially filled shells usually have distortions from a perfectly spherical shape. Clemenger [23] proposed shell models with spheroidal distortions to treat such cases. Ellipsoidal shell models have also been discussed in the literature [1]. When the distortions are not large, the molecular orbitals (MO) of the clusters can still be considered to be angular momentum eigenstates to a good accuracy, although the degeneracy of all the $2(l+1)$ states found for a spherical shape is now lifted. Measurement of photoelectron angular distribution from alkali clusters has established this point beyond doubt [24, 25]. Therefore, although the spherical shell models are only guides to our understanding of the electronic structure of simple metal clusters in a strict sense, they remain a very good guide, and this simple picture is used to interpret the results of more accurate first-principles calculations.

Only three of the 3d TM elements, Fe, Co and Ni, turn out to be ferromagnetic (FM) in their bulk phases although all of them have partially filled d states in the atoms. Mn and Cr turn out to have anti-ferromagnetic (AFM) ground states in the bulk. Usually, itinerant FM is understood in terms of the Stoner criterion [26]. This says that if the product of the exchange integral, and the density of states (DOS) at the Fermi energy in the paramagnetic state is larger than 1, the system spontaneously transforms to a broken symmetry FM state. The same criterion could explain magnetic properties of V clusters [27]. Khanna and co-workers, in their theoretical studies, found that a nine-atom V cluster in the body centered cubic (bcc) structure with inter-atomic distances as in the bulk, had an antiferro-magnetic (AFM) ground state. The spin on the atom at the body center was oriented opposite to the spins on the corner atoms. Changing the ‘lattice constant’ (R) changed the relative stabilities of the magnetic and non-magnetic states. For large $R/R_0$, $R_0$ being the cubic lattice constant of the bulk, the FM and AFM states were nearly degenerate, and were more favorable than the paramagnetic (PM) state. As the interatomic distances decreased, the AFM state became more favorable. This remained the ground state down to $R/R_0= 0.9$. For R smaller than this, the PM state became energetically favorable. This transition between FM/AFM and PM states correlates nicely with the change of DOS at the Fermi energy. At large inter-atomic separations, the DOS at the Fermi energy is large. This decreases with decreasing R, and finally almost vanishes at $R/R_0=0.8$.

In this work, Khanna et al. also explored the effect of coordination on the magnetic state. When six more V atoms were added to from a V₁₅ cluster in the bcc structure, moment on all the atoms vanished. The moment remained zero for V₂₇ and V₅₁ clusters in the bcc structure. In this context, it is also important to mention that in the V₉ cluster, the moment on the central atom was much smaller (1.38 μ _B ) than those on the corner atoms (3.82 μ _B ). To illustrate the role of coordination on magnetic moment, they also calculated properties of a linear chain of V atoms. Up to V₇ at bulk V-V separation, the moment per atom remained almost constant, and moment on all the atoms aligned ferromagnetically. For a dimer, the moment per atom turned out to be 4 μ _B at the bulk separation of ~2.5 Å. But it was found to be only 1 μ _B at the gas-phase equilibrium bond length of 1.7 Å. These findings again underscore the effect of coordination and inter-atomic separation on the magnetic moment on an atom.

In order to understand the role of reduced coordination on magnetic moment, magnetic properties of Fe, Co and Ni clusters were measured extensively by the groups of de Heer [28] and Bloomfield [29, 30]. The most significant conclusion of these works is that clusters have larger magnetic moment per atom than the corresponding bulk FM solids. Moreover, magnetic moment per atom varied non-monotonically with size. Larger moment per atom was understood in terms of reduced coordination on an average in the clusters compared to the bulk. The non-monotonicity in the variation of with size is related to the structural growth pattern of the clusters. Atoms in clusters with compact structures have higher coordination on an average, and tend to have small moment, while more open structures have larger moment [31]. Thus structural details played an important role in determining magnetic properties of these clusters. The de Heer and Bloomfield groups tried to find at which size the clusters reach their ‘bulk limit’ as far as the magnetic moment per atom is concerned. The de Heer group reported that Ni clusters reach bulk limit at ~150 atoms. Fe and Co clusters have average moment larger than the bulk up to sizes ~450 and ~550 respectively. In a later experiment, the Bloomfield group found that Ni clusters have larger than bulk moment even up to 740 atoms. The reason for the discrepancy between the two results is not clear, but both go on to show that a lower coordination leads to a larger moment.

The theoretical work on V clusters, and the experiments on Fe, Co and Ni clusters and the related theoretical works raised the question whether some of the 4d or 5d TM elements, all of which are paramagnetic in their bulk, can have finite magnetic moments in cluster form. Reddy, Khanna and Dunlap were the first to show the possibility of large magnetic moments in 4d TM clusters [32]. This generated a flurry of activities on these clusters. Here I will review some of the works on Rh clusters.

Hund’s Rule in Simple Metal Clusters

Origin of Hund’s Rule in Atoms

Before I go on to discuss applicability or otherwise of Hund’s rule to metal clusters, it is important to understand its microscopic origin in atoms. It was argued by Slater that Hund’s rule of spin maximization is a consequence of many-electron exchange effect [33]. Suppose we are to fill the electronic states in a carbon atom. The electronic configuration would be $1s^22s^22p^2$. According to Hund’s rule, the ground state will be a triplet (term symbol $^3$P$_0$). A simple way to understand this is as follows. Within a Hartree–Fock picture, two electrons with the same spin orientation ($S_z = 1/2$) will have a lower energy due to a finite negative contribution of the exchange term, than if the spins were oriented oppositely. In other words, parallel spin orientations lead to lower electron-electron interaction energies, and this is the origin of Hund’s rule. This idea prevailed for quite some time before it was scrutinized more closely. A crucial assumption in Slater’s argument, which remains unstated here, is that the atomic orbitals remain the same in both spin states. It is easy to argue that this cannot be true [34]. Each eigenstate must satisfy the virial theorem, $2T+V=0$. Here T is the kinetic energy and V is the total potential energy including electron-nucleus, electron-electron, Hartree and exchange contributions [35]. If the potential energy decreases, the kinetic energy must increase according to the virial theorem. But if the orbitals remain the same the kinetic energy also remains the same. So there is an inconsistency. Self-consistent calculations by Hongo et al. [34] in fact show that the orbitals are different in different spin states. The higher spin states have lower electron-nucleus interaction energy as a consequence of the orbitals getting more localized near the nucleus. This also leads to an increase in the kinetic energy in the higher spin state. More strikingly, a triplet state has a higher electron-electron interaction energy. Accurate diffusion Monte Carlo calculations by these authors [34] show that for a C atom in the singlet ($S=0$) and triplet ($S=1$) spin states, the kinetic energy, electron-nucleus interaction energy ($V_\mathrm{en}$) and the total electron-electron interaction energy ($V_\mathrm{ee}$) change as follows.

$$\begin{aligned} T^{S=1}> & {} T^{S=0}, \nonumber \\ V_\mathrm{ee}^{S=1}> & {} V_\mathrm{ee}^{S=0}, \\ V_\mathrm{en}^{S=1}< & {} V_\mathrm{en}^{S=0}. \nonumber \end{aligned}$$

(1)

As these relations show, the gain in $V_\mathrm{en}$ more than compensates for the increases in T and $V_\mathrm{ee}$, and is responsible for a high-spin state.

Validity of Hund’s rule in clusters

With the simple intuitive explanation for spin maximization turning out to be incorrect for elemental atoms, the issue for metal clusters is only expected to be more complex. The question whether small simple metal clusters, and clusters of non-magnetic 3d TM’s are magnetic has been addressed in only a few experimental works as far as I know. Cox et al. [36] were the first to explore magnetism in small aluminum clusters. They used a usual Stern-Gerlach apparatus for this. But instead of measuring the deflection of the cluster beams, they measured the decrease in intensity at the maximum of the beams due to the field gradient. The ratio of the intensities at the beam maximum with and without the field gradient present ($I_0/I_H$) was called the depletion factor. Al₂ and Al₃ showed significant depletion factors of 3.6 and 1.8 indicating magnetism in these clusters. These authors were unable to measure the depletion factors of Al₄ and Al₅ clusters because the energy of the ionizing ArF laser (6.4 eV) they used is lower than the ionization threshold of these clusters. Note that after passing through the inhomogeneous magnetic field, clusters are detected in a time-of-flight mass spectrometer for which ionization is essential. Al₆, Al₇ and Al₈ clusters also showed considerable depletion factors of 1.5, 1.9 and 1.7 respectively. If a cluster has spin S, the cluster beam is expected to split into $2S+1$ beams corresponding to the $2S+1$ allowed values of $S_z$ as it passes through the magnetic field. Moreover, for clusters having half-integer spins, the $S_z=0$ state is not allowed. Therefore, for sufficiently strong field gradients, the intensity along the original beam direction should be very small, and the depletion factor should be large. Since each Al atom has an odd number of electrons, all odd-sized clusters will have half-integer values of S, and should show large depletion ratios. However, as the above numbers show, some of the even-sized clusters (Al₂, for example) show larger depletion ratio than odd-sized clusters. Also, the depletion ratio becomes nearly 1 (no deflection) for all clusters larger than Al₈. These two observations, contrary to expectations, are explained as follows. To have large depletion ratios, even the clusters in the smallest $S_z$ states should have appreciable deflection so that they are removed out the portion of the beam near the center that gets exposed to the ionizing laser. Remembering that the amount of deflection (ξ) for a particular $S_z$ state is [2]

$$\begin{aligned} \xi \propto (S_z/M) (\partial B/ \partial z), \end{aligned}$$

(2)

M being the mass of the cluster, substantial deflection of the smallest $S_z$ states requires large enough field gradients. Limited deflecting power of the magnetic field, and a finite spatial extent of the ionizing laser prevent one from obtaining an ideal depletion ratio. The deflection is also inversely proportional to the mass of the cluster. Therefore, for the same value of spin, deflections of larger (heavier) clusters become smaller. This may explain why even the large odd-sized clusters show a depletion ratio close to 1.

These observations indicate that large clusters have small magnetic moments. Odd-sized clusters are perhaps doublets, while the even-sized clusters are singlets. Small even-sized clusters, Al₂, Al₆ and Al₈, on the other hand, are inferred to have triplet ground states.

In a second experiment, Douglass et al. [37] explored magnetic states of V, Cr, Pd and Al clusters. They measured the deflection of the cluster beams directly, and obtained the upper bound of the moment from the experimental uncertainties assuming a superparamgnetic model for the cluster spin. They explored size ranges 8-99 for V, 9-31 for Cr, 100-120 for Pd and 15-48 for for Al clusters. In all cases they could not detect any moment on the clusters within their experimental resolution. The situation is particularly interesting for the V clusters as Khanna and co-workers had found large magnetic moment on a V₉ cluster in a bcc structure with bulk inter-atomic separations. An absence of magnetic moment indicates that the structure of V₉ is not a bulk fragment. Unfortunately, ref [37] could not study Al clusters in the small size regime explored by Cox et al. [36].

The experimental scenario is a little unfortunate in the following way. Cox et al. did report non-zero magnetic moments on small Al clusters. Particularly important are the non-zero moments on Al₆ and Al₈ clusters, because odd-sized clusters always have spin unpaired electrons anyway. But Douglass et al. could not independently verify these results. They could do experiments only in the size range 15-48. Both these works, however, agree that the clusters are non-magnetic in the size range where they overlap. I will not get into any further discussions on the magnetic properties of V and Cr clusters as that is not our focus here. I focus on simple metal clusters.

There have only been a few works addressing the question of magnetic states of small Al clusters. A number of early studies using both ab initio and the local density approximation (LDA) within density functional theory (DFT) reported a triplet ground state for the Al₂ dimer, in agreement with the experiments of Cox et al. [38–41]. The situation for the size range of 3-6 atoms is less clear. Some authors have claimed Al₃, Al₄, and Al₅ to be quartet, triplet, and quartet in their respective ground states [42, 43]. Rao and Jena [40] found Al₄ to be a triplet, but Al₃ and Al₅ turned out to be doublets (low spin states) in their DFT calculations based on the generalized gradient approximation (GGA). They also found Al₆, Al₈ and Al₁₀ to have triplet ground states. These results are in complete agreement with the experiments of Cox et al, except for Al₁₀ for which Cox et al. found a depletion factor of 1, and Al₄ and Al₅ for which there were no measurements. Akola et al. [44], in their 1998 work using spin-polarized LDA, had predicted all Al clusters to have low spin ground states: doublet for odd-sized clusters, and singlet for even-sized clusters. Al₂ was the only exception, which they found to be a triplet. Upton [45], in his model calculation, predicted Al₂ and Al₆ to have nearly degenerate singlet and triplet states, but found Al₄ to be a singlet, and the odd-sized clusters Al₃ and Al₅ to be doublets. Phung et al. [46] found Al₂, Al₄, Al₆, Al₁₀, Al₁₂ and Al₁₆ to have triplet ground states in their DFT calculations. However, Al₈ was found to be a singlet, contrary to the conclusions of Cox et al. Al₁₄ also turned out to be a singlet. In a more recent set of calculations employing both hybrid DFT and quantum chemistry methods, Kiohara et al. [47] found Al₂ and Al₃ to have triplet and doublet ground states respectively. From Al₄ to Al₉, however, multi-reference character was detected in the ground state wave functions, implying significant static correlation. It is clear that all calculations agree that Al₂ is a triplet, but they disagree on the ground state spin configurations of clusters in the range 3-10. Even those works, that found high spin ground states for small Al clusters, did not address the question if these can be rationalized using Hund’s rule within a shell model picture.

A question further complicating the case of small Al clusters is whether Al atoms are monovalent or trivalent in these systems. Therefore, even if one attempted to view the magnetic ground states within a shell model, it is not immediately obvious what would be the valence electron count. Let us try to understand this with an example. If Al is a monovalent atom, Al₄ will have four valence electrons. If shell model is valid, its electron configuration will be 1S²1P². Now if Hund’s rule is valid, the total spin will be 1, and the cluster will have a triplet ground state. On the other hand, if Al atoms are trivalent, then the valence electron count will be twelve, and the electron configuration within the shell model will be 1S²1P⁶1D⁴. If Hund’s rule is valid, the ground state will be a quintet in this case. Although early works claimed that Al behaves as a monovalent atom in small clusters [12, 40], most recent works by Melko and Castleman [48], and Chauhan et al. [49] have shown that sp hybridization is present even at small sizes. Therefore, we conclude this discussion on Al clusters by noting that although the question of the validity or otherwise of Hund’s rule in this system is interesting, there is no conclusive evidence either way for clusters up to 8 or 9 atoms. For intermediate sizes, Al₁₃, Al₁₄ etc., shell model provides a good description of the electronic structure as shown by Bergeron et al. [14, 15], and Chauhan et al. [49]. However, both theory and experiments suggest that Hund’s rule is not valid, as low-spin ground states are obtained. It is worth mentioning that electronic structure of Al clusters is strongly affected by the geometric structure [45], and at still larger sizes shell model predictions are valid only at a few specific sizes [50].

Clusters have an additional degree of freedom, their atomic structure, that is absent in atoms. This also plays a crucial role in determining their ground state spin multiplicity. This point has been nicely explained through LDA calculations by Khanna et al. [51]. Although this particular work is quite old, by now it is well established that the ground state of the Na₄ cluster is a singlet in a rhombus structure. Khanna et al. found that the optimal rhombus structure has an apex angle (the smaller internal angle) of 52⁰. The triplet has a higher energy in this structure. As the apex angle was increased, the energy of the triplet decreased, and that of the singlet increased. At an apex angle of 76⁰, the two energies became equal, and after that the triplet became the lower energy state. In a perfectly symmetric square structure (apex angle of 90⁰), triplet is the lower energy state.

Fig. 1

Energies of the relevant MOs of Na₄ in the singlet and triplet states in square planar and rhombus structures. With kind permission from [51], Fig. 2

These results can be understood in terms of a competition between crystal-field splitting caused by Jahn–Teller (JT) distortions and exchange splitting of the MOs of the cluster. Energies of the MOs in different structures and spin states are shown in Fig 1. A perfectly square symmetry ensures that the $p_x$ and $p_y$ orbitals in the cluster are degenerate. In the triplet state in this structure, the $p_x$ and $p_y$ states in the $\alpha$ ($\uparrow$-spin) channel are occupied by two electrons. The states in the $\beta$ ($\downarrow$-spin) channel are at a higher energy and are unoccupied. In the singlet state, the $\alpha$ and $\beta$ states are also degenerate, and one each in the two spin channels are occupied. Consequently, there is a gain in exchange energy in the triplet state relative to the singlet. In the rhombus structure (apex angle between 52$^0$ to 76$^0$), the degeneracy between the $p_x$ and $p_y$ states are lifted by an amount that is greater than the exchange splitting in the triplet state. Thus, it is energetically favorable to occupy the $p_x$ states in the two spin channels leading to a singlet ground state. In fact, the partially filled highest occupied molecular orbital (HOMO) in the singlet state of the square structure represents an unstable situation. Our calculations show that after relaxation (within DFT) this structure distorts, and transforms to a rhombus.

To explore the interplay of crystal-field effect and exchange splitting further, Liu et al. [27] also studied a Li$_4$ cluster in a tetrahedral structure. In a perfect tetrahedron, the $p_x$, $p_y$ and $p_z$ orbitals are degenerate. Note that the $p_z$ orbital is removed to a higher energy in the planar square and rhombus structures, and it was not relevant to the discussion. In the singlet state of the tetrahedron, therefore, the HOMO is 1/3 filled (2 electron in 6 orbitals). In the triplet state there is an exchange splitting of the levels, and as a consequence a gain in exchange energy. However, a perfect tetrahedron still leaves the $p_x$, $p_y$ and $p_z$ orbitals degenerate in each spin channel giving a 2/3 filled HOMO in the $\alpha$ channel. A further gain in energy is achieved by a small distortion of the tetrahedron so that the three-fold degeneracy of the p orbitals now breaks into a (2+1)-fold degeneracy. Thus a local minimum is obtained for a distorted tetrahedron in a triplet state.

I would like to emphasize that the net result of this subtle interplay of crystal-field splitting (as dictated by the JT distortion) and exchange splitting is that the Na₄ and Li₄ clusters have global minima that are singlet in a rhombus structure. In fact, Na _n clusters have low spin ground states at all sizes up to n = 20: doublet for odd sizes, and singlets for even sizes [52]. At larger sizes, things could be different. The geometric packing effects become more important at larger sizes, and the role of electronic shell structure in determining the stable clusters diminishes [22, 53]. In such a regime, even alkali clusters may have high-spin ground states as the crystal-field splitting due to JT distortion is small. In fact, around n = 55, DFT calculations suggest that ground states of Na _n clusters have high spins: triplets for even sizes, and quartet for odd sizes. Na₇₁ is also found to have a quartet ground state. [53]. K _n clusters behave in a similar manner [22]. K₅₄ has a quintet ground state in DFT corrected for dispersion interactions; K₅₅ and K₇₁ are quartets. K₅₆ and, surprisingly, K₆₁ have triplet ground states. Although magnetic moments of these clusters have not been directly measured, a good match of the calculated and measured photo electron spectra (PES) of the Na _n cluster anions gives confidence that this could indeed be the case. A direct measurement of a finite moment will settle the issue decisively.

The case of Cs clusters, however, may be different even at intermediate sizes. Theoretical studies indicate that way. The reasons why Cs clusters will be different from the Na clusters are the following. (1) Relativistic effects are important in Cs atoms, but not in Na. Relativistic effects contract the valence 6s orbital of the Cs atom, making it of the same spatial extent as the 5d orbitals. Alongside this, the 6$s \rightarrow 5d$ and $6s \rightarrow 6p$ excitation energies are nearly the same in Cs, and both are ~0.4 eV lower than the $3s \rightarrow 3p$ excitation energy in Na. Therefore, sd hybridization is likely to play an important role in Cs systems. Indeed, significant sd hybridization is found near the Fermi level in bulk Cs [54–56]. There is practically no possibility of any sd hybridization in Na systems as there are no 2d states, and the 3d states are higher in energy. (2) Whenever a new electronic shell gets occupied for the first time in a simple metal cluster, there is a drop in IP. Experiments and theory have clearly established that there are drops in IP between alkali clusters of sizes 8 and 9, and between sizes 20 and 21 [8, 9, 11, 57]. Interestingly, the drops in IP’s in Cs clusters are much smaller than the corresponding drops in the Na clusters [57]. This suggests a weaker role of electronic shells in determining the stability of Cs clusters, and one expects a concomitantly greater role of geometric packing. Therefore, by the same argument as above, Cs clusters much smaller than 55 atoms can have magnetic ground states.

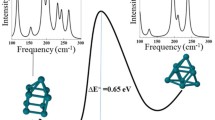
The idea is best explained with the example of the Cs₁₃ cluster as demonstrated by Aguado [58]. According to the shell model, electron configuration of Cs₁₃ (or other 13-atom alkali clusters) is 1S²1P⁶1D⁵. 1D is half-filled. Such clusters with partially filled HOMO levels undergo JT distortions to lift the degeneracy, as we already saw. Such JT distortions leading to low spin ground states are consequences of electron-vibron coupling. The 1D orbital being exactly half filled, prolate and oblate distortions are equally likely for 13-atom alkali clusters. This is found to be true for Na₁₃. Two nearly degenerate structures, one with a C ₂ symmetry and the other with C _s symmetry are found to be the ground states. The C ₂(C _s ) structure can be viewed as oblate(prolate) distorted relative to a more ‘spherical’ icosahedron. Both turn out to be spin doublets. In other words, JT distortions and consequent crystal-field effects win over exchange splittings in Na₁₃ to produce low spin ground states. But if the electron-vibron coupling is weak, one may have a perfectly symmetric icosahedron in high spin ground state. Occupation of all the five 1D orbitals in a single spin channel will make the shape of the electronic charge density congruent with the arrangement of the nuclear charges, thus lowering the electron-nuclear interaction energy. The C ₂ and C _s structures for Na₁₃ and the icosahedron structure for Cs₁₃ are shown in Fig. 2.

Fig. 2

Structures of Na₁₃ having C ₂ and C _s symmetries, and Cs₁₃ having I _h symmetry. Adapted from [58] © Am. Chem. Soc. 2012, and [78] with permission

Electronic structure calculations that Aguado performed [58] on the Cs₁₃ cluster, in fact, support this conjecture. He performed several calculations on the icosahedron (I _h ), C ₂ and C _s isomers. Two different exchange-corrleation functionals were used: the PBE gradient corrected functional, and a non-local correlation functional that describes van der Waals interactions within DFT (vdW-DFT). For both these approaches, he did calculations fixing the spin state to be doublet, and finding the spin state self consistently. Again, for both PBE and vdW-DFT methods, two different basis sets were used: one that included the 5d atomic orbitals, and one that did not. It turned out that both within PBE and vdW-DFT, a perfect icosahedron in the spin sextet state has the lowest energy when the d orbitals were included in the basis. If the d orbitals are not included, the C ₂ structure turns out to have the lowest energy followed by the C _s and the I _h . If the spin was fixed to be a doublet, even inclusion of the d orbitals led to the C ₂ (with vdW-DFT) or C _s (with PBE) structure to have the lowest energy. Thus, effect of the d orbitals in determining the ground state structure and spin configuration is crucial. But more importantly, Cs₁₃ does have a high-spin ground state in a perfectly symmetric icosahedron structure.

Aguado also reported contributions of different terms to the total energy in the sextet and doublet states. The nuclear arrangement was kept fixed at the lowest energy icosahedron structure of the sextet state so that the contribution of the nuclear interactions was the same in both cases. The electron-nucleus interaction energy is 0.127 eV lower in the sextet state. Unlike in an atom, where a higher spin state increases the electron kinetic energy, the kinetic energy was lower in the high spin sextet state. In an atom, there is a single nuclear attractor. Therefore, contraction of the orbitals closer to the nucleus increases the kinetic energy contribution. In clusters, presence of a number of attractors allows the electronic wave function to spread out while taking advantage of the nuclear attraction, thereby reducing the kinetic energy. The electron-electron interaction energy contribution is 0.105 eV higher in the sextet state. The overall result is that the sextet state is 0.124 eV lower compared to the doublet.

Cs₁₃ is a special case because it has an exactly half-filled 1D state. Therefore, once the exchange splitting lifts the degeneracy between the two spin channels, a filled sub-shell (of the majority spin 1D orbitals) is obtained, giving a large gap between the highest occupied and the lowest unoccupied molecular orbitals (HOMO-LUMO gap). But this is obviously not the case at every size. Cs₁₅ is an example that illustrates the point. Cs₁₅ has an electronic configuration 1S²1P⁶1D⁷. The ground state can have total spin of S = 3/2 or 1/2 depending on whether the spin is maximized or not. If the JT distortion is large, one would have a single unpaired spin in the majority spin channel, whereas a large exchange splitting would give a high spin ground state. Aguado’s calculations [58] showed that Cs₁₅ does undergo a JT distortion from the perfectly symmetric Kasper polyhedron of $D_{6d}$ symmetry to a lower symmetry $D_2$ structure. The associated splittings of the orbitals in both spin channels are smaller than 0.02 eV. Compared to this, the exchange splitting between the occupied 1D$_{\alpha }$ and 1D$_{\beta }$ levels in the reference $D_{6d}$ structure is 0.1 eV. Therefore, the JT distortion is unable to drive the cluster to a low spin ground state, and it remains a quartet. At other sizes also, the crystal-field splittings were typically an order of magnitude smaller than the exchange splittings, giving high spin ground states for Cs clusters. The reason for such smallness of the JT energy scale is a smaller electron-vibron coupling in Cs systems compared to Na systems.

This presents us with an exciting situation where clusters containing few Cs atoms, that form an ideal free electron paramagnetic metal in the bulk, is magnetic with the highest possible spin value. Na and K clusters containing ~55 atoms or more may also be magnetic. It would be interesting to have experimental confirmation of these.

Magnetism in Rhodium Clusters

Rh₁₃ cluster

I now come to the topic of magnetism in 4d TM clusters that are non-magnetic in the bulk. I will discuss Rh clusters only, as these turn out to be the most interesting ones. The first indication that small Rh clusters could have large magnetic moments came from theoretical calculations of Reddy et al. [32]. They studied 13-atom clusters of 4d TM atoms Rh, Pd and Ru using DFT. Rh₁₃ turned out to have a moment of 21 μ _B in an icosahedron structure. This result was very surprising and exciting because the per atom moment, 1.6 μ _B , was larger than the moment of 0.56 μ _B in bulk FM nickel. In fact, it was comparable to the moment of 1.64 μ _B per atom in FM bulk Co. The moments on all the individual Rh atoms were aligned, and the outer shell atoms had slightly larger moment than the central atom. Pd₁₃ and Ru₁₃ were also magnetic, but the moments were much smaller in these clusters. Two factors conspired to produce such a large moment on Rh₁₃. Firstly, high symmetry of the icosahedron structure increased degeneracy of the electronic states, producing sharp peaks in the density of states (DOS). In fact, in the non-magnetic Rh₁₃ cluster, the Fermi energy occurred near one of the peaks in the DOS. Secondly, a large number of surface atoms, having low coordination, gives a large moment. In an icosahedron, 12 of the 13 atoms are on the surface.

This path-breaking work prompted Cox et al. [59, 60] to look for magnetism in small Rh clusters in experiments. In a Stern-Gerlach setup, they indeed found all Rh clusters in the size range 12-32 to be magnetic [59]. Some sizes, Rh₁₅, Rh₁₆ and Rh₁₉ in particular, had significantly larger moments compared to their neighbors. In the first work (ref. [59]), Cox et al. reported a moment of $0.88 \pm 0.16$ μ _B /atom for Rh₁₃. It turned out there was a systematic error in their measurements [60]. They corrected this in ref. [60], and the moment on Rh₁₃ turned out to be $0.48 \pm 0.13$ μ _B /atom. Rh₁₅, Rh₁₆ and Rh₁₉ still had larger moments compared to their neighbors. In ref [60] all the Rh clusters up to size 34 were found to be magnetic. In a follow up of their original work, Reddy et al. [61] reported that there are a number of different spin states for icosahedral Rh₁₃ that are very close in energy. At very small inter-atomic distances, the moment on Rh₁₃ is very small. As the distances increase (keeping the icosahedron structure intact) the cluster makes a transition to a state with a total moment of 7 μ _B . With further increase in the distances, a state with 15 μ _B becomes favorable. In fact, this state, at an inter-atomic separation of 2.65 Å, turns out to be the lowest energy state. As the inter-atomic distances are increased further, the cluster goes to a state of 21 μ _B , and this is the state that Reddy et al. reported in their first work [32]. Energy difference between the 15 μ _B and 21 μ _B states was only 25 meV/atom, at the limits of accuracy of their DFT calculations. In a different calculation (using a different basis set), the 21 μ _B state in fact came out to have a lower energy. Reddy et al. also reported the variation of the binding energy per atom (BE) of Rh₁₃ for all spin states from 7 to 23 μ _B  [61]. The variation in BE over such a large range of moments was only 0.1 eV/atom. This clearly shows that different spin states in Rh clusters are very close in energy, and which state comes out to have the lowest energy may be influenced by the choice of the method of calculations. We discuss this point in more detail later. The most important point, despite the mismatch between the calculated and measured moments, is that Rh₁₃ cluster is magnetic.

Let us now look at some of the other important theoretical works on Rh₁₃. After the first theoretical work by Reddy et al. [32] and the experimental work by Cox et al. [59, 60], Jinlong et al. [62] performed a thorough calculation on Rh₁₃. They considered the I _h , cuboctahedron (O _h ), and a low symmetry D _3h structures. The I _h structure turned out to have the lowest energy, and was 0.45 eV and 1.35 eV lower than the D _3h and O _h structures respectively. Let us first focus on the magnetic properties of the I _h structure. Jinlong et al. [62] also found (this work actually preceded ref [61]) competing spin states for Rh₁₃ below interatomic separation of ~2.61 Å. Between 2.54 and 2.61 Å, there are three close-lying spin states with total moments of 7 μ _B , 15 μ _B and 21 μ _B . At 2.56 Å, the 15 μ _B state turns out to have the lowest energy, and this is the global minimum in agreement with ref. [61]. Interestingly, a later work by Bae et al. [63] found a completely different structure to be the ground state for Rh₁₃. We will discuss this later. The 7 μ _B and 21 μ _B states are 0.74 eV and 0.35 eV higher respectively at this interatomic distance. The 21 μ _B state becomes stable only above 2.54 Å, while it is the only stable state above 2.67 Å. Although the 7 μ _B state was found to exist over a large size range below 2.61 Å, it is never the ground state. This point is in disagreement with the results in ref [61] which find 7 μ _B to be the most favorable state below 2.6 Å.

Another interesting aspect of Jinlong et al’s results is that the moment of the I _h cluster is smaller than that of the O _h and D _3h clusters over a large range of interatomic distances below 2.65 Å. Common understanding is that the more symmetric a structure is, the more the degeneracy of the electronic levels, and hence less is the crystal-field splitting. Therefore, the exchange splitting wins, producing large magnetic moments. So a high symmetry structure having low moment is surprising. Jinlong et al. explain this in terms of an energy difference (ΔE) which was defined as follows. For clusters with a partially filled HOMO, which is the case with all Rh₁₃ clusters they studied, ΔE is the energy difference between the HOMO and the closest-in-energy spin-opposite molecular orbital (CSMO), which is the one-electron energy level in the opposite spin channel nearest to the HOMO in energy. This orbital may be occupied or unoccupied. The important point is that the minimum energy re-ordering of the orbitals necessary to change the spin state of the cluster is this difference. ΔE is ~0.5 eV for the O _h and the D _3h clusters, but it is only ~0.05 eV for the I _h cluster. Therefore, the magnetic state of the I _h cluster is changed more easily with change in structure, but the moments on the O _h and the D _3h clusters remain 19 μ _B at all interatomic distances. As a result, for distances below 2.6 Å, moment on the I _h cluster falls below that of the other two.

Bae et al. [63], as a departure from the earlier works, not only considered symmetric icosahedron, cuboctahedron and such structures, but explored other less symmetric structures for Rh₁₃. In fact, a cage structure without any central atom, with a magnetic moment of 17 μ _B , turned out to be the ground state. The icosahedron with 21 μ _B is 0.3 eV higher. An icosahedron with 17 μ _B was also found, and this is only 0.01 eV higher than the 21 μ _B state. Several other close-lying structural isomers and spin states were detected. A centered hexagonal prism-like structure having 11 μ _B is 0.04 eV higher than the ground state. Another prism-like structure having 15 μ _B moment lies 0.08 eV above the ground state. Surprisingly, these authors do not report either the 7 μ _B or the 15 μ _B I _h cluster. This shows that different methods within DFT can produce different energy orderings of structural and spin isomers. I will not get into a detailed discussion of the methods used in different works, which can be found in the original papers.

One aspect common to the works of Reddy et al, Jinlong et al. and Bae et al. is that the calculated moment in the ground state is much larger than that found in the experiments by Cox et al. While the experimental number is $0.48 \pm 13$ μ _B per atom, the value found in the three theoretical works are 1.15 μ _B , 1.15 μ _B and 1.30 μ _B respectively. There could be several reasons for this. Firstly, it is not entirely clear what is the ground state. Refs [61] and [62] considered only some high symmetry structures. Ref [63] did consider other isomers, but given the small energy differences between these isomers and various spin states, that are at the limit of accuracy of the DFT calculations, one cannot be absolutely certain about the ground state. Even if one assumes that the cage structure with 17 μ _B is the ground state, the low lying isomers and spin states, which have lower moments, can very well be produced in the cluster source, giving a lower value of the measured moment. Experimentally, what was measured is the effective moment, related to the true moment on the cluster by the Langevin function, under the assumption that the clusters behave as super-paramagnets [2],

$$\mu _\mathrm{eff} = \mu \left[ \coth {\left( \frac{N\mu B}{k_BT} \right) } - \frac{k_BT}{N\mu B} \right].$$

(3)

In this relation μ _eff and μ are the measured and the true moments per atom on an N-atom cluster. B is the average magnetic field in the Stern-Gerlach apparatus, k _B is the Boltzman constant and T is the cluster vibrational temperature. Any uncertainty in the cluster temperature, which is only known indirectly, can lead to error in the measured moment.

Smaller Rhodium Clusters

Now I discuss results, mostly theoretical, on smaller Rh clusters. Let us start with the smallest size, the Rh₂ dimer. Different theoretical methods give a wide range of values for the equilibrium bond length (d) and the binding energy (BE) for the dimer. Even different calculations using the same exchange-correlation functional in DFT by different authors give different numbers. LDA calculations by Chien et al. [64] give a bond length of 2.27 Å, and BE of 1.6 eV/atom. GGA calculations by the same authors as also by Reddy et al. [61] give d ~ 2.33 Å. Chien et al. found a BE ~1.32 eV/atom, but Reddy et al. found 1.88 eV/atom. Nayak et al. [65] found d = 2.26 Å  and BE = 1.51 eV/atom, again within GGA. Configuration interaction (CI) produced bond lengths over a wide range, d = 2.28–2.86 Å. These methods found a wide scatter in BE also, 0.43–1.05 eV/atom [66–68]. Given this wide spread of the results, it is comforting to note that all these calculations agreed on the ground state spin configuration of the dimer, which is a quintet. Recently, Beltran et al. [69] also found a quintet state using the B3LYP hybrid functional, with a bond length of 2.28 Å, and BE of 0.7 eV/atom.

One would imagine that in such a situation, a comparison with experimental results is the way to decide which method works best. But experiments are also limited for such small clusters. The moment is too small to get an appreciable deflection in a Stern-Gerlach set up, more so because Rh is a much heavier atom than Al. Two experiments have reported values of BE for the Rh₂ dimer. Gingerich et al. [70] found BE of 1.46 eV/atom. But the values of d and the vibrational frequency had to be assumed to get the BE. Wang et al. [71] calculated BE from the measured value of the anharmonic vibrational constant for Rh₂ in an Ar matrix. The value they obtained is 0.7 eV/atom. Whether this is the BE of an isolated Rh₂ dimer, or the matrix affects its properties significantly, is a point to ponder.

For Rh₃, different calculations using LDA, GGA, CI and B3LYP produced ground state structures that are either equilateral (D _3h ) or isosceles (C _2v ) triangles. The bond lengths also varied over a wide range from 2.4 Å  to 2.6 Å. Rather than giving a long list of all the results, I refer interested readers to the original papers and the references in those: [61, 64, 65, 69, 72]. The important point is that the calculations differ on the ground state spin configuration also. Within DFT, both the LDA calculations in refs. [64, 72] find a quartet state. GGAs differ. Nayak et al. [65] found a quartet while Reddy et al. [61], and Chien et al. [64] found a sextet using GGA. In all these calculations the energy difference between the quartet and sextet states is, however, rather small, only a few tens of meV/atom. The CI calculations differ more widely with each other. Das et al. [73] find a C _2v structure with BE of 2.72 eV/atom in a quartet state, but Dai et al. [74] find a C _2v structure in a sextet state with a much larger BE of 3.59 eV/atom.

Again, there are no direct measurements of the magnetic moment of the trimer. The previous calculations were not compared to any experiments. Only recently a couple of joint theory and experimental works have been published. Beltran et al. compared calculated anion PES for Rh _n clusters up to C _2v = 9 to the measurements of Bowen’s group [69]. The one by Harding et al. [75] focuses only on the cation clusters. The anion adiabatic and vertical detachment energies (ADE and VDE) that were calculated in ref [69] depend on the geometry and electronic structure of both the anion and neutral clusters. Compared with experiments, these can indirectly give information about the structure and spin states. Calculated ADE of 1.16 eV for the trimer is in very good agreement with the experimental value of 1.0 eV. This indicates that sextet in an isosceles triangle structure is indeed the ground state of Rh₃.

Rh₄ represents a good example as to how complicated finding out the ground state geometry and electronic state of these clusters can be. The calculations in refs [61, 64], [65] and [72] all agreed that the ground state geometry is a tetrahedron, and the spin state is singlet. Nayak et al. [65] and Reddy et al. [61] calculated the square planar structure also. This was found to have a quintet spin state and was marginally higher in energy. But Bae et al. [63] found the ground state to be a bent rhombus, with the angle of bent nearly 90⁰, in a septet state. Ghosh et al. [76] also found the ground state to be a septet but a tetrahedron. These authors also found a quintet square, and a singlet tetrahedron. These two isomers were nearly degenerate, and only 0.05 eV/atom higher than the ground state. Beltran at al’s [69] B3LYP calculations also produced a septet bent rhombus ground state. Their calculated ADE (1.02 eV) and VDE (1.12 eV) values for Rh₄ anion match closely the second peak in the measured PES [69]. The experimental PES is shown in Fig. 3. In fact, none of the isomers found in this work reproduced the first peak in the PES at 0.8 eV. It is possible that the peak at 0.8 eV is due to electron detachment from a spin excited state of the anion. Given the small energy differences between various isomers and spin states, it is difficult to identify the precise reason as the electronic structure calculations are always limited by the approximations for the exchange-correlation energy. Nevertheless, this shows the complexity of these clusters.

Fig. 3

Photoelectron spectra of Rh _n anion clusters. Reprinted from [69] with permission from Springer

A number of authors have studied different size ranges for Rh clusters larger than Rh₄. Here I will only mention the most important aspects keeping in mind that magnetism is our primary focus. For Rh₅, GGA and B3LYP calculations find the sextet and octet spin states in the square pyramid structure to be very close in energy [61, 63, 64, 69, 76]. The energy difference is only a few tens of meV. Different LDA calculations produce either a triangular bi-pyramid quartet [72] or a square pyramid sextet [64] as the ground state. The situation is not entirely clarified even after comparison with experiments. For the anion, Beltran et al. [69] find a square pyramid septet to be the lowest in energy. However, the calculated ADE and VDE values for both the square pyramid and the triangular bi-pyramid are in reasonable agreement with the measured values, making a unique identification difficult.

For Rh₆ Reddy et al. [61] predicted a singlet octahedron to be the ground state, though the septet was very close, only 0.01 eV/atom higher. GGA calculations of Bae et al. [63] find a septet, but in a triangular prism geometry, to be the ground state. The septet octahedron is only 0.01 eV/atom higher. Beltran et al’s [69] B3LYP calculations produce a septet in an octahedron structure. Jinlong et al’s [72] LDA calculations produce an octahedron singlet ground state, and the septet is 0.07 eV/atom higher. Such close energies for two very different spin states again illustrates the complexity of this problem. But the B3LYP ADE and VDE values are in very good agreement with the experiments, giving confidence about the septet octahedron ground state.

The ground state multiplicity of Rh₇ varied from 10 to 14 in different calculations [61, 63, 69, 72]. B3LYP calculations [69] produced a pentagonal bi-pyramid of multiplicity 14 as the ground state. But the calculated ADE (2.33 eV) and VDE (2.74 eV) values for this structure do not match the experiments (2.1 and 2.2 eV, respectively) very well. Curiously, the calculated values from the capped prism structure (multiplicity of 12 and 13 for the neutral and anion), ADE 2.07 eV and VDE 2.10 eV, match the experiments much better, although this isomer is ~0.3 eV higher for the neutral, and ~0.5 eV higher for the anion. It is possible that the higher energy isomer was produced in the cluster source due to kinetic reasons.

For clusters larger than Rh₇, Reddy et al. [61] did not report the multiplicities directly. Rather, they plotted the magnetic moment per atom for the ground states with increasing size. Reading their plot, it seems that the ground states they found had multiplicities 9, 10, 3, 4, and 9 for Rh₈ to Rh₁₂. Bae et al. [63] found a cube with multiplicity 13 as the ground state for Rh₈. A low coordination structure like a cube turning out to be the ground state is quite surprising. Jinlong et al’s [72] LDA calculations produced a tetrahedron with multiplicity 11. Beltran et al. [69] found a bi-capped octahedron with multiplicity 13 as the ground state. Calculated ADE (2.17 eV) and VDE (2.20 eV) for this structure match the experimental results (2.1 eV and 2.3 eV, respectively) very closely. Therefore, one can be confident that the ground state for the neutral is indeed a bi-capped octahedron of multiplicity 13. Bae et al. [63] found a capped cube of multiplicity 14 for Rh₉, whereas Beltran et al. [69] found a capped square anti-prism of multiplicity 18. With this structure, the calculated VDE (2.42 eV) matches the experimental result (2.4 eV) almost exactly. Rh₁₀ turned out to have a triplet ground state in Reddy et al’s [61] GGA calculations. Jinlong et al. [72], in LDA, obtained a septet ground state which was nearly degenerate with a singlet. Bae et al. [63] found a ground state multiplicity of 15. Reddy et al. [61] found a quartet ground state for Rh₁₁, as already mentioned. But Bae et al. [63] found it to have a multiplicity of 16. Rh₁₂ turned out to have a ground state of multiplicity 13 in Bae et al’s [63] GGA calculations. But Jinlong et al’s [72] LDA calculations found the ground state to have multiplicity 9. The singlet, and a state of multiplicity 15 were within a few tens of meV/atom of the ground state.

One can directly compare the calculated moments with the measurements of Cox et al. [60] for Rh₉ to Rh₁₂. The measured moments are reproduced in Table 1. Reddy et al. showed [61] that except for Rh₉ and Rh₁₂, their calculated moments do not match the measured moments. For Rh₉ none of the other calculations match the experiments. For Rh₁₀, Jinlong et al’s [72] LDA results (multiplicity 7) match the experiments within error bars. Reddy et al’s calculated moment is too small, while that obtained by Bae et al. is too large. For Rh₁₁ neither Reddy et al’s nor Bae et al’s calculations match the experiments. Reddy et al’s GGA and Jinglong et al’s LDA calculations match the experiments well for Rh₁₂. Bae et al’s calculated multiplicity is too large.

Table 1 Measured magnetic moment per atom (in μ _B ) for Rh₉-Rh₁₂ from Ref. [60]

The above discussion makes it clear that it is difficult to unequivocally identify the ground state of Rh clusters in many cases. There are several reasons for this. At each size, there are different structural and spin isomers very close in energy. Different theoretical methods often produce different energy orderings of these states. Sometimes, theoretical results from different isomers match experimental data for different physical quantities. For example, for Rh₉, ADE and VDE values for a capped square anti-prism structure [69] calculated with B3LYP match the experiments almost exactly. But the ground state multiplicity (18) does not match the results of Stern-Gerlach experiments. On the other hand, Reddy et al’s [61] calculated moment matches experiments, though the structure they found was very different. For Rh₁₁, none of the calculations matched the measured magnetic moment. Interpretation of the Stern-Gerlach experiments has its complications as well. Apart from the difficulty of knowing the exact vibrational temperature, close energy ordering of various isomers can lead to production of not just the ground state, but other clusters in the beam. Since the moment is estimated from the deflection of the cluster beam, which in turn depends on the moment on the clusters, presence of clusters with different moments in the beam leads to large error bars in the experiment [60], making experimental determination of the ground state moment difficult. Spin-orbit coupling can be significant for the 4d elements. But the moment on the clusters are estimated using Eqs. 2 and  3 assuming a super-paramagnetic behavior of the spins, and neglecting the orbital moment altogether.

Summary

I conclude this review with the following note. Experimentally, except for the very small Al clusters studied by Cox et al. [36], all other simple metal clusters are found to have the lowest possible spin in their ground states. Even in the Al clusters, the exact value of the spin could not be determined experimentally. Among the theoretical calculations, Rao and Jena’s [40] results largely agree with the experiments. But those of Akola et al. [44] do not. Most importantly, one cannot say for sure whether Hund’s rule is responsible for the magnetic ground states in these clusters because firstly, the valence of Al atoms in such small clusters is still a debated issue, and secondly, whether electrons in these clusters follow the shell model at all is not clear. Without clarity on these two points, one does not know what the highest possible spin state is. Alkali clusters present an interesting situation. Theoretical calculations suggest that one may have magnetic ground states in these clusters although the bulk is an ideal example of a PM metal. Measurements may pose challenges, though. For example, assuming that Cs clusters behave as super-paramagnets, a quick estimate shows that deflection of a Cs₁₃ cluster in a typical experimental set up (B = 1.2 T, vibrational temperature = 25 K) will be ~0.15 mm, which is at the limit of experimental resolution [77].

As for magnetism in small Rh clusters, the technical difficulties notwithstanding, it is conclusively found, both in theory and experiments, that these are magnetic, although the bulk metal is non-magnetic. This is an effect of low coordination at small sizes. As the cluster size increases, the per atom moment decreases rapidly [60]. By Rh₆₀, the moment is undetectable within experimental resolution. Discovery of large magnetic moments on clusters of non-magnetic metals have definitely given us new insights into the phenomenon of magnetism.