Introduction

Advances in technology in combination with a push for empirically justified outcomes [e.g., No Child Left Behind Act of 2001 (2002); Individuals with Disabilities Improvement Act of 2004 (2003); What Works Clearinghouse] have resulted in renewed research in single-case effect sizes (SCESs). The purpose of SCESs is to supplement visual analysis with a universally understandable metric that is resistant to bias and can potentially be combined across studies or individuals within a study. Recent iterations of these metrics attempt to address the observed complexities and assumption violations inherent in statistical analysis of single-case data (SCD) including autocorrelation, slope, non-normality, and random growth trajectories across participants (e.g., Maggin et al. 2011; Manolov and Solanas 2013; Parker et al. 2011b; Shadish et al. 2013). However, at the expense of addressing these data features, these newer procedures incur novel assumption violations readers may not be familiar with.

With this in mind, the current study has two purposes. The primary purpose is to explicitly outline assumptions that pertain to SCESs, using a handful of these newer metrics to anchor this discussion, and to strongly encourage readers to review assumptions in their own work so as to increase the validity of their findings. These assumptions generalize to many other SCESs that are not discussed presently. The secondary purpose of this paper is to address issues of scale and distribution by examining this sample of metrics more closely while accommodating certain assumption violations.

Recent Developments in SCESs

Suggestions for the extension of statistical analysis to SCD have been forthcoming for over 40 years, however, few, if any, methods have achieved both durability and empirical robustness (Allison and Gorman 1993; Shadish et al. 2008; Wolery 2013). Present in the literature are methods with foundations in non-overlap criteria (e.g., Ma 2006; Parker et al. 2007, 2011a), multiple regression (e.g., Allison and Gorman 1993; Gorsuch 1983), econometrics (Manolov and Solanas 2013), the modeling of autocorrelation (e.g., Gotman and Glass 1978; Swaminathan et al. 2010), and multi-level modeling (e.g., Shadish et al. 2013; Van de Noortgate and Onghena 2003). Such variety speaks to the continued philosophical issues regarding how single-case data should be interpreted and the difficulty in selecting which undesirable data characteristics should be controlled for, expending what is often a small pool of degrees of freedom (e.g., number of observations of behavior).

Nonetheless, more focused discussion of what a robust SCES should accomplish (e.g., Horner et al. 2009; Wolery 2013) has encouraged the development of contemporary methods that potentially control for multiple threats and may be more readily interpretable. These techniques were designed to accommodate violations of basic parametric assumptions. Non-normality is frequent in SCD (Solomon 2014) as is heterogeneity. The violation of independence—one of the defining characteristics of SCD—often results in baseline trend contributing most often to false positives when visual analysis (Mercer and Sterling 2012) or mean-level approaches are applied. A violation of independence also leads to potential autocorrelation (i.e., serial dependency), typically resulting in inflated summary statistics and overly optimistic visual analysis (Busk and Marascuilo 1988; Jones et al. 1978; Manalov and Solanas 2008; Matyas and Greenwood 1990; Shadish and Sullivan 2011). Autocorrelation is defined as how well a dataset can be explained by a lagged version of itself; one observation ideally does not predict the magnitude of the next datum point (Bence 1995; Huitema and McKean 1991). The finding that visual analysis is influenced by these violations further justifies the use of SCESs as a supplement.

Regardless of the positive attributions of newer procedures, corrective techniques still must fulfill an array of data assumptions depending on the procedure. A review of assumptions guides selection of the statistic and can influence the confidence placed in subsequent calculations and their interpretation. Assumption violations, particularly when paired with small sample sizes like those typically found with SCD (Shadish and Sullivan 2011), can have a significant effect on resulting parameters (Grissom 2000; Lix et al. 1996; Manalov and Solanas 2008). In our experience, we have found few researchers have provided any rationale for their selection of SCES beyond describing the theoretical virtues of the parameters themselves, overlooking the nature of the data to which the estimator is being applied. Several of these articles, including single-case meta-analyses, have appeared in the Journal of Behavioral Education.

Assumptions Related to SCES Estimation and Interpretation

Throughout this article, we draw upon a large database of synthesized data. This convenience sample included populations of studies focused on school-wide positive behavior support, teacher performance feedback, math interventions, and classroom-based individual behavior interventions originally used in Solomon et al. (2012a, b), Poncy et al. (in press) and Solomon (2014), respectively, for the purpose of SCD synthesis (see Table 1). We direct readers to these sources for further information on methods for study inclusion. All datasets were updated specifically for this study in January of 2014 using identical methods to those reported. We also included an additional five studies focused on individual elementary-level reading interventions, amounting to another 15 graphs. These articles were selected to broaden our overall pool and were the first five peer-reviewed articles that utilized a single-case framework focusing on elementary reading acquisition that appeared on EBSCO.

Table 1 Summary of included studies
Full size table

We begin with one of the most venerable effect sizes, Cohen’s d, which, despite limitations when applied to SCD, has been used frequently for single-case analysis (Beretvas and Chung 2008). Shadish et al. (2008) argued that these drawbacks are different, but no greater, than those of some more recently published techniques. Cohen’s d requires traditional group assumptions of basic parametric tests, and these conventions carry over to many of the more elaborate SCESs subsequently developed and reported presently.

Cohen’s d

Cohen’s d is a parametric effect size that standardizes the average difference between two independent groups, or in the single-subject case, between two adjacent phases. Cohen’s d assumes normality, homogeneity (constant variance across phases), and independence. Because independence is violated, researchers should assess its effect by evaluating data trend and autocorrelation. Cohen’s d for SCD can be defined as the difference between two adjacent phases in original scale units, divided by a within-phase standard deviation (SD) term, where \( d = (\bar{X}_{B} - \bar{X}_{A} )/S^{*} . \) S* can be a pooled term, where the SD of both phases is combined, which will be more precise when homogeneity has been fulfilled and can also be adjusted for small sample bias, resulting in Hedges’ g (see Borenstein 2009). S* can also be defined as the SD of Phase A when homogeneity is violated, resulting in Glass’s Δ. Busk and Serlin (1992) refer to Δ in the SCD case as the “no assumption effect size” (NAES). A review of the literature suggests the NAES was popular up until several years ago when nonparametrics appear to have increased in prevalence. Despite its title, the NAES is not assumption free and assumes normality and independence, while d also assumes homogeneity. It appears Busk and Serlin (1992) presented this statistic with the belief that researchers would frame interpretation of the effect within the limits of violations of non-normality, although this generally has not been the case.

Conditions for Use

If normality is violated, Cohen’s d may not be appropriate. Non-normality can be assessed using descriptive estimates of skew and kurtosis. Q–Q plots, boxplots, and histograms can also be visually inspected (see “Appendix”). Homogeneity will determine the form used (d or Δ), which can be tested with a Levene’s test. If moderate-to-high levels of trend are present, a trend-controlled procedure will be more appropriate. The standardized trend value and its significance can be inspected using a basic regression package (see “Appendix”) available in nearly all spreadsheet and statistics programs. Finally, if autocorrelation is present, d will be biased. A general rule-of-thumb for moderate autocorrelation is .20.

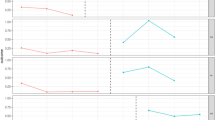
As an example, we generated random samples from two normal, homogenous population distributions representing phase A and B of a simple single-case design, with baseline mean = 2.71, SD = 1.38, and intervention mean = 4.20, SD = .77 (Fig. 1a). In this case, it is known that the population distributions for both phases were normal, homogenous, and without trend or autocorrelation. We calculate Cohen’s d, which equals 1.33. For all examples described presently, the quartile distributions under the “Interpretative Guidelines” section of this article are referenced. These benchmarks show that this value would be considered small.

Fig. 1
figure 1

Sample AB contrasts. a Data for Cohen’s d, b data for NAP, c data for GLS, d data for MPD

Full size image

Tau-U & Non-overlap of All Data (NAP)

Tau-U is a nonparametric statistic representative of the popular family of non-overlap procedures, originally published in Parker et al. (2011a). Such procedures are desirable for their immunity to threats to normality, higher power when normality is violated, and ease of calculation. Tau-U accounts for trend by taking advantage of the compatible additive properties of the overlap matrices used to calculate the Kendall Rank Correlation (KRC; Kendall 1970) and the Mann–Whitney U test of group/phase dominance. Because slope is measured as overlap within phase, and only reflects rising or lowering datum points, it is defined as monotonic slope. The procedure for comparing adjacent phase differences with Phase A slope controlled can be summarized as follows:

  1. 1.

    Sum both how many phase B datum points are greater than Phase A datum points (U L1) and how many Phase B datum points are less than Phase A datum points (U S1), where S AB  = U L1 − U S1 and N AB is equal to all overlap comparisons for S AB .

  1. 2.

    Sum both how many Phase A datum points are greater than all prior Phase A points (U L2) and those that are inferior (U S2), where S A  = U L2 − U S2 and N A is equal to all overlap comparisons for S A .

  1. 3.

    Tau = (S AB − S A )/(N AB  + N A ) and is a proportion between −1 and 1.

NAP, originally published in Parker and Vannest (2009), is calculated by computing step 1 as described above and then dividing S AB by N AB . In other words, NAP is equivalent to Tau-U absent trend control (Parker et al. 2011a) and is a nonparametric alternative to Cohen’s d. NAP, and the many other non-overlap procedures that make use of all datum points, such as the Percent of All Non-Overlapping Data (PAND; Parker et al. 2007), were intended to improve upon the Percent of Non-Overlapping Data (PND; Scruggs and Casto 1987). Although PND remains popular due to its ease of calculation (Beretvas and Chung 2008; Scruggs and Mastropieri 2013), researchers have warned of the severe limitations of this metric and typically do not recommend its use (e.g., Allison and Gorman 1993, 1994; Parker et al. 2007; Shadish et al. 2008; White 1987). NAP can be understood within the Common Language Effect Size framework, where .5 is equal to no effect (chance overlap), any value >.5 is equal to a positive effect, and any value <.5 an undesirable effect (Parker and Vannest 2009).

A critical issue pertaining to non-overlap procedures is one of validity (Wolery et al. 2010). At the expense of overcoming non-normality, nonparametric approaches are restricted to an ordinal interpretation. In Fig. 2, the difference in leaving one’s seat per instructional unit across phases may have little clinical value; however, any nonparametric ESs would be at an absolute maximum (e.g., 1). Academic interventions in particular are probably incompatible with such techniques, as the magnitude of improvement, a ratio metric, is of primary interest. However, numerous such academic intervention studies and meta-analyses have applied non-overlap procedures. In our convenience sample of math and reading data, 46 % of reviewed phase contrasts hit the maximum NAP ceiling of one, and as Wolery et al. (2010) observed, it is unlikely all these studies yielded similar effects. The researcher must consider whether non-overlap can preserve the validity of the behavioral response.

Fig. 2
figure 2

Loss of the interval scale with non-overlap

Full size image

Most non-overlap procedures are also vulnerable to high levels of autocorrelation, although tend to be more robust than their traditional parametric counterparts (Parker et al. 2011a). Serial dependency >.20 may visibly distort Tau-U (Parker et al. 2011a), and this level of autocorrelation is fairly common with SCD (Busk and Marascuilo 1988; Shadish et al. 2013; Solomon 2014).

The subtraction of overlap matrices also has drawbacks unique to Tau-U. Because phase A overlap is subtracted from AB phase overlap (recall the numerator, S AB  − S A ), and phase B has a maximum amount of overlap comparisons with phase A equal to N A  × N B , the monotonic slope control is confounded with phase B length. As an example, if one had three baseline points along a positive linear trajectory, S A equals three. If the intervention phase had three points, all of which were superior to all baseline points (S AB  = 9), Tau-U is (9 − 3)/(9 + 3) = .5. If the intervention phase had five superior points and nothing else was changed (S AB  = 15), Tau-U equals (15 − 3)/(15 + 3) = .67. Therefore, Tau-U’s ceiling is a function of phase length. This will limit inter-study comparisons, such as is typically done in meta-analysis. Tau-U can be adjusted to include phase B trend (Parker et al. 2011a)—another potentially desirable property of an intervention—where Phase B trend is comprised of a third additive overlap matrix and Tau-U = (S AB  + S B − S A )/(N A  + N B  + N C ), although the ceiling will still not be consistent across studies.

Conditions for Use

In selecting a nonparametric estimator, presumably because there is either direct or theoretical evidence for moderate-to-severe non-normality, researchers should first consider whether non-overlap could reflect substantive treatment goals. Second, trend should be evaluated. If trend is significant, Tau-U or a parametric trend-controlled procedure may be more appropriate. If autocorrelation is highly elevated, an autocorrelation-controlled method may be more appropriate.

As an example, in Fig. 1b, we provide sample data for an AB contrast. These sample data were drawn from a similar population as our previous example, except positive skew of 1.80 was introduced to both phases. d would mischaracterize the effect, so we calculate NAP, which in this case is .94. This value is toward the upper limit of the metric’s scale and would be considered medium to large.

Generalized Least Squares (GLS)

The goal of GLS is to estimate an unknown parameter—in this case a Lag-1 autoregressive term (AR1)—and model it in the linear regression error term. In doing so, GLS controls for autocorrelation that otherwise may result in a bias of the resulting parameter. The prospect of cleaning autocorrelation from SCD has been proposed before (see Gotman and Glass 1978); however, Swaminathan et al. (2010) offered a recently published method, an adapted version of GLS that also controls for trend, which initially appeared in a technical report to the Institute of Educational Sciences. The procedure is summarized in the peer-reviewed literature by Maggin et al. (2011) as:

  1. 1.

    Model AR1 using the Cochrane–Orcutt (CO) procedure. The CO models serial dependency in observed residuals around the time series Ordinary Least Squares (OLS) regression line (ρ) absent phase identification, and both y- and x-axes are subsequently adjusted by ρ.

  1. 2.

    Calculate a regression line between the AR1 corrected baseline data (β 1*) and time, and the AR1 corrected intervention data (β 2*) and time. Project β 1* through the intervention phase. The CO can be repeated if residual ρ remains large as indicated by the Durbin–Watson test.

  1. 3.

    Subtract each projected datum point along β 1* from its respective β 2* datum point at each observed time point. Averaging these values results in the final statistic, which is the mean difference of the data space between two regression lines.

The resulting statistic is unstandardized, which restricts researchers to comparisons across identical metrics. Maggin et al. (2011) offer the suggestion that the final output be divided by the scatter about the phase regression lines, resulting in a standardized value somewhat similar to a Cohen’s d. Absent any formal guidelines, we computationally defined this scatter using a simple pooled error term, \( SE_{B1 - B2} = \sqrt {(SE_{B1} )^{2} + (SE_{B2} )^{2} } , \) where \( SE_{B1} \) and \( SE_{B2} \) are equal to the average scatter around the individual OLS regression lines (Cohen et al. 2003). The potential issues with this standardization are not clear and have yet to be resolved. For example, the projected trend line has no residual error, although the intervention trend line does, creating potential estimation issues.

Parametric regression techniques which employ a trend control, including the GLS, can result in implausible scenarios were researchers must deal with regression lines that intercept the x-axis before the experiment has terminated, resulting in negative levels of projected behavior (Parker et al. 2011a). We define this presently as the intercept assumption. In Fig. 3, an OLS baseline trend is projected through the intervention phase and each intervention point compared to its hypothetical point absent treatment, which is the basis for several published procedures. In this case, the last two datum points would be compared to the implausible y-axis values of −1.7 and −3.67 incidents of behavior, respectively, inflating the effect. In our convenience sample, this assumption was violated 22 % of the time for the GLS, making such a case fairly common. If negative forecasted values emerge, the researcher must judge whether the problem is severe enough to terminate the analysis in favor of an alternative technique. Tau-U, which controls for monotonic trend, is not vulnerable to the intercept assumption.

Fig. 3
figure 3

Violation of the intercept assumption

Full size image

All parametric trend-controlled procedures carry the assumption of linear trend absent intervention. In other words, it must be assumed that—absent an intervention occurring—baseline trend levels would have continued unaltered through the intervention condition in a linear trajectory (Parker et al. 2011a). The cumulative distribution plots of Fig. 5, which graph SCESs for our entire sample, highlight a potential outcome of violating this assumption. Cohen’s d, a level difference metric, had only four negative values, whereas at the other extreme, GLS had 23 negative outcomes. A negative effect would certainly alter recommendations for a particular intervention, if not the prospect of publication entirely. If growth would not have continued post-baseline with the same degree of slope in these studies, then these procedures become overly punitive. For example, Solomon (2014) found that baseline OLS trend levels for math intervention studies were generally higher than those found in other fields, likely the result of practice effects on the measurement probes. Such practice would probably continue to yield growth given current literature on the effects of explicit timing interventions (e.g., Poncy et al. 2010), making a trend control more appropriate. It may be less appropriate to assume that, for example, a student’s on-task behavior would continue to improve in a linear fashion absent intervention.

The GLS, being a parametric estimator, assumes homoscedasticity and normality of the residuals. GLS carries with it the assumption that the true value of ρ is constant across phases or subjects, although there is no direct test for this because autocorrelation is not precisely estimated with small samples. Finally, it is worth noting that there currently is no statistics program that readily calculates the GLS as described by Maggin et al. (2011).

Conditions for Use

Researchers who use trend-controlled parametric procedures should first test for non-normality, heteroscedasticity, and negative projected y-axis values. Researchers should also consider whether projected values represent a plausible scenario had intervention not occurred. If not, level difference approaches will be more valid. Finally, researchers will want to examine autocorrelation for each phase; values should be, at the least, in the same direction and of moderate size for the GLS.

In Fig. 1c, we have taken our data from Cohen’s d and introduced heavy autocorrelation of .40 to raw datum points. d is now upwardly biased, d = 1.70. We respond by calculating the GLS, which equals −1.69. Due to the cleansing of both trend and autocorrelation, our standardized value actually suggests a medium-sized negative effect, highlighting several issues previously discussed.

Mean Phase Difference (MPD)

The MPD (Manolov and Solanas 2013) is similar in principle to the final two steps of the GLS, in that the goal is to project a baseline linear trend and remove that trend from intervention phase data. The MPD calculates linear trend line by employing differencing—a well-known concept in economics—making the procedure unique. Differencing limits the researcher to examination of linear trend, whereas the GLS and other parametric techniques can be modified to examine curvilinear trend, although we have observed few published examples of such. The MPD is more robust to individual outliers while preserving the parametric properties of the estimator. As described in the calculation steps outlined below, differencing is also easily accomplished using a spreadsheet program such as Microsoft Excel. The MPD can be summarized as follows:

  1. 1.

    Calculate a differenced baseline trend by subtracting each baseline datum point from each subsequent baseline datum points (e.g., X 2 − X 1, X 3 − X 2, X 4 −X 3, …, X k − X k−1). Average these values to calculate the slope of the differenced trend line.

  1. 2.

    Using this slope, project the differenced baseline trend through the intervention phase.

  1. 3.

    Subtract each projected point from each actual intervention datum point and average. This results in the unstandardized MPD.

Like the GLS, the standardization of the MPD is not clear and the intercept assumption can be violated. Interestingly however, in only 6 % of our sample did this violation occur for the MPD, in comparison with the 22 % for the GLS. The procedure is parametric, and therefore, standardized values are vulnerable to heteroscedasticity. With no built-in mechanism to control autocorrelation, this also is an assumption, although removing trend will typically reduce autocorrelation to some degree, because trend and autocorrelation are correlated (Yue et al. 2002). Manolov and Solanas (2013) also noted that controlling for both autocorrelation and trend within the same model, as is done with the GLS, might overcorrect both problems, resulting in a loss of sensitivity. Shadish et al. (2008) also suggested that, sample sizes typically being small in SCD, the presence of absolute ρ may be a random artifact of the data. Manolov and Solanas (2013) also demonstrated that the MPD is robust to moderate levels of autocorrelation.

Manolov and Solanas (2013) observed that phase B sample size might confound parametric trend-controlled statistics that measure the data space between two regression lines, which includes the MPD and the GLS. The authors reported to be working on a more appropriate standardization procedure that addresses this issue. In Fig. 4, we provide an example of this concept using OLS regression, where the average difference between the regression lines for the first three datum points (dashed arrows) is \( \bar{X} \) = .92. However, if we were unsatisfied with this value, we could extend the experiment through the next three datum points (solid arrows), and the difference is now \( \bar{X} \) = 2.56. This duration confound is neither exclusive to single-case designs nor the MPD/GLS. Any repeated measures design phase—group or single case—can be extended beyond original intent to exaggerate differences between levels of the IV, creating a higher likelihood of significance and the visual illusion of greater effectiveness of the target treatment. However, given the method of calculation, the GLS and MPD are particularly vulnerable. It is recommended that researchers either compare across interventions, whether it be within or across studies, if the duration of those experiments are generally equivalent, or account for time in some way, whether this be defined by observation points along the x-axis or, more precisely, by total instructional minutes of intervention (Cates et al. 2003; Joseph and Schsiler 2007; Poncy et al. in press).

Fig. 4
figure 4

Intervention duration as a confound

Full size image

We present the MPD because it is similar to the other metrics discussed (e.g., a single parameter that controls for trend); however Manalov and Solanas earlier presented a two-part effect estimator entitled the “slope and level change” (SLC; Solanas et al. 2010). The differenced slope of phase B minus the differenced slope of phase A comprises one element. The Phase B mean minus the phase A mean with both phase A and phase B trend controlled equals the second element. Separate estimation of slope and level differences avoids several issues, including the intercept assumption and confounds with study duration (Beretvas and Chung 2008). Similar two-parameter summaries could also be calculated using OLS regression, which would be more sensitive when normality is fulfilled and there are no outliers, or using nonparametric/non-overlap procedures similar to Tau-U (see Parker et al. 2011a), which would be more appropriate when normality is violated.

Recently proposed techniques for the use of multilevel modeling estimate slope and level changes separately and simultaneously, can accommodate alternative distributions, and have the added benefit of providing a single, flexible, summary for all study participants (Ferron et al. 2009; Shadish et al. 2013). Such models can also include interaction terms (trend × phase). Multilevel models have a higher power requirement (Shadish et al. 2013), require multiple subjects, typically utilize more specialized software, and require a background in advanced regression applications.

Conditions for Use

The MPD should be considered when non-normality is violated; however, maintaining an interval or ratio difference is important when there is evidence for linear trend in the data. If curvilinear trend is found, the MPD is not appropriate. Heteroscedasticity across phases should be evaluated and if high, the procedure avoided or results given less weight. Like the GLS, if the intercept assumption occurs, the procedure should be terminated in favor of the separate estimation of slope and level. Although robust against autocorrelation, high levels may warrant an alternative procedure.

In Fig. 1d, we use our skewed data for which we calculated NAP. However, a consistent trend over the baseline condition of .20 units/session and an intervention trend of .35 units/session have been introduced. Ignoring trend, d = 2.18. We calculate the MPD, with a differenced slope value for baseline of .22, and the standardized MPD = .25, a very different outcome than the mean-level approach. This effect would be considered small.

Summary of Assumptions

We have outlined some key assumptions of several extant SCESs, which we summarize in Table 2. In Table 3, we provide a basic guide for evaluating these assumptions using common approaches. These assumptions have rarely been reviewed in prior SCD literature, and we stress the need to account for them before selection of SCES and interpretation of results. As discussed, this may include normality (including floor and ceiling effects), homogeneity/homoscedasticity, experimental duration, trend and linearity, autocorrelation, and potential intercept violations. Many SCES may still be robust in the face of modest violations, although more inquiry is needed to delineate these nuances and researchers are advised to take a conservative approach.

Table 2 Summary of assumption requirements for described effect sizes
Full size table
Table 3 Various methods for reviewing assumptions
Full size table

Interpretative Guidelines

We now move to another facet of interpretability. Presuming assumptions are met, researchers need some context for explaining the size of the effect. Effect sizes with understandable distributions that lend to clear interpretation are most desirable. Such benchmarks are the well-known case of parametric large-N procedures, such as Cohen’s d (.2, .5, .8) and r (10, .30, .50) for small, medium, and large (Cohen 1988); however, there is no reason they should apply to the single case, largely because they are not drawn from the same sampling distribution. We have come across several recent published works where authors have mistakenly recommended group design benchmarks for single-case use, albeit usually encouraging caution. There also may be a misunderstanding that because the MPD and GLS result in a d-like statistic, they can be combined with group design statistics.

Model Generation

The assumptions discussed above were reviewed when constructing benchmarks. To preserve as much of our sample as possible, studies with very high levels of non-normality (skew or kurtosis <−4 or > 4), and high levels of autocorrelation among the raw values (ρ > .4) were removed for the parametric procedures (MPD, Cohen’s d). Graphs with high autocorrelation for the nonparametric procedures (Tau-U, NAP) were removed, as were graphs with non-normality for the GLS. We then averaged graphs within studies. To increase precision, we only reviewed studies with at least 15 datum points and five points per phase for the GLS, which Manolov and Solanas (2013) found to be acceptable. This is a more conservative process than has been utilized in prior studies, which typically report benchmarks without regard to assumption violations or overrepresentation of graphs from certain studies. This makes the current summary unique, although parallels are drawn to prior reports when appropriate. To avoid a confound with study duration, averages were not weighted. Finally, quartile estimates were bootstrapped to increase benchmark stability.

Benchmark Comparisons

Benchmark summaries are reported in Table 4. Negative results were removed to enhance interpretability and the sign of the effects adjusted to reflect the hypothesis of the experiment. Cohen’s d yielded the most uniform intervals. Benchmarks (1.81, 2.44, 3.55) were far greater than Cohen’s traditional benchmarks. The MPD also showed larger values relative to traditional benchmarks and positive skew, although values were more conservative than those of Cohen’s d. Among these three procedures, the GLS appeared to have quartiles that most resembled traditional benchmarks, but were still far greater. Tau-U yielded slight negative skew, although benchmarks stayed away from the scale’s potential range limits. The 3rd quartile of NAP was virtually at the range limit of the scale (Q3 = .98), similar to findings of Parker et al. (2011a, b) and Peterson-Brown et al. (2012), again highlighting issues with ceiling effects with NAP and other non-overlap procedures. Bootstrapped confidence intervals yielded moderate variability, particularly for the first quartile of d and the third quartiles of the parametric procedures, suggesting a certain amount of instability with these metrics across sampling iterations.

Table 4 Bootstrapped distribution benchmarks by SCES and confidence intervals
Full size table

Distribution of SCESs Across Studies

To further highlight differences in these distributions, we graphed our findings in the form of cumulative distribution plots (Fig. 5). As Parker et al. (2011a) noted, ideally these plots are uniform, indicating sensitivity across a wide range of effects. Tau-U yielded the most uniform CPD, with the densest cluster of scores falling between .35 and .6. This distribution was similar to that originally presented in Parker et al.’s (2011a) presentation of Tau-U. In contrast, NAP showed a significant ceiling, where the top 30 % of scores were nearly indistinguishable, again consistent with previous findings. The difference between these graphs is explained purely by the inclusion of monotonic trend, the implications of which were discussed previously.

Fig. 5
figure 5

Cumulative probability distributions of SCESs

Full size image

The MPD yielded a relative normal distribution except in the right tail, with sharp increases in scores after the 80th percentile. The GLS demonstrated a less desirable distribution, with significant kurtosis, and Cohen’s d yielded a more ideal distribution, with slight positive skew. The most extreme positive outlier distorts the plot.

The take-home message for researchers is that Tau-U yielded ideal sensitivity across studies, although researchers must be aware of ceiling effects, as described earlier, complicates this otherwise straightforward finding. Among the parametric procedures, Cohen’s d yielded relatively optimal sensitivity, followed by the MPD and then the GLS, although distributions were not ideal for the MPD and especially the GLS. Researchers should know that if using the GLS or the MPD, study results that appear different from visual inspection might yield similar ESs. This is particularly so for the GLS, which may overly cleanse data. Manolov and Solanas (2013) came to a similar conclusion in their Monte Carlo study, finding that although the GLS was generally more robust, the MPD was more sensitive to study-level effects.

Limitations

Several of the assertions we made were bolstered by results from our convenience sample. This convenience sample represents only a small sample of the published single-case literature. It is possible different results would have been reached had other discipline areas that utilize SCD been included.

We reviewed only a select few SCESs, as a full examination of all published SCESs is beyond the scope of a single article. These SCESs were purposefully chosen because they represent distinct areas of the field and were recently published. No judgment regarding the quality of these metrics should be inferred by their inclusion alone. For example, a recent proposal, the d-index (Shadish et al. 2014a, b), was described in the educational research after initial submission of this article. Readers are cautioned that different SCESs have different assumptions, although there is great overlap across procedures. Most of the assumptions described above will generalize to other variants of these procedures.

Due to limitations of space, we also did not discuss power in detail, a field of study focusing on the minimum sample size needed to reliably detect certain magnitudes of effect size or attain significance.

Conclusions

We have summarized a wide variety of assumptions applicable to single-case analysis. It was emphasized that these assumptions must be reviewed prior to estimation and should be used to guide both selection and interpretation of these metrics. We then presented sample distributions for the SCESs reviewed to demonstrate that group benchmarks do not apply and to provide some context for their application. We stress that assumption violations do not lead to direct recommendations for ES selection, making any decision tree on the subject potentially misleading. Such decisions depend on the severity of the assumption violation, sample size, and the type of data.

It is our opinion that SCESs nicely juxtapose many of the errors that can potentially occur with visual analysis. However, given the findings reported in this article and in other extant work, it is recommended that such statistics remain supplemental. Given prior research and the evidence currently presented, we find two or three parameter models where slope and level differences are estimated separately, such as the SLC or multilevel models, appealing given their flexibility and ability to avoid certain assumptions. However, there are circumstances when researchers may want a single indicator, the far more common statistic in the social sciences, such as for comparisons across studies or when differences in trend are not relevant to address research questions. Non-overlap techniques may be used when normality is severely violated and non-overlap can adequately address the research question. Curiously, many researchers have chosen such effects as their default method, even for meta-analysis. Controlling for autocorrelation may be applied when serial dependency is severe; however, we question whether this will be worth the effort in many cases when trend is also controlled for. We do not believe providing multiple SCESs (e.g., NAP and Cohen’s d) to cover all bases, whether it be for individual studies or meta-analysis, is appropriate, which is atheoretical and may lead to false positives. Rather, researchers should use their understanding of the data to select the single, most appropriate estimator, as is common practice in the group design literature.