Introduction

Biological macromolecules are inherently flexible objects and often accomplish their task through extensive conformational rearrangement (Sicheri and Kuriyan 1997; Pickford and Campbell 2004; Zhang and Zuiderweg 2004; Tonks 2006; Chuang et al. 2010). Characterization of such rearrangements and the relevant conformational states can provide important clues about the mechanisms underlying biological function. This however is a challenging task because the system is underdetermined, implying a large degeneracy in the reconstructed solutions, and requires extensive experimental work often involving multiple techniques (Bonvin and Brunger 1996; Choy and Forman-Kay 2001; Svergun et al. 2001; Burgi et al. 2001; Clore and Schwieters 2004; Schroeder et al. 2004; Iwahara et al. 2004; Bertini et al. 2004a; Blackledge 2005; Lindorff-Larsen et al. 2005; Fragai et al. 2006; Tolman and Ruan 2006; Boehr et al. 2006; Ryabov and Fushman 2006; Chen et al. 2007; Bernadò et al. 2007; Bertini et al. 2007; Ryabov and Fushman 2007; Lange et al. 2008; Hulsker et al. 2008; Korzhnev and Kay 2008; Nodet et al. 2009; Boehr et al. 2009; Stelzer et al. 2009; Huang and Grzesiek 2010; Fisher et al. 2010; Bashir et al. 2010; Rinnenthal et al. 2011; Bothe et al. 2011; Fisher and Stultz 2011; Berlin et al. 2013; Russo et al. 2013; Guerry et al. 2013; Kukic et al. 2014; Ravera et al. 2014; Torchia 2015). Therefore, it is important to know the information content provided by various experimental methods in order to decide on an optimal set of experiments a priori.

Residual dipolar couplings (RDC; Lohman and Maclean 1978) are widely used as a source of information on biomolecular structure and dynamics (Tolman 2001; Tolman and Ruan 2006; Berlin et al. 2013; Ravera et al. 2014). They arise in the presence of partial molecular orientation, which can be achieved by interactions with alignment media surrounding the molecule (Tolman et al. 1995; Tjandra and Bax 1997; Hansen et al. 1998; Losonczi and Prestegard 1998; Ramirez and Bax 1998; Wang et al. 1998; Al-Hashimi et al. 2000; Prestegard et al. 2000; Zweckstetter and Bax 2001; Lakomek et al. 2008) and/or by the preferential orientation of the molecule itself in a magnetic field due to its magnetic susceptibility anisotropy (Lohman and Maclean 1978; Tolman et al. 1995; Zhang et al. 2003; Latham et al. 2008; Ravera et al. 2014; Musiani et al. 2014). RDCs obtained by alignment induced by an external orienting medium, herein referred to as diamagnetic RDCs (dRDC), depend on the nature of the interactions of the biomolecule with the medium. These interactions can be steric and/or electrostatic and, because of this, dRDC are reporters also on the overall shape of the macromolecule and/or its charge distribution (Zweckstetter and Bax 2000; Zweckstetter 2008; Berlin et al. 2009; Maltsev et al. 2014). On the other hand, RDCs caused by molecular self-alignment, often induced by the presence of a paramagnetic center with an anisotropic magnetic susceptibility, herein termed paramagnetic RDCs (pRDC), only depend on the orientation of the internuclear vectors in the reference frame of the magnetic susceptibility tensor and are generally independent of the shape of the molecule. However, the presence of an anisotropic magnetic susceptibility also gives rise to pseudocontact shifts (PCS; Kurland and McGarvey 1970), which are reporters on the positions of the nuclei in the principal axis frame of the magnetic susceptibility tensor centered on the paramagnetic site, and therefore contain information about the structure/shape of a molecule. The use of paramagnetism-induced restraints (Gochin and Roder 1995a, b; Banci et al. 1996, 1998; Bertini et al. 2001a; Gaponenko et al. 2004; Bertini et al. 2005; Diaz-Moreno et al. 2005; Jensen et al. 2006; Bertini et al. 2008; Schmitz et al. 2012; Yagi et al. 2013b) is becoming increasingly popular because of the introduction of lanthanide binding tags (Barthelmes et al. 2011; Wöhnert et al. 2003; Rodriguez-Castañeda et al. 2006; Su et al. 2006; John and Otting 2007; Pintacuda et al. 2007; Zhuang et al. 2008; Su et al. 2008a, b; Keizers et al. 2008; Häussinger et al. 2009; Su and Otting 2010; Hass et al. 2010; Man et al. 2010; Das Gupta et al. 2011; Saio et al. 2011; Swarbrick et al. 2011a, b; Bertini et al. 2012a; Liu et al. 2012; Kobashigawa et al. 2012; Cerofolini et al. 2013; Yagi et al. 2013a; Gempf et al. 2013; Loh et al. 2013), that extend the range of applications from paramagnetic metalloproteins (Banci et al. 1996, 1997; or proteins in which the naturally occurring metal can be replaced by a paramagnetic one; Allegrozzi et al. 2000; Bertini et al. 2001a, b, c; Bertini et al. 2003, 2004b; Balayssac et al. 2008; Bertini et al. 2010a; Luchinat et al. 2012b) to, in principle, any protein.

Given the various possibilities and limited resources, choosing the optimal set of observables for the characterization of protein conformational heterogeneity is important. In this work we analyze the information content associated with the two commonly used types of experimental data (dRDC and paramagnetic data) and discuss their features and advantages and pitfalls. Specifically, we want to understand what information can be recovered and to what extent. Importantly, the methodology that we develop below is not limited to dRDC or paramagnetic data, and can be applied to any set of experimental observables.

Theory

Formulation of the ensemble problem

We focus on analyzing the ensemble information content of three specific types of NMR restraints, dRDC, pRDC, and PCS, in the case of proteins composed of two domains connected by a flexible linker. We have used the two-domain protein calmodulin (CaM) as a test case.

As done previously (Bertini et al. 2007; Berlin et al. 2013), we assume that all three types of NMR restraints considered here represent a population-weighted average of the corresponding values for the individual conformers, and therefore have a linear dependence on the ensemble populations, such that

$$ {\mathbf{y}} = {\mathbf{a}}_{1} x_{1} + \cdots + {\mathbf{a}}_{N} x_{N} + \varepsilon = {\mathbf{Ax}} + \varepsilon $$
(1)

where y is a length-L column vector representing the experimental data (dRDC, pRDC, PCS, or some combination thereof), A is an L × N prediction matrix consisting of N column-vectors a j (j = 1,…,N) representing the predicted data for each of the N conformers, x j is the population weight for the jth conformer, and ε is the difference between y and Ax due to the presence of experimental error. This assumption seems reasonable for pRDC and PCS (Bertini et al. 2012c), whereas for dRDC the interconversion between conformers can occur on a timescale that could be comparable to the one of the interaction with the alignment medium; additionally, the latter may perturb the system.

Since in general recovering x from Eq. 1 is an ill-posed problem, having an infinite number of solutions, we seek to recover the minimum ensemble (sparsest solution) satisfying the experimental observables, which we express as a constrained linear least-squares problem (Berlin et al. 2013),

$$ {\mathbf{x}}^{*} = \mathop {\arg \hbox{min} }\limits_{\text{x}} \left\| {{\mathbf{W}}\left( {{\mathbf{Ax}} - {\mathbf{y}}} \right)} \right\|_{2} {\text{ s}} . {\text{t}} . \,{ }{\mathbf{x}} \ge 0, \, \left\| {\mathbf{x}} \right\|_{0} = M $$
(2)

where W is the weight matrix that non-uniformly weighs the residuals between y and Ax, M is the desired ensemble size, ‖…‖2 is the Euclidian norm, and \( \left\| {\mathbf{x}} \right\|_{0} \) is the l 0 quasi-norm of x, i.e. the number of nonzero elements in x. Typically the experimental errors are assumed to be uncorrelated, in which case W is simply a diagonal matrix with W ii = 1/σi, where σi is the estimated experimental error of the ith observation y i . For simplicity, for the rest of the manuscript we will drop W from our equations by assuming that A and y are already multiplied by W. In the sparse ensemble selection (SES) method the ensemble size is chosen by solving the problem for reasonable values of M and using the L-curve to select the appropriate M value (Berlin et al. 2013). A different approach was also applied, based on the calculation of the maximum occurrence allowed for each conformer (MaxOcc, see below; Bertini et al. 2002a; Gardner et al. 2005; Longinetti et al. 2006; Bertini et al. 2007, 2010b, 2012b, c; Luchinat et al. 2012a; Andralojc et al. 2014).

Predicting RDC and PCS data

For steric dRDC data, we generate the prediction matrix A using program PATI (Berlin et al. 2009, 2013), which assumes the presence of a steric planar alignment medium (Fig. 1a). Electrostatically induced RDCs were similarly simulated using PALES (Zweckstetter 2008). The absolute scaling in the predicted dRDC values is regulated by changing the value of the parameter “liquid crystal concentration” (Zweckstetter and Bax 2000) that controls the distance between the planar steric barriers. In the SES model the absolute scaling of the predicted dRDC is treated as an implicit parameter since the sum of all weights (∑ j x j ) is not constrained (Berlin et al. 2013).

Fig. 1
figure 1

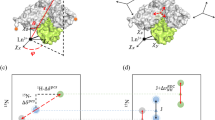
Schematic illustration of the relationship between the conformation of a multidomain protein and the alignment tensor for the two experimental methods considered her (or: alignment tensor caused by external and internal alignment). In the case of partial orientation induced by external orienting media the alignment tensor changes for different conformations of a two-domain protein (a) whereas in the case of partial orientation induced by a paramagnetic metal ion attached to the protein the alignment tensor is invariant with respect to the orientation of the domain where it is attached (b)

Full size image

For pRDC and PCS, without loss of generality, we can assume that a metal ion tag is located on the first (rigid) domain of the protein (Bertini et al. 2003). Therefore, the position of the metal ion relative to that domain is the same for all conformers. So, instead of performing the prediction of pRDC and PCS values for both domains, we obtain the prediction matrix A for a two-domain rigid system by first deriving the magnetic susceptibility anisotropy tensor (and metal ion’s position) from the experimental data for the first domain, and then use these tensors to predict the matrix A values for the second domain based on its position relative to the first domain (Fig. 1b). This formulation assumes that the distribution of the relative positions of the two domains is independent of the orientation of the magnetic susceptibility anisotropy tensor in the magnetic field (Bertini et al. 2002a).

Given a specific conformer, the pRDC values in the A matrix are thus predicted by first deriving the vector containing the 5 independent components of the alignment tensor, S *, directly from the experimental data for the first domain:

$$ {\mathbf{S}}^{*} = \mathop {\arg \hbox{min} }\limits_{\text{S}} \left\| {{\mathbf{V}}_{1} {\mathbf{S}} - {\mathbf{y}}_{1} } \right\|_{2} $$
(3)

where V 1 is a 5-column matrix, the elements of which depend on the orientations of the normalized bond vectors in the fixed frame (Losonczi et al. 1999; Valafar and Prestegard 2004; Berlin et al. 2009; Simin et al. 2014) and y 1 are the observed experimental pRDC values for the first domain. Then, using the derived S *, we predict the pRDC for the second domain of the jth conformer (A pRDC,j ) as

$$ {\mathbf{A}}_{pRDC,j} = {\mathbf{V}}_{2j} {\mathbf{S}}^{*} $$
(4)

where V 2j is the 5-column matrix of the bond vectors for the second domain in the jth conformer.

Similarly, the PCS values for the first domain can be used to derive the magnetic susceptibility anisotropy tensor T *, represented by a 3 × 3 traceless symmetric matrix, and the metal ion’s position p * (computed by alternating between solving a non-linear least-squares problem for p *, and a linear problem for T *). These values are then used to predict the PCS for the second domain of the jth conformer (A PCS,j ). The elements of the A PCS,j vector are the PCSs predicted for each nucleus i of the second domain, according to the relationship

$$ {\mathbf{A}}_{PCS,j,i} \approx \frac{1}{{12\pi \left\| {{\mathbf{r}}_{ij} } \right\|_{2}^{5} }}{\text{tr}}\left( {\left[ {\begin{array}{*{20}c} {3r_{ij,1}^{2} - \left\| {{\mathbf{r}}_{ij} } \right\|_{2}^{2} } & {3r_{ij,1} r_{ij,2} } & {3r_{ij,1} r_{ij,3} } \\ {3r_{ij,1} r_{ij,2} } & {3r_{ij,2}^{2} - \left\| {{\mathbf{r}}_{ij} } \right\|_{2}^{2} } & {3r_{ij,2} r_{ij,3} } \\ {3r_{ij,1} r_{ij,3} } & {3r_{ij,2} r_{ij,3} } & {3r_{ij,3}^{2} - \left\| {{\mathbf{r}}_{ij} } \right\|_{2}^{2} } \\ \end{array} } \right]\,{\mathbf{T}}^{*} } \right) $$
(5)

where \( {\mathbf{r}}_{ij} = [r_{ij,1} ,r_{ij,2} ,r_{ij,3} ] \) is the vector connecting the metal ion (located at p *) and the ith atom in the jth conformer, and tr(…) designates the trace of a matrix. The elements of the tensor T * and the components of the alignment tensor S * are related to one another by a proportionality constant (Bertini et al. 2002b), so that each of the two can be easily calculated from the other.

Similarly to dRDC for multiple alignment media, pRDC and PCS from multiple metal ion derivatives (determined from the S * and T * tensors, respectively, of the corresponding metals) can be combined together in a single A matrix of predicted data.

Methods

Constraining SES ensemble populations

Since the scaling of the predicted dRDC values has an uncertainty (Berlin et al. 2013), when recovering SES ensembles using dRDC, we allow the total sum of x, ∑ j x j , to float, and only use the restraint x ≥ 0 (see Eq. 2).

By contrast, the values of pRDC and PCS are determined without any adjustable scaling factor, and thus the two datasets can be directly combined into a single population-constrained pRDC + PCS SES problem,

$$ {\mathbf{x}}^{*} = \mathop {\arg \hbox{min} }\limits_{\text{x}} \left\| {\,\left[ {\begin{array}{*{20}c} {{\mathbf{y}}_{pRDC} } \\ {{\mathbf{y}}_{PCS} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {{\mathbf{A}}_{pRDC} } \\ {{\mathbf{A}}_{PCS} } \\ \end{array} } \right]{\mathbf{x}}} \right\|_{2} {\text{ s}} . {\text{t}} . \,{ }{\mathbf{x}} \ge 0,\sum\limits_{j} {x_{j} \le c} ,\left\| {\mathbf{x}} \right\|_{0} = M $$
(6)

where c is the upper bound on the total population weight. Since ∑ j x j represents the total population weight ∑ j x j should be 1. However, we allow for the sum of the weights to be <1, since we aim at recovering the sparsest ensemble representing the major states (potentially there could be a very large set of transient minor states). The validity of the recovered solution can be evaluated from the geometrical interpretation of pRDC: a solution is a convex combination of a set of conformers such that the averaged pRDC belong to the polyhedron with vertices in the conformers (see Figure S5; Gardner et al. 2005; Longinetti et al. 2006). Since the problem is underdetermined, there will be many solutions, and the SES method chooses to limit the number of vertices to M. In order to find a solution with this constraint, we need to use a c < 1 in Eq. (6). This is equivalent to shrinking the vertices of the polyhedron towards the origin by a factor c and renormalizing the weighting factors to 1. However, since the origin is an acceptable point (Sgheri 2010a) and the set is convex, the shrunk vertices will be anyway acceptable points. In other words, if c is relatively close to 1, the conformers representing the vertices are anyway good representatives of the conformational freedom of the system. Finally, the ∑ j x j  ≤ 1 restraint prevents from finding unphysical solutions.

SES algorithm implementation

SES ensemble recovery was implemented using the multi-orthogonal matching pursuit (MOMP) algorithm (Berlin et al. 2013). We modified the MOMP method to handle the ∑ j x j  ≤ c requirement using the active set method (O’Leary 2009) to restrain our solution for each iteration of MOMP. Given that there are two restraints on x: x ≥ 0 and ∑ j x j  ≤ c, during each iteration of the MOMP algorithm there are four possible sets of active restraints: (1) no restraints are active; (2) ∑ j x j  ≤ c restraint is active; (3) the x ≥ 0 restraint is active; or (4) both x ≥ 0 and ∑ j x j  ≤ c are active. To summarize, the constrained least-squares problem is solved as follows: update the solution using conjugate gradient (CG) method; if the solution violates x ≥ 0 or ∑ j x j  ≤ c, solve the linearly constrained linear least-squares problem by using a “feasible direction” method (O’Leary 2009); if the solution still violates x ≥ 0, drop this solution from a list of possible solutions stored in a priority queue. This procedure is repeated for all propagated solutions from the previous iteration.

The time versus accuracy tradeoff in the MOMP algorithm is controlled by how many top solutions, K, from the current iteration are propagated to the next iteration of MOMP (Berlin et al. 2013). In order to improve the memory requirement for running SES using very large K values (>106), we modified the algorithm used to solve the overdetermined linear least-squares problem for each iteration of SES, when a new solution must be computed right after one new column is added to the list of active columns [see Supporting Information in Berlin et al. (2013)]. In the previous implementation (Berlin et al. 2013), the least-squares solution was efficiently updated by doing a rank-1 update of the QR decomposition. However, this approach requires us to store K QR decompositions during each iteration. In our current updated version, we switched to an iterative CG least-squares solver, which requires that we only store the previous-iteration solution, rather than the QR decomposition. This significantly reduced the SES memory footprint for large K. The full A T A matrix required for the CG algorithm is never explicitly formed, and instead the multiplication step in the CG algorithm is computed as A T(Ax). With the CG implementation we are able to run SES on a 10 GB RAM desktop for K = 106, without any sacrifice in computational time or accuracy, as compared to the previous implementation.

MaxOcc calculations

The maximum occurrence (MaxOcc) of each and every conformer is defined as the maximum weight that it can obtain when part of a conformational ensemble without violating the constraints of the experimental data. No restriction is posed on the number of conformations to be included in the ensemble. Maximum occurrence (MaxOcc) can be interpreted as the maximum fraction of time that a conformation can exist, when taken together with any ensemble of conformations with optimized weights (Longinetti et al. 2006; Bertini et al. 2007; Sgheri 2010b; Bertini et al. 2010b; Das Gupta et al. 2011; Luchinat et al. 2012a; Bertini et al. 2012b, c; Cerofolini et al. 2013).

We formulate MaxOcc as a convex regularization problem, where for each conformer j we find the weight vector x which minimizes

$$ \mathop {\arg \hbox{min} }\limits_{\text{x}} \left\{ {\left\| {{\mathbf{Ax}} - {\mathbf{y}}} \right\|_{2}^{2} + \lambda (x_{j} - x_{MO} )^{2} + \lambda \left( {1 - x_{MO} - \sum\limits_{i = 1,i \ne j}^{N} {x_{i} } } \right)^{2} } \right\}{\text{ s}} .\,{\text{t}} .\, { }{\mathbf{x}} \ge 0 $$
(7)

where x MO is the desired weight of the conformation j, and λ is a weighting factor. The calculations are repeated for increasing values of x MO ; the MaxOcc of conformation j is defined as the highest x MO providing a value of the expression in Eq. 7 not exceeding the minimum value by more than a prefixed threshold, for example 20 %. The value of λ was fixed to 15, as found with the L-curve method, as a compromise between a good fit of the experimental observables and the proximity of the sum of the weights to 1. A frugal coordinate descent algorithm, combined with random coordinate search (Nesterov 2012), is used to solve Eq. 7.

Calculations are also performed to determine the maximum occurrence of a region (MaxOR) defined in the conformational space of the protein (Andralojc et al. 2014). The MaxOR, similar to MaxOcc, is defined as the maximum weight that a region in conformational space (composed of multiple structures) can have in an ensemble without causing a violation of the experimental restraints. First, the highest-MaxOcc structures are clustered according to their positions using a k-means algorithm as implemented in the Python library SciPy (Jones et al. 2001). The number of clusters is set to the highest value yielding reproducible clustering by the algorithm. Once the clusters are built, small regions are defined around the centers of the clusters, which include all conformations within a given distance Δ from the center of the cluster. The MaxORs of these regions are determined by solving

$$ \mathop {\arg \hbox{min} }\limits_{\text{x}} \left\{ {\left\| {{\mathbf{Ax}} - {\mathbf{y}}} \right\|_{2}^{2} + \lambda \left[ {\left( {x_{MO} - \sum\limits_{i \in C}^{{}} {x_{i} } } \right)^{2} - \left( {1 - x_{MO} - \sum\limits_{i \in D}^{{}} {x_{i} } } \right)^{2} } \right]} \right\}{\text{ s}} . {\text{t}} . \,{ }{\mathbf{x}} \ge 0 $$
(8)

where x MO is the fixed value that must correspond to the sum of the weights of all conformations within the region, and C and D indicate the structures within and outside that region, respectively. Again, the largest x MO providing a good fit of the experimental data defines the maxOR of the region.

Results and discussion

An important theoretical question that we would like to answer a priori, before performing any time-consuming simulation or experiment, is how much information for ensemble recovery is contained in dRDC versus pRDC versus PCS and in dRDC versus pRDC + PCS combined. For example, intuitively, dRDC should contain more information than pRDC, since dRDC contain shape/size-related information, while the relative informational content of PCS is harder to intuitively quantify. To what extent combining pRDC with PCS yields better results than each of these data separately? Is the information provided by pRDC + PCS similar to that provided by dRDC? Would using several different metal ions be needed to obtain results comparable to those obtained with multiple sets of dRDC, or do they produce a better set of experimental data for the characterization of the conformational heterogeneity?

In order to answer these questions, we analyzed several algebraic properties of eight experimentally feasible datasets: (1) single-alignment medium dRDC; (2) single-metal ion pRDC; (3) single-metal ion PCS; (4) single-metal ion pRDC + PCS combined; and (5–8) datasets analogous to (1–4) but with three alignment media or thee metal ions. We will refer to the one and three media/metal ions datasets as the one- and three-restraint datasets, respectively.

The datasets were generated for a pool of 32723 conformers of calmodulin (CaM), a protein composed of two rigid domains connected by a 4-residue flexible linker (Barbato et al. 1992; Tjandra et al. 1995; Chou et al. 2001; Kukic et al. 2014). This large pool of sterically allowed conformations of the protein was taken from reference (Bertini et al. 2010b), where it was generated using the program RanCh (Bernadò et al. 2007), For each conformer and for each aligning medium or metal ion, a set of dRDCs, pRDCs, and PCSs was generated, as described in the “Theory” section.

Simulated PCS and pRDC data

The paramagnetic restraints consisted of PCS of the amide H atoms and pRDC of amide N–H pairs of the C-terminal domain of CaM induced by the presence of a paramagnetic center in its N-terminal domain. Three metals with non-coinciding magnetic susceptibility tensors (corresponding to the experimental ones obtained for Tb(III), Tm(III), and Dy(III) CaM) were used to generate three sets of PCSs (132 observations in total) and pRDCs (112 observations in total). The magnetic susceptibility anisotropy tensors were taken from reference (Bertini et al. 2009).

Simulated dRDC data

The simulated diamagnetic restraints were amide 15N-1H dRDCs (219 in total) induced in both CaM domains by 3 independent external alignment media: flat uncharged discs and either positively or negatively charged rods. In the first case, dRDCs were generated using PATI (Berlin et al. 2009), in the other cases using PALES (Zweckstetter and Bax 2000; Zweckstetter 2008). In both cases, the calculation of the alignment tensors, and of the corresponding dRDC, are performed under the assumption that the protein’s conformations are rigid during the time course of its interaction with the alignment medium. As a word of caution we note that every interaction of a protein with the alignment medium might actually perturb its conformation, and these interactions can occur on a timescale that is slower than the conformational averaging itself. The assumption that the averaged dRDCs correspond to a weighted average of the RDCs calculated for the individual conformations, although universally used, might fall short in representing the real physical picture.

SVD of prediction matrices

The first and simplest analysis we performed was aimed at evaluating the theoretical information content of the eight different datasets described above. This was done through the spectral analysis of the prediction matrix A for each dataset. The spectral analysis measures the number of significant linearly independent components present in the data, by counting the eigenvalues corresponding to linearly independent eigenvectors. This directly provides an upper bound on the number of independent conformers we can hope to extract. Trying to recover a larger number of independent conformers would result in overfitting. The results are shown in Fig. 2a, d.

Fig. 2
figure 2

SVD decomposition (left panels), histogram of column correlations (center panels), and condition number of randomly subselected set of columns (right panels), for the eight described datasets. The results for a single medium/metal ion are shown on the top, and the results for the 3 media/metal ions are shown on the bottom. a–d The 35 largest singular values of the associated A matrices. b–e The distribution of the uncentered correlations between all pairs of columns in the A matrix, estimated by performing 20,000 random samples. c–f The expected mean and SD of the relative error for recovering population weights from an arbitrary M = 1,…,10 subset of columns

Full size image

As shown in Eq. 3, any vector of RDC values (either pRDC or dRDC) from a rigid domain can be expressed as a matrix V, which can be determined from the orientations of the bond vectors of that domain, multiplied by the 5 independent components of the alignment tensor matrix. Since there is a linear dependence of the observed data on the 5 components of the alignment tensor, we expect the A matrix for dRDC to have rank 10 (5 independent parameters for each of the two domains), and for pRDC to have rank 5, since only the second domain data are used for ensemble recovery. The number of unknowns in the paramagnetic case is also smaller because the alignment tensor for the first domain (5 parameters) can be easily determined from PCS and pRDC measured for this domain, as they are not averaged by conformational variability.

Numerical spectral analyses of the generated prediction matrices for dRDC and pRDC (Fig. 2a, d) support our theoretical analysis, and show that the number of singular values of matrix A for one-restraint dRDC and pRDC data is 10 and 5, respectively. Going from 1 to 3 alignment tensors triples the number of non-zero singular values for dRDC and pRDC, as would be expected for linearly independent alignments. The large decrease in the magnitude of singular values for the last 10 dRDC and 5 pRDC non-zero singular values in the three-restraint datasets likely reflects the difficulty in experimentally obtaining three fully independent alignment tensors. The larger magnitudes of dRDC singular values compared to the singular values for pRDC are not related to their information content, but merely reflect the relative strength of diamagnetic versus paramagnetic alignment in the simulated data. On the contrary, it is the decrease in the relative magnitude of the singular values with respect to the largest value, calculated from a set of data, that reflects the difficulty in exploiting the associated restraints, and is hence ultimately related to the information content.

Similarly, the observed PCS data for a rigid domain which is not containing the paramagnetic ion (i.e. for the second domain) can be expressed using 8 parameters: the 5 independent components/parameters defining the T tensor, and the 3 parameters describing the metal-ion’s position p with respect to this domain. However, since the observed PCS vector y is not linearly related to p, the rank of A PCS (calculated from the PCSs in the second domain) is much higher than 8, and greater than that for dRDC or pRDC datasets. The rank of A PCS is actually close to (up to) the number of observations; however as Fig. 2a, d show, the magnitude of the singular values decreases very rapidly. This decrease reflects the strong difference in the PCS values between conformers where the C-terminal (second) domain is close to the metal ion (paramagnetic center) and those where it is far away. After the first ≈15 entries, in the one-restraint case the singular values are very small because similar PCS values are calculated for conformers not very far from one another and for nuclei which are spatially close to several other nuclei. When using three sets of metal ions, the number of conformers with large and different PCS values increases. Thus, the decrease in the magnitude of the singular values is significantly slower than in the case of a single metal ion (Fig. 2a–d).

One major advantage of using metal ions instead of steric alignment is that both pRDC and PCS are collected from the same biochemical construct. Thus, two independent datasets can be directly combined, as described in Eq. 6. When combining these datasets, a significantly slower decay in singular values of A is obtained compared to the pRDC and PCS datasets analyzed independently. This supports the accepted intuition that pRDC and PCS provide orthogonal structural restraints (pRDCs are very sensitive to orientation, PCSs mostly provide distance restraints).

Histograms of prediction matrices

The spectral analysis of the A matrices suggests that pRDC + PCS and even PCS alone provide better restraints for ensemble selection than dRDC. However, singular values are not an exhaustive description of the overall vector distribution. Therefore, we directly analyzed the distribution of correlations between all columns of the matrix A calculated for dRDC, pRDC, and PCS. The uncentered correlation distributions between all pairs of columns are shown in Fig. 2b, e. The more uncorrelated the columns of each specific A (A dRDC, A pRDC, A PCS) the smaller the chance that an alternative conformer can explain the same subset of experimental data, thus decreasing the number of viable alternative ensembles. In the optimal case, all columns would have zero correlation, and the ensemble solution would be unique.

Figure 2b, e clearly demonstrate that even though the number of singular values of PCS is larger than that of dRDC and pRDC, the correlation distribution is actually significantly worse than for any other dataset, so that their information content could not be larger. The higher correlation for large fraction of the conformers reflects a distribution of PCS where very large changes occur in proximity of the metal ion only, whereas almost no change occurs far away from the metal ion. Additional metal ions can significantly improve the distribution of correlations, although it remains poor with respect to that of the other restraints.

Since pRDCs are distance-independent, they provide a more uniform distribution of values, so that their correlation distribution is much better than for PCS. The pRDC distribution is anyway worse than that of dRDC in the one-restraint case; it significantly improves, essentially to the level of dRDC, in the three-restraint case. Interestingly, the dRDC distribution changes only slightly between one and three restraints, which suggests that the information contained in the additional dRDC datasets is more redundant than in the pRDC case.

Combining pRDC with PCS results in a better correlation distribution than for pRDC and PCS individually. In turn, the correlation distribution of pRDC + PCS is very similar to that of dRDC in the one-restraint case and actually somewhat better in the three-restraint case.

Expected relative error

While the correlation plots in Fig. 2b, e provide an estimate of the A matrix column vector distribution, they do not directly tell how well ensembles greater than two can be recovered, nor do they take signal-to-noise ratio into account. To assess how well larger ensembles can be recovered, we computed the mean and standard deviation (SD) of the relative error from a synthetically generated y data (with added Gaussian error) for M = 1,…,10 columns. The mean and SD were computed by randomly sampling, for each M value, M columns and uniformly at random generating the associated population weights x. The synthetic y was generated as y = Ax + N(0,1), where N(0,1) is the zero-mean Gaussian distribution with σ = 1. The vector x * and the associated relative error, ||x − x *||2/||x||2, were recovered by solving Eqs. 2 and 6. In order to guarantee a <0.1 % relative error with >99.999 % confidence using Chernoff bound, the process was repeated 40,000 times for each M. The results for all datasets are shown in Fig. 2c, f.

For the one-restraint datasets, dRDC has lower relative error than pRDC, PCS, or pRDC + PCS. As expected, there is a rapid growth in pRDC errors due to the low matrix rank, and high errors overall in PCS due to the high correlation between columns. In the case of the three-restraint datasets, dRDC has significantly lower relative error than pRDC, even though on the correlation plot the two distributions are very similar. Interestingly, combining pRDC + PCS yields only slightly higher error rate than for dRDC.

Recovering the conformational variability from synthetic datasets

In the previous sections we theoretically analyzed the information content of 8 datasets of synthetic dRDC, pRDC and/or PCS data. Here we perform a direct comparison of the performance of the different restraints in recovering information on the structural variability of the system. To achieve this, we determined (1) the minimum-size sparsest ensemble solution using the SES method (Berlin et al. 2013) and (2) the conformations (as well as the regions in the conformational space) with the highest MaxOcc values. In this way it becomes possible to analyze the accuracy of the recovered solutions from the different sets of synthetic averaged data.

For this purpose, we devised three simulations modeling (1) extensive mobility around a single conformation, (2) two-site exchange with limited mobility around each center, and iii) two-site exchange with a reduced difference in the orientations of the two centers. In each of the simulations, the two-domain protein CaM was allowed to sample different, well defined, parts of its sterically allowed conformational space. Synthetic restraints were calculated as weighted averages over the values of dRDC, pRDC, and PCS of the individual conformations belonging to the sampled regions. These average data were perturbed with a Gaussian error with a SD of 1, 2, or 3 Hz for pRDC and dRDC and of 0.01, 0.02, or 0.03 ppm for PCS.

In the following descriptions of the simulated conformational ensembles, the N-terminal domain of CaM is taken as the frame of reference, and each conformation is described by the different position and orientation of the C-terminal domain with respect to the N-terminal domain. The exact details of each simulation, although described accurately for completeness, are not crucial for the success of the ensemble recovery attempts.

Simulation 1

In this first simulation we consider the case of conformational variability centered at a single extended conformation of CaM. The sampled ensemble consists of all the conformers, present in the pool of the 32723 sterically allowed conformers, within a distance Δ (measured as a combination of translation and rotation) from the central extended structure (Fig. 3a; Bertini et al. 2012b). Specifically, this distance is defined as:

$$ \Delta = d + f(1 - { \cos }\,\upalpha) $$
(9)

where d is the translation of the center of mass of the C-terminal domain from the central structure, and α is the angle of rotation from the central structure, calculated as α = arccos (|q c  · q|), where q c and q are the unitary quaternions describing the central structure and the other structure. Note that the two structures are actually 2α apart in Cartesian space (Kuffner 2004). Δ defines the largest allowed spatial displacement (when α is 0) and the largest allowed rotation (when d is 0; it also depends on the factor f) from the position of the central conformer. In the present simulation, conformations with Δ up to 30 Å (a reasonable estimate for this system) were accepted and the value of f was set to 84 Å. In this way, the conformers in the constructed ensemble can have the center of mass of the C-terminal domain at a maximum distance of 30 Å with respect to the conformer at the center of the distribution, if they have the same orientation (the distance decreases with increasing the difference in the orientation). Their C-terminal domain can be rotated up to 100° (α = 50°) with respect to the central conformer, if there is no translation of the center of mass (and gradually less and less as the translational component increases). The weight of each conformation in the ensemble depends on its Δ, and is fixed according to a Gaussian distribution centered at Δ = 0, with SD chosen to provide weights close to zero when Δ is close to 30 Å.

Fig. 3
figure 3

The simulated ensembles. Different positions of the C-terminal domain of CaM are represented by a triad of Cartesian axes, centered at the center of mass of the C-terminal domain. The conformers are color coded according to their relative weights (form red = high weight to blue = low weight). a Simulation 1, b Simulation 2, c Simulation 3. The ensembles are shown from two different points of view in the left and right panels. All the conformers are superimposed by the N-terminal domain, which is shown in cartoon representation

Full size image

Simulation 2

This simulation models the case of a two-site exchange, with limited mobility allowed around each of the two main conformers (Fig. 3b). The two centers were separated by approximately 30 Å and their C-terminal domains were rotated by ca. 140° with respect to each other. The mobility around each center was simulated as in the previous case with the threshold on Δ set to 10 Å and f equal to 42.7 Å, which corresponds to a maximum allowed angular displacement with respect to the central conformer of 80° (α = 40°).

Simulation 3

This simulation is similar to Simulation 2, with the difference that the angular distance between the two sites was decreased almost twofold (Fig. 3c). Sites with more similar orientations are likely to present a bigger challenge in ensemble recovery using restraints which depend on the domain orientations. The distance between the centers (both distinct from those used in Simulation 2) is 30 Å while the difference in orientation of the C-terminal domains is now 80°. The threshold of Δ and the value of f used to simulate the residual mobility around each center were the same as in Simulation 2, hence the same upper limit on the angle α.

SES ensembles

We applied the SES method to these simulated datasets and analyzed how the various restraints affect the recovery of the main conformations contained in the synthetic ensembles used to generate the data. The recovered ensembles were evaluated in terms of their sizes (number of major states) and of the proximity of recovered structures to the centers of the synthetic ensembles (in terms of spatial and angular displacement). As already mentioned in the “Theory” section, the ensemble size was chosen using the L-curve method (Berlin et al. 2013; see Figure S6).

The results are presented in Tables 1, 2 and 3. In general, dRDCs allowed a reasonably accurate recovery of the major states that were used to generate the synthetic datasets (see, for instance, Fig. 4a). However, in all three simulations, in some solutions one additional conformer was recovered, albeit with a relatively low weight. This additional conformer either belongs to the distribution of conformers around one of the main centers (as in Simulation 1 with error of 1 and 2 Hz, and in Simulation 2 with error of 2 Hz, Fig. 4b) or is positioned in-between the two major states (as in Simulation 2 with error of 1 Hz, Fig. 4c). In the first case its presence may reflect conformational heterogeneity; in the second case it is likely related to artifacts. The latter may arise because, ‘average conformers’ can be more compatible with the averaged experimental observables than any of the actually sampled conformations taken individually.

Table 1 Results of Simulation 1
Full size table
Table 2 Results of Simulation 2
Full size table
Table 3 Results of Simulation 3
Full size table
Fig. 4
figure 4

SES recovery using dRDC data. Color code for the C-terminal domain: green—simulated conformers in the centers of the regions, red, blue, and yellow—reconstructed conformers with highest, intermediate, and lowest weight, respectively. a An ensemble with correctly recovered major states (Simulation 3, 3 Hz error), b An ensemble with an additional state present next to one of the centers (Simulation 2, 2 Hz error), c An ensemble with an additional state (yellow) recovered (Simulation 2, 1 Hz error). The ensembles are shown from two different points of view in the left and right panels. All conformers are superimposed by the N-terminal domain

Full size image

In the case of pRDCs, the right number of major states was always recovered (Fig. S1), and in the corresponding conformers the domains were oriented with an accuracy comparable to that achieved with dRDC. It should be recalled that pRDCs contain no information whatsoever on the relative positions of the domains, which therefore results in inaccuracy of their positioning.

PCS data alone in two out of three simulations were sufficient to recover the correct solutions (Fig. S2) in terms of ensemble sizes and locations of the major states (with the accuracy similar to dRDC). However in Simulation 3, where the two states are more alike to one another, the calculations provide only a single state (Fig. S2B) situated in-between the two actual centers (in terms of both translation and orientation). The recovery of such an incorrect state is most likely, as already mentioned for dRDC, the outcome of the averaging of the experimental observables. Using all the paramagnetic data together (i.e. pRDC and PCS) improved the robustness of the recovery: both translations and orientations were satisfactory accurate in all cases (Fig. 5). The translation and rotation with respect to the conformers at the center of the distributions were within 4 Å and 16° for Simulation 1, 8 Å and 34° for Simulation 2, and 3 Å and 18° or 7 Å and 9° for Simulation 3 (1 Hz and 0.01 ppm error case). The ensemble recovery is robust, as increased errors did not noticeably affect the accuracy of solutions.

Fig. 5
figure 5

SES recovery with all the paramagnetic data. Color code for the C-terminal domain: green—simulated conformers in the centers of the regions, red, blue—reconstructed conformers with higher and lower weight, respectively. a Simulation 1, b Simulation 2, c Simulation 3, with 0.03 ppm and 3 Hz errors. The ensembles are shown from two different points of view in the left and right panels. All conformers are superimposed by the N-terminal domain

Full size image

In conclusion, diamagnetic RDC, as well as the combination of paramagnetic RDC and PCS, are both equally suitable restraints for the recovery of the major states present in conformational ensembles. Special attention should be paid to the fact that, occasionally, ‘average conformers’ may be recovered.

MaxOcc analysis

Similar to the SES analysis, we performed MaxOcc analysis on the same datasets. From the MaxOcc values, it is possible to determine which conformers can be sampled with the largest weights. In order to speed the computational analysis up, we used random sampling to detect regions of with potentially high MaxOcc conformers, and then expanded those regions, to find the globally best solution. To do this, we first computed MaxOcc for 400 conformers, randomly chosen from the generated pool (Bertini et al. 2010b, 2012b; Cerofolini et al. 2013). Then the conformers with the highest MaxOcc (up to 0.8 of the MaxOcc of the highest scoring conformer) were selected and the MaxOcc of their neighboring conformers (in the conformational space) were calculated. The procedure was repeated until no more neighbors with high MaxOcc were found. The neighboring conformers scored at each iteration were chosen using Eq. 9 with the threshold on Δ of 5 Å and f = 40 Å. If the final distribution of the highest MaxOcc conformers was broad, the analysis was supplemented by the maximum occurrence of regions (MaxOR) approach, which permitted to discriminate between the cases of high MaxOcc conformers corresponding to conformers actually sampled by the protein and the cases of high MaxOcc conformers corresponding to conformers arising from data averaging (Andralojc et al. 2014).

The results of the MaxOcc analysis are reported in Table 4 for all three simulations. In Simulation 1, for both the paramagnetic and diamagnetic data, the analysis revealed that all the conformers with the highest MaxOcc (from 0.8 to 1 of the highest MaxOcc, corresponding to 0.58–0.73 for the paramagnetic data and 0.57–0.71 for the dRDC) form a single, relatively compact, region in the conformational space (Fig. 6a, c). In order to quantify its agreement with the original distribution, the center of the region was calculated by averaging the translational and orientation parameters of the highest MaxOcc conformers. The conformation so obtained was then compared with the conformation at the center of the original distribution. As shown in Table 4 and Fig. 6b, d, the agreement was very good in terms of spatial and angular displacement for both the diamagnetic and the paramagnetic data, either for 1 Hz/0.01 ppm or for 3 Hz/0.03 ppm errors.

Table 4 The MaxOcc/MaxOR analysis
Full size table
Fig. 6
figure 6

MaxOcc results for Simulation 1. Each conformation is represented by a triad of Cartesian axes, centered at the center of mass of the C-terminal domain. Color code for a, c—according to the MaxOcc value (0.0—blue, 0.8—red), a The conformers with the highest MaxOcc recovered with the paramagnetic data (with error of 1 Hz for pRDC and 0.01 ppm for PCS), b The center of the distribution shown in panel a (red) versus the center of the simulated region (black), c The conformers with the highest MaxOcc recovered with dRDC (with error of 1 Hz), d The center of the distribution shown in panel c (red) versus the center of the simulated region (black). The results are shown from two different points of view in the left and right panels. All conformers are superimposed by the N-terminal domain, shown as a ribbon

Full size image

In simulation 2, i.e. the case of two well separated conformational regions, when dRDC are used, the highest MaxOcc conformers are positioned in two distinct, clearly separated regions (Fig. 7a), the centers of which are positioned very close to the centers of the actually sampled distribution (Table 4; Fig. 7b). When paramagnetic data (PCS + pRDC) are used, the highest MaxOcc (0.41–0.51) conformers are positioned in one elongated, banana-shape region in the conformational space (Fig. 8a), which includes the two actually sampled centers, but also many conformers situated between them (their high score is an outcome of conformational averaging as described in the SES results paragraph). From these results, one cannot conclude whether the studied conformational ensemble mainly reflects a two-site exchange case or the sampling of all the conformations within the determined region. In order to distinguish between these two cases, MaxOR calculations were performed. The highest MaxOcc conformers were clustered in 5 regions, shown in Fig. 8b, which include all conformations with distance Δ ≤ 5 Å from the central conformation (calculated using eq. 9, with f = 147 Å). The MaxOR values for these regions are reported in Table S1 (diagonal entries). All regions have similar MaxOR values (up to 0.60), not much higher than the largest MaxOcc values for the individual conformations. If however MaxOR values are calculated for pairs of regions (off-diagonal entries of Table S1), strong differences arise. All pairs yielding the highest MaxOR (0.90–1.00) are composed of regions at the opposite sides of the distribution of the highest MaxOcc conformers, whereas all pairs composed of the regions located on the same side of the distribution or more importantly containing a region in the middle, have significantly lower MaxOR (up to 0.63 and 0.78, respectively). This strongly suggests the occurrence of a two-site exchange model. The pair of regions with the highest MaxOR has their central conformations in nice agreement with the conformations in the center of the distributions in the synthetic ensemble, with an accuracy comparable to that obtained by SES (Table 4; Fig. 8d).

Fig. 7
figure 7

MaxOcc results for Simulation 2 with dRDC with error of 1 Hz. Each conformation is represented by a triad of Cartesian axes, centered at the center of mass of the C-terminal domain. a The conformers with the highest MaxOcc, color code: according to the MaxOcc value (0.0—blue, 0.6—red). b The center of the distribution shown in panel a (red) versus the center of the simulated region (black). All conformers are superimposed by the N-terminal domain, shown as a ribbon

Full size image
Fig. 8
figure 8

MaxOcc/MaxOR results for Simulation 2 with paramagnetic data (1 Hz error for pRDC and 0.01 ppm error for PCS). Each conformation is represented by a triad of Cartesian axes, centered at the center of mass of the C-terminal domain. a The conformers with the highest MaxOcc, color code—according to the MaxOcc value (0.0—blue, 0.6—red). b The five clusters formed by the conformers in panel a. c The centers of the clusters. d The centers of clusters with the largest MaxOR versus the centers of the simulated regions (black). All conformers are superimposed by the N-terminal domain, shown as a ribbon

Full size image

In simulation 3, for both the paramagnetic and diamagnetic data, the conformers recovered by MaxOcc form elongated regions comprising both the two centers and conformers situated between them (Figs. S3A and S4A). MaxOR was thus applied in both cases. As in the previous simulation, no single region has MaxOR significantly higher than the others, but the analysis of pairs of regions indicated again the occurrence of a two-site exchange (Tables S2 and S3). The two central conformations of the synthetic ensemble were identified with good accuracy (Table 4; Figs. S3D and S4D) using both kinds of experimental restraints. Again, the results are robust, as increased errors did not largely affect the accuracy of the solutions.

The performed MaxOcc/MaxOR analysis, as it appears from Table 4 as a whole, confirms the conclusion from the SES results that paramagnetic and diamagnetic restraints are equally useful for the recovery of conformational ensembles.

Conclusions

In many experimental studies RDCs have been shown to be precious restraints for analyzing molecular conformational freedom (Montalvao et al. 2014; Ravera et al. 2014; Camilloni and Vendruscolo 2015; Torchia 2015). Here we compared paramagnetic and diamagnetic RDCs and found substantial differences in their information content in the case of multidomain proteins. We found that the information content of dRDC is larger than that of pRDC in terms of number of singular values, and this reflects the shape dependence of dRDC. However, since the internal alignment due to paramagnetism also gives rise to PCSs, the total informational content recovered in a paramagnetic experiment is at least on par with dRDCs.

We have performed several simulations to evaluate the capability of recovering the conformational variability of two-domain proteins by the use of two different approaches, SES and MaxOcc/MaxOR. The main states of the protein were recovered reasonably well for both paramagnetic and diamagnetic datasets, with both approaches (see Tables 1, 2, 3, 4 and also Table S4). Even for rather large experimental errors, we have found that both datasets still retain the ability of recovering the main conformational states, thus resulting appealing for the analysis of averaged experimental data possibly also in the case of large systems, where RDCs are affected by large errors. Of course, since the problem is underdetermined, a correct reconstruction of the main states may be unsuccessful for different rather unpredictable conformational distributions.

Such analysis suggests that pRDC + PCS provide a very promising alternative to dRDC data. It is important to note that this analysis does not include modeling error, which is harder to quantify. Therefore, our analysis does not capture the principal advantages of pRDC + PCS over dRDC, in that it does not require assumption of a barrier model in order to predict the alignment. In addition, one has to consider that the interactions of the protein with the alignment medium might actually perturb the system, and that these interactions can occur on a timescale that is slower than the conformational averaging itself, so that the assumption that the measured dRDCs can be represented as a population-weighted average of the RDCs for the individual (rigid) conformers may fall short in representing the real physical picture.

Finally, the availability of a number of rigid lanthanide-binding tags nowadays may make the acquisition of three independent metal ion datasets more practical and safer than the acquisition and prediction of three independent alignment media. One current limitation of using metal ions is the low signal-to-noise ratio in pRDC and PCS data, which could potentially be improved with better technology and methodology.