Introduction

The impetus for the study reported in this paper grew out of the authors’ previous research on proportional reasoning, which showed that targeted professional development and explicit teaching can assist students to develop stronger proportional reasoning skills (Hilton et al. 2016). The study also builds on our previous research regarding the value of practitioner research for enhancing teachers’ professional growth (see Hilton and Hilton 2017). This paper reports on outcomes from the first year of an ongoing study being conducted in a primary school in a large provincial town in Queensland, Australia. Teachers of Years 3, 4, and 5 are participating in a 2-year professional development programme. The first year of the programme consisted of a series of workshops with supporting modelled lessons and interventions that enabled teachers to engage in practitioner research opportunities between each workshop. The purpose of this professional development programme is to enhance teachers’ content and pedagogical knowledge around the teaching and learning of proportional reasoning and its component elements. In the second year, workshops are continuing to support the teachers to promote the teaching and learning of proportional reasoning with a focus on integration across the curriculum and to further assist curriculum coordinators to embed proportional reasoning across the curriculum. In the first year of the project, the practitioner research cycles involved a series of three structured interventions that were designed by the researchers and implemented by the teachers. Each intervention aimed at enhancing certain aspects of proportional reasoning teaching and learning, including the use of mathematical language and student discussion; concepts of scale, fractions, relative and multiplicative thinking; and appropriate representations for teaching these concepts. This paper reports on the outcomes of implementing these structured interventions on teachers’ professional development from the perspectives of the teacher participants. It draws on data from workshop focus groups, participant interviews, and classroom video recordings.

Theoretical background

The importance of proportional reasoning

Proportional reasoning involves multiplicative thinking. Proportional reasoners have a sense of co-variation and are able to make comparisons among quantities (Fielding-Wells et al. 2014; Lesh et al. 1988). In order to be able to reason proportionally, students need a highly developed understanding of foundational concepts, which include multiplication and division, fractions, and decimals (Hilton and Hilton 2016; Boyer and Levine 2012; Lamon 2007; Lo and Watanabe 1997). This form of reasoning is needed in a range of situations beyond ratio and proportion, including the many aspects of rate and scale as well as relative thinking (in contrast to absolute thinking) (Ben-Chaim et al. 2007; Lamon 1993). Not only is proportional reasoning essential for students to succeed in a variety of mathematical contexts, it is also necessary in many other subject areas, such as art, geography, and science (Akatugba and Wallace 2009; Howe et al. 2011). Ahl et al. (1992) highlighted the importance of proportional reasoning, noting that it is a ‘pervasive activity that transcends topical barriers in adult life’ (p. 81). Further, it has been claimed that proportional reasoning is one of the most commonly used forms of mental computation in daily life and that a large proportion of the adult population cannot reason proportionally (Lamon 2007, 2012).

Children have an intuitive understanding of aspects of proportionality and it is now known that proportional reasoning develops gradually from the early years of schooling. Although Piaget and his colleagues claimed that the ability to formally reason proportionally develops in early adolescence (Piaget and Inhelder 1951/1975; Inhelder and Piaget 1958), research over several decades has shown that young children have an inherent sense of proportional relations and that if teachers can capitalise on their intuitive understandings, this can be useful in scaffolding more formal understanding later (see Boyer and Levine 2012; Jeong et al. 2007). According to Boyer and Levine, ‘early intuitive understanding continues to influence our mathematical skills even after the ability to perform formal mathematical operations emerges…’ (p. 517). According to Lesh et al. (1988), proportional reasoning is the capstone of elementary school mathematics.

Research has also shown that despite its importance for success in mathematics and other curricula as well as its centrality to everyday numeracy, proportional reasoning is rarely explicit in the school curriculum at any year level (Hilton and Hilton 2016) and many teachers need support in order to develop sufficient pedagogical content knowledge to teach it (Kastberg et al. 2012; Lobato et al. 2011; Sowder et al. 1998). These findings suggest that if teachers are to be able to promote students’ proportional reasoning, they must first have a strong understanding of the various elements and foundational concepts of proportional reasoning (subject matter knowledge) as well as pedagogical content knowledge that allows them to plan effective learning experiences to promote their students’ proportional reasoning. A key to addressing this situation is to identify effective ways of promoting teachers’ professional development in these important areas.

Challenges of teaching and learning proportional reasoning

A large corpus of research literature describes the difficulties that students experience with various aspects of proportional reasoning, and while it is not the purpose of this paper to discuss these, it is important to note that many of these difficulties are attributed to the ways in which proportional reasoning and its foundational concepts have been taught. These include teaching of concepts in isolation; failing to make connections between related topics, such as fractions and ratios; and not articulating differences between additive and multiplicative situations (Behr et al. 1992; English and Halford 1995; Sowder et al. 1998). Research has revealed that many teachers struggle with aspects of proportional reasoning concepts, making the same mistakes and experiencing the same difficulties as their students (Lobato et al. 2011) and as a consequence they may find it challenging to identify ways to support their students or they may lack the confidence to try. According to Sowder (2007), while teachers may be familiar with algorithms and procedures associated with proportional reasoning situations (e.g. fractions, multiplicative strategies), they may not have strong conceptual understanding. Further, Thompson and Thompson (1996) noted that even when teachers do have a strong understanding, they may still struggle to teach the concepts associated with multiplicative and fractional thinking to their students.

If teachers are to help their students develop strong proportional reasoning skills, they need the necessary content and pedagogical knowledge. These include having a deep knowledge of multiplicative concepts and how to use appropriate representations and learning experiences to develop them in students; an understanding of the developmental nature of proportional reasoning; the ability to distinguish between and characterise multiplicative and additive thinking and to provide appropriate contexts for students to engage in these forms of reasoning; the ability to recognise and build on students’ prior knowledge; and an awareness of potential misconceptions that may be held by students (Siebert 2002; Taber 2002). It follows that if this is the case, teachers need professional development opportunities that target their content knowledge as well as the development of their pedagogical skills and knowledge for teaching these important concepts to their students.

Teachers’ knowledge for teaching

Over the past 30 years, conceptions of teacher knowledge—what is needed and how teachers acquire it—have changed (van den Kieboom 2013). Since the 1980s, a common theme in much of the literature focused on the importance of teachers’ pedagogical content knowledge (PCK), a special form of content knowledge for teaching—knowing the most effective ways to present subject matter so that it is comprehensible to others (Shulman 1986). PCK enables teachers to identify concepts that are more fundamental or challenging for students and the most appropriate explanations, examples, demonstrations, analogies, and representations to support learners within the context of the learning environment (Loucks-Horsley et al. 2010; Park and Oliver 2008). For teachers to develop PCK, a strong knowledge of subject matter is necessary and without it, PCK development is limited (Veal and MaKinster 1999). Loughran et al. (2012) argued that in order to develop strong PCK, teachers must have ‘a rich conceptual understanding of the particular subject content that they teach’ (p. 7).

More recently, the importance of teachers having mathematical knowledge that is teaching-specific has been emphasised (Hoover et al. 2016). Hoover et al. (2016, p. 11) who conducted an extensive review of research literature on the topic, suggested that teaching teachers more disciplinary mathematics does little to enhance their knowledge ‘in ways that impact teaching and learning’. While there is no doubt that having sufficient content, knowledge is essential, skilfully teaching mathematics requires something more. Mathematics teachers must be able to make connections among different mathematical concepts, identify students’ misconceptions, evaluate representations, and use explicit mathematical language (Koellner et al. 2007). Hill and Ball (2009) also identified the types of mathematical understanding required by teachers, including the ability to pose appropriate questions, to interpret and analyse the answers given by students, knowing how to provide explanations and examples that are accessible to students, and choosing the most useful representations and making connections between representations in different modes. Ball et al. (2008) also argued that teachers must be able to unpack mathematical concepts and representations so as to make particular content visible and accessible to students. They were critical of Shulman’s original work (Shulman 1986), arguing that the definition of PCK lacked clarity, and suggested that after 2 decades, it remained inadequately understood. Ball et al. elaborated on Shulman’s model by subdividing two of his categories, subject matter knowledge and PCK, as shown in Table 1. These are known collectively as mathematical knowledge for teaching (MKT). Ball et al. described MKT as ‘the mathematical knowledge needed to carry out the work of teaching mathematics’ (p. 395), adding that they intended ‘teaching’ to include all that teachers must do in their work to support their students’ learning.

Table 1 Descriptions of the domains of mathematical knowledge for teaching with proportional reasoning examples.
Full size table

It is important to acknowledge that despite the amount of research conducted over the past decade on mathematical knowledge for teaching, the field continues to lack a well-defined and shared conception of what this actually entails (Hoover et al. 2016). There have been numerous approaches proposed to adapt or improve the original MKT model (Aslan-Tutak and Adams 2015). Carrillo and colleagues argued that all knowledge is specialised and that the MKT model requires refinement. Flores et al. (2013) based their arguments for refinement of the model on the notion of SCK as purely mathematical knowledge; however, this would appear to conflict with the way in which Ball et al. (2008) initially defined it—they included skills such as the ability ‘to select examples with pedagogically strategic intent’ (p. 401). Indeed, Flores et al. argued that specialised knowledge requires ‘more aspects than meanings, properties, and definitions’ (p. 8) and we agree, however, this statement seems more aligned with the original intention of the MKT model than these authors suggest. Carrillo et al. (2013) proposed that instead of focusing on SKT, or indeed MKT, there should be a recognition of mathematics teachers’ specialised knowledge and in response, they proposed the MTSK model. While this model has merit, it has not been widely adopted in the years since its development, whereas there continues to be widespread use of the MKT model for researching teachers’ mathematical knowledge, skills, and pedagogical approaches.

Research around MKT has shown that these forms of mathematical knowledge for teaching are strongly related to the quality of teachers’ mathematical instruction (Hill et al. 2008). The challenge is to identify ways in which to develop teachers’ MKT. Ball et al. (2008) argued that research is needed to examine the impact of different approaches to teacher professional development on teachers’ PCK and specialised content knowledge. Hurrell (2013) echoed these ideas advocating professional development to enhance teachers’ MKT. According to Hoover et al. (2016), recent studies have shown that professional development requires a combination of pedagogical and mathematical content to focus teachers on important mathematics for teaching. The following section outlines what is known about effective professional development in general and more specifically what is needed to develop teachers’ capacity to teach proportional reasoning and the MKT associated with it.

Professional development to promote proportional reasoning and MKT

The terms professional development and professional learning are sometimes used synonymously while at other times they are distinguished from one another. In this paper, a broad definition of professional development as offered by Day and Sachs (2004) is used:

… all natural learning experiences and those conscious and planned activities which are intended to be of direct or indirect benefit to the individual, group, or school and which contribute … to the quality of education in the classroom. It is the process by which, alone and with others, teachers review, renew and extend their commitment as change agents … by which they acquire and develop critically the knowledge, skills … essential to good professional thinking, planning and practice… (p. 34)

The need for professional development associated with multiplicative thinking and proportional reasoning has been widely recognised in the literature (e.g. Ben-Chaim et al. 2007; Sowder et al. 1998). Our previous research in a number of schools across Australia has also suggested the need for sustained professional development programmes to support teachers’ professional growth in proportional reasoning (see Hilton et al. 2016). According to Lobato et al. (2011), teachers who participate in proportional reasoning professional development can use more sophisticated strategies for solving problems involving proportional reasoning. They also noted the necessity to focus on enhancing teachers’ MKT.

Limited research has directly focused on the effects of professional development for improving mathematics teaching or students’ learning outcomes (Goldsmith et al. 2014; Hiebert and Grouws 2007). Too little teacher professional development is interactive or reflective, and much of it is disconnected from practice (Loucks-Horsley et al. 2010). Although Loucks-Horsley et al. suggested that professional development should provide opportunities for teachers to collaborate and engage in collegial reflection, they also cautioned that while essential, collaboration and reflection are not sufficient unless professional development focuses on addressing substantive content and pedagogical needs of teachers. This position has also been stressed by other researchers (e.g. Darling-Hammond and Richardson 2009; Hurrell 2013). According to Darling-Hammond and Richardson (2009) and Loucks-Horsley et al. (2010), research supports professional development that

  • is embedded in school reform and linked to curriculum and assessment;

  • provides opportunities for active hands-on learning, collaboration, and collegial discussion and reflection;

  • situates learning in familiar contexts and provides opportunities to apply it in practice;

  • creates cognitive dissonance;

  • supports teachers to develop teaching and formative assessment strategies;

  • uses formative assessment of teachers to provide a starting point for professional development;

  • supports teachers to become intentional in their selection of strategies and learning experiences; and

  • deepens teachers’ knowledge of how students learn specific concepts or content.

In order to teach effectively, teachers require procedural, conceptual, and metacognitive knowledge (Ammon and Kroll 2002). Kroll (2005) argued that these can be promoted through teachers using inquiry approaches as a way to analyse their own teaching. She added that coupling classroom-based inquiry with collaboration and reflection can assist teachers to develop stronger pedagogical understanding. This approach was also identified by Hoover et al. (2016) as an important finding from research that showed that ‘cycling through mathematical considerations, pedagogical considerations, and reflective enactment is vital to the design of professional development’ (p. 13). They added that such a cyclic design increases teachers’ motivation both during workshops and in their classroom practices. Further, the review of research conducted by Hoover et al. (2016) revealed that professional development that promotes teachers’ MKT engages them with mathematical knowledge that is situated in their practice. They called for professional development that provides opportunities for teachers to learn in and from their practice.

The use of inquiry approaches by teachers has also been advocated by other researchers as a means of improving teacher performance, and teachers have been urged to undertake continued professional development through reflective practice and research (e.g. Meijer et al. 2016; Scheerens 2010). Practitioner research as a form of inquiry has been described as an effective means through which educational practices can be investigated and consequently reconceptualised and transformed (Campbell and Groundwater-Smith 2010; Ellis 2012). The literature abounds with many definitions and descriptions of practitioner research. In the context of the current study, we regard practitioner research to be intentional and systematic research done by practitioners in their own contexts (Campbell and McNamara 2009; Heikkinen et al. 2016). Practitioner research may involve individual teachers, collaborative groups of teachers, or teachers working with researchers (as is the case in the current study) (Cohen et al. 2007; Willegems et al. 2017). Cohen et al. noted teachers will be more likely to change their attitudes or behaviours if they have been involved in practitioner research that demonstrates to them that change is needed and that it can be achieved.

Taken together, the findings about what makes teacher professional development effective and the research evidence around teachers’ need for further professional development about proportional reasoning support the design of professional development that involves cycles of workshops focused on subject matter and pedagogical knowledge interspersed with inquiry through practitioner research. Such a design allows the professional development to be participant-centred, collaborative, context-specific, and to target multiple aspects of teachers’ content knowledge and pedagogical needs. As argued by Thomas (2007), too many professional development programmes can be criticised for failing to promote transfer of knowledge to the classroom or to give teachers opportunities to apply their new knowledge or skills. The use of practitioner research has the potential to address this criticism when it engages teachers in enacting new knowledge or skills in their classroom and investigating and reflecting on the effects of their enactment on students’ outcomes.

This paper reports on the first year of an ongoing programme designed to focus on selected year levels each year and gradually expand across the school. A decision was made by the teachers in collaboration with school administration regarding which year levels would be involved in each year of the study, with the Year 3–5 teachers volunteering to be involved first. This small number of participants made it possible to focus deliberately on their learning needs and to devise very specific teaching interventions as a means of developing both their subject matter knowledge and their PCK. The research questions that are addressed in this paper are: (1) What is the impact of a professional development programme that utilises a series of structured mathematics interventions on primary school teachers’ MKT? (2) What aspects of this form of professional development make it effective for developing MKT?

Method

Setting and participants

The setting for this study is a large public primary school in a provincial town in Queensland, Australia. The students at the school are from mixed socio-economic backgrounds and the classes are mixed ability. The participants in the study were eight Year 3, 4, and 5 teachers and their students. All teacher participants volunteered to take part in the study. The two curriculum coordinators also participated in the study. The student participants were from four Year 3 classes, one Year 4 class, one composite Year 4/5 class, and three Year 5 classes. In total 98 Year 3 students (8 years of age), 37 Year 4 students (9 years of age), and 69 Year 5 students (10 years of age) participated. The focus of this paper is on the eight teacher participants. Informed consent was obtained from all participants before conducting the study. The data reported in this paper are from the eight teacher participants.

The professional development programme

The professional development workshops

Prior to the workshops, we conducted some activities to help us gain insights into the content and pedagogical needs of the teachers, thereby allowing the professional development to be designed to address these needs and to provide opportunities to connect the learning with the teachers’ classroom practice, as suggested in the literature (e.g. Hoover et al. 2016; Loucks-Horsley et al. 2010). The teachers attended a 3-h pre-programme information session about the professional development and the nature and importance of proportional reasoning. Following this session, several of the teachers self-identified as lacking confidence in their mathematical content knowledge and in their understanding of proportional reasoning. In fact, when asked about proportional reasoning in this session, most teachers were unable to explain what it is or to identify the key conceptual areas that it involves. They also asked for help with teaching strategies that would allow them to better develop their students’ proportional reasoning skills. The teachers also completed a diagnostic instrument (previously used with students in the middle years). This instrument’s development and use with over 2000 students have been published elsewhere (see Hilton et al. 2013, 2016). The items cover concepts and reasoning expected of students by the end of the middle years of schooling, which are commonly used in everyday situations. As such, the content addressed by the items focused on CCK. The teachers’ responses allowed us to identify the conceptual aspects of proportional reasoning that the teachers found most challenging, which provided us with important information to aid in the design of the workshops.

Given that the teachers’ needs were related to both subject matter knowledge and PCK, we designed a series of full-day workshops. We combined the extensive literature around teachers’ needs regarding proportional reasoning with our own research findings from the past 10 years to design workshops that would address teachers’ content and pedagogical needs by engaging them with a combination of content-specific materials, hands-on activities that illustrated how the teachers might teach the content in their classrooms, and reflection on practice. Table 2 provides a summary of the focus of the four workshops and the interventions. Each workshop was conducted over a full school day (i.e. 5–6 h), and all workshops were attended by all participants. The workshops occurred near the beginning of each school term (of which there are four each year). According to Hoover et al. (2016), the closeness of the relationship between the content taught in workshops and that subsequently taught by teachers influences the positive effects of professional development. This approach was supported by the researchers who taught model lessons as a follow-up to each of the workshops. The model lessons involved one of the researchers teaching a lesson about the content from the workshop, using some of the activities and resources discussed during the workshop. After model lessons, debriefing sessions were held with the teachers to discuss the lessons and resolve any questions they had.

Table 2 Workshop focus and sequence
Full size table

Much of the material presented in each workshop was designed for use by the teachers in their classrooms. The activities were presented as they would be to students and the teachers were taken through the activities themselves so that they could experience the intended thinking and learning that they might expect their students to experience. Each activity was discussed in terms of the mathematical concepts as well as the ways in which the teachers might use the activities and how they might plan to embed them in their programmes. The curriculum coordinators who attended the workshops also worked with the teachers between workshops to build on their learning from the workshops and interventions to plan learning activities in other curriculum areas, both within mathematics lessons and beyond. As the year progressed, the teachers began sharing resources and teaching lessons for one another to share their practices. These lessons were observed by the curriculum coordinators who provided feedback and planning support to the teachers.

The practitioner research interventions

As shown in Table 2, at each of the first three workshops, the teachers were given an intervention that they could implement in their classrooms between workshops. Each intervention was designed and timed to provide opportunities for the teachers to learn from integrating new ideas and activities into their teaching as suggested by Hill and Ball (2009), with the goal of promoting transfer of the workshop content into practice. The interventions aimed to:

  • Provide teachers with a scaffolded means of applying what they learned in each workshop;

  • Guide teachers in the development of aspects of proportional reasoning with their students;

  • Provide models for teachers to use in the development of classroom approaches, language, strategies, and resources; and

  • Allow teachers to reflect on and collect data about their students’ progress as a result of the implementations.

We also took the curriculum focus of each term into account.

All interventions were designed for teachers to use in their classrooms as whole-class discussions with student-focused activities. The interventions involved representations, either visual or physical, and in the case of Interventions 2 and 3, they required students to physically manipulate materials. Interventions 1 and 2 were heavily scripted to help the teachers to direct the students’ discussion and language development through prompts and questioning, while Intervention 3 was less prescriptive in timing and wording, which allowed the teachers to have more input into the interventions. There was space on each script for teachers to record observations and reflections.

These interventions were designed to engage the teachers in practitioner research. The teachers were not experienced in conducting structured, systematic, intentional research, having mostly conducted more informal inquiry that was directed by their school district. Each of the interventions was structured and scaffolded by means of scripts and discussion prompts to allow the teachers to develop knowledge in multiple areas and included data collection and reflection components. The researchers and teachers collaboratively developed the research questions and the researchers developed the data collection instruments; however, the teachers were able to choose when and how they collected the data and they spent time sharing, discussing, and reflecting on the data they collected, both in year level meetings and at the workshops. The second and third interventions included pre- and post-intervention instruments to allow the teachers to establish their students’ prior knowledge and to determine their progress as a result of the intervention. Intervention 1 had no quantitative data assessment because the concepts were being dealt with qualitatively, and there was minimal requirement in the first intervention for children to undertake calculations. The main goals of this intervention were to focus on development of mathematical language and conceptual understanding and to introduce the teachers to undertaking their own guided research in their classrooms. During this intervention, the teachers made classroom observations and recorded notes regarding the improvement in their children’s understanding and use of language and some teachers video recorded their lessons as a means of collecting data related to the intervention. The participating school engages all its teachers in ‘data cycles’ every term, which involve inquiries into a specified area of curriculum or teaching. The participating teachers decided that they would use the second and third interventions to research their students’ learning as their chosen ‘data cycles’ during the terms in which they conducted the interventions. They collected and analysed the data from the pre- and post-intervention instruments and met together with the curriculum coordinators to discuss the results for their own classes prior to the next workshop at which time was allocated for discussion and reflection about the outcomes of the intervention with the researchers. The teachers also spent time at the workshops reflecting on each intervention and the data they had collected and the intervention’s impact on their own learning as well as that of their students.

Table 3 shows the timeline and a summary of the nature of the interventions. A detailed description of the first two interventions can be found elsewhere (see Hilton and Hilton 2018; Hilton et al. 2015); however, sample activities from Interventions 1 and 2 are also provided in “Appendix 1”. For each of the first two interventions, the teachers were given a script that contained a structured series of discussion prompts and questions to be used on each of 4 days per week for 2–3 weeks (depending on the intervention) although some teachers extended interventions to 3–5 weeks in response to student or curriculum needs. It was envisaged that each day’s activities would require around 10 min, although the teachers noted that they often spent longer because of the depth of discussion or because they were able to focus on the use of language or target the children’s interests and learning needs. In addition to discussion prompts and suggested questions, the teachers were also provided with a glossary of terms to ensure that they all used accurate and consistent mathematical language when conducting the interventions (this is shown in “Appendix 3”). The main reasons for providing the scripts and glossary for the teachers were to ensure that the interventions were consistently implemented across all classes by all teachers and to support the teachers who felt unsure about their own subject matter knowledge or about how they could promote their students’ understanding of proportional reasoning and the language of proportion. That said, the teachers were teaching across Years 3, 4, and 5 so there was a need for teachers to exercise professional judgement in the ways that they implemented the interventions, the scaffolding and differentiation they chose to use, and the timing of the various components of the interventions. The third intervention was less heavily scaffolded (in that it did not include scripts) and contained more materials and lessons than would be usable within a 2–3 week timeframe. This allowed the teachers to build on their experience from the previous two interventions when selecting examples and representations, and when formulating their explanations and questions. It also allowed the teachers to use their own professional judgement as to which concepts were appropriate for the year level taught, their students’ learning needs, and curriculum requirements.

Table 3 Timing and focus of each intervention
Full size table

Data collection

Focus group discussions

Data were collected in several ways. Firstly, focus group discussion and reflection sessions were conducted at the workshop that followed each of the interventions. The teachers were asked to reflect on each intervention in terms of the resources, script/discussion prompts, and target concepts, as well as the benefits and challenges associated with its implementation. They were also asked to describe any changes that they would make should they use the intervention again with future classes and to reflect on the impact of the interventions on their own knowledge and teaching strategies. As mentioned previously, the teachers also collected data about their students’ progress during each intervention. These were also discussed in the focus group discussions. Field notes and audio-recordings were used to record focus group data.

Semi-structured interviews

Data were collected using semi-structured interviews at the end of the first year (after Intervention 3 and Workshop 4). The questions are shown in “Appendix 2”. Because of the small number of participants, it was possible to interview all of them. The two curriculum leaders who attended the workshops and participated in the focus group sessions at each workshop were also interviewed. Each interview was about 20 min in length and focused on the participants’ perceptions of how their content knowledge and pedagogical approaches had changed during the year. They were also specifically asked about the interventions, whether they had impacted on their learning, and if so, in what ways. The interviews were audio-recoded.

Classroom observations and reflections

For each of the interventions, the teachers were asked to annotate the scripts to indicate any reflections they made during the intervention. They also recorded observations of the ways in which students responded to the questions and activities and any changes, additions, or adaptations the teachers made. The teachers’ annotated scripts were collected and used to supplement the data from the focus group sessions. As mentioned previously, some teachers chose to video record their teaching of some of the interventions and the researchers conducted observations of some of the lessons taught during the interventions. As with the teachers’ scripts, the classroom recordings and observations were used to collect further evidence to support the analysis of data from focus group sessions and interviews.

Data analysis

All responses were transcribed verbatim and analysed using NVivo. A pragmatic approach guided the thematic analysis of the responses, which took both the theoretical framework and research questions into account (Patton 2002; Saldaña 2013). The responses were broken into idea units, each of which contained one key piece of information as suggested by Gee (2005). In order to address Research Question 1, responses from the focus groups and interviews were coded in terms of their alignment with the descriptions of the domains of MKT (shown in Table 1). The coding for Research Question 2 focused on identifying those aspects of the interventions that participants identified as impacting on their learning. Initial broad themes were generated, and as the review proceeded, sub-themes were generated to identify which aspects of MKT were impacted. All coding was carried out independently by each of the authors with outcomes of the coding compared and discussed. Re-coding was done where necessary until agreement was reached (Cohen et al. 2007). The classroom observations and video recordings of lessons as well as the teachers’ scripts were used to verify the interpretations of the teachers’ comments made during the focus group sessions and the interviews. In particular, these were used to identify illustrative evidence to support the thematic coding of the interview and focus group data in answering Research Question 2.

Results

Research Question 1: impact on MKT

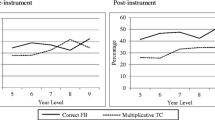
Research Question 1 was answered using data from the focus group sessions as well as the semi-structured interviews. There was evidence that using the interventions impacted on all six domains of MKT for most teachers, although some domains were impacted more than the others. Table 4 shows data from the analysis of the responses from the focus groups and semi-structured interviews of the eight participating teachers. It indicates each of the domains with the number of teachers who referred to them and an example of the response coded in each. As shown in the table, all teachers referred to SCK, KCS, and KCT, with most teachers also referring to CCK and KCC.

Table 4 Semi-structured interview and focus group data: sample response for each domain
Full size table

Research Question 2: aspects of the interventions that supported MKT development

A number of themes emerged relating to the ways in which teachers felt the interventions had influenced their learning. The themes related to the functioning of the interventions as formative assessment; support for development of teachers’ mathematical explanations; the embedded language use and focus on mathematical terminology; connectedness between proportional reasoning and other curricula; the nature of the representations used; and the structure of the interventions. Each of these themes is described in turn with representative quotes and the aspect of MKT they reflect. This is followed by a classroom vignette to illustrate these themes.

Interventions promoting formative assessment

The teachers felt that implementing the interventions and the pre- and post-intervention data collection instruments provided them with opportunities to learn about students’ understanding and gain feedback to inform their planning and teaching practices. Their comments suggested that this impacted on their KCS, KCT, and SCK. They felt that the interventions helped them to ‘see’ students’ thinking and analyse their errors (KCS). This in turn informed teachers’ planning to better address their students’ errors/difficulties (SCK). For example, ‘At the start, I didn’t have many applying multiplicative strategies, even though I tried to direct them towards that. The children used known values to find the interval value and then added or subtracted in order to find the missing numbers…’ (Teacher 2). The assessment opportunities afforded by the interventions also allowed teachers to plan an explicit focus and to differentiate their lessons (KCS, KCT) as well as promoting reflection on their teaching (KCT):

It is just wonderful to check on your teaching – whether you are being explicit enough or whether children understand, whether there is movement before or after, it is a brilliant tool to use. It can certainly pinpoint areas that we may need to focus on and to target with differentiation. (Teacher 6)

Modelled explanations

The intervention scripts included question prompts and explanations of target concepts. The teachers felt that this assisted them to learn new ways to explain proportional reasoning concepts more clearly to students (SCK, KCT), for example, ‘Sometimes you gave me exactly the sentence I needed to go back and explain it. They (the interventions) have been really beneficial and I have applied them… They help you to be really explicit in your teaching’ (Teacher 3). The teachers also stated that the interventions modelled ways in which to use mathematical language in their explanations (SCK) and provided ideas for explicit teaching strategies (KCT): ‘I make sure I use that kind of language explicitly, “OK Michael’s thinking multiplicatively but Ian is thinking additively—we got the same answer but we thought about it differently”’ (Teacher 5) (pseudonyms used).

Embedded language use

A specific goal of the interventions was to embed as much mathematical language as possible to assist the teachers in becoming familiar with the terminology and in modelling the use of the language to their students. The teachers made multiple comments about the ways in which this explicit focus on language impacted on their learning. An important aspect was that it helped them to consolidate their understanding of the terminology and the associated concepts (CCK): ‘It helped me to develop my own understanding of the content and the language first before I could feel confident to use it with the kids…,’ (Teacher 6). The teachers also mentioned that this changed their teaching approaches and ways of explaining (KCT): ‘Having the language to teach it to the kids has changed my teaching fundamentally really’ (Teacher 1); and it gave them a common vocabulary to use with students and one another (CCK, KCT): ‘Having a common vocabulary—to my mind that’s most important—you want to start the common vocab on the things that everybody does from Prep to 6’ (Teacher 4). The teachers felt that their use of mathematical language had impacted on their students and that developing students’ language use allowed the students to explain their thinking (KCS). The teachers noted that learning new mathematical language also increased students’ interest and motivation (KCS): ‘It’s just the enjoyment for them—being able to express themselves using that language, it’s incredibly powerful and very important’ (Teacher 5).

Highlighting connectedness

The interventions helped the teachers make and identify connections in multiple ways. Firstly, they helped the teachers make connections among different mathematical concepts (HCK):

I have tried to see more links between one bit and another. I find when I am teaching mathematics, I can’t help myself – you know – when I’m talking about multiplication, I end up talking about division and then I’m thinking, ‘Oh we can do place value at the same time,’ so I’ve got 120 and 12 going at the same time and I always keep layering on as much as possible. (Teacher 1)

They also allowed the teachers to see ways in which proportional reasoning could be emphasised in other curriculum areas (KCC): ‘The skills we learn in maths are going to be used in other subjects so I am probably much more aware of planning … looking where proportional reasoning can be identified in other subject areas’ (Teacher 2).

Use of multiple representations

The interventions used a range of representations in multiple modes. Intervention 1 used graphical, tabular, and pictorial representations while Interventions 2 and 3 used physical representations and symbolic representations. These were combined with textual and verbal representations through the scripts and discussion prompts. These multiple representations allowed teachers to make connections for students and highlighted ways to represent concepts that the teachers hadn’t previously considered (KCT):

The interventions offer it (the content) in different contexts and in different ways. Instead of always starting my number line at 0, which is what I would have done before, I really have thought about different ways of representing information or things to children’ (Teacher 5).

The teachers also talked about the physical resources supporting their students to think, visualise, and explain (KCS):

I think it is a result of both using physical material and also doing it more often. When we used the counters, you could just see the joy of manipulating them and making groups and then just being able to move them around and try out their thinking. They still need that concrete manipulation, they still can’t visualise … they have been able to change things and move things around – they like it.

Structured interventions

The sequenced lessons and accompanying scripts acted to model ways to sequence the learning to develop students’ concepts and language as well as to support teachers in their ability to pose mathematical questions (KCT): ‘It got easier as I got more practice at using the language and the questions—the ability to refer to the notes meant that I could make sure that I asked the right questions …’ (Teacher 7). The question prompts were also sequenced so that they allowed the teachers to move from situations involving less challenge to those requiring more complex reasoning. The teachers noted that this helped them to use questioning more effectively (KCT): ‘It was quite good because it had some of those prompts—the sorts of questions we should be asking to elicit that higher order thinking…’ (Teacher 8).

A classroom vignette to illustrate the results in practice

In the interests of brevity, this vignette comes from only one lesson in Intervention 1 by Teacher 3. The purpose of this vignette is to illustrate the themes described previously in a practical situation. Pseudonyms are used in the transcript. The photograph of the day was from a classroom in rural Africa. Without showing every desk, it showed enough detail to extrapolate the number of rows and desks per row. The following was included as the discussion prompt for the teacher:

  • Here is a classroom in Africa. We can’t see all the desks but is there a quick way of estimating how many desks there might be? ANS: count a row, and count a column/line and then multiply. (Multiplicative thinking)

  • If this was a Year 1 classroom, how many children do you think might sit at each desk? ANS: various but consider reality. How many Year 1 children could sit in this classroom according to your calculation? (Multiplicative thinking, relative thinking)

  • How many Year 7 students might fit in each desk? ANS: various but consider reality. How many Year 7 children could sit in the classroom according to your calculation? (Multiplicative thinking, relative thinking)

  • Why does the number of children able to sit in the room change? ANS: relative size of children and ratio of children per desk. (relative thinking, co-variation)

At the start of the lesson, the teacher revised the language that the class had been using. (These were written on the board)

T:

Let’s talk about the words that we might use when we look at the next slide in the proportional reasoning activity

S1:

Comparing

S2:

Width, length

S3:

Relative size

S4:

Multiplicative thinking

T:

(Showing the new slide) How many desks are in the classroom? (A student starts counting in twos).

T:

Yes, but we can’t see all the desks, so how can we work out how many are there?

S5:

18

T:

How did you find that answer?

S5:

I counted in twos in the row and then found how many across.

T:

Yes, how many in a row (counting to six) and how many across (counting to three). So, if there are three across and six in each row, how do we get 18?

S6:

Because 3 times 6 is 18

T:

(Creating a line drawing on the board to represent the desks producing a diagrammatic version of the photograph)

T:

(After creating the diagrammatic representation) Three multiplied by six equals 18 and writes 3 × 6 = 18 on the board at the same time.

T:

So, instead of counting all the desks in ones or twos, we can count the rows and the desks in each row and multiply. (Turning to a group of desks in the actual classroom) How many people would be able to sit over there?

S7:

Two times four is eight.

T:

Well done—you’ve just used multiplicative thinking. Now, there are 8 there, 8 there and 8 over there. How many people altogether sit at these desks?

S8:

24?

T:

Yes, because three lots of eight make 24. So, we can do the same kind of thinking in our own classroom even though there are different shapes and different arrangements. Let’s look back at the photograph. Think about the relative size of the books on the desk. How many children do you think could sit at each desk?

S1:

I think you could fit three children.

T:

Yes, I agree—aha—immediately, I see that Jenny has begun counting in threes—so we know there are 18 children in each row of desks so what next?

S9:

We times 18 by 3?

T:

Yes, how do we do that? (writing the calculation out on the board)

S10:

54.

T:

(Representing the three children per desk on the previous line diagram). The answer could be obtained by finding 10 × 3 and 8 × 3 and adding together. Using multiplicative thinking means that instead of having to count all the children you can use multiplication to help. Now please turn around.

(Children move to face the back of the room)

T:

There are some posters here. How many are there in each row?

Students:

4

T:

How many rows are there?

Students:

3

T:

So how many posters are there?

Students:

12

…

T:

What about the windows on the side wall—two rows of three—how many?

Students:

6

T:

Excellent, two lots of three make six.

(Returning to the photograph)

T:

Now before we guessed three children per desk, and I think that was a pretty good guess for children who are like you in Year 3. But what if—imagine this is a Year 9 classroom. Will that change the number of people you can get in the classroom? What do you think?

S5:

It will change because Year 9 children are bigger.

T:

(Sitting on his chair) How many men can fit on my chair?

Students:

1

T:

How many Year 3 students fit on the chair? (Asking volunteers to sit on the chair)

Students:

2

T:

Two, so what can we say about the relative size of people and how many fit on the chair? Let’s think about what Benjamin just said about the Year 9 students being bigger. Are we going to fit more or less people in this room?

Students:

Less

T:

I hear Andrew Smith saying 2—why are you saying that?

S11:

Because there would be two Year 9 s in each desk.

T:

So, if we have two per desk, let’s change our array (goes to diagram on board and modifies it to show two students per desk). So, if we now have two per desk, how many students will fit in this room?

Students:

36

T:

So, as the size of the people goes up, the number you can fit in the room goes down. That’s co-variation. What about if you had pre-schoolers?

S11:

Five to a desk

T:

Wow OK, so eighteen desks and five to a desk would make (working together with class on board).

How many?

Students:

90

T:

90 preppies—is that realistic?

S12:

I think the teacher would be frustrated—you’d need three teachers.

T:

So, the older the students are, what happens to the number of teachers? (discussion about pre-school, high school, university classes, class debriefs and lesson ends).

The following brief descriptions aim to show how the activity supported the teacher and to illustrate the themes identified in the analysis of the teachers’ responses:

Promoting formative assessment The teacher asked the questions suggested in the script (shown at the beginning of the vignette in italics), sometimes of individual students and sometimes of the class as a whole group. Apart from these, all other questions in the vignette are the teacher’s own question, which the teacher used to determine the reasons for giving certain answers and to check for understanding. The questions about the students’ own classroom were designed to check the students’ understanding in a different context using desks, windows, posters.

Modelled explanations The script for this photograph included prompts that were used by the teacher as a guide, but he clearly adapted some and added his own questions to direct the learning experience to include more than the suggested prompts. The prompts were written for teachers of Year 3–5 students, and there was no expectation that they would all use them verbatim but rather adapt them as appropriate for their students. In this case, the teacher chose to ask the questions in different ways to accommodate his students, who were in Year 3.

Embedded language use At the start of the lesson, the teacher revised the language that the class had previously used with other photographs. He then used the situation in the photograph and the students’ responses to his questions to continue to use certain language (e.g. multiplicative thinking, relative size, array, co-variation).

Highlighting connections Throughout the lesson, the teacher made connections between the situation in the photograph and the students’ own context. He asked questions to make links between the photograph and the desks in the actual classroom as well as the posters on the wall and the arrangement of the windows. He also made connections between the number of students and the number of teachers that would be required in different situations.

Using multiple representations The teacher used multiple representations in multiple modes. He re-represented the photograph in diagrammatic format. He then used the information in the diagrammatic array to discuss how to calculate the number of desks in the room, adjusting it to represent different numbers of children. He wrote the calculation on the board and also said it aloud. He showed the children multiple ways to find the answer (e.g. 18 × 3 = 54; 10 × 3 + 8 × 3 = 54).

Scaffolded interventions At the beginning of the intervention, the video recordings showed that the teacher followed the scaffolding script and prompts almost verbatim. As he progressed through the lessons, he began to adapt and extend the activity to include his own ideas. The lesson described in this vignette occurred towards the end of the intervention. In the teacher’s own words,

This has really helped me to become better at spotting things and being able to analyse what I do and why I do it. I went from using the script closely to being able to take it further. The ways in which I explain it to the children have changed a lot. I’m now learning to incorporate more of the vocabulary from the glossary as much as possible. (Teacher 3)

Discussion

The goal of the study was to promote the teaching and learning of proportional reasoning; however, in this paper, we have focused on the impact on teachers rather than on student learning. The professional development implemented with the teachers in the first year of the study was designed to respond to teachers’ needs around both subject matter knowledge and PCK around proportional reasoning. Initial discussion with the teachers revealed that they were facing the same challenges as have been described elsewhere in the literature (e.g. Behr et al. 1992; Lobato et al. 2011; Sowder 2007). These challenges included lacking confidence in content or pedagogical knowledge; not being cognisant of the connections between the different aspects of proportional reasoning; teaching individual concepts without making connections between topics; and not explicitly articulating the foundational concepts that underpin proportional reasoning, such as relative thinking, fractional concepts, and distinguishing additive from multiplicative thinking; and not being familiar with the mathematical terms associated with these areas.

This paper has addressed two research questions. The first research question focused on how the implementation of structured interventions as a form of professional development supported teachers in the development of their mathematical knowledge for teaching (MKT). The results indicate that using this approach was beneficial for the teachers across all aspects of MKT, including their horizon content knowledge (HCK), knowledge of content and curriculum (KCC), and their common curriculum knowledge (CCK), but that the strongest influences occurred in teachers’ specialist content knowledge (SCK), their knowledge of content and teaching (KCT), and their knowledge of content and students (KCS). This is perhaps due in part to the design of the interventions, which were focused on supporting these aspects of the teachers’ MKT, whereas the workshops placed more emphasis on developing the teachers’ CCK—their fundamental understanding of proportional reasoning concepts, terminology and representations, and the relationships among the various elements and foundational concepts of proportional reasoning (i.e. rate, ratio, scale, and relative, multiplicative, and fractional thinking). It makes sense to conclude that the transfer of this more fundamental knowledge into practice in the classroom via the interventions had a stronger impact on the key domains of PCK and teachers’ SCK. As Loucks-Horsley et al. (2010) argued, teachers’ PCK is reflected in their ability to identify concepts that are fundamentally important or that may be challenging for students and to choose best representations, examples, explanations, and demonstrations to make those concepts accessible to their students. The information presented in the workshops provided teachers with the concepts, connections between them, and ways of teaching them, focusing on CCK, SKT, and HCK development, whereas the interventions provided a scaffolded process through which the teachers could engage with these ideas in the contexts of their own practice, thereby enhancing SCK, KCT, and KCS. This supports the argument made by Hoover et al. (2016) that teachers’ MKT is developed when they undertake professional development that engages them with mathematical knowledge that is situated in their practice.

The second research question focused on identifying those characteristics of the interventions that promoted the teachers’ MKT. Two clear aspects emerged from the results. The first is that the interventions and the data collection opportunities acted as diagnostic tools for the teachers on multiple levels. They allowed the teachers to identify students’ prior knowledge and to monitor their understanding on an ongoing basis through the focus on student questions and the interactive nature of the activities. This provided the teachers with insights into the concepts that the students found challenging and their misconceptions (KCS). Through this ongoing formative assessment, the interventions also allowed the teachers to reflect on the effectiveness of various aspects of their teaching (e.g. their use of questions, explanations, and language and their choice of representations) (KCT). It also allowed them to analyse students’ errors and misconceptions and to develop ways to explain why their strategies were not valid (SCK). The second aspect of the interventions that led to improvements in the teachers’ MKT was that the interventions were scaffolded using scripts and discussion prompts and acted as models for the teachers by providing lesson sequences and explanations, modelling the use of mathematical language in explanations and questioning; providing questions that targeted multiple levels of thinking from recall through to higher order thinking, and drawing attention to the interconnectedness of the different areas of proportional reasoning (KCT, SCK). By providing these scripted model lesson sequences, the teachers were supported to implement the interventions and to enact their learning from the workshops.

At the beginning of the programme, as has been found in other research (e.g. Lobato et al. 2011), most of the teachers said that they lacked confidence to engage their students with some of the areas of proportional reasoning and as with many teachers, because the connections between the different areas were unclear, they were unsure how the focus on proportional reasoning might be relevant to their curriculum. After the first workshop and intervention, the teachers became much more responsive to engaging with further practitioner research because they started to make connections, became familiar with the mathematical language and concepts, and they realised that the consistent use of the mathematical language not only supported their students’ understanding but also allowed their students to articulate their reasoning more clearly. They also valued and used the data they collected about their students. This had numerous outcomes. The first was the immediate benefit that the teachers could identify the students’ reasoning. Secondly, the scaffolding and scripted nature of the interventions helped the teachers to feel more confident in their own understanding and in their ability to explain the concepts to their students. More broadly, these outcomes convinced the teachers of the need for changes in their practice and they were motivated to engage with further interventions as a means of enhancing both their own MKT and their students’ proportional reasoning. This finding aligns with that of Cohen et al. (2007) who suggested that teachers are more likely to change their practices, attitudes, and behaviours if they are involved in practitioner research that demonstrates both the need for change and how to they might achieve it. This also prompted the teachers to request model lessons from the researchers and to teach lessons for one another.

Thompson and Thompson (1996) noted that some teachers who have a strong understanding of proportional reasoning may still struggle to teach the concepts to their students. This was the case with some of the teachers in the current study. Those teachers who felt they had stronger content understanding initially felt that they would have no problems explaining concept to their students but when they began the interventions, the teachers discovered that they relied on the strategies with which they themselves were familiar or comfortable to explain the concepts. These teachers described the ways in which they benefited from the focus on language and multiple representations because this helped them to develop alternative ways of explaining the concepts to students and it supported them to explain to struggling students why their approaches were not working. This is further evidence that for these teachers, the interventions helped to develop their KCT and SCK.

Teacher change in general happens slowly. However, we believe that in the first year of this study that the teachers did make significant progress. The intensive nature of the professional learning workshops and the ongoing support from the researchers and curriculum coordinators while the teachers were implementing the classroom interventions resulted in the total number of hours in which the teachers were engaging in some form of professional development being far more than 4 days. They participated in an introductory session (3 h), four full-day workshops and implemented the interventions in each of the school terms. In addition, throughout each term the teachers worked with the curriculum coordinators to build on their learning from the workshops and interventions to plan learning activities in other curriculum areas, both within mathematics lessons and beyond. The teachers also watched model lessons presented by the researchers and they watched one another teach lessons planned around the intervention or workshop materials. These were supported by the curriculum coordinators who observed the lessons and provided feedback to the teachers. They used the outcomes of their research, especially the data collected during interventions to plan further lessons or to differentiate according to their students’ needs.

This paper has reported on the first year of a longer-term study, and the data reported are from a small sample of teachers in only one school. While this circumstance was considered an opportunity to focus specifically on the individual needs of the participating teachers, the study was limited to a single school context and teachers of only 3 year levels. For the participants in the first year of the study, the data show that the approaches used, and in particular the use of structured interventions as practitioner research to help teachers contextualise and make connections between the workshop content and their classroom practice, were effective for developing aspects of the teachers’ MKT. While the data indicate that all aspects of MKT were impacted, it is clear that for the teachers in this study, engaging with the interventions influenced some aspects more than others. Further research might focus on ways to help teachers further develop these other aspects of MKT. As the study proceeds, the possibility to conduct similar interventions with teachers of other year levels will be possible, which may extend the findings. In addition, ongoing work with the teachers who participated in the first year will allow us to investigate whether there are further changes in their MKT. Future research might also examine ways to support teachers to develop their own classroom-based practitioner research in which they devise their own interventions and use them to reflect on their practice and their students’ outcomes.

Conclusion

The broad outcomes of the professional development programme described in this paper included increased teacher confidence, ability to identify students’ problems, ability to determine strategies and materials that allow teachers to support student understanding, greater knowledge of content and how to represent it, as well as better understanding of how proportional reasoning connects within and beyond the mathematics curriculum. Now in the second year of the study, the same Year 3, 4, and 5 teachers who participated in the first year are continuing to develop resources and activities to support their students. They have built on the original interventions to adapt them for further use in their data cycles and they continue to invite one another into their classrooms to share practice around proportional reasoning. This study has implications for teachers, teacher educators, and policy makers. It has demonstrated that in addition to professional learning workshops, the use of short interventions that allow teachers to engage in practitioner research through which they can learn in and about their own practice can have a powerful influence on teachers’ mathematical knowledge for teaching. Utilising such an approach with cycles of professional development through workshops and practitioner research allows teachers to progressively build their knowledge and pedagogical strategies as they transfer their learning from the workshops into their practice, thereby promoting the development of stronger MKT.