Mathematics, lenses and videotapes: a framework and a language for developing reflective practices of teaching

Abstract

The VIDEO-LM project (Viewing, Investigating and Discussing Environments of Learning Mathematics) is aimed at enhancing mathematics teachers’ reflection on their professional practice, through watching and discussing videotaped lessons of unknown teachers. The discussions are guided by the use of an analytic framework, comprised of six detailed “viewing lenses.” In this article, we first provide a brief historical context of practicing teacher education, followed by the description of the framework we developed. We then present selected data from 17 implementation sites that illustrate the impact of VIDEO-LM courses on the professional growth of participants. Findings show that using the six-lens framework in video-based peer conversations supports the development of a reflective language, with which mathematics teachers engage in deep discussions about core issues of their profession.

Introduction

The importance of practicing teacher education was recognized long before mathematics education became an academic discipline of inquiry. Traditionally, it had diverse goals, such as improving the background and effectiveness of teachers, supporting the implementation of new curricula and strengthening teaching “skills” (e.g., Gibb et al. 1970; Bruckheimer and Hershkowitz 1983). Over the past three decades, four major developments have deeply influenced practicing teacher education: (a) Research findings have advanced the field’s understanding of student cognition and classroom functioning; (b) Standards-oriented educational reforms became widespread; (c) Theoretical advances in teacher knowledge and (e.g., Shulman 1986) were made; and (d) Many comprehensive international studies, assessments and classroom comparisons across the world were conducted (e.g., TIMSS and PISA), scrutinizing mathematics classrooms in different countries (e.g., Clarke et al. 2006; Shimizu et al. 2010).

These developments influenced the field of teacher education and are still shaping it. The very name “in-service education” (let alone “training”) gave way to “teacher professional development,” sometimes preceded by the adjective “continuous” or “ongoing.” From this perspective, professionalization processes need to be designed in ways that regard teachers as “serious learners in and around their practice, rather than amassing strategies and activities” (Ball and Cohen 1999, p. 4). Thus, nowadays the focus of professional development (PD) aspires to be much wider than at any time before: Both the content and the pedagogy of teacher professional education go beyond the knowledge of mathematics, the exercising of certain teaching techniques, the knowledge of curriculum and the knowledge of student difficulties. It certainly includes all the above but also much more. PD programs aim at professionalism which encompasses all “the internal workings of a profession and the concern of a profession’s members to do the best possible job for their clients” (Noddings 2001, p. 102). This also implies the “finding of ways to use practice as a site for inquiry, in order to center professional learning in practice” (Ball and Cohen 1999, p. 19), and it aspires to encourage and support the building of strong teacher communities which “can foster teacher learning and instructional improvement” (Borko 2004, p. 6). In our view, a main common component of these new directions is the need for development of sound professional tools such as reflection and informed decision-making. In the next section, we refer to several theoretical frameworks, which guided us in the design of tools that can be both meaningful and productive for teacher professional development.

Theoretical background

Following the target stated above, i.e., the design of sound professional tools for mathematics teacher development, we sought to create a sufficiently detailed “language” with which teachers can reflect on the mathematics teaching profession and on processes of decision-making within it. Our work in this direction is rooted in two main theoretical frameworks: “teaching in context” (Schoenfeld 2010) and “mathematical knowledge for teaching” (Ball et al. 2008). Another source of inspiration is the widespread and successful practical model, implemented on nationwide scales—the Japanese model of lesson study (e.g., Fernandez and Yoshida 2004) in which teachers communicate with each other within collaborative environments and develop established ways and norms to deeply reflect on their professional work.

The “teaching in context” framework (Schoenfeld 2010) presumes, firstly, that teaching is goal-oriented; that is, that when teachers are teaching at any particular moment, they are trying to achieve one or more goals. Such goals can be to present certain material; to have students discuss a topic or an idea; to establish or maintain a particular kind of classroom community; or, when things are going badly, to simply survive the lesson. Secondly, the theory asserts that teachers have a body of knowledge resources they can call upon, for both expected and unexpected situations. Thirdly, the theory suggests that teachers, like everyone else, have a series of orientations, including predispositions, biases and beliefs about mathematics, about students and about teaching, that shape their choice of actions. Schoenfeld proposes that goals, resources and orientations interact to shape how teachers teach (and therefore shape much of what students learn). It follows that PD programs for teachers should meaningfully involve explicit awareness to, and reflection of, these core elements of goals, resources and orientations in and around practice.

The “mathematical knowledge for teaching” framework (Ball et al. 2008) is based on the assertion that what teachers need to know in order to be competent goes beyond the mathematical content itself; it also requires a specialized kind of knowledge, such as acquaintance with students’ ways of reasoning and communicating; fluency in providing different types of examples; connections to previous and future mathematical ideas encountered by students; alternative ways to accessing new ideas and concepts; alertness to alternative and nonstandard ways of solving problems; and more. As with Schoenfeld’s theory, we believe that PD programs need to explicitly address the continuous development, revision and reflection upon this specialized knowledge.

These theoretical frameworks led us to suggest that teachers can and should be actively involved in a productive and deep reflection and analysis of their own (and others’) goals, resources and orientations and of their mathematical knowledge for teaching. Reflection and analysis not only include looking backwards per se, but they also involve pursuing and seizing opportunities to learn from such scrutiny in order to re-encounter the professional practice with new tools, insights and horizons. Reflection is not a new idea in education; Dewey (1910) was one of its explicit pioneers, although there may be earlier sources. Schön (1983) introduced the ideas of reflection on action and reflection in action, proposing that professional practitioners become action researchers. Based on the ideas of both Dewey and Schön, Ricks (2011) distinguished two broad categories of teacher reflection: incident reflection (isolated mental incidents not necessarily connected explicitly to future action) and process reflection, defined as an “active form of reflection that extends and links together separate reflective incidents into a cohesive mental continuum as ideas develop through action” (p. 252). Clarke (2000) proposed to differentiate reflection in, on and for practice. Reflection in practice occurs during classroom time and depends to a large extent on how the teacher interprets “live events” in light of his or her goals. Reflection on practice is usually contextualized within a wider setting, e.g., in conversations with school or PD colleagues, and can refer to occurrences that are not necessarily experienced personally. The third category, reflection for practice, is defined by Clarke as a purposeful action that refines knowledge or leads to new insights, and informs—and even predicts—teacher actions. Some theoretical models have been developed (e.g., McAlpine and Weston 2002) to describe the metacognitive processes of reflection on teaching, linking it to teachers’ decision-making and monitoring of actions.

Based on this literature, we define reflection as the detailed, analytical and careful observation of “what was done” in order to attempt to understand intentions, plans, actions and utterances and to consider alternative decisions and their possible implementation. We are aware that teacher learning is a very complex phenomenon, shaped by social contexts, school and national policies, teachers’ prior knowledge and predispositions, and more. However, we assume that an appropriate “curriculum for professional learning” as well as “a pedagogy for professional development” (Ball and Cohen 1999, p. 20, 25), developed in and around the study of practice, would also play a significant role in supporting teachers’ deep reflection; thus, such learning can potentially lead to modifications and enrichment of the teachers’ their own practices.

In the following, we describe the rationale of the VIDEO-LM project, the design of the 6-lens analytical framework, drawing on the models mentioned above, and the study conducted to evaluate the effects of VIDEO-LM professional development courses.

The VIDEO-LM project

Video as a stimulus for knowledge growth and reflection

The affordances of videotaped episodes as a source for several types of reflection have been investigated in a growing number of studies (e.g., Borko et al. 2011; Coles 2010, 2014; Lampert and Ball 1998; Santagata and Yeh 2013; Sherin and van Es 2009). Whether teachers watch their own or others’ lessons, there is initial evidence that reflection, noticing and ultimately revision of routine thinking and actions are enhanced (Clarke and Hollingsworth 2000; Santagata et al. 2005; Sherin 2004; Sherin and van Es 2009).

Generally speaking, there are three main objectives for using videotaped lessons as resources for mathematics teacher development. Firstly, video is utilized for introducing and modeling the implementation of new curricula, activities, pedagogical strategies, etc. (e.g., Seago et al. 2010). A second objective, which is becoming more and more prevalent (particularly in the USA), is to provide feedback and evaluation. Videos are watched using a preconstructed rubric, such as the TRU Math Scoring Rubric (Schoenfeld 2015) or the Mathematical Quality of Instruction rubric (Hill et al. 2008), in order to evaluate and improve the quality of teaching. A third objective is to enhance teachers’ proficiency to notice, understand and discuss students’ mathematical thinking (Sherin et al. 2011), usually in the form of “video clubs” (Sherin and van Es 2009).

The VIDEO-LM project (Viewing, Investigating and Discussing Environments of Learning Mathematics) was designed to address a fourth objective: The elaboration and use of tools for reflection on practice, in the senses described above, and the development of a productive language that supports deep conversations, i.e., conversations in which seemingly known issues are re-inspected in a new light and approaches not previously considered, are discussed. For that purpose, a special framework was carefully designed (see below). VIDEO-LM was envisioned as an intimate collaboration between teachers, teacher educators and researchers in mathematics education in order to promote mutual scaffolding of deep reflection and some reconceptualization of the mathematics teaching profession as frequently advocated (e.g., Clarke 2000; Potari et al. 2010).

The design of “viewing lenses”

In VIDEO-LM, we endeavored to design an analytic framework that teachers can use for watching and discussing videotaped lessons of colleagues unknown to them, which would bring to the fore which underlies the conceptualization of the mathematics teaching practice. Following previous initial experimentation with video-based discussions that centralize these ideas (Arcavi and Schoenfeld 2008), we further defined which analytical tools may be entailed in reflecting on resources, orientations and goals. In our view, resources refer mainly to the mathematical knowledge for teaching (Ball et al. 2008) and the ways this knowledge inspires, influences and drives the mathematical and meta-mathematical ideas that teachers choose to focus on when preparing a lesson and in class. Thus, reflection in this case refers to making explicit the mathematics around a certain lesson and providing opportunities to enhance and strengthen it. The goals for the lesson are derived by teachers from their implicit and explicit views of the mathematics at stake; thus, productive reflection further consists of explicating those goals, considering alternative goals, weighing decisions about which goals to pursue and which to postpone. Those goals are realized on the shoulders of tasks, and the Japanese lesson study model (Fernandez and Yoshida 2004) demonstrates how much attention may be devoted to the careful selection of a task, and how teachers can deeply reflect on its nuances and on different ways to implement it. Implementing a task in class implies conducting interactions with the students which pose dilemmas for the teacher and the need for immediate decision-making. The identification, articulation and discussion of these dilemmas and the ensuing decisions to be taken or to be dismissed are another key component of reflection. Finally, the teacher’s beliefs and values that guide actions and decisions are also a central element shaping the teaching practice. Thus, we envisioned the above elements as the focus of the reflection and the language to be developed. The outcome was a six-lens framework consisting of (1) mathematical and meta-mathematical ideas around the lesson’s topic; (2) explicit and implicit goals that may be ascribed to the teacher; (3) the tasks selected by the teacher and their enactment in class; (4) the nature of the teacher–student interactions; (5) teacher dilemmas and decision-making processes; and (6) beliefs about mathematics, its learning and its teaching as inferable from the teacher’s actions and reactions. This six-lens framework (henceforth, SLF) and its utilization in PD programs are characterized by the following features.

The teacher is at the center

Although students’ voices and actions are taken into account, the focus of the reflection is on the teacher’s actions and choices, whether these are derived from his or her decisions prior to the lesson, or developed as a result of classroom events.

Acknowledgement of different “best” practices

We believe that although there may be some agreed features of good teaching, for different teachers there may exist different best practices, contingent upon personal traits, contextual factors and cultural settings. Thus, the choice of lessons for observation is based on whether they can serve as springboards for meaningful discussions on different aspects of practice, rather than on alignment with criteria of how teaching should look like. In this sense, we adopted the motto “better than best practice” coined by Lefstein and Snell (2014).

Focus on the mathematics

This framework shuns generic discussions on teaching. Issues of classroom management, the teachers’ body language and other generic aspects are not the focus of conversations around videotaped lessons. Instead, SLF centers on what lies at the heart of mathematics teaching, that is, mathematical concepts, processes, and meta-mathematical issues. Furthermore, we chose to focus on middle and high school mathematics, and in particular on the advanced topics within it, that are often regarded as challenging to teach.

Away from evaluation and feedback

In line with the works of Jaworski (1990) and Coles (2013), the use of SLF attempts to establish nonjudgmental norms of discussion, through the redirection of highly evaluative comments into “issues to think about.”

Whole lessons as the units of analysis

Rather than clips or short episodes edited from a lesson, teachers’ discussions refer to the complete lesson, in which a more comprehensive “story” can unfold, with a beginning, a development and a closure.

Implementation of the six-lens framework (SLF) in professional development settings

As mentioned above, the six lenses are meant to accompany the observation and discussion of videotaped mathematics lessons and to trigger and guide reflective discussions. In a sense, the lenses support “vicarious experiences” which allow for indirect exploration of one’s own perceptions, experiences, ideas and credos through the observation of a third person. Our aim was that the repeated and guided use of this framework would become both an internalized tool for reflection on practices and a language with which mathematics educators and teachers can communicate with each other.

A typical VIDEO-LM course is built as a sequence of workshops around collective watching of videotaped mathematics lessons. Different watching modes may apply, depending on the lesson itself, and on the lenses we want to emphasize in the discussions. For example, prior to screening the video, the facilitator might ask the participants to elicit all the mathematical and meta-mathematical ideas (lens #1) they can associate with the topic of the lesson. These ideas, documented on the board, may later be compared to those pursued by the teacher in the videotaped lesson, leading to a discussion on what goals can be ascribed to this teacher (lens #2) that may explain the selection of some ideas over others. Another mode consists of requesting the teachers to first solve the tasks presented in the film they are about to watch (lens #3) and discuss their solutions and sometimes their possible uses in class (especially when these uses are expected to differ from the way the task was implemented in the videotaped lesson). The lesson itself may be either screened in predetermined sections or paused at points of interest raised by participants. Such pausing can also be performed with a subsequent invitation to predict the direction a lesson may take and to unpack those predictions. The role of the facilitator is to initiate a conversation related to one or several of the lenses, for instance, by asking teachers to consider one lens which may be strongly relevant to the specific video [e.g., interactions with students (lens #4) or the teacher’s dilemmas and decisions (lens #5)]. A technique we often use is to distribute different lenses and have groups of teachers within the same workshop watch the lesson with a specific lens. This compels teachers to concentrate on one aspect of the lesson and has the potential to generate lively exchanges when the results of the observations are shared, compared and contrasted. A central design principle is to lead a process of gradual exposure to the norms of VIDEO-LM. These include accepting a basic working assumption that the filmed teacher is acting in the best interest of his/her students; practicing the exercise of “stepping into the shoes” of the filmed teacher in an attempt to understand his/her goals, decisions and beliefs; maintaining a nonevaluative and respectful conversation; justifying suggested alternatives not as better or worse courses of action, but rather as a way to enrich the span of possible options, while considering the trade-offs involved.

The effects of VIDEO-LM: an evaluative study

A main question we posed to ourselves was: To what extent does VIDEO-LM attain its main overarching goals of (a) stimulating deep reflections about the practice of mathematics teaching; (b) fostering the internalization of the SLF framework as a tool for planning, acting and reviewing one’s own teaching; and (c) improving, or sharpening, teachers’ MKT?

Simply phrased: Does it work? And if so, how? In order to find answers to these questions, we conducted repeated implementations of our workshops around many videotaped lessons with different teacher populations, as detailed in the next section. Although the systematic analysis of our findings is still ongoing, we can already report interesting results.

Sources of data

During 2012–2015, we conducted 17 VIDEO-LM courses in nine different venues in Israel. Most of these courses were given in Regional Teacher Centres (RTCs) and open to secondary school mathematics teachers of the region.¹

Participants in each course met about 7–8 times throughout the academic year, each time for a 3–4 h session (total of 30 PD hours). A total of 212 teachers participated in these courses; all were mathematics teachers teaching in middle or high schools in various locations across Israel, including schools of minority sectors such as the Arab, Druze and Ultra-Orthodox Jewish sectors. The participating teachers’ levels of experience varied—there were new teachers, experienced teachers, lead teachers and a few teacher educators and school principals. All courses were facilitated by VIDEO-LM team members or by teachers who were specifically trained for this pursuit. Courses were somewhat different from one another, according to each facilitator’s approach and the evolving dynamic of the group, but all were aligned with the aims and agenda of the VIDEO-LM as described above, and in all of them SLF was used as a base for peer discussions. We documented a sample of these sessions (at least one session in each course). Documentation was mainly by video (in 11 out of the 17 sites). Due to some constraints², we had to use audio recording or field notes as the sole means of documentation (2 and 4 sites, respectively). In total, 45 sessions were documented, and selected episodes from recorded data were transcribed. In certain sites, we also collected written reflection assignments (7 sites) or answers to feedback questionnaires (5 sites), submitted by teachers at the end of the course as part of their final course duties.³ Finally, some RTC’s conducted external evaluation of the courses offered under their auspices. This was done for 8 of the VIDEO-LM courses, and these evaluations were collected. A table summarizing the course details and the data collection means appears in “Appendix”.

Data analysis methods

The analysis of the data is a continuous and complex effort that began on 2013–2014 (with the data gathered during 2012–2013), and is still ongoing. Various qualitative content analysis methods were applied, in an attempt to find evidence to diverse kinds of impact of VIDEO-LM courses. No single mode of analysis was utilized on the complete data corpus, as this would have been unfeasible in light of the data extent and the meticulous nature of analyses; rather, we applied each method to selected parts of the data, according to both availability of data at the time of analysis and the target of the analysis. Analysis methods include:

• (a) Comparing the language used by teachers in the beginning of the PD, to that used at the final sessions and in the assignments or questionnaires. Comparisons related to the frequency of judgmental comments, the nature of reflective expressions and the references made to the six lenses comprising the framework.

• (b) Analysis of teachers’ discussions based on the six MKT categories (Ball et al. 2008), which was performed using the following sequence of steps: Transcribing video or audio records of a PD session; Tracing all utterances of participants’ associated with MKT (i.e., unpacking mathematical concepts or relating to teaching these concepts); Grouping utterances into units of analysis that share similar ideas; Using the units to form “discussion maps” that convey the evolution of knowledge throughout different parts of sessions (Karsenty et al. 2015; Nurick 2015); Comparing utterances in the discussions before and after watching the video, using the six MKT categories. This type of analysis is exemplified below (see Example 1).

• (c) Characterizing teachers’ types of reflections through implementing a sequence of steps, based on the Grounded Theory methods (Glaser and Strauss 1967), as follows: Reading all the documented materials—both spoken and written—relating to the same lesson watched in various sites, and identifying themes associated with reflection on practice; Categorizing participants’ utterances by the themes identified; Building “theme narratives” in order to characterize teachers’ reactions in each category; Re-examining and refining the narratives.

Some evidence of growth in teachers’ knowledge was already reported (Karsenty et al. 2015), as well as preliminary findings concerning self-reflections (Karsenty and Schwarts 2016). In this article, we concentrate on the affordances of the six lenses as a distinctive viewing instrument for teachers. In the following, we present in detail each of the lenses and illustrate their use through examples and findings. Thus, for each lens we introduce a triple-layer account that interweaves (1) an elaborated description of the lens; (2) examples of its use; and (3) representative-related findings.

The framework, its nature and its functioning: some key findings

Lens #1: mathematical and meta-mathematical ideas

Using this lens in a VIDEO-LM course consists of scanning the space of the many possible mathematical and meta-mathematical ideas related to the topic of the lesson. We acknowledge that as mathematics educators, we do not always embark explicitly on such an exercise, but rather take these ideas for granted (based on our previous experiences, on what textbooks offer, on what students would need for upcoming exams, etc).

We found that for different PD participants, the notion of a “mathematical idea” may have different connotations. Take, for example, the following idea is related to the topic of functions and its representations: “In the Cartesian plane, f(x) = 0 is represented as the intersection of the graph with the x-axis.” Compare this to: “The main ideas behind the concept of function are dependency and variability.” This diversity in the “grain size” of elicited ideas allows for discussions about “the idea of idea,” leading to considerations of which ideas one may take into account and why, when it comes to preparing a lesson. We also found that many teachers are not used to discussing meta-mathematical ideas and the role they may play (or should play) in a lesson, whether implicitly or explicitly. Thus, elaborating on the status of a counterexample, for instance, or on the possible benefits of changing a representation or on heuristics for problem solving is an engaging and often unfamiliar activity for many teachers.

Our data analysis shows that discussing mathematical and meta-mathematical ideas explicitly with teachers triggers very productive conversations. Our criteria for identifying a productive conversation in this context are that (a) the discussion consists of open dialogues in which most teachers in the group are engaged; (b) participants consider the topic of discussion to be relevant to their practices; (c) teachers elucidate mathematical topics, and as a result, they enhance their knowledge; and (d) opportunities are created and seized for elaborating or re-inspecting mathematical and meta-mathematical issues, in ways which are viewed by teachers as novel or fresh.

When the space of mathematical and meta-mathematical ideas is made explicit, explored and discussed, teachers may have clearer reasons for choosing some ideas over others, since not everything is relevant or possible to be brought up in a lesson. Thus, one main question to be discussed under this lens is: Which ideas would we (fellow teachers) have chosen and which ideas were actually chosen by the videotaped teacher? How can we account for discrepancies between these choices, if any? This question not only enables teachers to overtly explore ideas related to a certain topic; it also helps to refine, rethink and re-connect among them, and sometimes even to learn something new, as we illustrate through two examples.

Example 1

(Data from site#1⁴). The discussions before and after watching a 7th grade lesson on the associative and commutative laws were coded in terms of the MKT categories (Ball et al. 2008). As explained above in the data analysis methods description, each unit of analysis was coded as reflecting Common Content Knowledge (CCK), Specialized Content Knowledge (SCK), Knowledge at the Mathematical Horizon (HCK), etc. Before the video was shown, teachers were asked to list mathematical ideas related to this topic. They suggested several ideas, from the simple fact that addition and multiplication satisfy both laws, while subtraction and division do not, to efficient solutions of multi-term exercises using them. The following excerpt demonstrates a unit of analysis from this part of the discussion, coded as KCS (Knowledge of Content and Students):

64:

T1: In 7th grade it’s difficult to construct a serious generalization, so you smooth it over to things that work or don’t work. As ideas, the associative and commutative laws are too early for 7th grade and it’s difficult to create learning.

65:

T2: There is use in it, applications, for example 99 + 3232 + 1. A student that looks at it intuitively will do it.

66:

T3: They will do it without us calling it the commutative law and generalizing it.

The main issue discussed in this PD session prior to watching the video was whether and how to teach the associative and commutative laws in middle school.

In the videotaped lesson, the teacher led the exploration of unusual arithmetical operations in which one of the laws holds, but not necessarily the other (see Fig. 1). Watching this lesson opened up an aspect of the topic which was initially overlooked, i.e., that the two laws are not interdependent.

Fig. 1

Operations discussed in the ‘commutative and associative laws’ lesson

One participant described the teacher’s goal as “undermining the perception that an operation can either satisfy both the associative and commutative laws, or none of them.” The teachers used concepts from set theory to express this idea, noting that addition and multiplication are in the intersection of the commutative operations and the associative operations sets, while subtraction and division are in the complement of the union of these sets. Teachers also discussed the use of finite operation tables. Some teachers asserted that operations on small finite groups are not equivalent, mathematically and pedagogically, to operations defined on the real numbers. Thus, they challenged the group to find an operation, defined on the real numbers and relevant to students’ school learning, for which only one of the laws holds. Eventually, two such examples were found: a □ b = (a + b)² and a □ b = |a + b|. In both cases, the operation satisfies the commutative law, but not the associative law. Thus, our analysis revealed that watching the video triggered a shift in the participants’ utterances toward the eliciting of more mathematical ideas, and that the span of ideas discussed was considerably enriched. This was also evident from the noticeable increase in the percentage of units coded as Common Content Knowledge (CCK) (see Table 1).

Table 1 Distribution of units of analysis coded by the MKT categories, before and after watching the ‘commutative and associative laws’ lesson

One of the pedagogical implications debated within the discussion was whether 7th graders should meet this type of tasks (that imply defining unusual arithmetical operations) and what might be the mathematical “benefit” for them. The discussion included ideas regarding diverse operations that may be encountered by students in their mathematical horizon, such as composition of functions, and how awareness to seemingly obvious properties, that actually do not hold, can avoid common errors (Nurick 2015).

Example 2

(Data from site#3). The teachers watched an 11th grade Calculus class, in which students explored the notion of inflection points of functions (i.e., points in which the graph of the function changes its concavity). The video triggered a heated conversation about this concept and the possible deficiencies of two of its characterizations brought up in the lesson: the point for which the second derivative is zero or the point in which the first derivative has an extremum. The teachers engaged in an active and enthusiastic attempt to challenge these characterizations by looking for counterexamples. They arrived at a graphic representation of how a prototypic counterexample may look (see Fig. 2), yet could not find an algebraic counterpart. An intensive exchange of e-mail messages followed this session, lasting a few days, in which participants continued looking for algebraic representations of counterexamples. Among the counterexamples, they correctly proposed were $f\left( x \right) = \sqrt[3]{x}$ (which has an inflection point at (0, 0), but neither the first derivative nor the second derivative is defined in that point), and f(x) = x|x|, in which f′(0) = 0, but f″(0) is not defined.

Fig. 2

A teacher presenting a graphic example of an inflection point where the first derivative does not exist

The conversation also included pedagogical implications of the mathematical ideas brought up. One teacher proposed to turn these ideas into a task for students: “Are there any functions in which an inflection point is not an extremum of the first derivative?” Since the characterization of an inflection point as a point where the second derivative is zero suffices for all functions students in this level will handle in the final examination, the above question triggered a debate: How far should teachers go beyond what is delimited by the curriculum? This issue elicited an “ethical” concern: To what extent are we allowed to “sacrifice” mathematical rigor in favor of our students’ immediate practical interests? One possible consideration raised was that in many occasions in their mathematical trajectory, students learn certain generalizations, which are later on readjusted when needed for more advanced topics.

The two examples above illustrate that observing a lesson through the lens of the mathematical and meta-mathematical ideas it offers, and with the explicit objective of specifying them, may trigger important and rich reflective discussions with implications for the refinement of the relevant mathematical knowledge for teaching (Ball et al. 2008).

Lens #2: goals

The possible space of mathematical and meta-mathematical ideas is the basis on which teachers can choose their goals for specific lessons. This lens focuses on attributing the (general or local) goals underlying the teacher’s actions or decisions, on the basis of what was observed in the video. Since we generally screen authentic lessons taught by teachers who are not present in the workshops, it is not possible to talk with the filmed teacher about his/her actual goals, and even if it was, this is not our intention. The exercise of ascribing goals to the filmed teacher centers on inferring and attributing, regardless of how “right” or “wrong” these inferences and attributions are; thus, it compels teachers to delve into the space of possible reasons for a certain action, decision or choice. Even when a certain action seems strange, accepting the working assumption that the teacher acted in the best interests of the students means that one can engage in uncovering or imagining what could have been the underlying motives. As said, this exercise is clearly not about revealing the “real” reason for the teacher’s actions; instead, it is aimed at supporting the articulation of possible goals. Many times teachers are surprised to find that a certain action can be explained through various goals (which may even contradict each other), as in the following case.

Example 3

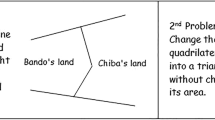
(Data from sites #1, 12, 13, 14). One of the lessons analyzed in VIDEO-LM courses is a famous TIMSS Japanese video named Changing Shape without Changing Area, a geometry lesson for 8th grade. Several analyses of this lesson can be found in the literature (e.g., Lopez-Real and Leung 2001; Siegel 2004). The main problem discussed in this lesson is presented in Fig. 3.

Fig. 3

Problem of Changing Shape without Changing Area

The solution of this problem relies on a theorem reviewed by the teacher in the opening of the lesson (triangles with the same base on a given line and the third vertex on a parallel line have equal areas).

The snapshots in Fig. 4 show how, after posing the problem, the teacher slides a stick to depict the straight boundary sought.

Fig. 4

The teacher illustrates the straight borderline. The snapshots are taken from the video available at: http://www.timssvideo.com/67

The facilitators in several sites asked the teachers what may have been the goal of such an action. We have documented very different suggestions (Schwarts 2016):

• 1. To hint at the way by which the right solution may be found:

  • He wants them first of all to have in mind that it must pass through the vertex, and then, they can think parallel to what (T2, site#12, turn 284).

• 2. To discard extreme cases, and estimate where the line can be:

  • He made them understand where it [the solution] can be obtained; he gave them an estimation, first of all estimate where it can be (T5, site#13, turn 181)

• 3. To make things harder on students, by hinting at a reasonable yet erroneous guess:

  • He wants them not to miss the pitfall […] it’s tempting to take the midsegment, and he wants them to fall into this trap and then get out of it (T8, site#1, turns 266, 271).

  • Looks like he is even teasing them a little (T7, site#14, turn 307)

In addition, the space of possible goals could also include the following two:

• 4. To clarify what the problem is asking for.

• 5. To illustrate how straightening the borderline involves compensation of areas.

As noted earlier, we cannot know what the actual goals of the teacher were; rather, the quotes above reflect the teachers’ own ideas about possible goals. We believe that the “ascribing” exercise can sharpen participants’ awareness of different possible goals and provide opportunities to negotiate the benefits and pitfalls of preferring certain goals over others.

Lens #3: tasks

Goals are carried out “on the shoulders of tasks.” Watching the video of a lesson not only allows to see how the goals are carried out using a certain task, but it also shows in a very vivid way how that task comes alive in a specific class. The task as enacted by the teacher and the students may develop differently than expected, and in this process, its intended goals may shift. Sometimes, the same task unfolds very differently in two different classes, and this is worth noticing and discussing. We refer to this as an “a posteriori task analysis,” an additional angle to that of the “a priori analysis.” Another reason for focusing on this lens is to provide opportunities for teachers to discuss tasks they find valuable and thus might be used in their lessons versus tasks that are discarded, and why. For example, the task presented in the Japanese lesson mentioned in the previous section (Fig. 3) was frequently a source of passionate debates focusing on its characteristics, affordances and limitations (Karsenty and Schwarts 2016; Schwarts 2016). In site#1, teachers debated about the suitability of such a task for their own classrooms. Some teachers strongly argued that the task is very difficult and could be frustrating for their students; thus, they would never use it:

328:

T2: When I pictured to myself how in my classroom, and I have an excellent class […] I’ll introduce such a task, [I’ll get] much more noise, much more of “what do you want” and where does this come from and this and that, and after that I don’t know how it will look here, 3–4 students might try it, the others, even good and strong ones, will sit and wait for me and get terribly bored because they are not used to this at all.

374:

T3: The task is tricky, it doesn’t give, it paralyzes, and this task is paralyzing. For most students, it is paralyzing, for most teachers it is paralyzing.

One of the more vocal teachers taking this stance (T2 in the excerpt above) finally decided to nevertheless try it in her own classroom, mostly due to the positive opinions on the task by many of her course peers, as she later testified. Her lesson, which was also videotaped, turned out to be very different than the Japanese lesson (in style, in the intensity of interactions and in many other aspects); however, both the teacher’s excitement and the students’ excitement were apparent. This phenomenon was not uncommon; we know of at least 11 teachers, in various sites, who have tried this task in their classrooms after discussing it in the VIDEO-LM workshop.

When using the tasks lens to watch a lesson, one of the issues that often arise is the sequencing of problems and exercises within a lesson. One strategy used in VIDEO-LM courses was found to be particularly useful for discussing this issue, as described below.

Example 4

(Data from site#17). The topic of the lesson, filmed in a 10th grade low-track class, was the calculation of sums of arithmetic series. After watching the part of the lesson in which the teacher led students to find the method for calculating such sums, the facilitator stopped the video and handed each group of teachers a set of eight cards containing the exercises included in the worksheet prepared by the teacher for seatwork (e.g., a ₁ = 6, d = −3, find S ₁₃; a ₁ = 87.5, d = 1.5, find S ₉; a ₁ = 7, d = 0, find S ₈). Teachers were asked to order the cards in a sequence they thought was best for using in a lesson, and explain their choice. The outcomes from five groups of teachers were five different sequences, which then were compared with the sequence chosen by the filmed teacher and the subsequent effect it had on students. The ensuing discussion focused on different criteria for designing a worksheet, particularly for low-track students, such as increasing the level of difficulty assigned to a problem; representing a variety of number groups (positive, negative, whole numbers, decimals, etc.); presenting cases that may be puzzling for students (e.g., can d be zero?); the degree of repetitiveness and the related dilemma of dreariness versus effectiveness.

Lens #4: interactions

Teachers interact with their students in diverse ways; for example, they may pose further questions to those included in the task, they may listen to (or ignore) questions, comments or difficulties raised by students, they may promote (or discourage) discussions, and they may or may not delegate responsibilities in the process of knowledge generation. These interactions are the object of observation, description and analysis and are connected when appropriate to the other lenses of this framework. Of special interest are those interactions in which the teacher may follow up in detail a comment or a question of a student, while in another part of the lesson the same teacher may dismiss another response. The assignment in these cases is to try to infer the possible reasons for these differences.

Overall, we attempt to turn teachers’ comments about interactions into general issues of discussion. For example, a participant’s comment that the teacher in the video did not ask any “why” questions could be directed toward considering whether it is always desirable to ask “why” questions, and in which cases would one choose to insist or alternatively to refrain from asking such questions. The following example demonstrates how a general issue for discussion emerges as a result of analyzing a lesson through the lens of interaction.

Example 5

(Data from site#14). In this session, the teachers watched a lesson on alternative solutions to a problem, commonly solved by using geometrical considerations. It was filmed in an 11th grade advanced class, and the teacher’s expectations from students appeared to be high. Students were called to the board to present their different solutions and received encouraging feedbacks and compliments. This type of interaction was tagged by the observing teachers as empowering. However, they noticed that for one student this was not the case; although the teacher accepted his solution as legitimate, she did so in a rather unenthusiastic tone, perhaps because it was not the type of elegant solution she aimed to nurture. One of the teachers thought that this was a demotivating response, and described a recent episode from her own classroom, when she complimented a shy and insecure student for her comment although it was far from being mathematically relevant. Moreover, the teacher said that the next day she was purposefully planning to bring a new problem to her class, for which the student’s comment will be useful and relevant, in order to encourage her. The facilitator took this conversation to open up a fundamental issue: Assuming that we have certain goals and some students fail to meet them, do we adapt the mathematics to the students, or do we demand that students adapt themselves to the mathematical requirements? The teachers were engaged with this question, speaking about a spectrum of possible interactions between these two opposed stances.

Example 6

(Data from site#17). In the lesson watched, students were struggling to find a solution to a homework problem given in the previous lesson, to which none of them found the answer. They elicited many ideas, yet the teacher did not comment on the correctness of any of these ideas, until about 15 min later, when he summed up the process and explained the mathematical logic behind the solution (which was actually offered by a student in the midst of this interaction). In a written reflection, one PD participant noted:

In this lesson the teacher hardly speaks, and in doing so he allows the students to be the ones who speak. Moreover, what I found fascinating in this film is that the teacher hardly uses explicit positive feedbacks. He almost doesn’t use words such as ‘excellent’, ‘great’ or ‘well done’. His conduct is not judgmental […] he doesn’t hint to the ‘correct’ answer as many of us tend to do. By minimizing his interventions, even those we perceive as positive, […] he enables students to express themselves instead of being constantly occupied with searching for the teacher’s approval of their attempts

This reflection demonstrates how the lens of interaction may lead to re-seeing a well-intended and frequent practice (i.e., providing positive feedbacks), and daring to elicit and inspect a potential shortcoming that may be attached to it.

Lens #5: dilemmas and decision-making

Unforeseen events in a lesson, such as an unexpected student question, an “almost correct” answer, an alternative way to reason or to solve a problem proposed by a student, may pose dilemmas for the teacher. In our context, we define a dilemma as a situation for which there is no apparent optimal course of action, and thus, each of the options available to the teacher may entail “costs” and “benefits” which need to be weighed. However, such dilemmas require immediate decision-making (i.e., whether to ignore the event or, alternatively, to abandon the planned course of action and confront the situation, and how to do it). Using this lens consists of asking the participating teachers to identify the filmed teacher’s dilemmas, to describe them, to discuss the way they were resolved and to consider alternative resolutions and their consequent trade-offs. These alternatives are not elicited in order to consider “better” ways to act, but rather for serving the purpose of reflection that unfolds the complex and nuanced nature of a predicament a teacher may find herself in, and the several possible ways to resolve it. The workshops offer the opportunity to discuss dilemmas in a friendly and relaxed context, away from the pressing need of an immediate action. These discussions have the potential to equip teachers with tools for a more informed and reflective on-site decision-making and for more explicit a posteriori justifications of it. For many teachers, the “diving” into another teacher’s decisions is a novel experience, and using this lens often involves the risk of drifting into criticism and judgmental talk. Thus, the facilitator needs to walk a fine line between, on the one hand, listening to teachers’ free comments and, on the other hand, encouraging them to consider constraints and affordances of the filmed teacher’s choices, rather than evaluating actions and decisions. We have found that teachers gradually adapt and internalize the norm of weighing alternatives instead of passing judgments, as illustrated in the next example.

Example 7

(Data from site#9). Participants in this site were lead teachers, who were also regional teacher mentors, employed by the Ministry of Education. In the course of this job, they were accustomed to giving feedback to teachers after watching their lessons, and some of them were highly evaluative in their approach. In one session, participants watched a videotaped Calculus lesson and discussed a dilemma faced by the teacher. One participant, Sarah, was extremely critical about a decision taken by the filmed teacher, arguing that it left students confused and that she would have handled the situation better. The facilitator challenged Sarah to nevertheless find possible advantages of the teacher’s move, and then, a simulation took place, where Sarah was invited to enact her alternative strategy, while all participants discussed the pros and cons of each approach. Reflecting on the course a year later,⁵ Sarah said:

[It] completely changed the nature of my observations on teachers’ lessons […] all of the conversation, the conversation that I hold now with a teacher, after visiting his classroom for observation, is more like ‘what’s your motivation, and what brought you [to do this], and what were your considerations’, and it leads to a different kind of meaningful conversation […] something changed, even in the way I observe.

Lens #6: beliefs

The issue of how teachers’ beliefs shape their practice has been widely studied (e.g., Schoenfeld 1998; Li and Moschkovich 2013). In fact, some of the previously mentioned lenses (goals, tasks, dilemmas) are likely to be guided by the beliefs the teacher brings into the classroom (Schoenfeld 2010). Facilitating discussion about beliefs is a delicate matter; for many teachers, this theoretical construct is foreign (and sometimes even strange); thus, it needs to be carefully presented, often by talking about orientations and values, followed by examples. The questions we focus on within this lens are: On the basis of the observed actions, what may be the teacher’s vision of the nature of mathematics? How does the teacher perceive her role in the lesson? How does the teacher envision the role of students in the lesson? What are the teacher’s beliefs regarding on students’ capabilities in general and on the capabilities of specific students in her classroom? What is the teacher’s perspective on teaching and on learning? As with the goals lens, we invite teachers to infer and attribute beliefs to the filmed teacher. This is not a trivial exercise, but in many workshops it turned out to trigger catalytic comments, such as the one we heard in site#2: “And what about me, what do I believe in?” Insights like this reflect the attainment of a main aim of VIDEO-LM, namely using videotaped lessons of unknown colleagues as vicarious experiences, a springboard for reflection with implications for re-examining one’s own practices and ideas, as demonstrated clearly in the following example.

Example 8

(Data from site#3). The topic of the lesson was sketching, for a given function f(x), the graphs of e ^f(x) and lnf(x). The teaching in this lesson was frontal for the whole period, with the teacher’s tight control over the development of the mathematical knowledge. Students appeared to be highly engaged in the questions posed by the teacher, who never left her position near the board. Analyzing this lesson, one teacher said:

The lesson really challenges our beliefs. […] If you’d ask me at the beginning, before watching the video, what… how should a lesson look like, I would have said many nice things […] such as you need to have a discussion, you need to have shared thinking, students should experiment right and wrong things, you need to have interaction in the class, and dynamics, and then suddenly I see something that… doesn’t have these things—there’s no discussion, or just a very short one, and I’m looking at it and I say ‘what a beautiful lesson!’ […] so now I have an internal conflict, really, I have an internal conflict, because on the one hand everything I know about teaching is missing here, but on the other hand I like what I see. So I’m trying to settle this dissonance, so I say okay, maybe it’s class dependent, maybe it’s student dependent.

This example is an existence proof that, when given the opportunity to interact within a respectful and candid reflective space, teachers may re-inspect their deepest convictions and practices and confront the complexities of teaching. This may or may not lead to changes in one’s own beliefs, but it certainly opens up new ways of interacting with peers and understanding different stances in a thoughtful manner.

Further indications of impact

In the previous section, we have described in detail the six lenses and provided illustrative evidence of how their use supports the development of reflective conversations. In this section, we present additional findings that emerged from the data analyses. Some of these findings (e.g., change in perspectives and influence on practice) highlight the role that reflective conversations may have on teachers, not only in opening up significant channels of communication among peers, but also in impact on approaches and actions.

• 1. Change in perspectives. The analysis of the written reflections (henceforth, WR) and the answers to feedback questionnaires (FQ), collected from different sites, revealed that many teachers were able to identify and even describe quite vividly a change in their perspective during the course, as exemplified by the following citations:

  • At the beginning, I related to videos differently. I was inclined to criticize what I saw, and it was hard for me to abandon that approach. It took me time to understand what I can get from these videos (WR, site#6)

  • These are really tools that now I use to look at lessons, and also when I plan lessons, I heavily think about dilemmas […] everything suddenly has names, selecting tasks as well. There are many kinds of spectacles that now became natural to me (FQ, site#1)

  • Theoretically, I know that there is an infinite variety of teachers that I can regard as “good teachers,” and still they will be different from one another, and in various decision crossroads they may take totally opposite decisions. However, each time I witness this it is a refreshing discovery, and I feel that slowly it wears out my inherent belief that there ate absolute “rights” and “wrongs,” in teaching too (WR, site#17)

  • During the video watching and discussions […], I found myself engaged in questions: Where do I stand? What would I have done? How come I never thought of this? […] In what ways am I different? What should I keep? What should I change? (WR, site#6)

• 2. Influence on practice. We found two kinds of evidence for such impact. Firstly, the analysis of WR and FQ pointed to declared or intended changes; for example,

  • I promised myself that next year I will present in class at least one problem with multiple solutions taken from various mathematical domains (WR, site#6)

  • In one of the lessons, we saw that the students construct the definition themselves and now I use this a lot (WR, site#10)

  • I pay attention to the way the classroom conversation unfolds, to the way I speak and communicate with students (WR, site#14)

Although we cannot asses the degree to which these declared or intended changes were realized in the teachers’ classrooms, the sincere manner that characterizes these reflections points to teachers’ readiness to inspect and modify their practice. Secondly, we found evidence of actual impact on practice. As already mentioned, we know of at least 11 teachers who tried the Japanese task in their classrooms. This occurred with other tasks watched in various videos. For instance, in site#7 two teachers reported to the group on the implementation of a graphing task, appearing in a previously watched video, in their classrooms. The information that in one classroom students were successful while in the other students failed to solve the task initiated a discussion about possible reasons for this difference. In site#13, two teachers reported on an inquiry task they developed and implemented after watching the lesson on inflection points, and there are other documented experiences. Despite the fact that implementing tasks watched in videos is not one of the VIDEO-LM goals, and is not required of teachers, it is notable that impact in that direction was quite common. Other directions of impact reported were uses of pedagogical strategies (e.g., having students think on their own, then in pairs and then present on the board) and the embrace of the norm of “stepping into another’s shoes.” In this respect, we highlight a report from a teacher about a surprising, albeit wrong, student’s answer that she read in a test. She described how, instead of her usual habit of immediately rejecting such an answer, she invested efforts in understanding and appreciating the underlying idea. This teacher ascribed this change to the norms and the perspectives she developed in the course.

• 3. Positive external evaluation. All eight external evaluations carried out by independent reviewers, nominated by Regional Teacher Centers hosting the VIDEO-LM courses, were extremely positive. Details about the list of means used and precise outcomes are beyond the scope of this article. However, in general findings from these evaluations show that the vast majority of teachers (80–100%, depending on the site and on the specific question) characterized the VIDEO-LM course they enrolled in as (a) eliciting authentic experiences that enable peer learning; (b) including relevant examples of practice; (c) contributing to personal improvement in practice; (d) centralizing active teacher learning; (e) offering tools that are applicable to actual teaching; (f) empowering professional capabilities; and (g) a safe environment for sharing and exposing difficulties and dilemmas associated with teaching.

• 4. Continuous involvement in video-based activities. Of the 212 participants in the in-service courses during 2012–2015, 74 (35%) continued on to participate in various activities (initiated either by the project or by other sources), involving video as a major tool for reflection. These activities include advanced VIDEO-LM courses conducted as of the 2015–2016 academic year; training courses for video-based discussion facilitators; and more. The development of an ongoing interest in this direction of professional development is a promising sign regarding the impact of VIDEO-LM.

• 5. Expanding use of the VIDEO-LM Website. About 1400 users are signed up for the website,⁶ in which more than 50 videotaped lessons and guiding materials are presented, and the number is growing daily. This is a considerable figure in Israeli terms (there are about 7000 secondary mathematics teachers in Israel).

Final thoughts

The use of videos of unknown colleagues within professional development, in order to promote reflection about the mathematics teaching practice, is a novel experience for most teachers involved in VIDEO-LM courses. It implies the opening of the usually closed door of someone else’s classroom and the development of new ways to deeply reflect about macro- and microaspects of mathematics teaching. Our framework of analysis proved to be a useful tool for this endeavor. However, its implementation requires a certain adaptation time and skillful facilitation. A main challenge to be faced by a facilitator of VIDEO-LM workshops is to cope with the inevitable (and usually unproductive) judgmental comments (e.g., “excellent class,” “I would have done it better”). These habits are hard to abandon. The facilitator should respectfully and subtly, but steadily shift the focus of the discussion from criticism to reflection using the six lenses.

Our experiences so far, as presented in the findings section above, seem to indicate that such shifts in teachers’ talk and the development of reflective skills are not only possible, but also productive. The workshops are met with visible enthusiasm and excitement by most participants. It remains to be seen whether this enthusiasm is just transient or if it indeed turns into a sustainable transformational experience. Although we did not identify strong voices of dissent or visible opposition to the VIDEO-LM experience as a whole, we acknowledge that any interventional program in education is not expected to affect all participants. Some teachers may be less interested in the demanding task of reflection or less likely to be influenced by it. However, given the widespread tendency to establish, support and nurture teacher communities, the ideas of VIDEO-LM may provide tools for use in the activities of such communities, and thus, it may influence, through peer interactions, even those teachers who are less inclined to actively reflect on their practice and to implement subsequent changes. Further research is needed in order to probe, characterize and follow up the processes of change that many of the teachers seem to undergo during their participation in the project. Some of the questions that we are now pursuing in follow-up studies include: Are changes reported by teachers provisional or more stable? To what degree do teachers internalize the SLF language and use it after the course is over? Do teachers experience significant shifts in their practice in a conscious way? In what ways can VIDEO-LM courses support communication among teachers toward the creation of teacher communities?

As mentioned in the introduction section of this article, the evolution from in-service training to teacher professional development was much more than a mere change of names; it consisted of expanding the scope of what teachers’ ongoing learning may mean. VIDEO-LM is a means to such an expansion. The discussions around the six-lens framework aim to make space for teachers’ ideas to emerge, for “big questions” to be formulated and for different stances and voices to be heard. After being intensively exposed to a range of ideas not previously accessed or considered, and to collective discussions about these ideas, we believe that teachers will be prepared to make and defend their own informed decisions and choices, according to their contexts and pedagogical orientations. In our view, this is an essential part of ongoing professional learning.

Appendix

See Table 2.

Table 2 VIDEO-LM courses 2012–2015: details and data collected