The relationship between deep-level defects and high resistivity characteristic in CdZnTe crystals

Abstract

The internal defects of CdZnTe crystals grown by the modified vertical Bridgman (MVB) method act as trapping centers or recombination centers in the band gap, which have effects on its resistivity. The relationship between deep-level defects and high resistivity characteristic in Cd_0.9Zn_0.1Te:In single crystal was studied. The deep-level defects were identified by thermally stimulated current (TSC) spectroscopy and thermoelectric effect spectroscopy (TEES) in the temperature range of 18–315 K. The trap-related parameters, e.g., activation energy, capture cross section, trap density were characterized by the simultaneous multiple peak analysis (SIMPA) method and Arrhenius fitting. The deep donor level (${{E}_{\text{DD}}}$) dominating dark current was about 0.664 eV near the middle gap by fitting the plots of the natural logarithm of dark current intensity ln(I _DC) versus 1/(kT). The doubly ionized Te antisite ($\text{Te}_{\text{Cd}}^{\text{2+}}$) below the conduction band acting as a deep donor level was mainly the origin of ${{E}_{\text{DD}}}$ level. The energy value of Fermi-level was about 0.671 eV characterized by current–voltage (I–V) measurements of temperature dependence in the temperature range from 275 K to 315 K. The resistivity was about 8.17 × 10⁹ Ω·cm measured by I–V measurement at room temperature. The high resistivity performance of Cd_0.9Zn_0.1Te:In crystal is mainly due to the Fermi-level pinned near the middle gap by the ${{E}_{\text{DD}}}$ level.

1 Introduction

Cadmium zinc telluride (Cd_1−xZn_xTe or CZT) single crystal is a promising nuclear radiation detector at room temperature. It can be used to detect X-ray and gamma-ray in astronomy, environmental monitoring and nuclear medicine imaging fields because it has high charge collection efficiency for carriers and can work normally in a large electric field. This is mainly related to the performance of high resistivity and good mobility-lifetime products [1–4]. The high resistivity characteristic of CZT crystals is usually obtained by using group III (Al, In) or group VII (Cl) elements as dopant to compensate the native defects of Cd vacancies (V_Cd) effectively [5, 6]. Although many researchers have successfully grown CdZnTe crystals of high resistivity, there is no a unified and impeccable mechanism for the formation of high resistivity.

In this work, The deep-level defects were identified by thermally stimulated current (TSC) spectroscopy and thermoelectric effect spectroscopy (TEES). Then, the trap-related parameters were characterized by the simultaneous multiple peak analysis (SIMPA) method and Arrhenius fitting. The deep donor level (${{E}_{\text{DD}}}$) was evaluated by fitting the plots of the natural logarithm of dark current intensity ln(I _DC) versus 1/(kT). The Fermi level was evaluated by current–voltage (I–V) measurements of temperature dependence. The resistivity was measured by I–V measurement at room temperature. Finally, the high resistivity performance of Cd_0.9Zn_0.1Te:In crystal was explained by the relationship between the Fermi level and a near mid-gap deep donor level defect.

2 Experimental procedure

Cd_0.9Zn_0.1Te:In crystal used in our experiments was grown by the modified vertical Bridgman (MVB) method. From the ingot the 5 × 5 mm² wafer with thickness 2 mm was cut. Next, the wafer was mechanically polished and then chemically polished by MgO turbid liquid and the solution mixed by Si sol and solution of H₂O₂ to remove surface scratches. The deionized water and acetone solution were used to clean the wafer subsequently. Finally the wafer was chemically etched in 2% bromine methanol solution to remove the damaged surface layer. The wafer was deposited with electroless Au contacts on opposite surfaces in a planar structure or on both edges in a strip structure using an AuCl₃ solution for further measurements.

The deep level defects were characterized on the strip structure via TSC spectroscopy and TEES. In TSC measurement, the sample was placed in a closed-cycle cryostat with liquid helium (Sumitomo DE-202) and cooled to 18 K in darkness, where the deep traps were filled using a halogen lamp. Then, the trapped carriers were released by thermal emission in the dark until 315 K at a certain bias voltage and a constant heating rate. The experiments choose 10 V bias voltage and 0.10, 0.15, 0.18, 0.21, 0.24, 0.27 K/s heating rate respectively, the resulting TSC spectrums were obtained. Besides, the temperature dependence of dark current I _DC was determined by implementing the above described steps without illumination at low temperatures. The TEES measurement, which is similar to TSC measurement, was performed to identify the type of traps (electrons or holes). A thermal gradient across the sample is imposed for TEES, while an electric field is applied for TSC. The experiment chooses 10 V bias voltage, 0.21 K/s and a small temperature gradient of several degrees to avoid perturbing the dynamics of cooling/heating cycle of the cryostat.

The planar electrode structure was selected for current–voltage (I–V) measurements of temperature dependence. The sample was placed in a cryostat to cool by liquid nitrogen and then was researched by I–V curves of temperature dependence with the bias voltages from −10 to 10 V. The temperature was 275, 285, 295, 305, 315 K respectively. The resistivity of wafer was measured by an Agilent 4155 °C semiconductor parameter analyzer with the bias voltage from −1 to 1 V at room temperature.

3 Results and discussions

3.1 TSC and TEES analysis

Figure 1a presents the heating rate dependence of TSC spectra as a function of temperature ranging from 18 to 315 K. It shows that the peak positions shift toward high temperatures as the heating rate β increases from 0.10 to 0.27 K/s. Figure 1b shows the effect of heating rate on the corresponding dark current spectra, and the inset illustration is the part of dark current spectra in the temperature range of 265 to 315 K.

Fig. 1

a Heating rate dependence of TSC spectra in the temperature of 18–315 K measured from 0.10 to 0.27 K/s for the CZT wafer. b The effect of heating rate on the corresponding dark current spectra. The inset illustration is the part of dark current spectra in the temperature range of 265–315 K

Generally, the relationship between TSC peak temperature T _m and heating rate β is described by the expression [7]:

$${{E}_{\text{a}}}=k{{T}_{\text{m}}}\ln \left( \frac{{{N}_{c,v~}}~\sigma vkT_{\text{m}}^{2}}{\beta \left( {{E}_{\text{a}}}+2k{{T}_{\text{m}}} \right)} \right)$$

(1)

In the case of ${{E}_{\text{a}}}\gg 2k{{T}_{\text{m}}}$, Eq. (1) can be simplified as

$${{E}_{\text{a}}}=k{{T}_{\text{m}}}\ln \left( \frac{{{N}_{c,v~}}~\sigma vkT_{m}^{2}}{\beta {{E}_{a}}} \right)$$

(2)

Equation (2) can be transformed into the form of $\text{In}(T_{\text{m}}^{2}/\beta )$ as a function of 1/T _m in Eq. (3), which is called Arrhenius formula,

$$\ln \left( \frac{T_{\text{m}}^{2}}{\beta } \right)=\frac{{{E}_{\text{a}}}}{k{{T}_{\text{m}}}}-\ln \left( \frac{{{N}_{c,v~}}\sigma vk}{{{E}_{a}}} \right)$$

(3)

where ${{E}_{\text{a}}}$ is the thermal activation energy of a specific trap level, k Boltzmann’s constant, ${{N}_{c,v~}}$ is the effective density of states in the valence (conduction) band, $\sigma$ is the trap capture cross section, and $v$ is the thermal velocity of the holes (electrons). The value of ${{E}_{\text{a}}}$ can be determined by the slope of Eq. (3).

In order to reduce the mutual interference of overlapping peaks and determine all trap levels simultaneously from the TSC spectrum in the CZT crystal, the simultaneous multiple peak analysis (SIMPA) method reported by Pavlovic and Desnica [8] is introduced. The fitting function I _SIMPA, including the sum of TSC peaks belonging to the specific deep levels I _TSC and dark current I _DC, is defined by

$${{I}_{\text{SIMPA}}}\left( T \right)=\underset{i=1}{\overset{m}{\mathop \sum }}\,I_{\text{TSC}}^{i}\left( T \right)+{{I}_{\text{DC}}}(T),$$

(4)

where $I_{\text{TSC}}^{i}\left( T \right)$ represents the ith individual TSC peak current, m is the number of deep traps in the calculation and ${{I}_{\text{DC}}}\left( T \right)=C~\text{exp}~\left( -{{E}_{DD}}/kT \right)$. C is a constant, k is the Boltzmann constant and ${{E}_{\text{DD}}}$ is the deep donor activation energy. The ${{E}_{\text{DD}}}$ level plays a significant role in the dark current and electrical compensation.

In the ‘first order kinetics’ approximation, the ith individual TSC peak current can be described as

$$I_{TSC}^{i}\left( T \right)={{N}_{{{T}_{i}}}}e{{\mu }_{n}}AE{{\tau }_{n}}{{D}_{t,i}}{{T}^{2}}\text{exp}\left\{ -\frac{{{E}_{a,i}}}{kT}-\frac{k{{D}_{t,i}}}{\beta {{E}_{a,i}}}{{T}^{4}}{{e}^{-{{E}_{a,i}}/kT}}\times \text{exp}\left[ 1-4\frac{kT}{{{E}_{a,i}}}+20{{\left( \frac{kT}{{{E}_{a,i}}} \right)}^{2}} \right] \right\},$$

(5)

where ${{N}_{{{T}_{i}}}}$ is the carrier concentration of the filled ith trap level, $e$ is the electron charge, ${{\mu }_{n}}$ is the carrier mobility, A is the area of the electrode, E is the applied electric field, ${{\tau }_{n}}$ is the carrier lifetime, ${{D}_{t,i}}$ is the temperature-dependent coefficient of the filled ith trap level, T is the absolute temperature, $k$ is the Boltzmann constant, $\beta$ is the heating rate and ${{E}_{a,i}}$ is the thermal activation energy of the filled ith trap level.

Besides, the effective collected charge ${{Q}_{{{T}_{i}}}}$ released by the filled ith trap level can be accurately calculated by SIMPA method, which can be described as

$${{Q}_{{{T}_{i}}}}=\mathop{\int }^{}I_{TSC}^{i}dt=\frac{1}{\beta }\underset{{{T}_{0}}}{\overset{T}{\mathop \int }}\,I_{TSC}^{i}dT.$$

(6)

And then ${{N}_{{{T}_{i}}}}$ can be calculated from

$${{N}_{{{T}_{i}}}}=\frac{{{Q}_{{{T}_{i}}}}}{2{{\mu }_{n}}({{T}_{i}}){{\tau }_{n}}({{T}_{i}})eAE}\text{ }\!\!~\!\!\text{ }.$$

(7)

In addition, ${{D}_{t,i}}$ can be defined as ${{D}_{t,i}}=3.0\times {{10}^{21}}\left( {{m}^{*}}/{{m}_{0}} \right){{\sigma }_{i}}$, where ${{m}^{*}}$ is the electron (or hole) effective mass, ${{m}_{0}}$ is the electron (or hole) rest mass and ${{\sigma }_{i}}$ is the capture cross section. The Zn concentration in Cd_0.9Zn_0.1Te crystal is relatively low, so we can use ${{m}^{*}}=0.14{{m}_{0}}$ for electrons and ${{m}^{*}}=0.37{{m}_{0}}$ for holes in CdTe [9, 10]. Therefore, the trap-related parameters (${{E}_{a,i}},~{{N}_{{{T}_{i}}}}$ and ${{\sigma }_{i}}$) in Cd_0.9Zn_0.1Te:In wafer were characterized by the above calculations.

Take the TSC measurement of 10 V bias voltage and 0.21 K/s heating rate for example, Fig. 2a shows that the SIMPA results of three deep trap levels, named from T ₁ to T ₃ along the high temperature direction. In order to clarify the type of traps (electron or hole), TEES was obtained in Fig. 2b. To get the thermal activation energy of this three trap levels, Fig. 2c indicates the relationship between $\text{ln}(T_{\text{m}}^{2}/\beta )$ and 1/T _m adopted Arrhenius fitting according to the Eq. (3). In addition, Fig. 2d shows that a deep donor level dominated by the dark current. The trap parameters of observed traps are presented in Table 1 by calculation with the SIMPA method.

Fig. 2

a TSC spectrum of 10 V bias voltage and 0.21 K/s heating rate from Cd_0.9Zn_0.1Te:In and its SIMPA fitting results. The dashed curve represents the experimental TSC spectrum and the solid curve above it represents the fitting TSC spectrum, the other three solid curves show the individual fitting TSC peaks belonging to specific trap levels. b The corresponding TEES spectrum. c Arrhenius fitting for trap levels in TSC spectra. d Determination of the corresponding ${{E}_{\text{DD}}}$ level by the linear fit of ln(I_DC)−1/(kT)

Table 1 Trap parameters of observed trap levels in Cd_0.9Zn_0.1Te:In crystal determined with the SIMPA method

Among these traps, trap T ₁ (0.063 eV, 7.5 × 10¹⁴ cm⁻³, 1.68 × 10⁻¹⁷ cm²) may correspond to the shallow acceptor of the so-called A center originated from V_Cd-In_Cd complex [11]. Trap T ₂ (0.102 eV, 6.1×10¹⁴ cm⁻³, 4.72 × 10⁻¹⁷ cm²) may be related with the point defect $\text{In}_{\text{Cd}}^{+}$ derived from the indium element dopant [12]. Trap T ₃ (0.571 eV, 1.4 × 10¹⁴ cm⁻³, 2.54 × 10⁻¹⁷ cm²) may be attributed to Cd vacancy [13]. Besides, the deep donor level ${{E}_{\text{DD}}}$ related to doubly ionized Te antisite ($\text{Te}_{\text{Cd}}^{\text{2+}}$) dominating the dark current in Cd_0.9Zn_0.1Te:In crystal is 0.664 eV, which is similar to the ‘EL 2’ middle gap level in SI-GaAs [14].

3.2 Current–voltage analysis

The relationship between resistivity (ρ) and Fermi level (E _F) can be described by the expression [15]:

$$\text{ln}\rho \propto ~\frac{{{E}_{\text{F}}}}{kT}$$

(8)

where $k$ is Boltzmann’s constant and $T$ is thermodynamic temperature.

At a certain temperature, the resistivity (ρ) can be calculated by the following equation:

$$\rho =\frac{U}{I}\frac{S}{d}$$

(9)

where U is bias voltage, I is current, S is the electrode area and d is the thickness of the wafer.

In order to get the value of Fermi level, the bias voltages between −10 and 10 V were chosen and the temperature selected 275, 285, 295, 305, 315 K respectively. The current–voltage (I–V) measurement under a low bias voltage can reflect the bulk resistivity of sample at room temperature [16], so the bias voltages between −1 and 1 V were chosen at room temperature.

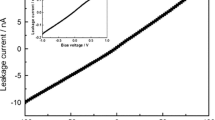
Figure 3a shows the I–V curves of temperature dependence in the temperature range from 275 to 315 K. Fig. 3b shows the relationship between resistivity (ρ) and Fermi level (E _F), E _F was evaluated to be 0.671 ± 0.005 eV near the mid-gap of CdZnTe according to the expression (8). Figure 4 shows the I–V curve between −1 and 1 V at room temperature, the bulk resistivity of Cd_0.9Zn_0.1Te:In wafer is about 8.17 × 10⁹ Ω cm, which meets the performance requirement for nuclear radiation detector at room temperature.

Fig. 3

a I–V measurements of temperature dependence for Cd_0.9Zn_0.1Te:In wafer and b linear fit of Fermi level by the plots of ln ρ versus 1/(kT)

Fig. 4

I–V fitting result of Cd_0.9Zn_0.1Te:In wafer applied on the bias voltages from −1 to 1 V

4 Conclusions

In this study, The deep-level defects of Cd_0.9Zn_0.1Te:In crystal grown by the MVB method were identified by TSC and TEES measurement, and the trap-related parameters were characterized by the SIMPA method and Arrhenius fitting. The energy value of Fermi-level was characterized by I–V measurements of temperature dependence. The resistivity was measured by I–V measurement at room temperature.

• • Based on the SIMPA method, three trap levels and a deep donor level ${{E}_{\text{DD}}}$ dominating the dark current and their origin are identified.

• • The ${{E}_{\text{DD}}}$ derived from $\text{Te}_{\text{Cd}}^{\text{2+}}$ is about 0.664 eV and the Fermi-level is about 0.671 eV.

• • The resistivity of Cd_0.9Zn_0.1Te:In crystal is about 8.17 × 10⁹ Ω·cm. The high resistivity performance of Cd_0.9Zn_0.1Te:In crystal is mainly due to the Fermi-level pinned near the middle gap by the ${{E}_{\text{DD}}}$ level.