Trans-interface-diffusion-controlled coarsening of γ′ particles in Ni–Al alloys: commentaries and analyses of recent data

Abstract

Recently published data on coarsening of γ′ precipitates in a binary Ni–Al alloy are critically reviewed within the framework of the trans-interface diffusion-controlled theory of particle coarsening. These data are shown to be remarkably consistent in every respect with the predictions of theory using the temporal exponent n = 2.2, which was arrived at by fitting experimental histograms and experimental cumulative distribution functions to their theoretical counterparts. This is the best procedure for evaluating the temporal exponent n, but plotting the average radius, 〈r〉, as 〈r〉ⁿ versus aging time t is a suitable alternative. Semiquantitative agreement is obtained with all the data, including the kinetics of solute depletion as well as the temporal dependencies of the volume fraction and number density, N_v. The inverse time dependency of N_v is shown once again to be incorrect, failing the simplest test of internal consistency, specifically constancy of the product N_vt. The notion that there exists a “quasi-stationary” regime of γ′ precipitate coarsening is seriously questioned and shown to be untenable. Analysis of the data enables quantitative prediction of the interfacial free energy, σ. In combination with previous work, this provides the first concrete experimental evidence for a linear decrease of σ with increasing temperature.

Introduction

A polydisperse array of particles coarsens in order to lower its interfacial area, hence energy. During coarsening smaller particles shrink, surrendering their mass to the larger particles that grow at their expense. Coarsening thus involves the transport of matter from smaller shrinking particles to larger-growing ones. Any of a number of different processes can control the rate of transport. Among these, diffusion in the medium supporting the particles (the matrix phase) or an unspecified reaction at the interface between the matrix and the particles are two processes of historical importance, though there are quite a few more. Matrix-diffusion-controlled (MDC) transport was envisioned by Greenwood [1] and Todes and Khrushchov [2], for example, whose early incomplete theories were ultimately replaced nearly simultaneously by the seminal work of Lifshitz and Slyozov [3] and Wagner [4], leading to what is now universally known as the LSW theory. LSW derived not only the kinetics of growth of a particle of average radius 〈r〉 in a polydisperse assembly, but also the particle size distribution (PSD). The variation of 〈r〉 with aging time t is represented by the familiar equation

$$\langle r\rangle^{3} - \langle r_{\text{o}} \rangle^{3} = kt,$$

(1)

where k is a rate constant that depends on the important thermodynamic and kinetic parameters of the system and 〈r_o〉 is taken as the average radius at the onset of coarsening. Equation (1) is sometimes written alternatively as 〈r〉³ = k(t – t_o), where t_o is a different constant of integration which ostensibly represents a fictional time at which coarsening is supposed to have commenced. However, from a physical and mathematical perspective there is only one constant of integration, and the only parameter of true physical significance in Eq. (1) is the rate constant k.

In a representative metallurgical aging experiment on precipitation from supersaturated solid solution, the particles form by nucleation and growth, spinodal decomposition or some combination of the two, depending on the composition of the alloy and its phase diagram. Whatever the process is that governs the initial stages of decomposition, the onset of coarsening typically overlaps the end of the initial stage, after the matrix has been depleted of excess solute to the extent that the residual supersaturation is small. In practical terms both 〈r_o〉 and t_o are both ill-defined and t in Eq. (1) is simply taken as the total aging time of an experiment. If the major objective of an experiment on coarsening is to evaluate the magnitude of the rate constant k, it is necessary only to determine the slope of a plot of 〈r〉³ versus t.

Wagner [4] also considered the problem of interface reaction-controlled (IRC) coarsening, wherein the rate-limiting process is the transport of solute through the precipitate-matrix interface by an unspecified interface reaction. The equation for coarsening under these conditions is

$$\langle r\rangle^{2} - \langle r_{\text{o}} \rangle^{2} = k_{R} {\kern 1pt} t,$$

(2)

where k_R is a new rate constant that depends quite differently from k on the thermo-kinetic parameters of the system. As is the case for MDC coarsening, the parameters 〈r_o〉 and t_o are also fictitious, though their magnitudes are also expected to be small. In his classic paper Wagner also derived the PSD associated with IRC coarsening and showed that it is broader than the PSD for MDC coarsening.

The LSW theory, as written, is strictly speaking valid for a simple thermodynamic system in which the host matrix phase is an ideal solid solution, the dispersed precipitate phase is a pure element, and the dispersion itself is infinitely dilute, meaning in practical terms that its equilibrium volume fraction, f_e, is zero. These physical restrictions are never satisfied in real 2-phase systems. Solid solutions are almost never close to being infinitely dilute and the dispersed phases are never pure, but are usually solid solutions or intermetallic compounds. Under these more general conditions the most widely accepted equation for the rate constant for MDC coarsening is that of Calderon et al. [5] for binary alloys,

$$k = k(0) = \frac{{8\tilde{D}V_{{\text{m}\gamma^{\prime}\text{e}}} \sigma }}{{9G^{\prime\prime}_{{\text{m}\gamma \text{e}}} \left( {X_{{\gamma^{\prime}\text{e}}} - X_{{\gamma \text{e}}} } \right)^{2} }}.$$

(3)

Equation (3) is written here specifically for γ/γ′ alloys, where the γ phase is a Ni (or Co)-base solid solution and the γ′ phase is an ordered intermetallic compound based on Ni₃Al, which has the Cu₃Au (L1₂) crystal structure. In Eq. (3) $\tilde{D}$ is the chemical diffusion coefficient in the majority γ phase, X_γe and X_γ′e are the equilibrium compositions of the γ and γ′ phases, respectively, σ is the interfacial free energy of the γ/γ′ interface, V_mγ′e is the molar volume of the γ′ precipitates, and $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ is the curvature of the Gibbs free energy of the γ phase; V_mγ′e and $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ are evaluated at their equilibrium compositions. All the parameters in Eq. (3) are temperature dependent, some more weakly so than others, so the activation energy for coarsening is generally not equal to the activation energy for chemical diffusion.

The equality k = k(0) in Eq. (3) emphasizes its limitation to describe the rate of coarsening in systems in which the equilibrium volume fraction is formally equal to zero. As already stated, f_e can never be zero in real systems. This was realized not only by Lifshitz and Slyozov [3] themselves, but also by many others, leading to numerous publications on the effect of f_e on the kinetics of coarsening as well as other consequences of nonzero volume fraction, especially spatial correlations which are nonexistent when f_e = 0. The numerous approaches to solving the multi-particle diffusion problem can be found in several review articles on this topic [6,7,8,9]. There are three major consequences of the effect of f_e on MDC coarsening, only two of which are important in this paper; 1. The temporal dependence of particle growth is identical to that in Eq. (1), i.e., the temporal exponent remains n = 3, but the rate constant k becomes a function of f_e, k(f_e), which increases monotonically as f_e increases, i.e., k(f_e)/k(0) > 1; 2. The PSD broadens as f increases. The third consequence of finite f_e is that spatial correlations develop among randomly spaced spherical precipitates in systems that are free of internal strains, such as solid or liquid particles coarsening in a liquid matrix, or perfectly lattice-matched precipitates in a solid matrix. In such systems the spatial correlations loosely resemble the atomic or molecular arrangements in liquids or amorphous solids, with no specific directionality. In solid systems containing coherent misfitting precipitates, elastic interactions engender alignment of the precipitates along elastically soft cube directions [10]. These complications are not relevant to the overall objectives of this paper and are mentioned only for the sake of completeness.

The mathematical approach used by Lifshitz and Slyozov [3] has been readily adapted to other kinds of problems in the coarsening pantheon, some leading to temporal exponents that differ from n = 3. In no particular order, it has been used to formulate a theory of grain growth [11] (n = 2), MDC coarsening in 2-dimensions [12,13,14] (n = 3), coarsening of grain boundary precipitates, which is grain boundary diffusion-controlled [15,16,17,18] (n = 4), coarsening of precipitates on dislocation networks, in which diffusion through dislocations in the network is the rate-limiting step [18] (n = 5). In these processes the rate constants can no longer be predicted by Eq. (3), but are instead related to the thermo-kinetic parameters of the specific situation, which are not germane to the objectives of this article.

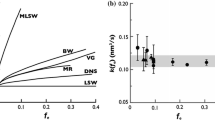
Even though k(f_e) is theoretically predicted to increase as f_e increases, it does not do so in numerous binary and multi-component Ni-base γ/γ′ alloys. The absence of the effect of volume fraction on coarsening kinetics is so contrary to theoretical expectation that a brief review of findings is in order. Binary Ni–X alloys containing Ni₃X precipitates, where X = Al [19,20,21,22,23,24,25], Ga [26, 27], Ge [28, 29], Si [30,31,32] and Ti [33] have been extensively investigated. The most compelling evidence for the absence of an effect of f_e on k(f_e) is provided by the results on the coarsening of Ni₃Al precipitates in Ni–Al alloys [22, 23] and Ni₃Si precipitates in Ni–Si alloys [31, 32], where measurements have been taken over very large ranges of volume fraction, up to f_e ~ 0.3. The dependency of k(f_e) on f_e in Ni–Si alloys aged at 650 °C is shown in Fig. 1. It is evident that k ≈ 0.11 nm³ s⁻¹ from 0.08 < f_e ≤ 0.30. There is a hint in Fig. 1 of an anomalous dependency of k(f_e) on f_e in that k(f_e) appears to decrease with f_e at small values of f_e (< 0.08). It turns out that this is a robust observation, which is also observed in the coarsening behavior of γ′-type precipitates in Ni–Al [34], Ni–Ga [27], Ni–Ge [29] and Ni–Ti [33] alloys. To date, there is no satisfactory explanation for this behavior although it has been found in 2-dimensional phase-field computer simulations of coarsening in γ/γ′ alloys [35, 36].

Figure 1

Illustrating the dependence of the rate constant for coarsening, k(f_e), on the equilibrium volume fraction, f_e of γ′-type Ni₃Si precipitates in binary Ni–Si alloys aged at 650 °C. k(f_e) is essentially constant within the shaded area. Data of Meshkinpour and Ardell [30], Cho and Ardell [32] and Sauthoff and Kahlweit [37]

There is also quite convincing evidence for the absence of an effect of f_e on the kinetics of coarsening in multi-component alloys. Examples are Ni₃(Al, Cr) precipitates in ternary Ni–Al–Cr alloys [38, 39], with compositions lying along the same tie line [40]. The experimentally measured PSDs in ternary Ni–Al–Cr alloys [22, 24] are also unaffected by volume fraction. Other examples of similar behavior are found in the coarsening of γ′ precipitates in ternary Ni–Co–Al alloys [41] and quaternary Ni–Co–Cr–Ti [42] and Ni–Cr–Al–Ti and Ni–Cr–Al–Nb alloys [43], although the compositions in these alloys do not necessarily lie on the same tie line.

The absence of the effect of volume fraction on coarsening behavior in Ni-base γ/γ′ alloys is one of the critical factors that led to the development of the theory of trans-interface diffusion-controlled (TIDC) coarsening [44]. However, there are two other important components of the TIDC coarsening theory. One of them is the discovery that the γ/γ′ interface is not sharp, but diffuse [45], transitioning chemically from the γ to γ′ compositions over a distance, δ, the order of ~ 2–4 nm. The third important factor is the relatively large difference between chemical diffusion in the ordered γ′ and disordered γ phases; for example diffusion is much more sluggish in Ni₃Al, typically by 2 orders of magnitude, than in disordered Ni–Al solid solutions [46,47,48].

The initial observations on the diffuse nature of the γ/γ′ interface were made using atom probe tomography (APT) by Harada et al. [45]. Although there was some early disagreement [49] over that finding, subsequent investigations by APT on a variety of different Ni-base γ/γ′ alloys [50,51,52] now leave no doubt that γ/γ′ interfaces are indeed diffuse. Atomistic Monte Carlo simulations [44, 53] are consistent with the experimental observations. It has also been shown using high-resolution transmission electron microscopy that the transition from order to disorder occurs over a distance smaller than the interface width [54, 55]. There is therefore a component of the interface width, δ_lro, over which the order–disorder transition occurs and, as noted, δ_lro < δ.

The TIDC coarsening theory predicts that for small particles, in the earlier stages of coarsening, the rate constant should be independent of f_e because the kinetics is controlled by diffusional transport THROUGH the ordered interface region rather than by diffusion in the disordered matrix TO the interface. Any mechanism of coarsening that involves interfacial processes that control the growth of individual precipitates will lead to a rate law like Eq. (2) (see for example Shiflet et al. [56]). The physical reason behind the transition from TIDC to LSW coarsening kinetics is that when the particles are large enough, the concentration gradients in the matrix are so small that MDC becomes the rate-limiting step. Ardell and Ozolins [44] showed that this prevails when the particle radius r satisfies the condition $r > \delta \tilde{D}_{\gamma } /\tilde{D}_{I}$. This condition is the most likely reason that MDC coarsening of γ′ precipitates is operative in Ni and/or Co-base superalloys aged at very high temperatures.

The TIDC coarsening theory is also consistent with the coarsening behavior in so-called inverse γ/γ′ alloys. The geometries of the (γ + γ′)/γ′ phase boundaries in the Ni–Al and Ni–Ge phase diagrams (the γ solvus in both cases) enable the γ′ phases Ni₃Al and Ni₃Ge to be supersaturated at temperatures below the γ solvus and therefore to exhibit normal precipitation behavior. In these circumstances the precipitates are the Ni–Al and Ni–Ge solid solutions, respectively. In principle the structure of the γ/γ′ interfaces should be the same irrespective of which is the majority phase, though a recent report [57] suggests that this might not be the case. Since the matrices in both inverse alloys are the ordered γ′-type phases, chemical diffusion is now substantially slower in the ordered matrix than in the disordered precipitate phase or in the interface itself. Under these conditions MDC coarsening is expected to dominate, and that is precisely what happens. Experiments on “inverse” Ni–Al [58, 59] and Ni–Ge [60] alloys demonstrate that the rate constants are strongly dependent on volume fraction, as shown in Fig. 2. The ranges of f_e over which the data were measured are quite small, but the dependencies of k(f_e) on f_e are very strong and the antitheses of the behavior in normal alloys.

Figure 2

Illustrating the dependencies of the rate constant for coarsening, k(f_e) of the LSW theory on the equilibrium volume fraction, f_e, of disordered Ni–Al precipitates (a) and Ni–Ge precipitates (b) in “inverse” Ni₃Al and Ni₃Ge alloys aged at 650 and 600 °C, respectively. The data in a are from Ma and Ardell [59], and the data in b are from Ma and Ardell [60]. The dashed curves in a and b represent the predictions of the MLSW theory of Ardell [61], modified by the calculations of Tsumuraya and Miyata [62]

A few years after the publication of the TIDC theory of coarsening, a review of the literature on coarsening of γ′ precipitates in binary Ni–Al alloys was undertaken to evaluate extant data [63]. The focus of that work centered on three aspects of the TIDC theory, namely the PSDs and the kinetics of particle growth and solute depletion. The TIDC theory was shown to be quantitatively consistent with the available data. Since the publication of that paper there has been one new thorough investigation of precipitation in Ni–Al alloys, specifically a comprehensive study by Plotnikov et al. [64] of nucleation, growth and coarsening of γ′ precipitates in a binary Ni–12.5 at.%Al alloy aged at 823 K. The authors concluded that coarsening during the later stages of precipitation was fully consistent with the predictions of the LSW theory. No effort was made to evaluate the efficacy of the TIDC theory. That effort constitutes the focal of this paper, which is organized as follows. The foundational equations of the TIDC coarsening theory are presented in order to provide a background for the subsequent sections that deal with the analyses and evaluation of data on the PSDs, kinetics of particle growth and solute depletion, as well as the temporal evolution of the volume fraction and number density of precipitates. The data of Plotnikov et al. [64] are re-evaluated and demonstrated to be in remarkably good agreement with the predictions of the TIDC theory of coarsening. The data are also shown to be internally self-consistent only in the context of TIDC coarsening, but not otherwise. New calculations of σ are extracted from the data, and for the first time σ is confirmed experimentally to be a function of temperature. The final section of the paper summarizes the main findings, presents a number of conclusions and offers final thoughts on work that remains to be done.

Brief review of quantitative predictions of the TIDC theory of coarsening

In the TIDC theory of coarsening the rate of growth of the average particle is given by the equation

$$\frac{{\text{d}\langle r\rangle^{n} }}{{\text{d}t}} = k_{n} ,$$

(4)

where the rate constant k_n differs from that in Eq. (3). Instead, it is given by an equation of the form

$$k_{n} = \left( {\frac{n - 1}{n}} \right)^{{( {n - 1} )}} K_{T} ,$$

(5)

where K_T is a constant that depends in different ways on the thermo-kinetic parameters of the alloy system, as well as assumptions about the dependencies of the interface width, δ, and the interfacial diffusion coefficient, $\tilde{D}_{I}$, on r [63, 65]. For purposes of this discussion the exact equation for K_T is irrelevant. The important points to note here are that the temporal exponent, n, satisfies the condition 2 ≤ n ≤ 3 and that the growth rate of the average particle is given by Eq. (4), the integration of which leads to the equation for the growth of the average precipitate, namely

$$\langle r\rangle^{n} -\langle r_{\text{o}} \rangle^{n} = k_{n} t.$$

(6)

The kinetics of solute depletion of the matrix phase varies with aging time as

$$X_{\gamma } - X_{{\gamma \text{e}}} \approx \left( {\kappa_{n} t} \right)^{ - 1/n} ,$$

(7)

where Xγ_e is the concentration of solute in the γ phase at thermodynamic equilibrium and κ_n is a rate constant related to k_n by the equation

$$\left( {\frac{{k_{n} }}{{\kappa_{n} }}} \right)^{1/n} = \langle z\rangle {\ell},$$

(8)

where ${\ell }$ is the capillary length determined by the Gibbs–Thomson equation, namely

$${\ell } = \frac{{2V_{{\text{m}\gamma^{\prime}\text{e}}} \sigma }}{{{\kern 1pt} \Delta X_{\text{e}} G^{\prime\prime}_{{\text{m}\gamma \text{e}}} }}.$$

(9)

In Eq. (9) ∆X_e = X_γ′e − X_γe and 〈z〉 = 〈r〉/r*, where r* is a critical radius in all coarsening theories. It is the radius of a particle that is neither growing nor shrinking at time t; 〈z〉 is of order unity and can be calculated from the theoretical PSD (discussed later). An equation similar to Eq. (7) governs the kinetics of solute depletion in the minority γ′ phase, but the rate constant differs from κ_n because it involves different thermo-kinetic parameters. The main assumption in the derivation of Eq. (7) is that the later stages of coarsening have obtained, so that 〈r〉ⁿ is truly much greater than 〈r_o〉ⁿ, hence 〈r〉 ≈ (k_nt)^1/n.

The other two quantities that vary with aging time are the volume fraction, f, and the number of precipitates per unit volume, N_v. The asymptotic time dependence of f is given by the equation

$$f = f_{\text{e}} - \frac{{\left( {\kappa_{n} t} \right)^{ - 1/n} }}{{\Delta X_{\text{e}} }},$$

(10)

while the asymptotic variation of N_v with aging time is

$$N_{v} = \frac{{f_{\text{e}} }}{{\psi S\left( {k_{n} t} \right)^{3/n} }}\left\{ {1 - \frac{{\left( {\kappa_{n} t} \right)^{ - 1/n} }}{{f_{\text{e}} \Delta X_{\text{e}} }}} \right\},$$

(11)

where the constant S depends on the shape of the precipitate phase and enters into the kinetics via the relationship among f, N_v and the average volume of the precipitate phase, 〈V〉, i.e.,

$$\langle V\rangle N_{v} = f,$$

(12)

where 〈V〉 = ψS〈r〉³. For spherical particles S = 4π/3 while for cube-shaped particles S = 8 and r is taken as a/2, where a is the edge length of the cube. The parameter ψ = 〈r³〉/〈r〉³ depends on the PSD and varies from ~ 1.36 to ~ 1.13 as n increases from n = 2 to n = 3; it is evaluated in “Appendix A.” Equations (10) and (11) differ slightly from previous versions [6, 20, 66] because in the general expression for f from the lever rule, f = (X_o − X_γ)/(X_γ′ − X_γ), it is assumed that the denominator (X_γ′ − X_γ) ≈ ∆X_e. It will be shown later that this is an excellent approximation, and better than the one used previously, i.e., (X_γ′ − X_γe) ≈ ∆X_e. The origin of the second term in curly brackets in Eq. (11) is the first term in the series expansion for the time dependence of f; it is not the second term in a series expansion for the time dependence of N_v. This is presented in detail in “Appendix B.”

The PSD is calculated using the equations¹

$$h(z) = - 3\phi (z)\exp \left\{ {\xi (z)} \right\},$$

(13)

$$\xi ( z ) = 3\int_{0}^{z} {\phi ( x )\text{d}x} ,$$

(14)

and

$$\phi (z) = \frac{{z^{{( {n - 1} )}} }}{{( {z - 1} )\frac{{n^{n} }}{{( {n - 1} )^{{(n - 1)}} }} - z^{n} }}.$$

(15)

Comparison with experimentally measured PSDs or histograms must be made using the variable u = r/〈r〉, since r* cannot be measured experimentally. To compare an experimental PSD or histogram with a theoretically predicted PSD, it is necessary to transform h(z) to the PSD expressed in terms of the variable u, i.e., g(u), which is done using the equation

$$g(u) = \langle z\rangle h\langle z\rangle$$

(16)

which follows from the equality g(u)du = h(z)dz. The maximum theoretical particle size in the PSD is z_max = n/(n − 1). It follows that u_max = n/〈z〉(n − 1).

Analytical solutions of Eqs. (13)–(15) are possible only for n = 2 (〈z〉 = 8/9) and n = 3 (〈z〉 = 1). In these 2 cases the PSDs are identical to those for IRC and MDC coarsening [3, 4], respectively.

Re-analysis of the data of Plotnikov et al. [64] in the context of TIDC coarsening

The particle size distributions

The most important parameter needed for the analysis of the data on kinetics of coarsening within the framework of the TIDC coarsening theory is the temporal exponent, n. As stated earlier n is best obtained by fitting experimental PSDs, which are typically published as histograms. The method used here differs from the Mathematica subroutine used previously for analysis of the histograms of the PSDs in binary Ni–Al [63], Ni–Ti [67] and Ni–Ga, Ni–Ge and Ni–Si [68] alloys. Instead, it is based on equating the standard deviations of the experimental PSDs to those predicted by the TIDC coarsening theory for values of n in the range 2 ≤ n ≤ 3. This method is very easy to implement and is of far greater utility than that used previously because no special computer programming is needed. However, it is imperfect because probability distributions are typically characterized by additional parameters, so the method is expected to be useful mainly as a guide because most of the theoretical TIDC PSDs are not heavily skewed. To proceed it is necessary to integrate Eqs. (13)–(15) numerically, with n as a free parameter. Numerical integration is possible using a variety of methods. The one chosen here involves implementation of the trapezoid method in Microsoft Excel^®. The procedure is presented in “Appendix A”, the result of which produces the theoretical dependency of n on the standard deviation, σ_SD, normalized by the average particle radius 〈r〉. The relationship between n and σ_SD/〈r〉 is expressed by the empirical equation

$$n = 8.199 - 40.764\frac{{\sigma_{{\text{SD}}} }}{\langle r\rangle } + 95.032\left( {\frac{{\sigma_{{\text{SD}}} }}{\langle r\rangle }} \right)^{2} - 82.958\left( {\frac{{\sigma_{{\text{SD}}} }}{\langle r\rangle }} \right)^{3}.$$

(17)

Between the limits 2 < n < 3, σ_SD/〈r〉 varies between a maximum value of 0.3536 (for the broad PSD of the IRC theory of coarsening) to and a minimum value of 0.2154 (for the narrow PSD of the LSW theory).

Plotnikov et al. [64] published PSDs in the form of histograms for all their aging times except 2607 h; they are presented in the Supplementary Material to the paper. The histograms for 16, 64, 256, 1024 and 4096 h are ostensibly representative of the PSDs of the γ′ precipitates in the coarsening regime of their aging experiments. The ratio σ_SD/〈r〉 was calculated from their histograms using the formula

$$\frac{{\sigma_{{\text{SD}}} }}{\langle r\rangle } = \left\{ {\sum\limits_{i} {g_{i} \left( {u_{i} - 1} \right)^{2} } } \right\}^{1/2} ,$$

(18)

where the subscript i denotes the value of u in the center of the ith bin, the sum being taken over all the bins in the histograms. It is important to point out that the values of σ_SD/〈r〉 calculated using Eq. (18) are not equal to the values reported by Plotnikov et al. [64] in Table D1 of the Supplementary Material, which is most likely a consequence of the fact that only those γ′ particles fully contained within the APT tip were included in the statistics. To compare the scaled standard deviations with the reported standard deviations it is necessary only to divide σ_SD by the reported values of 〈r〉. The results of the calculations are summarized in Table 1.

Table 1 Standard deviations of the particle size distributions in a Ni–12.5%Al alloys aged at 550 °C

A glance at the 4th column of Table 1 shows that σ_SD/〈r〉 lies within the acceptable limits of 0.3536 and 0.2154 for only 2 of the 5 PSDs (1024 and 4096 h), with the PSD for t = 256 h of aging right at the limit for the smallest allowable value of n = 2. On substituting the values of σ_SD/〈r〉 for these last two aging times (Table 1) into Eq. (17), the values of n obtained are 2.16 and 2.06, respectively.

Taking a cue from the results in Table 1, we consider here the histograms only for the aging times of 256, 1024 and 4096 h and analyze them by comparison with the theoretical PSDs of the TIDC coarsening theory for n = 2.0, 2.2 and 2.4. These 3 values of n were chosen because n = 2.0 is the smallest possible value in the TIDC coarsening theory and representative of the histogram for the specimen aged for 256 h, while n = 2.4 is the value of n that best fits the vast majority of data on the PSDs in Ni–Al alloys [63]. The approximate nature of the fitting routine by no means excludes analysis of the other two PSDs (16 and 64 h). but for our purposes it is sufficient to consider just the data on the last three aging times. The results are shown in Fig. 3a. It appears that the theoretical PSDs describe the experimental distributions equally well or poorly, depending on one’s perspective. In terms of visual appearance, the theoretical PSD for n = 2 appears to best fit the tail of the experimental histograms, while the PSD for n = 2.4 appears to best fit the data at the smaller values of u. The PSD for n = 2.2 is clearly a good compromise fit to the overall data on the histograms. As will be seen in an upcoming section, the intermediate value of n = 2.2 also happens to be one that comes close to best fitting the data on the kinetics of growth of γ' precipitates in the alloy investigated by Plotnikov et al. [64] and is close in magnitude to the value n = 2.16 for the alloy aged for 1024 h.

Figure 3

a Experimentally measured particle size distributions of γ′ precipitates in a binary Ni–12.5Al alloy aged at 823 K, data of Plotnikov et al. [64]. Each data point represents the center of a bin in the originally published histograms. The curves represent the theoretical PSDs of the TIDC coarsening theory for n = 2.0, 2.2 and 2.4; b the data of Plotnikov et al. in Fig. 3a presented as experimental cumulative distribution functions, ECDF, compared with G(u), the CDFs predicted by the TIDC coarsening theory for n = 2.0, 2.2 and 2.4. The data on the ECDFs are taken at the maximum value of u for each bin in the experimental histograms

Since the data on the experimental PSDs are limited and of questionable statistical significance given the small number of particles measured (as noted by Plotnikov et al. themselves) and the fits to the PSDs are inconclusive, it is useful to explore an additional option for fitting the data on the PSDs to find an acceptable value of n. The option chosen is to convert the PSDs of Plotnikov et al. to experimental cumulative distribution functions, ECDFs, and compare them empirically with theoretical CDFs of the TIDC coarsening theory calculated for n = 2.0, 2.2 and 2.4. The virtue of comparing ECDFs with theoretical CDFs is that there are established statistical tests of goodness of fit, which utilize ECDFs rather than PSDs for comparing theoretical and experimental statistical distributions (see, for example, the paper by Stephens [69]).

The CDFs predicted by the TIDC coarsening theory were calculated using the formula published by Ardell [70], who showed that the CDFs for several different types of coarsening problems can be calculated quite simply using the equation

$$H( z ) = 1 - \text{exp}\left\{ {\xi ( z )} \right\},$$

(19)

where H(z) is the theoretical CDF and ξ(z) is given by Eq. (14) with z as the upper limit of the integral. Even though the theoretical CDFs must be calculated using the variable z = r/r*, they are identical to those expressed in terms of u, taking into account the equality H(z) = G(u) [70]. To compare the ECDFs with the theoretical CDFs, using u as the convenient scaled particle size coordinate, it is essential to transform the coordinate z to u. Keeping this in mind, the ECDFs for the data of Plotnikov et al. [64] are shown in Fig. 3b for n = 2.0, 2.2 and 2.4, where it is apparent from a visual perspective that the ECDFs confirm the assessments based on the evaluations of the PSD in Fig. 3a, namely that the tail of the histograms appears to be most consistent with n = 2.0, while the data for smaller values of u are most consistent with n = 2.4, n = 2.2 being a reasonable compromise value. It is emphasized here that the fits to the ECDF data are not rigorous, and that tests of goodness of fit are possible using known methods of statistical analysis [69]; goodness-of-fit testing will be implemented in future work.

Based on the analyses of the PSDs and ECDFs, n = 2.2 was selected as representative of the temporal exponent for the analysis of the data of Plotnikov et al. [64] on the kinetics of γ' precipitate coarsening. Even though the choice of n = 2.2 is arbitrary to some extent, it can be stated with confidence that the theoretical PSDs shown in Fig. 3a fit the data as well as the theoretical PSDs predicted by the MLSW theory of Ardell [61], the theory of Brailsford and Wynblatt [71] and the theory of Akaiwa and Voorhees [72], shown in Fig. E1 in the Supplementary Material [64]. Those 3 theories predict that the PSD depends on the volume fraction of precipitate. Given that the coarsening behavior of γ′ precipitates is independent of volume fraction, any agreement between these theories and the experimental histograms can only be regarded as fortuitous.

Kinetics of particle growth

The most accurate values of the rate constant k_n and the TIDC coarsening theory are best obtained by plotting 〈r〉ⁿ versus t, in accordance with Eqs. (4) and (6); this is true irrespective of the value of n (= 3 for LSW, 2 for IRC or between 2 and 3 for TIDC coarsening). In order to obtain meaningful values of the parameters that govern any coarsening process it is essential to use the equations that best represent the kinetics and PSDs. Having chosen a value of n it is imperative to insist that analyses of all the data survive the test of internal consistency. In particular, we need only to plot 〈r〉ⁿ versus t, X versus t^−1/n and f versus t^−1/n to see whether all the data not only obey the appropriate rate laws, but also provide a consistent set of thermo-kinetic parameters. There are different ways of plotting the temporal dependency of N_v, but the same standard applies to this variable as well.

We begin by examining the kinetics of growth of the average particle, plotted as 〈r〉^2.2 versus t in Fig. 4. The error bars represent the standard deviations of 〈r〉^2.2, calculated from the standard deviations of 〈r〉 reported in Table D1 of the Supplementary Material of Plotnikov et al. The inset shows the correlation coefficients, R², of the fits as a function of the temporal exponent, n. The best fit to the data, i.e., the maximum value of R², is obtained for n = 2.24, which is in exceptionally good agreement with the value of n = 2.2 used to fit the CDF in Fig. 3b. The rate constant obtained from the slope of the curve in Fig. 4 is k_n = 3.460 ± 0.450 × 10⁻²⁵ m^2.2 s⁻¹.

Figure 4

The data of Plotnikov et al. [64] on average radius, 〈r〉, raised to the 2.2 power, as a function of aging time, t. The data plotted are for t ≥ 16 h, within the coarsening regime. The blue curve shows the linear fit to the data. The plot inset shows the correlation coefficient, R², for the same data as a function of the temporal exponent n derived from plots of 〈r〉ⁿ for different values of n. The best fit is obtained for n = 2.24

The kinetics of solute depletion

The kinetics of solute depletion is shown in Fig. 5 for both the γ and γ′ phases. The time dependencies of both X_γAl and X_γ′Al are identical to that in Eq. (7), i.e., they both vary as t^−1/2.2 at long aging times, but the rate constants differ [5]. Here we are concerned only with the rate constant κ_n obtained from the analysis of the data on X_γAl (Fig. 5a) The usefulness of both plots in Fig. 5 is that the extrapolation to t^−1/2.2 = 0 (t = ∞) provides values of the equilibrium solubilities of Al in both the γ and γ′ phases at the temperature of the experiment on coarsening. One of the great benefits of APT is that it is able to provide data on the solute concentration in the minority phase, which is difficult to obtain by other means.

Figure 5

Plots illustrating the kinetics of solute depletion for the γ and γ′ phases in a Ni–12.5Al alloy aged at 823 K. The concentrations of Al in the γ phase are shown in a, while the concentrations of Al in the γ′ phase are shown in b. The concentrations in both phases are plotted against aging time raised to the inverse 1/n power, with n = 2.2. Data of Plotnikov et al. [64]. The data in red and green were used in the linear fit, while the datum in black in each figure was excluded

Owing to the asymptotic nature of Eq. (7), only the data for t ≥ 64 h are included in Fig. 5. The additional datum for 16 h of aging is also shown; it clearly deviates from the linear fit to the data and its omission is justified by fact that Eq. (7) is expected to be valid only at longer aging times, even in the coarsening regime. The slope of the curve in Fig. 5a is $\kappa_{n}^{ - 1/2.2}$ = 1.0426 ± 0.2575 s^1/2.2. The intercepts indicate that the equilibrium solubilities of Al in the γ and γ′ phases are X_γAle = 0.1121 ± 0.0005 and X_γ′Ale = 0.2365 ± 0.0004, respectively. What is not seen in Fig. 5 is that the difference (X_γ′ − X_γ) ≈ 0.125 for the aging times t ≥ 256 h is essentially equal to ∆X_e ≈ 0.124 from the extrapolated equilibrium values in Fig. 6. This nicely justifies the assumption used to derive Eq. (10); this assumption is more fully justified later.

Figure 6

Data on the measurements of the volume fraction, f, of γ′ precipitates in a Ni–12.5Al alloy aged at 823 K, plotted versus aging time, t, raised to the − 1/2.2 power. Data of Plotnikov et al. [64]. The datum in green was omitted from the fit, which includes only the data for t ≥ 64 h

Dependence of volume fraction on aging time

Plotnikov et al. [64] reported data on the variation of f with aging time but did not analyze the kinetics. The variation of the volume fraction, f, with aging time is shown in Fig. 6, where f is plotted versus t^−1/2.2 in accordance with Eq. (10). Once again, only the data for t ≥ 64 h are included in the analysis since the level of approximation is the same as for the kinetics of solute depletion. The extrapolation to t^−1/2.2 = 0 provides an estimate of the equilibrium volume fraction at the temperature of the experiment, 823 K. The results of the analysis of the data yield the slope of the curve $\kappa_{n}^{ - 1/2.2} \text{/}\Delta X_{\text{e}}$ = − 12.930 ± 2.993 s^1/2.2, with f_e = 0.1350 ± 0.0053. Using the data obtained from the analysis of the data in Fig. 5, the calculated slope of the curve in Fig. 6 is − 10.427 ± 2.414 s^1/2.2. Given the errors in the experimentally measured values of f and the only fair agreement between the data and the predictions of Eq. (10), the semiquantitative agreement between the measured and calculated values of the slope is about as good as can be expected.

The time dependency of N_v

It has been known for quite some time [6, 66] that the time dependency of N_v is given by Eq. (11). The physics behind Eq. (11) derives from the relationship among 〈r〉, N_v and f, which for spherical particles leads from Eq. (12) to the result

$$\frac{{4\pi \psi \langle r\rangle^{3} }}{3}N_{v} = f,$$

(20)

recalling that 〈V〉 = 4πψ〈r〉³/3. Equation (20) is valid for all aging times. The frequently invoked inverse time dependency of N_v arises from the asymptotic relationship 〈r〉³ ≈ kt, which on substitution into Eq. (20) leads to the result

$$N_{v} = \frac{3f}{4\pi \psi k}t^{ - 1} .$$

(21)

Examination of Eq. (11) suggests two options for analyzing experimental data. On the one hand, data plotted as N_vt^3/n versus t^−1/n should be linear, with slope ${{ - \kappa_{n}^{ - 1/n} } / {\Delta X_{\text{e}} \psi S k_{n}^{3/n} }}$ and intercept ${{f_{\text{e}} } / \psi S k_{n}^{3/n} }$. On the other hand a plot of Nvt^4/n versus t^1/n should also be linear, with the slope and intercepts interchanged, along with their signs. Unless the data are exceptionally reliable, they do not produce comparable results. This is evident on examining the data analyzed in Ref. [66]. For the data of Plotnikov et al. [64] the more reliable method is to plot the product N_vt^4/2.2 versus t^1/2.2, the results of which are shown in Fig. 7. The linearity expected from Eq. (11) is approximately observed only for aging times satisfying t ≥ 256 h. Exclusion of the other data is justified by the arguments presented in “Appendix B.” As predicted by Eq. (11) the intercept in Fig. 7 is negative, with a magnitude of 3.430 ± 1.719 × 10³⁴ s^4/2.2 m⁻³. The slope of the curve is 6.946 ± 1.332 × 10³¹ s^−1/2.2 m⁻³. Using the previously measured values of k_n, f_e, $\kappa_{n}^{ - 1/2.2}$ and ∆X_e ≈ 0.124, the calculated values of the slope and intercept of the curve in Fig. 7 are 6.649 × 10³¹ s^−1/2.2 m⁻³ and 4.128 × 10³³ s^4/2.2 m⁻³, respectively. The agreement between the measured and calculated slopes is remarkably good, but the calculated intercept is about a factor of 8 too small. It will be shown later that the authors’ reported values of 〈r〉³, N_v and f are themselves internally inconsistent. Given the uncertainties of the experimentally measured values of N_v, it is unrealistic to expect the re-analysis of the data to yield results that are better than those obtained.

Figure 7

The data of Plotnikov et al. [64] on the variation of the product of the number density, N_v, and aging time, t, raised to the 1/2.2 power. Only the data on the 4 longest aging times, in red, were used in the linear fit, indicated by the blue line. The 2 data points in black represent the data at 16 and 64 h and were not used in the fit

Comments and criticisms

The discussions in this section focus on the primary distinctions between the approaches used herein to analyze the data of Plotnikov et al. [64] compared with those used by the authors themselves. These approaches differ in significant ways, and the objective here is to present the interested reader with persuasive and pedagogically useful arguments that the approaches used by Plotnikov et al. are flawed, in some cases mildly and in others quite seriously.

Analyses of the data on the kinetics of particle growth

The standard practice of Plotnikov et al. [64] is to treat all the parameters in Eqs. (6) and (7) as unknowns, to be determined numerically using multivariate nonlinear regression analysis (MNRA) of the data. There would be no particular problem with this approach if all the parameters in the equations were physically meaningful, but they are not. The main problem with using MNRA is that the inclusion of 〈r_o〉 and t_o unnecessarily compromises the values of the really important parameters in the kinetics of particle growth, specifically k_n and n.

To illustrate this, consider the data on the kinetics of particle growth in Fig. 4. Plotnikov et al. write the equation governing the kinetics of particle growth as

$$\langle r\rangle^{n} - \langle r_{\text{o}} \rangle^{n} = k_{n} \left( {t - t_{\text{o}} } \right),$$

(22)

which includes 3 disposable parameters, the exponent n and two constants of integration, 〈r_o〉 and t_o. The only parameters with true physical significance are n and k_n, and there is only one arbitrary constant on integrating Eq. (4), not two. Nevertheless, the authors use the Microsoft Excel^® Solver macro to extract the “best” values of the three parameters, which is done by first rewriting Eq. (22) as

$$\langle r\rangle = \left\{ {k_{n} \left( {t - t_{\text{o}} } \right) + \langle r_{\text{o}} \rangle^{n} } \right\}^{1/n} .$$

(23)

The target variable in the Solver macro (the “model” variable in the language of Solver) is 〈r〉.

MNRA of the data using Eq. (23) produces the curve shown in Fig. 8a, with n ≈ 2.917, k_n ≈ 0.528 nm^2.917 h⁻¹, t_o ≈ − 1.403 h and 〈r_o〉 = 2.50 nm. From the simple standpoint of internal consistency, it is expected that a plot of 〈r〉^2.917 versus t should be characterized by the very same values of k_n and 〈r_o〉, with t_o = − 〈r_o〉ⁿ/k_n, the expectation being that alternative representations of the very same set of data would yield consistent results provided that the parameter values produced by MNRA are robust. A plot of 〈r〉^2.917 versus t is shown in Fig. 8b. The values of k_n and 〈r_o〉 obtained from analysis of the data in Fig. 8b differ from those obtained from MNRA, k_n = 0.552 nm^2.917 h⁻¹ being ~ 4% larger than the MNRA result and 〈r_o〉ⁿ = − 5.465 nm^2.917 being negative. The value of t_o consistent with these parameters is 9.9 h, which is not only positive, but 7 times larger in magnitude than the value of t_o extracted from MNRA of the same set of data. The negative value of 〈r_o〉^2.917 and positive value of t_o are clearly visible in the graph inset in Fig. 8b. These discrepancies are untenable and entirely attributed to the misapplication of MNRA to the data. MNRA is not at fault here. Instead, it is the elevation of both 〈r_o〉 and t_o to physical significance when in fact they have none. It should also be noted in passing that the fit to the data using n = 2.917 is not as good as the fit using n = 2.2 (Fig. 4).

Figure 8

a Plot of the average particle size 〈r〉 versus aging time, t, compared with the prediction of Eq. (23), solid red curve; b plot of 〈r〉^2.917 versus t with the linear fit indicated by the red line. The insert shows the data on the 2 smallest aging times, 16 and 64 h, and the same fit to the data nearest the origin, illustrating the positive value of t_o and the negative value of 〈r〉^2.917. The units in the inset are h for the abscissa and nm^2.917 for the ordinate. Data of Plotnikov et al. [64]

The variation of volume fraction with aging time and quasi-steady coarsening kinetics

It seems that since f increases slowly with aging time toward its equilibrium value, but is not constant, Plotnikov et al. [64] as well as Sudbrack et al. [38] and Booth-Morrison et al. [39, 73] before them, assert that coarsening proceeds under “quasi-steady-state” conditions. The inference is that true steady-state coarsening, as opposed to quasi-steady-state coarsening, is possible only when f is constant and equal to its equilibrium value. In fact, however, there is nothing quasi at all about the conditions under which γ′ precipitates coarsen. The volume fraction must increase with aging time as a natural consequence of the depletion of solute from the matrix. This is unarguable and has been an undisputed fact at least since its publication in 1969 [20]. It is perhaps most easily appreciated by considering Fig. 9.

Figure 9

The Ni-rich region of the Ni–Al phase diagram, illustrating the approximate compositions of the γ and γ′ phases during coarsening, from which the volume fraction of any alloy, composition X_o, can be calculated using the lever rule. The residual supersaturations of the γ and γ′ phases X_γAle − X_γAl and X_γ′Ale − X_γ′Al, respectively, are greatly exaggerated for clarity

The volume fraction² of the γ′ phase during coarsening is f ≈ (X_o − X_γAl)/(X_γ′Al − X_γAl). The equilibrium volume fraction is f_e ≈ (X_o − X_γAle)/(X_γ′Ale − X_γAle). Since X_γ′Al − X_γAl ≈ X_γ′Ale − X_γAle, it is easy to see graphically from Fig. 9, using the lever rule, why f increases with aging time. It is simply because the “distance” X_o − X_γAl increases as X_γAl approaches its equilibrium value X_γAle, while the “distance” X_γ′Al − X_γAl ≈ X_γ′Ale − X_γAle remains approximately constant. The increase in f is therefore not an accidental feature of particle coarsening or the signature of some kind of “quasi-steady-state” condition, waiting for the eventual arrival of “steady-state.” Instead, it is part and parcel of the normal Ostwald ripening process.

Variation of the number density with aging time

There has been considerable reluctance in some quarters to accept Eq. (11) as the proper description of the kinetics of depletion of the number density of particles with aging time, preferring instead Eq. (21). Plotnikov et al. [64] are no exception. We consider here some of the implications of Eq. (21) that any set of data must obey. These implications also provide additional theoretical justification for the validity of Eq. (11).

Temporal dependency of the product N_vt

The easiest way to check the validity of Eq. (21) is to calculate the product N_v t. If Eq. (21) were correct the product N_v t would be constant, independent of aging time. To this end we examine the data of Plotnikov et al. [64] using their tabulated data as input (Table D1, Supplementary Material). The results are presented in Table 2. It is obvious by inspection that the product N_vt is not even close to being constant, increasing with aging time by over an order of magnitude. Granted, there are uncertainties in the measurements of N_v, but the trend is unmistakable and completely belies the longstanding belief that N_v varies as t⁻¹. The reason for this is obvious. According to Eq. (21) the inverse dependency of N_v on t would be valid if f were constant and equal to f_e. Is it not.

Table 2 Calculations of the product N_vt as a function of aging time for the data of Plotnikov et al. [64] on a binary Ni–12.5Al alloy

Internal consistency among 〈r〉, N_v and f

In any series of experiments the results must be internally consistent to assure credibility and confidence that the reported data are as error-free as possible on the one hand and truly meaningful on the other. It is also important to examine any set of data that fails this requirement with a view to providing alternative explanations. The data of Plotnikov et al. [64] are evaluated in this context. There is one easy check of internal consistency, which involves the independent measurements of 〈r〉, N_v and f.

Equation (20) describes the relationship among 〈r〉, N_v and f for spherical particles. Internal consistency of the data demands agreement with this equation, which does not involve any approximations apart from the assumption of spherical shape. The data on γ′ coarsening in Ni–Al alloys are examined in this light, yielding the results shown in Table 3 where it is seen that most of the discrepancies exceed 15%. There is no rational explanation other than to assert that something is seriously amiss with the data. It is impossible to know the source of the large discrepancies, but they are far too great to be attributed to the errors reported in the publication. Since Eq. (20) is valid at all aging times, the discrepancies cannot be attributed to assumptions about whether or not the γ′ microstructure has entered the coarsening regime. The suspicion here is that the values of N_v are inaccurate, which is perhaps not surprising because N_v is generally very difficult to measure. Moreover, the inaccuracies in the reported values of N_v do not appear to be systematic. The behavior shown in Table 2 and the lack of internal consistency seen in Table 3 are consistent with the assertion that the accuracy of the reported values of N_v is highly suspect.

Table 3 Comparison of the measured values of the volume fraction (f_meas) of γ′ precipitates in the Ni–12.5%Al alloy with those calculated (f_calc) using Eq. (20); data of Plotnikov et al. [64]

The role of second-order terms in the asymptotic expansions of coarsening variables

Detractors of the validity of Eq. (11) and proponents of Eq. (21) wonder why the time-dependent variables are not impacted by second-order terms.³ Consideration of higher-order corrections to the time dependencies of 〈r〉, X, f and N_v is presented in “Appendix B”, where the answer is provided. In the particular case of N_v, the second term in Eq. (11) does not arise from a series expansion of its time dependency. Instead, it is a consequence of the temporal dependency of f_e.

Comparison with literature data

The re-analysis of the data of Plotnikov et al. [64] in the context of TIDC coarsening has demonstrated nearly perfect self-consistency, exceeding expectations given the flaws in the data. The internal agreement includes the data on the ECDFs as well as the data on kinetics. In this section the results of the TIDC theory re-analysis are compared with the data expected from reports in the literature. The parameters in question are the equilibrium solubilities of Al in the γ and γ′ phases, X_γAle = 0.1121 ± 0.0005 and X_γ′Ale = 0.2365 ± 0.0004, the equilibrium volume fraction, f_e, and the interfacial free energy, σ, at the aging temperature of 550 °C (823 K).

The equilibrium compositions of the γ and γ′ phases at 823 K are readily available from the solubility curves published by Ardell (X_γAle) [74] and Ma and Ardell (X_γ′Ale) [75]. The results are X_γAle = 0.1074 and X_γ′Ale = 0.2313, respectively, which differ by ~ 0.05 at.% from the values obtained from the extrapolations in Fig. 6. The equilibrium volume fraction of γ′ precipitates at 823 K for an alloy containing 12.50 at.% Al is 0.15, which is ~ 10% larger than f_e obtained from the intercept in Fig. 10. Interestingly, the values of X_γAle, X_γ′Ale and f_e happen to be in excellent agreement with those reported by Plotnikov et al. themselves, specifically 0.1114 ± 0.0032, 0.2314 ± 0.0047 and 0.128, respectively. All these values are within the acceptable range of uncertainty.

Figure 10

Data on the temperature dependence of the interfacial free energy of the γ/γ′ interface compared with the predictions of several theories. The two data points attributed to Ardell are taken from Ref. [68]. The labeled theoretical curves are taken from the work of Mao et al. [79], Yang et al. [81] and Liu et al. [82]

The interfacial free energy, σ, is readily calculated from the equation

$$\sigma = \frac{{\Delta X_{e} G^{\prime\prime}_{{\text{m}\gamma \text{e}}} }}{{2V_{{\text{m}\gamma^{\prime}\text{e}}} \langle z\rangle }}\left( {\frac{{k_{n} }}{{\kappa_{n} }}} \right)^{1/n} ,$$

(24)

which is valid for the LSW theory with n = 3 (〈z〉 = 1) and for the TIDC theory for any value of n. Equation (24) has already been used to estimate σ in 5 binary γ/γ′ alloys, Ni–Al, Ni–Ga, Ni–Ge, Ni–Si and Ni–Ti [68]. That effort was undertaken for two main reasons: 1. Thermodynamic modeling was finally available to provide reliable estimates of $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ for all 5 alloys, thereby eliminating the need for simplifying approximations of the curvature of the Gibbs free energy of the γ phase; 2. the values of σ predicted by both the LSW and TIDC theories of coarsening could be easily compared. The main conclusions were that the magnitudes of σ were all in the expected range and that the TIDC analysis produced values of σ about 2/3 as large as the LSW values.

Proper application of Eq. (24) demands that ∆X_e, V_mγ′e and $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ have their thermodynamic equilibrium values, which of course depend on the equilibrium compositions of the γ and γ′ phases at the temperature of the experiment that produces the values of k_n and κ_n. Since the equilibrium values of ∆X_e, V_mγ′e and $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ as functions of T have not been reported previously, they are presented in “Appendix C” along with empirical equations that can be used to calculate their temperature dependencies. The source material used in the calculation of ∆X_e is the temperature dependencies of X_γe reported by Ardell [74] and X_γ′e reported by Ma and Ardell [75]. V_mγ′e was calculated using the equilibrium lattice constants of the γ′ phase as a function of temperature [76]. The equilibrium curvatures of the Gibbs free energies of mixing were calculated using the thermodynamic data base of Ansara et al. [77] in conjunction with the equilibrium solubilities of the γ phase as a function of T [74].

Using as input the data extracted from Figs. 4 and 5a, in conjunction with $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ = 338,173 J mol⁻¹ [77], V_mγ′e = 7.03 × 10⁻⁶ m³ mol⁻¹ and 〈z〉 = 0.9242, Eq. (24) predicts σ = 25.73 ± 0.653 mJ m⁻². The large errors are due entirely to the scatter in the values of X_γAl at the longer aging times (see Fig. 5). Computational modeling of the γ/γ′ interfacial free energy [78,79,80,81,82] indicates that it is temperature dependent, decreasing with increasing temperature. Values of σ for Ni–Al alloys are also available for aging temperatures of 898 and 988 K [68], specifically 22.33 ± 1.31 and 19.52 ± 0.90 mJ m⁻², respectively. The data on σ as a function of aging temperature T for the 3 available aging temperatures are shown in Fig. 10. Within the limits of experimental error the decrease of σ with T is linear. These results, all obtained from data on coarsening in binary Ni–Al alloys analyzed using the TIDC coarsening theory, confirm that the energy of coherent γ/γ′ interfaces is temperature dependent, as predicted theoretically. The comparison between theory and experiment seen in Fig. 10 indicates that the temperature dependence of σ is much stronger than that predicted by Mao et al. [79] and more closely resembles the temperature dependencies predicted by the theories of Yang et al. [81] and Liu et al. [82], the latter of which is within striking distance of good quantitative experimental agreement. The decrease of σ with increasing T has been noted before [81,82,83], using the Ni–Al/Ni₃Al interfacial free energies calculated by Ardell [68], but the addition of the third value places the temperature dependency on a much firmer footing.

The values of σ reported by Plotnikov et al. [64], 28.55 ± 1.61 and 29.94 ± 1.69 mJ m⁻² depending on which thermodynamic data base is used in the calculation (see their Table 7) are comparable in magnitude to the value of σ calculated herein from their data, but with much smaller errors. The main factors responsible for the differences, apart from their assumption that MDC coarsening kinetics prevail, is their use of incorrect values of V_mγ′e and $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$, both of which are smaller than the correct values but compensate each other to some extent in Eq. (24). Specifically, Plotnikov et al. used $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ ≈ 270 kJ mol⁻¹ in their calculations of σ (cf. ~ 338 kJ mol⁻¹), which suggests that they might have used the curvature of the excess Gibbs free energy rather than the curvature of the total Gibbs free energy, which is about 25% larger. Also, their reported value of V_mγ′e (6.98 × 10⁻⁶ m³ mol⁻¹) is slightly smaller than the one used herein.

The equation used by Plotnikov et al. to calculate σ also includes a fudge factor, F(f) (= 1.83 in their Table 6) which purports to “correct” for the dependence of the rate constant k on f. Since there is no effect of f on coarsening in Ni–Al alloys, it is clearly inappropriate to employ a phantom fudge factor to account for a phantom effect. The Plotnikov et al. values of σ are about a factor of 1.22 smaller when the fudge factor is excluded, bringing their values of σ much closer to that reported in this work.

The source of the small error bars on their reported values of σ appears to be related to an underestimate of the error in the rate constant κ, reported in their Table 6. The value of κ^−1/3 reported by Plotnikov et al. is 0.25 ± 0.01 s^1/3; the value calculated herein using their last five data points in a plot of X_Al versus t^−1/3 is 0.263 ± 0.068 s^1/3. Whereas the magnitudes of κ are comparable, the error in their data is actually over a factor of 6 larger than that reported, which accounts for the discrepancy between the error reported by Plotnikov et al. and the error calculated in this work.

Summary, conclusions and final thoughts

• 1. Fitting the PSDs to the theoretical PSD of the TIDC coarsening theory is the best way to evaluate n. If PSDs have not been measured, a suitable alternative is to plot 〈r〉ⁿ versus t for different values of n and then determine n from a plot of the correlation coefficient, R², versus n, as shown inset in Fig. 4. Plotnikov et al. disavow this method, but do not offer any scientific or statistical basis for their opinion. A glance at Fig. A1 of the Supplementary Material to Ref. [64] shows quite clearly that of the 4 plots shown n = 2.4 provides the best fit to their own data.

• 2. Regarding the time dependency of N_v, it has been shown repeatedly [6, 40, 66] that the inverse time dependency predicted by Eq. (21) is incorrect. It truly does not take much effort on the part of any researcher to check the constancy of the product N_vt. The data in Table 2 are easily checked in a matter of minutes, and it requires little knowledge of mathematics to see that N_vt is not even close to being constant. Simple scientific curiosity would stimulate most researchers to at least try to understand why Eq. (21) fails so miserably. Perhaps it is because Eq. (21) dates so far back to the early days of the theory of coarsening that it is accepted without question. But its failure, and the relative, if imperfect, success of Eq. (11) [6, 40, 66] to describe data on the time dependency of N_v in so many different types of coarsening problems suggests that the refusal to accept Eq. (11) is truly staggering. Plotnikov et al. [64] assert that Eq. (21) is justified by the theoretical work of Marqusee and Ross [84] who indeed report a “second-order correction” to the t⁻¹ dependency of Eq. (20) (as do Umantsev and Olson [85]). However, the second term in Eq. (11) is not a consequence of a series expansion of the time dependency of N_v (see “Appendix B”). Instead, it is due to the time dependency of f and is much too large to ignore.

• 3. The existence of “quasi-steady-state” or “quasi-stationary state” coarsening has been a consistent thread in the papers written by Sudbrack et al., Booth-Morrison et al. and Plotnikov et al. The usage first appears in the Ph.D. dissertation of Sudbrack [86], who associated it with solute depletion during coarsening and attributed it to Kuehmann and Voorhees (K–V) [87]. K–V themselves, however, refer only to the quasi-stationary approximation used to solve Laplace’s equation for steady-state diffusion. K–V themselves never use the term quasi-steady-state coarsening. In subsequent publications [38, 39, 64, 73] the notion of quasi-steady-state coarsening appears to have taken on a life of its own, possibly attributed to the experimentally measured variation of f with aging time. The upcoming discussion involving the lever rule (see Fig. 8) illustrates convincingly that the volume fraction of γ′ precipitates must increase with aging time toward its equilibrium value as an integral component of Ostwald ripening behavior. There is nothing “quasi-steady” about the way this occurs. The idea of quasi-steady or quasi-stationary state coarsening is misleading terminology and should be abandoned.

• 4. Despite the misgivings accompanying the lack of internal consistency of some of the data of Plotnikov et al. [64], their results are entirely consistent with the predictions of the TIDC coarsening theory. This conclusion is inescapable. Indeed, it is almost as if the authors set out to provide a critical test of the TIDC coarsening theory, which nearly perfectly describes their data both semiquantitatively (Figs. 4, 5, 6, 7) and quantitatively. The excellent visual fit between the experimental and theoretical CDFs seen in Fig. 3b provides additional reassurance that the TIDC coarsening theory is correct. The only discrepancy with previous work [63, 68] is the difference between the values of the temporal exponent used to fit the data, n = 2.4 previously and 2.2 in this study. It is most likely the case that self-consistent results would obtain using the same value of n to analyze all the data, but that is work for the future. Lending further credence to the validity of the TIDC coarsening theory is the consistency among the values of σ obtained from analysis of the data on Ni–Al alloys. We see in Fig. 10 a consistent linear decrease of σ with T over the range of T investigated and good agreement with at least some of the temperature dependencies predicted theoretically.

• 5. In the original TIDC coarsening theory [44] the interface width, δ, was assumed to be independent of the particle size. The original justification for temporal exponents satisfying 2 ≤ n ≤ 3 arose from a conjecture that δ should increase as 〈r〉 increases [44]. The work of Plotnikov et al. [52] shows that this is not the case, δ instead decreasing very slowly with aging time during the γ′ coarsening regime in a binary Ni–Al alloy. As demonstrated recently [65], the diffusion coefficients at the γ/γ′ interface in binary Ni–Al alloys can also impact coarsening in such a way that the temporal exponent is noninteger, leading to a temporal exponent that satisfies the condition 2 ≤ n ≤ 3. The influence of other factors remains to be explored. One is whether δ_lro, the transition region between long-range order in the γ′ particle to disorder within the interface [54, 55], varies with particle size. After all, it is diffusion within this region of the interface, not within the entire interface itself (recalling that δ_lro < δ), that will have quantitative consequences for TIDC coarsening. Another, perhaps more subtle, factor is the change in equilibrium shape that occurs during coarsening in elastically misfitting γ/γ′ alloys, typified by Ni–Al alloys, where the shapes of the γ′ precipitate evolve from spherical to cuboidal as the size increases. This means that the parameter S, which satisfies the condition 4π/3 ≤ S ≤ 8 increases with aging time and should be incorporated into the Gibbs–Thomson equation which is used to specify the solute concentration in the matrix at the γ/γ′ interface.

Appendices

Appendix A

The procedures described in this appendix provide an alternative method of fitting the theoretical PSD of the TIDC coarsening theory to experimentally measured histograms when a more rigorous mathematical subroutine is not available. The method utilizes Microsoft Excel^® to implement simple integration routines using the trapezoid approximation. A side benefit of the new method is the calculation of other important parameters related to the PSDs. The first task is numerical integration of Eqs. (13)–(15) to calculate h(z) for values of n over the interval 2 ≤ n ≤ 3. After this is done, 〈z〉, 〈z²〉 and 〈z³〉 are calculated numerically over the same range of n, thus enabling calculation of g(u), Eq. (16) and H(z), Eq. (19), as well as σ_SD and ψ. Fitting of the experimentally measured histograms is done by calculating their unique values of σ_SD/〈r〉 and equating them to the theoretically calculated values of σ_SD/〈r〉, which depend on n via Eq. (17). The numerical integrations were all performed using the trapezoid approximation with ∆z = 0.005. The numerical calculations for n = 2 and n = 3 were compared with the analytical solutions for IRC and MDC coarsening, respectively, and found to agree to at least the 8th decimal place.

Numerical calculation of 〈z〉, 〈z²〉 and 〈z³〉 is straightforward, making use of Eqs. (13) and (15), and recalling that z_max = n/(n − 1):

$$\langle z\rangle = - 3\int\limits_{0}^{{z_{{\text{max}}} }} {z\,\phi ( z )} \,\text{exp}\left\{ {\xi ( z )} \right\}\text{d}z;$$

(25)

$$\langle z^{2} \rangle = - 3\int\limits_{0}^{{z_{{\text{max}}} }} {z^{2} \,\phi ( z )} \,\text{exp}\left\{ {\xi ( z )} \right\}\text{d}z;$$

(26)

$$\langle z^{3} \rangle = - 3\int\limits_{0}^{{z_{{\text{max}}} }} {z^{3} \,\phi ( z )} \,\text{exp}\left\{ {\xi ( z )} \right\}\text{d}z.$$

(27)

To calculate σ_SD/〈r〉, note that σ_SD for the distributed variable radius r is given by the equation

$$\sigma_{{\text{SD}}} = \left( {\langle r^{2} \rangle - \langle r\rangle^{2} } \right)^{1/2} = \langle r\rangle \left\{ {\frac{{\langle r^{2} \rangle }}{{\langle r\rangle^{2} }} - 1} \right\}^{1/2} = \langle r\rangle \left\{ {\frac{{\langle z^{2} \rangle }}{{\langle z\rangle^{2} }} - 1} \right\}^{1/2} .$$

(28)

Equation (28) is valid for the theoretical PSD in any type of coarsening problem. Implementation of Eq. (28) involves the calculation of both 〈z〉 and 〈z²〉 using Eqs. (25) and (26). Comparison with experimentally measured PSDs or histograms must be made using the variable u = r/〈r〉. Since 〈z〉 = 〈r〉/r*, and 〈u²〉 = 〈z²〉/〈z〉², the expression for σ_SD/〈r〉 from Eq. (28) becomes

$$\frac{{\sigma_{{\text{SD}}} }}{\langle r\rangle } = \left\{ {\langle u^{2} \rangle - 1} \right\}^{1/2} .$$

(29)

Since 〈u²〉 depends on n via the dependencies of 〈z〉 and 〈z²〉 on n, it is then a simple matter to find the empirical equation relating n and σ_SD/〈r〉 The result is the empirical Eq. (17), which helps to find the value of n associated with an experimental histogram. To this end Eq. (18) is used to calculate an “experimentally measured” value of σ_SD/〈r〉, which is then used as input in the empirical equation, Eq. (17).

On taking Eqs. (15)–(17) into account, the integrals in Eqs. (25), (26) and (27) are calculated numerically to obtain 〈z〉 and ψ as a function of n, and then for n as a function of σ_SD/〈r〉. The variations of these parameters are depicted in Fig. 11. For the sake of completeness, the empirical equations relating 〈z〉 and ψ on n are presented as Eqs. (30) and (31):

$$\langle z\rangle = - \, 0.2891 \, + \, 1.1229n- \, 0.3386n^{2} + \, 0.0358n^{3}$$

(30)

and

$$\psi = 4.6236-3.2765n + 1.0605n^{2} -1.1888n^{3} .$$

(31)

Figure 11

Illustrating the dependencies of: a the average value of 〈z〉 = 〈r〉/r*; b the value of ψ = 〈r³〉/〈r〉³ as a function of the temporal exponent n for the PSDs in TIDC coarsening; c illustrating the dependency of n on the normalized standard deviation of the PSDs, σ_SD/〈r〉

Appendix B

We begin with Eq. (1), the kinetics of growth of the average particle, written in the alternative form

$$\langle r\rangle^{n} = k\left( {t - t_{\text{o}} } \right) = kt\left( 1 - \frac{t_{\text{o}}} {t} \right) = kt( {1 - \tau } ),$$

(32)

where τ = t_o/t is a dimensionless time variable. Even though τ cannot be measured experimentally, we expect it to be a small quantity for all practical aging times during coarsening, and especially so at long aging times, when 〈r〉 ≫ 〈r_o〉 and t ≫ t_o; note that τ → 0 as t → ∞. Equation (32) can be rewritten as

$$\langle r\rangle = ( {kt} )^{1/n} ( {1 - \tau })^{1/n} \approx ( {kt} )^{1/n} \left( {1 - \frac{\tau }{n}} \right)$$

(33)

on discarding quadratic and higher-order terms in the series expansion of (1 − τ)^1/n. Equation (33) justifies the approximation 〈r〉 ≈ (kt)^1/n at long aging times when τ ≪ 1.

The kinetics of solute depletion is described by the equation

$$X_{\gamma } - X_{{\gamma \text{e}}} = \frac{\ell \langle z\rangle }{\langle r\rangle } = \frac{\ell \langle z\rangle }{{( {kt} )^{1/n} \left( {1 - {\tau /n}} \right)}}.$$

(34)

On recalling Eq. (8) and expanding the denominator, Eq. (34) can be rewritten as

$$X_{\gamma } - X_{{\gamma \text{e}}} = ( {\kappa t} )^{ - 1/n} \left( {1 + {\tau /n}} \right).$$

(35)

Equation (7) is recovered when τ ≪ 1. Note that Eq. (35) involves a higher level of temporal expansion than Eq. (33).

From the discussion involving Fig. 3, the volume fraction, f, is expressed as

$$f = f_{\text{e}} - \frac{{X_{\gamma } - X_{{\gamma \text{e}}} }}{{\Delta X_{\text{e}} }} = f_{\text{e}} - \frac{{( {\kappa t} )^{ - 1/n} }}{{\Delta X_{\text{e}} }}\left( {1 + \frac{\tau }{n}} \right).$$

(36)

On substitution of Eq. (35) into the denominator, Equation (10) is recovered to the same level of approximation as Eq. (35) as τ → 0.

To derive the time dependency of N_v at long aging times Eq. (12) is rewritten as

$$N_{v} = \frac{f}{{\psi S\langle r\rangle^{3} }} \approx \frac{{f_{\text{e}} }}{{\psi S( {k t} )^{{3/n}} \left( 1 - {3 \tau / n} \right)}}\left\{ {1 - \frac{{\ell \langle z\rangle \left( {1 + {\tau /n}} \right)}}{{f_{\text{e}} \Delta X_{\text{e}} \left( {k t} \right)^{{1/n}} }}} \right\} \approx \frac{{f_{\text{e}} \left( {1 + 3\tau /n} \right)}}{{\psi S\left( {k t} \right)^{{3\text{/}n}} }}\left\{ {1 - \frac{{\ell \langle z\rangle \left( {1 + {\tau /n}} \right)}}{{f_{\text{e}} \Delta X_{\text{e}} \left( {k t} \right)^{{1\text{/}n}} }}} \right\}.$$

(37)

Equation (11) is recovered at long aging times, as τ → 0. The level of approximation is even higher than those of Eqs. (35) and (36), which is why Eq. (11) is expected to be valid at aging times exceeding the validity of Eqs. (7) and (10). It is important to realize and acknowledge that the second term in brackets in Eq. (37), which depends on time as t^−1/n, does not arise from a series expansion involving N_v versus t.

Appendix C

This Appendix provides the reader with the temperature dependencies of several important parameters associated with the γ and γ′ phases of thermodynamic equilibrium compositions, namely ∆X_e, V_mγ′e and $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$. ∆X_e was calculated using the equilibrium solute concentrations of the γ and γ′ phases [74, 75], respectively. The equilibrium solubility of the γ′ phase was then used to calculate V_mγ′e, in conjunction with the empirical equation describing its equilibrium lattice constants [76] as a function of temperature. The results are presented in Fig. 12.

Figure 12

a The dependencies of the difference between the equilibrium compositions of the γ and γ′ phases, $\Delta X_{\text{e}} = X_{{\gamma^{\prime}\text{e}}} - X_{{\gamma \text{e}}}$; b the equilibrium molar volume of the γ′ phase, V_mγ′e, on temperature, T

The empirical equation that describes the difference between the equilibrium compositions of the γ and γ′ phases is

$$\Delta X_{\text{e}} = 0.1957-5.9259 \times 10^{ - 4} T-3.3796 \times 10^{ - 4} T^{2} .$$

(38)

The empirical equation that describes the equilibrium molar volume of the γ′ phase is

$$V_{{\text{m}\gamma^{\prime} \text{e}}} = 6.7487 + 3.1836 \times 10^{ - 4} T,$$

(39)

where V_mγ′e is in 10⁶ m³ mol⁻¹. In both equations T is in K. The errors associated with these parameters are difficult to estimate with any precision because errors in both the equilibrium compositions and lattice constants contribute. Equations (38) and (39) are estimated to be accurate to within ± 0.2%, which is twice the uncertainty reported in Ref. [76].

The temperature dependency of $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ was calculated using the parameters published in the thermodynamic model of the binary Ni–Al alloy system due to Ansara et al. [77]. It is shown in Fig. 13. The temperature dependency of $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ is given by the empirical equation

$$G^{\prime\prime}_{{\text{m}\gamma \text{e}}} = 203.3014 \, + \, 0.2127T-6.8338 \times 10^{ - 5} T^{2} ,$$

(40)

where $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ is in kJ mol⁻¹ and T is in K. The uncertainties associated with $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ are also difficult to estimate because there are no reported errors associated with the Redlich–Kister interaction terms used by Ansara et al. [77] in their thermodynamic model of the Ni–Al alloy system. The origin of the curve labeled “Dupin” is a personal communication (Dupin 1999). Her calculations of $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ are about 3% larger because she used slightly larger values of the equilibrium Al concentration of the γ′ phase (Dupin, personal communication, 1999).

Figure 13

The temperature dependencies of the curvature of the total Gibbs free energy of mixing of the γ phase of equilibrium composition, $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$, as a function of temperature, T (curve in red). The curve labeled “Dupin” represents her calculation of $G^{\prime\prime}_{{\text{m}\gamma \text{e}}}$ (Dupin, personal communication 1999)