Introduction

As the functionality demands on engineering materials continue to rise, multi-phase materials become more popular. A number of technologically important alloys, composites, and precipitated hardened materials consist of phases with different properties. In these materials, the desired functional and mechanical properties can largely be tailored by the properties of the individual constituent phases. Moreover, some material properties, including the mechanical and electrical properties, are influenced by the grain size and spatial arrangement of the phases. Many of the enhanced properties in multi-phase materials are mainly attributed to the inherently different phase boundary and grain boundary properties.

Although coarsening in multi-phase materials involves both, Ostwald ripening and grain growth, several previous studies performed for dual-phase coarsening of systems with a conserved volume fraction of phases in 2D [1,2,3,4,5,6] and 3D [7,8,9,10,11] and recent coarsening simulations for 3D three-phase systems [12], confirm that Ostwald ripening is the controlling coarsening mechanism at steady-state coarsening.

In multi-phase materials and under diffusion-controlled growth, the structural evolution is then mainly controlled by the chemical energy, interfacial energies, volume fractions of the phases, and the diffusivities of the different chemical elements in the constituent phases. When the bulk chemical energy and volume fraction of phases are assumed to be equal, the microstructural evolution is governed by the grain boundary and interface energies and the diffusivities in the different phases. Sheng et al. [13] performed 2D simulations for a two-phase system, formed by spinodal decomposition, with highly disparate diffusion mobilities for the two phases and obtained a different growth behavior for different ratios of the diffusion mobilities in the two phases. The evolved phase arrangements during the microstructural evolution was not meaningfully affected by the diffusion mobilities of the phases in this study. Moreover, for a 3D ternary three-phase system with different diffusivities in the different phases, but equal grain boundary and interface energies, Ravash et al. [12] showed that the phase with the lowest diffusivity coarsens fastest and the two other phases grow at a nearly equal rate. Chang et al. [14, 15] and Holm et al. [16] studied the effect of the interfacial energy ratio (this is the ratio of the energy of the boundaries between grains of the same phase and that of boundaries between grains of dissimilar phases) on the microstructure evolution for two-phase systems. They found that the interfacial energy ratio determines largely the grain topology, phase arrangement, and coarsening kinetics in a microstructure.

So far, the effects of different diffusivities in the different phases and those of phase arrangement on the evolving morphology of a multi-phase system have not been considered simultaneously. Moreover, practical conclusions from 2D two-phase systems to 3D three-phase systems may not be relevant.

In the present study, the microstructural evolution in 3D three-phase systems was simulated considering different phase arrangements and assuming different diffusion mobilities in the different phases. A ternary system is considered, since it follows from Gibbs phase rule that at least three components should be present to have three-phase regions in a phase diagram at given temperature and pressure. Different phase arrangements are obtained by using different interfacial energy conditions. If \(\sigma _{\text{gb}}\) is the energy of boundaries between grains of the same phase and \(\sigma _{\text{pb}}\) represents the energy of boundaries between grains of dissimilar phases, the interfacial energy ratio is defined as \(ER = \sigma _{\text{gb}} / \sigma _{\text{pb}}\). Simulations were conducted for microstructures with (a) phase boundary energy smaller than grain boundary energy (\(ER = 1.78\)), (b) phase boundary energy larger than grain boundary energy (\(ER = 0.566\)) and (c) misorientation-dependent grain boundary energy with \(\sigma _{{\text{gb}},\max} = \sigma _{\text{pb}}\) (\(0.06 < ER \le 1\)), assuming a Read–Shockley misorientation dependence. For cases (a) and (b), the ER ratio was chosen so that there is a considerable difference between the grain boundary and interface energy to observe an obvious effect on the spatial distribution of the phases, but with \(0.5< ER < 2\) to avoid the possibility of complete wetting of certain boundaries and obtain fully connected grain structures. For case (c), the lowest ER-value is obtained for a grain boundary between two grains with a misorientation of \(0.18^{\circ }\), the lowest misorientation that is resolved in the simulations. In this system, there is a possibility to observe complete wetting of an interphase or high-angle grain boundary, as it is energetically favorable to replace such a boundary by two low-energy grain boundaries when locally present in the structure. The grain size and topology evolution and the grain size and topological class distributions were determined from the simulated microstructures. Moreover, the growth behavior of the individual phases is analyzed considering the selected diffusion mobilities and different phase arrangements. The results are also compared with results from a previous study [12] for a system with the same chemical and diffusion properties as those considered in the present study, but an equal energy for the phase and grain boundaries (i.e., \(ER = 1\)).

Model and methodology

Model

An extended description of the model used in this study was presented before [12]. Only a summary is given here.

To represent the different grain orientations of the different phases, large sets of non-conserved phase-field variables, \({\eta }_{1,1},\ldots ,{\eta }_{{p}_{1},1}\); \({\eta }_{1,2},\ldots ,{\eta }_{{p}_{2},2}\); \(\ldots \), \({\eta }_{1,N},\ldots ,{\eta }_{{p}_{j},N}\), were used, with \(p_{j}\) the number of grain orientations of phase j and N the number of phases present in the system. The second index refers to the phase and the first index to the grain number or grain orientation within each phase. A ternary system is considered and the local composition at each point of the system is described using two conserved phase-field variable \(c_{s}\), with \(s=1, 2\), representing the local molar fractions of the two independent components.

The evolution equations of these conserved and non-conserved phase-field variables were obtained according to the principles of non-equilibrium thermodynamics, namely to ensure a monotonous decrease of the Gibbs energy in time and mass conservation throughout the system, giving for each phase-field variable \(\eta _i\), with \(i=1\ldots p\) and p the total number of non-conserved phase-field variables, \(N=3\) the number of phases and \(n=3\) the number of chemical components,

$$\begin{aligned} \frac{\partial \eta _{i}}{\partial t} &= -L\left\{ m\left( \eta _{i}^3-\eta _{i}+2\gamma _{i,j} \sum _{j=1, j\ne 1}^{p}\eta _{i}\eta _{j}^2\right) -\kappa \nabla ^2\eta _{i}\right. \\&\quad+A\left[ \sum _{k=1}^{n-1}\left( \left( c_{k}-\sum _{l=1}^{N} c_{k,l}^{0}H_{l}(\eta _{1}\ldots \eta _{p})\right) \left( -\sum _{l=1}^{N}c_{k,l}^{0}\frac{\partial H_{l}((\eta _{1}\ldots \eta _{p}))}{\partial \eta _{i}}\right) \right) \right] \\&\quad\left. +\sum _{l=1}^{N} G_{l}\frac{\partial H_{l}((\eta _{1}\ldots \eta _{p}))}{\partial \eta _{i}}\right\} , \end{aligned}$$
(1)

and for the two independent conserved composition fields \(c_{s}\),

$$\begin{aligned} \frac{1}{V_{m}}\frac{\partial c_{s}({\mathbf{r}}, t)}{\partial t} = \nabla \cdot \left[ \sum _{r=1}^{n-1} M_{s,r} \nabla \widetilde{\mu }_r\right] \end{aligned}$$
(2)

with \(\widetilde{\mu }_r = V_m(\partial f_{\text{chem}}/\partial c_r) = V_m A (c_r -\sum _{j=1}^{N} H_j c_{r,j}^0)\) the interdiffusion potential and \(M_{s,r} = \sum _{j=1}^{N} H_j M_{s,r}^{j}\) with \(M_{s,r}^{j}\) the interdiffusion mobility of element s under the chemical potential gradient of element r for phase j.

The model parameters m, \(\gamma _{i,j}\) and \(\kappa \) in (1) are related to the interfacial energy \(\sigma _{i,j}\) and width of the diffuse interface assumed in a phase-field representation \(l_{i,j}\) of a boundary between two grains as

$$\begin{aligned} \sigma _{i,j}=g(\gamma _{i,j})\sqrt{\kappa m} \end{aligned}$$
(3)

and

$$\begin{aligned} l_{i,j}=\sqrt{\kappa /(mf_{0,\max}(\gamma _{i,j}))} \end{aligned}$$
(4)

with \(g(\gamma _{i,j})\) and \(f_{0,\max}(\gamma _{i,j})\) functions that were evaluated numerically as described in Ref. [17] (the function values are given in the additional material for a wide range of \(\gamma _{i,j}\)-values).

The model parameters \(G_{l}\), \(c_{k,l}^{0}\) and A relate to the bulk chemical energy of phase l as a function of the composition variables \(c_{1}\) and \(c_{2}\). The bulk chemical energy is formulated following the model of Folch and Plapp [18]. Since for the present simulations the equilibrium compositions are taken far from the dilute limit and coarsening phenomena are considered—the composition remains thus close to the equilibrium composition—a parabolic composition dependence can be applied to simplify the model equations. These parameters must be chosen so that the equilibrium compositions of the phases are reproduced.

The functions \(H_{l}\), where the suffix l refers to the three phases, are used to interpolate between the chemical energies of the different phases and are taken from the multi-phase model of Moelans [19],

$$\begin{aligned} H_{l} (\eta _{i, k}) = {\phi _l} = \frac{\sum _{i=1}^{p_{l}} {\eta ^2_{i,l}}}{\sum _{k=1}^{N} \sum _{i=1}^{p_{k}}{\eta ^2_{i,k}}} \end{aligned}$$
(5)

where k is taken over the different phases and i over all grain orientations of phase k, and which equals per definition the phase fraction \(\phi _l\) of phase l.

The kinetic coefficient L is formulated as a function of the kinetic constants related to the different grain boundary and interface boundary mobilities as \(L=\left[ \sum _{i=1}^{p}\sum _{j=i+1}^{p} L_{i,j}\eta _i^2\eta _j^2\right] /\left[ \sum _{i=1}^{p}\sum _{j=i+1}^{p}\eta _i^2\eta _j^2\right] \), with p again the total number of non-conserved phase-field variables used in the model. This expression is chosen so that at each interface where only two non-conserved phase-field variables have a value different from 0 \((\eta _{(k\ne i,\ne j)}=0)\), \(L= L_{i,j}\) with i and j the numbers of the two phase-field variables representing the adjacent grains. For an interface between two grains of the same phase, \(L_{i,j}\) is related to the grain boundary mobility \(\mu _{i,j}\) as \(L_{i,j}\kappa =\sigma _{i,j}\mu _{i,j}\) [17]. The \(L_{i,j}\) for the interfaces between grains of a different phase are chosen to obtain diffusion-controlled growth [19].

In the equation for the conserved concentration fields, \(M^{j}_{s, r}\) is defined as the interdiffusion mobility of element s in phase j under the chemical potential gradient of element r [20]. The elements in the diffusion mobility matrix can be expressed as a function of the atomic mobilities of the individual elements. In this study, the atomic mobilities are assumed to be equal for all elements within a phase, i.e., \(\beta _{(1),j} = \beta _{(2),j} = \beta _{(3),j} = \beta _{(1,2,3),j}\), but different in the different phases. For a ternary system, and considering a number-fixed frame, the matrix of diffusion mobilities in each phase \({\mathbf{M}} ^{j}\) has then the form

$$\begin{aligned} {\mathbf{M}} ^{j}= \left[ {\begin{array}{cc} c_{1}(1-c_{1}) & -c_{1}c_{2} \\ -c_{1}c_{2} & c_{2}(1-c_{2}) \\ \end{array} } \right] \cdot \frac{\beta _{(1,2,3),j}}{V_{m}}, \end{aligned}$$
(6)

with \(c_{1}\) and \(c_{2}\) the molar fractions of the independent components.

Implementation

Three-dimensional grain growth and coarsening simulations for polycrystalline structures containing a statistically relevant number of grains based on Eqs. (1)–(2) are extremely computationally intensive due to the large number of phase-field variables for which an evolution equation has to be solved. Therefore, the bounding-box algorithm based on a sparse data structure representation as developed by Vanherpe et al. [21, 22] and extended for multi-phase systems by Ravash et al. [12] was used. Like many sparse data structure algorithms, the bounding-box technique exploits the fact that at a given time t and a given grid point \({\mathbf{r}} \) of the microstructure, only a few phase-field variables \(\eta _{i}\) are active, this means that they have a value different from 0. The method offers a significant speedup for phase-field models for polycrystalline structures compared to the conventional techniques, as the computational requirements only scale with the system size and not with the number of phase-field variables used to represent the microstructure. For the presented simulations, an explicit finite difference method with Forward-Euler time stepping and a second-order central scheme for the Laplacian was used to discretize the partial differential equations (1) and (2).

Post processing

For analysis of the simulated microstructures, a so-called sharp-interface representation was generated from the resulting phase-fields \(\eta _{i}\) at different time steps, by taking at each grid point the number of the phase-fields with the value closest to 1. The grain volume of the different grains was obtained from this sharp-interface representation as the number of grid points represented by a same number in the sharp-interface representation multiplied by the volume of a grid point, i.e., \((\Delta x)^3\). The grain radius was obtained as the equivalent radius of a sphere with a volume equal to that of the grain.

Input parameters

The parameters in the bulk chemical energy were taken as \(c^{0}_{1,1} = 0.5\), \(c^{0}_{2,1} = 0.3\) for phase 1, \(c^{0}_{1,2} = 0.4\), \(c^{0}_{2,2} = 0.2\) for phase 2, \(c^{0}_{1,3} = 0.6\), \(c^{0}_{2,3} = 0.1\) for phase 3, \(G_{1} = G_{2} = G_{3} = -1 \times 10^{5}\, \hbox {J/m}^3\), and \(A= 5 \times 10^{8}\,\hbox {J/m}^3\).

The atomic diffusion mobilities of elements 1, 2 and 3 were set as \(\beta _{(1,2,3), 1}/V_{m}\) \( = 5 \times 10^{-13}\,{\text{mol}}^{2}/({\text{m}}\,{\text{J}}\,{\text{s}})\) for phase 1, \(\beta _{(1,2,3),2}/V_{m} = 1 \times 10^{-12}\,\hbox{mol}^{2}/(\hbox{m}\,\hbox{J}\,\hbox{s})\) for phase 2 and \(\beta _{(1, 2, 3), 3} /V_{m} = 2 \times 10^{-13}\,\hbox {mol}^{2}/(\hbox{m}\,\hbox{J}\,\hbox{s})\) for phase 3. Diffusion will thus be fastest in phase 2 and slowest in phase 3 with a mobility ratio of 0.2 between the phases 3 and 2, 0.4 between the phases 3 and 1 and 0.5 between the phases 1 and 2.

For each system, the model parameters \(\kappa \), m, \(\gamma _{i,j}\) and \(L_{\text{gb}}\) were calculated to reproduce in the simulations the selected interface energies \(\sigma _{\text{gb}}\) and \(\sigma _{\text{pb}}\) and grain boundary mobility \(\mu _{\text{gb}}\). Figure 1 presents the selected energies for boundaries between grains of the same phase and between grains of dissimilar phases for the different interfacial energy conditions considered in this paper. In each simulation, grains with an orientation number ranging between [0 499], [500 999] and [1000 1499] belong to phase 1, 2 and 3, respectively. In this figure, each color or symbol represents one phase and the given values represent the \(\sigma / \sigma _{\max }\) associated with the interface between the first selected grain of each phase (namely grains with types 0, 500 and 1000) and the other grains in the system.

Figure 1
figure 1

The selected interface energies, expressed as \(\sigma /\sigma _{\max }\) with \(\sigma _{\max } = 0.25\,\hbox {J/m}^{2}\) for the considered structures with \(ER = 1.78\), \(ER = 0.566\) and \(0.06 < ER \le 1\). Each color or symbol represents one phase and the given values represent the interface energy between the first selected grain of each phase (namely grains with types 0, 500 and 1000) and the other grains in the system

Full size image

For all simulations, the maximum boundary energy was taken \(\sigma _{\max } = 0.25\,\hbox {J/m}^{2}\) and the diffuse interface width of these boundaries was taken \(\ell _{i,j} = 3 \times 10^{-7}\)m, resulting in the model parameters \(\kappa = 5.62 \times 10^{-8}\, \hbox {J/m}\), \(\gamma _{\max } = 1.5\) and \(m = 5 \times 10^6\,\hbox {J/m}^3\). This is for the grain boundary energy for \(ER = 1.78\), the interphase boundary energy for \(ER = 0.566\) and for the interphase boundary and high-angle grain boundary energies for \(0.06 < ER \le 1\).

For \(ER = 1.78\) and 0.566, the minimum boundary energy is \(\sigma _{\min } = 0.14\,\hbox {J/m}^{2}\), resulting in \(\gamma _{\min } = 0.68\) and a diffuse interface width \(\ell _{i,j} = 5.3 \times 10^{-7}\)m for these boundaries.

These values for \(\sigma _{\max }\) and \(\sigma _{\min }\) were chosen to obtain the intended ER-values and independent of a particular material system. They are slightly lower, but of the same order of magnitude, than the experimentally measured and MD calculated values of high-angle grain boundary energies reported for a number of fcc materials [23]. For the considered model, the width of the diffuse boundaries between grains and phases is smaller for boundaries with a higher energy. Therefore, the diffuse interface width of the boundaries with energy \(\sigma _{\max }=0.25\,\hbox {J/m}^{2}\) is taken as \(\ell _{i,j} = 3 \times 10^{-7}\hbox {m} = 5 \times \Delta x\) (\(\Delta x\) is specified further). It was verified before for grain growth [24] and individual grain boundary [17] and diffusion-controlled phase boundary [19] migration that accurate velocities (i.e., with a relative error smaller than \(5\%\) compared to the analytically expected values for particular grain structure geometries) are obtained for \(\ell \ge 0.5 \Delta x\). The diffuse interface width of the boundaries with lower energy follows from this choice and will be slightly larger; they are given by Eq. (3).

In the system with misorientation-dependent grain boundary energy (\(0.06 < ER \le 1\)), the crystallographic orientations of the grains are assumed to be identical in one direction and random in the plane perpendicular to this direction. For certain types of deformation processes, such a structure is observed after mechanical deformation in metals; for example, compression of fcc metals causes a fiber texture with \(\langle 110 \rangle \) aligned with the fiber axis [25]. In this study, however, the assumption was made merely to simplify the formalism while still having the opportunity to study the effect of varying grain boundary properties within the phases. A crystal with fourfold symmetry and \(p_{j} = 500\) grain orientations for each phase were assumed resulting in an orientation discretization \(\triangle (\theta )= 90^\circ /p_{j} = 0.18 ^{\circ }\) within one quadrant. The misorientation angle \(\theta \) associated with the boundary between two neighboring grains assigned by orientations i and j is calculated using

$$\begin{aligned} \theta _{i,j} = {\left\{ \begin{array}{ll} \triangle \theta \cdot |j-i| &{\text{if}}\,\,\, |j-i| \le \frac{p_{j}}{2} \\ -90^\circ + \triangle \theta \cdot |j-i| &{\text{if}}\,\,\, |j-i| > \frac{p_{j}}{2} \end{array}\right. }. \end{aligned}$$
(7)

For fourfold symmetry \(\theta _{i,j}\) ranges from \(-45^\circ \) to \(+45^\circ \). The minimum interfacial energy ratio \(ER = 0.06\) corresponds to the boundaries with the lowest misorientation angle \(({\le}0.18^{\circ })\). The corresponding boundary energies \(\sigma _{i,j} = \sigma _{\text{gb}}(\theta _{i,j})\) are obtained, assuming the Read–Shockley dependence for low misorientations, using Eq. (8) [26], giving

$$\begin{aligned} \sigma _{\text{gb}}(\theta ) = {\left\{ \begin{array}{ll} \sigma _{m}\frac{|\theta |}{\theta _{m}}\left( 1-ln \left( \frac{|\theta |}{\theta _{m}}\right) \right) &{\text{ if} } \quad |\theta |<\theta _{m} \\ \sigma _{m} &{\text{ if} } \quad |\theta |\ge \theta _{m} \end{array}\right. }, \end{aligned}$$
(8)

where \(|\theta |<\theta _{m}\) and \(|\theta |\ge \theta _{m}\) correspond to the low-angle and high-angle boundaries. In the presented simulation, \(\theta _{m} = 15^{\circ }\) and \(\sigma _{m} = 0.25\,\hbox {J/m}^{2}\) are assumed. The grain boundary energy varied between \(\sigma = 0.016\,\hbox {J/m}^{2}\) (\( \theta _{i,j} = 0.18\)) and \(\sigma = 0.25\,\hbox {J/m}^{2}\) (\(\theta _{i,j} \ge 15\)). The \(\gamma _{i,j}\) parameters reproducing this Read–Shockley dependence were calculated using the MATLAB script given in the additional material.

For all grain boundaries between grains of a same phase, a grain boundary mobility \(\mu _{\text{gb}} = 2.25 \times 10^{-12}\,\hbox {m}^{2}\)s/kg was assumed, giving \(L_{\text{gb}} = 10^{-5}\,\hbox {m}^{3}\)/Js for the grain boundaries with \(\sigma _{\text{gb}} = 0.25\,\hbox {J/m}^2\) and \(L_{\text{gb}} = 0.56\times 10^{-5}\,\hbox {m}^{3}\)/Js for boundaries with \(\sigma _{\text{gb}} = 0.14\,\hbox {J/m}^2\) for the kinetic coefficients in the Ginzburg–Landau equations. The \(L_{\text{gb}}(\theta _{i,j})\) for the system with misorientation-dependent grain boundary energy was calculated such that the grain boundary mobility was the same and equal to \(\mu _{\text{gb}} = 2.25 \times 10^{-12}\,\hbox {m}^{2}\)s/kg for all misorientations using the MATLAB script given in the additional material. The grain boundary mobility of materials can vary over orders of magnitude, depending on among others temperature, the amount of solutes segregated to the boundary and boundary orientation. In the present study, the grain boundary mobility was chosen based on computational considerations, namely sufficiently large to reach the steady-state regime with growth controlled by long-range bulk diffusion within the accessible simulation time, however not larger to allow for a reasonably large time step.

The kinetic coefficients for boundaries between grains of different phases were taken from previous work [12] and estimated to approach diffusion-controlled phase boundary movement [19]. The kinetic coefficient for a boundary between grains of the phases 1 and 2 was taken as \(L_{12}= L_{21} = 4.7 \times 10^{-5}\,\hbox {m}^{3}\)/Js, between the phases 1 and 3 as \(L_{13}= L_{31} = 2.2 \times 10 ^{-5}\,\hbox {m}^{3}/\hbox {Js}\) and between the phases 2 and 3 as \(L_{23}= L_{32} = 3.7 \times 10 ^{-5}\,\hbox {m}^{3}/\hbox {Js}\).

For all simulations, a threshold value for the bounding box of \(\epsilon = 10^{-5}\), a system size of \(256 \times 256 \times 256\) grid points with grid size \(\triangle x = 6 \times 10^{-8}\,\hbox {m}\) and \(\triangle t = 1.8 \times 10^{-4}\,\hbox {s}\) were chosen.

Initial microstructure

To generate initial polycrystalline three-phase microstructures, the following steps were taken. First, for every phase-field variable \(\eta _{i}\), a grid point \(C_{i}\) was chosen according to a uniform distribution over the domain of the microstructure. Second, a spherical grain region with small radius was defined around each center \(C_{i}\). Next, for every spherical grain region, the corresponding phase-field variable \(\eta _{i}\) was initialized such that \(\eta _{i}\) equals 1 inside and 0 outside the respective grain region. Then, the phase-field equations for grain growth of a single-phase material were solved using the bounding-box algorithm as explained in [21]. Once the polycrystalline microstructure was fully developed, it was used as the initial microstructure for the three-phase system simulation by distributing the grains among the phases based on their numbers, namely 1–499 to phase 1, 500–999 to phase 2 and 1000–1499 to phase 3. Finally, the composition variables at each grid point were set equal to the equilibrium composition of the phase present at that point. Figure 2a represents such an initial microstructure composed of phases 1, 2 and 3.

Figure 2
figure 2

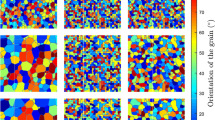
3D images with 2D cross section of the evolved microstructures for a \(ER=1.78\) at time \(t = 200 \times 10^{3} \Delta t\), b \(ER=0.566\) at time \(t = 150 \times 10^{3} \Delta t\) and c \(0.06 < ER \le 1\) at time \(t = 150 \times 10^{3} \Delta t\). The white squares indicate stable quadruple junctions. The red square indicates an unstable triple junction of the type 111 penetrated by another phase

Full size image

Large-scale simulations were performed for a cubic system containing three solid phases each with volume fraction \(f_{p} \approx 0.333\) for a total simulation time of \(t = 300 \times 10^{3} \Delta t\). During the simulation time, the number of grains decreases from approximately 1500 to approximately 150–200 grains, which is a considerable number of grains and evolution time. Considering the recent findings from normal grain growth simulations [15, 27, 28], however, a larger initial structure may be required to draw firm conclusions on the true steady-state characteristics. Since three-phase coarsening may be affected by several processes (not only grain boundary movement, but also diffusion-controlled phase boundary movement), we can expect that an even longer time and substantially more grains will be required to obtain true steady-state behavior. It is possible, for example, that the systems pass several regimes with close to self-similar behavior before true steady-state is reached depending on the relative kinetics of grain boundary and interphase boundary movement. With the current knowledge on multi-phase multi-component coarsening, it is impossible to predict how large the compute power required to investigate such a scenario is. Therefore, we have chosen the initial number of grains as large as possible but such that the simulations can be performed with the available compute power within a reasonable time. For all considered systems, we find an extended regime where the average grain size as a function of time evolves according to the power growth law with growth coefficient 3, which makes it anyway interesting to compare the growth behavior within this regime for different system properties.

To improve the statistical relevance of the conclusions, all simulations were performed for three different initial structures, each containing an initial number of 1500 grains, and the measured properties of the grain structures were averaged over the three simulations for identical system properties but with different initial grain structure, every 2000 time steps.

Results

Microstructural features

Figure 2 presents 3D images and 2D sections of the simulated microstructures for \(ER = 1.78\) (a), \(ER = 0.566\) (b) and \(0.06 \le ER \le 1\) (c) at time \(t = 150 \times 10^{3} \Delta t\). From Fig. 2a, it is evident that grains of different phases evolve next to each other in an alternating pattern for \(ER = 1.78\). On the other hand, the microstructure attained for \(ER = 0.566\) is characterized by a continuous clustering of grains of a same phase (see Fig. 2b). In the simulation with misorientation-dependent grain boundaries (\(0.06 \le ER \le 1\)), there is clearly tendency to form clusters of grains of a similar phase, as well (Fig. 2c). Moreover, the elongated and curvy boundaries are characteristic for this microstructure. We even observe isolated grains.

Quadruple junctions consisting of two grain and two phase boundaries, persisting for a considerable time are seen in the simulations for \(ER=1.78\) (indicated with the white boxes in the 2D section in Fig. 2a), but not in the simulations for the other ER conditions considered in this study. In the system with misorientation-dependent grain boundary energy (\(0.06< ER \le 1\)), quadruple junctions formed of four grain boundaries can be observed.

Grain coarsening

The mean grain radius as obtained from the simulations as a function of time was fitted with a power growth law,

$$\begin{aligned} \langle r_{p}(t)\rangle ^{n}-\langle r_{p}(0)\rangle ^{n} = Kt \end{aligned}$$
(9)

where \(\langle r \rangle \), n and K denote the average grain radius, growth rate exponent and rate constant, respectively.

For all three systems a constant growth exponent \(n = 3.01 \pm 0.02\) is obtained over an extended simulation time. The rate constants K varied with the interfacial energy conditions: \(K = 60 \times 10^{-21} \pm 2 \times 10^{-21} \) was obtained for \(ER=1.78\), \(K = 121 \times 10^{-21} \pm 6 \times 10^{-21} \) for \(ER=0.566\) and \(K = 135 \times 10^{-21} \pm 3 \times 10^{-21} \) for \(0.06 < ER\le 1\). The error indicates the maximum deviation from the mean value over the three simulations performed for each interfacial energy condition. For \(ER=1\) and all system properties the same as in the current simulations, \(K = 102 \times 10^{-21} \pm 1 \times 10^{-21} \) was found in previous work [12]. As shown in Fig. 3, the simulation for \(ER = 1.78,\) where \(\sigma _{\text{pb}}=0.14\) and with alternating phases, shows a clearly lower growth rate than the other systems, for which \(\sigma _{\text{pb}}=0.25\). The K-value obtained for \(ER = 1.78\) is also considerably lower than those obtained for the other conditions.

Figure 3
figure 3

Mean grain radius as a function of time as obtained in the different simulations within the time frame \(10^5 \times \Delta t\) to \(3\times 10^5 \times \Delta t\): curve 1 was obtained in previous work for \(ER=1\) [12] and is added for comparison with the curves obtained in this work, curve 2 is obtained for \(ER=1.78\), curve 3 for \(ER=0.566,\) and curve 4 for \(0.06 < ER \le 1\). Broken lines are the least-square fits of the power growth law with \(\langle R \rangle \) the mean grain radius and n the growth rate exponent, as fitted to the data points over a time frame where \(n=3\) is constant. For curve 2, this constant growth rate coefficient is reached at approximately \(10^5 \times \Delta t\). For curves 1, 3 and 4, the constant growth rate coefficient was obtained at a slightly later time; therefore, the earliest data points in this figure, which were not included in the fit, deviate slightly from the linear line for these curves

Full size image

Comparison of the growth rate of the individual phases over the time interval, where \(n=3\) (Fig. 4), shows that phase 3 has the highest growth rate of the three phases for all considered interfacial energy conditions. When grains of different phases alternate (\(ER=1.78\)), phase 1 and phase 2 grow at a fairly similar rate, while in the case of clustering (\(ER=0.566\), \(0.06 < ER \le 1\)), phase 2 has a higher growth rate than phase 1. The different growth rates of the phases are related to the different diffusion mobilities in the different phases.

Figure 4
figure 4

Mean grain size evolution obtained in the simulations for the three individual phases and for the overall microstructure for \(ER=1.78\), \(ER=0.566\) and \(0.06 < ER \le 1\)

Full size image

The grain size distributions obtained for the different interfacial energy conditions, always normalized with the average grain size, are presented in Fig. 5. They are obtained by averaging the distributions measured between \(t = 100 \times 10^{3} \Delta t\) and \(t = 200 \times 10^{3} \Delta t\) and averaging over the three simulations for each ER-value. Over this time interval, the grain growth exponent is close to 3 and almost constant, the normalized grain size distributions tend to be self-similar and topologically self-similar evolution is found for the three interfacial energy conditions considered in the figure (see ‘Topology evolution’ section), while there are still sufficient grains remaining in the system to obtain meaningful results. Since no topologically self-similar evolution was found for \(0.06 < ER\le 1\), where grain boundary energies are misorientation dependent, the grain size distribution was not included in this figure. For all three cases, the grain size distributions are found to be symmetrical around their mean, as also found for 3D simulations of two-phase coarsening for equal volume fractions of the two phases [7, 10]. There are no significant differences between the grain size distribution curves obtained for \(ER=1\), \(ER=1.78\) and \(ER=0.566\). It is possible, however, that smaller deviations in the shape of the grain size distributions may become clear if considerably larger grain structures can be considered. For comparison, the grain size distributions obtained from 3D simulations for two-phase coarsening with equal volume fraction of the two phases (\(f_{p}= 50 \% \)) of Poulsen et al. [7] and from experimental data of two-phase coarsening with \(f_{p}= 52 \% \) and \(f_{p}= 78 \% \) from Rowenhorst et al. [29] for Sn-rich particles dispersed in a Pb-Sn eutectic matrix are added in Fig. 5, showing that the shape and range of the steady-state normalized grain size distributions obtained for two- and three-phase coarsening in conserved systems are very similar.

Figure 5
figure 5

Steady-state normalized overall (including all phases) grain size distribution obtained from the simulations for \(ER=1\) (taken from [12] for comparison), \(ER=1.78\) and \(ER=0.566\). For each system, the grain size is normalized with respect to its mean grain size. For comparison, the distribution obtained from a simulation of two-phase coarsening with 50% volume fraction of each phase [7] and experimental data [29] obtained for two-phase structures with volume fraction of one of the phases 52 and 78%, respectively, are added

Full size image

Figure 6 shows for \(ER=1.78\) and \(ER=0.566\) the grain size distribution of each phase normalized with respect to the mean grain size of that phase. They are also obtained by averaging the distributions measured between \(t = 100 \times 10^{3} \Delta t\) and \(t = 200 \times 10^{3} \Delta t\) and averaging over the three simulations for the same ER-value. Although the statistics obtained for the individual phases are much lower than those for the whole system, it seems that for the considered systems with equal volume fractions of the three phases, the normalized grain size distributions of the individual phases have a similar shape as the overall normalized grain size distribution.

Figure 6
figure 6

Steady-state normalized grain size distributions of the individual phases 1, 2 and 3 and the overall microstructure for a \(ER = 1.78\) and b \(ER = 0.566\). The grain sizes of an individual phase are normalized with respect to the mean grain size of that phase

Full size image

Topology evolution

Figure 7 shows the evolution of the mean number of grain faces for all simulations over the total simulation time (the curves in the upper part of the graphs). For \(ER=1.78\) and \(ER=0.566\), the average number of grain faces evolves toward a constant value which is measured to be \(\langle F \rangle = 14.12 \pm 0.1\). The measured values are averaged over the last \(10^{5}\) time steps of the simulations. A same value was found in our previous work for \(ER=1\) [12]. For \(0.06 < ER \le 1\), the average number of faces increases from \(\langle F \rangle = 14.29\) to \(\langle F \rangle = 18.94\) during the considered simulation time, indicating that the evolution is topologically not self-similar, although fitting of the growth curve gave \(n = 3\) over a considerable simulation time. The curves in the lower part of the graphs represent the average values of faces shared between grains of the same phase and shared with grains of a different phase. When comparing the average number of grain faces for the different phases, it is clear that phase 3 has the highest number of faces in all cases.

Figure 7
figure 7

Evolution of the mean number of grain faces for phase 1, 2 and 3 and the overall microstructure obtained in the simulations for a \(ER = 1.78\), b \(ER = 0.566\), and c \(0.06 \le ER \le 1\). The curves in the lower part of the figures represent the average number of faces shared between the grains of each phase with grains of the same phase or grains of other phases. For example, \(F_{11}\) is the average number of faces shared between grains of phase 1 and \(F_{12}\) is the average number of faces shared between grains of phase 1 and phase 2. For \(ER = 1.78\) (a), \(\langle F_{11} \rangle =3.92< \langle F_{13} \rangle = 4.46< \langle F_{12} \rangle = 5.19, \langle F_{22} \rangle = 3.70< \langle F_{23} \rangle = 4.51 < \langle F_{21} \rangle = 5.36\) and \(\langle F_{33} \rangle =3.60< \langle F_{32} \rangle = 6.11 < \langle F_{31} \rangle = 6.25\). For \(ER = 0.566\) (b), \(\langle F_{11} \rangle = 4.17< \langle F_{13} \rangle = 4.61< \langle F_{12} \rangle = 4.73, \langle F_{22} \rangle = 4.07< \langle F_{23} \rangle = 4.80 < \langle F_{21} \rangle = 5.48\) and \(\langle F_{33} \rangle = 4.04< \langle F_{32} \rangle = 5.03 < \langle F_{31} \rangle = 5.61 \). For \(0.06 < ER \le 1\) (c), no topologically self-similar evolution was found

Full size image

For \(ER = 1.78\), the average number of faces for phase 1 and phase 2 \(\langle F_{1} \rangle = \langle F_{2} \rangle = 13.50 \pm 0.03 \) are equal and considerably smaller than that of phase 3 \(\langle F_{3} \rangle = 15.92\). Furthermore, it is noted that the mean numbers of faces of phase 3 shared with phases 1 and 2 are almost equal and the most frequent types of interface, while the mean number of faces shared between grains of phase 3 are lowest. In addition, the number of grain faces which are shared between phase 1 and phase 2 are almost equal (see Fig. 4), which is expected as they exhibit fairly similar growth behavior. These observations are very similar to our previous findings for \(ER=1\) [12].

For \(ER = 0.566\), the average number of faces for phase 1 \(\langle F_{1} \rangle = 13.46 \), phase 2 \(\langle F_{2} \rangle = 14.26\) and phase 3 \(\langle F_{3} \rangle = 14.64\) are obtained. Here, phase 2 shows a higher average number of faces than phase 1, but still lower compared to that of phase 3. This can be correlated with the results of the average grain size evolution of the different phases which shows that phase 2 grows at a higher rate than phase 1 for \(ER=0.566\). The mean number of faces shared between grains of the same phase is also higher than for \(ER=1\) and \(ER=1.78\). This is in good agreement with the clustering feature of the evolved microstructure seen for \(ER=0.566\).

Finally, for \(0.06 \le ER \le 1\), the maximum increase in average number of faces is seen for phase 3, while the least increase is seen for phase 1. A more detailed study on the evolution of the average number of faces for each phase reveals that the largest increase is seen for boundaries shared between grains of phase 3, namely \(F_{33}\).

Figure 8 shows the normalized grain size in the different topological classes for the simulated microstructures with different interfacial energy conditions at \(t = 250 \times 10^{3} \Delta t\). It should be noted that the normalization for each simulation is made with respect to the average grain size in that particular simulation. It is evident that for most of the topological classes, the normalized grain size associated with each class is smaller for the simulation with \(0.06 \le ER \le 1\) than that of the other simulations. The average number of faces for grains with a size equal to the average grain size is 15.5, 15.9 and 15.8 for \(ER=1\), \(ER=1.78\) and \(ER=0.566\), respectively, and 17 for the system with varying grain boundary energies \(0.06 < ER \le 1\).

Figure 8
figure 8

Normalized grain size as a function of the number of grain faces obtained for the four considered interfacial energy ratios (the data for \(ER = 1\) were taken from [12]). Individual values are marked with small symbols and the average values over each topological class are marked with large symbols for the simulations with different interfacial energy conditions

Full size image

Evolution of the grain boundary characteristics for misorientation-dependent grain boundary energy

For \(0.06 < ER \le 1\), the area-weighted misorientation distribution function continues to evolve during the simulation. In the initial microstructure, grain orientations were assigned randomly and consequently the initial misorientation distribution is close to uniform. During grain evolution, the fraction of low misorientation boundaries (those with the lowest energy) increases in time, while the fractions of boundaries with another misorientation decreases in time. The area-weighted misorientation distribution obtained at \(t = 250 \times 10^3 \Delta t\) is shown in Fig. 9. Since the applied boundary energy skim is symmetric, the grain boundary properties can be studied within the range of \(\theta \in [0, 45^{\circ }]\) with \(\Delta \theta = 0.18^{\circ }\). Similar evolution was observed in single-phase systems with misorientation-dependent grain boundary energies [30,31,32]. It is unclear from the present simulations whether the evolution of the misorientation distribution function was stagnated by the end of the simulation time.

Figure 9
figure 9

Area-weighted misorientation distribution obtained in the simulation with \(0.06 \le ER \le 1\) after \(t = 250 \times 10^{3} \Delta t\). The displayed area fraction on the vertical axis is the ratio of the total boundary area associated with the misorientation angle corresponding to each bin with respect to the total grain boundary area

Full size image

Discussion

Microstructural features

The presented simulation results show clearly that the characteristics of the evolved microstructures are affected by the interfacial energy ratios. For \(ER = 0.566\) and \(0.06 < ER \le 1\), grains of a same phase tend to cluster, while for \(ER = 1.78\), grains of different phases tend to alternate in the microstructure. Furthermore, in our previous study [12] on the coarsening of a similar three-phase system with \(ER = 1\), we also found that grains of different phases have the tendency to alternate. These findings are in essence similar to those obtained in several studies on two-phase coarsening in 2D [14, 16, 33] and 3D [7, 10]. For example, for 2D grain structures, Holm et al. [16] observed that for \(ER<1\), the microstructure favors interfaces shared between grains of the same phase while for \(ER>1\), it favors the interfaces shared between grains of dissimilar phases. Furthermore, for 3D two-phase systems, Poulsen et al. [7] found for \(ER=0.8\) a tendency for clustering, and Yadav et al. [10] found for \(ER=1\) that phases rather have the tendency to alternate. The fact that the same observations are made about the tendency to cluster or to alternate for conserved and non-conserved systems and two- and three-phase systems indicates that this feature is determined by the ER-value (i.e., the interphase boundary and grain boundary energies), while the chemical and diffusion properties of the individual phases seem not to have an important effect on the mutual spatial arrangement of the phases.

Extending Cahn’s [33] analysis and the findings from other studies [14,15,16] on the stability of triple and quadruple junctions for two-phase systems to three-phase systems, gives that

  1. (i)

    for \(ER < \sqrt{2}\,\approxeq\,1.41\) only triple junctions are stable,

  2. (ii)

    quadruple junctions are stable for \(ER \ge \sqrt{2}\),

  3. (iii)

    type 111 (this is a triple junction in which 3 grain boundaries between grains of a same phase, here phase 1, end), 222 and 333 triple junctions are only stable for \(ER \le \sqrt{3}\,\approxeq\,1.73\), and

  4. (iv)

    for \(ER > \sqrt{3}\) triple junctions (other than type 111, 222 and 333) coexist with quadruple junctions,

which are all confirmed by our simulation results. Analysis of the 2D sections of the simulated microstructures in Fig. 2 namely shows that while for \(ER = 0.566\) and \(ER = 1\) (see [12]), triple lines are the only stable type of junctions, for \(ER = 1.78\), both triple and quadruple lines exist, as marked with white boxes in the 2D section in Fig. 2a. Moreover, for \(ER = 1.78\), triple lines of type 111, 222 and 333 are not stable, and when occurring, were penetrated by another phase, as can be observed in Fig. 2a, where a triple line of type 111 is destabilized and being penetrated by another phase (indicated with the red box). In the simulations for \(0.06 < ER \le 1\), the grain boundary energy varies over a sufficiently large range, so that quadruple junctions formed of two high-angle grain boundaries and two low-angle grain boundaries can be stable, namely when \(\sigma _{high}/\sigma _{low} > \sqrt{2}\), which is also observed in the simulations.

Furthermore, in the evolved microstructure for \(0.06 \le ER \le 1\) (Fig. 2c), an interesting feature is found where the formation of one grain inside another one occurs, as marked by the white frames. This is devoted to the fact that all grain boundaries have the same mobility in this simulation study, as the grain boundaries with low energy move consequently relatively slow. In reality, low-angle grain boundaries have typically also a lower mobility and will thus migrate even slower, increasing the frequency of this feature in the microstructure.

Coarsening mechanism

The grain growth exponent \(n \approx 3 \) measured for the different simulations shows that for all considered interfacial energy conditions, grain coarsening is mainly controlled by long-range diffusion (Ostwald ripening) and that a reduction of the boundaries between different phases is the controlling driving force for coarsening. Since all simulations consider phases with a similar thermodynamic behavior around the equilibrium composition (i.e., the second derivative of the free energy is equal for all phases, namely equal to A in Eq. 2) and equal volume fractions, the coarsening rates of the individual phases are determined by the diffusion mobilities in the different phases and the phase arrangement developed during coarsening.

In [12], where only the condition \(ER=1\) was considered, a difference in diffusion mobility in the different phases was found to be the responsible for the different growth rates of the different phases. Phase 3, the phase with the lowest diffusivity, i.e., 0.2 of that of phase 2 and 0.4 of that of phase 1, was shown to have the highest growth rate, while the phases 1 and 2 were growing at a nearly equal rate. This was explained by the rate-controlling effect of long-range diffusion. The growth rate of the phases 1 and 2 is namely determined by the long-range diffusion of elements through phase 3, the phase with the slowest diffusivity. The growth of phase 1 requires long-range diffusion through phases 2 and 3; however, as the diffusion through phase 3 is slower, diffusion through phase 3 is rate limiting; and similar for phase 2. The growth rate of phase 3 is determined by the diffusion rate of the elements through phase 1, which has a lower diffusivity than phase 2, but a higher than phase 3.

In the current study, we have added the effect of phase arrangement, by changing the ER-value, while keeping the diffusivities of the three phases the same. While phase 3 still shows the highest growth rate for all considered interfacial energy conditions, the growth rate of phases 1 and 2 are found to be equal only for \(ER=1\) and \(ER=1.78\), namely when grains of a different phase tend to alternate. In the simulations with \(ER =0.566\) and \(0.06 < ER \le 1\), where grains of a same phase tend to form chains and clusters, the growth rate of phase 2 is found to be higher than that of phase 1. These results show that the spatial arrangement of the phases has an important effect on the long-range diffusion of atoms and the growth behavior of the different phases. One explanation for this effect could be that the disappearance of another type grain within a cluster of grains of a similar type is controlled by diffusion through the major type grains in the cluster. Therefore, a type 1 or 3 grain within a type 2 cluster will disappear faster than a type 2 or 3 grain within a type 1 cluster, resulting in a faster growth of type 2 grains in the case of clustering.

Comparing the growth rate obtained in the different simulations (see Fig. 3) reveals that the microstructure with \(ER = 1.78\) shows by far the lowest growth rate and the microstructure with \(0.06 < ER \le 1\) grows at the highest rate. The differences in the overall growth rate between the different systems can be related to the different values of the energy of the boundaries between different phases \(\sigma _{\text{pb}}\) and the different phase arrangements in the different simulations. The energy of the boundaries between different phases is the lowest in the simulation with \(ER=1.78\), while it has a same value for the three other cases \(ER = 1\), \(ER = 0.566\) and \(0.06 < ER \le 1\) (see Fig. 1). The smaller differences in coarsening rate between simulations with \(ER = 1\), \(ER = 0.566\) and \(0.06 < ER \le 1\) are mainly attributed to the different diffusion patterns introduced by the different phase arrangement in these microstructures. Note that although the grain boundaries in the simulation with \(ER=1\) had a higher energy than those in the simulation with \(ER = 0.566\), and the low-energy grain boundaries when \(0.06 < ER \le 1\), a higher growth rate is obtained for \(ER = 0.566\) and \(0.06 < ER \le 1\), where grains of a same phase tend to form clusters. This shows that the phase arrangement has a more important effect on the overall growth rate than the grain boundary energy itself.

In the current study considering only systems with equal volume fractions of the three phases, we did not find a significant difference between the grain size distributions for \(ER=1\), \(ER=1.78\) and \(ER=0.566\). Phase-field simulations [7, 10] of coarsening in two-phase systems, with equal diffusivities in the two phases, have shown however that the peak of the grain size distribution shifts toward lower grain sizes and the distribution seems to be slightly wider for systems where the volume fractions of the two phases is different. If the volume fraction of one of the two phases is very low, e.g., a volume fraction of \(10\%\), the distribution becomes bimodal. Similar effects can be expected for the grain size distribution of three-phase systems with different volume fractions of the phases. The current modeling approach would be particularly suited to study in the future the influence of different volume fractions of the different phases on the coarsening behavior and grain size distribution in two- and three-phase systems and the effect of different diffusivities in the different phases on this.

Topological evolution

The evolution of the mean number of grain faces in the microstructures with \(ER = 1\) (see [12]), \(ER = 1.78\) and \( ER = 0.566\) reveals that the mean number of faces does not change in time over de considered regime, for the overall microstructures as well as for the individual phases. In all three cases with constant grain boundary energy within the phases, the average value of grain faces is found to be \(\langle F \rangle = 14.12 \pm 0.01\), which is almost similar to the average number of grain faces obtained from 3D simulations for dual-phase materials with \(\langle F \rangle = 14.09 \pm 0.05\) as determined by Poulsen et al. [7] and \(\langle F \rangle = 14.13 \pm 0.14\) for 50–50 percent volume fractions of the two phases by Yadav et al. [10]. This is a slightly higher value than the average number of grain faces typically obtained for single-phase materials by Rowenhorst et al. [29] and Krill and Chen [34], where \(\langle F \rangle = 13.7\). Since Yadav et al. obtained \(\langle F \rangle = 13.7\) for non-conserved growth and \(\langle F \rangle = 14.09 \pm 0.05\) for conserved growth under similar simulation conditions, we conclude that the average number of phases is different for conserved and non-conserved growth, but is not affected by the number of phases involved or the diffusion properties of the phases.

Conclusion

In this study, three-dimensional phase-field simulations were performed to study the coarsening behavior of ternary three-phase materials. The effects of the diffusivities of the individual phases and of the spatial arrangement of the phases were analyzed. Different phase arrangements were obtained using different interfacial energy ratios ER, defined as the ratio of the energy of the interphase boundaries and grain boundaries. A microstructure with the phase boundary energy smaller than the grain boundary energy (\(ER = 1.78\)), a microstructure with the phase boundary energy larger than the grain boundary energy (\(ER = 0.566\)) and a microstructure with misorientation-dependent grain boundary energy within the phases with the maximum grain boundary energy equal to the phase boundary energy (\(0.06 < ER \le 1\)) were considered. The results from this work were also compared with results from previous work considering a microstructure with equal energy for the phase boundaries and grain boundaries (i.e., \(ER = 1\)) and the same thermodynamic and diffusion properties as the systems considered in this work.

We found that for the interfacial energy ratios \(ER = 1.78\) and \(ER = 1\), different phases tend to alternate in the microstructure and for \(ER = 0.566\) and \(0.06 < ER \le 1\) grains of a same phase tend to cluster.

For all cases, a growth rate exponent of \(n\approx 3\) was obtained, indicating long-range diffusion-controlled growth, but different average growth rates were found, which was attributed to the different values of the energy of the phase boundaries and the different phase arrangements. In all cases, the phase with the lowest diffusivity had the highest growth rate and on average a larger number of grain faces. The growth rate of the other two phases was equal in the cases where different phases tend to alternate and different in the cases where grains of a same phase tend to cluster, showing the effect of phase arrangement on the coarsening kinetics of a microstructure.

In the microstructures with \(ER = 1\), \(ER = 1.78\) and \(ER = 0.566\), the mean number of grain faces evolved toward a value that is constant in time and close to the mean number of faces found in three-dimensional two-phase coarsening simulations, revealing topologically self-similar growth behavior. However, in the microstructure with misorientation-dependent grain boundary energy, \(0.06 < ER \le 1\), the average number of grain faces continued to increase. A longer simulation time using a substantially larger domain and higher number of grains is required to further verify this effect.

The presented results show that the applied modeling approach is particularly suited to study the effect of various parameters on the coarsening behavior of three-phase systems. In particular, interesting for further work is an investigation of the combined effects of different volume fractions and different diffusivities for the different phases on the growth characteristics of the individual phases and the overall grain structure, as well as, a study of the effect of the grain boundary mobility on the grain structure evolution and coarsening characteristics during initial transient growth, i.e., in the time before steady-state diffusion-controlled growth is reached. Furthermore, the model has the possibility to include more than three phases.