Deformable Groupwise Image Registration using Low-Rank and Sparse Decomposition

Abstract

Groupwise image registration describes the problem of simultaneously aligning a series of more than two images through individual spatial deformations and it is a common task in the processing of medical image sequences. Variational methods with data fidelity terms based on robust PCA (RPCA) have proven successful in accounting for structural changes in image intensity stemming, e.g., from the uptake of a contrast agent in functional imaging. In this article, we investigate the drawbacks of the most commonly used RPCA data term and derive an improved replacement that employs explicit constraints instead of penalties. We further present a multilevel scheme with theoretically justified scaling to solve the underlying fully deformable registration model. Our numerical experiments on synthetic and real-life medical data confirm the advanced adaptability of RPCA-based data terms and showcase an improved registration accuracy of our algorithm when compared to related groupwise approaches.

1 Introduction

1.1 Groupwise Image Registration

The problem of aligning one image with another image of the same object is a well-studied problem in image processing and variational methods have proven successful for the task [25, 34]. However, many application scenarios involve data comprised of more than two images as in the case of image data gathered over time. This necessitates so-called groupwise methods. One example that we are primarily concerned with in this article is medical applications where the movements of a patient (or those of certain organs) have to be corrected in image sequences for further analysis.

Naive pairwise techniques that select one image from the group as a fixed reference and register all other images to the reference have been shown to be inconsistent as registration accuracy frequently depends on the choice of the reference. They are therefore generally deemed inferior to groupwise methods [21, 24] which allow all images of the group to be deformed simultaneously and operate only on an implicit reference.

A variational model for groupwise registration problems typically reads as follows: Given N images $T_i: \mathbb {R}^d \rightarrow \mathbb {R}$ (with $i = 1, \ldots , N$), deformations $u_i: \Omega \rightarrow \mathbb {R}^d$ over a fixed image domain $\Omega \subset \mathbb {R}^d$ are sought that minimize an energy of the form

$$\begin{aligned} \inf _{u_1, \ldots , u_N \in \mathcal {U}} \, D(T_1 \circ u_1, \ldots , T_N \circ u_N) + \sum \limits _{i = 1}^N S(u_i). \end{aligned}$$

(1)

Therein, $\mathcal {U}$ denotes a suitable set of spatial deformations—in our application, these will be nonparametric, i.e., fully deformable. Furthermore, D is a distance measure that quantifies the dissimilarity between the given images and S is a regularization term that accounts for the ill-posed nature of the registration problem by measuring solution candidates and penalizing ill-suited ones.

A crucial step in solving any image registration problem is the selection of a suitable dissimilarity measure on pairs or groups of images. In the past, both generalizations of established dissimilarity metrics for the classical two image problem and new concepts have been proposed to measure the distance between a group of $N > 2$ images. Examples for the former case include the variance-measure found in [2, 24] that extends the well-known sum of squared distances, different generalizations of the mutual information from [21, 30] and a multi-image version of the normalized gradient fields measure in [7].

One concept that is both central to many of the above-mentioned measures as well as the method proposed in this work is that of the Casorati matrix. Given a set of N discrete¹ images $T_i \in \mathbb {R}^{m \times n}$, such a matrix is defined as

$$\begin{aligned} M_{T_1, \ldots , T_N} := [ {{\,\mathrm{vec}\,}}(T_1) | \ldots | {{\,\mathrm{vec}\,}}(T_N) ] \in \mathbb {R}^{m n \times N}, \end{aligned}$$

(2)

where ${{\,\mathrm{vec}\,}}(\cdot )$ denotes a column-major vectorization.

The motivation behind definition (2) is, in broad terms, the fact that the rank of $M_{T_1, \ldots , T_N}$ quantifies the degree of linear dependence between the images $T_i$ which can in turn be used as a groupwise dissimilarity measure. As the rank function is however highly discontinuous and sensitive to the smallest of distortions, more sophisticated and adaptive techniques such as Robust Principal Component Analysis (RPCA) are usually employed in practice.

1.2 Robust PCA

Robust PCA techniques were originally developed to overcome the issue of high sensitivity toward sparse outliers that the classical PCA is known for and that render it unsuited for image sequence with strong local changes in intensity over time. Among the different proposed RPCA methods—see [16] for an extensive comparison—the most widely used variant is arguably the Principal Component Pursuit (PCP) from [8, 10].

PCP is derived as a convex relaxation of the combinatorial optimization problem

$$\begin{aligned} \min _{L, E \in \mathbb {R}^{p \times q}} {{\,\mathrm{rank}\,}}(L) + ||E||_0 \quad \text{ s.t. } M = L + E \end{aligned}$$

(3)

for given data $M \in \mathbb {R}^{p \times q}$—note that the field of application for RPCA techniques is much larger than image processing and that M need not necessarily be comprised of images. The term $||E||_0$ denotes the number of nonzero entries of E.

Replacing both summands of (3) with their convex hulls yields

$$\begin{aligned} \min _{L \in \mathbb {R}^{p \times q}} ||L||_* + ||M - L||_1, \end{aligned}$$

(4)

which is convex in L and thus poses a more tractable optimization problem. $||L||_*$ is the so-called nuclear norm, defined as the sum of all singular values of L (see [14]) and

$$\begin{aligned} || M - L ||_1 := \sum \limits _{i = 1}^p \sum \limits _{j = 1}^q | M_{i, j} - L_{i, j} | \end{aligned}$$

(5)

is an $\ell _1$-type norm. An intuitive connection to (3) is established via the relationship

$$\begin{aligned} {{\,\mathrm{rank}\,}}(A) = \#\{\sigma _i(A) > 0\} \end{aligned}$$

(6)

between the singular values $\sigma _i$ and the rank of a matrix (see again [14]). The decomposition of M generated by (4) is usually referred to as a low-rank and sparse decomposition, in which L is of low rank and $E := M - L$ is sparse.

PCP has previously been used in the context of groupwise image registration by [18, 19, 23, 28]. Primarily tackled therein are datasets for which low-dimensional approximations using classical PCA-based techniques are ill-suited due to occlusions, local changes in image intensity, e.g., in dynamic contrast enhanced MRI (DCE-MRI), or general pathologies in medical image data. In all these publications, the data matrix M for (4) is constructed as a Casorati matrix (2). The authors of [18, 23] however only use low-rank and sparse decompositions as a preprocessing step and subsequently perform registrations of the generated low-rank components L with different algorithms. Contrary to that, [19, 28] both use the optimal value of (4) as a metric for the similarity of a set of given images $T_1, \ldots , T_N$.

Section 2 of this paper will present an in-depth analysis of PCP as a distance measure. We argue that PCP has some inherent drawbacks: Perfect alignments of all $T_i$ often constitute local minimizers of PCP in only very narrow neighborhoods while at the same time degenerated deformations result in comparatively lower energies. To overcome these issues, we present in this work a modification of PCP that is free from these issues while still being convex and therefore easy to optimize.

1.3 Proposed Approach

Precisely, we propose to use the following groupwise dissimilarity measure:

$$\begin{aligned}&D_{\delta \text {-RPCA}}(T_1, \ldots , T_N) :=\nonumber \\&\min _{L \in \mathbb {R}^{m n \times N}} || M_{T_1, \ldots , T_N} - L ||_1 \quad \text{ s.t. } || L - \bar{L} ||_* \le \nu . \end{aligned}$$

(7)

Here, $M_{T_1, \ldots , T_N}$ is again the Casorati matrix (2), $\bar{L}$ is the repeated columnwise mean of L and $\nu \ge 0$ is a suitable threshold for the nuclear norm. The intuition behind (7) is to jointly measure the $\ell _1$-distance between the input images and their optimal approximations in a low-dimensional linear subspace centered around the mean of L. Details are given in Sect. 2.

Our main contributions include the following:

• A novel technique for low-rank and sparse decompositions that results in a more suitable distance measure (7) for groupwise registration tasks than previous approaches.

• A less restrictive uniqueness constraint for groupwise registration problems (see Sect. 3.2) than the one commonly employed in the literature.

• A multilevel strategy with theoretically justified scaling (see Sect. 4.2) to solve the overall registration model.

1.4 Delimitation from Related Work

Major differences between our approach and related methods for groupwise registration are as follows.

The publications [2, 3, 15, 21, 24, 30] all propose groupwise registration algorithms in which the deformation model is based on B-Splines and therefore handle regularization implicitly. Contrary to that, our method allows for a flexible regularization via an adaptively selected regularization term S in (1). Most closely related to our method in terms of their distance measures are [15, 21] as both penalize the eigenvalues of the correlation matrix

$$\begin{aligned} K := \frac{\Sigma ^{-1} (M_{T_1, \ldots , T_N} - \bar{M})^{\top } (M_{T_1, \ldots , T_N} - \bar{M}) \Sigma ^{-1}}{N - 1} \end{aligned}$$

(8)

with $\bar{M}$ as the mean of the Casorati matrix and $\Sigma ^{-1}$ as an (diagonal) correction factor for the empirical standard deviation. The fact that these eigenvalues correspond to the squared singular values of the Cholesky factor $(M_{T_1, \ldots , T_N} - \bar{M}) \Sigma ^{-1} / \sqrt{N-1}$ of K underlines the similarity to (7) as a rank-minimization approach.

Concerning the two PCP-based registration approaches [19, 28], the former is restricted to affine deformations, while the latter operates on light-field data, for which a geometric relationship between input images is known a priori and is exploited in the registration process.

Another nonparametric approach is presented in [7]. While also based on rank minimization, the authors use normalized image gradients as feature vectors and define alignments locally (instead of global alignments and image intensities as features as in this article). A continuation of [7] is found in [6], which generalizes the former approach to different kinds of feature vectors and formulates alignments globally.

Furthermore and for the sake of avoiding confusion, let it be mentioned that several optical flow estimation algorithms exist that are based on the idea of low-dimensional motion fields (instead of low-dimensional motion-corrected images as in our scenario). Examples can be found in [13, 31]. Interestingly, a follow-up study of [13] in [20] found models with explicit constraints to outperform models with soft constraints in this context, which is (at a broader level) very much along the lines of our findings in this article.

Lastly, another interesting approach for motion correction in DCE-MRI data which is based on Dynamic Mode Decomposition (DMD) [33] is found in [35]. However, since the results of this method are generated through the blackbox mechanism of DMD instead of spatial transformations of the input images, its outputs cannot be retraced analytically which might be a disqualifying criterion for medical applications.

1.5 Outline and Contributions

The remainder of this article is organized as follows: In Sect. 2, we analyze the established PCP-metric and derive our proposed approach as a replacement. In Sect. 3, different regularizers for our model are recapitulated and a new uniqueness constraint for groupwise image registration algorithms is introduced. In Sect. 4, an account of our solution strategy via a multilevel scheme with theoretically justified scaling is given. Numerical experiments on synthetic and real-life medical data are presented in Sect. 5, including a quantitative comparison to related approaches. Section 6 gives concluding remarks.

2 RPCA-Based Distance Measures

2.1 Analysis of Classical Approach

The classical PCP image distance as it is used in [19, 28] is given by

$$\begin{aligned} D_{\text {PCP}} (T_1, \ldots , T_N) := \min _{L \in \mathbb {R}^{m n \times N}} || L ||_* + \mu || M - L ||_1 \end{aligned}$$

(9)

with M as a Casorati matrix². The parameter $\mu > 0$ controls the weighting between the requirement on the approximation L to be of low rank and the requirement on the residual $E := M - L$ to be sparse.

Fig. 1

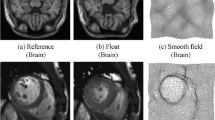
Input frames for the four experiments depicted in Fig. 2. In order to analyze the behavior of a groupwise dissimilarity measure, its energy is determined in an experiment in which one frame remains stationary (here: $T_1$) while the remaining frames ($T_2, \ldots , T_N$) are warped uniformly in a predefined manner. The above images are consecutive frames from a cardiac MRI sequence and can be regarded as aligned due to their short temporal offset

In order to assess the general applicability of (9) in the context of nonparametric groupwise image registration, we conducted the following experiment: Given N aligned images $T_1, \ldots , T_N \in \mathbb {R}^{m \times n}$, one image, say $T_1$, is selected as a reference. The remaining images $T_2, \ldots , T_N$ are then warped uniformly by a series of spatial deformations $(u^{j})_{j=-k, \ldots , k} \subset \mathbb {R}^{m \times n \times 2}$, yielding new images $T_2 \circ u^j, \ldots , T_N \circ u^j$ for every j³. Finally, we analyze the energy (9) corresponding to

$$\begin{aligned} M = \left[ {{\,\mathrm{vec}\,}}(T_1) | {{\,\mathrm{vec}\,}}(T_2 \circ u^j) | \ldots | {{\,\mathrm{vec}\,}}(T_N \circ u^j) \right] \end{aligned}$$

(10)

in dependence of the deformation index j.

Let it briefly be mentioned that this experiment requires solving (9) for L for every j or, respectively, M from (10). As (9) is convex in L, this can easily be done using the well-known PDHG algorithm from [9]. A comparative study with further details on existing RPCA methods can be found in [16].

In total, four different deformation sequences $(u^j)_j$ were employed describing firstly a translation, secondly a rotation, thirdly a scaling and fourthly a shearing—see the first row of Fig. 2 for a visualization. All deformation sequences are centered around the center of the image domain $\Omega$, so that $u^0 = 0$ corresponds to a perfect alignment in every experiment. As a perfect result, the energy (9) would therefore be expected to exhibit a global minimum at $j = 0$.

Our test data was comprised of $N = 5$ consecutive frames from a cardiac MRI sequence (see Fig. 1). As suggested by [8, Theorem 1.1], the weighting parameter for (9) was set to the provably optimal value of ${\mu = (m n)^{-1/2}}$ across all experiments.

The results of the above-described experiment are displayed in the second row of Fig. 2. Alongside the actual $D_{\text {PCP}}$-energies, their respective decompositions into the two summands $||L^*||_*$ and $\mu ||M - L^*||_1$ are shown as well (where $L^*$ denotes the minimizer of (9) with respect to the variable L).

Fig. 2

Experiments on the distance measures $D_{\text {PCP}}$ and $D_{\delta \text {-RPCA}}$. The classical $D_{\text {PCP}}$ energies (second row) exhibit only very narrow minima at the position $u^0 = 0$ of perfect alignment. Even worse so, global minimizers for all experiments except the rotation are found at the left or right endpoint of each curve and therefore correspond to degenerated transformations such as a translation out of the image domain. The proposed modification $D_{\delta \text {-RPCA}}$ (third row) resolves these issues: $u^0 = 0$ constitutes a global minimizer across all experiments. Furthermore, degenerated deformations generally result in high energies and are therefore not favored by this measure

Figure 2 indicates two major shortcoming of $D_{\text {PCP}}$ that are unfavorable for the purposes of image registration. Firstly, the point $u^0 = 0$ of perfect alignment only marks a local minimizer of $D_{\text {PCP}}$ in a very narrow neighborhood of $u^0$ in the translation experiment. In the scaling experiment, $u^0$ even constitutes a global maximizer. Secondly, both the left or the right endpoints of each energy plot, i.e., the most degenerated of all evaluated deformations $u^j$, represent global minimizers in every experiment except for the rotation.

This is especially problematic in case of translations, since constant translations are also not penalized by any regularizer based on derivatives. In practice, this problem is known to lead to trivial solutions in which all images are shifted out of the image domain. As a result, we consider $D_{\text {PCP}}$ unsuitable as a distance metric for general nonparametric registration tasks.

2.2 Proposed Modified Measure

Based on the above observations, we propose a new distance metric that modifies $D_{\text {PCP}}$ in two aspects. As a first step, the $||\cdot ||_*$-penalty term in (9) is replaced by a hard constraint to the set $\{|| \cdot ||_* \le \nu \}$ for some suitable threshold $\nu \ge 0$.

As a second step, we propose not to constrain the nuclear norm of L itself, but to consider that of the centered variable $L - \bar{L}$ in its stead. To this end, let $\bar{L} := (\sum _{i = 1}^{N} \frac{l_i}{N}) \cdot \mathbf {1}_{1 \times N} \in \mathbb {R}^{m n \times N}$ denote the matrix, in which every column is given by the arithmetic mean of the columns $l_i$ of L.

In the following, we will use the compact notation

$$\begin{aligned}&D_{\delta \text {-RPCA}}(T_1, \ldots , T_N) :=\nonumber \\&\min _{L \in \mathbb {R}^{m n \times N}} ||M - L||_1 + \delta _{\{||\cdot ||_* \le \nu \}}(L - \bar{L}) \end{aligned}$$

(11)

for our proposed dissimilarity measure (7), which we term $\delta$-RPCA. Therein, we use the convention of denoting the constraint of a variable x onto a set S via an indicator function $\delta _{S}(x)$ that evaluates to 0 for $x \in S$ and $+\infty$ for $x \notin S$ as is common in convex analysis [32].

The first modification is based on the observation that all energy curves of the $||\cdot ||_*$-term in Fig. 2 exhibit at least a local maximum at $u^0$ and therefore counteract the local minima of the $||\cdot ||_1$-term in the joint $D_{\text {PCP}}$-energy. Remodeling the low-rank requirement on L as a hard constraint resolves this issue by removing the nuclear norm from the energy as a summand.

The second modification of centering L further acts to model the low-rank requirement appropriately: As a short example, consider the nuclear norm of the two matrices

$$\begin{aligned} A_1&= a \cdot (1, 0, \ldots , 0) \in \mathbb {R}^{p \times q}, \end{aligned}$$

(12)

$$\begin{aligned} A_2&= a \cdot \mathbf {1}_{1 \times q} \in \mathbb {R}^{p \times q} \end{aligned}$$

(13)

for some $a \in \mathbb {R}^p \setminus \{0\}$. While both matrices are obviously of rank one, a short derivation shows that one has

$$\begin{aligned} ||A_1||_* = ||a||_2 < \sqrt{q} ||a||_2 = ||A_2||_* \end{aligned}$$

(14)

for all $q > 1$. In terms of the registration model, this means that a smaller nuclear norm for the uncentered variable L can be achieved by shifting all deformable images out of the image domain—thereby replacing them with the boundary value of zero—than by aligning them inside the image domain.

The continuation of the above example shows that this situation, which is highly undesirable for the purpose of image registration, is reversed when dealing with centered variables. These are given by

$$\begin{aligned} A_1 - \bar{A_1}&= a \cdot (1-q^{-1}, -q^{-1}, \ldots , -q^{-1}), \end{aligned}$$

(15)

$$\begin{aligned} A_2 - \bar{A_2}&= 0, \end{aligned}$$

(16)

respectively, and in fact, the equivalent of relation (14) now reads

$$\begin{aligned} ||A_2 - \bar{A_2}||_* = 0 < \sqrt{1 - q^{-1}} ||a||_2 = ||A_1 - \bar{A_1}||_*. \end{aligned}$$

(17)

As a consequence, (11) does not favor shifting the deformable images out of the image domain and is therefore more suited for image registration purposes.

Crucially, $D_{\delta \text {-RPCA}}$ is still convex in the variable L, since $\{|| \cdot ||_* \le \nu \}$ constitutes the level set of a convex function and is therefore convex [32, Theorem 4.6].

Repeating the above experiments for $D_{\delta \text {-RPCA}}$ with the empirical choice⁴ of $\nu = 0.9 ||M - \bar{M}||_*$ for every M from (10) yields the energies displayed in the third row of Fig. 2. In contrast to $D_{\text {PCP}}$, the modified metric $D_{\delta \text {-RPCA}}$ exhibits the desired global minimizers at $u^0 = 0$ across all experiments. Additionally, the global maximizer of each curve is found toward its left or right endpoint and consequently results from a degenerated deformation. While it should be mentioned that the global minimizers of $D_{\delta \text {-RPCA}}$ at $u^0$ are still confined to restricted convex neighborhoods in the translation and scaling experiments, this did not cause issues in practical registration tasks. We ascribe this to the facts that these regions are sufficiently wide and that, more importantly, the distance measure is accompanied by regularizer and uniqueness constraint terms (see Sect. 3) in our registration model which counteract the undesired drift process during optimization. In conclusion, the modifications that set $D_{\delta \text {-RPCA}}$ apart from $D_{\text {PCP}}$ succeed in tackling the most crucial shortcomings of the classical approach.

Apart from the interpretation of $D_{\delta \text {-RPCA}}$ as a modified version of $D_{\text {PCP}}$, it can also be interpreted in the following sense. First consider the case $\nu = 0$. This implies $L = \bar{L}$, which in turn implies constant columns $l_1 = \ldots = l_N$ of L. Using this fact, one can solve (11) analytically for L by recalling that $\ell _1$-distance minimization problems of the type

$$\begin{aligned} {{\,\mathrm{argmin}\,}}_{x \in \mathbb {R}} \sum \limits _{i = 1}^K |x - y_i| \end{aligned}$$

(18)

are solved by the median of $(y_1, \ldots , y_K)$ [4, p. 433]. As a consequence, the constant columns of L in the problem above are given by the pointwise median of $T_1, \ldots , T_N$ and $D_{\delta \text {-RPCA}}$ represents the residual of an $\ell _1$-distance between the input images and that median.

In the case of $\nu > 0$, $D_{\delta \text {-RPCA}}$ can more generally be interpreted as the joint $\ell _1$-distance between the images $T_1, \ldots , T_N$ and their individual (optimal) approximations $l_1, \ldots , l_N$ in a low-dimensional linear subspace centered around $\bar{l} := \sum _{i = 1}^N \frac{l_i}{N}$.

Thanks to the additional adaptability granted by its decomposition properties, we deem (11) especially suited for image sequences with intricate features such as temporal repetition or changes in image intensity. While conventional approaches based on matching predefined image features like intensity or edges might not be able to account for such characteristics, these can very well be captured by suitable low-rank and sparse components. Our experiments on complex medical image data in Sect. 5 aim at highlighting these capabilities.

3 Regularization

3.1 Choice of Regularizer

For our numerical experiments in Sect. 5, we employ two different types of regularizers S to accompany the data term $D_{\delta \text {-RPCA}}$ in the overall registration model (1). As these are standard concepts in variational image processing, we refrain to short recapitulations.

Firstly, we consider a Total Variation (TV) regularization as given by

$$\begin{aligned} {{\,\mathrm{TV}\,}}(\upsilon ) := \int _{\Omega } \mathop {}\!\mathrm {d}|D \upsilon | \end{aligned}$$

(19)

for continuous vector fields $\upsilon$ in the space $BV(\Omega , \mathbb {R}^d)$ of functions of bounded variation. For all details, we refer to [1].

In our practical experiments, we employ a straightforward discretization of (19) via finite forward differences. That is, given a discrete deformation $u \in \mathbb {R}^{m \times n \times 2}$ defined over a rectangular $(m \times n)$-grid⁵ with grid widths $h_1, h_2 > 0$, we approximate (19) by

$$\begin{aligned} {{\,\mathrm{TV}\,}}^h(u) := h_1 h_2 \Vert \nabla ^h {{\,\mathrm{vec}\,}}(u) \Vert _{2, 1}, \end{aligned}$$

(20)

where $\nabla ^h$ implements the afore-mentioned finite differences and $\Vert y \Vert _{2, 1} := \sum _{i = 1}^m\sum _{j = 1}^n \Vert y_{i, j} \Vert _2$ is a sum over the numerical gradients at every grid point.

While TV regularization is known to favor piecewise constant deformations, smooth solutions—as they are often more plausible in medical applications—can be obtained by using different concepts such as curvature regularization [12]. In the continuous setting, this is defined as

$$\begin{aligned} {{\,\mathrm{CURV}\,}}(\upsilon ) := \frac{1}{2} \sum \limits _{c = 1}^d \int _{\Omega } (\Delta \upsilon _c)^2 \mathop {}\!\mathrm {d}x \end{aligned}$$

(21)

for $\upsilon \in C^2(\Omega , \mathbb {R}^d)$. Using a point- and channelwise five-point stencil discretization of the two-dimensional Laplacian that is denoted by $\Delta ^h$, a discretization of (21) can be phrased compactly as

$$\begin{aligned} {{\,\mathrm{CURV}\,}}^h(u) := \frac{h_1 h_2}{2} \Vert \Delta ^h {{\,\mathrm{vec}\,}}(u) \Vert _2^2 \end{aligned}$$

(22)

where $u \in \mathbb {R}^{m \times n \times 2}$ is as above.

3.2 Uniqueness Constraint

As our model does not make use of an explicit reference image that all other images are aligned to, we need to employ an additional constraint on the displacements $(u^k)_k$ in order to ensure the uniqueness of a solution.

This can be seen from the simple example in which $T_1, \ldots , T_N$ display uniform objects, e.g., white rectangles, before a black background. Now consider the case of a perfect alignment

$$\begin{aligned} T_1(u^1) = \ldots = T_N(u^N) \end{aligned}$$

(23)

of these rectangles inside the image domain $\Omega$. If all deformations $u^k$ are uniformly modified by a sufficiently small translation $t \in \mathbb {R}^2$, such that the new deformations $\hat{u}^k$ still align all rectangles inside the common domain⁶, then the new deformations $(\hat{u}^k)_{k=1,\ldots ,N}$ constitute a solution equal to $(u^k)_{k=1,\ldots ,N}$ both in terms of $D_{\delta \text {-RPCA}}$ and in terms of any derivative-based regularizer S.

For the regularizer S, this is explained by the simple fact that any derivative of a deformation field is invariant under a constant translation.

The invariance for $D_{\delta \text {-RPCA}}$ is due to the equivalence of an offset by t and a simple reordering of the pixels between $T_k(u^k)$ and $T_k(\hat{u}^k)$ (due to the zero boundary condition). Clearly, the $\ell _1$-term in (11) is invariant to any reordering and the same is true for the nuclear norm constraint, since a consistent reordering of all $T_k(u^k)$ results in a row permutation of the Casorati matrix

$$\begin{aligned} M = [{{\,\mathrm{vec}\,}}(T_1 \circ u^1) | \ldots | {{\,\mathrm{vec}\,}}(T_N \circ u^N)]. \end{aligned}$$

(24)

As a short derivation shows, a row permutation does not affect the singular values of a matrix: Let $A \in \mathbb {R}^{p \times q}$ be an arbitrary matrix and let $P \in \{0, 1\}^{p \times p}$ be a permutation. If a singular value decomposition (SVD) of A is given by $A = U \Sigma V^{\top }$, then $P A = (P U) \Sigma V^{\top }$ constitutes a valid SVD of PA due to PU still being orthogonal, i.e.,

$$\begin{aligned} (P U)^{\top } (P U) = U^{\top } P^{\top } P U = U^{\top } U = I. \end{aligned}$$

(25)

Thus, the singular values on the diagonal of $\Sigma$ stay unaffected and so does the nuclear norm $||P A||_* = ||A||_*$.

In order to eliminate this remaining degree of freedom from our model, we impose an additional constraint on the deformations $(u^k)_k$ which enforce the mean (or equivalently the sum) over all deformations and grid points to be zero in each coordinate direction:

$$\begin{aligned} \frac{1}{(N m n)} \sum \limits _{k = 1}^N \sum \limits _{i = 1}^m \sum \limits _{j = 1}^n u_{i, j, c}^k \overset{!}{=} 0 \quad \forall c \in \{1, 2\}. \end{aligned}$$

(26)

Note that [15, 21, 24, 30] constrain their deformations in a related manner by demanding the mean of all deformations to be zero at every grid point as introduced by [3]. The difference however is, that (26) only imposes one constraint per dimension instead of one constraint per grid point and dimension. As a result, (26) restricts the space of feasible solutions much less severely while still ensuring uniqueness.

4 Implementation and Optimization

In this section, we present an optimization scheme for our groupwise registration model that is related to the works in [19, 36].

First, we combine all components derived in the previous sections into a complete registration model

$$\begin{aligned} {\begin{matrix} \min _{(u^k)_k, L} \ &{}h_1 h_2 \Vert [{{\,\mathrm{vec}\,}}(T_1 \circ u^1) | \ldots | {{\,\mathrm{vec}\,}}(T_N \circ u^N)] - L \Vert _1 \\ &{}+ \delta _{\{\Vert \cdot \Vert _* \le \nu \}}( L - \bar{L} ) + \mu \sum \limits _{k = 1}^N S(u^k)\\ &{}+ \sum \limits _{c = 1}^2 \delta _{ \{ \langle \mathbf {1}, \cdot \rangle = 0 \} } ((u_{\cdot , \cdot , c}^1, \ldots , u_{\cdot , \cdot , c}^N)), \end{matrix}} \end{aligned}$$

(27)

in which $\mu > 0$ controls the regularization strength.

Note that we also factored in a weighting of the $\ell _1$-term by the size of the grid cells $h_1 h_2$ in order to account for a consistent scaling of the different terms in the multilevel scheme that will be the subject of Sect. 4.2.

4.1 Linearized Subproblems

As our goal is to apply convex optimization methods to (27), one needs to deal with the nonlinearity of the expressions $T_k \circ u^k$ that leads to a non-convexity of the overall model. As in [19, 28, 29, 36], an iterative linearization of the deformed images is used to overcome this issue. Note that while a one-time linear approximation would be possible in theory, the strong locality of such an approximation becomes prohibiting when larger deformations are required to align the images.

In the following, we assume all variables to be in vector format (including the values of all $T_k$) and for brevity’s sake omit the explicit notation of reshaping operations like ${{\,\mathrm{vec}\,}}(\cdot )$. A linearization of $T_k$ can then be expressed as

$$\begin{aligned} T_k(u^k) \approx T_k(\tilde{u}^k) + \nabla T_k(\tilde{u}^k)^{\top } \cdot (u^k - \tilde{u}^k) \end{aligned}$$

(28)

for a suitable point $\tilde{u}^k$. This enables one to approximate the $\ell _1$-term in (27) by

$$\begin{aligned} \sum \limits _{k = 1}^N \Vert T_k(\tilde{u}^k) + \nabla T_k(\tilde{u}^k)^{\top } \cdot (u^k - \tilde{u}^k) - l_k \Vert _1. \end{aligned}$$

(29)

Using vectorized variables further allows one to rewrite the centering of L as a linear operation KL with

$$\begin{aligned} K = \left( I_{N \times N} - \frac{\mathbf {1}_{N \times N}}{N} \right) \otimes I_{m n \times m n} \in \mathbb {R}^{m n N \times m n N}. \end{aligned}$$

(30)

Therein, $\otimes$ denotes the Kronecker product of matrices.

Since solving (27) through iterative (re-)linearization amounts to solving a series of subproblems, we propose to treat it as a process, in which the threshold $\nu$ is successively decreased to one final threshold value.

Assuming a predefined number $n_{\text {iter}}$ of linearization steps and denoting the final threshold by $\nu$, we therefore employ a finite series of thresholds

$$\begin{aligned} \nu _1> \nu _2> \ldots > \nu _{n_{\text {iter}}} = \nu \end{aligned}$$

(31)

for the iterative solution of the individual subproblems.

As a strategy to select these parameters, we propose a simple scheme in which these thresholds are successively decreased by a constant factor $\alpha \in (0, 1)$. Using the nuclear norm of the centered input images as a baseline, one obtains

$$\begin{aligned} \nu _t := \alpha ^t \Vert M - \bar{M} \Vert _* \quad \text {for} \quad t = 1, \ldots , n_{\text {iter}} \end{aligned}$$

(32)

with M as the input image Casorati matrix (2) and $\bar{M}$ as its repeated columnwise mean.

Regarding the practical choice of the involved parameters, we found values of $\alpha \in (0.9, 0.95)$ to work reasonably well in all of our experiments. Note, however, that since $\alpha$ is directly related to $\nu$ via $n_{\text {iter}}$ in (32), it has to be chosen in conjunction with $n_{\text {iter}}$. In practice, we recommend using parameters tuples $(\alpha , n_{\text {iter}})$ that yield values of $\alpha ^{n_{\text {iter}}} \in (0.1, 0.4)$, depending on the degree of disturbance present in the image sequence.

At last, we solve the linearized—and therefore now convex—subproblems using the aforementioned Primal-Dual Hybrid Gradient (PDHG) method [9, Alg. 1]. In short, we assign all terms of the linearized version of (27) except for the uniqueness constraints to the expression F(Ax) in the primal problem formulation

$$\begin{aligned} \inf \nolimits _{x \in \mathbb {R}^p} F(A x) + G(x). \end{aligned}$$

(33)

Obviously, this leaves the remaining uniqueness constraints for G. The primal variables x are comprised of all deformations $(u^k)_k$ as well as the low-rank components L and the linear operator $A \in \mathbb {R}^{q \times p}$ captures all relevant linear transformations of these variables, i.e., the linearization in (29), the centering of the low-rank components L by (30) and the differential operator corresponding to the chosen regularizer S.

Clearly, both F and G fulfill the usual requirements of convexity, lower-semicontinuity and properness, so that the saddle point formulation

$$\begin{aligned} \inf \nolimits _{x \in \mathbb {R}^p} \sup \nolimits _{y \in \mathbb {R}^q} \ \langle A x, y \rangle + G(x) - F^*(y) \end{aligned}$$

(34)

of (33) can be solved using the PDHG algorithm. For all required proximal operators, we refer to [27] as an extensive reference.

4.2 Multilevel Scheme and Parameter Scaling

As is common in image registration, we couple the scheme derived in the previous subsection with a multilevel approach, also known as coarse-to-fine strategy. This serves the two purposes of lowering the computational effort of our solution strategy and of avoiding unwanted local minimizers.

An image pyramid of $n_{lev}$ resolution stages serves as input to our multilevel scheme in which images are downsampled by a factor of 2 in each dimension between consecutive stages⁷.

The inverse operation, i.e., the prolongation that all primal variables x are subject to, is implemented as depicted in Fig. 3. As proposed in [36], the dual variables y are simply reinitialized with 0 for every new stage. Note that while more sophisticated prolongation strategies for the primal variables exist (see, e.g., [26, Chpt. 9.4]), this approach simplifies the subsequent analysis and we found it to perform well in practice.

Fig. 3

Prolongation scheme. Variable values for the index (i, j) in the low-resolution coordinate system (left) are propagated to the variables indexed by ${(2 i - 1, 2 j - 1)}$, ${(2 i - 1, 2 j)}$, ${(2 i, 2 j - 1)}$, (2i, 2j) in the high-resolution system (right)

In order to guarantee a consistent scaling of both the $\ell _1$-term and the regularizer S in (27), we adapt the grid widths $h_1$ and $h_2$ in between stages.

Moreover, we require a scaling of the thresholds $\nu _t$ from (32) since the low-rank variable L changes in resolution as well. To this end, we need to derive by what factor the nuclear norm of a Casorati matrix M changes when it is prolongated to the next higher resolution. In accordance with Fig. 3, we can express the prolongation of $M \in \mathbb {R}^{m n \times N}$ as

$$\begin{aligned} P \begin{bmatrix} M\\ M\\ M\\ M \end{bmatrix} \in \mathbb {R}^{4 m n \times N} \end{aligned}$$

(35)

where $P \in \mathbb {R}^{4 m n \times 4 m n}$ is a suitable permutation.

As the singular values of a matrix are invariant under row-permutations (see Eq. (25)), one can restrict the analysis of the singular values of (35) to the simple case $P = I$. Let an economic SVD of M now be given by $M = U \Sigma V^{\top }$ with $U \in \mathbb {R}^{m n \times N}$ and $\Sigma , V \in \mathbb {R}^{N \times N}$ [14, Chpt. 2.5]. Then, it holds

$$\begin{aligned} \underbrace{\begin{bmatrix} M\\ M\\ M\\ M \end{bmatrix}}_{=: \hat{M}} = \underbrace{\begin{bmatrix} U\\ U\\ U\\ U \end{bmatrix}}_{=: \hat{U}} \Sigma V^{\top }. \end{aligned}$$

(36)

Equation (36) does not constitute a valid (economic) SVD of $\hat{M}$ however, since the columns of $\hat{U}$ are no longer normalized: Rather, one has

$$\begin{aligned} (\hat{U}^{\top } \hat{U})_{i, j} = {\left\{ \begin{array}{ll} 4, &{} i = j,\\ 0, &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(37)

In order to regain a valid SVD, a factor of 2 has to be redistributed from $\hat{U}$ to $\Sigma$, i.e.,

$$\begin{aligned} \hat{M} = (\hat{U} / 2) (2 \Sigma ) V^{\top }. \end{aligned}$$

(38)

This implies $||\hat{M}||_* = 2 ||M||_*$ which in turn implies that the sought factor is given by 2. Note that this result can easily be generalized to the case of d-dimensional images, where that factor is then given $2^{(d / 2)}$.

Fig. 4

(Top row) Exemplary images from the synthetic dataset described in Sect. 5.1. The elliptic object describes a semicircular motion and alternates in texture between two patterns in between images. The frame and rectangle objects remain stationary throughout the sequence. (Bottom row) Motion correction of the above frames using the proposed method. The axis ticks indicate the respective position of the ellipse’s center within each image. It can be seen easily, that nearly all motion was corrected successfully without disturbing the ellipses’ stripe patterns. Note also that no artificial motion was introduced to the frame or rectangle objects thanks to a TV regularizer that allows for piecewise constant deformations

The overall multilevel strategy is shown in Alg. 1. Therein, we assume grid widths $h_1 = h_2 = 1$ at maximum resolution. Further assumed is a partition of the number of relinearization steps $n_{\text {iter}}$ from Sect. 4.1 among the different stages j, i.e.,

$$\begin{aligned} n_{\text {iter}} = \sum \limits _{j = 1}^{n_{lev}} n_{\text {iter}}^j. \end{aligned}$$

(39)

Clearly, it is advisable to begin with a sufficient number of iterations $n_{\text {iter}}^1$ at the lowest resolution in order to obtain a rough initial alignment and to perform only a small number of refinement steps $n_{\text {iter}}^j$ at each following stage j.

5 Numerical Experiments

5.1 Synthetic Data: Textured Ellipse

As a first experiment, we employ a synthetic dataset to illustrate the ability of our model to simultaneously correct motion and to generate low-dimensional embeddings of the corresponding output data.

The sequence is comprised of a total of 10 frames that display the semicircular motion of an elliptic object before a uniform background where other stationary objects are present as well. Crucially, the ellipse’s texture alternates between vertical and horizontal stripes for all oddly and all evenly indexed frames, respectively. This means that, assuming a perfect motion correction of the ellipse, the output images would be expected to be embedded in a subspace of dimension two. Exemplary frames from this sequence are displayed in the top row of Fig. 4.

As befits the motion present in this sequence, we employ a TV regularization by (20) with homogenous Dirichlet boundary conditions for the differential operator. Further parameters for Alg. 1 are chosen as

• $\alpha = 0.9$, $\mu = 0.2$,

• $n_{lev} = 3$ with $n_{\text {iter}}^1 = 16$ and $n_{\text {iter}}^j = 2$ for $j = 2, 3$.

Results of the motion correction are shown in the bottom row of Fig. 4. Clearly, the proposed algorithm is capable of correcting motion near perfectly in this simple example.

Regarding the low-rank components generated alongside the actual motion correction, we point to Fig. 5. Note that the low-rank approximations can be regarded as equal to the actual outputs ${T_i \circ u^i}$ for this synthetic dataset since it is (by nature) void of any intensity distortions. Figure 5 shows that a two-dimensional representation of the motion-corrected output sequence is in fact generated by our method. This is formed from the mean of L and the leading left singular vector of the mean-adjusted low-rank components $L - \bar{L}$.

Fig. 5

(Left) Development of the singular values of $L - \bar{L}$ over the course of the multilevel scheme from Alg. 1 (scaling of the singular values adjusted as discussed in Sect. 4.2). As the scheme progresses, the influence of the leading singular value $\sigma _1$ (solid red line) on the nuclear norm (dashed blue line) increases. This corresponds to a vanishing of motion artifacts from the low-rank components L. Note that these can be regarded as equal to the output images ${T_i \circ u^i}$ (see Fig. 4) since the dataset is synthetic in nature and therefore free from irregular intensity distortions. (Right) Low-dimensional embedding of the output images. As expected, a two-dimensional basis representation of the output sequence is generated by our method. This is formed from the mean of L and the leading (left) singular vector of $L - \bar{L}$ (corresponding to the red line in the left-hand figure). As is intuitive, frames with horizontal stripe patterns are reconstructed by adding the two basis vectors and frames with vertical stripes are reconstructed by subtracting them. The influence of all remaining singular vectors is negligible due to the small magnitude of their singular values in the left-hand figure

5.2 Medical Data I: Cardiac MRI

As a more challenging task, we test the applicability of our model on real-world medical data. Concretely, we consider a MRI sequence of a beating heart in the so-called two-chamber view that displays the left atrium and ventricle. Seven repetitions of the heart cycle with blood flow in and out of the two chambers as well as breathing-induced motions of several structures like the thorax, the diaphragm and the heart itself are seen in this sequence.

Note that while different repetitions of the same phase of the heart cycle exhibit visual similarities, the turbulent nature of the blood flow leads to irregular object appearances which make it an interesting test case for our method.

In order to reduce the enormous magnitude of the dataset, we confine the registration task to one frame per each repetition of the following phases of the heart cycle: systole, diastolic relaxation and diastolic filling. This makes for 21 frames to register in total. See the left-hand side of Fig. 6 for exemplary frames from this dataset.

Fig. 6

(Left) Exemplary frames from the cardiac MRI dataset overlaid with the corresponding deformation fields generated by our method. Per heart cycle and phase, one frame is chosen as part of the registration task. (Right) Difference images per phase between the selected frames of the first and seventh heart cycle before and after registration. While these difference images present only a selective account of the overall motion correction quality, it is still apparent that misalignments, i.e., the “motion shadows” found in the diaphragm, thorax, heart apex and artery regions of the initial difference images, are largely absent in the output images

Parameters for this experiment remained the same as in the previous section except for

• $\alpha = 0.95$, $\mu = 10$,

where we now use a curvature regularizer (22) with homogenous Neumann boundary conditions.

The difference images before and after registration in the right-hand side of Fig. 6 show that misalignments due to the patients’ breathing motion are in fact successfully corrected by our method.

Before we present a comparative analysis of the registration accuracy against related groupwise registration algorithms in Sect. 5.2.1, we investigate the effect of the low-rank and sparse decomposition on this dataset. To this end, we present exemplary sparse components ${T_i \circ u^i - l_i}$ generated by our method in Fig. 7. These describe, as expected, those parts of the output sequence that are too irregular to be explained by a low-dimensional basis. In the present dataset, these are the visual details of the blood flow. Moreover, the images in Fig. 7 show these components to be in fact sparse as derivations from zero are locally restricted throughout.

Fig. 7

Sparse components $e_i := T_i \circ u^i - l_i$ generated by our algorithm for the cardiac MRI dataset (with $l_i$ as the i-th column of L). The displayed images correspond to the frames shown in Fig. 6. It is visually clear that the sparse components first and foremost capture the irregularities of the blood flow, i.e., that part of the output sequence that cannot be explained in a low-dimensional subspace

5.2.1 Comparative Analysis

In order to rank the registration accuracy of our method, we compare its results to the following registration techniques for image stacks:

• 1. The classical PCP image distance $D_{\text {PCP}}$ from (9) whose problematic aspects were discussed in Sect. 2. Nevertheless, this approach presents an interesting benchmark for the modifications introduced in this article. To make for a fair comparison, we exchange only the data term of (27) by $D_{\text {PCP}}$ and keep all other parts of the registration model (and its implementation) the same. Moreover, the weighting parameter for $D_{\text {PCP}}$ is chosen as suggested in [8].

• 2. The simple variance-based dissimilarity measure

  $$\begin{aligned} D_{\text {VAR}} (T_1, \ldots , T_N) := \frac{1}{2} \sum _{i = 1}^N \Vert T_i - \bar{T} \Vert _2^2 \end{aligned}$$

  (40)

  with $\bar{T} := \frac{1}{N} \sum _{i=1}^N T_i$ as it is used in [2, 24]. Just as with $D_{\text {PCP}}$, this data term can be integrated easily into our proposed registration model (27) and multilevel strategy without adjusting any of other part of the model.

• 3. The more sophisticated PCA-based measure $D_{\text {PCA2}}$ from [21] which is defined as

  $$\begin{aligned} D_{\text {PCA2}} (T_1, \ldots , T_N) := \sum \limits _{i=1}^N i \lambda _i(K) \end{aligned}$$

  (41)

  with $\lambda _i(K)$ as the i-th largest eigenvalue of the correlation matrix K from (8). For this measure, a public implementation is available in the elastix-toolbox [22]. Note however that, as stated in Sect. 1.4, this implementation is parametric and therefore does not use explicit regularization.

• 4. A pairwise registration approach using a discretized version of the intensity-invariant normalized gradient fields measure

  $$\begin{aligned} D_{\text {NGF}} (R, T) := \frac{1}{2} \int _{\Omega } 1 - \left\langle \frac{\nabla R}{\Vert \nabla R \Vert _{\eta }}, \frac{\nabla T}{\Vert \nabla T \Vert _{\eta }} \right\rangle ^2 \mathop {}\!\mathrm {d}x \end{aligned}$$

  (42)

  with $\Vert z \Vert _{\eta } := \sqrt{\Vert z \Vert _2 + \eta ^2}$ (see [17] for details). Like all other presented approaches that make use of explicit regularization, we combine (42) with a curvature regularizer (21). Since any pairwise registration method for image stacks $T_1, \ldots , T_N$ requires a fixed reference $R = T_r$ for some $r \in 1, \ldots , N$, we employ the simple strategy of selecting that image as the reference R that exhibits the smallest accumulated SSD-distance to all other images, respectively. Experiments for this approach were conducted in the publicly available Matlab library FAIR [26] and using the provided spline-based image interpolation model (cf. [26, Sec. 3.4]).

Fig. 8

(Left) Selected landmarks in the cardiac MRI dataset. (Right) Comparison of landmark registration accuracy as measured by (43) (smaller values indicate better accuracy, especially note the logarithmic scaling of the y-axis). The competing approaches are the one proposed in this work (blue line), the elastix-implementation of $D_{\text {PCA2}}$ (red), the variance-based approach (40) (green), the pairwise method based on $D_{\text {NGF}}$ (orange) and the classical RPCA implementation termed $D_{\text {PCP}}$ (purple). For comparison, the accuracy of the unregistered landmarks is shown as well (gray line). The landmarks’ numbering on the horizontal axis corresponds to the one displayed on the left. Clearly, our approach outperforms the competing methods on most landmarks most of the time. Despite being based on the classical (instead of robust) PCA, $D_{\text {PCA2}}$ performs surprisingly well—the rather simplistic variance-measure on the other hand performs worst of the five

We quantify registration accuracy through the use of landmarks. Specifically, we annotate 22 corresponding landmarks in each of the 21 input frames of the cardiac MRI dataset—see Fig. 8 for their positioning on one representative frame. Then, we measure per specified landmark the mean Euclidean distance of each warped representative of that landmark from its average warped position. That is, if $y_i^k \in \mathbb {R}^2$ is the position of the k-th landmark in the i-th input frame and $\tilde{y}_i^k$ is the position that $y_i^k$ is warped to by a specified registration algorithm, we compute

$$\begin{aligned} \frac{1}{N} \sum \limits _{i=1}^N \Vert \tilde{y}_i^k - \bar{y}^k \Vert _2 \text { with } \bar{y}^k := \frac{1}{N} \sum \limits _{i=1}^N \tilde{y}_i^k \end{aligned}$$

(43)

as a measure for the accuracy with which that algorithm was able to register the k-th landmark.

The intuition behind (43) is that the position of each landmark should ideally be fixed across all frames after registration. This means that smaller values for (43) indicate better accuracy.

Parameters for the competing approaches were chosen as follows:

For the $D_{\text {PCA2}}$-measure, we increased the elastix-parameters recommended by the authors of [21] to Parameters for the

• 3 resolution stages (recommended: 2),

• 2.000 iterations per stage (rec.: 1.000),

• 25.000 random coordinates per stage (rec.: 2.048)

to ensure that the method is granted sufficient computational capacity to produce accurate solutions.

For the pairwise approach using $D_{\text {NGF}}$, we employed an edge parameter of $\eta = 25$ as well as a regularization strength of $\mu = 10$.

Lastly, the regularization strengths for the $D_{\text {PCP}}$-based and the $D_{\text {VAR}}$-based algorithms were chosen as $\mu = 0.1$ and $\mu = 10$, respectively.

The results of all methods are displayed in the right-hand side of Fig. 8 in which the proposed $\delta \text {-RPCA}$ approach outperforms its competitors for the majority of the selected landmarks. While $D_{\text {PCA2}}$, $D_{\text {PCP}}$ and even the pairwise approach using $D_{\text {NGF}}$ are occasionally close to $D_{\delta \text {-RPCA}}$ in terms of registration accuracy, the variance approach based on (40) is inferior many times over.

Moreover and for the sake of completeness, an exemplary visual comparison of warped mages generated by the different methods is presented in Fig. 9.

Fig. 9

Visual comparison of registration results of the competing methods/distance measures $D_{\delta \text {-RPCA}}$, $D_{\text {PCP}}$, $D_{\text {PCA2}}$, $D_{\text {VAR}}$ and $D_{\text {NGF}}$. Per considered phase of the heart cycle, the warped output frames of the first heart cycle in the cine are displayed along the figure’s rows (cf. also Fig. 6). Note that while differences in registration accuracy (as they are considered in Fig. 8) are hard to distinguish upon visual examination, the challenge that the registration task poses to simple and arguably underdeveloped approaches like $D_{\text {VAR}}$ becomes apparent

5.3 Medical Data II: Renal DCE-MRI

To further showcase the versatility of our algorithm, we consider a second real-world medical dataset with breathing motion to be corrected. This dataset was acquired using dynamic contrast-enhanced MRI (DCE-MRI) and shows the contrast agent uptake in a human kidney. In total, we consider a sequence of 16 consecutive frames to register in this experiment. Exemplary frames are shown in the top row of Fig. 10.

Fig. 10

(Top row) Exemplary input frames from the renal DCE-MRI dataset. The horizontal lines are aligned to different structures in the first input frame (marked by crosses) and indicate the misalignments of these structures across time. Especially note the intensity changes in the kidney region—these are due to contrast agent uptake and make out the intricacy of this registration task. (Bottom row) Registered output frames generated by our method. As the horizontal lines show, misalignments caused by breathing motion are successfully resolved

As the contrast agent uptake in the kidney region causes structural changes in image intensity, simple registration methods based on the principle of matching intensities (or the corresponding edges) are ill-suited for this dataset.

Using the parameters

• $\alpha = 0.95$, $\mu = 20$,

• $n_{lev} = 4$ with $n_{\text {iter}}^1 = 16$, $n_{\text {iter}}^j = 2$ for $j = 2, \ldots , 4$

for Alg. 1 as well as a curvature regularization (22) with homogenous Dirichlet boundary conditions, our approach was able to perform a successful motion correction as displayed in the bottom row of Fig. 10.

Moreover, we carried out the same comparative analysis as in Sect. 5.2.1 for this dataset. Parameters for the $D_{\text {PCA2}}$-measure were kept the same as previous while parameters for the variance-approach were adapted from those employed for $D_{\delta \text {-RPCA}}$. However, we were not able to identify a regularization strength $\mu$ that resulted in acceptable performance for the latter approach which is why we adhered to the choice of $\mu = 20$. Regularization strengths for the $D_{\text {PCP}}$ method and the pairwise $D_{\text {NGF}}$-based algorithm were chosen as $\mu = 0.1$ and $\mu = 10$, respectively.

See Fig. 11 for a visualization of the results.

Fig. 11

Comparative analysis of landmark registration accuracy for the renal DCE-MRI dataset. (Left) Landmark positions and numbering. (Right) Landmark registration accuracy measured in terms of (43) (y-axis scaling is again logarithmic). The proposed approach (blue) produces the most accurate results for many of the landmarks numbered 1–16. Largely on a par is the pairwise strategy using normalized gradient fields (orange) while $D_{\text {PCA2}}$ (red) is in close succession. For the variance-based method (40, green) and the classical RPCA approach using (9, purple), we were not able to identify parameters that resulted in acceptable performance. Note also that the landmarks numbered 17–22 exhibit more motion after registration (for all five methods) than without registration (gray). This is due to the fact that these landmarks are positioned along the patients’ spine and that all algorithms assume a smooth deformation model which is not compatible with the sliding motion between the spine and the surrounding organs. However, as the spine is usually not part of the region of interest for renal DCE-MRI data, we deem this a minor issue for practical applications

As in the previous dataset, we found our registration strategy to perform well against the competing approaches in terms of accuracy. Especially striking is the gain in accuracy over the classical $D_{\text {PCP}}$ measure which failed to produce a viable motion correction for any regularization strength $\mu$ we employed via grid search. Note that this comparison serves as an ablation study and provides justification for the modifications introduced by $D_{\delta \text {-RPCA}}$.

While the performance of $D_{\text {PCA2}}$ was only mildly inferior to that of $D_{\delta \text {-RPCA}}$, the results generated by $D_{\text {VAR}}$ are largely unusable. We attribute this failure of $D_{\text {VAR}}$ to its lack of adaptability to the variations in image intensity caused by the contrast agent.

Most noteworthy however is the accuracy of the pairwise registration strategy using $D_{\text {NGF}}$ which is overall on a par with that of the successful groupwise approaches $D_{\text {PCA2}}$ and $D_{\delta \text {-RPCA}}$. While the choice of the reference image is a debatable question when registering image stacks using pairwise techniques—leading to biased registration results in a worst case scenario—, our experiments show that they are able to produce accurate registration results and should not be discarded generally.

Lastly, we mention the fact that the landmarks along the spine were not successfully registered by any of the three methods as Fig. 11 shows. This is due to the sliding motion between the spine and the surrounding organs which cannot be represented aptly by smooth deformations such as those assumed by the curvature regularizer or implicit B-Spline regularization. For practical purposes, we deem this a minor shortcoming since the region of interest for renal DCE-MRI data is inside the kidneys and a suitable registration result is available for this region. If one was however interested in deformations that capture this sliding behavior accurately, a spatially dependent regularization as in [11] could be conceived and integrated into the model.

5.4 A Note on Computational Cost

Let us briefly analyze the computational cost of the proposed registration algorithm on a fixed resolution level of Alg. 1. As we require the evaluation of the proximal operators of all individual terms in (27) to perform a PDHG iteration, it is useful to categorize them with respect to computational cost and parallelizability.

Both the proximal operators corresponding to the $\ell _1$-term and the discussed regularizers S are separable with respect to the image grid points and have an overall linear cost in the number of grid points mn and images N (cf. [27]).

While it cannot be evaluated in a decoupled manner, the proximal operator corresponding to the uniqueness constraint resolves to two simple projections onto a linear subspace of dimension one and can be evaluated with linear cost in (mnN) as well.

The bottleneck in computational cost however is given by the proximal operator corresponding to the nuclear norm constraint as it requires the computation of a singular value decomposition of a $(m n) \times N$ matrix in each iteration. Assuming $m n > N$, the cost of a single SVD is given by $\mathcal {O}(m n N^2)$ [14] and is therefore quadratic in the number of images N. Moreover, the SVD algorithm does not allow for a pointwise separation of the computation, i.e., parallelization.

In terms of memory usage, the PDHG scheme employed in Alg. 1 operates on 3Nmn primal and 4Nmn dual floating point variables for a fixed spatial resolution $m \times n$.

Regarding the application scenario presented in this article, i.e., medical image processing, the fact should be noted that temporal image data is usually acquired in three instead of two spatial dimensions. Experiments in 3D+t data would therefore increase the computational and memory cost by another linear factor corresponding to the number of sampling points along that third dimension. As the runtimes reported below indicate, an application of the proposed method to 3D+t data of medium or high resolution as well as close-to-real-time data processing is out of reach at the current time.

Our practical runtimes ranged around $\sim 38 \, \text {min.}$ for the synthetic data from Sect. 5.1 (with an input resolution of $m = n = 200$), $\sim 80 \, \text {min.}$ for the cardiac MRI data from Sect. 5.2 ($m = n = 220$) and $\sim 93 \, \text {min.}$ for the renal DCE-MRI data from Sect. 5.3 ($m = n = 256$) on a 64Bit Linux system with an Intel Core i7-4770 CPU and 8GB of RAM. Our implementation in Matlab is publicly available at https://github.com/roland1993/d_RPCA.

6 Concluding Remarks

In this work, we have investigated a novel dissimilarity measure for groupwise image registration based on low-rank and sparse decompositions. The proposed term aims at correcting the major drawbacks of the RPCA-image distance from [19, 28] as discussed in Sect. 2.

Our numerical experiments confirm the adaptibility of this approach when registering image sequences with intricate features such as structural and/or recurring changes in object appearance. Our experiments on real-life medical data further confirm the advantage of sophisticated distance measures such as ours over simple ones like the variance-measure (40). Moreover, we have shown a notable lead of our approach when compared to the already highly engineered $D_{\text {PCA2}}$-measure from [21] or the often-employed $D_{\text {PCP}}$-measure.

A multilevel approach with theoretically justified scaling serves as a solution strategy to our model. Apart from tweaking our optimization algorithm, further possible avenues of research could include the combination of our data-term with more sophisticated regularizers like the total generalized variation [5] (as used, e.g., in [19]), the replacement of the rather simple linear interpolation model in our implementation by a spline-based model⁸ or the application of our explicitly constrained decomposition approach to other tasks than image registration.