Measure-Valued Variational Models with Applications to Diffusion-Weighted Imaging

Abstract

We develop a general mathematical framework for variational problems where the unknown function takes values in the space of probability measures on some metric space. We study weak and strong topologies and define a total variation seminorm for functions taking values in a Banach space. The seminorm penalizes jumps and is rotationally invariant under certain conditions. We prove existence of a minimizer for a class of variational problems based on this formulation of total variation and provide an example where uniqueness fails to hold. Employing the Kantorovich–Rubinstein transport norm from the theory of optimal transport, we propose a variational approach for the restoration of orientation distribution function-valued images, as commonly used in diffusion MRI. We demonstrate that the approach is numerically feasible on several data sets.

1 Introduction

In this work, we are concerned with variational problems in which the unknown function $u:\varOmega \rightarrow \mathcal {P}(\mathbb {S}^2)$ maps from an open and bounded set $\varOmega \subseteq \mathbb {R}^3$, the image domain, into the set of Borel probability measures $\mathcal {P}(\mathbb {S}^2)$ on the two-dimensional unit sphere $\mathbb {S}^2$ (or, more generally, on some metric space): Each value $u_x := u(x) \in \mathcal {P}(\mathbb {S}^2)$ is a Borel probability measure on $\mathbb {S}^2$ and can be viewed as a distribution of directions in $\mathbb {R}^3$.

Such measures $\mu \in \mathcal {P}(\mathbb {S}^2)$, in particular when represented using density functions, are known as orientation distribution functions (ODFs). We will keep to the term due to its popularity, although we will be mostly concerned with measures instead of functions on $\mathbb {S}^2$. Accordingly, an ODF-valued image is a function $u:\varOmega \rightarrow \mathcal {P}(\mathbb {S}^2)$. ODF-valued images appear in reconstruction schemes for diffusion-weighted magnetic resonance imaging (MRI), such as Q-ball imaging (QBI) [75] and constrained spherical deconvolution (CSD) [74].

Fig. 1

Top left: 2D fiber phantom as described in Sect. 4.1.2. Bottom left: peak directions on a $15 \times 15$ grid, derived from the phantom and used for the generation of synthetic HARDI data. Center: The diffusion tensor (DTI) reconstruction approximates diffusion directions in a parametric way using tensors, visualized as ellipsoids. Right: The QBI-CSA-ODF reconstruction represents fiber orientation using probability measures at each point, which allows to accurately recover fiber crossings in the center region

Applications in diffusion MRI. In diffusion-weighted (DW) magnetic resonance imaging (MRI), the diffusivity of water in biological tissues is measured noninvasively. In medical applications where tissues exhibit fibrous microstructures, such as muscle fibers or axons in cerebral white matter, the diffusivity contains valuable information about the fiber architecture. For DW measurements, six or more full 3D MRI volumes are acquired with varying magnetic field gradients that are able to sense diffusion.

Under the assumption of anisotropic Gaussian diffusion, positive definite matrices (tensors) can be used to describe the diffusion in each voxel. This model, known as diffusion tensor imaging (DTI) [7], requires few measurements while giving a good estimate of the main diffusion direction in the case of well-aligned fiber directions. However, crossing and branching of fibers at a scale smaller than the voxel size, also called intra-voxel orientational heterogeneity (IVOH), often occurs in human cerebral white matter due to the relatively large (millimeter-scale) voxel size of DW-MRI data. Therefore, DTI data are insufficient for accurate fiber tract mapping in regions with complex fiber crossings (Fig. 1).

More refined approaches are based on high angular resolution diffusion imaging (HARDI) [76] measurements that allow for more accurate restoration of IVOH by increasing the number of applied magnetic field gradients. Reconstruction schemes for HARDI data yield orientation distribution functions (ODFs) instead of tensors. In Q-ball imaging (QBI) [75], an ODF is interpreted to be the marginal probability of diffusion in a given direction [1]. In contrast, ODFs in constrained spherical deconvolution (CSD) approaches [74], also denoted fiber ODFs, estimate the density of fibers per direction for each voxel of the volume.

In all of these approaches, ODFs are modeled as antipodally symmetric functions on the sphere which could be modeled just as well on the projective space (which is defined to be a sphere where antipodal points are identified). However, most approaches parametrize ODFs using symmetric spherical harmonics basis functions which avoids any numerical overhead. Moreover, novel approaches [25, 31, 45, 66] allow for asymmetric ODFs to account for intra-voxel geometry. Therefore, we stick to modeling ODFs on a sphere even though our model could be easily adapted to models on the projective space.

Fig. 2

Horizontal axis: angle of main diffusion direction relative to the reference diffusion profile in the bottom left corner. Vertical axis: distances of the ODFs in the bottom row to the reference ODF in the bottom left corner ($L^1$-distances in the top row and $W^1$-distance in the second row). $L^1$-distances do not reflect the linear change in direction, whereas the $W^1$-distance exhibits an almost-linear profile. $L^p$-distances for other values of p (such as $p=2$) show a behavior similar to $L^1$-distances

Variational models for orientation distributions. As a common denominator, in the above applications, reconstructing orientation distributions rather than a single orientation at each point allows to recover directional information of structures— such as vessels or nerve fibers—that may overlap or have crossings: For a given set of directions $A \subset \mathbb {S}^2$, the integral $\int _A d u_x(z)$ describes the fraction of fibers crossing the point $x\in \varOmega$ that are oriented in any of the given directions $v\in A$.

However, modeling ODFs as probability measures in a nonparametric way is surprisingly difficult. In an earlier conference publication [78], we proposed a new formulation of the classical total variation seminorm (TV) [4, 14] for nonparametric Q-ball imaging that allows to formulate the variational restoration model

$$\begin{aligned} \inf _{u:\varOmega \rightarrow \mathcal {P}(\mathbb {S}^2)} \int _\varOmega \rho (x,u_x) \,\hbox {d}x + \lambda {\text {TV}}_{W_1}(u), \end{aligned}$$

(1)

with various pointwise data fidelity terms

$$\begin{aligned} \rho :\varOmega \times \mathcal {P}(\mathbb {S}^2) \rightarrow [0,\infty ). \end{aligned}$$

(2)

This involved in particular a nonparametric concept of total variation for ODF-valued functions that is mathematically robust and computationally feasible: The idea is to build upon the ${\text {TV}}$ formulations developed in the context of functional lifting [52]

$$\begin{aligned} \begin{aligned}&{\text {TV}}_{W_1}(u) := \sup \left\{ \int _\varOmega \langle -{\text {div}}p(x,\cdot ), u_x \rangle \,\hbox {d}x :~\right. \\&\quad \left. p \in C^1_c(\varOmega \times \mathbb {S}^2; \mathbb {R}^3), ~p(x,\cdot ) \in {\text {Lip}}_1(\mathbb {S}^2; \mathbb {R}^3) \right\} , \end{aligned} \end{aligned}$$

(3)

where $\langle g, \mu \rangle := \int _{\mathbb {S}^2} g(z)\,\hbox {d}\mu (z)$ whenever $\mu$ is a measure on $\mathbb {S}^2$ and g is a real- or vector-valued function on $\mathbb {S}^2$.

One distinguishing feature of this approach is that it is applicable to arbitrary Borel probability measures. In contrast, existing mathematical frameworks for QBI and CSD generally follow the standard literature on the physics of MRI [11, p. 330] in assuming ODFs to be given by a probability density function in $L^1(\mathbb {S}^2)$, often with an explicit parametrization.

As an example of one such approach, we point to the fiber continuity regularizer proposed in [67] which is defined for ODF-valued functions u where, for each $x \in \varOmega$, the measure $u_x$ can be represented by a probability density function $z \mapsto u_x(z)$ on $\mathbb {S}^2$:

$$\begin{aligned} R_{{\mathrm {FC}}}(u) := \int _\varOmega \int _{\mathbb {S}^2} (z \cdot \nabla _x u_x(z))^2 \,\hbox {d}z \,\hbox {d}x \end{aligned}$$

(4)

Clearly, a rigorous generalization of this functional to measure-valued functions for arbitrary Borel probability measures is not straightforward.

While practical, the probability density-based approach raises some modeling questions, which lead to deeper mathematical issues. In particular, comparing probability densities using the popular $L^p$-norm-based data fidelity terms—in particular the squared $L^2$-norm—does not incorporate the structure naturally carried by probability densities such as nonnegativity and unit total mass and ignores metric information about $\mathbb {S}^2$.

To illustrate the last point, assume that two probability measures are given in terms of density functions $f,g \in L^p(\mathbb {S}^2)$ satisfying ${\text {supp}}(f) \cap {\text {supp}}(g) = \emptyset$, i.e., having disjoint support on $\mathbb {S}^2$. Then, $\Vert f - g\Vert _{L^p} = \Vert f\Vert _{L^p} + \Vert g\Vert _{L^p}$, irrespective of the size and relative position of the supporting sets of f and g on $\mathbb {S}^2$.

One would prefer to use statistical metrics such as optimal transport metrics [77] that properly take into account distances on the underlying set $\mathbb {S}^2$ (Fig. 2). However, replacing the $L^p$-norm with such a metric in density-based variational imaging formulations will generally lead to ill-posed minimization problems, as the minimum might not be attained in $L^p(\mathbb {S}^2)$, but possibly in $\mathcal {P}(\mathbb {S}^2)$ instead.

Therefore, it is interesting to investigate whether one can derive a mathematical basis for variational image processing with ODF-valued functions without making assumptions about the parametrization of ODFs nor assuming ODFs to be given by density functions.

1.1 Contribution

Building on the preliminary results published in the conference publication [78], we derive a rigorous mathematical framework (Sect. 2 and Appendices) for a generalization of the total variation seminorm formulated in (3) to Banach space-valued¹ and, as a special case, ODF-valued functions (Sect. 2.1).

Building on this framework, we show existence of minimizers to (1) (Theorem 1) and discuss properties of ${\text {TV}}$ such as rotational invariance (Proposition 2) and the behavior on cartoonlike jump functions (Proposition 1).

We demonstrate that our framework can be numerically implemented (Sect. 3) as a primal-dual saddle-point problem involving only convex functions. Applications to synthetic and real-world data sets show significant reduction of noise as well as qualitatively convincing results when combined with existing ODF-based imaging approaches, including Q-ball and CSD (Sect. 4).

Details about the functional-analytic and measure-theoretic background of our theory are given in Appendix A. There, well-definedness of the ${\text {TV}}$-seminorm and of variational problems of form (1) is established by carefully considering measurability of the functions involved (Lemmas 1 and 2). Furthermore, a functional-analytic explanation for the dual structure that is inherent in (3) is given.

1.2 Related Models

The high angular resolution of HARDI results in a large amount of noise compared with DTI. Moreover, most QBI and CSD models reconstruct the ODFs in each voxel separately. Consequently, HARDI data are a particularly interesting target for post-processing in terms of denoising and regularization in the sense of contextual processing. Some techniques apply a total variation or diffusive regularization to the HARDI signal before ODF reconstruction [9, 28, 47, 53] and others regularize in a post-processing step [25, 29, 80].

1.2.1 Variational Regularization of DW-MRI Data

A Mumford–Shah model for edge-preserving restoration of Q-ball data was introduced in [80]. There, jumps were penalized using the Fisher–Rao metric which depends on a parametrization of ODFs as discrete probability distribution functions on sampling points of the sphere. Furthermore, the Fisher–Rao metric does not take the metric structure of $\mathbb {S}^2$ into consideration and is not amenable to biological interpretations [60]. Our formulation avoids any parametrization-induced bias.

Recent approaches directly incorporate a regularizer into the reconstruction scheme: Spatial TV-based regularization for Q-ball imaging has been proposed in [61]. However, the TV formulation proposed therein again makes use of the underlying parametrization of ODFs by spherical harmonics basis functions. Similarly, DTI-based models such as the second-order model for regularizing general manifold-valued data [8] make use of an explicit approximation using positive semidefinite matrices, which the proposed model avoids.

The application of spatial regularization to CSD reconstruction is known to significantly enhance the results [23]. However, total variation [12] and other regularizers [41] are based on a representation of ODFs by square-integrable probability density functions instead of the mathematically more general probability measures that we base our method on.

1.2.2 Regularization of DW-MRI by Linear Diffusion

In another approach, the orientational part of ODF-valued images is included in the image domain, so that images are identified with functions $U:\mathbb {R}^3 \times \mathbb {S}^2 \rightarrow \mathbb {R}$ that allow for contextual processing via PDE-based models on the space of positions and orientation or, more precisely, on the group SE(3) of 3D rigid motions. This technique comes from the theory of stochastic processes on the coupled space $\mathbb {R}^3 \times \mathbb {S}^2$. In this context, it has been applied to the problems of contour completion [59] and contour enhancement [28, 29]. Its practical relevance in clinical applications has been demonstrated [65].

This approach has been used to enhance the quality of CSD as a prior in a variational formulation [67] or in a post-processing step [64] that also includes additional angular regularization. Due to the linearity of the underlying linear PDE, convolution-based explicit solution formulas are available [28, 63]. Implemented efficiently [54, 55], they outperform our more computationally demanding model, which is not tied to the specific application of DW-MRI, but allows arbitrary metric spaces. Furthermore, nonlinear Perona and Malik extensions to this technique have been studied [20] that do not allow for explicit solutions.

As an important distinction, in these approaches, spatial location and orientation are coupled in the regularization. Since our model starts from the more general setting of measure-valued functions on an arbitrary metric space (instead of only $\mathbb {S}^2$), it does not currently realize an equivalent coupling. An extension to anisotropic total variation for measure-valued functions might close this gap in the future.

In contrast to these diffusion-based methods, our approach is able to preserve edges by design, even though the coupling of positions and orientations is able to make up for this shortcoming at least in part since edges in DW-MRI are, most of the time, oriented in parallel to the direction of diffusion. Furthermore, the diffusion-based methods are formulated for square-integrable density functions, excluding point masses. Our method avoids this limitation by operating on mathematically more general probability measures.

1.2.3 Other Related Theoretical Work

Variants of the Kantorovich–Rubinstein formulation of the Wasserstein distance that appears in our framework have been applied in [51] and, more recently, in [32, 33] to the problems of real-, RGB- and manifold-valued image denoising.

Total variation regularization for functions on the space of positions and orientations was recently introduced in [16] based on [18]. Similarly, the work and toolbox in [69] is concerned with the implementation of so-called orientation fields in 3D image processing.

A Dirichlet energy for measure-valued functions based on Wasserstein metrics was recently developed in the context of harmonic mappings in [49] which can be interpreted as a diffusive ($L^2$) version of our proposed ($L^1$) regularizer.

Our work is based on the conference publication [78], where a nonparametric Wasserstein-total variation regularizer for Q-ball data is proposed. We embed this formulation of TV into a significantly more general definition of TV for Banach space-valued functions.

In the literature, Banach space-valued functions of bounded variation mostly appear as a special case of metric space-valued functions of bounded variation (BV) as introduced in [3]. Apart from that, the case of one-dimensional domains attracts some attention [27] and the case of Banach space-valued BV functions defined on a metric space is studied in [57].

In contrast to these approaches, we give a definition of Banach space-valued BV functions that live on a finite-dimensional domain. In analogy with the real-valued case, we formulate the TV seminorm by duality, inspired by the functional-analytic framework from the theory of functional lifting [42] as used in the theory of Young measures [6].

Due to the functional-analytic approach, our model does not depend on the specific parametrization of the ODFs and can be combined with the QBI and CSD frameworks for ODF reconstruction from HARDI data, either in a post-processing step or during reconstruction. Combined with suitable data fidelity terms such as least-squares or Wasserstein distances, it allows for an efficient implementation using state-of-the-art primal-dual methods.

2 A Mathematical Framework for Measure-Valued Functions

Our work is motivated by the study of ODF-valued functions $u:\varOmega \rightarrow \mathcal {P}(\mathbb {S}^2)$ for $\varOmega \subset \mathbb {R}^3$ open and bounded. However, from an abstract viewpoint, the unit sphere $\mathbb {S}^2 \subset \mathbb {R}^3$ equipped with the metric induced by the Riemannian manifold structure [50]—i.e., the distance between two points is the arc length of the great circle segment through the two points— is simply a particular example of a compact metric space.

As it turns out, most of the analysis only relies on this property. Therefore, in the following we generalize the setting of ODF-valued functions to the study of functions taking values in the space of Borel probability measures on an arbitrary compact metric space (instead of $\mathbb {S}^2$).

More precisely, throughout this section, let

• 1. $\varOmega \subset \mathbb {R}^d$ be an open and bounded set, and let

• 2. (X, d) be a compact metric space, e.g., a compact Riemannian manifold equipped with the commonly used metric induced by the geodesic distance (such as $X = \mathbb {S}^2$).

Boundedness of $\varOmega$ and compactness of X are not required by all of the statements below. However, as we are ultimately interested in the case of $X = \mathbb {S}^2$ and rectangular image domains, we impose these restrictions. Apart from DW-MRI, one natural application of this generalized setting is two-dimensional ODFs where $d = 2$ and $X = \mathbb {S}^1$ which is similar to the setting introduced in [16] for the edge enhancement of color or grayscale images.

The goal of this section is a mathematically well-defined formulation of ${\text {TV}}$ as given in (3) that exhibits all the properties that the classical total variation seminorm is known for: anisotropy (Proposition 2), preservation of edges and compatibility with piecewise-constant signals (Proposition 1). Furthermore, for variational problems as in (1), we give criteria for the existence of minimizers (Theorem 1) and discuss (non-)uniqueness (Proposition 3).

A well-defined formulation of ${\text {TV}}$ as given in (3) requires a careful inspection of topological and functional-analytic concepts from optimal transport and general measure theory. For details, we refer the reader to the elaborate Appendix A. Here, we only introduce the definitions and notation needed for the statement of the central results.

2.1 Definition of ${\text {TV}}$

We first give a definition of ${\text {TV}}$ for Banach space-valued functions (i.e., functions that take values in a Banach space), which a definition of ${\text {TV}}$ for measure-valued functions will turn out to be a special case of.

For weakly measurable (see Appendix A.1) functions $u:\varOmega \rightarrow V$ with values in a Banach space V (later, we will replace V by a space of measures), we define, extending the formulation of ${\text {TV}}_{W_1}$ introduced in [78],

$$\begin{aligned} \begin{aligned}&{\text {TV}}_{V}(u) := \sup \left\{ \int _\varOmega \langle -{\text {div}}p(x), u(x) \rangle \,\hbox {d}x :~\right. \\&\quad \left. p \in C_c^1(\varOmega , (V^*)^d), ~\forall x \in \varOmega :\Vert p(x)\Vert _{(V^*)^d} \le 1 \right\} . \end{aligned} \end{aligned}$$

(5)

By $V^*$, we denote the (topological) dual space of V, i.e., $V^*$ is the set of bounded linear operators from V to $\mathbb {R}$. The criterion $p \in C_c^1(\varOmega , (V^*)^d)$ means that p is a compactly supported function on $\varOmega \subset \mathbb {R}^d$ with values in the Banach space $(V^*)^d$ and the directional derivatives $\partial _i p:\varOmega \rightarrow (V^*)^d$, $1 \le i \le d$ (in Euclidean coordinates) lie in $C_c(\varOmega , (V^*)^d)$. We write

$$\begin{aligned} {\text {div}}p(x) := \sum _{i=1}^d \partial _i p_i(x). \end{aligned}$$

(6)

Lemma 1 ensures that the integrals in (5) are well defined and Appendix D discusses the choice of the product norm $\Vert \cdot \Vert _{(V^*)^d}$.

Measure-valued functions. Now we want to apply this definition to measure-valued functions $u:\varOmega \rightarrow \mathcal {P}(X)$, where $\mathcal {P}(X)$ is the set of Borel probability measures supported on X.

The space $\mathcal {P}(X)$ equipped with the Wasserstein metric $W_1$ from the theory of optimal transport is isometrically embedded into the Banach space $V = K\!R(X)$ (the Kantorovich–Rubinstein space) whose dual space is the space $V^* = {\text {Lip}}_0(X)$ of Lipschitz-continuous functions on X that vanish at an (arbitrary but fixed) point $x_0 \in X$. This setting is introduced in detail in Appendix A.2. Then, for $u:\varOmega \rightarrow \mathcal {P}(X)$, definition (5) comes back to (3) or, more precisely,

$$\begin{aligned} \begin{aligned}&{\text {TV}}_{K\!R}(u) := \sup \left\{ \int _\varOmega \langle -{\text {div}}p(x), u(x) \rangle \,\hbox {d}x :~\right. \\&\quad \left. p \in C_c^1(\varOmega , [{\text {Lip}}_0(X)]^d), ~\Vert p(x)\Vert _{[{\text {Lip}}_0(X)]^d} \le 1 \right\} , \end{aligned} \end{aligned}$$

(7)

where the definition of the product norm $\Vert \cdot \Vert _{[{\text {Lip}}_0(X)]^d}$ is discussed in Appendix D.3.

2.2 Properties of ${\text {TV}}$

In this section, we show that the properties that the classical total variation seminorm is known for continue to hold for definition (5) in the case of Banach space-valued functions.

Cartoon functions. A reasonable demand is that the new formulation should behave similarly to the classical total variation on cartoonlike jump functions $u:\varOmega \rightarrow V$,

$$\begin{aligned} u(x) := {\left\{ \begin{array}{ll} u^+, &{} x\in U, \\ u^-, &{} x \in \varOmega \setminus U, \\ \end{array}\right. } \end{aligned}$$

(8)

for some fixed measurable set $U \subset \varOmega$ with smooth boundary $\partial U$, and $u^+, u^- \in V$. The classical total variation assigns to such functions a penalty of

$$\begin{aligned} \mathcal {H}^{d-1}(\partial U)\cdot \Vert u^+ - u^-\Vert _V, \end{aligned}$$

(9)

where the Hausdorff measure $\mathcal {H}^{d-1}(\partial U)$ describes the length or area of the jump set. The following proposition, which generalizes [78, Proposition 1], provides conditions on the norm $\Vert \cdot \Vert _{(V^*)^d}$ which guarantee this behavior.

Proposition 1

Assume that U is compactly contained in $\varOmega$ with $C^1$-boundary $\partial U$. Let $u^+, u^- \in V$ and let $u:\varOmega \rightarrow V$ be defined as in (8). If the norm $\Vert \cdot \Vert _{(V^*)^d}$ in (5) satisfies

$$\begin{aligned}&\left| \textstyle {\sum _{i=1}^d x_i} \langle p_i, v \rangle \right| \le \Vert x\Vert _2 \Vert p\Vert _{(V^*)^d} \Vert v\Vert _V, \end{aligned}$$

(10)

$$\begin{aligned}&\Vert (x_1 q, \dots , x_d q)\Vert _{(V^*)^d} \le \Vert x\Vert _2 \Vert q\Vert _{V^*} \end{aligned}$$

(11)

whenever $q \in V^*$, $p \in (V^*)^d$, $v \in V$, and $x \in \mathbb {R}^d$, then

$$\begin{aligned} {\text {TV}}_{V}(u) = \mathcal {H}^{d-1}(\partial U) \cdot \Vert u^+ - u^-\Vert _V. \end{aligned}$$

(12)

Proof

See Appendix B. $\square$

Rotational invariance. Property (12) is inherently rotationally invariant: We have ${\text {TV}}_V(u) = {\text {TV}}_V({\tilde{u}})$ whenever ${\tilde{u}}(x) := u(Rx)$ for some $R \in SO(d)$ and u as in (8), with the domain $\varOmega$ rotated accordingly. The reason is that the jump size is the same everywhere along the edge $\partial U$. More generally, we have the following proposition:

Proposition 2

Assume that $\Vert \cdot \Vert _{(V^*)^d}$ satisfies the rotational invariance property

$$\begin{aligned} \Vert p\Vert _{(V^*)^d} = \Vert R p\Vert _{(V^*)^d} \quad \forall p \in (V^*)^d, R \in SO(d), \end{aligned}$$

(13)

where $Rp \in (V^*)^d$ is defined via

$$\begin{aligned} (Rp)_i = \sum _{j=1}^d R_{ij} p_j \in V^*. \end{aligned}$$

(14)

Then, ${\text {TV}}_V$ is rotationally invariant, i.e., ${\text {TV}}_V(u) = {\text {TV}}_V({\tilde{u}})$ whenever $u \in L_w^\infty (\varOmega , V)$ and ${\tilde{u}}(x) := u(Rx)$ for some $R \in SO(d)$.

Proof

(Proposition 2) See Appendix C. $\square$

2.3 ${\text {TV}}_{{\textit{KR}}}$ as a Regularizer in Variational Problems

This section shows that, in the case of measure-valued functions $u:\varOmega \rightarrow \mathcal {P}(X)$, the functional ${\text {TV}}_{K\!R}$ exhibits a regularizing property, i.e., it establishes existence of minimizers.

For $\lambda \in [0,\infty )$ and $\rho :\varOmega \times \mathcal {P}(X) \rightarrow [0,\infty )$ fixed, we consider the functional

$$\begin{aligned} T_{\rho ,\lambda }(u) := \int _\varOmega \rho (x, u(x)) \,\hbox {d}x + \lambda {\text {TV}}_{K\!R}(u). \end{aligned}$$

(15)

for $u:\varOmega \rightarrow \mathcal {P}(X)$. Lemma 2 in Appendix F makes sure that the integrals in (15) are well defined.

Then, minimizers of energy (15) exist in the following sense:

Theorem 1

Let $\varOmega \subset \mathbb {R}^d$ be open and bounded, let (X, d) be a compact metric space and assume that $\rho$ satisfies the assumptions from Lemma 2. Then, the variational problem

$$\begin{aligned} \inf _{u \in L_w^\infty (\varOmega , \mathcal {P}(X))} T_{\rho ,\lambda }(u) \end{aligned}$$

(16)

with the energy

$$\begin{aligned} T_{\rho ,\lambda }(u) := \int _\varOmega \rho (x, u(x)) \,\hbox {d}x + \lambda {\text {TV}}_{K\!R}(u). \end{aligned}$$

(17)

as in (15) admits a (not necessarily unique) solution.

Proof

See Appendix F. $\square$

Non-uniqueness of minimizers of (15) is clear for pathological choices such as $\rho \equiv 0$. However, there are non-trivial cases where uniqueness fails to hold:

Proposition 3

Let $X = \{0,1\}$ be the metric space consisting of two discrete points of distance 1 and define $\rho (x,\mu ) := W_1(f(x),\mu )$ where

$$\begin{aligned} f(x) := {\left\{ \begin{array}{ll} \delta _1, &{} x \in \varOmega \setminus U, \\ \delta _0, &{} x \in U, \end{array}\right. } \end{aligned}$$

(18)

for a non-empty subset $U \subset \varOmega$ with $C^1$ boundary. Assume coupled norm (D.22) on $[{\text {Lip}}_0(X)]^d$ in definition (7) of ${\text {TV}}_{K\!R}$.

Then, there is a one-to-one correspondence between feasible solutions u of problem (16) and feasible solutions $\tilde{u}$ of the classical $L^1$-${\text {TV}}$ functional

$$\begin{aligned} \inf _{{\tilde{u}} \in L^1(\varOmega ,[0,1])} \tilde{T}_{\lambda }(u),\; \tilde{T}_{\lambda }(u):= \Vert \mathbf {1}_U - {\tilde{u}}\Vert _{L^1} + \lambda {\text {TV}}({\tilde{u}}) \end{aligned}$$

(19)

via the mapping

$$\begin{aligned} u(x) = {\tilde{u}}(x) \delta _0 + (1 - {\tilde{u}}(x)) \delta _1. \end{aligned}$$

(20)

Under this mapping $\tilde{T}_{\lambda }(\tilde{u}) = T_{\rho ,\lambda }(u)$ holds, so that problems (16) and (19) are equivalent.

Furthermore, there exists $\lambda > 0$ for which the minimizer of $T_{\rho ,\lambda }$ is not unique.

Proof

See Appendix E. $\square$

2.4 Application to ODF-Valued Images

For ODF-valued images, we consider the special case $X = \mathbb {S}^2$ equipped with the metric induced by the standard Riemannian manifold structure on $\mathbb {S}^2$, and $\varOmega \subset \mathbb {R}^3$.

Let $f \in L_w^\infty (\varOmega , \mathcal {P}(\mathbb {S}^2))$ be an ODF-valued image and denote by $W_1$ the Wasserstein metric from the theory of optimal transport (see equation (A.8) in Appendix A.2). Then, the function

$$\begin{aligned} \rho (x,\mu ) := W_1(f(x),\mu ), ~x \in \varOmega , ~\mu \in \mathcal {P}(\mathbb {S}^2), \end{aligned}$$

(21)

satisfies the assumptions in Lemma 2 and hence Theorem 1 (see Appendix F).

For denoising of an ODF-valued function f in a post-processing step after ODF reconstruction, similar to [78] we propose to solve the variational minimization problem

$$\begin{aligned} \inf _{u:\varOmega \rightarrow \mathcal {P}(\mathbb {S}^2)} \int _\varOmega W_1(f(x),u(x)) \,\hbox {d}x + \lambda {\text {TV}}_{K\!R}(u) \end{aligned}$$

(22)

using the definition of ${\text {TV}}_{K\!R}(u)$ in (7).

The following statement shows that this in fact penalizes jumps in u by the Wasserstein distance as desired, correctly taking the metric structure of $\mathbb {S}^2$ into account.

Corollary 1

Assume that U is compactly contained in $\varOmega$ with $C^1$-boundary $\partial U$. Let the function $u:\varOmega \rightarrow \mathcal {P}(\mathbb {S}^2)$ be defined as in (8) for some $u^+, u^- \in \mathcal {P}(\mathbb {S}^2)$. Choosing norm (D.22) (or (D.1) with $s=2$) on the product space ${\text {Lip}}(\mathbb {S}^2)^d$, we have

$$\begin{aligned} {\text {TV}}_{K\!R}(u) = \mathcal {H}^{d-1}(\partial U) \cdot W_1(u^+, u^-). \end{aligned}$$

(23)

The corollary was proven directly in [78, Proposition 1]. In the functional-analytic framework established above, it now follows as a simple corollary to Proposition 1.

Moreover, beyond the theoretical results given in [78], we now have a rigorous framework that ensures measurability of the integrands in (22), which is crucial for well-definedness. Furthermore, Theorem 1 on the existence of minimizers provides an important step in proving well-posedness of variational model (22).

3 Numerical Scheme

As in [78], we closely follow the discretization scheme from [52] in order to formulate the problem in a saddle-point form that is amenable to standard primal-dual algorithms [15, 37,38,39, 62].

3.1 Discretization

We assume a d-dimensional image domain $\varOmega$, $d = 2,3$, that is discretized using n points $x^1, \dots , x^n \in \varOmega$. Differentiation in $\varOmega$ is done on a staggered grid with Neumann boundary conditions such that the dual operator to the differential operator D is the negative divergence with vanishing boundary values.

The framework presented in Sect. 2 applies to arbitrary compact metric spaces X. However, for an efficient implementation of the Lipschitz constraint in (7), we will assume an s-dimensional manifold $X = \mathcal {M}$. This includes the case of ODF-valued images ($X = \mathcal {M}= \mathbb {S}^2$, $s=2$). For future generalizations to other manifolds, we give the discretization in terms of a general manifold $X = \mathcal {M}$ even though this means neglecting the reasonable parametrization of $\mathbb {S}^2$ using spherical harmonics in the case of DW-MRI. Moreover, note that the following discretization does not apply to arbitrary metric spaces X.

Now, let $\mathcal {M}$ be decomposed (Fig. 3) into l disjoint measurable (not necessarily open or closed) sets

$$\begin{aligned} m^1, \dots , m^l \subset \mathcal {M}\end{aligned}$$

(24)

with $\bigcup _k m^k = \mathcal {M}$ and volumes $b^1, \dots , b^l \in \mathbb {R}$ with respect to the Lebesgue measure on $\mathcal {M}$. A measure-valued function $u:\varOmega \rightarrow \mathcal {P}(\mathcal {M})$ is discretized as its average $u \in \mathbb {R}^{n,l}$ on the volume $m^k$, i.e.,

$$\begin{aligned} u_k^i := u_{x^i}(m^k)/b_{k}. \end{aligned}$$

(25)

Functions $p \in C_c^1(\varOmega , {\text {Lip}}(X,\mathbb {R}^d))$ as they appear, for example, in our proposed formulation of ${\text {TV}}$ in (5) are identified with functions $p:\varOmega \times \mathcal {M}\rightarrow \mathbb {R}^d$ and discretized as $p \in \mathbb {R}^{n,l,d}$ via $p_{kt}^i := p_t(x^i, z^k)$ for a fixed choice of discretization points

$$\begin{aligned} \forall k=1,\dots ,l: \quad z^k \in m^k \subset \mathcal {M}. \end{aligned}$$

(26)

The dual pairing of p with u is discretized as

$$\begin{aligned} \langle u, p \rangle _b := \sum _{i,k} b_{k} u_k^i p_k^i. \end{aligned}$$

(27)

3.1.1 Implementation of the Lipschitz Constraint

The Lipschitz constraint in definition (A.8) of $W_1$ and in definition (7) of ${\text {TV}}_{K\!R}$ is implemented as a norm constraint on the gradient. Namely, for a function $p:\mathcal {M}\rightarrow \mathbb {R}$, which we discretize as $p \in \mathbb {R}^{l}$, $p_k := p(z^k)$, we discretize gradients on a staggered grid of m points

$$\begin{aligned} y^1, \dots , y^m \in \mathcal {M}, \end{aligned}$$

(28)

such that each of the $y^j$ has r neighboring points among the $z^k$ (Fig. 3):

$$\begin{aligned} \forall j=1,\dots ,m: \quad \mathcal {N}_j \subset \{1, \dots , l\},\quad \#\mathcal {N}_j = r. \end{aligned}$$

(29)

The gradient $g \in \mathbb {R}^{m,s}$, $g^j := Dp(y^j)$ is then defined as the vector in the tangent space at $y^j$ that, together with a suitable choice of the unknown value $c := p(y^j)$, best explains the known values of p at the $z^k$ by a first-order Taylor expansion

$$\begin{aligned} p(z^k) \approx p(y^j) + \langle g^j, v^{jk} \rangle , \quad k \in \mathcal {N}_j, \end{aligned}$$

(30)

where $v^{jk} := \exp ^{-1}_{y^j}(z^k) \in T_{y^j}\mathcal {M}$ is the Riemannian inverse exponential mapping of the neighboring point $z^k$ to the tangent space at $y^j$. More precisely,

$$\begin{aligned} g^j := \mathop {\hbox {arg min}}\limits _{g \in T_{y^j}\mathcal {M}} \min \limits _{c\in \mathbb {R}} \sum _{k \in \mathcal {N}_j} \left( c + \langle g, v^{jk} \rangle - p(z^k)\right) ^2. \end{aligned}$$

(31)

Writing the $v^{jk}$ into a matrix $M^j \in \mathbb {R}^{r,s}$ and encoding the neighboring relations as a sparse indexing matrix $P^j \in \mathbb {R}^{r,l}$, we obtain the explicit solution for the value c and gradient $g^j$ at the point $y^j$ from the first-order optimality conditions of (31):

$$\begin{aligned}&c = p(y^j) = \frac{1}{r}(e^T P^j p - e^T M^j g^j), \end{aligned}$$

(32)

$$\begin{aligned}&(M^j)^T E M^j g^j = (M^j)^T E P^j p, \end{aligned}$$

(33)

where $e := (1,\dots ,1) \in \mathbb {R}^r$ and $E := (I - \frac{1}{r}ee^T)$. The value c does not appear in the linear equations for $g^j$ and is not needed in our model; therefore, we can ignore the first line. The second line, with $A^j := (M^j)^T E M^j \in \mathbb {R}^{s,s}$ and $B^j := (M^j)^T E \in \mathbb {R}^{s,r}$, can be concisely written as

$$\begin{aligned} A^j g^j = B^j P^j p, \text { for each } j \in \{1, \dots , m \}. \end{aligned}$$

(34)

Following our discussion about the choice of norm in Appendix D, the (Lipschitz) norm constraint $\Vert g_j\Vert \le 1$ can be implemented using the Frobenius norm or the spectral norm, both being rotationally invariant and both acting as desired on cartoonlike jump functions (cf. Proposition 1).

Fig. 3

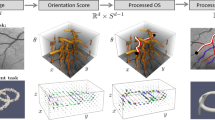
Discretization of the unit sphere $\mathbb {S}^2$. Measures are discretized via their average on the subsets $m^k$. Functions are discretized on the points $z^k$ (dot markers), and their gradients are discretized on the $y^j$ (square markers). Gradients are computed from points in a neighborhood $\mathcal {N}_j$ of $y^j$. The neighborhood relation is depicted with dashed lines. The discretization points were obtained by recursively subdividing the 20 triangular faces of an icosahedron and projecting the vertices to the surface of the sphere after each subdivision

3.1.2 Discretized $W_1$-${\text {TV}}$ Model

Based on the above discretization, we can formulate saddle-point forms for (22) that allow to apply a primal-dual first-order method such as [15]. In the following, the measure-valued input or reference image is given by $f \in \mathbb {R}^{l,n}$ and the dimensions of the primal and dual variables are

$$\begin{aligned}&u \in \mathbb {R}^{l,n},&p \in \mathbb {R}^{l,d,n},&g \in \mathbb {R}^{n,m,s,d}, \end{aligned}$$

(35)

$$\begin{aligned}&p_0 \in \mathbb {R}^{l,n},&g_0 \in \mathbb {R}^{n,m,s}, \end{aligned}$$

(36)

where $g^{ij} \approx D_z p(x^i, y^j)$ and $g_0^{j} \approx D p_0(y^j)$.

Using a $W_1$ data term, the saddle-point form of the overall problem reads

$$\begin{aligned} \min _{u} \max _{p,g} \quad&W_1(u,f) + \langle Du, p \rangle _b \end{aligned}$$

(37)

$$\begin{aligned} \text {s.t.}\quad&u^i \ge 0, ~\langle u^i, b \rangle = 1, ~\forall i, \end{aligned}$$

(38)

$$\begin{aligned}&A^j g^{ij}_t = B^j P^j p^i_t ~\forall i,j,t, \end{aligned}$$

(39)

$$\begin{aligned}&\Vert g^{ij}\Vert \le \lambda ~\forall i,j \end{aligned}$$

(40)

or, applying Kantorovich–Rubinstein duality (A.8) to the data term,

$$\begin{aligned} \min _{u} \max _{p, g, p_0, g_0} \quad&\langle u-f, p_0 \rangle _b + \langle Du, p \rangle _b \end{aligned}$$

(41)

$$\begin{aligned} \text {s.t.}\quad&u^i \ge 0, ~\langle u^i, b \rangle = 1 ~\forall i, \end{aligned}$$

(42)

$$\begin{aligned}&A^j g^{ij}_t = B^j P^j p^i_t, ~\Vert g^{ij}\Vert \le \lambda ~\forall i,j,t, \end{aligned}$$

(43)

$$\begin{aligned}&A^j g^{ij}_0 = B^j P^j p^i_0, ~\Vert g^{ij}_0\Vert \le 1 ~\forall i,j. \end{aligned}$$

(44)

3.1.3 Discretized $L^2$-${\text {TV}}$ Model

For comparison, we also implemented the Rudin–Osher–Fatemi (ROF) model

$$\begin{aligned} \inf _{u:\varOmega \rightarrow \mathcal {P}(\mathbb {S}^2)} \int _\varOmega \int _{\mathbb {S}^2} (f_x(z) - u_x(z))^2 \,\hbox {d}z \,\hbox {d}x + \lambda {\text {TV}}(u) \end{aligned}$$

(45)

using ${\text {TV}}={\text {TV}}_{K\!R}$. The quadratic data term can be implemented using the saddle-point form

$$\begin{aligned} \min _{u} \max _{p,g} \quad&\langle u-f, u-f \rangle _b + \langle Du, p \rangle _b \end{aligned}$$

(46)

$$\begin{aligned} \text {s.t.}\quad&u^i \ge 0, ~\langle u^i, b \rangle = 1, \end{aligned}$$

(47)

$$\begin{aligned}&A^j g^{ij}_t = B^j P^j p^i_t, ~\Vert g^{ij}\Vert \le \lambda ~\forall i,j,t. \end{aligned}$$

(48)

From a functional-analytic viewpoint, this approach requires to assume that $u_x$ can be represented by an $L^2$ density, suffers from well-posedness issues and ignores the metric structure on $\mathbb {S}^2$ as mentioned in Introduction. Nevertheless, we include it for comparison, as the $L^2$ norm is a common choice and the discretized model is a straightforward modification of the $W_1$-${\text {TV}}$ model.

3.2 Implementation Using a Primal-Dual Algorithm

Based on saddle-point forms (41) and (46), we applied the primal-dual first-order method proposed in [15] with the adaptive step sizes from [39]. We also evaluated the diagonal preconditioning proposed in [62]. However, we found that while it led to rapid convergence in some cases, the method frequently became unacceptably slow before reaching the desired accuracy. The adaptive step size strategy exhibited a more robust overall convergence.

The equality constraints in (41) and (46) were included into the objective function by introducing suitable Lagrange multipliers. As far as the norm constraint on $g_0$ is concerned, the spectral and Frobenius norms agree, since the gradient of $p_0$ is one-dimensional. For the norm constraint on the Jacobian g of p, we found the spectral and Frobenius norm to give visually indistinguishable results.

Furthermore, since $\mathcal {M}= \mathbb {S}^2$ and therefore $s=2$ in the ODF-valued case, explicit formulas for the orthogonal projections on the spectral norm balls that appear in the proximal steps are available [36]. The experiments below were calculated using spectral norm constraints, as in our experience this choice led to slightly faster convergence.

4 Results

We implemented our model in Python 3.5 using the libraries NumPy 1.13, PyCUDA 2017.1 and CUDA 8.0. The examples were computed on an Intel Xeon X5670 2.93GHz with 24 GB of main memory and an NVIDIA GeForce GTX 480 graphics card with 1,5 GB of dedicated video memory. For each step in the primal-dual algorithm, a set of kernels was launched on the GPU, while the primal-dual gap was computed and termination criteria were tested every $5\,000$ iterations on the CPU.

Fig. 4

Top: 1D image of synthetic unimodal ODFs where the angle of the main diffusion direction varies linearly from left to right. This is used as input image for the center and bottom row. Center: solution of $L^2$-${\text {TV}}$ model with $\lambda =5$. Bottom: solution of $W_1$-${\text {TV}}$ model with $\lambda =10$. In both cases, the regularization parameter $\lambda$ was chosen sufficiently large to enforce a constant result. The quadratic data term mixes all diffusion directions into one blurred ODF, whereas the Wasserstein data term produces a tight ODF that is concentrated close to the median diffusion direction

For the following experiments, we applied our models presented in Sects. 3.1.2 ($W_1$-${\text {TV}}$) and 3.1.3 ($L_2$-${\text {TV}}$) to ODF-valued images reconstructed from HARDI data using the reconstruction methods that are provided by the Dipy project [34]:

• For voxel-wise QBI reconstruction within constant solid angle (CSA-ODF) [1], we used CsaOdfModel from dipy.reconst.shm with spherical harmonics functions up to order 6.

• For voxel-wise CSD reconstruction as proposed in [73], we used ConstrainedSphericalDeconvModel as provided with dipy.reconst.csdeconv.

The response function that is needed for CSD reconstruction was determined using the recursive calibration method [72] as implemented in recursive_response, which is also part of dipy.reconst.csdeconv. We generated the ODF plots using VTK-based sphere_funcs from dipy.viz.fvtk.

It is equally possibly to use other methods for Q-ball reconstruction for the preprocessing step, or even integrate the proposed ${\text {TV}}$-regularizer directly into the reconstruction process. Furthermore, our method is compatible with different numerical representations of ODFs, including sphere discretization [35], spherical harmonics [1], spherical wavelets [46], ridgelets [56] or similar basis functions [2, 43], as it does not make any assumptions on regularity or symmetry of the ODFs. We leave a comprehensive benchmark to future work, as the main goal of this work is to investigate the mathematical foundations.

4.1 Synthetic Data

4.1.1 $L^2$-${\text {TV}}$ vs. $W_1$-${\text {TV}}$

We demonstrate the different behaviors of the $L^2$-${\text {TV}}$ model compared to the $W_1$-${\text {TV}}$ model with the help of a one-dimensional synthetic image (Fig. 4) generated using the multi-tensor simulation method multi_tensor from dipy.sims.voxel which is based on [71] and [26, p. 42]; see also [78].

Fig. 5

Numerical solutions of the proposed variational models (see Sects. 3.1.2 and 3.1.3) applied to the phantom (Fig. 1) for increasing values of the regularization parameter $\lambda$. Left column: solutions of $L^2$-${\text {TV}}$ model for $\lambda = 0.11,\,0.22,\,0.33$. Right column: solutions of $W_1$-${\text {TV}}$ model for $\lambda = 0.9,\,1.8,\,2.7$. As is known from classical ROF models, the $L^2$ data term produces a gradual transition/loss of contrast toward the constant image, while the $W_1$ data term stabilizes contrast along the edges

Fig. 6

Slice of size $15 \times 15$ from the data provided for the ISBI 2013 HARDI reconstruction challenge [24]. Left: peak directions of the ground truth. Right: Q-ball image reconstructed from the noisy (${\text {SNR}}=10$) synthetic HARDI data, without spatial regularization. The low ${\text {SNR}}$ makes it hard to visually recognize the fiber directions

Fig. 7

Restored Q-ball images reconstructed from the noisy input data in Fig. 6. Left: result of the $L^2$-${\text {TV}}$ model ($\lambda =0.3$). Right: result of the $W_1$-${\text {TV}}$ model ($\lambda =1.1$). The noise is reduced substantially so that fiber traces are clearly visible in both cases. The $W_1$-${\text {TV}}$ model generates less diffuse distributions

By choosing very high regularization parameters $\lambda$, we enforce the models to produce constant results. The $L^2$-based data term prefers a blurred mixture of diffusion directions, essentially averaging the probability measures. The $W_1$ data term tends to concentrate the mass close to the median of the diffusion directions on the unit sphere, properly taking into account the metric structure of $\mathbb {S}^2$.

4.1.2 Scale-Space Behavior

To demonstrate the scale-space behavior of our variational models, we implemented a 2D phantom of two crossing fiber bundles as depicted in Fig. 1, inspired by [61]. From this phantom, we computed the peak directions of fiber orientations on a $15 \times 15$ grid. This was used to generate synthetic HARDI data simulating a DW-MRI measurement with 162 gradients and a b-value of $3\,000$, again using the multi-tensor simulation framework from dipy.sims.voxel.

We then applied our models to the CSA-ODF reconstruction of this data set for increasing values of the regularization parameter $\lambda$ in order to demonstrate the scale-space behaviors of the different data terms (Fig. 5).

As both models use the proposed ${\text {TV}}$ regularizer, edges are preserved. However, just as classical ROF models tend to reduce jump sizes across edges, and lose contrast, the $L^2$-${\text {TV}}$ model results in the background and foreground regions becoming gradually more similar as regularization strength increases. The $W_1$-${\text {TV}}$ model preserves the unimodal ODFs in the background regions and demonstrates a behavior more akin to robust $L^1$-${\text {TV}}$ models [30], with structures disappearing abruptly rather than gradually depending on their scale.

4.1.3 Denoising

We applied our model to the CSA-ODF reconstruction of a slice (NumPy coordinates [12:27,22,21:36]) from the synthetic HARDI data set with added noise at ${\text {SNR}}=10$, provided in the ISBI 2013 HARDI reconstruction challenge. We evaluated the angular precision of the estimated fiber compartments using the script (compute_local_metrics.py) provided on the challenge homepage [24].

The script computes the mean $\mu$ and standard deviation $\sigma$ of the angular error between the estimated fiber directions inside the voxels and the ground truth as also provided on the challenge page (Fig. 6).

The noisy input image exhibits a mean angular error of $\mu = 34.52$ degrees ($\sigma = 19.00$). The reconstructions using $W_1$-${\text {TV}}$ ($\mu = 17.73$, $\sigma = 17.25$) and $L^2$-${\text {TV}}$ ($\mu = 17.82$, $\sigma = 18.79$) clearly improve the angular error and give visually convincing results: The noise is effectively reduced and a clear trace of fibers becomes visible (Fig. 7). In these experiments, the regularizing parameter $\lambda$ was chosen optimally in order to minimize the mean angular error to the ground truth.

4.2 Human Brain HARDI Data

One slice (NumPy coordinates [20:50, 55:85, 38]) of HARDI data from the human brain data set [68] was used to demonstrate the applicability of our method to real-world problems and to images reconstructed using CSD (Fig. 8). Run times of the $W_1$-${\text {TV}}$ and $L^2$-${\text {TV}}$ model are approximately 35 minutes ($10^5$ iterations) and 20 minutes ($6\cdot 10^4$ iterations).

As a stopping criterion, we require the primal-dual gap to fall below $10^{-5}$, which corresponds to a deviation from the global minimum of less than $0.001 \%$ and is a rather challenging precision for the first-order methods used. The regularization parameter $\lambda$ was manually chosen based on visual inspection.

Fig. 8

ODF image of the corpus callosum, reconstructed with CSD from HARDI data of the human brain [68]. Top: noisy input. Middle: restored using $L^2$-${\text {TV}}$ model ($\lambda =0.6$). Bottom: restored using $W_1$-${\text {TV}}$ model ($\lambda =1.1$). The results do not show much difference: Both models enhance contrast between regions of isotropic and anisotropic diffusion, while the anisotropy of ODFs is conserved

Overall, contrast between regions of isotropic and anisotropic diffusion is enhanced. In regions where a clear diffusion direction is already visible before spatial regularization, $W_1$-${\text {TV}}$ tends to conserve this information better than $L^2$-${\text {TV}}$.

5 Conclusion and Outlook

Our mathematical framework for ODF- and, more general, measure-valued images allows to perform total variation-based regularization of measure-valued data without assuming a specific parametrization of ODFs, while correctly taking the metric on $\mathbb {S}^2$ into account. The proposed model penalizes jumps in cartoonlike images proportional to the jump size measured on the underlying normed space, in our case the Kantorovich–Rubinstein space, which is built on the Wasserstein-1-metric. Moreover, the full variational problem was shown to have a solution and can be implemented using off-the-shelf numerical methods.

With the first-order primal-dual algorithm chosen in this paper, solving the underlying optimization problem for DW-MRI regularization is computationally demanding due to the high dimensionality of the problem. However, numerical performance was not a priority in this work and can be improved. For example, optimal transport norms are known to be efficiently computable using Sinkhorn’s algorithm [21].

A particularly interesting direction for future research concerns extending the approach to simultaneous reconstruction and regularization, with an additional (non-) linear operator in the data fidelity term [1]. For example, one could consider an integrand of the form $\rho (x,u(x)) := d(S(x),Au(x))$ for some measurements S on a metric space (H, d) and a forward operator A mapping an ODF $u(x) \in \mathcal {P}(\mathbb {S}^2)$ to H.

Furthermore, modifications of our total variation seminorm that take into account the coupling of positions and orientations according to the physical interpretation of ODFs in DW-MRI could close the gap to state-of-the-art approaches such as [28, 63].

The model does not require symmetry of the ODFs and therefore could be adapted to novel asymmetric ODF approaches [25, 31, 45, 66]. Finally, it is easily extendable to images with values in the probability space over a different manifold, or even a metric space, as they appear, for example, in statistical models of computer vision [70] and in recent lifting approaches [5, 48, 58] for combinatorial and non-convex optimization problems.

Appendices

Appendix A: Background from Functional Analysis and Measure Theory

In this appendix, we present the theoretical background for a rigorous understanding of the notation and definitions underlying the notion of ${\text {TV}}$ as proposed in (5) and (7). Section A.1 is concerned with Banach space-valued functions, and Sect. A.2 focuses on the special case of measure-valued functions.

1.1 Banach Space-Valued Functions of Bounded Variation

This subsection introduces a function space on which the formulation of ${\text {TV}}$ as given in (5) is well defined.

Let $(V, \Vert \cdot \Vert _V)$ be a real Banach space with (topological) dual space $V^*$, i.e., $V^*$ is the set of bounded linear operators from V to $\mathbb {R}$. The dual pairing is denoted by $\langle p, v \rangle := p(v)$ whenever $p \in V^*$ and $v \in V$.

We say that $u:\varOmega \rightarrow V$ is weakly measurable if $x \mapsto \langle p, u(x) \rangle$ is measurable for each $p \in V^*$ and say that $u \in L_w^\infty (\varOmega , V)$ if u is weakly measurable and essentially bounded in V, i.e.,

$$\begin{aligned} \Vert u\Vert _{\infty ,V} := \hbox {ess}\,\hbox {sup}_{x \in \varOmega } \Vert u(x)\Vert _V < \infty . \end{aligned}$$

(A.1)

Note that the essential supremum is well defined even for non-measurable functions as long as the measure is complete. In our case, we assume the Lebesgue measure on $\varOmega$ which is complete.

The following Lemma ensures that the integrand in (5) is measurable.

Lemma 1

Assume that $u:\varOmega \rightarrow V$ is weakly measurable and $p:\varOmega \rightarrow V^*$ is weakly* continuous, i.e., for each $v \in V$, the map $x \mapsto \langle p(x), v \rangle$ is continuous. Then, the map $x \mapsto \langle p(x), u(x) \rangle$ is measurable.

Proof

Define $f:\varOmega \times \varOmega \rightarrow \mathbb {R}$ via

$$\begin{aligned} f(x, \xi ) := \langle p(x), u(\xi ) \rangle . \end{aligned}$$

(A.2)

Then, f is continuous in the first and measurable in the second variable. In the calculus of variations, functions with this property are called Carathéodory functions and have the property that $x \mapsto f(x,g(x))$ is measurable whenever $g:\varOmega \rightarrow \varOmega$ is measurable, which is proven by approximation of g as the pointwise limit of simple functions [22, Proposition 3.7]. In our case, we can simply set $g(x) := x$, which is measurable, and the assertion follows. $\square$

1.2 Wasserstein Metrics and the KR Norm

This subsection is concerned with the definition of the space of measures $K\!R(X)$ and the isometric embedding $\mathcal {P}(X) \subset K\!R(X)$ underlying the formulation of ${\text {TV}}$ given in (7).

By $\mathcal {M}(X)$ and $\mathcal {P}(X) \subset \mathcal {M}(X)$, we denote the sets of signed Radon measures and Borel probability measures supported on X. $\mathcal {M}(X)$ is a vector space [40, p. 360] and a Banach space if equipped with the norm

$$\begin{aligned} \Vert \mu \Vert _\mathcal {M}:= \int _X \,\hbox {d}|\mu |, \end{aligned}$$

(A.3)

so that a function $u:\varOmega \rightarrow \mathcal {P}(X) \subset \mathcal {M}(X)$ is Banach space-valued (i.e., u takes values in a Banach space). If we define C(X) as the space of continuous functions on X with norm $\Vert f\Vert _{C} := \sup _{x \in X} |f(x)|$, under the above assumptions on X, $\mathcal {M}(X)$ can be identified with the (topological) dual space of C(X) with dual pairing

$$\begin{aligned} \langle \mu , p \rangle := \int _{X} p \,\hbox {d}\mu , \end{aligned}$$

(A.4)

whenever $\mu \in \mathcal {M}(X)$ and $p \in C(X)$, as proven in [40, p. 364]. Hence, $\mathcal {P}(X)$ is a bounded subset of a dual space.

We will now see that additionally, $\mathcal {P}(X)$ can be regarded as subset of a Banach space which is a predual space (in the sense that its dual space can be identified with a “meaningful” function space) and which metrizes the weak* topology of $\mathcal {M}(X)$ on $\mathcal {P}(X)$ by the optimal transport metrics we are interested in.

For $q \ge 1$, the Wasserstein metrics $W_q$ on $\mathcal {P}(X)$ are defined via

$$\begin{aligned} \begin{aligned} W_q(\mu , \mu ') :=&\left( \inf _{\gamma \in \varGamma (\mu ,\mu ')} \int _{X \times X} d(x,y)^q \,\hbox {d}\gamma (x,y) \right) ^{1/q}, \end{aligned} \end{aligned}$$

(A.5)

where

$$\begin{aligned} \varGamma (\mu ,\mu ') := \left\{ \gamma \in \mathcal {P}(X \times X):~\pi _1 \gamma = \mu , ~\pi _2 \gamma = \mu ' \right\} . \end{aligned}$$

(A.6)

Here, $\pi _i\gamma$ denotes the ith marginal of the measure $\gamma$ on the product space $X \times X$, i.e., $\pi _1\gamma (A) := \gamma (A \times X)$ and $\pi _2\gamma (B) := \gamma (X \times B)$ whenever $A, B \subset X$.

Now, let ${\text {Lip}}(X,\mathbb {R}^d)$ be the space of Lipschitz-continuous functions on X with values in $\mathbb {R}^d$ and ${\text {Lip}}(X) := {\text {Lip}}(X,\mathbb {R}^1)$. Furthermore, denote the Lipschitz seminorm by $[\cdot ]_{{\text {Lip}}}$ so that $[f]_{{\text {Lip}}}$ is the Lipschitz constant of f. Note that, if we fix some arbitrary $x_0 \in X$, the seminorm $[\cdot ]_{{\text {Lip}}}$ is actually a norm on the set

$$\begin{aligned} {\text {Lip}}_0(X,\mathbb {R}^d) := \{ p \in {\text {Lip}}(X,\mathbb {R}^d):p(x_0) = 0 \}. \end{aligned}$$

(A.7)

The famous Kantorovich–Rubinstein duality [44] states that, for $q=1$, the Wasserstein metric is actually induced by a norm, namely $W_1(\mu , \mu ') = \Vert \mu - \mu '\Vert _{K\!R}$, where

$$\begin{aligned} \Vert \nu \Vert _{K\!R} := \sup \left\{ \int _{X} p \,\hbox {d}\nu : ~p \in {\text {Lip}}_0(X), ~[p]_{{\text {Lip}}} \le 1 \right\} , \end{aligned}$$

(A.8)

whenever $\nu \in \mathcal {M}_0(X) := \{ \mu \in \mathcal {M}:\int _X d\mu = 0\}$. The completion $K\!R(X)$ of $\mathcal {M}_0(X)$ with respect to $\Vert \cdot \Vert _{K\!R}$ is a predual space of $({\text {Lip}}_0(X), [\cdot ]_{{\text {Lip}}})$ [79, Theorem 2.2.2 and Cor. 2.3.5].² Hence, after subtracting a point mass at $x_0$, the set $\mathcal {P}(X) - \delta _{x_0}$ is a subset of the Banach space $K\!R(X)$, the predual of ${\text {Lip}}_0(X)$.

Consequently, the embeddings

$$\begin{aligned} \mathcal {P}(X)&\hookrightarrow (K\!R(X), \Vert \cdot \Vert _{K\!R}), \end{aligned}$$

(A.9)

$$\begin{aligned} \mathcal {P}(X)&\hookrightarrow (\mathcal {M}(X), \Vert \cdot \Vert _{\mathcal {M}}) \end{aligned}$$

(A.10)

define two different topologies on $\mathcal {P}(X)$. The first embedding space $(\mathcal {M}(X), \Vert \cdot \Vert _{\mathcal {M}})$ is isometrically isomorphic to the dual of C(X). The second embedding space $(K\!R(X), \Vert \cdot \Vert _{K\!R})$ is known to be a metrization of the weak*-topology on the bounded subset $\mathcal {P}(X)$ of the dual space $\mathcal {M}(X) = C(X)^*$ [77, Theorem 6.9].

Importantly, while $(\mathcal {P}(X), \Vert \cdot \Vert _{\mathcal {M}})$ is not separable unless X is discrete, $(\mathcal {P}(X), \Vert \cdot \Vert _{K\!R})$ is in fact compact, in particular complete and separable [77, Theorem 6.18] which is crucial in our result on the existence of minimizers (Theorem 1).

Appendix B: Proof of ${\text {TV}}$-Behavior for Cartoonlike Functions

Proof

(Prop. 1) Let $p:\varOmega \rightarrow (V^*)^d$ satisfy the constraints in (5) and denote by $\nu$ the outer unit normal of $\partial U$. The set $\varOmega$ is bounded, p and its derivatives are continuous and $u \in L_w^\infty (\varOmega , V)$ since the range of u is finite and U, $\varOmega$ are measurable. Therefore, all of the following integrals converge absolutely. Due to linearity of the divergence,

$$\begin{aligned}&\langle {\text {div}}p(x), u^\pm \rangle = {\text {div}}(\langle p(\cdot ), u^\pm \rangle ), \end{aligned}$$

(B.1)

$$\begin{aligned}&\langle p(x), u^\pm \rangle := ( \langle p_1(x), u^\pm \rangle , \dots , \langle p_d(x), u^\pm \rangle ) \in \mathbb {R}^d. \end{aligned}$$

(B.2)

Using this property and applying Gauss’ theorem, we compute

$$\begin{aligned} \begin{aligned}&\int _\varOmega \langle -{\text {div}}p(x), u(x) \rangle \,\hbox {d}x \\&\quad = -\int _{\varOmega \setminus U} {\text {div}}(\langle p(x), u^- \rangle ) \,\hbox {d}x - \int _{U} {\text {div}}(\langle p(x), u^+ \rangle ) \,\hbox {d}x \\&\quad \overset{\text {Gauss}}{=} \int _{\partial U} \sum _{i=1}^d \langle \nu _i(x) p_i(x), {u^+} - {u^-} \rangle \,\hbox {d}\mathcal {H}^{d-1}(x) \\&\quad \le \mathcal {H}^{d-1}(\partial U) \cdot \Vert {u^+} - {u^-}\Vert _V. \end{aligned} \end{aligned}$$

(B.3)

For the last inequality, we used our first assumption on $\Vert \cdot \Vert _{(V^*)^d}$ together with the norm constraint for p in (5). Taking the supremum over p as in (5), we arrive at

$$\begin{aligned} {\text {TV}}_{V}(u) \le \mathcal {H}^{d-1}(\partial U) \cdot \Vert {u^+} - {u^-}\Vert _V. \end{aligned}$$

(B.4)

For the reverse inequality, let ${\tilde{p}} \in V^*$ be arbitrary with the property $\Vert {\tilde{p}}\Vert _{V^*} \le 1$ and $\phi \in C_c^1(\varOmega , \mathbb {R}^d)$ satisfying $\Vert \phi (x)\Vert _2 \le 1$. Now, by (11), the function

$$\begin{aligned} p(x) := (\phi _1(x) {\tilde{p}}, \dots , \phi _d(x) {\tilde{p}}) \in (V^*)^d \end{aligned}$$

(B.5)

has the properties required in (5). Hence,

$$\begin{aligned} {\text {TV}}_{V}(u)&\ge \int _\varOmega \langle -{\text {div}}p(x), u(x) \rangle \,\hbox {d}x \end{aligned}$$

(B.6)

$$\begin{aligned}&= -\int _\varOmega {\text {div}}\phi (x) \,\hbox {d}x \cdot \langle {\tilde{p}}, u^+ - u^- \rangle . \end{aligned}$$

(B.7)

Taking the supremum over all $\phi \in C_c^1(\varOmega , \mathbb {R}^d)$ satisfying $\Vert \phi (x)\Vert _2 \le 1$, we obtain

$$\begin{aligned} {\text {TV}}_{V}(u)&\ge {\text {Per}}(U, \varOmega ) \cdot \langle {\tilde{p}}, u^+ - u^- \rangle , \end{aligned}$$

(B.8)

where ${\text {Per}}(U, \varOmega )$ is the perimeter of U in $\varOmega$. In the theory of Caccioppoli sets (or sets of finite perimeter), the perimeter is known to agree with $\mathcal {H}^{d-1}(\partial U)$ for sets with $C^1$ boundary [4, p. 143].

Now, taking the supremum over all ${\tilde{p}} \in V^*$ with $\Vert {\tilde{p}}\Vert _{V^*} \le 1$ and using the fact that the canonical embedding of a Banach space into its bidual is isometric, i.e.,

$$\begin{aligned} \Vert u\Vert _V = \sup _{\Vert p\Vert _{V^*} \le 1} \langle p, u \rangle , \end{aligned}$$

(B.9)

we arrive at the desired reverse inequality which concludes the proof. $\square$

Appendix C: Proof of Rotational Invariance

Proof

(Proposition 2) Let $R \in SO(d)$ and define

$$\begin{aligned} R^T\varOmega := \{ R^T x : x \in \varOmega \}, ~{\tilde{p}}(y) := R^T p(Ry). \end{aligned}$$

(C.1)

In (5), the norm constraint on p(x) is equivalent to the norm constraint on ${\tilde{p}}(y)$ by condition (13). Now, consider the integral transform

$$\begin{aligned} \int _\varOmega \langle -{\text {div}}p(x), u(x) \rangle \,\hbox {d}x&= \int _{R^T\varOmega } \langle -{\text {div}}p(R y), {\tilde{u}}(y) \rangle \,\hbox {d}y \end{aligned}$$

(C.2)

$$\begin{aligned}&= \int _{R^T\varOmega } \langle -{\text {div}}{\tilde{p}}(y), {\tilde{u}}(y) \rangle \,\hbox {d}y. \end{aligned}$$

(C.3)

where, using $R^T R = I$,

$$\begin{aligned} {\text {div}}{\tilde{p}}(y)&= \sum _{i=1}^d \partial _i {\tilde{p}}_i(y) = \sum _{i=1}^d \sum _{j=1}^d R_{ji} \partial _i \left[ p_j(R y)\right] \end{aligned}$$

(C.4)

$$\begin{aligned}&= \sum _{i=1}^d \sum _{j=1}^d \sum _{k=1}^d R_{ji} R_{ki} \partial _k p_j(R y) \end{aligned}$$

(C.5)

$$\begin{aligned}&= \sum _{j=1}^d \sum _{k=1}^d \partial _k p_j(R y) \sum _{i=1}^d R_{ji} R_{ki} \end{aligned}$$

(C.6)

$$\begin{aligned}&= \sum _{j=1}^d \partial _j p_j(R y) = {\text {div}}p(R y), \end{aligned}$$

(C.7)

which implies ${\text {TV}}_V(u) = {\text {TV}}_V({\tilde{u}})$. $\square$

Appendix D: Discussion of Product Norms

There is one subtlety about formulation (5) of the total variation: The choice of norm for the product space $(V^*)^d$ affects the properties of our total variation seminorm.

1.1 Product Norms as Required in Proposition 1

The following proposition gives some examples for norms that satisfy or fail to satisfy conditions (10) and (11) in Proposition 1 about cartoonlike functions.

Proposition 4

The following norms for $p \in (V^*)^d$ satisfy (10) and (11) for any normed space V:

• 1. For $s = 2$:

  $$\begin{aligned} \Vert p\Vert _{(V^*)^d,s} := \left( \sum _{i=1}^d \Vert p_i\Vert _{V^*}^s \right) ^{1/s}. \end{aligned}$$

  (D.1)

• 2. Writing $p(v):=(\langle p_1,v\rangle ,\dots ,\langle p_d,v\rangle )\in \mathbb {R}^d$, $v \in V$,

  $$\begin{aligned} \Vert p\Vert _{\mathcal {L}(V, \mathbb {R}^d)} := \sup _{\Vert v\Vert _V \le 1} \Vert p(v)\Vert _{2} \end{aligned}$$

  (D.2)

On the other hand, for any $1 \le s < 2$ and $s > 2$, there is a normed space V such that at least one of the properties (10), (11) is not satisfied by corresponding product norm (D.1).

Remark 1

In the finite-dimensional Euclidean case $V = \mathbb {R}^n$ with norm $\Vert \cdot \Vert _2$, we have $(V^*)^d = \mathbb {R}^{d,n}$; thus, p is matrix-valued and $\Vert \cdot \Vert _{\mathcal {L}(V, \mathbb {R}^d)}$ agrees with the spectral norm $\Vert \cdot \Vert _\sigma$. The norm defined in (D.1) is the Frobenius norm $\Vert \cdot \Vert _F$ for $s=2$.

Proof

(Prop. 4) By Cauchy–Schwarz,

$$\begin{aligned} \left| \textstyle {\sum _{i=1}^d} x_i \langle p_i, v \rangle \right|&\le \Vert x\Vert _2 \left( \textstyle {\sum _{i=1}^d} \left| \langle p_i, v \rangle \right| ^2 \right) ^{1/2} \end{aligned}$$

(D.3)

$$\begin{aligned}&\le \Vert x\Vert _2 \left( \textstyle {\sum _{i=1}^d} \Vert p_i\Vert _{V^*}^2 \Vert v\Vert _V^2 \right) ^{1/2} \end{aligned}$$

(D.4)

$$\begin{aligned}&\le \Vert x\Vert _2 \Vert v\Vert _V \left( \textstyle {\sum _{i=1}^d} \Vert p_i\Vert _{V^*}^2 \right) ^{1/2}, \end{aligned}$$

(D.5)

whenever $p \in (V^*)^d$, $v \in V$, and $x \in \mathbb {R}^d$. Similarly, for each $q \in V^*$,

$$\begin{aligned} \left( \textstyle {\sum _{i=1}^d} \Vert x_i q\Vert _{V^*}^2 \right) ^{1/2} = \Vert x\Vert _2 \Vert q\Vert _{V^*}. \end{aligned}$$

(D.6)

Hence, for $s = 2$, properties (10) and (11) are satisfied by product norm (D.1).

For operator norm (D.2), consider

$$\begin{aligned} \left| \textstyle {\sum _{i=1}^d} x_i \langle p_i, v \rangle \right|&\le \Vert x\Vert _2 \left( \textstyle {\sum _{i=1}^d} \left| \langle p_i, v \rangle \right| ^2 \right) ^{1/2} \end{aligned}$$

(D.7)

$$\begin{aligned}&= \Vert x\Vert _2 \Vert p(v)\Vert _2 \end{aligned}$$

(D.8)

$$\begin{aligned}&\le \Vert x\Vert _2 \Vert p\Vert _{\mathcal {L}(V, \mathbb {R}^d)} \Vert v\Vert _V, \end{aligned}$$

(D.9)

which is property (10). On the other hand, (11) follows from

$$\begin{aligned} \Vert (x_1 q, \dots , x_d q)\Vert _{\mathcal {L}(V, \mathbb {R}^d)}&= \sup _{\Vert v\Vert _V \le 1} \left( \textstyle {\sum _{i=1}^d} |x_i q(v)|^2 \right) ^{1/2} \end{aligned}$$

(D.10)

$$\begin{aligned}&= \Vert x\Vert _2 \sup _{\Vert v\Vert _V \le 1} |q(v)| \end{aligned}$$

(D.11)

$$\begin{aligned}&= \Vert x\Vert _2 \Vert q\Vert _{V^*}. \end{aligned}$$

(D.12)

Now, for $s > 2$, property (10) fails for $d = 2$, $V = V^* = \mathbb {R}$, $p = x = (1,1)$ and $v = 1$ since

$$\begin{aligned} \left| \sum _{i=1}^d x_i \langle p_i, v \rangle \right|&= 2 > 2^{1/2} \cdot 2^{1/s} = \Vert x\Vert _2 \Vert p\Vert _{(V^*)^d,s} \Vert v\Vert _V. \end{aligned}$$

(D.13)

For $1 \le s < 2$, consider $d = 2$, $V^* = \mathbb {R}$, $q = 1$ and $x = (1,1)$, then

$$\begin{aligned} \Vert (x_1 q, \dots , x_d q)\Vert _{(V^*)^d,s}&= 2^{1/s} > 2^{1/2} = \Vert x\Vert _2 \Vert q\Vert _{V^*}, \end{aligned}$$

(D.14)

which contradicts property (11). $\square$

1.2 Rotationally Symmetric Product Norms

For $V = (\mathbb {R}^n, \Vert \cdot \Vert _2)$, property (13) in Proposition 2 is satisfied by the Frobenius norm as well as the spectral norms on $(V^*)^d = \mathbb {R}^{d,n}$. In general, the following proposition holds:

Proposition 5

For any normed space V, rotational invariance property (13) is satisfied by operator norm (D.2). For any $s \in [1,\infty )$, there is a normed space V such that property (13) does not hold for product norm (D.1).

Proof

By definition of the operator norm and rotational invariance of the Euclidean norm $\Vert \cdot \Vert _2$,

$$\begin{aligned} \Vert Rp\Vert _{\mathcal {L}(V, \mathbb {R}^d)}&= \sup _{\Vert v\Vert _V \le 1} \Vert Rp(v)\Vert _{2} \end{aligned}$$

(D.15)

$$\begin{aligned}&= \sup _{\Vert v\Vert _V \le 1} \Vert p(v)\Vert _{2} = \Vert p\Vert _{\mathcal {L}(V, \mathbb {R}^d)}. \end{aligned}$$

(D.16)

For product norms (D.1), without loss of generality, we consider the case $d = 2$, $V := (\mathbb {R}^2, \Vert \cdot \Vert _1)$, $p_1 = (1,0)$, $p_2 = (0,1)$ and

$$\begin{aligned} R := \begin{pmatrix} 1/2 &{} -\sqrt{3}/2 \\ \sqrt{3}/2 &{} 1/2 \end{pmatrix} \in SO(2). \end{aligned}$$

(D.17)

Then, $V^* := (\mathbb {R}^2, \Vert \cdot \Vert _\infty )$ and

$$\begin{aligned} \Vert p\Vert _{(V^*)^d,s} = \left( \textstyle {\sum _{i=1}^2} \Vert p_i\Vert _\infty ^s \right) ^{1/s} = 2^{1/s} \end{aligned}$$

(D.18)

whereas

$$\begin{aligned} (Rp)_1&= (1/2, -\sqrt{3}/2), ~(Rp)_2 = (\sqrt{3}/2, 1/2), \end{aligned}$$

(D.19)

$$\begin{aligned} \Vert Rp\Vert _{(V^*)^d,s}&= \left( \textstyle {\sum _{i=1}^2} (\sqrt{3}/2)^s \right) ^{1/s} \end{aligned}$$

(D.20)

$$\begin{aligned}&= 2^{1/s} \cdot \sqrt{3}/2 \ne 2^{1/s} = \Vert p\Vert _{(V^*)^d,s}, \end{aligned}$$

(D.21)

for any $1 \le s < \infty$. $\square$

1.3 Product Norms on ${\text {Lip}}_0(X)$

We conclude our discussion about product norms on $(V^*)^d$ with the special case of $V = K\!R(X)$: For $p \in [{\text {Lip}}_0(X)]^d$, the most natural choice is

$$\begin{aligned}{}[p]_{{\text {Lip}}(X,\mathbb {R}^d)} := \sup _{z \ne z'} \frac{\Vert p(z) - p(z')\Vert ^2_2}{d(z,z')}, \end{aligned}$$

(D.22)

which is automatically rotationally invariant. On the other hand, the product norm defined in (D.1) (with $s=2$), namely $\sqrt{\sum _{i=1}^d [p_i]_{{\text {Lip}}}^2}$, is not rotationally invariant for general metric spaces X. However, in the special case $X \subset (\mathbb {R}^n, \Vert \cdot \Vert _2)$ and $p \in C^1(X,\mathbb {R}^d)$, norms (D.22) and (D.1) coincide with $\sup _{z\in X} \Vert Dp(z)\Vert _\sigma$ (spectral norm of the Jacobian) and $\sup _{z\in X} \Vert Dp(z)\Vert _F$ (Frobenius norm of the Jacobian), respectively, both satisfying rotational invariance.

Appendix E: Proof of Non-uniqueness

Proof

(Prop. 3) Let $u \in L_w^\infty (\varOmega , \mathcal {P}(X))$. With the given choice of X, there exists a measurable function ${\tilde{u}}:\varOmega \rightarrow [0,1]$ such that

$$\begin{aligned} u(x) = {\tilde{u}}(x) \delta _0 + (1 - {\tilde{u}}(x)) \delta _1. \end{aligned}$$

(E.1)

The measurability of ${\tilde{u}}$ is equivalent to the weak measurability of u by definition:

$$\begin{aligned} \langle p, u(x) \rangle&= {\tilde{u}}(x) \cdot p_0 + (1 - {\tilde{u}}(x)) \cdot p_1 \end{aligned}$$

(E.2)

$$\begin{aligned}&= {\tilde{u}}(x) \cdot (p_0 - p_1) + p_1. \end{aligned}$$

(E.3)

The constraint

$$\begin{aligned} p \in C_c^1(\varOmega , [{\text {Lip}}_0(X)]^d), ~[p(x)]_{{\text {Lip}}(X,\mathbb {R}^d)} \le 1 \end{aligned}$$

(E.4)

from the definition of ${\text {TV}}_{K\!R}$ in (7) translates to

$$\begin{aligned} p_0, p_1 \in C_c(\varOmega ,\mathbb {R}^d),~\Vert p_0(x) - p_1(x)\Vert _2 \le 1. \end{aligned}$$

(E.5)

Furthermore,

$$\begin{aligned}&\langle -{\text {div}}p(x), u(x) \rangle \end{aligned}$$

(E.6)

$$\begin{aligned}&\quad = -{\text {div}}p_0(x) \cdot {\tilde{u}}(x) - {\text {div}}p_1(x) \cdot (1-{\tilde{u}}(x)) \end{aligned}$$

(E.7)

$$\begin{aligned}&\quad = -{\text {div}}(p_0 - p_1)(x) \cdot {\tilde{u}}(x) - {\text {div}}p_1(x). \end{aligned}$$

(E.8)

By the compact support of $p_1$, the last term vanishes when integrated over $\varOmega$. Consequently,

$$\begin{aligned}&{\text {TV}}_{K\!R}(u) = \sup \left\{ \int _\varOmega -{\text {div}}(p_0 - p_1) (x) \cdot {\tilde{u}}(x) \,\hbox {d}x : \right. \end{aligned}$$

(E.9)

$$\begin{aligned}&\qquad \left. p_0, p_1 \in C_c(\varOmega ,\mathbb {R}^d),~\Vert (p_0 - p_1)(x)\Vert _2 \le 1 \right\} \end{aligned}$$

(E.10)

$$\begin{aligned}&\quad = \sup \left\{ \int _\varOmega -{\text {div}}p(x) \cdot {\tilde{u}}(x) \,\hbox {d}x : \right. \end{aligned}$$

(E.11)

$$\begin{aligned}&\qquad \left. p \in C_c(\varOmega ,\mathbb {R}^{d}),~\Vert p(x)\Vert _2 \le 1 \right\} \end{aligned}$$

(E.12)

$$\begin{aligned}&\quad = {\text {TV}}({\tilde{u}}). \end{aligned}$$

(E.13)

and therefore

$$\begin{aligned} T_{\rho ,\lambda }(u)&= \int _{\varOmega \setminus U} {\tilde{u}}(x) \,\hbox {d}x + \int _U (1-{\tilde{u}}(x)) \,\hbox {d}x + \lambda {\text {TV}}({\tilde{u}}) \end{aligned}$$

(E.14)

$$\begin{aligned}&= \int _\varOmega |\mathbf {1}_U(x) - {\tilde{u}}(x)| \,\hbox {d}x + \lambda {\text {TV}}({\tilde{u}}) \end{aligned}$$

(E.15)

$$\begin{aligned}&= \Vert \mathbf {1}_U - {\tilde{u}}\Vert _{L^1} + \lambda {\text {TV}}({\tilde{u}}). \end{aligned}$$

(E.16)

Thus we have shown that the functional $T_{\rho ,\lambda }$ is equivalent to the classical $L^1$-${\text {TV}}$ functional with the indicator function $\mathbf {1}_U$ as input data and evaluated at ${\tilde{u}}$ which is known to have non-unique minimizers for a certain choice of $\lambda$ [17]. $\square$

Appendix F: Proof of Existence

1.1 Well-Defined Energy Functional

In order for the functional defined in (15) to be well defined, the mapping $x \mapsto \rho (x, u(x))$ needs to be measurable. In the following lemma, we show that this is the case under mild conditions on $\rho$.

Lemma 2

Let $\rho :\varOmega \times \mathcal {P}(X) \rightarrow [0,\infty )$ be a globally bounded function that is measurable in the first and convex in the second variable, i.e., $x \mapsto \rho (x,\mu )$ is measurable for each $\mu \in \mathcal {P}(X)$, and $\mu \mapsto \rho (x,\mu )$ is convex for each $x \in \varOmega$. Then, the map $x \rightarrow \rho (x,u(x))$ is measurable for every $u \in L_w^\infty (\varOmega , \mathcal {P}(X))$.

Remark 2

As will become clear from the proof, the convexity condition can be replaced by the assumption that $\rho$ be continuous with respect to $(\mathcal {P}(X), W_1)$ in the second variable. However, in order to ensure weak* lower semicontinuity of functional (15), we will require convexity of $\rho$ in the existence proof (Theorem 1) anyway. Therefore, for simplicity we also stick to the (stronger) convexity condition in Lemma 2.

Remark 3

One example of a function satisfying the assumptions in Lemma 2 is given by

$$\begin{aligned} \rho (x,\mu ) := W_1(f(x),\mu ), ~x \in \varOmega , ~\mu \in \mathcal {P}(\mathbb {S}^2). \end{aligned}$$

(F.1)

Indeed, boundedness follows from the boundedness of the Wasserstein metric in the case of an underlying bounded metric spaces (here $\mathbb {S}^2$). Convexity in the second argument follows from the fact that the Wasserstein metric is induced by a norm (A.8).

Proof

(Lemma 2) The metric space $(\mathcal {P}(X), W_1)$ is compact, hence separable. By Pettis’ measurability theorem [10, Chapter VI, §1, No. 5, Proposition 12], weak and strong measurability coincide for separably valued functions, so that u is actually strongly measurable as a function with values in $(\mathcal {P}(X),W_1)$. Note, however, that this does not imply strong measurability with respect to the norm topology of $(\mathcal {M}(X), \Vert \cdot \Vert _{\mathcal {M}})$ in general!

As bounded convex functions are locally Lipschitz continuous [19, Theorem 2.34], $\rho$ is continuous in the second variable with respect to $W_1$. As in the proof of Lemma 1, we now note that $\rho$ is a Carathéodory function, for which compositions with measurable functions such as $x \mapsto \rho (x,u(x))$ are known to be measurable. $\square$

1.2 The Notion of Weakly* Measurable Functions

Before we can go on with the proof of existence of minimizers to (15), we introduce the notion of weak* measurability because this will play a crucial role in the proof.

Analogously with the notion of weak measurability and with $L_{w}^\infty (\varOmega , K\!R(X))$ introduced above, we say that a measure-valued function $u:\varOmega \rightarrow \mathcal {M}(X)$ is weakly* measurable if the mapping

$$\begin{aligned} x \mapsto \int _X f(z) \,\hbox {d}u_x(z) \end{aligned}$$

(F.2)

is measurable for each $f \in C(X)$. $L_{w*}^\infty (\varOmega , \mathcal {M}(X))$ is defined accordingly as the space of weakly* measurable functions.

For functions $u:\varOmega \rightarrow \mathcal {P}(X)$ mapping onto the space of probability measures, there is an immediate connection between weak* measurability and weak measurability: u is weakly measurable if the mapping

$$\begin{aligned} x \mapsto \int _X p(z) \,\hbox {d}u_x(z) \end{aligned}$$

(F.3)

is measurable whenever $p \in {\text {Lip}}_0(X)$. However, since, by the Stone–Weierstrass theorem, the Lipschitz functions ${\text {Lip}}(X)$ are dense in $(C(X), \Vert \cdot \Vert _{\infty })$ [13, p. 198], both notions of measurability coincide for probability measure-valued functions $u:\varOmega \rightarrow \mathcal {P}(X)$, so that

$$\begin{aligned} L_w^\infty (\varOmega , \mathcal {P}(X)) = L_{w*}^\infty (\varOmega , \mathcal {P}(X)). \end{aligned}$$

(F.4)

However, as this equivalence does not hold for the larger spaces $L_{w*}^\infty (\varOmega , \mathcal {M}(X))$ and $L_{w}^\infty (\varOmega , \mathcal {M}(X))$, it will be crucial to keep track of the difference between weak and weak* measurability in the existence proof.

1.3 Proof of Existence

Proof

(Theorem 1) The proof is guided by the direct method from the calculus of variations. The first part is inspired by the proof of the fundamental theorem for Young measures as formulated and proven in [6].

Let $u^k:\varOmega \rightarrow \mathcal {P}(X)$, $k \in \mathbb {N}$, be a minimizing sequence for $T_{\rho ,\lambda }$, i.e.,

$$\begin{aligned} T_{\rho ,\lambda }(u^k) \rightarrow \inf _{u} T_{\rho ,\lambda }(u) ~\text { as }~ k \rightarrow \infty . \end{aligned}$$

(F.5)

As $\mathcal {M}(X)$ is the dual space of C(X), $L_{w*}^\infty (\varOmega , \mathcal {M}(X))$ with the norm defined in (A.1) is dual to the Banach space $L^1(\varOmega , C(X))$ of Bochner integrable functions on $\varOmega$ with values in C(X) [42, p. 93]. Now, $\mathcal {P}(X)$ as a subset of $\mathcal {M}(X)$ is bounded so that our sequence $u^k$ is bounded in $L_{w*}^\infty (\varOmega , \mathcal {M}(X))$ (here we use again that $L_{w*}^\infty (\varOmega , \mathcal {P}(X)) = L_{w}^\infty (\varOmega , \mathcal {P}(X))$).

Note that we get boundedness of our minimizing sequence “for free”, without any assumptions on the coercivity of $T_{\rho ,\lambda }$! Hence we can apply the Banach–Alaoglu theorem, which states that there exist $u^\infty \in L_{w*}^\infty (\varOmega , \mathcal {M}(X))$ and a subsequence, also denoted by $u^k$, such that

$$\begin{aligned} u^k \overset{*}{\rightharpoonup } u^\infty \text { in } L_{w*}^\infty (\varOmega , \mathcal {M}(X)). \end{aligned}$$

(F.6)

Using the notation in (A.4), this means by definition

$$\begin{aligned}&\int _\varOmega \langle u^k(x), p(x) \rangle \,\hbox {d}x \rightarrow \int _\varOmega \langle u^\infty (x), \,p(x) \rangle \,\hbox {d}x \end{aligned}$$

(F.7)

$$\begin{aligned}&\quad \forall p \in L^1(\varOmega , C(X)). \end{aligned}$$

(F.8)

We now show that $u^\infty (x) \in \mathcal {P}(X)$ almost everywhere, i.e., $u^\infty$ is a nonnegative measure of unit mass: Convergence (F.7) holds in particular for the choice $p(x,s) := \phi (x)f(s)$, where $\phi \in L^1(\varOmega )$ and $f \in C(X)$. For nonnegative functions $\phi$ and f, we have

$$\begin{aligned} \int _\varOmega \phi (x) \langle u^k(x), f \rangle \,\hbox {d}x \ge 0 \end{aligned}$$

(F.9)

for all k, which implies

$$\begin{aligned} \int _\varOmega \phi (x) \langle u^\infty (x), f \rangle \,\hbox {d}x \ge 0. \end{aligned}$$

(F.10)

Since this holds for all nonnegative $\phi$ and f, we deduce that $u^\infty (x)$ is a nonnegative measure for almost every $x \in \varOmega$. The choice $f(s) \equiv 1$ in (F.7) shows that $u^\infty$ has unit mass almost everywhere.

Therefore, $u^\infty (x) \in \mathcal {P}(X)$ almost everywhere and we have shown that $u^\infty$ lies in the feasible set $L_{w}^\infty (\varOmega , \mathcal {P}(X))$. It remains to show that $u^\infty$ is in fact a minimizer.

In order to do so, we prove weak* lower semicontinuity of $T_{\rho ,\lambda }$. We consider the two integral terms in definition (15) of $T_{\rho ,\lambda }$ separately. For the ${\text {TV}}_{K\!R}$ term, for any $p \in C_c^1(\varOmega , {\text {Lip}}(X,\mathbb {R}^d))$, we have ${\text {div}}p \in L^1(\varOmega , C(X))$ so that

$$\begin{aligned} \lim _{k\rightarrow \infty } \int _\varOmega \langle {\text {div}}u^k(x), p(x) \rangle \,\hbox {d}x = \int _\varOmega \langle {\text {div}}u^\infty (x), p(x) \rangle \,\hbox {d}x. \end{aligned}$$

(F.11)

Taking the supremum over all p with $[p(x)]_{[{\text {Lip}}(X)]^d} \le 1$ almost everywhere, we deduce lower semicontinuity of the regularizer:

$$\begin{aligned} {\text {TV}}_{K\!R}(u^\infty ) \le \liminf _{k\rightarrow \infty } {\text {TV}}_{K\!R}(u^k). \end{aligned}$$

(F.12)

The data fidelity term $u \mapsto \int _\varOmega \rho (x,u(x)) \,\hbox {d}x$ is convex and bounded on the closed convex subset $L_w^\infty (\varOmega , \mathcal {P}(X))$ of the space $L_{w*}^\infty (\varOmega , \mathcal {M}(X))$. It is also continuous, as convex and bounded functions on normed spaces are locally Lipschitz continuous. This implies weak* lower semicontinuity on $L_w^\infty (\varOmega , \mathcal {P}(X))$.

Therefore, the objective function $T_{\rho ,\lambda }$ is weakly* lower semicontinuous, and we obtain

$$\begin{aligned} T_{\rho ,\lambda }(u^\infty ) \le \lim \inf _{k\rightarrow \infty } T_{\rho ,\lambda }(u^k) \end{aligned}$$

(F.13)

for the minimizing sequence $(u^k)$, which concludes the proof.

$\square$