Modal Space: A Physics-Based Model for Sequential Estimation of Time-Varying Shape from Monocular Video

Abstract

This paper describes two sequential methods for recovering the camera pose together with the 3D shape of highly deformable surfaces from a monocular video. The nonrigid 3D shape is modeled as a linear combination of mode shapes with time-varying weights that define the shape at each frame and are estimated on-the-fly. The low-rank constraint is combined with standard smoothness priors to optimize the model parameters over a sliding window of image frames. We propose to obtain a physics-based shape basis using the initial frames on the video to code the time-varying shape along the sequence, reducing the problem from trilinear to bilinear. To this end, the 3D shape is discretized by means of a soup of elastic triangular finite elements where we apply a force balance equation. This equation is solved using modal analysis via a simple eigenvalue problem to obtain a shape basis that encodes the modes of deformation. Even though this strategy can be applied in a wide variety of scenarios, when the observations are denser, the solution can become prohibitive in terms of computational load. We avoid this limitation by proposing two efficient coarse-to-fine approaches that allow us to easily deal with dense 3D surfaces. This results in a scalable solution that estimates a small number of parameters per frame and could potentially run in real time. We show results on both synthetic and real videos with ground truth 3D data, while robustly dealing with artifacts such as noise and missing data.

1 Introduction

The combined inference of 3D scene structure and camera motion from monocular image sequences, or rigid Structure from Motion (s f m), is one of the most active areas of research in computer vision. In the last decade, s f m methods have made significant progress in simultaneously retrieving camera motion and 3D shape in real time for a sparse set of salient points [16, 27, 34] and even per-pixel dense reconstructions from video sequences acquired with a hand-held camera [36, 37] or with a micro aerial vehicle [62]. While s f m is now considered to be a mature field, these methods cannot be applied to structures undergoing nonrigid deformations, where the problem remains a challenge. In these cases, recovering the 3D structure of a deformable object from a monocular image sequence is an ill-posed problem since many different 3D shapes can have the same image measurements, producing severe ambiguities.

Fig. 1

On-line camera motion and nonrigid 3D shape from monocular image sequence. Our approaches consist of two stages: initialization and on-line estimation. Left In stage one, we use a few initial frames to estimate a shape at rest that we model by means of a soup of elastic triangular finite elements and to estimate the stiffness and mass matrices. Finally, we compute a shape basis by solving a simple eigenvalue problem using modal analysis. For dense cases, we present two strategies: a frequency-based and a coarse-to-fine approach. Right In stage two, we estimate camera motion and deformable 3D shape in a sequential manner over a sliding temporal window of frames. When a new frame $f+1$ is available, the temporal window shifts—blue window—and the new frame is processed. For this stage, we propose two approaches: a BA based using temporal smoothness priors and an EM-based using spatial ones (Color figure online)

Nonrigid structure from motion (nrs f m) addresses this limitation and methods from this field are now capable of estimating simultaneously accurate 3D reconstructions of nonrigid objects and camera motion from monocular video. The underlying principle behind most approaches is to model deformations using a low-rank shape basis [9, 12, 15, 21, 39, 40, 57] or a trajectory basis [8, 41]. However, nrs f m methods remain behind their rigid counterparts when it comes to real-time performance. The main reason behind this is that they are typically limited to batch operations where all the frames in the sequence are processed at once, after the whole acquisition, preventing them from on-line and real-time performance applications. Only recently, have nrs f m methods been extended to sequential processing [3, 40, 51] using a small set of salient points. However, they remain slow [40, 51] or do not scale to the use of a large number of points [3, 40, 51].

In this paper, we push monocular nrs f m forward toward real-time operation by proposing two fast sequential algorithms to simultaneously recover the nonrigid 3D shape and camera pose of strongly deforming surfaces under realistic real-world assumptions. Our approaches can deal with significant occlusions; they are suitable for modeling a wide variety of deformations from inextensible to highly extensible without the need for a pre-trained model, and they can be used to handle both sparse and dense data. To this end, we employ a linear combination of mode shapes—computed using continuum mechanics from a 3D rest shape estimation—to model the nonrigid 3D shape. Our on-line approaches work in two stages (see Fig. 1). In stage one, we estimate a shape at rest from the first few frames by means of a rigid factorization and then obtain a physics-based shape basis by solving a simple eigenvalue problem. In stage two, equipped with this low-rank shape constraint, the operation in a sequential manner over a sliding temporal window of frames is possible. To perform this stage, we propose two algorithms. The first is based on bundle adjustment (BA) with temporal smoothness priors, where the only parameters to estimate per-frame are the camera pose and the basis coefficients. The second uses a probabilistic model of the linear subspace with a Gaussian prior on each mode to encode the nonrigid 3D shape, i.e., spatial smoothness priors are assumed. Since the basis weights in the subspace are marginalized out, this method only optimizes per every frame the camera pose and a measurement noise by using expectation maximization (EM). In both cases, the number of parameters to estimate per frame is small, and our methods are fast and may potentially run in real time at frame rate. Although our shape basis is computed considering only the rest shape, it has proven experimentally to be able to code subsequent scene deformations without the need for 3D pre-learned data. It is worth pointing out that this shape basis is able to describe future deformations of the shape at rest (see experimental section). So for the same rest shape, our shape basis can code very different types of deformations.

Regarding the computation of mode shapes, while our methods can be directly applied from sparse to dense reconstructions, solving the stage one for dense cases could become prohibitive (see Fig. 1) in terms of computational load. To efficiently encode the deformations in these cases, we also propose two methods: (1) a frequency-based method where the dense mode shapes are computed using an interval of frequencies obtained in a low-resolution mesh, and (2) a coarse-to-fine approach where the dense shape at rest is down-sampled to a sparse mesh where modal analysis is applied at a low computational cost. These sparse 3D shapes are grown back to dense by exploiting the shape functions¹ to encode the geometry into the finite elements.

This paper combines and extends two conference publications [4, 5]. Here, we integrate these preliminary publications into a comprehensive presentation of our sequential approach to retrieve 3D nonrigid shapes together with camera motion from monocular video. We also present a novel frequency-based algorithm to compute stretching modes at low computational cost. In addition, we conduct new experiments to measure our algorithm’s resilience to corrupted observations such as noise and missing data, and to compare the performance of its different variants. We also show more extensive comparisons of our results with other methods reported in the literature. The paper is organized as follows. In section two, we discuss the related work and describe the contributions of our work. Section three defines our novel physics-based deformation model. In section four, we formulate the problem of on-line recovery of camera motion and time-varying shape from a monocular sequence. This is followed in section five by a description of our sequential algorithms used to solve the previous problem using different priors. In section six, we show our experimental results and present a comparison with respect to state-of-the-art techniques. Our conclusions are set out in section seven. Finally, to keep the paper self-contained, we provide an appendix with mathematical details.

2 Related Work

nrs f m is an inherently ill-posed problem unless additional a priori knowledge of the shape and camera motion is considered. A seminal work by [12] proposed a low-rank shape constraint as an extension of the [54] factorization algorithm to the nonrigid case. Their key insight was to model time-varying shape as a linear combination of an unknown shape basis under orthography. Although this prior has proved to be a powerful constraint, it is insufficient to solve the inherent ambiguities in nrs f m. It was shown in [7] that the low-rank shape prior in addition to orthonormality constraints on camera motion are sufficient for noise-free observations. Recently, [15] imposed the low-rank shape constraint directly on the time-varying shape matrix via a trace norm minimization approach.

Most approaches have required the use of additional priors using different optimization schemes to include temporal smoothness [3, 9, 17, 57, 61], smooth-time trajectories [8, 25], inextensibility constraints [61], rigid priors [6], and spatial smoothness [21, 57]. BA has become a popular optimization tool for refining an initial rigid solution [54] optimizing the pose, shape basis, and coefficients while incorporating both motion and deformation priors [9, 17]. A solution in [39] recovers motion matrices that lie on the correct motion manifold where the metric constraints are exactly satisfied. More recently, [21] combined a low-rank shape and local smoothness priors within a variational approach to produce per-pixel dense vivid reconstructions. A dual formulation using a trajectory basis was proposed in [8], where predefined discrete cosine trajectory bases are used to express the trajectory of each 3D point, considering each point as an independent object. Smoothness for the time-trajectory of each single point was assumed in [25].

Piecewise models have been proposed to encode more accurately strong local deformations. Piecewise planar [60], locally rigid [13, 52], or quadratic [20] approaches rely on common features shared between patches to enforce global consistency. [45] proposed a formulation to automate the best division of the surface into local patches. Later, [3] proposed a finite element method (FEM) formulation providing support for a piecewise approach where the local elements are stretchable triangles. The FEM modeling assures deformable surface continuity without additional constraints.

The alternative strand of methods known as template based [33, 38, 46, 47] rely on correspondences between the 2D points in the current image and a reference 3D shape which is assumed to be known in advance. In [33, 47], the unknown shape was encoded as a linear combination of deformation modes learnt in advance from a relatively large set of training data. [38] introduced the Laplacian formalism in computer vision to regularize 3D meshes without requiring any training data. To avoid inherent ambiguities, additional shape constraints are required such as inextensibility [33, 38]. Recently, [61] showed the exclusive use of these constraints, and it is sufficient to perform nonrigid reconstruction but only for isometric deformations, limiting the applicability of method.

On the other hand, spatial smoothness can be coded by means of probabilistic priors, although they have not been extensively used to recover nonrigid structure and camera motion. These priors allow the marginalization of hidden data that does not have to be explicitly computed, simplifying the optimization problem and avoiding over-fitting. Probabilistic Bayesian priors have been used in nrs f m  to model deformation weights in a low-dimensional subspace based on principal component analysis (PCA) [56], the remaining model parameters being estimated by EM. These priors have also been used in template-based methods, where a Gaussian process latent variable model was employed to learn a prior over the deformations of local surface patches [47]. More recently, [28] proposed a Procrustean normal distribution to model shape deformation without additional constraints. The unknown shape is encoded as a linear combination of deformation modes learned on-the-fly for a relatively small deformation [56], or in advance from a relatively large set of training data [47]. However, the large deformations of real-world shapes may need larger values of rank, and hence the reconstruction becomes under-constrained for methods that learn deformation modes on the fly [56]. This ambiguity can be reduced using a predefined basis in terms of shape or trajectory which acts as a representative basis while reducing the number of parameters to be estimated. A shape basis could be estimated with a learning step over nonrigid 3D training data, but this information is not always available in advance in which case alternative methods to obtain a predefined basis are necessary. Probabilistic priors have also been used to model nodal forces in a physics-based deformation model combining an extended kalman filter (EKF) with the FEM to predict nonrigid displacements [2, 3].

Mechanical priors have also been proposed to constrain the deformations of nonrigid objects. Early approaches used deformable superquadrics [32], balloons [14] or spring meshes [26], although these approaches were only valid to code relatively small deformations. The FEM was proposed to accurately represent specific materials [59, 65] with known material properties. To tackle the high dimensionality of these physics-based models, a low-rank representation was proposed by applying modal analysis over a known structure discretized in 3D finite elements [35, 42]. This method was then applied to image segmentation [43], medical imaging [35], and deformable 2D motion tracking [48, 50]. [42] integrated the incremental updates of the basis coefficients over time using an EKF. This resulted in inevitable drift that eventually destroyed the ability to accurately reconstruct the nonrigid object. Recently, linear elasticity models have been proposed in [3, 30] to code the extensible deformation of nonrigid objects, factorizing out the material properties into a normalized forces vector [3] or optimizing a stretching energy with respect to these [30].

Despite these advances, previous approaches to nrs f m typically remain batch and process all the frames in the sequence at once, after video capture. While sequential real-time s f m [27, 34, 36] solutions exist for rigid scenes, on-line estimation of nonrigid shape from a single camera based only on the measurements up to that moment remains a challenging problem. Sequential formulations have emerged only recently [3, 40, 51]. The first sequential nrs f m system was proposed in [40], based on BA over a sliding window with an implicit low-rank shape model. In [51], an incremental principal component analysis was proposed to model the shape basis. However, these approaches did not achieve real-time performance and were only demonstrated for a small number of feature points and small deformations. The first real-time on-line solution for nrs f m including feature tracking and outliers detection in a single process was proposed in [2, 3], combining an EKF with FEM to estimate a small set of salient points which belong to a deformable object.

In this work, we present two sequential approaches over a sliding window to solve the nrs f m problem as the data arrive. In both cases, we use a predefined physics-based model to define a number of meaningful deformation mode shapes to obtain a low-rank shape model. To compute this shape basis, we only need an estimation of the shape at rest from a few initial frames of the image sequence. We discretize the scene into elastic triangular finite elements to code the behavior of the object with a thin-plate model and unknown material properties (see Fig. 1). We then propose two sequential algorithms to solve for the parameters of the model. The first combines the low-rank shape model with temporal smoothness priors and uses BA to estimate the parameters. The second combines the shape basis with probabilistic priors and solves the latent variable problem by EM. In both cases, the number of parameters to be estimated is small, resulting in a system with low computational cost that may potentially run in real time. Similarly to [3], our methods also use FEM to encode the nonrigid shape. However, while [3] had to compute a stiffness matrix at every step, in contrast, we here use FEM to solve a single modal analysis problem which provides a shape basis able to encode scene deformations. Our methods are valid for large displacements caused by strong deformations and can cope with both isometric and elastic warps. Note that most deformations in nrs f m, such as a smiling face or a waving flag, are produced with respect to a mean shape, and hence our method can model this type of deformations without updating the shape basis per frame. Exploring this way forward will be part of our future work.

3 Continuum Mechanics Deformation Model

A common way to model nonrigid 3D shapes in computer vision is to represent the 3D shape as a linear combination of shape basis [9, 12, 15, 21, 39, 40, 47, 55]. The complexity of the problem can be reduced using dimensionality reduction techniques such as PCA [11, 33] or modal analysis [42, 48, 50]. In this work, we only need an estimation of the shape at rest (from rigid structure-from-motion) to apply modal analysis and compute a shape basis, instead of using nonrigid 3D training data. We propose a method to compute the shape basis from a continuum mechanics physics-based model of the scene. Our approach is valid for both sparse and dense data and for encoding both bending and stretching deformations. We first review some dynamics concepts from continuum mechanics that will lead to our formulation of the estimation of the deformable shape basis.

Fig. 2

Left Representation of some nonrigid mode shapes of a plate surface discretized into triangular elements with $\#$176 nodes. We show the effect of adding the mode shape (colored mesh) to the shape at rest (black mesh) using an arbitrary weight. Note that the effect of subtracting can be obtained using the opposite weight. First and second column: bending mode shapes. Third and fourth column: stretching mode shapes. Right Eigen-frequencies $\omega _{k}$ for the previous black mesh in logarithmic scale. Rigid, bending, and stretching mode shape intervals in green, blue and red line, respectively. Best viewed in color (Color figure online)

3.1 Dynamics Overview

The dynamic response of a nonrigid solid under external actions has been widely studied in mechanical engineering [10, 66]. Numerical methods are mandatory to approximately solve the partial differential equations modeling this behavior, with FEM being the most common approach.

A continuous object $\varOmega$ can be discretized into a number of finite elements $\varOmega _e$ (Fig. 2). Each element is defined by the 3D location of its nodes, ${\bar{\mathbf {s}}}_{j}$ for a generic node j. Hence the geometry of the undeformed solid is encoded as $\bar{\mathbf {S}} \in \mathbb R^{3\times p}$ where the matrix columns are the 3D coordinates defining the location of the p discretization nodal points:

$$\begin{aligned} {\bar{\mathbf {S}}}= \begin{bmatrix} {{\bar{\mathbf {s}}}_{1}}&{\ldots }&{{\bar{\mathbf {s}}}_{j}}&{\ldots }&{{\bar{\mathbf {s}}}_{p}} \end{bmatrix}=\begin{bmatrix} {X_{1}}&{\ldots }&{X_{j}}&{\ldots }&{X_{p}} \\ {Y_{1}}&{\ldots }&{Y_{j}}&{\ldots }&{Y_{p}}\\ {Z_{1}}&{\ldots }&{Z_{j}}&{\ldots }&{Z_{p}}\end{bmatrix}. \end{aligned}$$

(1)

Alternatively, for later computations, we also define the vectorized form of ${\bar{\mathbf {S}}}$ as ${\bar{\mathbf {S}}}\in \mathbb R^{3p\times 1}$.

The fundamental equations of discrete structural mechanics are elaborate versions of Newtonian mechanics formulated as force balance statements. The dynamic response of the object $\varOmega$ is governed by the laws of physics and can be modeled using the general damped forced vibrations equation as

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {u}}(t)+\mathbf {C}\dot{\mathbf {u}}(t)+\mathbf {K}\mathbf {u}(t)=\mathbf {r}, \end{aligned}$$

(2)

where $\mathbf {M}$, $\mathbf {C}$, and $\mathbf {K}$ are the global mass, damping, and stiffness $3p\times 3p$ matrices, respectively. $\mathbf {u}$ and $\mathbf {r}$ are the $3p\times 1$ 3D nodal displacement and external forces vectors, respectively. The motion at each node j is specified by means of $\mathbf {u}_j=\left( \varDelta X_j, \varDelta Y_j, \varDelta Z_j \right) ^\top$. Derivatives with respect to t are denoted by $\dot{\mathbf {u}}(t)\equiv \frac{d\mathbf {u}(t)}{d t}$ and $\ddot{\mathbf {u}}(t)\equiv \frac{d^2\mathbf {u}(t)}{d t^2}$. In the linear case, both matrices $\mathbf {K}$ and $\mathbf {M}$ are independent of $\mathbf {u}$ and $\mathbf {r}$ since they are evaluated at the nondeformed state $\mathbf {u}=\mathbf {0}$.

However, the previous force balance can be replaced in practice by an undamped free vibrations equation as

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {u}}(t)+\mathbf {K}\mathbf {u}(t)=\mathbf {0} . \end{aligned}$$

(3)

In this case, in the absence of external loads $\mathbf {r}=\mathbf {0}$, the displacement can be determined from the initial conditions, i.e., only knowing a shape at rest ${\bar{\mathbf {S}}}$. The internal elastic forces $\mathbf {K}\mathbf {u}$ balance the negative of the inertial forces $\mathbf {M}\ddot{\mathbf {u}}$ which can be interpreted as assigning a certain mass and a certain stiffness between nodal points. This undamped model gives conservative answers and is easier to handle numerically. The equation is linear and homogeneous, and its solution is a linear combination of exponentials modulated by the mode shapes, i.e., of the form $\mathbf {u}=\varvec{\psi }\sin \left( \omega t\right)$ with $\varvec{\psi }$ a 3p-dimensional vector and $\omega$ a real scalar.

3.2 Proposed Model Matrices

This section is devoted to the computation of the matrices $\mathbf {K}$ and $\mathbf {M}$ in Eq. (3). We discretize the surface of the observed solid into m linear triangular elastic finite elements with $\mathcal {E}$ connectivity. We compute the stiffness matrix $\mathbf {K}$ by means of a model for thin-plate elements. The deformation is modeled as a combination of plane-stress and Kirchhoff’s plate, using the free-boundary conditions matrix for linear elastostatic objects with isotropic and homogeneous material properties, as proposed by [3]:

(4)

where $\mathbf {B}_e$ is the strain-displacement matrix defined in terms of the approximation function derivatives, i.e., this matrix relates the strain and displacement fields. $\mathbf {D}$ is the constitutive matrix depending on the elastic properties of the material: Young’s modulus E and Poisson’s ratio $\nu$ (for more details, see [10]). We assume near incompressible materials $\nu \approx 0.5$, valid for rubber, papers, and human tissue such as a face. $\mathcal {T}$ is the local-to-global displacement transformation matrix. Finally, represents the assembly operator, i.e., the global matrix is assembled from the piecewise contributions.

To model the mass matrix $\mathbf {M}$, we assume a lumped mass at the nodes, leading to the mass matrix being computed as

(5)

preserving the total element mass $\sum _{a}\tilde{M}^{e}_{aa}=\int _{\varOmega _e} \rho \, d\varOmega _e$, where $\tilde{M}^{e}_{aa}$ is the mass per component, and $\rho$ is the material density (mass-density). For simplicity, the surface thickness h is the same for all elements. $A_e$ represents the element area. While a lumped mass provides less rigidity to the shape with respect to a distributed mass (the physical configuration), in our domain this difference is negligible and the accuracy of both models is roughly the same. Since a lumped mass provides a more efficient model, we always use this model.

3.3 Modal Analysis

According to structural engineering FEM analysis [10], the deformed object at a given sample time can be approximated as a linear combination of some mode shapes which can be computed by solving a generalized eigenvalue problem from the undamped free vibration dynamics (see Eq. (3)). Modal analysis is standard in structural engineering and has also been applied in computer vision to the spring mesh model in medical imaging [43]. In [35, 42], it was used for motion analysis and to track and recover heart motion, and in [48, 50] for nonrigid 2D tracking. Modal analysis was used to decouple the equilibrium equations by obtaining a closed-form solution of Eq. (2).

In this work, we propose to apply modal analysis to a soup of elastic triangles with unknown material properties $(E,\rho )$. Hence, the stiffness matrix $\mathbf {K}$ and mass matrix $\mathbf {M}$ are computed per unit of E and $\rho$, respectively. This does not limit the generality of our model. The only implication is that the estimated displacement will be up to scale. Our algorithm does not require boundary conditions, i.e., rigid points, but we could exploit them if they were available by solving a constrained eigenvalue problem with Dirichlet constraints to fix the values of several points $\mathbf {u}_j=\mathbf {0}$. It is worth pointing that since our method employs a triangulated mesh of 2D finite elements, a subset of deformations like articulated motion cannot be modeled. To solve this, we would have to incorporate another type of finite elements, such as springs or beams. In a similar way, to model balloon-like objects 3D finite elements are required. Exploring this way is part of our future work. Finally, we directly use the mode basis without using the decoupled system in Eq. (2), avoiding having to estimate the applied forces.

The undamped free vibration response of the 3D structure caused by a disturbance with respect to the shape at rest—modeled by Eq. (3)—can be estimated by solving the generalized eigenvalue problem in $\omega ^2$:

$$\begin{aligned} \mathbf {K}\varvec{\psi }_k=\mathbf {M}\omega ^2_k\varvec{\psi }_k \;, \end{aligned}$$

(6)

where $\left\{ \varvec{\psi }_k, \omega _k^2\right\}$, $k\in N_m$ are the mode shapes (eigenvectors) and frequencies (eigenvalues), respectively. $N_m:=\{1\ldots 3p\}$ is the index set. Each eigenmode $\varvec{\psi }_k$ is a $3p \times 1$ vector and its components are the displacements for all p nodes in the discretization. The modes are normalized to satisfy the orthonormality conditions $\varvec{\psi }_{k}^{\top }\mathbf {M}^{-1}\mathbf {K}\varvec{\psi }_{l}=\omega ^{2}_{k}\varvec{\psi }_{k}^{\top } \varvec{\psi }_{l}$ and $\varvec{\psi }_{k}^{\top } \varvec{\psi }_{l}=\delta _{kl}$, where $\delta _{kl}$ is the Kronecker delta and $l\in N_m$, such that $\Vert \varvec{\psi }_{k}\Vert _{2}=1$.

3.4 Mode Shape Basis: Analysis and Selection

Modal analysis yields 3p orthonormal modes—provided $\mathbf {K}$ and $\mathbf {M}$ are symmetric positive definite—[see some examples in Fig. 2(left)]. To analyze the mode shapes or vibration modes, we sort them according to the energy they need to be excited, using a frequency spectrum from lower to higher frequencies (see Fig. 2(right)). In the case, where no boundary conditions are imposed, we can approximately identify three practical mode families, instead of the two proposed in [48], separating the intermediate modes into bending and stretching ones as follows:

• Rigid motion modes (R) Theoretically the first 6 frequencies should be zero, because they correspond to 6 degree of freedom rigid body motions. However, in practice, the rank of stiffness matrix $\mathbf {K}$ is 4 instead of 6 due to the thin-plate approximation [3]. Hence, the first 4 frequencies are zero up to numerical error. This is consistent with our model having 4 rigid modes instead of the normal 6 in a full 3D FEM model [42]. These 4 rigid motion modes are excluded from the basis when coding nonrigid deformations.

• Bending modes (B) Bending, out-of-plane deformations, are mainly represented by the modes localized in the interval $\left[ 5, p+4\right]$ (see Fig. 2). These modes can represent elastic bending deformations (with low stretching in-plane). Moreover, selecting a few of the first bending modes provides an accurate mode basis to model bending deformations.

• Stretching modes (S) Stretching deformations can be modeled as a linear combination of the modes in the interval $\left[ p+5, 2p\right]$. Similarly, selecting only the first stretching modes provides a basis to accurately represent the stretching in-plane deformations.

The rest of the mode shapes $\left[ 2p+1,3p\right]$—the higher frequencies—do not correspond to physical deformations but to artifacts resulting from the discretization process. When at least three noncollinear rigid points are considered, the rigid motion of the modes does not appear in the frequency spectrum. The first modes are similar to the linear, quadratic, and twist modes in [20, 45], but our shape basis is more general including additional modes such as high order modes, not available in the quadratic model. The mode shapes capture decreasingly important details in the shape deformation, following a coarse-to-fine approach. Hence, the lower frequencies within each interval model the global deformations and the higher frequencies the local details.

Fig. 3

Fitting real 3D models with the proposed mode shape basis as a function of the number of mode shapes. Left We display a specific shape for each dataset using different values of $r=\{10, 20, 40, 100\}$. Reconstructed 3D shape and the corresponding 3D ground truth are shown with red dots and black circles, respectively. Right Results for serviette and carton datasets, respectively (Color figure online)

To sum up, any nonrigid 3D displacement $\mathbf {u}$ can be modeled by a basis that contains only $\left\{ k_1, \ldots , k_r\right\} , r<<3p$ mode shapes. For notational simplicity, it is assumed that the r selected modes are renumbered $k=1,\ldots ,r$, so any displacement field vector can be approximated by a linear combination of the mode shapes expressed as

$$\begin{aligned} \mathbf {u}\approx \mathcal {S}\varvec{\gamma }=\begin{bmatrix} {\varvec{\psi }_1}&{\ldots }&{\varvec{\psi }_k}&{\ldots }&{\varvec{\psi }_r} \end{bmatrix} \begin{bmatrix} {\gamma _{1}}&{\ldots }&{\gamma _{k}}&{\ldots }&{\gamma _{r}}\end{bmatrix}^{\top }, \end{aligned}$$

(7)

where the transformation matrix $\mathcal {S}\in \mathbb R^{3p\times r}$ concatenates r mode shapes, and $\varvec{\gamma }$ is a weight vector to obtain a low-rank representation. It is worth pointing that the mode shapes $\varvec{\psi }_k$ do not depend on the material properties $(E,\rho )$. For the same shape at rest, the normalized modes are the same irrespective of $(E,\rho )$. Different $(E,\rho )$ would produce the same deformation but with a different amplitude, which can be absorbed into the deformation weights $\gamma _{k}$.

3.5 Fitting Real Deformations

To empirically demonstrate the suitability of the mode shape basis for coding real deformations, we propose to use our basis to fit 3D deforming objects. To this end, we use two datasets with 3D ground truth acquired from motion capture systems. Particularly, we employ the serviette and carton datasets² that consist in 102 shapes with 63 nodal points and in 53 shapes with 81 nodal points, respectively. Figure 3 show the effect on 3D errors of varying the rank of the subspace, observing a consistent reduction of the error as more mode shapes r are considered (some examples are also shown in figure). It is worth pointing that just a few mode shapes reduce the error by half, observation that we exploit in this paper by proposing a low-rank shape constraint. To make a fair comparison, we also consider two configurations to train a PCA-based approach. The PCA-1 in which the PCA basis is trained with first 10 samples; the PCA-2 where all data are used to train. Note that our approach consistently outperforms PCA-1, without explicitly using 3D deformable training data. Even though PCA-based methods can become very accurate if appropriate learning data are available (such as PCA-2), this method have used an accurate deformation model learned from the ground truth of the whole data, which may be difficult to obtain in real applications such as medical videos we process in experimental section. This limitation is outperformed by our method, which in contrast just needs a rest shape estimation.

Fig. 4

Left Representation of some stretching mode shapes of a plate surface discretized into triangular elements with three meshes. First row $5\times 10$ mesh in dark cyan. Second row $10\times 20$ mesh in magenta. Third row $15\times 30$ in orange. The shape at rest is always displayed with a black mesh. Right Eigen-frequencies $\omega _{k}$ for the previous black multiple meshes in logarithmic scale. We display the interval $\left[ \omega _{low},\omega _{high}\right]$ to find stretching mode shapes in green, being similar for all meshes. Best viewed in color (Color figure online)

3.6 Computational Cost

In this section, we analyze the computational complexity of obtaining mode shapes when solving the eigenvalue problem. To do this, we first compute $\mathbf {M}^{-1}\mathbf {K}$ to transform the generalized eigenvalue problem into a standard one. In the case of the lumped mass matrix—a diagonal matrix—in Eq. (5), the inverse computation cost is negligible. The actual computation and assembly of both $\mathbf {K}$ and $\mathbf {M}$ has a $\mathcal {O}\left( p\right)$ complexity that is only significant for dense maps, where the process could easily be parallelized.

The second step is the computation of the mode shapes as eigenvectors. For computational efficiency, we propose to use orthogonal iteration with Rayleigh–Ritz acceleration [18, 24]. This returns the eigenvectors (mode shapes), sequentially in ascending frequency order, hence the complexity scales with the number of computed modes. If the r mode shapes to be included in the basis correspond only to low frequencies (bending modes), the computation is efficient with a complexity scaling with $4+r$ even for dense meshes. However, if both bending and stretching modes have to be computed, the complexity scales with $4+r+p$, which may become prohibitive in both computation time and memory requirements, especially for dense meshes.

3.7 Computation of Mode Shapes for Dense Meshes

The mode shapes have been classified into two families: bending and stretching modes. The first family of modes is affordable to compute even in the dense case by solving Eq. (6), but it can only encode out-of-plane bending deformations. In contrast, for scenes with stretching in-plane deformations, a few stretching modes have to be included to have a representative basis. Unfortunately, computing these dense modes may become prohibitive in terms of computational and memory requirements. To solve this limitation, in this work, we propose two algorithms to compute mode shape at a lower cost. The first computes the eigenvalue problem in a sparse mesh to obtain the frequencies of vibration and then computes the stretching modes applying the frequency-based mode shapes method to the dense mesh. The second approach computes the eigenvalue problem in a sparse mesh and, exploiting the approximation functions within finite elements, computes modes in the dense mesh applying a robust coarse-to-fine approach. This enables dense problems to be easily solved and drastically reduces the computational and memory requirements to compute all frequencies in the spectrum.

3.7.1 Frequency-based Dense Mode Shape Estimation

In this section, we present our frequency-based method to compute dense stretching mode shapes. Our approach begins by solving the eigenvalue problem in Eq. (6) for a sparse mesh of q points where $q<<p$, allowing us to easily obtain all the frequencies in the spectrum. As we can locate the stretching modes in the ordered frequency spectrum (see section 3.4), we can obtain a finite interval of frequencies for these modes situated between $\omega _{low}$ and $\omega _{high}$. Next, we can formulate the problem to estimate mode shapes over the dense mesh of p points as

$$\begin{aligned} \mathop {\hbox {arg min}}\limits _{\varvec{\psi }_k}&\Vert&\left( \mathbf {M}^{-1}\mathbf {K}- \omega ^2_k \mathbf {I}\right) \varvec{\psi }_k \Vert ^{2} \nonumber \\ \text {subject} \,\,&\text {to}&\,\,\, \omega _{low} \le \omega _k\le \omega _{high}, \end{aligned}$$

(8)

where $\varvec{\psi }_k$ are the mode shapes with frequencies between $\omega _{low}$ and $\omega _{high}$. Although this approach is valid for both bending and stretching modes, our aim is to obtain the stretching modes while avoiding having to compute the bending modes. Figure 4 displays the frequency spectrum for three meshes and some stretching modes applying this approach over the dark cyan sparse mesh. It can be seen that the frequency $\omega _{low}$ remains unchanged for all meshes. We can obtain this frequency over a sparse mesh, and then solve Eq. (8) over a dense mesh by linear least squares. The computed mode shapes using this method are not an approximation and they can code both low and high frequencies.

While this approach offers new theoretical insights, it is very sensitive to changes in the rest shape. Due to this sensitive, this approach is particularly relevant for regular meshes (such as the used in registration) where the sub-sampling process is trivial. For instance, it could easily be employed in template-based methods [33, 46, 47] using multiple regular meshes and a template where the 3D shape is accurately known.

Fig. 5

Coarse-to-fine approach to modal analysis. a Reference image plane to compute optical flow. b Dense 2D tracking of p points. c Subsample of dense shape into q points (green points). d Delaunay triangulation for sparse mesh. e Active search to match every point in the sparse mesh. Please zoom into the electronic images for a detailed view (Color figure online)

3.7.2 Coarse-to-Fine Mode Shape Estimation

In this section, we propose our second efficient approach to compute dense mode shapes. We exploit the approximation functions used to define the displacement field within a finite element [10]. Therefore, as in the previous method, we solve the eigenvalue problem for $q<<p$ scene points obtaining $\mathcal {S}^{*} \in \mathbb R^{3q\times r}$ basis shapes and then compute $\mathcal {S}\in \mathbb R^{3p\times r}$ for p points using the approximation functions. First, we subsample the scene points to convert the p-dimensional map—dense mesh—(see Fig. 5b) into a q-dimensional map- –sparse mesh—(see Fig. 5c, d). Each point in the dense mesh must then be matched with an element of the sparse mesh (see Fig. 5e). The q-dimensional map has to ensure a sparse mesh where every p point can be matched. To find an element in the sparse mesh $\triangle \left( {\bar{\mathbf {s}}}_{a}{\bar{\mathbf {s}}}_{b}{\bar{\mathbf {s}}}_{c}\right)$ with nodal labels $\{a,b,c\}$ per point ${\bar{\mathbf {s}}}_{j}$, we suggest an active search by computing several cross products over a two-dimensional space:

$$\begin{aligned}&\sum _{\begin{array}{c} \tau =0 \\ \tau +1 \in \text {mod(3)} \end{array}}^{2} \left( \chi _{\iota } \left( \overrightarrow{{\bar{\mathbf {s}}}_\tau \, {\bar{\mathbf {s}}}_{j}} \times \overrightarrow{{\bar{\mathbf {s}}}_{\tau } \, {\bar{\mathbf {s}}}_{\tau +1}}\right) = {\left\{ \begin{array}{ll} {1} &{} {\text {if} \left( \overrightarrow{{\bar{\mathbf {s}}}_\tau \, {\bar{\mathbf {s}}}_{j}} \times \overrightarrow{{\bar{\mathbf {s}}}_{\tau } \, {\bar{\mathbf {s}}}_{\tau +1}}\right) \in \iota }\\ {0} &{} {\text {if} \left( \overrightarrow{{\bar{\mathbf {s}}}_\tau \, {\bar{\mathbf {s}}}_{j}} \times \overrightarrow{{\bar{\mathbf {s}}}_{\tau } \, {\bar{\mathbf {s}}}_{\tau +1}}\right) \notin \iota } \end{array}\right. } \right) \nonumber \\&\quad ={\left\{ \begin{array}{ll} {3} &{} {\text {if}\;\; {\bar{\mathbf {s}}}_{j}\in \triangle \left( {\bar{\mathbf {s}}}_{0}{\bar{\mathbf {s}}}_{1}{\bar{\mathbf {s}}}_{2}\right) }\\ {\le 2} &{} {\text {if}\;\;{\bar{\mathbf {s}}}_{j}\notin \triangle \left( {\bar{\mathbf {s}}}_{0}{\bar{\mathbf {s}}}_{1}{\bar{\mathbf {s}}}_{2}\right) } \end{array}\right. } \end{aligned}$$

(9)

where the labels $\{a,b,c\}\equiv \{0,1,2\}$ are renumbered and $\chi _{\iota }$ represents a step function with $\iota \equiv \left[ 0,\infty \right)$. ${\bar{\mathbf {s}}}_{j}$ is inside the triangle element $\triangle \left( {\bar{\mathbf {s}}}_{a}{\bar{\mathbf {s}}}_{b}{\bar{\mathbf {s}}}_{c}\right)$ when all the cross products are nonnegative, three in our case. Note that this two-dimensional space is a dimensional reduction of the shape at rest, and hence it can be obtained either by projecting the shape at rest onto the image plane or using the reference image plane (see Figs. 5a, 6). When the active search is completed, we need to compute its natural coordinates $(\xi _j,\eta _j)$ within the element $\triangle \left( {\bar{\mathbf {s}}}_{a}{\bar{\mathbf {s}}}_{b}{\bar{\mathbf {s}}}_{c}\right)$. First, we transform from the global system to a $\mathcal {L}$ local one $\triangle \left( {\bar{\mathbf {s}}}_{a}^{\mathcal {L}}{\bar{\mathbf {s}}}_{b}^{\mathcal {L}}{\bar{\mathbf {s}}}_{c}^{\mathcal {L}}\right)$ defined on the plane of each triangle element and then obtain the natural coordinates as

$$\begin{aligned} \begin{bmatrix} \xi _j \\ \eta _j \end{bmatrix}= \bigg [\Big [{\bar{\mathbf {s}}}_{b}^{\mathcal {L}} \, \, {\bar{\mathbf {s}}}_{c}^{\mathcal {L}} \Big ] - \Big [{\bar{\mathbf {s}}}_{a}^{\mathcal {L}} \otimes \mathbf {1}^{\top }_{2} \Big ] \bigg ]^{-1} \Big [ {\bar{\mathbf {s}}}_{j}^{\mathcal {L}}-{\bar{\mathbf {s}}}_{a}^{\mathcal {L}}\Big ], \end{aligned}$$

(10)

where $\mathbf {1}_{2}$ is a vector of ones and $\otimes$ indicates the Kronecker product. The 3D displacement can be obtained using the linear approximation functions $\mathfrak {N}^{l}(\xi _j,\eta _j) \equiv \left[ N_{1}^{l} \, N_{2}^{l} \, N_{3}^{l} \right]$ [10] within the element. The 3D displacement for every mode shape can be computed as

$$\begin{aligned} \mathcal {S}_{j} =\Big [\mathfrak {N}^{l}(\xi _j,\eta _j) \otimes \mathbf {I}_{3}\Big ] \begin{bmatrix} \mathcal {S}_{a}^{*}&\mathcal {S}_{b}^{*}&\mathcal {S}_{c}^{*}\end{bmatrix} ^{\top }, \end{aligned}$$

(11)

where $\mathcal {S}_{a}^{*}$, $\mathcal {S}_{b}^{*}$, and $\mathcal {S}_{c}^{*}$ are $3 \times r$ displacement vectors for the mode shapes basis corresponding to the triangle element $\{a,b,c\}$ to which ${\bar{\mathbf {s}}}_{j}$ belongs. Finally, $\mathcal {S}_{j}$ is placed in rows $3j-2$ through 3j in $\mathcal {S}$. Note that for coding nonrigid shapes, the high-frequency details are included in the shape at rest with dense mesh, while these have been lost in the shape basis for the approximation of this method. However, our approximation is accurate even using a sparse mesh with a 10 $\%$ of points in the dense mesh, as we show in the experimental section.

Fig. 6

Left A dense shape of p nodes (red points) is reduced to q nodes (green points) to solve the eigenvalue problem. In this case, the 2D space can be obtained by projecting the 3D shape at rest estimation. Right Active search to match the p points with triangular elements of the sparse mesh. Please zoom into the electronic images for a detailed view (Color figure online)

Regarding complexity, we drastically reduce the computational cost of computing dense mode shapes using this approach. To compute and assemble both FEM matrices, the complexity is reduced from $\mathcal {O}\left( p\right)$ to $\mathcal {O}\left( q\right)$, with q being the number of points in the sparse mesh, representing under 10 $\%$ of the points in the dense mesh. This allows us to easily compute the full frequency spectrum—including stretching shapes with high frequencies—solving a simple eigenvalue problem of low dimension. It is worth to point that for the frequency-based algorithm, the complexity to solve the eigenvalue problem over a sparse mesh is similar, but later it is necessary to compute a few mode shapes over the dense mesh and the performance is reduced.

4 Problem Formulation

Let us consider a 3D structure $\mathbf {S}_f$ of p points on an image frame f. The orthographic projection $\mathbf {W}_f$ is expressed as

$$\begin{aligned} \mathbf {W}_f=\begin{bmatrix} {u_{f1}}&{\ldots }&{ u_{fj}}&{\ldots }&{u_{fp}} \\ {v_{f1}}&{\ldots }&{ v_{fj}}&{\ldots }&{v_{fp}} \end{bmatrix} = \varvec{\Uppi }\mathbf {Q}_f \mathbf {S}_f + \mathbf {T}_f + \mathbf {N}_{f}, \end{aligned}$$

(12)

where $\varvec{\Uppi }$ is the $2\times 3$ orthographic camera matrix, and $\mathbf {Q}_f$ is the $3\times 3$ rotation matrix. Next, $\mathbf {R}_f=\varvec{\Uppi }\mathbf {Q}_f$ are the first two rows of a full rotation matrix (i.e., $\mathbf {R}_f\mathbf {R}^{\top }_f=\mathbf {I}_{2}$). Due to the orthographic projection, the depth coordinate of the translation vector cannot be resolved. Considering this ambiguity, we model 2D translations $\mathbf {t}_{f}$ defined as $\mathbf {T}_{f}=\mathbf {1}^{\top }_{p} \otimes \mathbf {t}_{f}$ with $\mathbf {1}_{p}$ a vector of ones and $\mathbf {t}_{f}=\mathbf {R}_{f}\mathbf {d}_{f}$, where $\mathbf {d}_{f}$ is a 3D-translation vector. Finally, $\mathbf {N}_f$ is a $2\times p$ zero-mean Gaussian noise process matrix for modeling the noise in image tracks. The noise vector for a generic point j is $\mathbf {n}_{fj} \sim \mathcal {N}\left( 0;\sigma ^2 \mathbf {I}\right)$ with variance of the measurements $\sigma$ in each dimension.

Alternatively, the orthographic projection $\mathbf {w}_f$ into vectors can be expressed as

$$\begin{aligned} \mathbf {w}_f= \big [ {u_{f1}} \, \, { } \, \, {v_{f1}} \, \, { } \, \, {\ldots } \, \, { } \, \, {u_{fp}} \, \, {v_{fp}} \big ]^{\top } = \mathbf {G}_f \mathbf {S}_f + \bar{\mathbf {t}}_f + \mathbf {n}_{f}, \end{aligned}$$

(13)

where $\mathbf {G}_{f}=\mathbf {I}_{p} \otimes \mathbf {R}_{f}$ with $\mathbf {I}_{p}$ a $p\times p$ identity matrix, and $\bar{\mathbf {t}}_{f}$ and $\mathbf {n}_{f}$ are the vectorized form of $\mathbf {T}_f$ and $\mathbf {N}_f$, respectively.

Our problem is to simultaneously estimate camera motion $\left( \mathbf {R}_f,\mathbf {t}_f\right)$ and the nonrigid 3D shape $\mathbf {S}_f$ as the data arrive, in every frame f from uncalibrated 2D point correspondences in a monocular video $\mathbf {W}_f$. Note that our measurements can have occlusions and lost tracks, and the measurement matrix $\mathbf {W}_f$ is not full. For these cases, only a set $\mathcal {V}$ of visible points $\varrho$ is observed, but always all p scene points have to be reconstructed.

4.1 Proposed Linear Subspace Deformation Model

We propose to model the nonrigid shape at each instant as a linear combination of a mean shape and r deformation mode shapes from modal analysis. Hence the estimation of the 3D structure at each frame f comes down to estimating the corresponding weight vector $\varvec{\gamma }_f$. It is also useful in our formulation to represent $\mathcal {S}$ using a permutation operator $\mathcal {R}(\mathcal {S})$ that rearranges the entries of $\mathcal {S}$ into a $3r\times p$ matrix such that the j-th column of $\mathcal {R}(\mathcal {S})$ contains all the displacement ${\varDelta X_{rj}}, {\varDelta Y_{rj}}, and {\varDelta Z_{rj}}$ coordinates of the point j for all r modes. Considering Eq. (7), the 3D displacement field into matrices can be rewritten as $\mathbf {U}=\left( \mathbf {I}_3 \otimes \varvec{\gamma }^{\top } \right) \mathcal {R}(\mathcal {S})$ where $\mathbf {I}_3$ is a $3\times 3$ identity matrix. The deformed structure at frame f can be written as

$$\begin{aligned} \mathbf {S}_{f}={\bar{\mathbf {S}}}+\mathbf {U}_f={\bar{\mathbf {S}}}+\left( \mathbf {I}_3 \otimes \varvec{\gamma }^{\top }_f \right) \mathcal {R}(\mathcal {S}). \end{aligned}$$

(14)

Assuming noise-free observations, we can rewrite the orthographic projection Eq. (12) as

$$\begin{aligned} \mathbf {W}_f = \mathbf {R}_f \left( {\bar{\mathbf {S}}}+\left( \mathbf {I}_3 \otimes \varvec{\gamma }^{\top }_f \right) \mathcal {R}(\mathcal {S}) \right) + \mathbf {T}_f . \end{aligned}$$

(15)

In section 5.1, we propose an on-line BA-based algorithm to solve this nonlinear problem as the data arrive.

4.2 Proposed Probabilistic Modal Analysis Model

We also propose to replace the linear subspace model described above with a probabilistic model using a Gaussian prior on each shape in the subspace, inspired by probabilistic PCA [44, 53, 56]. The weight coefficients $\varvec{\gamma }_f$ are modeled with a Gaussian prior distribution with zero-mean as

$$\begin{aligned} \varvec{\gamma }_f \sim \mathcal {N}\left( \mathbf {0};\mathbf {I}_{r}\right) . \end{aligned}$$

(16)

These deformation weights $\varvec{\gamma }_f$ become latent variables that can be marginalized out and are never explicitly computed. Employing this Gaussian prior over $\varvec{\gamma }_f$, the weights for each shape are similar to each other, the nonrigid shape distribution being $\mathbf {s}_{f}\sim \mathcal {N}\left( {\bar{\mathbf {s}}};\mathcal {S}\mathcal {S}^{\top }\right)$, producing smooth deformations with respect to shape at rest. The r principal axes are modeled using an orthogonal fixed basis $\mathcal {S}$. In this case, the nonrigid structure at frame f, considering Eq. (7) can be written as

$$\begin{aligned} \mathbf {s}_{f}={\bar{\mathbf {s}}}+\mathbf {u}_{f}={\bar{\mathbf {s}}}+\mathcal {S}\varvec{\gamma }_{f}= \tilde{\mathcal {S}} \tilde{\varvec{\gamma }}_{f}, \end{aligned}$$

(17)

where $\tilde{\mathcal {S}}=\left[ {\bar{\mathbf {s}}}\,\,\, \mathcal {S}\right]$ is the concatenation matrix of the shape at rest together with the mode shapes, and $\tilde{\varvec{\gamma }}_{f}=\left[ 1\,\,\,\varvec{\gamma }_{f}^{\top } \right] ^{\top }$.

By assuming Gaussian noise over the shape and the observations, considering Eq. (13) the distribution to be estimated over the projected points $\mathbf {w}_f$ is also Gaussian:

$$\begin{aligned} \mathbf {w}_f \sim \mathcal {N}\left( \mathbf {G}_{f}{\bar{\mathbf {s}}}+\bar{\mathbf {t}}_{f};\mathbf {G}_f\mathcal {S}\mathcal {S}^{\top } \mathbf {G}_{f}^{\top } + \sigma ^2 \mathbf {I}\right) . \end{aligned}$$

(18)

This is equivalent to solving the nrs f m  problem. In Sect. 5.2, we propose an on-line EM-based algorithm to solve the maximum likelihood estimation as the data arrive in this latent variable problem.

5 Sequential NRSfM

Our aim is to sequentially estimate camera motion and time-varying 3D shape from 2D point tracks. This section is devoted to describing the details of our sequential approaches to nrs f m. Note that we just need to tune the number of mode shapes r in the subspace. While most state-of-the-art techniques are very sensitive to the choice of the specific rank, our methods do not require fine tuning (see experimental Sect. 6). Obtaining a sequential system in real time could easily be fixed in terms of computational cost.

5.1 On-line BA Algorithm

We use a sliding temporal window approach as proposed in [40] to perform BA [58] on the last $\mathcal {W}$ frames. As the deformation modes, $\mathcal {S}$ are computed in a previous step following the modal analysis described in Sect. 3, and only an estimate of the shape at rest ${\bar{\mathbf {s}}}$ is required, the trilinear sequential nrs f m  problem is reduced to the estimation of per-frame camera motion $\left( \mathbf {R}_i,\mathbf {t}_{i}\right)$ and deformation weights $\varvec{\gamma }_{i}$, i.e., a bilinear problem. This involves the estimation of a very small number of parameters r to encode the shape at each frame, which leads to a low computational cost system. The model parameters are estimated on the fly by minimizing the image re-projection error of all the observed points $\varrho$ over all frames in the current temporal window $\mathcal {W}$ by means of the following cost function $\mathcal {A}\left( \mathbf {R}_{i}, \mathbf {t}_i, \varvec{\gamma }_{i}\right)$:

$$\begin{aligned}&\mathop {\hbox {arg min}}\limits _{\mathbf {R}_{i}, \mathbf {t}_i,\varvec{\gamma }_i} \lambda _{\gamma } \sum _{i=f-\mathcal {W}+2}^{f} \Vert \varvec{\gamma }_{i}^{\top } - \varvec{\gamma }_{i-1}^{\top } \Vert ^{2}_{\mathcal {F}} \nonumber \\&\quad + \, \lambda _{t} \sum _{i=f-\mathcal {W}+2}^{f} \Vert \mathbf {t}_i - \mathbf {t}_{i-1} \Vert ^{2}_{\mathcal {F}} \nonumber \\&\quad + \,\sum _{i=f-\mathcal {W}+1}^{f} \sum _{\varrho \in \mathcal {V}} \Vert \mathbf {W}_{i\varrho } - \mathbf {R}_i \left( {\bar{\mathbf {S}}}_{\varrho }+\left( \mathbf {I}_3 \otimes \varvec{\gamma }^{\top }_i \right) \mathcal {R}(\mathcal {S}_{\varrho }) \right) \nonumber \\&\quad -\,\mathbf {T}_i \Vert ^{2}_{\mathcal {F}} + \lambda _{q} \sum _{i=f-\mathcal {W}+2}^{f} \Vert \mathbf {R}_i (\mathbf {q}_i) - \mathbf {R}_{i-1} (\mathbf {q}_{i-1}) \Vert ^{2}_{\mathcal {F}}, \end{aligned}$$

(19)

where $\Vert \cdot \Vert ^{ }_{\mathcal {F}}$ is the Frobenius norm. The rotation matrices $\mathbf {R}_i (\mathbf {q}_i)$ are parameterized using quaternions to guarantee orthonormality $\mathbf {R}^{ }_{i} \mathbf {R}^{\top }_{i}=\mathbf {I}_2$. We add temporal smoothness priors to penalize strong variations in the deformation weights $\varvec{\gamma }_{i}$, translations $\mathbf {t}_i$, and camera matrices $\mathbf {R}_i (\mathbf {q}_i)$. The positive regularization weights $\lambda _{\gamma }$, $\lambda _{t}$, and $\lambda _{q}$ govern the relative importance of the regularization terms, and they are determined empirically. These coefficients are fixed in all the experiments we describe in the experimental section. This problem can be solved using a sparse Levenberg–Marquardt nonlinear minimization algorithm.

To initialize the parameters for a new incoming frame, we consider the smoothness priors for both camera motion and nonrigid deformation, penalizing far solutions from the previous frame. The mode shape weights $\varvec{\gamma }_{i}$ are initialized assuming rigid motion $\varvec{\gamma }_{i}=\varvec{\gamma }_{i-1}$, and the camera pose is initialized as $\mathbf {R}_{i}=\mathbf {R}_{i-1}$ and $\mathbf {t}_{i}=\mathbf {t}_{i-1}$.

5.2 On-line EM Algorithm

We propose an on-line version of the EM algorithm—similar to EM for factor analysis [23]—over a sliding window on the last $\mathcal {W}$ frames, similar to the algorithm described above. In this case, we denote the set of model parameters to be estimated by $\Theta _{f}\equiv \{\mathbf {R}_{f},\mathbf {t}_{f},\sigma ^{2} \}$, the hidden data by $\varvec{\gamma }_{f}$, and the complete data as $\{\mathbf {w}_{f},\varvec{\gamma }_{f}\}$. Given the observable data $\mathbf {w}_{f-\mathcal {W}+1:f}$ over the sliding temporal window of frames with indexes $_{f-\mathcal {W}+1:f}$, we estimate the model parameters over all the frames in the current window denoted as ${\hat{\mathcal {W}}}$. For dealing with missing data, we consider all the observed points $\varrho \in \mathcal {V}$ over all the frames in the current window. Note that for full measurements, the number of visible points $\varrho$ is equal to p. The joint probability of $\mathbf {w}$ over a sliding window, assuming that the samples are independent and identically distributed, may be computed considering the Gaussian distribution per frame, Eq. (18), as

$$\begin{aligned} p\big (\mathbf {w}_{{\hat{\mathcal {W}}}} | \mathbf {G}_{{\hat{\mathcal {W}}}}, \bar{\mathbf {t}}_{{\hat{\mathcal {W}}}},\sigma ^2 \big ) \,\, = \prod _{i=f-\mathcal {W}+1}^{f} p\big (\mathbf {w}_{i\varrho } | \mathbf {G}_{i}, \bar{\mathbf {t}}_{i},\sigma ^2 \big ).\nonumber \\ \end{aligned}$$

(20)

The EM algorithm estimates iteratively until convergence the likelihood, alternating between two steps: the E-step and M-step. In the E-step, the expectation of the data likelihood with respect to the latent variable distribution is computed. For this, we compute the posterior distribution over latent variables $p\left( \varvec{\gamma }_{{\hat{\mathcal {W}}}}|\mathbf {w}_{{\hat{\mathcal {W}}}},\Theta _{{\hat{\mathcal {W}}}} \right) \propto p\left( \mathbf {w}_{{\hat{\mathcal {W}}}}|\varvec{\gamma }_{{\hat{\mathcal {W}}}},\Theta _{{\hat{\mathcal {W}}}} \right) p\left( \varvec{\gamma }_{{\hat{\mathcal {W}}}}|\Theta _{{\hat{\mathcal {W}}}} \right)$ given the measurements and the current parameter model on the sliding window as

$$\begin{aligned} p\big (\varvec{\gamma }_{{\hat{\mathcal {W}}}}|\mathbf {w}_{{\hat{\mathcal {W}}}},\Theta _{{\hat{\mathcal {W}}}} \big ) \sim \prod _{i=f-\mathcal {W}+1}^{f} \mathcal {N}\Big (\varvec{\mu }_i;\varvec{\varSigma }_i\Big ), \end{aligned}$$

where $\varvec{\mu }_{i}=\beta _i\left( \mathbf {w}_{i}-\mathbf {G}_{i}{\bar{\mathbf {s}}} - \bar{\mathbf {t}}_{i} \right)$ and $\varvec{\varSigma }_{i}=\mathbf {I}_{r}- \beta _{i}\mathbf {G}_{i}\mathcal {S}$, with $\beta _i=\mathcal {S}^{\top }\mathbf {G}_{i}^{\top }\left( \sigma ^{2}\mathbf {I}_{2p}+\mathbf {G}_{i}^{\top }\mathcal {S}(\mathbf {G}_{i}\mathcal {S})^{\top }\right) ^{-1}$ that is efficiently computed using the Woodbury matrix identity [63].

Note that for the missing data case, $\mathbf {G}_{i}=\mathbf {I}_{\varrho } \otimes \mathbf {R}_{i}$ with $\mathbf {I}_{\varrho }$ being a $\varrho$-order identity matrix. $\mathcal {S}$, ${\bar{\mathbf {s}}}$, and $\mathbf {w}_{i}$ are only evaluated for visible points.

In the M-step, the expected value of the log-likelihood function is optimized by replacing the latent variables by their expected values to update the model parameters. We update motion variables maximizing the likelihood with respect to parameters $\Theta$ holding hidden distribution fixed, or equivalently minimizing its expected negative log-likelihood function $\nabla _{\Theta _{i}^{t}} \;\mathcal {B}\left( \Theta _{i}^{t-1}\right) \mid ^{ }_{\Theta _{i}^{t}=\Theta _{i}^{t-1}}=0$, because the logarithm is strictly monotonous:

$$\begin{aligned} \mathcal {B}\left( \Theta _{i}\right)= & {} \mathop {\hbox {arg min}}\limits _{\Theta _{i}} \,\,\,\, \mathbb {E} \left[ - \sum _{i=f-\mathcal {W}+1}^{f} \sum _{\varrho \in \mathcal {V}} \log p\left( \mathbf {w}_{i \varrho }|\Theta _{i} \right) \right] \nonumber \\= & {} \mathop {\hbox {arg min}}\limits _{\mathbf {R}_{i},{\mathbf {t}}_{i},\sigma ^{2}} \,\, \frac{1}{2\sigma ^2}\sum _{i=f-\mathcal {W}+1}^{f} \sum _{\varrho \in \mathcal {V}} \mathbb {E}\, \Big [ \Vert \mathbf {w}_{i\varrho }\nonumber \\&-\mathbf {G}_{i}\left( {\bar{\mathbf {s}}}_\varrho +\mathcal {S}_\varrho \varvec{\gamma }_{i} \right) - \bar{\mathbf {t}}_{i} \Vert _{2}^{2} \Big ] \nonumber \\&+\varrho \mathcal {W}\log \left( 2\pi \sigma ^2\right) , \end{aligned}$$

(21)

where $\mathbb {E}[\cdot ]$ represents the expectation operator.

Note that using the Gaussian prior, we do not need to add additional temporal smoothness priors to penalize strong variations, avoiding tuning regularization weights [21, 40, 45]. This function cannot be optimized in closed form to compute a global optimum, and partial M-steps are necessary. The model parameters are individually updated in closed form, except for camera rotation (see Appendix for update rules).

In order to initialize the model parameters for a new incoming frame, the camera pose is initialized as $\mathbf {R}_{i}=\mathbf {R}_{i-1}$ and $\mathbf {t}_{i}=\mathbf {t}_{i-1}$, while the latent variables are initialized assuming a rigid motion as $\mathbb {E}\left[ \varvec{\gamma }_{i}\right] =\mathbb {E}\left[ \varvec{\gamma }_{i-1}\right]$.

5.3 Missing Data on BA-FEM and EM-FEM Algorithms

Unlike other methods [8, 12, 15], our formulations can cope with incomplete image tracks resulting from occlusions or tracking outliers, always reconstructing all the scene points. Both algorithms have the capability of dealing with missing data since the cost function is only evaluated on the set of visible points $\mathcal {V}$. After that, we exploit our global model to estimate the 2D location ${\hat{\mathbf {W}}}_{fj}$ of the missing data entries in the observation matrix:

$$\begin{aligned} {\hat{\mathbf {W}}}_{fj} = \mathbf {R}_f \left( {\bar{\mathbf {S}}}_j+\left( \mathbf {I}_3 \otimes \varvec{\gamma }^{\top }_f \right) \mathcal {R}(\mathcal {S}_j) \right) + \mathbf {t}_f. \end{aligned}$$

(22)

5.4 Shape at Rest Estimation

Our sequential approaches assume that the shape at rest can be estimated similarly to batch [20, 45] and sequential [1, 40] approaches, using a rigid factorization algorithm [31] on a few initial frames. To this end, we consider that the observed sequence contains some nr initial frames where the object is mostly rigid and does not deform substantially. Our method does not require the surfaces to be planar or developable, and modal analysis can be applied on general nonplanar rest shapes. Note that using rigid s f m to initialize is standard practice in the nrs f m community and, moreover, initialization is one of the challenges in sequential methods, including the rigid case [27].

The rest shape is a tuple $\left( \mathcal {P},\mathcal {E}\right)$ where $\mathcal {P}=(n_{1},\ldots ,n_{p})$ is a finite set of p nodes and $\mathcal {E}=(e_{1}, \ldots , e_{m})$ is a finite set of m triangular elements—over q points for dense cases—obtained by means of a Delaunay triangulation [10] on the image plane or on the reference image for dense cases [21, 22]. For simplicity, we have used the Delaunay triangulation, although we could take advantage of having an estimation of the 3D shape at rest and easily use alternative connectivity algorithms.

5.5 On-line Complexities

In this section, we show both the complexity of the memory and the computational complexity of our sequential approaches. Our nrs f m methods ensure that the computation time per image is bounded and does not grow with the number of frames, as occurs with batch approaches [20, 21, 39, 52]. We show how our methods could potentially achieve real-time performance at frame rate and, more importantly, how both methods process the video sequence as the data arrive, frame by frame.

First, we analyze the memory complexity. Our on-line algorithms store only the latest $\mathcal {W}$ frames with complexity $\mathcal {O}\left( \mathcal {W}\right)$, unlike batch algorithms where all the frames are stored with complexity $\mathcal {O}\left( f\right)$. This is an important feature for real applications where the computational resources are often much lower than in a desktop setting [62]. Next, we analyze the computational complexity for the BA-FEM and EM-FEM algorithms.

5.5.1 BA-FEM Algorithm

An efficient BA implementation consists of three principal parts: the computation of the residuals and sparse Jacobians used for the Levenberg–Marquardt algorithm with $\mathcal {O}\left( p\mathcal {W}r\right)$, building the linear system with $\mathcal {O}\left( p\mathcal {W}^2r^2\right)$ and, finally, solving the linear system with $\mathcal {O}\left( \mathcal {W}^3r^3\right)$. Since in our domain the number of frames on the sliding window $\mathcal {W}$ is relatively small, and the number of modes r is significantly smaller than the number of points in the structure shape p, and the cubic term of solving the linear system is negligible. Thus, the complexity of sequential-mode BA over a sliding window is dominated by building the linear system and computing residuals and Jacobians, dominated by $\mathcal {O}\left( p\mathcal {W}^2r^2\right)$.

5.5.2 EM-FEM Algorithm

The complexity of sequential-mode EM over the sliding window is dominated by the E-step and can be approximated on the order of $\mathcal {O}\left( t \mathcal {W}p r^{2}\right)$ as a function of the number of iterations t per frame until convergence to the desired precision. The likelihood function is increased at each iteration until convergence, i.e., $\mathcal {B}\left( \Theta _{i}^{t+1}\right) -\mathcal {B}\left( \Theta _{i}^{t}\right) < \epsilon$, where the superscript $^{t}$ represents the EM iteration. In practice, only a few iterations are necessary to achieve convergence. Moreover, in our on-line EM-FEM algorithm, we use a temporal smoothness by means of the sliding window that is initialized as the last frame, but we do not implicitly use regularizations within the sliding window as in our BA-FEM algorithm, reducing the complexity order from $\mathcal {W}^2$ to $\mathcal {W}$. The total complexity becomes $\mathcal {O}\left( p r^{2}\right)$ considering $\mathcal {W}$ to be negligible, 5 in our experiments. Furthermore, this complexity over r can be reduced when sparsity is exploited. Our sliding window approach may potentially achieve real-time performance since it could easily be parallelized for the i.i.d. assumption.

6 Experimental Results

In this section, we show the experimental results for both synthetic and real sequences, providing comparisons with respect to state-of-the-art methods. We present results from sparse to dense shapes, for isometric and elastic deformations, and finally we show our performance against corrupted observations, such as noise or missing data. In all the experiments, we report the error $e_{3\mathcal {D}}=\frac{1}{f}\sum _{i=1}^{f}\frac{\Vert \mathbf {S}_{i}^{ } - \mathbf {S}_{i}^{GT} \Vert ^{ }_{\mathcal {F}}}{\Vert \mathbf {S}_{i}^{GT} \Vert ^{ }_{\mathcal {F}}}$ where $\mathbf {S}_{i}^{ }$ is the 3D reconstruction and $\mathbf {S}_{i}^{GT}$ is the ground truth. Before computing this 3D error, the 3D reconstruction is aligned with the corresponding ground truth using Procrustes analysis over all the frames.

6.1 Synthetic Data

In this section, we compare our sequential methods BA-FEM and EM-FEM to state-of-the-art techniques, for both sparse and dense observations. In addition, we also analyze the two proposed strategies to compute stretching modes. In all cases, the synthetic deformation is observed by an orthographic camera.

6.1.1 Elastic Sequences

First, we propose two synthetic sequences of a deforming elastic plate with irregular (Syn. 1) and regular (Syn. 2) discretization, respectively. In both cases, we have considered a nonlinear hyperelastic Yeoh material [64] to model large deformations, but just consider a different discretization. The Yeoh model for incompressible materials is a function only of the first strain invariant $I_{1}$, and its deformation energy is defined as $W=C_{10}(I_{1}-3)+C_{20}(I_{1}-3)^2+C_{30}(I_{1}-3)^3$, where the parameters $\{C_{10},C_{20},C_{30}\}$ define the material properties. Particularly, we set $C_{10}=10$MPa, $C_{20}=-0.01$MPa and $C_{30}=10$MPa for these experiments. We refer the reader to previous paper for further details. Both sequences were generated using Abaqus for which the material properties, boundary conditions and nodal forces are required a priori to compute the deformation. In contrast, our methods based on linear elasticity do not require any prior knowledge to constrain the deformation.

Table 1 Quantitative comparison for synthetic sequences

We use our BA-FEM and EM-FEM algorithms for this test and present a comparison against state-of-the-art nrs f m methods, both batch and sequential algorithms. For batch methods, we consider EM-LDS [57], MP [39], PTA [8], KSTA [25], the block matrix approach SPM [15], and EM-PND [28]. We also compare with the sequential BA based on implicit models SBA [40]. The parameters of these methods were set in accordance with their original papers. Table 1 summarizes the comparison of the results for each method, while the 3D reconstruction of a typical frame for some methods are displayed in Fig. 7. Figure 8 displays the effect on 3D errors of varying the rank of the subspace, showing the consistent reduction of the error as more modes r are considered. We do not address the selection of r in this paper, since our results suggest that the proposed methods are not extremely sensitive to this choice.

Fig. 7

Synthetic sequences. Comparing results of our BA-FEM and EM-FEM algorithms with respect to EM-LDS [57], PTA [8], MP [39] and SBA [40] for frame $\#200$. Reconstructed 3D shape and the 3D ground truth are shown with red dots and black circles, respectively. Top Results for Syn. 1 sequence. Bottom Results for Syn. 2 sequence

We also evaluate the sensibility of including nonrigid motion in the initial frames that affects to the initialization and hence to the shape basis computation. To this end, we quantify this nonrigid motion by the metric $\Vert \mathbf {U}_{nonrigid}\Vert _{\mathcal {F}}$, where $\mathbf {U}_{nonrigid}$ represents the nonrigid 3D displacement of the shape in these frames. Even though in both experiments, the deformation is not produced concerning a mean shape, causing rest shapes more inaccurate, our methods produce accurate results and even outperform the rest of techniques evaluated. Figure 9 shows this effect on 3D errors varying the level of deformation in the initial frames. We can conclude that our methods outperform the state-of-the-art methods in terms of accuracy, with the additional advantage of being sequential, allowing us process frames in an on-line fashion. In addition, we achieve with an unoptimized Matlab code a frame rate of about 3 fps when dealing with a model of 81 points using 10 modes, and hence these results could still be significantly speeded up. We consider our method may potentially achieve real-time performance at frame rate with an efficient implementation.

Parameter selection The contribution of each smoothness term in the cost function of Eq. (19) can be controlled by means of the weights $\lambda _{\gamma }=0.15$, $\lambda _t=0.03$, and $\lambda _q=0.03$. We have tuned these parameters on these sequences, and used the same values for the rest of experiments. Yet, these parameters do not need to be carefully tuned. For instance, we test the 3D reconstruction error over the two elastic sequences after changing these weights by a $\div /\times$10 their original value. We obtain an error of 3.90(10)–4.01(10) for Syn.1 and 3.06(10)–3.17(10) for Syn.2. Observe that the reconstruction results barely change.

6.1.2 Dense Face Sequences

We now present results applying boundary conditions, i.e., rigid points, to show how our model can easily incorporate these constraints if they are available. We use only these priors to obtain the shape basis, managing both kinds of points—rigid and nonrigid points—in a single framework, unlike [17, 30] where both kinds of points are independently considered. Note that these constraints do not fix the absolute location of these points in the space, but produce sensitive changes in the mode shape basis. We only use these priors in these sequences to show the qualities of our shape basis estimation.

Fig. 8

Mean normalized error $e_{3\mathcal {D}}$ with varying number of mode shapes for synthetic sequences. Left Results for Syn. 1 sequence. Right Results for Syn. 2 sequence (Color figure online)

Fig. 9

Mean normalized error $e_{3\mathcal {D}}$ with varying level of deformation in initial frames for synthetic sequences. Left Results for Syn. 1 sequence. Right Results for Syn. 2 sequence (Color figure online)

Fig. 10

Dense Face 1 sequence. Reconstruction of the dense face for selected frames: $\#30$, $\#40$, $\#79$, and $\#95$. Top Ground truth 3D shapes. Bottom Our dense 3D reconstruction (Color figure online)

Table 2 Quantitative comparison for dense face sequences

Fig. 11

Stretching ribbon sequence. 3D reconstruction of the 275 point ribbon at frames $\#20$, $\#60$, and maximum deformation at $\#109$. Shape at rest is displayed behind with a black mesh. Top Ground truth deformation with a magenta mesh. Middle 3D reconstruction using the frequency-based method. Bottom 3D reconstruction using the coarse-to-fine approach. In both cases, the sparse mesh is shown in thick lines. Best viewed in color (Color figure online)

We use both 3 and 4 synthetic dense face sequences with $p=$ 28,887 points as proposed in [21] that we denominate Dense Face 1 and Dense Face 2, respectively. Both sequences are challenging owing to the density of the data and the strong deformations that combine bending and stretching, and they are similar with the exception of the camera motion. Thanks to the ability of our method to handle boundary point priors, we can compute just the first $r=$ 4 modes that combine both stretching and bending deformations, and experimentally show that they are sufficient to encode the face deformations. In this case, boundary conditions correspond to face points that have a null displacement with respect to the shape at rest. They are selected by means of a connectivity analysis. We show the error $e_{3\mathcal {D}}$ and a quantitative comparison with respect to batch and sequential state-of-the-art methods in Table 2, applying our algorithms. It is worth pointing out that we are not able to provide results for KSTA [25], SPM [15], and EM-PND [28], as they could not handle the large dimensionality of the problem. Our sequential approaches outperform in average the batch PTA [8] and MP [39] approaches, and the sequential approach SBA [40], but they provide an error higher than that of the variational batch method VNR [21], where all frames need to be available in advance. We show our 3D reconstruction for few frames in Fig. 10, using the BA-FEM algorithm.

6.1.3 Efficient Dense Mode Shape Computation

Finally, we propose a synthetic sequence of 109 frames where we simulate an elastic ribbon deformation of $p=$ 275 points with a nonlinear Yeoh hyperelastic material [64]. A dense shape basis is computed applying both the frequency-based and the coarse-to-fine approaches. In both cases, we use a low-dimensional mesh of $q=$ 78 points and then obtain a mesh of $p=$ 275 points. In order to estimate the nonrigid shape for this challenging 43 $\%$ stretching deformation, we use our EM-FEM algorithm—similar results are obtained by BA-FEM—and achieve the following performance $e_{3\mathcal {D}}$: (i) for the frequency-based method, we obtain 3.15 $\%$ for 5 modes, 1.08 $\%$ for 20 modes, and 0.86 $\%$ for 40 modes; (ii) for the coarse-to-fine approach, we obtain 3.11 $\%$, 1.57 $\%$ and 0.84 $\%$ for 5, 20, and 40 stretching modes, respectively. Figure 11 shows our 3D reconstructions with $r=$ 40 for a few selected frames including where the stretching is maximum, as well as a qualitative comparison with respect to ground truth. We conclude both methods provide similar 3D reconstructions, but note that the frequency-based method is more sensitive—due to the rigid factorization—and slightly more expensive. For this reason, we propose always to use the coarse- to-fine approach.

Fig. 12

Facial MoCap sequence. Original viewpoint and side views for selected frames #71, #188, #252, and #288 with ground truth (black mesh) and 3D reconstruction (red mesh) using r=55. Top BA-FEM algorithm. Bottom EM-FEM algorithm. Best viewed in color (Color figure online)

Table 3 Quantitative comparison for MoCap sequences using sequential methods

6.2 Motion Capture Data

In this section, we quantitatively evaluate our approaches using several existing datasets of motion capture (MoCap) to present an analysis of scalability with respect to sequential state-of-the-art nrs f m. We consider our approaches BA-FEM and EM-FEM, and the sequential method SBA [40]. Moreover, the performance of our methods is also analyzed when adding noise. We report results when zero-mean Gaussian noise with standard deviation $\sigma =\frac{\varepsilon }{100}\kappa$ is added to every point in the mesh following [39], where $\varepsilon$ is the noise percentage, and $\kappa$ is the maximum distance of an image point to the centroid of all the points. For each method, we use exactly the same $\mathbf {W}_{1:nr}$ to compute the shape at rest, i.e., the same initialization. Finally, we also report a comparison w.r.t. batch baselines.

Fig. 13

Flag MoCap sequence. 3D Reconstruction for a few frames with red dots. We display a few examples in Table 3 using the EM-FEM algorithm. We also show the corresponding 3D reconstruction error $e_{3\mathcal {D}}$[%]. First row Selected frames #10, #20, #32, and #45. Second row Sparse 594 points flag. Ground truth is overlaid with a black mesh and black circles. Third row Dense 9,622 points flag using the coarse-to-fine approach (CtF). Fourth row Dense 9,622 points flag without CtF. Please zoom in to the electronic images for a detailed view (Color figure online)

6.2.1 Facial MoCap Sequence

First, we use 316 frames from the facial MoCap sequence [57] with ground truth, where a subject is talking and moving his head while wearing 40 markers. With this sequence, we show the performance of our mesh-based approach using a reduced set of points. We show quantitative results for this sequence in Table 3 and qualitative results for both BA-FEM and EM-FEM in Fig. 12. We can achieve similar accuracy at a lower computational cost with respect to SBA [40]. However, when the measurements are noisy, the performance of SBA is worse since the shape basis is estimated on-the-fly while our algorithms provide a similar solution with respect to the noise-free case. It is worth noting that with the same basis, our EM-FEM algorithm is faster and more accurate compared to the BA-FEM algorithm, since this deformation is well modeled by Gaussian priors. However, our methods obtain less performance than batch methods in terms of error $e_{3D}[\%]$. Their results are 2.74(5), 2.69(3), 2.12(4), 1.82(7), and 1.40 for the methods MP [39], PTA [8], KSTA [25], SPM [15], and EM-PND [28], respectively. This is due to the low resolution of the object, which is insufficient to establish the FEM constraints. Despite this, our methods can obtain a competitive solution for this sequence w.r.t. batch ones, without requiring all frames to be available in advance.

Fig. 14

Actress sequence. Selected frames $\#31$, $\#48$, $\#84$ and $\#102$. First row Image frame sequence with 3D reprojected mesh. Second and third rows Original viewpoint and side views of the 3D reconstruction in the cases of full data and 40 $\%$ missing data, respectively, using the BA-FEM algorithm. Fourth and fifth row The same views applying the EM-FEM algorithm in the cases of full data and 40 $\%$ missing data, respectively. Visible points are displayed in red dots, and occluded points in blue circles (Colorfigure online)

6.2.2 Flag MoCap Sequence

We now evaluate our approaches using a challenging dense sequence [22] with $p=$ 9,622, corresponding to a fabric waving in the wind. To validate the scalability of our method, we also propose a $p=$ 594 sparse sequence version of the dense flag sequence, a result of the subsample process used to apply the coarse- to-fine approach (see Fig. 6). We have included a few initial frames corresponding to the camera observing the rigid shape. As the deformation contains little stretching, the first bending mode shapes can accurately encode the deforming scene.

We show quantitative 3D reconstructions for both sparse and dense flag sequences in Table 3 and qualitative results in Fig. 13. Both the BA-FEM and EM-FEM algorithms consistently outperform the SBA [40] method in terms of accuracy and efficiency from sparse to dense case and when applying noise. Although SBA [40] estimates the mode shapes on-the-fly—with shorter initialization computation time only for shape at rest—it is not able to overcome the mode shapes for this sequence. Note that the three methods use exactly the same initialization, although both BA-FEM and EM-FEM exploit the shape at rest to compute a mode shape basis. Our sequential methods are also more accurate than the batch methods MP [39], PTA [8], EM-PND [28], and KSTA [25] which for the sparse case obtain an error $e_{3D}[\%]$ of 16.02(2), 14.11(2), 8.65(2), and 8.61, respectively. Regarding the dense case, we obtain an error $e_{3D}[\%]$ of 21.94(2), 14.83(2), and 9.64(4) for the methods MP [39], PTA [8], and KSTA [25], respectively. SPM [15] and EM-PND [28] did not manage to process this sequence due to their nonscalable nature.

Fig. 15

Missing data pattern. Patterns used in the actress and paper bending sequences, respectively. Each row is a nonrigid frame and each column is a point track. Points in black and in white are marked as visible and occluded, respectively. Left 40 $\%$ random missing data. Right 22 $\%$ structured missing data

Fig. 16

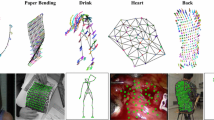
Paper Bending Sequence. We show the 3D reconstruction of a deformed scene for a few selected frames: $\#25$, $\#50$, $\#60$, $\#75$, and $\#100$. Up to 22 $\%$ structured occlusion is introduced (blue points) to show the robustness with respect to self-occlusion. Top Frames with 2D tracks. Middle General view using BA-FEM. Bottom General view using EM-FEM. (Color figure online)

Fig. 17

Niko’s sequence: dense 3D point cloud estimation. Top Selected frames $\#17$, $\#43$, $\#55$, $\#75$, $\#100$, and $\#121$ with 3D reprojected mesh. We display the mesh we use to obtain the mode shape basis. Middle Textured original viewpoint. Bottom Textured general view

Fig. 18

Heart sequence. 3D reconstruction of a beating heart during bypass surgery. Top Selected frames $\#9$, $\#24$, $\#32$, $\#58$, and $\#74$ with 3D reprojected mesh. Middle Textured general view subtracting the rigid motion for our BA-FEM method. Bottom Same views using KSTA [25]

In both cases, the error $e_{3\mathcal {D}}$ when applying EM-FEM is smaller than that of the BA-FEM algorithm. For this sequence, the Gaussian prior is more accurate and produces better solutions. Note that the initialization computation time for the sparse case is the same using both approaches since we do not use the coarse-to-fine approach. When we apply this algorithm for the dense case, the increase in the computation time is negligible—0.03 sec—compared to the sparse case, and it is dominated by the rigid factorization step with 25.67sec, similar to SBA [40]. However, the computation basis for the dense case without applying the coarse-to-fine approach is more expensive. It is worth noting that the reconstructions applying the coarse-to-fine approximation are less accurate than the standard method without significantly degrading the estimation, and the shape basis computation is much more efficient. For the sequential estimation, we obtain more efficient results using EM-FEM, with a better scalability in the number of modes. Concerning the sensitive when the rank is selected, we also observe a stability in our estimates with respect to this parameter, by obtaining more accurate solutions but at higher computational cost. Our conclusions can be extended to the noise case, showing the robustness of our methods.

We can conclude that our methods outperform the sequential state-of-the-art methods in terms of accuracy and efficiency. Although our method is implemented in unoptimized Matlab code without parallelization over a commodity computer Intel core i7@2.67 GHz, the results show a low computational cost per frame and the results can still be significantly speeded up.

6.3 Real Images

In this section, we evaluate our methods qualitatively using several existing datasets. We show the scalability of our methods for sparse to dense sequences of real images. Moreover, we show the robustness of our methods in the cases of structured and random missing data.

6.3.1 Actress Sequence

First, we use the sequence and tracks provided by [9] to report qualitative results for the actress sequence, which consists of 102 frames where an actress is talking and moving her head. We use a rigid model for the first 30 frames to compute the shape at rest for both approaches, similarly to [40]. In Fig. 14, we show our estimated 3D reconstruction applying both BA-FEM and EM-FEM algorithms with $r=$ 10 stretching mode shapes. Our results are comparatively similar to those reported by [40]. Moreover, we provide results in the case of corrupted observations. The missing data were generated by randomly deleting entries in the 2D input tracks. We report comparatively similar results to those of the full data case applying 40 $\%$ of missing data for both the BA-FEM and EM-FEM algorithms, showing their robustness to artifacts. We show the 40 $\%$ missing data mask in Fig. 15(left).

6.3.2 Paper Bending Sequence

In this case, we use the first 100 frames of a paper bending sequence proposed in [9] to provide a qualitative evaluation of our methods with respect to a structured missing data pattern. We use the sparse tracking of 828 points obtained by dense tracking data reported in [22]. We process the sequence using r= 10 bending mode shapes and 5 frames to compute the shape at rest. Between frames $\#48$ and $\#76$, a 22 $\%$ band of missing data is introduced simulating strong self-occlusion. Our performance is close to the full data case for both BA-FEM and EM-FEM, and our 3D reconstruction does not degrade significantly. We show both 3D reconstructions with missing data for this sequence in Fig. 16, the 22 $\%$ structured missing data mask in Fig. 15(right).

6.3.3 Niko’s Sequence

We now evaluate our approach using dense 28,332 tracks provided by [22] to show a qualitative evaluation for the face sequence compared to [21], where Niko is performing natural expressions and moving his head. Since we obtain similar results with both algorithms, in Fig. 17, we show a few frames with our 3D reconstruction using our EM-FEM algorithm with $r=$ 30 stretching mode shapes. We compute mode shapes with $q=$ 1,442 points and applying a coarse-to-fine approach to $p=$ 28,332 points (see Fig. 5).

6.3.4 Heart Sequence

Finally, we process a challenging Heart sequence of a beating heart captured during bypass surgery.³ This shows the generality of our approach to retrieve the 3D reconstruction of extensible objects. In this case, we track 3,024 points computed by [22] without any sub-sampling technique. Figure 18 shows some images and our 3D reconstruction using our BA-FEM algorithm with $r=$ 30 stretching mode shapes (similar results are provided by EM-FEM). Since 3D ground truth is not available for this experiment, we provide a qualitative comparison with respect to KSTA [25] using a rank in the basis of 5, which obtained one of better performance in quantitative experiments of the previous subsection. Even though this method is known to be very accurate, the estimated 3D shapes do not seem very realistically plausible being almost planar for some frames.

7 Conclusion

We have proposed two sequential algorithms to estimate camera motion and nonrigid 3D shape from monocular sequences in close to real-time operation. Our systems work with significant missing data, with both elastic or isometric deformations and, crucially, without a training step. Our methods can be used to model either sparse or dense data and are robust to noisy measurements. We use a thin-plate model with unknown material properties to code the behavior of a nonrigid 3D object by applying a force balance equation. This equation is directly solved by FEM modal analysis for sparse meshes, and we also propose two efficient methods to solve the equation for dense meshes. The resulting physics-based shape basis is combined with temporal and spatial smoothness constraints without using restrictive additional distance constraints such as inextensibility, allowing us to model elastic deformations. Both approaches provide a competitive solution in terms of accuracy versus per-frame computation time. Our claims have been experimentally validated for both synthetic and real sequences showing a performance better than or comparable to state-of-the-art methods, with the additional advantage that our methods are sequential, accurate, and scalable.

Our future work is to pursue the goal of merging feature tracking and outliers detection to provide a unified framework. Additionally, we plan to apply our methods to the problem of 3D reconstruction from endoscopic videos, where accurate FEM biomechanical models for internal organ tissues are available. We expect that our method will be able to exploit the rich priors available and provide new avenues of research for the challenging use of nrs f m in minimally invasive surgery.

Rotation Update on the Stiefel Manifold

The camera rotation $\mathbf {Q}_{i}^{t}$ is subject to orthonormality constraints, and a closed-form update is not possible. The rotation matrix lies exactly on a smooth manifold based on the orthogonal group SO(3), where it is possible to generalize a Riemannian-Newton algorithm [19, 49]. We define the problem as that of minimizing the function $\mathcal {B}\left( \mathbf {Q}^{t}_{i} \right)$, where $\mathbf {Q}^{t}_{i}$ is constrained to the set of matrices such that ${\mathbf {Q}^{t}_{i}}^{\top }\mathbf {Q}^{t}_{i}=\mathbf {I}$, i.e., a Stiefel matrix. In this work, we use the Riemannian manifold optimization to update the rotation matrices. First, we rewrite the expected negative log-likelihood function Eq. (21) dropping the dependence on $\sigma ^{2}$ and $\mathcal {B}\left( \mathbf {Q}^{t}_{i} \right)$ can be expressed as:

$$\begin{aligned} \mathop {\hbox {arg min}}\limits _{\mathbf {Q}^{t}_{i}\in SO(3)} \, \, \sum _{i=f-\mathcal {W}+1}^{f} \sum _{\varrho \in \mathcal {V}} \mathbb {E} \left[ \Vert \mathbf {w}_{i\varrho }-\varvec{\Uppi }\mathbf {Q}^{t}_{i} \tilde{\mathcal {S}}_{\varrho } \tilde{\varvec{\gamma }}_{i} -\mathbf {t}_{i} \Vert _{\mathcal {F}}^{2} \right] \end{aligned}$$

(23)

where $\mathbf {Q}^{t}_{i}\in SO(3)$ and its tangent $\varDelta _{Q^{t}_{i}}\in T_{Q^{t}}(SO(3))$ can be expressed as $\varDelta _{Q^{t}_{i}}=\mathbf {Q}^{t}_{i}\left[ \varvec{\delta }\right] _{\times }$ with $\left[ \varvec{\delta }\right] _{\times }$ being the skew-symmetric matrix. On SO(3), the geodesic at $\mathbf {Q}^{t}_{i}$ in the tangent direction can be expressed by means of the Rodrigues’ rotation formula:

$$\begin{aligned} \mathbf {Q}^{t+1}\big (\hat{\varvec{\delta }},\alpha \big )= \mathbf {Q}^{t}\left( \mathbf {I}_{3}+\left[ \hat{\varvec{\delta }}\right] _{\times } \sin (\alpha )+ \left[ \hat{\varvec{\delta }}\right] _{\times }^{2}\left( 1-\cos (\alpha )\right) \right) \end{aligned}$$

(24)

where $\left[ \varvec{\delta }\right] _{\times }\in \mathfrak {so}(3)$ is the Lie algebra of SO(3) the group and $\left[ \varvec{\delta }\right] _{\times }=\alpha \left[ \hat{\varvec{\delta }}\right] _{\times }$. This explicit formula for geodesics is necessary for computing the gradient $d\mathcal {B}(\varDelta _{Q^{t}_{i}})$ and the Hessian $Hess \,\mathcal {B}(\varDelta _{Q^{t}_{i}},\varDelta _{Q^{t}_{i}})$ of the cost function Eq. (23) along the geodesics on the manifold. Given the previous definition, we can obtain both the gradient and Hessian in a tangent direction $\varDelta _{Q_{i}^{t}}$ as:

$$\begin{aligned}&d \,\mathcal {B}(\varDelta _{Q_{i}^{t}})\equiv \left. {\frac{d \,\mathcal {B}\left( \mathbf {Q}_{i}^{t}(\alpha ) \right) }{d\alpha }} \right| _{\alpha =0} \nonumber \\&\quad =\left( \mathbf {R}_{i}^{t}\sum _{\varrho \in \mathcal {V}} \left( \tilde{\mathcal {S}}_{\varrho }\tilde{\varvec{\phi }}_{i}\tilde{\mathcal {S}}_{\varrho }^{\top } \right) -\sum _{\varrho \in \mathcal {V}}\left( \left( \mathbf {w}_{i\varrho }-\mathbf {t}_{i}\right) \tilde{\varvec{\mu }}_{i}^{\top } \tilde{\mathcal {S}}_{\varrho }^{\top }\right) \right) \varDelta _{R_{i}^{t}}^{\top } \end{aligned}$$

(25)

$$\begin{aligned}&Hess \,\mathcal {B}(\varDelta _{Q_{i}^{t}},\varDelta _{Q_{i}^{t}})\equiv \left. \frac{d^{2} \,\mathcal {B}\left( \mathbf {Q}_{i}^{t}(\alpha ) \right) }{d\alpha ^{2}}\right| _{\alpha =0}\nonumber \\&\quad =\left( \mathbf {R}_{i}^{t}\sum _{\varrho \in \mathcal {V}} \left( \tilde{\mathcal {S}}_{\varrho }\tilde{\varvec{\phi }}_{i}\tilde{\mathcal {S}}_{\varrho }^{\top } \right) - \sum _{\varrho \in \mathcal {M}}\left( \left( \mathbf {w}_{i\varrho }-\mathbf {t}_{i}\right) \tilde{\varvec{\mu }}_{i}^{\top } \tilde{\mathcal {S}}_{\varrho }^{\top }\right) \right) \varDelta _{Q_{i}^{t}}^{\top }\mathbf {Q}_{i}^{t} \varDelta _{R_{i}^{t}}^{\top }\nonumber \\&\qquad +\varDelta _{R_{i}^{t}}\sum _{\varrho \in \mathcal {V}} \left( \tilde{\mathcal {S}}_{\varrho }\tilde{\varvec{\phi }}_{i}\tilde{\mathcal {S}}_{\varrho }^{\top } \right) \varDelta _{R_{i}^{t}}^{\top } \end{aligned}$$

(26)

where $\varDelta _{R_{i}^{t}}=\varvec{\Uppi }\varDelta _{Q_{i}^{t}}$ are the first two rows of a full tangent vector. The expectations are $\tilde{\varvec{\mu }}_{i}=\mathbb {E}\big [\tilde{\varvec{\gamma }}_{i} \big ]$ and $\tilde{\varvec{\phi }}_{i} = \mathbb {E} \Big [\tilde{\varvec{\gamma }}_{i} \tilde{\varvec{\gamma }}_{i}^{\top }\Big ]$. The Hessian can be obtained by polarizing $Hess \,\mathcal {B}(\varDelta _{Q_{i}^{t}},\varDelta _{Q_{i}^{t}})$ [29, 49]. Assuming that the Hessian is nondegenerate, we compute the optimal updating vector for a generalized Newton method as $\varDelta _{Q_{i}^{t}}=-Hess^{-1}G$, where G is the gradient on the manifold. To compute the Hessian, we use an orthonormal basis $\mathbf {E}_{b}$ of the tangent space on SO(3). For simplicity, we can choose the standard basis $\mathbf {e}_{b}$ for $\mathbb R^{3}$. The Hessian matrix $\mathbf {H}$ and gradient vector $\mathbf {g}$ can be obtained as:

$$\begin{aligned} \mathbf {g}_{b}= & {} d \,\mathcal {B}(\mathbf {E}_{b}), \end{aligned}$$

(27)

$$\begin{aligned} \mathbf {H}_{bc}= & {} Hess \,\mathcal {B}(\mathbf {E}_{b},\mathbf {E}_{c}). \end{aligned}$$

(28)

Finally, the optimal updating vector can be computed as $\varDelta _{Q_{i}^{t}}=-Hess^{-1}G=\mathbf {Q}_{i}^{t}\left[ \varvec{\delta }\right] _{\times }$ and to move it in the tangent direction along the geodesic on SO(3). The outline of the algorithm is shown in Algorithm 1.

Next, the noise variance and the translation vector can be updated in an on-line manner as:

$$\begin{aligned} \sigma ^2= & {} \frac{1}{2\varrho \mathcal {W}} \sum _{i=f-\mathcal {W}+1}^{f} \sum _{\varrho \in \mathcal {V}}\Big ( - 2\left( \mathbf {w}_{i\varrho }- \bar{\mathbf {t}}_{i}\right) ^{\top } \mathbf {G}_{i} \tilde{\mathcal {S}}_\varrho \tilde{\varvec{\mu }}_{i}\\&+ \Vert \mathbf {w}_{i\varrho } - \bar{\mathbf {t}}_{i}\Vert ^{2} + \text {tr}\left( \tilde{\mathcal {S}}_\varrho ^{\top } \mathbf {G}_{i}^{\top } \mathbf {G}_{i}\tilde{\mathcal {S}}_\varrho \tilde{\varvec{\phi }}_{i} \right) \Big ), \\ \mathbf {t}_{i}= & {} \frac{1}{\varrho } \sum _{\varrho \in \mathcal {V}} \left( \mathbf {w}_{i\varrho } -\mathbf {R}_{i}\tilde{\mathcal {S}}_{\varrho } \tilde{\varvec{\mu }}_{i}\right) . \end{aligned}$$