Simulation-based metaheuristic optimization algorithm for material handling

Abstract

Modern technologies and the emergent Industry 4.0 paradigm have empowered the emergence of flexible production systems suitable to cope with custom product demands, typical in this era of competitive marketplaces. However, production flexibility claims periodic changes in the setup of production facilities. The level of flexibility of a production process increases as the reconfiguration capacity of its facilities increases. Nevertheless, doing that efficiently requires accurate coordination between productive resources, task planning, and decision-making systems aiming to maximize value for the client, minimizing non-added-value production tasks, and continuous process improvement. In a manufacturing system, material handling within manufacturing facilities is one of the major non-value-added tasks strongly affected by changes in plant floor layouts and demands for producing customized products. This work proposes a metaheuristic simulation-based optimization methodology to address the material handling problem in dynamic environments. Our proposed approach integrates optimization, discrete event simulation, and artificial intelligence methods. Our proposed optimization algorithm is mainly based on the ideas of the novel population-based optimization algorithm called Q-learning embedded Sine Cosine Algorithm, inspired by the Sine Cosine Algorithm. Unlike those, our proposed approach can deal with discrete optimization problems. It includes in its formulation a reinforcement learning embedded algorithm for the self-learning of the parameters of the metaheuristic optimization algorithm, and discrete event simulation is used for simulating the shop floor operations. The performance of the proposed approach is evaluated through an exhaustive analysis of simple to complex cases. In addition, a comparison is made with other comparable optimization methodologies.

Introduction

Today’s manufacturing companies are facing a wide range of obstacles and challenges. Production tends to be personalized, and demands are rapidly changing and diversifying. In addition, the speed of change in the environment is increasing. In this context, the paradigm of Industry 4.0 (I4.0) or the Fourth Industrial Revolution refers to a set of productive and institutional transformations. The concept of smart factories appears, where physical objects, machines, products, and even parts are integrated into the company’s information networks and communicate in real-time horizontally with each other and vertically with customers, users, and suppliers.

Computer systems monitor manufacturing processes, creating a virtual copy of the physical world and making decentralized decisions (Motta et al., 2019). This concept, called Digital Twin (DT), has recently generated much interest in academia and industry (Stączek et al., 2021). Furthermore, this has been accompanied by an increase in related publications. There is excellent potential in operating digital twins as agent-based systems that cooperate towards specific goals, with emerging benefits for the overall system (Jones et al., 2020).

I4.0 also includes technologies such as Cyber-Physical Systems, the Internet of Things, Big Data, Cloud Computing, Cloud Manufacturing, Robotics, and Simulation. Therefore, it considers a broad set of new technologies (software and hardware) that operate in integrated systems (Benitez et al., 2023) intending to achieve greater process flexibility. Moreover, even in these times, there is already talk of Industry 5.0 as a new paradigm, which includes concepts such as a humanized vision of the industry, circular and sustainable manufacturing, and future needs of society (Lu et al., 2023; Barata and Kayser, 2023; Golovianko et al., 2023; Pizoń and Gola, 2023).

On the other hand, Lean Manufacturing is a management philosophy of a company or organization and a long-term strategy (Womack et al., 2007). It was developed in the 1950 s in Japan at the Toyota Company and can be summed up with the phrase “do more with less”. In other words, it implies making more efficient use of available resources. Time and material waste are identified and eliminated to maintain quality and reduce manufacturing costs (Alkhoraif et al., 2019). The fundamental part of this philosophy is to focus on the company’s activities that add real value. This concept includes several engineering and management tools and methods, some of which are: 5 S, Just in Time (JIT), Total Productive Maintenance (TPM), Continuous Improvement (Kaizen), Total Quality Management (TQM), Zero Defects, Kanban, Standardization of Tasks, Value Stream Mapping (VSM), among others (Shah and Patel, 2018; Akkari and Valamede, 2020).

The Lean methodology identifies eight wastes of an organization that must be minimized to achieve efficiency and effectiveness in production systems, seven of which were raised by Taiichi Ohno (Ohno, 1988). These wastes are overproduction, waiting, unnecessary movements, transportation, inventory, defects, overprocessing, and unused talent. The minimization of these factors directly impacts production costs and the company’s competitiveness. And identifying these wastes is always the first step.

The ideas of Lean Manufacturing and I4.0 have been integrated into a new organizational paradigm called “Lean 4.0” (Langlotz et al., 2021). Methods from one paradigm can be supplemented by technology from another, and vice versa. While these paradigms, Lean Manufacturing and I4.0, may seem quite different, Lean 4.0 offers promising opportunities for the future of organizations if they can combine them synergistically to improve efficiency (Marinelli et al., 2021).

Returning to Lean wastes, transportation may be defined as a necessary operation that adds no value to a manufacturing process. Concerning the plant floor, material handling (MH) is vital in a manufacturing facility, but it frequently adds unnecessary time and expense (Adeodu et al., 2023; Yamazaki et al., 2017). The inefficient transportation of raw materials or products in the process directly influences the business’s productivity and profitability. It also impacts other Lean wastes, such as waiting in manufacturing and finished and in-process inventories.

This situation is related to two fundamental problems that have been treated for years in operations optimization: the traveling salesman problem (TSP) and the capacitated vehicle routing problem (CVRP). These problems are considered NP-hard combinatorial problems. In the TSP, given a list of nodes and the distance between them, one must find the shortest possible path to visit each node and return to the original one (Wang and Tang, 2021). Formally, an instance of a TSP can be defined in a graph as a set of nodes and edges. Each node has its characteristics, and a possible solution to the problem involves defining a path, that is, a specific sequence of nodes that satisfies the problem’s constraints. On the other hand, in the specific case of a CVRP, there is another node called the warehouse, and the original nodes represent clients, each with a particular demand. Each route starts from the depot and visits a subset of clients sequentially (Yaoxin et al., 2022). It is a directed graph. And the goal is to minimize the distance of the tour. This situation is the case with the MH problem on the plant floor, where, given an initial point, different workstations are visited to supply it.

However, in flexible production systems, the shop floor could be modified. Consequently, using graphs-based optimization methods to address lean minimization problems could be cumbersome since they must be refactorized every time there is a change in the configuration of the productive system. Instead, using discrete-event simulation-based methods or, even more, digital twin-based strategies gives a more realistic description of the system.

In this context, this study makes a proposal that combines discrete event simulation (DES), optimization, and artificial intelligence (AI) for the MH problem on the plant floor that has been little explored in the literature for flexible workshop floors in manufacturing plants. Our proposed optimization algorithm is mainly based on the ideas of the novel population-based optimization algorithm called Q-learning embedded Sine Cosine Algorithm (QLESCA) (Hamad et al., 2022), inspired by the Sine Cosine Algorithm (SCA) (Mirjalili, 2016) and its discrete version recently presented in the work of Gupta et al. (2022). In addition, to improve the convergence performance of our proposal, we embed a reinforcement learning algorithm into the formulation. In this way, our proposal can learn a behavioral law of the exploration/exploitation parameter that significantly influences the algorithm’s performance.

Notably, during the literature review, a non-significant amount of previous works in SCA applications have been identified for discrete optimization problems and even less so for the MH problem in flexible production systems. In summary, this work’s main contributions address minimizing a non-value-added task, mainly focusing on the MH problem where multiple resources are considered, vehicle routing and resource synchronization are posed, and a methodology for solving the proposed formulation is developed.

The paper is structured as follows: in section “Related work”, the related work; in section “Methodological background”, the methodological background; in section “Metaheuristic DSCA using RL-optimized parameterization laws for MH optimization”, the proposal developed and applied to the case study; in section “Results and discussions”, the corresponding results; and finally, in section “Conclusion and future work”, the conclusions and future work.

Related work

The concept of Lean 4.0 has emerged strongly in several investigations lately, combining the Lean philosophy with the new paradigm of I4.0 and treating them as complementary elements. Several works can be found where concepts regarding this combination of factors are reviewed or raised, or possible methodologies for their application are specified (Dillinger et al., 2021, 2022; Kolla et al., 2019). Some researchers suggest that a combination of Lean, simulation, and optimization may be crucial in the future to improve organizations’ efficiency. This combination can improve the traditional decision-making process, accelerate system improvements and re-configurations, and support organizational learning (Uriarte et al., 2018). However, there are few concrete articles of application in various case studies.

In Cifone et al. (2021), two current forms are proposed for this integration. The first perspective suggests Lean as a foundation for I4.0 implementation, arguing that controlled and optimized processes can be a prerequisite for any digitization process. In contrast, the second perspective shows I4.0 as a necessary complement to Lean, based on the great personalization of the demand that the current situation implies, where I4.0 represents a means that Lean can exploit to adapt to new trends in the world. In this work, we demonstrated this last trend using I4.0 tools for optimizing the MH problem and eliminating Lean waste in a conjunction of both paradigms.

On the other hand, the intersection of advanced technologies and industrial applications implies the development of DT technology and strategies for human–machine collaboration to make more efficient operational environments. In this sense, for the MH task, integrating Autonomous Mobile Robots and robot manipulators (Ghodsian et al., 2022) in the shopfloor could bring new ways for managing the material along the processes of transformation and their manipulation in the warehouses. In the recent work of Stączek et al. (2021), DT technology was used to assess the correctness of the design assumptions adopted for the early phase of implementing an autonomous mobile vehicle in a company’s production hall. However, the work mainly focuses on efficiently developing the DT. A step forward is discussed in Kiyokawa et al. (2023), where a review analyzes the prevalent approaches focusing on understanding the current difficulty and complexity definitions and outstanding human-robot collaboration assembly system issues. Similarly, this new trend of human–machine integration is addressed in Lu et al. (2023), where a DT-based framework is presented for coordinating teams of humans and robots, focusing on DT technology as a central communication hub to enable collaboration between these entities. All these advances should allow us to have more precise and real-time information about the operating environment, which means that the case of MH, whether carried out solely by robots or in collaboration with humans, requires efficient optimization algorithms to solve such problems.

Concerning the TSP and the CVRP, it can find several methodologies for solving these problems, such as evolutionary algorithms (Akhand et al., 2015; Zhang and Yang, 2022; Skinderowicz, 2022), various optimization methods (Dündar et al., 2022; Singh et al., 2022), reinforcement learning (RL) (Nazari et al., 2018; Ottoni et al., 2022), and neural networks (Hu et al., 2020; Luo et al., 2022). Within the wide range of optimization, a simple meta-heuristic algorithm called SCA (Mirjalili, 2016) emerged a few years ago, showing excellent results in various types of problems. Currently, it is being used in a plethora of applications and can be found in multiple research in several fields. For example, in Karmouni et al. (2022), it is used to control and improve monitoring performance in a photovoltaic system; in Issa (2021), it contributes to measuring pairs of biological sequences in the context of COVID-19, in Kuo and Wang (2022) it is used in a classification problem with mixed data, in Lyu et al. (2021) it is used for the prediction of the resistance to axial compression of circular columns and in Daoui et al. (2021) it is used for the copyright protection of images.

However, despite the potential of SCA, at least during our literature review, we have not found relevant applications in decision-making systems for the manufacturing process.

The original article shows that the SCA can be highly effective in solving real problems with restricted and unknown search spaces and that it converges, avoiding local optimum. In addition, it has a reasonable execution time and a straightforward implementation (Benmessaoud et al., 2021). Although this is true, several authors developed improvements or variants of this algorithm that increased its robustness or speed of convergence by adding certain meta-heuristics or hybridizations, such as Abdel-Baset et al. (2019); Li et al. (2018) and Al-qaness et al. (2018).

However, few articles have been found where problems with solutions of a discrete nature are dealt with (Yang et al., 2020), and no works have been developed where SCA can be applied to manufacturing systems or MH problems. We have rescued the article developed by Gupta et al. (2022), where they implement the Discrete Sine Cosine Algorithm (DSCA) and apply it to the programming of urban traffic lights as a basis for our proposal.

On the other hand, to solve routing problems, many works use graph theory for its resolution (Gouveia et al., 2019; Lei et al., 2022; Duhamel et al., 2011). However, using DES and digital models of manufacturing systems, we can not only represent a static layout but also take advantage of the potential of simulators to study complete systems. This allows us to have production statistics, stock, and failures, among others, and get a more realistic representation of the production process for the problem formulation.

In this work, we demonstrate that successful results are obtained without expert knowledge when using the proposed optimization method together with process simulation. This makes it easier for established industries to implement Lean 4.0 ideas, and this concept has been little addressed in the literature for flexible shop floor applications in manufacturing plants.

Methodological background

Discrete event simulation

In the current context, the decision-makers of productive companies are increasingly facing complex situations where they must maximize both production, economic, and sustainability objectives that often conflict with each other. The simulation of systems for the development of virtual models constitutes an essential tool to support decision-making so that companies can evaluate their operational policies to maximize the use of resources and quickly adapt to environmental changes.

Among the simulation methodologies available, DES is mainly used in manufacturing systems to evaluate, test, and improve the performance of processes at low cost, without intervening in them or their actual operation (Furian et al., 2015). DES is the process of encoding the behavior of a complex system as an ordered sequence of well-defined events. These events occur at particular times and mark a state change in the system (Kiran, 2019). Because no changes occur between events, discrete event models can directly simulate the occurrence time of the next event, and long time intervals can be significantly reduced.

I4.0 has even given way to the concept of digital twins, given the decisive irruption of the industrial Internet of things together with cyber-physical systems, where physical systems are connected with their simulated virtual twins in real-time. This makes monitoring and controlling them efficiently possible (Saavedra Sueldo et al., 2022). According to Semeraro et al. (2021), digital twins are “a set of adaptive models that emulate the behavior of a physical system in a virtual system, obtaining data in real-time to update throughout its life cycle. They replicate the physical system to predict failures and opportunities for change, prescribe actions in real-time to optimize or mitigate unexpected events, and observe and evaluate the operating profile of the system”.

Briefly, discrete event simulation offers the opportunity to test multiple solutions within a short time efficiently. It enables the analysis of various scenarios until the optimal one is discovered. In the context of MH problems, discrete event simulation using a manufacturing plant simulator provides the advantage of working with dynamic environments. It allows for considering perturbations and changes that are challenging to model using traditional methods commonly used in routing problems, such as graphs with vertices and arcs to represent the shop floor. Moreover, DES facilitates comprehensive data collection on industrial systems and different Lean wastes, in addition to evaluating factors like distances, routes, and statistical information across areas like maintenance, production, and quality management. This holistic approach ensures a precise assessment of the impacts of implemented actions on the entire production system (Ben Moussa et al., 2019).

Optimization

Optimization is finding the optimal values of the parameters or variables involved in a problem and maximizing or minimizing the final result. Thus, in an optimization problem formulation, we aim to maximize or minimize an objective function f(x) subject to certain constraints. The objective function can be linear or non-linear. Values that can be controlled and influence the system are called decision variables (Winston, 2004).

There are several approaches to solving different optimization problems (Thirunavukkarasu et al., 2023; Gambella et al., 2021). We can locate stochastic algorithms among the many methods for tackling this sort of issue. These techniques treat optimization problems as black boxes. This means that the derivation of mathematical models is unnecessary because such optimization paradigms simply modify the system’s inputs and monitor its outputs to maximize or minimize them. Another significant advantage of viewing problems as black boxes is their high adaptability, which means that stochastic algorithms adapt to problems in various domains. In addition, black-box optimization methods are designed to deal with complex systems with complex behavior to be accurately modeled without making excessive simplifications and assumptions that may affect the representation of the system. However, these methods can converge slowly or get stuck in local minima. On the other hand, metaheuristics are fundamental for solving complex optimization problems because they can produce acceptable results in a reasonable amount of time, making them suitable replacements for accurate algorithms (Karimi-Mamaghan et al., 2022).

The stochastic and metaheuristic optimization algorithm used in this article is based on the one developed by Mirjalili (2016) called SCA. This algorithm is simple and effective, and it was proposed to optimize real problems with unknown search spaces. It is a population-based optimization algorithm; that is, it starts with several random initial candidate solutions that are updated when compared with the best available solution. These solutions are close to or far from the best solution based on a mathematical model based on sine and cosine functions. In addition, there are four parameters integrated into the algorithm $r_{1}, r_{2}, r_{3}$ and $r_{4}$ that allow managing the exploration and exploitation of the search space or feasible zone. The fundamental equation is the following:

$$\begin{aligned} X_{i}^{t+1}= \left\{ \begin{array}{ll} X_{i}^{t}+r_{1}*\sin (r_{2})*|r_{3}P_{i}^{t}-X_{i}^{t}|, &{}\quad r_{4}<0.5 \\ X_{i}^{t}+r_{1}*\cos (r_{2})*|r_{3}P_{i}^{t}-X_{i}^{t}|, &{}\quad r_{4}\ge 0.5\end{array}\right. \end{aligned}$$

(1)

where $X_{i}^{t}$ is the position of the current solution at iteration t and dimension i and $P_{i}^{t}$ is the position of the best solution found so far at this moment. The formula of $r_{1}$ is $r_{1}= a - t \frac{a}{T}$, where a is a constant, t the current iteration and T the maximum number of iterations of the algorithm. $r_{2}$ is a random number that varies between 0 and $2\pi$, $r_{3}$ is a random number that varies between 0 and 2, and $r_{4}$ is a random number ranging between 0 and 1. The SCA pseudocode is shown below in Algorithm 1.

Algorithm 1

Sine Cosine Algorithm

The MH problem in a productive system involves finding the sequence of stations that make up a punctual route that minimizes the distance traveled. In this sense, the optimization problem requires dealing with discrete variables. Therefore, it is impossible to use the SCA directly since it is an algorithm for continuous variables. It is decided to adopt a variant called DSCA developed by Gupta et al. (2022). The fundamental equation of the SCA is discretized as follows for the DSCA:

$$\begin{aligned} X_{i,new}^{t+1}&= X_{i}^{t} \oplus (C_{i}^{t}\otimes (X_{d}^{t}\ominus X_{i}^{t})) \end{aligned}$$

(2)

$$\begin{aligned} C_{i}^{t}&= \left\{ \begin{array}{ll} |r_{1}*\sin (r_{2})|, &{}\quad r_{3} > 0.5 \\ |r_{1}*\cos (r_{2})|, &{}\quad r_{3} \le 0.5 \end{array}\right. \end{aligned}$$

(3)

where the parameter $r_{1}= \frac{t}{T}$ is linearly ascending between 0 and 1, $r_{2}$ is a random number ranging between 0 and $2\pi$, and $r_{3}$ is a random number ranging between 0 and 1.

As in the original SCA, $X_{i}^{t}$ is the position of the current solution, where $X_{d}^{t }$ is the best solution obtained so far. The parameter $C_{i}^{t}$ is used to decide the required change amount in the current candidate’s position vector to obtain a new state. That is, in $X_{d}^{t}\ominus X_{i}^{t}$ the difference of positions of the vectors is calculated: how many components in the solution vector $X_{i}$ are different from the best solution found $X_{d}$. After the multiplication in Eq. 2, the final value is rounded to update the solution, changing the number of characteristics or components obtained. As can be seen by comparing Eq. (1) and (2), in the discrete algorithm, there is one less parameter to consider ($r_1, r_2, r_3$) concerning SCA. The DSCA pseudocode is shown in Algorithm 2.

Algorithm 2

Discrete Sine Cosine Algorithm

The performance of the DSCA is highly dependent on the $r_i$ parameters. In this sense, we propose a version with an embedded RL algorithm for the parameters self-tuning policy learning.

Reinforcement learning

Within the different types of existing AI techniques, we can highlight RL as being fundamental to the developments of recent years. This AI technique involves the interaction of an intelligent agent with its environment, where it learns based on trial and error. Learning from interaction is a fundamental idea underlying almost all theories of learning and intelligence. RL is learning what to do, that is, how to assign situations to actions to maximize a numerical reward signal (Sutton and Barto, 1998).

Formally, the RL problem is described as a Markov decision problem (MDP), which requires the definition of a state vector of the system, the set of possible actions to be taken in each system state, and a reward function that rewards the effects of the actions taken. In this way, the agent generates its knowledge base and adapts its action policy $\pi$ according to the defined reward function. A policy describes the agent’s behavior. In broad terms, it is a mapping from perceived system states to actions to be conducted in those states.

MDPs are a classic formalization of sequential decision-making, where actions influence immediate rewards and subsequent situations or states. In more detail, the agent and the environment interact in a series of discrete time steps $t = 0, 1, 2, 3\ldots$. At each time step t, the agent receives some representation of the state of the system $s_{t}$ and chooses an action $a_{t}$ based on that representation. One step forward, due to the taken action, the system evolves to a new state $s_{t + 1}$, and the agent gets a numerical reward $r_{w_{t}}$.

One of the RL’s problems is the compensation between exploration and exploitation. An RL agent should choose actions aiming to maximize the obtained rewards. However, to discover such actions, the agent must try some actions that it has never tried before. Thus, the agent must exploit what it has already experienced to gain a reward, but it must also explore to make better decisions for future action. Neither exploration nor exploitation can be entirely carried out; the agent must try a variety of acts and gradually improve its behavior. Therefore, it is necessary to consider which hyperparameters are used in the chosen algorithm and how to balance this scenario (Sutton and Barto, 1998).

The Q-learning algorithm is one of the best-known RL tabular algorithms. It was developed by Watkins in 1989, and it is an incremental method that works by successively improving the quality of particular actions in particular states (Watkins and Dayan, 1992). The standard Q-learning was developed to deal with finite and discrete state and action spaces, S and A. The actualization values of the state-action value function are shown in Eq. (4):

$$\begin{aligned} Q(S_{t},A_{t}){} & {} \leftarrow Q(S_{t},A_{t}) \\{} & {} \quad + \alpha [R_{t+1} + \gamma \max \limits _{{a}} Q(S_{t+1},a) - Q(S_{t},A_{t})]\nonumber \end{aligned}$$

(4)

where Q is the state-action value function, which can be stored in a tabular way, $s_t \in S$ is the system state at time t, $a_t \in A$ is the action taken at time t, $\alpha$ is the learning rate, and $\gamma$ is the discount factor. Regardless of which policy is used, the learned action-value function Q directly approximates the optimal action-value function $Q^*$. Once $Q^*$ is known through interactions, then the optimal policy $\pi ^*(s)$ can be obtained directly through:

$$\begin{aligned} \pi ^*(s) = \max \limits _{{a}} Q(S,a) \end{aligned}$$

(5)

It is proven that Q-learning converges to optimal action values with probability one as long as all actions are sampled repeatedly in all states and action values are represented discretely (Watkins, 1989). As we will develop in the following section, in our proposal, we embed an RL formulation for optimal setting up the parameter $r_1$ of the optimization algorithm.

Metaheuristic DSCA using RL-optimized parameterization laws for MH optimization

As we mentioned earlier, our proposed approach focuses on the utilization of simulation, optimization, and RL techniques to address MH challenges within a manufacturing facility. Following, the performance of the proposed approach will be tested in a case study, encompassing scenarios ranging from less to more complex. This evaluation aims to assess the proposal’s effectiveness across various realistic situations, providing insights into its practical applicability and adaptability. Finally, we will test the algorithm’s effectiveness in reducing waste in the system.

Reinforced discrete sine cosine algorithm

MH optimization in production systems refers to efficiently moving raw materials, work-in-progress (WIP), and finished goods within a production facility during manufacturing. The MH problem commonly requires decisions that involve choosing a specific action from a finite set of options or choices, where the variables involved can only take on discrete values.

As we stated in section “Optimization”, the DSCA could be used to solve the MH problem. Although SCA has been utilized in several previous works, DSCA is a novel method that has received little attention and has yet to be used to address MH problems. The pseudocode shown above in Algorithm 2 outlines the main steps of the DSCA. However, as we will see in section“Results and discussions”, the standard DSCA underperforms our proposed algorithm to solve the MH problem. This is mainly due to its convergence being affected by the established values of the parameters $r_i$ in Eq. (3).

In order to improve the DSCA performance, we have been inspired by another algorithm, based on SCA, called QLESCA, recently proposed by Hamad et al. (2022). QLESCA includes a Q-learning formulation for the SCA parameters selection. The algorithm Q-learning helps each QLESCA agent to move adaptively in the search space according to its performance, where the reward (or penalty) is given based on the agent’s achievement. Each agent has a Q − table, where the parameters $r_{1}$ and $r_{3}$ are obtained based on the chosen state and action. Algorithm 3 outlines the QLESCA original pseudocode. Although QLESCA improves the performance of SCA, it was developed to deal with optimization problems in continuous domains, and the MH optimization problem requires discrete solutions. So, taking Algorithms 2 and 3 into account, we develop the proposed Reinforced Discrete Sine Cosine Algorithm, referred as $R^*DSCA$ outlined in the pseudocode shown in Algorithm 4.

Algorithm 3

Q-learning embedded Sine Cosine Algorithm

Algorithm 4

$R^*DSCA$

An important novelty of our proposed $R^*DSCA$ is that we have developed a mechanism for finding an optimal way to learn to increase the $r_1$ parameter. The coefficient $r_1$ is known as a transition control parameter, and its main function is to strike a balance between diversity and convergence during the search procedure (Gupta et al., 2022). The value of this parameter should preferably be increased across iterations to provide a transition from exploration to exploitation of the search space. As we see below, including a learning mechanism for $r_1$ selection substantially improves the algorithm’s performance. In this way, the transition control parameter $r_1$ could be updated following some behavior law. However, the possibility of learning a behavior law introduces an additional degree of freedom to the algorithm that can be taken advantage of to improve its performance. That is, instead of fixing a function that describes that behavior in advance, we can learn to build a monotonic increasing function from a finite set ${\mathcal {R}}$ of more elementary functions $r_{1,j} \in {\mathcal {R}}, j=1,\ldots N$ using the Q-learning algorithm. So, in order to implement a tabular version of the $Q-$learning algorithm in a simple way, we must have a set of finite states. Still, to convert the $r_1$ selection problem into a purely discrete finite MDP, defining a strategy to deal with discrete states remains. Therefore, we must define the states of the MDP. We define the space of states S in the domain [0, 1], such that each $s_\tau$ is an interval contained in S, such that $s_\tau \subset S$ with $s_\tau = 1,..,m$ and the states $s_1, \ldots s_m$, are congruent intervals into the domain of S. Additionally, we define the current relative distance $\delta _i^t$ between the solutions found and the optimal solution as:

$$\begin{aligned} \delta _i^t = \frac{X_{d}^{t}\ominus X_{i}^{t}}{l} \end{aligned}$$

(6)

where the numerator indicates the number of feature differences between the solution found and the optimal solution, and the denominator indicates the length of these solution vectors. So, the current state $s_t$ will be that $s^* \in S$ closest to the current value $\delta _i^t$. That is, for each agent at each instant, $\delta _i^t$ will be calculated, and the corresponding state will be found. In this way, using this strategy, we obtain a finite-state machine to describe the MDP, and consequently, the Q-learning algorithm could be used to obtain the optimal function for $r_1$ according to the current state $s_t$, following the state-action value function given in Eq. (4).

Returning to the step-by-step explanation of Algorithm 4, we see that it starts from a random solution. Then, each agent is evaluated by means of the objective function, and the proposed solution is saved. Then, the best solution is obtained. Continuing with the central part, which is the population evolution, as we can see, sometimes, with a probability $\varepsilon$, a random solution is taken (line 7, 8) and is evaluated through simulation, following on the other hand with the evolution of the algorithm.

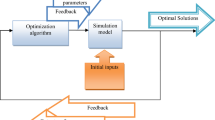
It can be seen in lines 10–17 the $Q-$learning section, where for each agent is obtained the current state and the action execution, as explained above. Once the value of $r_1$ is calculated, $r_2$ and $r_3$ are randomly updated. Using Eq. (2) and (3), the agent’s positions are updated, and their function’s evaluation results are saved. The exact elements are kept to update the agent’s position, and the order of the different features is updated randomly to generate a new solution. For the $Q-$learning reward, we compare the best solutions obtained for each agent with the current agent solution, and then the Q − tables are updated. Finally, the best solution for the population is returned. For a better comprehension of the developed algorithm, Fig. 1 shows a flowchart of it.

Fig. 1

$R^*DSCA$ flowchart

Case study

Problem definition

In the present work, the problem presented in Gola and Kłosowski (2019) is adapted as a case study. In particular, the benchmark problem has a high complexity where an MH problem is stated for a manufacturing plant, and it is solved by optimizing the routes of automated guided vehicles (AGV). The presented problem has a manufacturing system comprising 20 workstations and an autonomous vehicle.

The transport system of the case study has two fundamental tasks at certain times: delivery of parts to the workstations and collection of parts from the workstations. There is only one point of departure and arrival for the vehicle: the dispatch station. Once the vehicle has departed from this point, the route remains fixed, and there are no further changes.

Several aspects of the original problem are maintained in this work. For example, the plant layout and the stations’ working times. Also, the load sizes for each station. And the initial stocks are equal to the load at each station. These data can be consulted in Table 1. The dispatch station is located at point (0, 0).

Table 1 Case study data (Gola and Kłosowski, 2019)

The final objective of the study is to minimize the distance traveled by the vehicle on each route that must be developed. Before this, it is decided by predetermined fixed rules to which stations the vehicle should travel. It is also determined whether the transport should carry or remove materials from these stations. This will depend on the state of the stations, that is to say, the time remaining until the stock runs out and the amount of final stock in each.

$R^*DSCA$ Setup

For this particular problem presented in the previous subsection it will be defined here the main characteristics of our proposal. As mentioned, Q-learning finds the best values of $r_{1,j}$ for each iteration. Four increasing functions were chosen for the parameter $r_{1,j}$. Three of them were worked in the interval (0, 1) and the rest in the interval (0, 0.5). The formulas are shown below, and Fig. 2 shows the graphs corresponding to an interval of 30 iterations. Therefore, the actions $A_{t}$ of the algorithm will be the different functions $\hbox {r}_{1,j}$ whit $j=1,\ldots 4$.

$$\begin{aligned} r_{1_1}&= \frac{t}{T} \end{aligned}$$

(7)

$$\begin{aligned} r_{1_2}&= \frac{t}{2T} \end{aligned}$$

(8)

$$\begin{aligned} r_{1_3}&= 1 - \epsilon ^ {-(t^{0.5})}\end{aligned}$$

(9)

$$\begin{aligned} r_{1_4}&= \frac{t^2}{T^2} \end{aligned}$$

(10)

Fig. 2

Functions to apply for the parameter $r_{1}$

Regarding the necessary space of states S in the domain [0, 1] to apply the RL, five states were defined based on the current relative distance $\delta _i^t$ (Eq. (6)), such that $s_\tau \subset S$ with $s_\tau = 1,\ldots ,5$. The states can be seen in Table 2. Therefore, in our proposal, each Q − table has five states and four actions.

Table 2 States for $R^*DSCA$ setup

Regarding the reward, what is detailed in Algorithm 3 was maintained; that is, if the solution found by the agent is better than the one obtained so far, the reward is 1; otherwise, it is -1.

Finally, $\varepsilon$ was set at 0.20. And, when applying Q-learning, the internal parameters $\alpha$ and $\gamma$ were set to values of 0.1 and 0.9, respectively. These values are the most commonly used empirically in the literature. In addition, the agent was trained following an $\epsilon$-greedy exploration strategy, with a decay of $\epsilon$ with the course of the episodes from $\epsilon$ = 1 to a minimum value $\epsilon$ = 0.01, to improve the exploration-exploitation strategy.

Computational environment setup

For the modeling of the system and environment for the execution of the algorithms, it was decided to use the software Tecnomatix Plant Simulation (TPS) from Siemens. This software allows us to easily and quickly model and visualize productive systems. It is an object-oriented software that can customize and adapt these objects by adding specific programming. Figure 3 shows the model built in TPS for the problem in question. As can be seen, the routes are fixed, and the stations have a single place for loading and another for unloading.

The proposed optimization algorithm $R^*DSCA$ was developed in Python language. In addition, the computational implementation uses the software architecture SimulAI (Perez Colo et al., 2020) previously developed in the group (Saavedra Sueldo et al., 2022, 2021). This architecture was developed by our team earlier and allowed us to interconnect different entities and exchange information between them. SimulAI is a library that facilitates the use of AI techniques to optimize variables derived from the Simulation of Flexible Manufacturing Systems. The objective is to improve the decision-making process in organizations, making it more efficient and safe. In this case, we mainly use SimulAI to encapsulate the TPS simulations with our computational algorithmic formulation.

Fig. 3

Simulation model of the case study

The Python code comprises a general simulation of the plant and similar simulations that are opened and closed by running a specific path in the optimization algorithm to test a point solution. The overall simulation for the first phase of the problem (deciding where to go) is continuously monitored, and the algorithms are used to find the best possible route sequence.

The complexity of the developed model is $O(T *|X|)$, with T the number of iterations and |X| the number of initial solutions. The algorithmic developments of this work, as well as the details of the case study, are available in the digital repository https://github.com/carosaav/SimulAI/tree/master/RDSCA%20algorithm

Results and discussions

Initially, in section “R*DSCA assessment” to show the performance of our proposed $R^*DSCA$ optimization algorithm, we consider four sub-problems (or scenarios) with different complexity levels based on the problem presented in section “Problem definition”. We start addressing the least complex sub-problems, then another with intermediate complexity, and finally, a more complex sub-problem than the other two are addressed. When dealing with tractable problems with a few workstations, we can find the global optimal solutions by simulating all possible solutions. In this way, we take advantage of having the plant simulator, which allows us to simulate all possible solutions and accurately identify the optimal one. Thus, the solution that gives the best objective function value will be the optimal one. Then, this optimal solution will be used to compare the solution found using our proposal.

Once we demonstrate the performance of our proposal, in section “$R^*DSCA$ assessment for waste reduction”, we address the whole problem presented in section “Problem definition” and illustrate the applicability of our proposed algorithm for a large case considering waste reduction. However, finding the optimal global solution using intensive computational simulations is impracticable when faced with complex scenarios with several workstations since extremely large (or prohibitively) computational processing times will be required. As we have previously stated, the main problem has 20 workstations. Therefore, this gives rise to 2.432902e+18 (20!) possible routes (feasible solutions).

R*DSCA assessment

As detailed above, we consider four sub-problems explained below to assess the performance of $R^*DSCA$. Following, in section. “Results for $R^*DSCA$”, we show the results obtained when $R^*DSCA$ is used to solve these cases. Then, in section “Performance comparison”, we compare performance against another comparable methodology, the DSCA, for the same cases.

Results for $R^*DSCA$

Sub-problem A

To begin with, the initial sub-problem is simple, made up of only five stations out of the 20 that make up the complete original system. In this case, only workstations $\#1$, $\#4$, $\#6$, $\#15$, and $\#16$ are considered, and Fig. 4 shows the configuration of the resulting system. To analyze the performance of the proposed algorithm, we designed four testing experiments for this sub-problem. The results of each experiment are summarized in Table 3.

Fig. 4

Simulation model of sub-problem A

In order to determine how the initialization affects the solution found by the algorithm, we have run experiments with a fixed initial population and with a random one (mentioned in the 2nd column of Table 3). In both cases, the initial population includes six initial feasible solutions. In addition, to determine how the number of iterations affects the solution found by the algorithm, we have run experiments with different numbers of iterations, T, given in the 3rd column of Table 3. As previously explained, for this problem, the optimal theoretical solution, denoted as $O_{ts}$, is found by simulation of all feasible solutions. It is given in the 4th column of Table 3.

For each experiment, due to the stochastic nature of the proposed $R^*DSCA$, the value ${\bar{D}}$, shown in the 5th column of Table 3, corresponds to the average of the results ($D_{t_i}$) obtained for $m = 10$ repetitions of such an experiment. It is computed as in Eq. (11). The optimal solution, $D^*$, found by the algorithm is given in the last column of Table 3, and it is obtained as in Eq. (12).

$$\begin{aligned} \bar{D_{t}}&= \frac{\sum _{i=1}^{m} D_{t_i}}{m} ; \quad t=1\ldots T \end{aligned}$$

(11)

$$\begin{aligned} D^*_{t}&= \max _{j}\{D_{t_j}\} \quad ; \quad j=1\ldots m \end{aligned}$$

(12)

Table 3 $R^*DSCA$ experiments on sub-problem A

It can be verified that, for this simplified sub-problem, the algorithm always finds the optimal solution and that most of the tests are close to this solution since the average solution of each one is very close to the optimal one.

Sub-problem B

In this case, we address a variant with the same complexity as in the previous case, i.e., we take into account only five workstations too, but now we take into account the workstations $\#2$, $\#7$, $\#9$, $\#14$, and $\#19$. Therefore, the resulting shop floor setup is as in Fig. 5. In the same way, as in the previous case, we repeat the same experiments, and the obtained results are given in Table 4. Once again, the successful performance of the algorithm can be seen in all the tests since Algorithm 4 consistently achieves the optimal solution, that is, $D^* = O_{ts}$. Also, another issue that can be observed is that the initialization of the algorithm does not affect its performance. Therefore, we will consider only random initiations for the following experiments to avoid bias.

Fig. 5

Simulation model of sub-problem B

Table 4 $R^*DSCA$ experiments on sub-problem B

This is to highlight that in the case of a flexible production system, the periodic reconfiguration of production facilities is a frequent issue since the facilities must be reconfigured to meet different production requirements.

For both sub-problem A and sub-problem B, the proposed optimization algorithm successfully reached the optimal solution of the problem. This demonstrates that, in addition to arriving at the optimal solution for MH, our proposal is appropriate for use in these types of reconfigurable production systems. Next, to demonstrate the successful performance of our proposal, we will present other considerably more complex cases.

Sub-problem C

This sub-problem is more complex than the previous ones, and it is composed of seven workstations, which are $\#2$, $\#5$, $\#7$, $\#9$, $\#11$, $\#14$, and $\#19$, and the resulting shop floor setup is shown in Fig. 6.

This sub-problem is larger than the previous ones because the space of feasible solutions increases. Consequently, giving the algorithm a greater possibility of exploration is logical. Therefore, we include three additional experiments by increasing the maximum number of iterations, T.

Table 5 summarizes the results obtained. As can be seen, the algorithm always finds the optimal solution, $D^* = O_{ts}$, even when it runs with low iterations. As in the previous cases, in the 4th column of Table 5, it can be seen that as T increases, the algorithm’s performance improves since the mean of the found optimal solutions decreases.

Fig. 6

Simulation model of sub-problem C

Table 5 $R^*DSCA$ experiments on sub-problem C

Sub-problem D

To finish with the performance analysis of the algorithm, we are going to consider a complex problem in which we have ten workstations: $\#1$, $\#2$, $\#4$, $\#8$, $\#9$, $\#11$, $\#12$, $\#14$, $\#15$, and $\#19$ and the production system setup results as in Fig. 7. Unlike the previous cases, we do not have the theoretical optimal solution $O_{ts}$. Thus, we analyze the algorithm’s performance as the number of iterations T increases.

Table 6 shows the obtained experimental results. It is observed that the greater the number of iterations T, the smaller the average distances obtained. Therefore, the optimal solutions found $D^*$ are also better.

Fig. 7

Simulation model of sub-problem D

Table 6 $R^*DSCA$ experiments on sub-problem D

As we have hinted, the proposed simulation-based metaheuristic algorithm, $R^*DSCA$, contributes to determining MH policies for flexible production systems, where the reconfiguration of the facilities can be carried out frequently to meet different production requirements.

Performance comparison

Following, we continue with a performance comparison of our proposal against another comparable methodology to address sub-problems A to D. Specifically, we use the original DSCA. For the DSCA application (Gupta et al., 2022), the difference in features of the vectors implies the discrepancy in the sequence of the routes tested. In addition, with a certain probability ($p=0.20$), the choice of random solutions is added to increase the exploration of feasible solutions.

In the same way, as in the previous case, all the tests were repeated ten times with six initial solutions for each experiment. Summarizing, below in Table 7 are the results of the experiments with the DSCA for these four different sub-problems. It is verified that in almost all cases, DSCA finds the optimal solution, but the $R^*DSCA$ achieves better average results, demonstrating better performance than DSCA.

Table 7 DSCA experiments on the four sub-problems

Finally, to carry out this performance comparison, we have only considered those experiments for which we have the optimal solution $O_{ts}$. So, for each experiment carried out for each sub-problem, in Table 8, we computed the deviation between the obtained ${\bar{D}}$ by DSCA and $R^*DSCA$, respectively, and the optimal solution $O_{ts}$.

Analyzing the results presented in Table 7 and Table 8, it can be inferred that the performance of our proposed $R^*DSCA$ is higher than DSCA, reaching fewer deviations in 11 of the 13 first cases with known optimal solutions.

In the case of sub-problem D, for the comparison, we build some graphs that show the convergence curves for both algorithms (Fig. 8) used to find an optimal solution for this stated problem. By having a random start to the algorithm, there are different starter points, but a convergence at smaller distances can be observed in $R^*DSCA$ in all the figures.

Table 8 Experiment deviations

Fig. 8

Convergence curves $\bar{D_{t}}$ comparison on sub-problem D

$R^*DSCA$ assessment for waste reduction

Summarizing up to this point, we have tested the algorithms on different sub-problems with different configurations and verified their effectiveness. We have demonstrated that the DSCA with RL parameterizing laws has the best performance. Now, another testing stage begins, where experiments are run for the complete system of 20 stations (Fig. 3). Therefore, this problem is even more complex than the previous ones and has too many feasible solutions. In addition, we verify that the developed proposal not only optimizes the distances but also helps to reduce other Lean wastes.

For this stage, several rules based on different transport route sequences that organizations may use in their daily operations are tested against the performance of $R^*DSCA$. The objective will be to verify if the $R^*DSCA$ optimization of MH impacts the Lean waste of the system, specifically transportation, waiting, and inventories, which we will check in the simulator.

The first three cases have no built-in optimization system, so the transport is directed in a given order to fulfill the required route following a rule. In case 1, the order of the sequence or scheduling rule is random. This would be the case for an organization that does not provide any planning for the transport of materials due to a lack of knowledge or resources. In case 2, the vehicle is directed in ascending numerical order to the stations, following the layout. In case 3, transport maintains the priorities given by the initial part of the system. This part is mentioned and explained in section “Case study”, the scenario with more logic for handling materials because it considers the state of the stations and their buffers. Finally, case 4 is the application of our proposal $R^*DSCA$ with T=100. The limit for the number of workstations to be covered by the transport on the same trip remains ten.

Ten repetitions of cases 1 and 4, which contain randomness, are carried out. Cases 2 and 3 are fixed for a given initial situation. It is verified in the TPS software that the distances traveled by the vehicle, the time that the stations must wait for parts, and the remaining stock at the end of the simulations are lower with the developed algorithm. Therefore, it is possible to reduce three significant wastes in any production system, significantly impacting costs and business productivity.

Tables 9 and 10 show the best results obtained for each case. The production period tested in the first table is 2 h for each test, while in the second table, it is 8 h. In all cases, we start from the same initial situation to be able to compare. The last column of these tables shows the waiting time of the system station that most had to wait from the twenty stations.

Tables 11 and 12 show the Lean waste reduction percentages when comparing the first three cases against our proposal $R^*DSCA$. In a few tests and with a small number of algorithm iterations ($\hbox {T}=100$), minimizing such waste is significant in both cases.

Table 9 Results for 2-hour production period with $\hbox {T}=100$

Table 10 Results for 8-hour production period with $\hbox {T}=100$

Table 11 Waste reduction for 2-hour production period with $\hbox {T}=100$

Table 12 Waste reduction for 8-hour production period with $\hbox {T}=100$

Finally, to conclude this section and with the experiments carried out, the general 8-hour production period simulation was tested with the four rules but no longer with restrictions on the number of stations that can cover the transport in a single tour. In this scenario, the application of $R^*DSCA$ is performed with T=200. The results are shown in Tables 13 and 14. Once again, the algorithm’s high performance and waste reduction results are confirmed, mainly in the waiting time of stations.

Table 13 Results for 8-hour production period with $\hbox {T}=200$

Table 14 Waste reduction for 8-hour production period with $\hbox {T}=200$

Advantages of the developed $R^*DSCA$

It is worth highlighting some central aspects of our proposal. One of the main contributions of this work is the development of an optimization algorithm to deal with optimization problems involving discrete decision variables since many plant floor problems can be formulated as discrete decision-making problems.

In summary, our proposal stated a discrete formulation of the Sine Cosine Algorithm with an RL-embedded algorithm that allows for self-learning of the behavior law for the exploration/exploitation parameters. Including reinforcement learning to update a parameter provides more excellent performance to the algorithm while generating a greater degree of autonomy and independence from the intervention of a human expert. However, this could even be considered to extend the idea to address the determination of other parameters not considered in this study.

On the other hand, a central contribution of our work is using a discrete envent simulator like Tecnomatix since several previous works use graph theory for this type of problem, providing less information. In addition, using a plant simulator would allow not only measurements of the roads but also other conditions, such as, to name a few, energy consumption, equipment failures, and others. In this way, involving the interconnection with a plant simulator paves the way to interact with a digital twin of the system in the future. In this sense, for example, we can more easily monitor system variables like waste in our case. In addition to having greater use in the industry and much development, these technologies allow migrating over time to a digital twin of the entire organization. This is a central issue for the future of Industry 4.0, including new industrial metaverses (Alimam et al., 2023).

Finally, there is a stretch relationship between lean manufacturing and material handling optimization algorithms. Lean principles provide the global philosophy for minimizing waste and continuous improvement. At the same time, optimization algorithms offer the tools and methodologies to implement and enhance these principles in the context of material handling and production processes. Together, they contribute to creating more efficient, flexible, and responsive manufacturing systems. The presented result demonstrated a high performance and waste reduction for the stated material handling problem.

Conclusion and future work

This work proposes a metaheuristic simulation-based optimization methodology to address the MH problem in dynamic environments. Our proposed approach integrates optimization, discrete event simulation, and artificial intelligence methods. A complex benchmark problem was addressed to assess the performance of our proposal deeply. In addition, based on that MH problem, more manageable sub-problems were stated to test and compare our proposal against other methodologies rigorously, and successful results were obtained.

Furthermore, using a plant simulator like Tecnomatix allowed us to study the complete production system and monitor Lean waste linked to MH. It was determined that our proposal contributes to reducing three wastes: transportation, inventory, and station waiting.

Another contribution of our work worth noting is our implementation since it uses a discrete-event plant simulator with the SimulAI architecture. This fact opens a course of action for future work since it allows, with a negligible effort, interchanging information between a decision-support system and a digital twin of a production system. This would enable us to deal with diverse environments, face even more dynamic problems, and address behavioral disturbances.

On the other hand, new trends in production sectors claim for developments supporting flexible production systems driven by customized product demand. The Lean 4.0 paradigm can significantly contribute to this requirement by promoting combining the concept of harnessing waste reduction with 4.0 technologies. Our proposal was conceived mainly to contribute to this issue since it was precisely raised to address the MH problem for flexible manufacturing systems. As previously emphasized throughout the manuscript, MH is one of the tasks that cause the most significant inefficiency in a production process. The time invested in moving materials within a shop floor is a task with no added value in the final product.

Also, as subsequent future work, it would be interesting to assess the performance of our proposal for other kinds of optimization problems related to the Lean 4.0 philosophy, like minimizing the environmental impacts of manufacturing activities in flexible plants. In addition, the developed proposal could be used in other engineering optimization problems, mainly those that can be formulated as optimal control problems with partial information on the environmental conditions.

Furthermore, another issue for future work is the configuration of the algorithm’s hyperparameters, both those of SCA and those related to the Reinforcement Learning setup. Techniques such as Bayesian Optimization are possible new paths for this topic.