Trajectory clustering method based on spatial-temporal properties for mobile social networks

Abstract

As an important issue in the trajectory mining task, the trajectory clustering technique has attracted lots of the attention in the field of data mining. Trajectory clustering technique identifies the similar trajectories (or trajectory segments) and classifies them into the several clusters which can reveal the potential movement behaviors of nodes. At present, most of the existing trajectory clustering methods focus on some spatial properties of trajectories (such as geographic locations, movement directions), while the spatial-temporal properties (especially the combination of spatial distances and semantic distances) are ignored, and thus some vital information regarding the movement behaviors of nodes is probably lost in the trajectory clustering results. In this paper, we propose a Joint Spatial-Temporal Trajectory Clustering Method (JSTTCM), where some spatial-temporal properties of the trajectories are exploited to cluster the trajectory segments. Finally, the number of clusters and the silhouette coefficient are observed through simulations, and the results show that JSTTCM can cluster the trajectory segments appropriately.

1 Introduction

Currently, with the rapid development of location-aware technology, most of mobile communication devices have been equipped with GPS positioning modules. In mobile social networks (MSNs), nodes (the nodes denotes the human beings carrying communication devices in the mobile social networks) always carry the communication devices when they travel or walk, and the geographic locations of nodes are recorded at intervals. Then, these sequential location records can be transformed into some trajectories. Note that a great deal of information regarding the movement behaviors of nodes is hidden in these trajectories, and the information can be extracted by analyzing these trajectories and can be widely used in many applications, such as the location recommendations (Bao et al. 2015), destination predictions (Besse et al. 2018) and personal navigations (Li et al. 2015). Some valuable results can be mined and exploited through trajectory data mining techniques, e.g., the movement behaviors of nodes are obtained and are integrated into some location-based services where some personalized recommendations should be provided for nodes.

The mass of trajectory data contains the movement patterns and activity rules of group objects, such as the movement and activity characteristics of the crowds, the driving routes and the parking positions of vehicles, etc. These mobile patterns and activities reflect the mobile behaviors and living habits of the group objects. In addition, we can obtain some valuable information through a trajectory clustering process, and apply the valuable information to various applications such as traffic systems and location service applications. For example, (1) Path recommendation. The map service company analyzes the users’ mobile routes by collecting the trajectory data, we can mine the ubiquitous movement patterns from the large-scale trajectory data, and then according to the real-time background environment and users’ behaviors, reasonable paths are recommended for the users. (2) Personalized service recommendation. The trajectory data can record the user’s locations in mobile social networks, and the user’s movement trajectories are exploited for the understanding of trajectory behaviors, the characterization of users’ characteristics, the mining of users’ behavior patterns and so on. According to the implication of users’ activities, the search engines will recommend satisfactory business services or personal services.

Trajectory data mining typically consists of the parts of trajectory classification, trajectory clustering, outlier detection and trajectory pattern mining. The trajectory classification belongs to the field of supervised learning, which relies on the labeled trajectory data. Actually, most of the trajectory data is unlabeled, and the cost of labeling the trajectory data manually is extremely large. In contrast, the trajectory clustering is a kind of unsupervised learning technique, and it does not require to label the training data, which seems more available in MSN applications than the trajectory classification.

By observing the movement behaviors of nodes in some real MSNs, there are two findings: (a) the nodes may exhibit a frequent movement trend when traveling on some road segments, as shown in Fig. 1a, the similar movement trends exist in the four trajectories of the same node; (b) there are common movement trends among different nodes, as illustrated in Fig. 1b, where the trajectories of node A, B, C and D have a common movement trend. The movement similarities between nodes are usually related to the number of similar road segments, i.e., more similar road segments give rise to a larger movement similarity (a closer relationship between the movements of two nodes). In order to exploit the common movement trends from a large amount of trajectories, the trajectory clustering technique is expected to allocate the similar trajectory segments into the same clusters.

Fig. 1

Two types of movement trends

The existing trajectory clustering techniques are divided into two categories: global trajectory clustering and sub-trajectory clustering. The global trajectory clustering methods classify the complete trajectories according to the trajectory similarities, whereas the complete trajectories are always of little similarities. The similarities between sub-trajectories are much easier to be explored than those between different complete trajectories, the original trajectories are first partitioned into several sub-trajectories (or trajectory segments), and then the similarities between these sub-trajectories (or trajectory segments) are calculated for further clustering process. In addition, most existing clustering methods consider the spatial-positions or temporal-information attached to the trajectories respectively in the similarity measurements of sub-trajectories, and the spatial properties and temporal properties of trajectories are not taken into account jointly, which makes some trajectory segments allocated into wrong clusters inevitably.

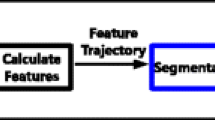
In this paper, we focus on the human trajectories, and the human beings carrying communication devices play the role of nodes in mobile social networks, so that the simulation dataset is also human related. A spatial-temporal distance function combining the spatial distances and semantic distances is designed to measure the similarities between trajectory segments, and then a density-based trajectory clustering method is proposed. To obtain the preferable clusters of trajectory segments, this work is consisted of two stages, as depicted in Fig. 2:

• trajectory partition, which partitions the original trajectories into trajectory segments;

• trajectory clustering, which clusters the trajectory segments through investigating the similarities between trajectory segments.

Fig. 2

Trajectory partition and trajectory clustering

The rest of the paper is organized as follows: Section 2 gives some related works. Section 3 introduces the joint spatial-temporal trajectory clustering method. Section 4 reports the simulation results of trajectory clustering. Finally, Section 5 concludes the paper.

This work is a significant extension of our early work (Tang et al. 2019b). Specifically, many related works are investigated, and our research motivation is introduced. The proposed JSTTCM is improved and explained with more details, e.g., a kernel function is give to measure the trajectory clustering results, and some example results regarding the combination and the normalization are provided to illustrate these mechanisms. Besides, much more simulation results are provided to further clarify the merits of JSTTCM.

2 Related work

The issue of trajectory clustering has attracted lots of attention. For example, Gaffney et al. propose a hybrid model-based trajectory clustering algorithm (Gaffney and Smyth 1999), which models each trajectory as a measurement sequence given by a time function, and then the objects generated by the core trajectory and Gaussian noise are aggregated by the EM algorithm. Alon propose a clustering method on the basis of a model in which each cluster is expressed by a Markov model (Alon et al. 2003), and the parameter estimation is also completed by the EM algorithm. However, all these methods treat each trajectory as a clustering object, and thus it is difficult to find the local similarities of the trajectories.

The trajectory clustering algorithms typically denote a trajectory by an eigenvector. Each dimension in the eigenvector is related to an attribute of the trajectory, and hence the number of the dimensions is equal to that of attributes. Besides, the distance between eigenvectors is applied to measure the similarities between trajectories, and a shorter distance is concerned with a larger similarity. Notice that the dimensions of different eigenvectors may be different, and this fact makes some existing trajectory clustering algorithms become unavailable, this is because the trajectories can embody many attributes, such as the lengths, shapes and sampling rates of trajectories. Therefore, the trajectory segments should be comprehensively compared according to their differences. Fortunately, there are some distance indices to measure the similarities between trajectories: the Longest Common Sub-Sequence (LCSS) distance aims to find the longest common sub-trajectory (Michail et al. 2006); Hausdorff distance is used to measure how far two trajectories are from each other (Liu et al. 2014); Dynamic Time Warping (DTW) targets to seek out an optimal alignment between two trajectory sequences (Chen et al. 2005); Chen and Ng treat each trajectory as a time series and then design an edit distance with actual penalty to measure the trajectory similarities (Chen and Ng 2004). The aforementioned distance indices are more suitable to calculate the distances of different trajectories rather than those of different trajectory segments.

Considering the difficulty of dealing with the complete trajectories, Lee et al. put forward a density-based trajectory clustering method TraClus (Lee et al. 2007), which first divides the trajectories into continuous trajectory segments by Minimum Description Length (MDL), and then the similar segments are clustered using this density-based clustering algorithm. A hierarchical trajectory clustering algorithm utilizing HDBSCAN (Zhang et al. 2018) based on TraClus is presented in Campello et al. (2013), where some semantic information (such as direction, speed and time) is considered. In addition, a trajectory clustering algorithm CTHD (clustering of trajectory based on hausdorff distance) is proposed (Chen et al. 2011), where a sequence of flow vectors are described and partitioned into a set of sub-trajectory. Then, the similarity between trajectories is measured by their respective Hausdorff distances (including the positions and directions). Finally, the trajectories are clustered by the DBSCAN clustering algorithm.

Besides, some existing literatures analyze the semantic trajectory data to find interesting places, such as CB-SMoT (Palma et al. 2008) and DB-SMoT (Rocha et al. 2010). In CB-SMoT, a trajectory clustering method based on velocity variation is provided to estimate the trajectory sample points and then form the clusters. In DB-SMoT, the changes in movement directions are taken as the key index for the clusters, and the proposed method is verified by the trajectory data of marine fishing vessels. An adaptation of a density-based clustering algorithm to trajectory data based on a simple notion of distance between trajectories is proposed (Nanni and Pedreschi 2006), and a new approach called temporal focusing to the trajectory clustering problem is sketched, which having the aim of exploiting the intrinsic semantics of the temporal dimension to improve the quality of trajectory clustering. A visually-driven analysis of movement data by progressive clustering is proposed (Rinzivillo et al. 2008), which focus in more detail on the use of cluster analysis with different similarity measures. In particular, the authors assume that each distance function aggregates objects according to its own semantics, the user can choose a sequence of functions to be used progressively. In Andrienko et al. (2016) the spatial-temporal aggregation is applied to traffic data consisting of vehicle trajectories, and a spatially abstracted transportation network consisting of areas in geographic space and the possible paths is generated, which is used to traffic analysis, forecasting and simulation leveraging spatial abstraction. The literature (Trasarti et al. 2011) introduces the concept of the mobility profile of a user as the set of his routine trips, and define a general method based on trajectory clustering to extract such profiles; then an instantiation of the method on the GPS data of vehicles with a route similarity function is shown; finally, the downgrading of the spatial-temporal richness of the data is studied.

In 2015, an unsupervised trajectory clustering method based on adaptive multi-kernel shrinkage is presented (Xu et al. 2015), where an adaptive multi-kernel-based estimation process is performed to estimate the “reduction” positions and the velocities of the track points. Further, a speed regularization optimization process that utilizes the estimated velocity is introduced to adjust the optimal shrunk points to ensure the smoothness and discriminant mode of the final shrunk trajectory. However, the proposed method does not take into account the time information attached to trajectories. In 2017, a trajectory clustering method via deep representation learning is proposed (Yao et al. 2017), where the trajectory clustering problems are re-examined by learning the low-dimensional trajectory representations. Especially, a sliding window is used to extract a set of movement behavior features that capture the spatial-temporal invariant features in the trajectories, and then each trajectory is converted into a sequence of features that can describe the object movements. Finally, the K-means clustering algorithm is utilized to cluster the learned trajectory representations.

In fact, many existing works have focused and addressed the trajectory clustering problem, and most of them ususally employ some spatial properties or temporal properties to cluster the trajectories. Yes, there are also some work taking into account of spatial properties or temporal properties simultaneously. We add some explanations about the motivation of this paper:

• Although some works have considered the spatial-temporal properties, there are some differences in terms of the problem objectives and application scenarios. The objective of our work is to explore the human trajectories, which indicates that there are some spatial-temporal properties hidden in human trajectories, and thus it is very necessary to analyze the mobile behaviors of human beings. However, the existing works mainly focus the vehicle trajectories, and the movement behaviors of vehicles are much different from those of human beings.

• We take the human beings carrying communication devices as nodes in the mobile social networks, i.e, the nodes have some social attributes. We observe that there are some similarities between these nodes due to the social attributes. Therefore, a spatial-temporal trajectory clustering method is appropriate to exploit the relations between nodes.

• This paper consists of two parts: trajectory partition and trajectory cluster. We consider some movement features of nodes in the process of trajectory partition, the results of which are served for the trajectory cluster. Therefore, we think the proposed method is quite different from other works.

In this paper, the spatial-temporal properties of the trajectories are investigated to cluster the trajectory segments, especially, a spatial-temporal distance function combining the spatial distances and semantic distances is defined to measure the similarities between trajectory segments, and then a Joint Spatial-Temporal Trajectory Clustering Method (JSTTCM) is proposed.

3 Joint spatial-temporal trajectory clustering method

JSTTCM is consisted of the stages of trajectory partition and trajectory clustering. In this section, we first introduce the trajectory partition method to partition the original trajectories into trajectory segments. Then, a new density-based trajectory clustering method is given to cluster the trajectory segments. To clarify the description, several definitions are provided as following:

Definition 1

A GPS point: a GPS point p_i is expressed as a triple (lat_i,lng_i,t_i), which is composed of the latitude, longitude and timestamp of the i-th point, where i = 1,2,⋯ ,n, and n is the number of GPS points in a trajectory.

Definition 2

A trajectory: a trajectory is a sequence of GPS points arranged in a chronological order and is denoted by TR = p₁,p₂,⋯ ,p_n, as shown in Fig. 3, the label of Axis Y indicates time stamp.

Fig. 3

An example trajectory

Definition 3

A trajectory segment: a trajectory segment L_i = {p_s,p_e} is denoted by the start point and the end point, where p_s denotes the start point, and p_e denotes the end point.

3.1 Trajectory partition

In MSNs, we note three significant characteristics regarding the node movements: (i) the moving speed of nodes changes greatly due to the switches of different travel modes or some special events (e.g., sudden braking or abrupt deceleration in driving) (Zheng et al. 2010a); (ii) the nodes are prone to visit some locations intentionally or unintentionally, and the locations visited frequently or stayed for a long period can be marked as stop points; (iii) the moving directions of nodes are varied frequently when some travel modes (such as the walking mode) are adopted. To this end, we provide a Trajectory Partition mechanism based on Movement Features(TPMF) (Tang et al. 2019a).

In TPMF, the stop points and change points are extracted according to the moving speeds and the speed changes, respectively, and then the extracted stop points and change points are treated as feature points. Finally, a Douglas-Peucker algorithm based on Direction changes and Perpendicular Euclidean Distance (DPDPED) is applied to simplify the sub-trajectories between the adjacent feature points.

3.2 Trajectory clustering

In this section, we define a spatial-temporal distance function and raise a density-based clustering method to cluster the similar trajectory segments. Besides, a clustering validation is given to evaluate the clustering results.

3.2.1 Spatial-temporal distance function

As mentioned above, it is hard to identify the similar movement behaviors in different trajectories, and thus we exploit the similarities between trajectory segments. Especially, some spatial-temporal properties are taken into account to calculate the similarities between trajectory segments. As shown in Fig. 4, the spatial distances include the perpendicular Euclidean distance and the parallel distance, and the spatial distances can measure the spatial relationships between trajectory segments. The semantic distances include the direction distance, duration distance, velocity distance and time distance, i.e., the semantic distances integrate the temporal dimension to explore the temporal relationships between trajectory segments.

Fig. 4

Spatial distances and Semantic distances

The spatial-temporal distance function considers the spatial distances and semantic distances jointly:

(a) Note that the perpendicular Euclidean distance remains the same unless the two trajectory segments are parallel to each other. Therefore, we first compare the lengths of two trajectory segments, and then calculate the perpendicular Euclidean distance from the shorter trajectory segment (such as L_i in Fig. 5) to the longer trajectory segment (such as L_j in Fig. 5). The perpendicular Euclidean distance is given by:

$$ d_{\perp}=\frac{l_{\perp 1}^{2}+l_{\perp 2}^{2}}{l_{\perp1}+l_{\perp 2}}, $$

(1)

where

$$ \left\{ \begin{array}{l} l_{\perp 1}=\sqrt{\Vert\overrightarrow{p_cp_a}\Vert^{2}-(\frac{\overrightarrow{p_cp_a}\cdot\overrightarrow{p_cp_d}}{\Vert\overrightarrow{p_dp_c}\Vert})^{2}},\\ l_{\perp 1}=\sqrt{\Vert\overrightarrow{p_dp_b}\Vert^{2}-(\frac{\overrightarrow{p_dp_b}\cdot\overrightarrow{p_dp_c}}{\Vert\overrightarrow{p_dp_c}\Vert})^{2}}. \end{array} \right. $$

(2)

Fig. 5

Perpendicular Euclidean distance and parallel distance

(b) In Fig. 5, the parallel distance consists of l_∥1 and l_∥2. We take the maximum value of l_∥1 and l_∥2 as the parallel distance, and the parallel distance is expressed as:

$$ d_{\parallel}=max(l_{\parallel 1},l_{\parallel_{2}}), $$

(3)

where l_∥1 and l_∥2 are calculated as:

$$ \left\{ \begin{array}{l} l_{\parallel 1}=\frac{\overrightarrow{p_cp_a}\cdot\overrightarrow{p_cp_d}}{\Vert\overrightarrow{p_cp_d}\Vert},\\ l_{\parallel 2}=\frac{\overrightarrow{p_dp_b}\cdot\overrightarrow{p_dp_c}}{\Vert\overrightarrow{p_dp_c}\Vert}. \end{array} \right. $$

(4)

The semantic distances focus on the trajectory differences in temporal dimensions. As depicted in Fig. 6, the angle between two trajectory segments denotes the directional deviation.

Fig. 6

Illustration of direction distance

(c) The direction distance can be expressed by an angle cosine and is written as:

$$ d_{\theta}=\left\{\begin{array}{rcl} 1-\cos\theta, & & {0 \leq \theta<\frac{\pi}{2}}\\ 1, & & {\frac{\pi}{2}\leq \theta \leq \pi} \end{array} \right. $$

(5)

where 𝜃 denotes the angle between two trajectory segments.

(d) The duration distance reflects the difference of time intervals between trajectory segments. The duration distance is computed as:

$$ d_{\Delta t}=\left\{\begin{array}{rcl} 1-\frac{\Delta t^{(L_{i})}}{\Delta t^{(L_{j})}}, & & {\Delta t^{(L_{i})}\leq{\Delta} t^{(L_{j})}},\\ 1-\frac{\Delta t^{(L_{j})}}{\Delta t^{(L_{i})}}, & & {otherwise}, \end{array} \right. $$

(6)

where ${\Delta } t^{(L_{i})}=t_{e}^{(L_{i})}-t_{s}^{(L_{i})}$, and ${\Delta } t^{(L_{j})}=t_{e}^{(L_{j})}-t_{s}^{(L_{j})}$.

(e) The velocity distance measures the difference of traffic modes between nodes. The velocity distance is given by:

$$ d_{v}=\left\{\begin{array}{rcl} 1-\frac{v_{i}}{v_{j}}, & & {v_{i}\leq v_{j}},\\ 1-\frac{v_{j}}{v_{i}}, & & {otherwise}, \end{array} \right. $$

(7)

where $v_{i}=\frac {\Vert L_{i} \Vert }{\Delta t^{(L_{i})}}$, and $v_{j}=\frac {\Vert L_{j} \Vert }{\Delta t^{(L_{j})}}$.

(f) The time distance is to measure how close are the time stamps of the trajectory segments, and it is defined as:

$$ d_{t}=\left|t_{s}^{(L_{i})}-t_{s}^{(L_{j})}\right|+\left|t_{e}^{(L_{i})}-t_{e}^{(L_{j})}\right|. $$

(8)

In order to combine the different kinds of distances technically, a nonlinear function is introduced for normalization, and it is expressed as:

$$ f(x)=\frac{1}{1+e^{-ax+b}}, $$

(9)

where a and b are preset parameters. Some example results for the combination and normalization are given in Fig. 7.

Fig. 7

Normalization curves under different values of a and b

3.2.2 Comparisons of different distance functions

Three types of distance functions (weighted summation function, kernel function and time focusing function) are applied to construct the spatial-temporal distance function, respectively. The weighted summation distance function is written as:

$$ dist_{w}(L_{i},L_{j})=w_{1}\cdot d_{\perp^{\prime}}+w_{2}\cdot d_{\parallel^{\prime}}+w_{3}\cdot d_{\theta}\\ +w_{4}\cdot d_{v}+w_{5}\cdot d_{\Delta t}+w_{6}\cdot d_{t^{\prime}}, $$

(10)

where $d_{\perp ^{\prime }}$, $d_{\parallel ^{\prime }}$ and $d_{t^{\prime }}$ denote the normalizations of perpendicular Euclidean distance, parallel distance and time distance, respectively.

The kernel distance function is similar to the Gaussian kernel, and it is written as:

$$ dist_{k}(L_{i},L_{j})=1-e^{-\frac{\Vert \textbf{\textit{F}}\Vert^{2}}{2\sigma^{2}}}, $$

(11)

where $\textit {\textbf {F}}=(d_{\perp ^{\prime }},d_{\parallel ^{\prime }},d_{\theta },d_{v},d_{\Delta t},d_{t^{\prime }})$ denotes an eigenvector, and σ denotes a reduction factor.

The time focusing distance function is written as:

$$ dist_{T}(L_{i},L_{j})=\frac{{\sum}_{t_{0}}^{t_{0}+T}d\left( L_{1}\left( t \right),L_{2}\left( t\right)\right)}{\left|T\right|}, $$

(12)

where $t\in \left (t_{0},t_{0}+\left |T\right |\right )$, t₀ indicates a start moment, T is the temporal interval over which trajectories L₁ and L₂ exist. Such a definition requires a temporal domain common to all objects, in general, it is a hard requirement. Actually, it is hard to find a common temporal domain between two different trajectory segments in real-life dataset. However, it is unnecessary to require common temporal interval in our work. Although such a definition considers the temporal property, the speed and direction was not taken into account in time focusing distance function.

Firstly, we compare the different characteristics between the weighted summation distance function and kernel distance function. Suppose there are two trajectory segments L₁ = {(4.25,2.53,12 : 00 : 15), (5.65,10.24,12 : 30 : 45)} and L₂ = {(4.26,2.535,11 : 50 : 25), (5.64,10.25,12 : 45 : 10)}. A trajectory segment consists of a start point and an end point, and each point consists of latitude, longitude and time stamp. For example, L₁ contains two points, and note that the latitude and longitude should be transformed to adapt the coordinate system. The start point of L₁ is (4.25, 2.53, 12:00:15), where 4.25 and 2.53 represent the transformed latitude and transformed longitude, respectively, and 12:00:15 denotes the timestamp. We have defined six different distance measures in pages 8 and 9, and provided a nonlinear function to normalize these distances.

Therefore, we get F = (0.995,0.277,0.000,0.442,0.442,0.277), $d_{\perp ^{\prime }}=0.995$ is the normalized perpendicular Euclidean distance between L₁ and L₂ with a = 1 and b = 5, which indicates the perpendicular Euclidean distance is very large. $d_{\parallel ^{\prime }}=0.277$ is the normalized parallel distance between L₁ and L₂ with a = 0.5 and b = 5, which indicates the parallel distance is relatively small. Note that d_𝜃 = 0.000 represents the directions of L₁ and L₂ remain almost parallel. d_v = 0.442 represents the speed distance by (7), and d_Δt = 0.442 represents the duration distance by (6). $d_{t^{\prime }}=0.277$ is the normalized time distance by (9) with a = 10 and b = 5. Then, the distance between L₁ and L₂ calculated by the weighted summation function is equal to 0.406, and the distance calculated by the kernel function is equal to 0.536. From the results of F, the perpendicular Euclidean distance between L₁ and L₂ is relatively large, which indicates that L₁ and L₂ are not similar. However, we cannot determine that whether L₁ and L₂ are similar or not according to the distances calculated by two distance functions. Note that there is an obvious difference between the results calculated by the two distance functions. The reason is that the kernel distance function is sensitive to the variation of each distance. In fact, the difference will be reduced when all the distances are not large. For example, we set the spatial positions of L₁ and L₂ be equal, which gives rise to 0.195 (the result obtained by the weighted summation distance function) and 0.209 (the result obtained by the kernel distance function), respectively, and it is obvious that the difference is reduced significantly.

We also compare the different characteristics between the weighted summation distance function and the time focusing distance function. Suppose there are two different trajectory segments L₁ = {(4.25,2.53,8 : 00 : 00), (5.65,10.24,8 : 10 : 00)} and L₂ = {(4.26,2.535,8 : 00 : 00), (5.64,10.25,8 : 10 : 00)}, which have a common temporal domain. Therefore, we get $\left |T\right |$= 600s, it’s easy to get the average distance $dist_{T}(L_{i},L_{j})=\frac {11.180 + 14.142}{600}=0.042$ by the time focusing distance function. In our work, both the time distance and the duration distance are equal 0. In addition, the distance dist_w(L_i,L_j) = 0.212 between L₁ and L₂ by the weighted summation function. From the results of two different distance functions, it indicates that the value of dist_w(L₁,L₂) is five times more than the value of dist_T(L_i,L_j), which is attributed to the fact that our distances have considered spatial-temporal properties. In fact, if the temporal distances are very small, yet the spatial distance are much large, which makes the similarity of trajectories extremely low.

3.2.3 Density-based clustering

We propose a density-based clustering algorithm, which is an improved version of DBSCAN (Ester et al. 1996). The outstanding advantage of DBSCAN is that it can filter out the noise and automatically identify the number of clusters. DBSCAN characterizes the closeness of the distribution of trajectory segments based on the neighborhood parameters (𝜖,MinPts). The basic idea is that each cluster continues to grow, until the trajectory segments in its neighborhood (the range of 𝜖) cannot become the core trajectory segments. Some definitions are first given to illustrate our proposed density-based clustering algorithm:

• 𝜖-neighborhood: there is L_i ∈D (trajectory segment dataset), if its 𝜖-neighborhood contains the trajectory segments whose distances to L_i are not larger than 𝜖, i.e, $N_{\epsilon }(L_{i})=\left \lbrace L_{j}\in \textit {\textbf {D}}|dist_{w}(L_{i},L_{j})\leq \epsilon \right \rbrace$.

• Core trajectory segment: if L_i’s 𝜖-neighborhood contains at least MinPts other trajectory segments, i.e., $\left |\epsilon (L_{i})\right |\geq MinPts$, and then L_i is taken as a core trajectory segment.

• Directly density-reachability: if L_j falls into the L_i’s 𝜖-neighborhood, and L_i is a core trajectory segment, then L_j is directly density-reachable to L_i.

• Density-reachability: if there is a set of trajectory segments p₁,p₂,⋯,p_n, where p₁ = L_i, p_n = L_j and p_i+ 1 is directly density-reachable to p_i, then L_j is considered to be density-reachable to L_i.

• Density-connectivity: if L_j and L_i are density-reachable to the same trajectory segment L_k, and then L_j and L_i are density-connected to each other.

An example is given to illustrate the definitions in Fig. 8, where L₁ is a core trajectory segment, and L₂ is directly density-reachable to L₁. L₃ is density-reachable to L₁, and L₃ is density-connected to L₄.

Fig. 8

Relations of trajectory segments

All core trajectory segments can be identified when the parameters 𝜖 and MinPts are set. Then, the core trajectory segments can “carry” all trajectory segments of their 𝜖-neighborhoods into density regions according to the directly density-reachable relationships. Furthermore, the density-reachable relationships are utilized to connect the small density regions with the centers of core trajectory segments. Finally, each core trajectory segment and the density-connected neighbors will constitute a density region (cluster). The time complexity of the above steps reaches O(n²) due to the fact that all of the neighborhoods of trajectory segments must be searched. In order to reduce the time complexity, we reduce the neighborhoods through exploiting some temporal attributes:

• 1. The trajectory segment dataset is sorted in a chronological order.

• 2. $t_{s}^{(L_{i})}$ and $t_{e}^{(L_{i})}$ are found from each trajectory segment L_i, and $t_{s}^{(L_{i})}-{\Delta } t$, $t_{e}^{(L_{i})} +{\Delta } t$ are calculated, respectively, where Δt is a preset offset.

• 3. The binary search is used to find the index l of $t_{s}^{(L_{i})}-{\Delta } t$ and the index r of $t_{e}^{(L_{i})} +{\Delta } t$ in the sorted dataset.

• 4. The initial neighborhood range is obtained according to l and r, and the distances between trajectory segments in the neighborhoods are recalculated.

The pseudo-code of our proposed density-based clustering algorithm is shown in Algorithm 1.

3.3 Clustering validation

To evaluate the clustering results, such as the number of appropriate clusters and the cluster structures, some unsupervised metrics have been applied to validate the clustering results, and these unsupervised metrics can be typically classified into two categories: the metric cohesion measures how closely related are the trajectory segments falling into the same cluster; the metric separation measures how distinctly separated are the trajectory segments in a cluster from those in other clusters.

In this paper, we use the silhouette coefficient (Rousseeuw 1987) to evaluate the clustering results, because the silhouette coefficient is a combination metric of cohesion and separation. Given the obtained results $\textit {\textbf {C}}=\left \lbrace C_{1}, C_{2}, \cdots , C_{k} \right \rbrace$, $\mathcal {A}(C_{i})$ represents the average distance of the trajectory segments in C_i, and ${\mathscr{B}}(C_{i})$ represents the minimum average distance from C_i to other clusters, where i = 1,2,⋯ ,k. $\mathcal {A}(C_{i})$ and ${\mathscr{B}}(C_{i})$ are given by:

$$ \mathcal{A}(C_{i})=\frac{1}{|C_{i}|}\cdot{\sum\limits_{L\in C_{i}}\frac{{\sum}_{L'\in C_{i}}dist(L,L')}{|C_{i}|-1}}, $$

(13)

$$ \mathcal{B}(C_{i})=\min_{1\leq j\leq k,j\neq i}\frac{1}{|C_{i}|}\cdot{\sum\limits_{L\in C_{i}}\frac{{\sum}_{L'\in C_{j}}dist(L,L')}{|C_{j}|}}. $$

(14)

Besides, the silhouette coefficient of C_i is defined as:

$$ \mathcal{S}(C_{i})=\frac{\mathcal{B}(C_{i})-\mathcal{A}(C_{i})}{max\left\lbrace \mathcal{A}(C_{i}),\mathcal{B}(C_{i})\right\rbrace} $$

(15)

A smaller $\mathcal {A}(C_{i})$ gives rise to a larger cohesion, and a larger ${\mathscr{B}}(C_{i})$ gives rise to a larger separation. The average of the silhouette coefficient of all clusters can measure the quality of clustering results effectively. Notice that the value of the silhouette coefficient falls into the interval $\left [-1,1\right ]$, and the best clustering results are achieved when $\mathcal {S}(C_{i})$ is equal to 1.0.

4 Simulations

The simulations are run on a PC equipped with Windows 7, 3.20GHz CPU and 4 GB memory. The trajectory clustering methods are realized by Java language.

4.1 Simulation setup

GPS trajectory dataset is obtained from (Microsoft Research Asia) Geolife project (Zheng et al. 2010b), which collects the trajectories of 182 users (nodes) during five years (from April 2007 to August 2012). The GPS trajectory of the dataset is represented by a sequence of time stamps, each of which contains latitude, longitude and altitude information. The dataset contains 17621 trajectories with a total distance of 1251654 km and a total duration of 48203 hours. These trajectories record different GPS loggers and GPS telephones, and have various sampling rates. The trajectory of 91% is recorded in dense representation, for example, every 1 to 5 seconds or 5 to 10 meters per point. The trajectory data set can be used in many research fields, such as mobile pattern mining, user activity recognition, location-based social networks, location privacy and location recommendation. Table 1 provides some distance parameter settings.

Table 1 Distance parameter settings

We set an upper bound for each distance parameter, which indicates that each kind of distance between two trajectory segments should be confined to an upper bound. As the road length is typically far larger than the road width, we set the upper bound of the perpendicular Euclidean distance to 5 meters, and then its normalized value is equal to 0.500 by (9). Likewise, we set the upper bound of the parallel distance to 10 meters, and its normalized value is equal to 0.500 as well. Besides, we assume that the upper bound of the angle between two trajectory segments is within π/6, so that we can obtain the normalized value of direction distance equal to 0.134 by (5). With regard to speed distance and duration distance, the upper bounds of speed ratio and duration ratio between two trajectory segments are set to 2/3, and both the two distances are 0.333 by (6) and (7), respectively. The time stamps of two trajectory segments are close to each other, and the upper bound of time distance is set to 30 minutes by (8), which indicates that its normalized value is equal to 0.500.

The upper bound of the parameter 𝜖 is calculated by the weighted summation function: dist_w(L_i,L_j) ≈ 0.394, which is close to the result calculated by the kernel function dist_k(L_i,L_j) ≈ 0.389. Thus, the weighted summation function is chosen as the distance function in our simulations, and the value of the 𝜖 falls into interval [0,0.394].

4.2 Trajectory clustering

In this section, we observe the impacts of the time sequences and the number of nodes on the trajectory clustering results, in terms of the number of clusters and the silhouette coefficient, as illustrated in Fig. 9.

Fig. 9

Number of clusters and silhouette coefficient (Eps(𝜖) = 0.35,MinPts = 15)

From Fig. 9a, the number of clusters becomes more stable as the number of nodes increases from 1 to 4, which indicates that the number of clusters is irrelevant with the input order of trajectory segments when enough trajectory data has been provided. Besides, it is obvious that the curve with trajectories of more nodes is much higher than those with trajectories of less nodes. In Fig. 9b, the silhouette coefficient fluctuates slightly with the increase of time sequences while the number of clusters almost keeps as a constant, which is due to the density differences in the trajectory clustering results.

Figure 10 illustrates that the variations of the number of clusters and silhouette coefficient under different MinPts. In Fig. 10a, the number of clusters decreases with the increase of MinPts when Eps is fixed. Notice that the number of clusters decreases significantly when the value of MinPts increases from 10 to 25, while the number of clusters reduces slowly when the value of MinPts is larger than 25. In Fig. 10b, the silhouette coefficient increases with the rise of MinPts, and we find that the silhouette coefficient is slightly varied when the value of MinPts increases from 25 to 30. As discussed above, MinPts is set to 25 in the following simulations.

Fig. 10

Numbers of cluster and silhouette coefficient vs. MinPts

Likewise, Fig. 11 shows the number of clusters and silhouette coefficient under different settings of Eps. In Fig. 11a, two observations are obtained: (a) the curves rise quickly when Eps is smaller than 0.36, and the reason is that the neighborhood of each core trajectory segment rapidly increases with the increase of Eps, and thus more clusters are produced; (b) the curves descend slowly when Eps is larger than 0.36, which is attributed to the fact that the density of neighborhood of each core trajectory segment has exceeded the size of cluster when Eps continues to increase, while the number of clusters is reduced. Hence, Eps is set to 0.36 in the following simulations. In Fig. 11b, the curves first drop quickly because of the increasing number of cluster, and then the curves rise slowly because the number of clusters number is reduced as aforementioned phenomenon in Fig. 11a.

Fig. 11

Numbers of cluster and silhouette coefficient vs. Eps

Therefore, the main parameter settings of JSTTCM are provided in Table 2. The distance radius (𝜖) and the minimum number of neighbors (MinPts) are vital to trajectory clustering methods, they are determined by simulations in Figs. 10 and 11. In addition, the time interval threshold (Δt) is preset to 0.5 hour, which indicates the maximum error of time interval between two trajectory segments does not exceed 30 minutes, it can be considered that it’s similar between two trajectory segments in time dimension when setting time interval to 0.5 hour. As for the weight of different distance measures, in fact, it is indeed very hard to estimate the weight settings by a theoretical analysis, and the optimal settings are always related to the parameters of environments or applications. At the beginning each distance measure is assigned the same weight while the sum of these weights is equal to 1, and then the weight settings can be gradually adjusted through observing the clustering results.

Table 2 Parameters setting

4.3 Comparisons of different trajectory clustering methods

Firstly, we compare JSTTCM with trajectory clustering method using Optics, the mechanism of Optics algorithm is very similar to that of JSTTCM, because both of them belong to the density-based clustering algorithms. However, there are differences between JSTTCM and Optics in the clustering process. The Optics algorithm does not generate the clusters explicitly, i.e., it sorts the objects in the data object set and outputs an ordered list of objects. The ordered list contains enough information to extract the clusters. The most outstanding advantage of Optics is that it is typically insensitive to the input parameters. The simulation results are given in Fig. 12.

Fig. 12

Comparisons of different trajectory clustering methods

In Fig. 12a, we can observe the variations of the number of clusters and the silhouette coefficient when the number of nodes is varied from 1 to 10. Obviously, the number of clusters increases gradually with the increase of the number of nodes. Specially, Optics always generates more clusters than JSTTCM when a large number of trajectories need to be processed, which is attributed to the fact that Optics has a stronger ability to resist the outlier noise, so that a larger cluster can be divided into several smaller clusters. Besides, note that the number of clusters generated by JSTTCM ascends much more slowly than that of Optics. In Fig. 12b, the silhouette coefficient of JSTTCM outperforms that of Optics especially when there are a large number of trajectories need to be processed, and this is because more clusters generated by Optics probably lead to a higher coupling of these clusters.

We compare JSTTCM with other trajectory clustering methods including TraClus, CTHD and Extended TraClus. In TraClus, there is an additional filter operation performed to remove the clusters where the number of trajectory segments are less than a preset threshold. CTHD uses Hausdorff distance that the flow vectors include the positions and directions. Extended TraClus extends HDBSCAN to handle line segments and plug it into TraClus to detect hierarchical clusters. We compare these methods from the aspects of the number of clusters and the silhouette coefficient, and the simulation results are shown in Fig. 13.

Fig. 13

Comparisons of different trajectory clustering methods (The dashed segment in Fig. 13b indicates that the silhouette coefficient cannot be obtained while the number of clusters is equal to 0)

We have observed the variations of the number of clusters and the silhouette coefficient with the increase of the number of nodes (from 1 to 10), as shown in Fig. 13. The number of clusters increases gradually when the number of nodes is varied from 1 to 10, and this is because the number of clusters is proportional to the number of trajectories. Specially, the least clusters are produced by TraClus due to its filter mechanism, which filters some clusters where the number of trajectory segments are less than a preset threshold. However, the most clusters are generated by CTHD, which is attributed to the fact that CTHD only considers the positions and directions, so that more clusters are generated due to some simple properties. Extended-TraClus generates more clusters than TraClus due to the discovery of layered clusters. Note that the number of clusters generated by JSTTCM is always between CTHD and Extended TraClus, and this is attributed to the fact that JSTTCM considers spatial-temporal trajectory properties, which brings less clusters than CTHD. From Fig. 13b, the silhouette coefficients of all methods decrease with the increase of the number of nodes slowly, however, the silhouette coefficient of JSTTCM is always larger than those of other methods, which indicates that better clustering results are obtained by JSTTCM. Especially, such gaps are much larger when the trajectories of more nodes have been provided. This is because JSTTCM clusters the trajectory segments through considering these spatial-temporal properties of trajectories, and hence JSTTCM can obtain the cluster structures more appropriately (Fig. 13).

With regard to the time complexity, the trajectory clustering methods in Fig. 13 have the same time complexity equal to O(n²). Essentially, these trajectory clustering methods are based on DBSCAN algorithm, our proposed method has improved the algorithm efficiency by introducing the timestamp as described in Section 3.2.3.

5 Conclusions

In this paper, we propose a Joint Spatial-Temporal Trajectory Clustering Method (JSTTCM), where some spatial-temporal properties of the trajectories are exploited to cluster the trajectory segments. The simulation results demonstrate that JSTTCM can be used to cluster the trajectory segments appropriately. Future research will focus on an enhancement of JSTTCM, which improves the running efficiency of JSTTCM by building an index structure, and a comprehensive evaluation over various datasets of MSNs will be performed.