Trajectory similarity clustering based on multi-feature distance measurement

Abstract

With the development of GPS-enabled devices, wireless communication and storage technologies, trajectories representing the mobility of moving objects are accumulated at an unprecedented pace. They contain a large amount of temporal and spatial semantic information. A great deal of valuable information can be obtained by mining and analyzing the trajectory dataset. Trajectory clustering is one of the simplest and most powerful methods to obtain knowledge from trajectory data, which is based on the similarity measure between trajectories. The existing similarity measurement methods cannot fully utilize the specific features of trajectory itself when measuring the distance between trajectories. In this paper, an enhanced trajectory model is proposed and a new trajectory clustering algorithm is presented based on multi-feature trajectory similarity measure, which can maximize the similarity of trajectories in the same cluster, and can be used to better serve for applications including traffic monitoring and road congestion prediction. Both the intuitive visualization presentation and the experimental results on synthetic and real trajectory datasets show that, compared to existing methods, the proposed approach improves the accuracy and efficiency of trajectory clustering.

1 Introduction

Nowadays, with the rapid development of satellites, wireless communication, storage and various positioning (such as GPS, GSM and RFID) technologies, it is possible to collect and store a large number of trajectory data of moving objects, recording information about vehicle location, mobile user activity, animal migration, hurricane movement, etc. A trajectory is a sequence of time-ordered locations for a moving object. It contains a lot of spatial and temporal semantic information. Therefore, analysis on trajectory data has become practically useful [1,2,3,4,5]. For example, the moving trajectories of mobile users can reflect their interests and favorites. Analysis of these trajectories can help in planning road system, recommending tourist routes and sharing life experience [6]. One of the typical analysis tasks is trajectory clustering, which is also one of the simplest and most powerful methods for acquiring knowledge from trajectory data [7,8,9].

Trajectory clustering is a process of assigning a set of similar trajectories into groups (called clusters), so that the trajectories within each cluster are highly similar, and there is low similarity among different clusters [10, 11]. Its purpose is to extract the common motion characteristics of similar moving objects, in order to predict the behaviors of moving objects or to provide the decision-making guidance for management in many fields, such as location recommendation, market research, vehicle destination prediction, urban planning, weather forecast [1, 2, 7, 12,13,14], etc. Much has been achieved in clustering research. The representative algorithms include k-means [15], DBSCAN [16], BIRCH [17] and OPTICS [18], which mainly focus on clustering of point data objects but cannot be directly used in trajectory clustering, because the distance measurement between trajectories is very complicated. In traditional clustering, each data point is a separate object. However, in trajectory clustering, each trajectory including several closely related sampling points is the basic object. Clustering of time series is another kind of clustering problem. Some application results have been achieved [19, 20]. For example, Literature [19] produced day-ahead forecasts of wind power by time series cluster analysis, where a Quality Threshold (QT) algorithm is adopted to cluster the time series. There are some similarities between time series and trajectories because both of them are sequences with time attributes, but the dissimilarity calculation in both problems cannot be generalized. The intrinsic characteristics and the movement trend of a trajectory cannot be utilized by these traditional clustering algorithms. New methods are needed to address the trajectory clustering problem. The key issue is how to measure the similarity degree between trajectories. An appropriate and valid model for defining the similarity between trajectories is critical to the quality of trajectory clustering. Clustering results with high accuracy play an important role in management decisions. For example, the municipal traffic department can plan urban roads and alleviate road congestion problems based on the cluster analysis of vehicle trajectories. The higher the accuracy of clustering results, the greater the guiding significance provided, otherwise misdirection will occur.

This paper presents a new similarity measurement method based on multiple trajectory features and a corresponding trajectory similarity clustering algorithm. The key contributions of this paper include:

1):

An enhanced trajectory model is introduced for trajectory analysis.

2):

A Multi-feature Trajectory Similarity Measure algorithm (MFTSM) is proposed to calculate the distance between any two trajectories based on multiple features of trajectories. In particular, the location distance based on area calculation is used to address the continuity problem of trajectory.

3):

A trajectory clustering algorithm based on MFTSM is proposed, denoted as TC_MFTSM, in which the initial centers of the clusters are optimized based on contemporary trajectories.

4):

Several comparative experiments are performed to verify the effectiveness and evaluate the efficiency of the proposed algorithms. The experimental results demonstrate that our algorithms outperform the prior work on trajectory similarity clustering.

The rest of this paper is organized as follows. Section 2 introduces the related work. In Section 3, we introduce an enhanced trajectory model. In Section 4, we describe the rate and time interval of contemporary trajectories, as well as an algorithm RTofCT, which will be used later. Section 5 introduces the trajectory similarity measure algorithm, MFTSM. Section 6 introduces the trajectory clustering algorithm based on MFTSM. Experimental results and analysis are presented in Section 7. Section 8 concludes the paper and provides future research directions.

2 Related work

There are mainly two ways to address the problem of trajectory clustering: 1) Define a specific trajectory clustering algorithm based on the intrinsic properties of trajectories. For example, Wei et al. [21] proposed a trajectory clustering method based on the regression model. In their method, a trajectory is approximately represented by fitting polynomial. 2) Two-stage method. Firstly, design a similarity (distance) measurement method based on trajectory data. Secondly, improve some traditional clustering algorithm to realize trajectory clustering. The vast majority of studies are carried out in the second way. This paper also focuses on trajectory clustering in this way, where the emphasis is trajectory similarity measurement [2, 22,23,24,25]. At present, there are many related research results in this field.

Lee et al. [12] proposed a partition-and-group framework for clustering trajectories, i.e., to divide each trajectory into several t-partitions according to the idea of line segment Hausdorff distance in image processing, in order to represent the local features of complex trajectories. And then they used the traditional density-based clustering method DBSCAN to find the general sub-trajectories from the trajectory database. This method solves the problem of comparisons between complex trajectories. However, the distance calculation between two trajectories is based on spatial locations. Each t-partition is only the line between two endpoints of the trajectory segment, which is an approximate description of the trajectory, resulting in the loss of local features. Lin et al. [26] proposed a similarity measurement method named OWD (One Way Distance), which merely focuses on spatial shapes of moving trajectories without considering the time dimension. Morris et al. [27] compared various trajectory similarity clustering methods, and proposed that performance is actually dictated by the trajectory properties encountered in a dataset. Ferreira et al. [24] proposed a trajectory similarity measurement method based on vector field, and then used k-means clustering method to achieve trajectory clustering. Domingo-Ferrer et al. [28] proposed a trajectory similarity calculation method based on the Euclidean distance between each point pair on the trajectory, which considers the time and space dimensions while ignoring other factors such as trajectory orientation, moving speed and continuity feature. Similarly, Wang et al. [29] proposed a similarity measurement method that takes trajectory shape into account on the basis of Literature [28]. It also does not consider the continuity of the trajectory. Gudmundsson et al. [30] proposed a subtrajectory clustering approach based on Fréchet distance, which merely considers a trajectory as a directed curve in 2D. Besse et al. [31] proposed a new distance SSPD (Symmetrized Segment-Path Distance). It is time insensitive and compares the shape and physical distance between two trajectories. Sanchez et al. [7] proposed hashing techniques based on DBH (Distance-Based Hashing) and LSH (Locality Sensitive Hashing) for fast trajectory similarity clustering. In their method, trajectory similarity measurement is based on DTW (Dynamic Time Warping) distance [32, 33] and trajectory clustering is realized using k-means algorithm. The above methods ignore the comprehensive impact of the internal and external characteristics of trajectory itself on the similarity between trajectories.

When calculating the distance between two trajectory segments, most existing methods use the center point and the length of trajectory segment as standards. For example, Zhang et al. [34] proposed a new trajectory clustering algorithm which considers semantic spatio-temporal information based on Traclus algorithm [12], where spatial distance consisting of perpendicular distance and horizontal distance is calculated based on those standards. Such methods ignore the continuity of trajectory. In this paper, the location distance is calculated using the area of quadrangle formed by two trajectory segments. For each pair of segments, our value of location distance is more accurate. In addition, we propose an enhanced trajectory k-means clustering method, in which the selection of initial trajectory centers is optimized based on the temporal features of trajectories. So we have made improvements in both stages of trajectory clustering.

In summary, there are a variety of trajectory similarity clustering methods, but almost none of them is widely approved. Aiming at the above problems, based on the characteristics of orientation, speed, shape, location and continuity of the trajectory, we propose a more accurate similarity measurement method based on trajectory multi-feature. And a trajectory similarity clustering algorithm is consequently proposed in this paper.

3 Preliminary concept and problem definition

3.1 Trajectory model

Definition 1

(Time-stamped location) [28]: Let t be a timestamp and (x,y) be a location in $\mathbb {R}^{2}$. A time-stamped location is defined as a triple (t,x,y), which means that an object is at location (x,y) at time t.

Hereinafter, triple and location will be used as synonyms for time-stamped location.

Definition 2

(Trajectory): A trajectory is an ordered set of time-stamped locations, denoted as T.

$$ T=\{Tid,(t_{1},x_{1},y_{1}),(t_{2},x_{2},y_{2}),\dots,(t_{n},x_{n},y_{n})\} $$

(1)

where t_r < t_r+ 1 for all 1 ≤ r < n, Tid is the identification of the trajectory, and n is the number of sampled points in the trajectory.

Consider a set of p trajectories TS = {T₁, T₂,…,T_p}, where $T_{i}=\{i,({t^{i}_{1}},{x^{i}_{1}},{y^{i}_{1}}),\dots ,({t^{i}_{m}},{x^{i}_{m}},{y^{i}_{m}})\}$ represents the i-th trajectory in TS, 1 ≤ i ≤ p.

Figure 1 shows an example in which four trajectories are provided. The sampled points in each trajectory can be projected to the $\mathbb {R}^{2} (x\text {-}y)$ plane.

Fig. 1

The motion trajectories of different moving objects and their projections in the 2D-plane

Definition 3

(Length of trajectory): Consider a trajectory T. The length of T is defined as the number of triples in T. It is denoted as |T|.

For example, |T| = n in (1).

Definition 4

(Sub-trajectory) [28]: Consider a trajectory S. $S=\{Sid,(t_{i_{1}},x_{i_{1}},y_{i_{1}}),(t_{i_{2}},x_{i_{2}},y_{i_{2}}),\dots ,(t_{i_{m}},x_{i_{m}} ,y_{i_{m}})\}$ is defined as a sub-trajectory of T in (1), denoted as $S\preccurlyeq T$, where 1 ≤ i₁ < ⋯ < i_m ≤ n.

Definition 5

(Trajectory segment): Consider a trajectory T. A trajectory segment is defined as the line segment between any adjacent pair of time-stamped locations ((t_r, x_r, y_r),(t_r+ 1, x_r+ 1, y_r+ 1)) in the trajectory T, 1 ≤ r < n.

In analyzing trajectory data, it is necessary to know the interrelation between different trajectories. We use pt%-contemporary defined below to indicate whether two trajectories have common timestamps or not.

Definition 6

(pt%-contemporary trajectories) [28]: Consider two trajectories $T_{i}=\{i,({t^{i}_{1}},{x^{i}_{1}},{y^{i}_{1}}),\dots ,({t^{i}_{m}},{x^{i}_{m}},{y^{i}_{m}})\}$ and $T_{j}=\{j,({t^{j}_{1}},{x^{j}_{1}},{y^{j}_{1}}),\dots ,({t^{j}_{n}},{x^{j}_{n}},{y^{j}_{n}})\}$. Their pt%-contemporary value pt is defined as:

$$ pt= 100{{\cdot}}min\left( \frac{{\Delta} t}{{t^{i}_{m}}-{t^{i}_{1}}},\frac{{\Delta} t}{{t^{j}_{n}}-{t^{j}_{1}}}\right), $$

(2)

where Δt is calculated as

$$ {\Delta} t=max((min({t^{i}_{m}},{t^{j}_{n}})-max({t^{i}_{1}},{t^{j}_{1}})),0). $$

(3)

If pt = 0, the two trajectories are not contemporary. If and only if they start at the same time and end at the same time, then pt = 100. Denote the overlap time of two trajectories T_i and T_j as ol(T_i, T_j), which starts at $max({t^{i}_{1}},{t^{j}_{1}})$ and ends at $min({t^{i}_{m}},{t^{j}_{n}})$. Hence, $ol(T_{i},T_{j})=\{max({t^{i}_{1}},{t^{j}_{1}} ),\dots ,min({t^{i}_{m}},{t^{j}_{n}})\}$.

Consider any two pt%-contemporary trajectories T_i and T_j for pt > 0, we assume that they have the same number of time-stamped locations within ol(T_i, T_j) and those correspond to the same time-stamps. Therefore, in our following method, a process of locations interpolation is firstly conducted for the original trajectory dataset TS according to the algorithm proposed in Literature [28].

Definition 7

(Trajectory outlier): ∀T_i ∈ TS, it is called as a trajectory outlier (also known as an outlying trajectory) if it is not contemporary with any other trajectory T_j in TS. That is, pt = 0 for T_i and T_j, j = 1…p,j ≠ i.

3.2 Distance between two trajectories

As described in Sections 1 and 2, it is most important to design a suitable similarity measurement method (a certain type of distance between two trajectories) in trajectory clustering. Because trajectories have temporal and spatial characteristics, many existing methods [28, 35] for measuring distance between two trajectories mainly consider the temporal and spatial factors while ignoring the shape and other trajectory characteristics, such as trajectory segment orientation, speed, continuity, etc. We propose a new trajectory similarity measure based on multiple features. Some related concepts and notions are given as follows.

Definition 8

(The r-th segment vector): The r-th segment vector of T_i, denoted as $se{g^{i}_{r}}$, refers to the directed path of a moving object in the r-th trajectory segment of the i-th trajectory. It is defined as:

$$ se{g^{i}_{r}}=(t^{i}_{r + 1}-{t^{i}_{r}},x^{i}_{r + 1}-{x^{i}_{r}},y^{i}_{r + 1}-{y^{i}_{r}}) $$

(4)

where $({t^{i}_{r}},{x^{i}_{r}},{y^{i}_{r}})$ and $(t^{i}_{r + 1},x^{i}_{r + 1},y^{i}_{r + 1})$ respectively represent the r-th and (r+ 1)-th locations of the i-th trajectory, 1 ≤ r < m.

Definition 9

(The r-th segment speed): The r-th segment speed of T_i, denoted as $seg{\_sp^{i}_{r}}$, refers to the movement speed of a mobile object in the r-th trajectory segment of the i-th trajectory. It is defined as:

$$ seg{\_sp^{i}_{r}}=\frac{\sqrt{(y^{i}_{r + 1}-{y^{i}_{r}})^{2}+(x^{i}_{r + 1}-{x^{i}_{r}})^{2}}}{t^{i}_{r + 1}-{t^{i}_{r}}} $$

(5)

where $({t^{i}_{r}},{x^{i}_{r}},{y^{i}_{r}})$ represents the r-th triple of the i-th trajectory, 1 ≤ r < m.

Definition 10

(Trajectory orientation distance): ∀T_i, T_j ∈ TS, the trajectory orientation distance, denoted as dist_o (T_i, T_j), refers to the distance between the two trajectories calculated based on the angles between two segment vectors. If T_i and T_j are pt%-contemporary trajectories with pt > 0,

$$\begin{array}{@{}rcl@{}} dist_{o}(T_{i},T_{j})&=&\frac{1}{pt\%\cdot(|ol(T_{i},T_{j})|-1)}\sum\limits_{r=st_{ij}}^{et_{ij}-1}\arccos\\&&\times\left( \frac{se{g^{i}_{r}} \bullet se{g^{j}_{r}}}{|se{g^{i}_{r}}|{{\cdot}}|se{g^{j}_{r}}|}\right) \end{array} $$

(6)

where “ ∙ ” is the dot product operator, “arccos” function is used to calculate the angle between two vectors, pt is calculated by (2), st_ij and et_ij are respectively the start time and end time of ol(T_i, T_j), which is defined in Definition 6, and finally $se{g^{i}_{r}}$ and $se{g^{j}_{r}}$ are calculated by (4).

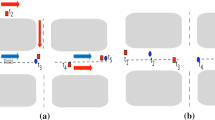
Based on the different trajectory orientations, there are four different scenarios for the angle 𝜃 between two trajectory segment vectors, which are shown in Fig. 2.

Fig. 2

Four different scenarios for the angle 𝜃 between two trajectory segment vectors

Definition 11

(Trajectory speed distance): ∀T_i, T_j ∈ TS, the trajectory speed distance, denoted as dist_s(T_i, T_j), refers to the distance between the two trajectories calculated based on segment speed. If T_i and T_j are pt%-contemporary trajectories with pt > 0,

$$\begin{array}{@{}rcl@{}} dist_{s}(T_{i},T_{j})&=&\frac{1}{pt\%\cdot(|ol(T_{i},T_{j})|-1)}\\&&\times\sqrt{\sum\limits_{r=st_{ij}}^{et_{ij}-1} (seg{\_sp^{i}_{r}}-seg{\_sp^{j}_{r}})^{2}}, \end{array} $$

(7)

where $seg{\_sp^{i}_{r}}$ and $seg{\_sp^{j}_{r}}$ are calculated by (5), and the other parameters are the same as defined earlier.

Definition 12

(Trajectory location distance): We call $\mathit {tripl}{e_{r}^{i}}$$=({t_{r}^{i}},{x_{r}^{i}},{y_{r}^{i}})$ the r-th time-stamped location of trajectory T_i. ∀T_i, T_j ∈ TS, the trajectory location distance, denoted as dist_l(T_i, T_j), refers to the distance between the two trajectories calculated based on the time-stamped locations. If T_i and T_j are pt%-contemporary trajectories with pt > 0,

$$ dist_{l}(T_{i},T_{j})=\frac{1}{pt\%\cdot(|ol(T_{i},T_{j})|-1)}{\sum}_{r=st_{ij}}^{et_{ij}-1}\sqrt{\sigma_{r}}, $$

(8)

where σ_r represents the sum of areas of two triangles consisting of the four time-stamped locations $tripl{e_{r}^{i}}$, $tripl{e_{r}^{j}}$, $triple_{r + 1}^{i}$ and $triple_{r + 1}^{j}$, it is calculated based on the following equations, 1 ≤ r,s < n and 1 ≤ i,j ≤ p.

$$ dt(tripl{e_{r}^{i}},tripl{e_{s}^{i}})=\sqrt{({x_{r}^{i}}-{x_{s}^{i}})^{2}+({y_{r}^{i}}-{y_{s}^{i}})^{2}} $$

(9)

$$ \alpha^{i}=dt(tripl{e_{r}^{i}},triple_{r + 1}^{i}) $$

(10)

$$ \beta_{r}=dt(tripl{e_{r}^{i}},tripl{e_{r}^{j}}) $$

(11)

$$ \gamma=dt(triple_{r + 1}^{i},tripl{e_{r}^{j}} ) $$

(12)

$$ \mu_{1}=\frac{\alpha^{i}+\beta_{r}+\gamma}{2} $$

(13)

$$ \sigma_{r,1}=\sqrt{|\mu_{1}(\mu_{1}-\alpha^{i})(\mu_{1}-\beta_{r})(\mu_{1}-\gamma)|} $$

(14)

$$ \mu_{2}=\frac{\alpha^{j}+\beta_{r + 1}+\gamma}{2} $$

(15)

$$ \sigma_{r,2}=\sqrt{|\mu_{2}(\mu_{2}-\alpha^{j})(\mu_{2}-\beta_{r + 1})(\mu_{2}-\gamma)|} $$

(16)

$$ \sigma_{r}=\sigma_{r,1}+\sigma_{r,2} $$

(17)

Definition 13

(Trajectory distance): ∀T_i, T_j ∈ TS, the trajectory distance, denoted as dist(T_i, T_j), refers to the distance between the two trajectories. If T_i and T_j are pt%-contemporary trajectories with pt > 0, we define

$$\begin{array}{@{}rcl@{}} dist(T_{i},T_{j})&=&\eta_{o}{{\cdot}}dist_{o}(T_{i},T_{j})+\eta_{s}{{\cdot}}dist_{s}(T_{i},T_{j})\\ &+&(1-\eta_{o}-\eta_{s}){{\cdot}}dist_{l} (T_{i},T_{j}), \end{array} $$

(18)

where η_o, η_s ∈ [0,1], respectively represent the weights of trajectory orientation distance and speed distance.

If pt = 0, i.e. T_i and T_j are not contemporary, but there is at least one trajectory T_ijk ∈ τ ⊆ TS, such that both (T_i, T_ijk) and (T_j, T_ijk) are pt%-contemporary with pt > 0, then

$$ dist(T_{i},T_{j} )=min_{T_{ijk}\in\tau}(dist(T_{i},T_{ijk})+dist(T_{j},T_{ijk})). $$

(19)

Otherwise, dist(T_i, T_j) is not defined. Where τ is a set of trajectories being contemporary with both T_i and T_j.

4 Rate and time interval of contemporary trajectories

A schematic diagram for the proposed trajectory clustering algorithm is provided in Fig. 3. After pre-processing the original trajectory dataset, the pt values and distances between each pair of trajectories are calculated, and then the trajectory clustering process is completed. The various technical aspects of the proposed algorithm will be described in detail in this section and the next two sections.

Fig. 3

Schematic diagram for the proposed trajectory clustering algorithm

In our trajectory similarity measurement method, we take the temporal factor into consideration. The calculation of trajectory distance is based on the rate and time interval of contemporary trajectories, which are calculated by Algorithm 1, denoted with RTofCT.

The notations used in the RTofCT algorithm are listed in Table 1.

Table 1 Notations used in the RTofCT algorithm

There are three steps in Algorithm 1. First, we pre-process the trajectory dataset TS in order to formalize each trajectory according to (1) (Line 1), and initialize the related variables used later (Lines 2-3). Second, the start time and the end time of each trajectory in TS are calculated and saved into the matrix TIME (Lines 4-9). Third, the pt values between each pair of trajectories in TS are calculated and saved into the matrix PT (Lines 10-17). The matrixes PT and TIME are calculated based on Definition 6.

The pseudo code of the RTofCT algorithm is given as follows:

The time complexity of Algorithm 1 depends on the following two parts: (a) the time for computing the TIME matrix, whose time complexity is O(p), where p is the number of trajectories in dataset TS, i.e. p = |TS|; (b) the time to calculate the PT matrix. From Lines 10-17 in Algorithm 1, we know that the values of pt must be calculated between each pair of trajectories. Hence, the number of calculations for this part is p⋅(p − 1)/2. If the value of p is close to infinity, the time complexity of this part is O(p²). So the total approximate time complexity of Algorithm 1 is O(p²). The space complexity of Algorithm 1 is O(p²), which is mainly due to storing the PT matrix.

Before all the algorithms are executed, TS has been interpolated based on the method mentioned in Section 3.1. In the following algorithms, TS as an input dataset, is assumed to have been pre-processed in the same way as the first step in Algorithm 1.

5 Trajectory similarity measure algorithm

According to the clustering results of trajectory dataset, a great deal of valuable information can be extracted. The similarity measure between trajectories is the basis of trajectory clustering.

Figure 4 shows two trajectories, each of which contains five time-stamped locations at times 0, 1, 2 ,3 and 4, respectively. Each pair of the corresponding trajectory segments moves in the same direction. By calculating the Euclidean distance between each pair of the corresponding sampling points, it is easy to get the distance between these two trajectories. However, according to the moving directions and projections on the x-y plane of the two trajectories, we find that the similarity calculation method based only on the distance of the corresponding sampling points of the trajectories is not adequate to achieve accuracy in the similarity measure. As is shown in Fig. 4, the path in the period of time 2-4 of Trajectory 1 is exactly the same as the one in the period of time 0-2 of Trajectory 2. The similarity degree of these two trajectories will be very high if only the shape and locations in the x-y plane are considered. Obviously, if time factor is ignored in distance calculation, the distance between two trajectories will not reflect the real situation. An analysis based on this distance may cause erroneous conclusions, which may lead to wrong guidance in the real applications.

Fig. 4

Two trajectories having the same locations at different time stamp

Therefore, in calculating the distance between two trajectories, time, location, shape, speed, continuity and other features of trajectory should be taken into account. The smaller the distance between two trajectories is, the greater the degree of similarity between them is.

The trajectory similarity measurement algorithm based on multiple features is described in Algorithm 2, which is the basis of our trajectory clustering algorithm. According to the value of pt, it is divided into three cases. Lines 8-26 give the distance calculation method. First, if pt > 0, the two trajectories are contemporary. The distance between them is calculated based on trajectory orientation distance, speed distance, and location distance. In the calculation of each of the three distances, the time aspect of trajectory is considered based on the value of pt. Equations (4)–(18) are used in this case (Lines 8-15). Second, if pt is equal to 0, the two trajectories are not contemporary. The distance measurement between them is based on the intermediate ones that overlap partially each of them. For this case, the two trajectories have a certain connection in terms of time attribute, but the absolute time can not be obtained for distance calculation. So the third party trajectories are used to realize the distance measurement between them. Equation (19) is used here (Lines 16-23). Third, if pt can not be obtained, indicating that at least one of the trajectories has a single location, which is most likely to be a noisy point. The distance related to such trajectory is meaningless, therefore, it is assigned with Inf in this case.

To make the MFTSM algorithm better understood, a specific example is given as follows:

Example 1

Consider two trajectories T₁₆ and T₁₇ selected from the synthetic dataset introduced in Section 7.1. In order to facilitate demonstration, the two trajectories we choose are relatively short. T₁₆ = {16,2,7827,17747,3, 7882.24, 17767.72 ,⋯ , 49, 11437.04, 17720.53}, T₁₇ = {17,2, 4286, 15523, 3, 4265.75, 15467.59, ⋯ , 19, 3817.73, 14642.22}. According to Lines 1-2 of Algorithm 2, (start₁₆, end₁₆)=(2,49), (start₁₇, end₁₇)=(2,19). Then, as is shown in Lines 3-6, the Δt and pt values between T₁₆ and T₁₇ are calculated based on (2) and (3). That is, Δt = max ((min(end₁₆, end₁₇) − max(start₁₆, start₁₇)),0) = max((19 − 2),0) = 17, and pt = 100⋅min(Δt/(end₁₆ − start₁₆),Δt/(end₁₇ − start₁₇)) = 100⋅min(17/(49 − 2),17/(19 − 2)) = 36.17. Based on Line 7, the value of (et_ij − st_ij) is calculated, the result is 17. Because pt > 0, the value of dist(T₁₆, T₁₇) is calculated based on Lines 8-15. According to the corresponding steps, the result is as follows: dist(T₁₆, T₁₇) = 19.0441.

Note that MFTSM algorithm is able to compare trajectories that are time-wise overlapping only partially or not at all. A lemma proved in Literature [28] guarantees that any two trajectories at minimum distance for clustering must have some overlapping time span. Therefore, the distance between two non-overlapping trajectories can be calculated but is too large. So any pair of non-overlapping trajectories is hard to be clustered.

Algorithm 2 is used to calculate the distance between any two trajectories, whose time complexity mainly depends on the distance calculation. For one thing, the time complexity of Algorithm 2 is O(interval) when pt > 0, where interval is the common duration of any two trajectories. For another, from Lines 16-23 in Algorithm 2, we know that if the condition pt == 0 is met, the number of calculations for the MFTSM algorithm is interval⋅|TS|. The other steps in the algorithm only need to be calculated once. Hence, the total approximate time complexity of Algorithm 2 is O(interval⋅|TS|). In general, interval is much smaller than |TS|. For example, in our later experiments, the maximum value of interval is 101 and |TS| is 1000 for synthetic dataset. The space complexity of Algorithm 2 is O(|TS|), which is mainly due to storing TIME (size: |TS|⋅3) and the intermediate results dist(T_i, T_ijk) and dist(T_j, T_ijk).

Based on the MFTSM algorithm, we calculate the distance matrix with a size of |TS|⋅|TS| to better serve the later research. The distances between each pair of trajectories need to be calculated and stored, so the time complexity of this calculation process is O(interval⋅|TS|²). The space complexity is O(|TS|²).

6 Trajectory clustering algorithm based on MFTSM

There are similarities and differences between trajectory clustering and point data objects clustering. The same thing is the general idea of clustering, the main difference is the distance calculation method. The original trajectories are partitioned into several clusters based on some similarity measure metric. Compared with the original k-means algorithm, our method makes several improvements to address the different object — trajectory.

In our trajectory clustering algorithm, there are two main features: 1) The distance between any two trajectories is calculated based on Algorithm 2 (MFTSM). 2) The trajectory clustering method is an enhanced k-means clustering process. First, trajectory outliers are removed from the original trajectory dataset based on the concept of contemporary trajectories. Second, instead of randomly generating, our method selects initial trajectory centers based on the time duration of each trajectory. In particular, the top num_c trajectories with the longest time duration are used as the initial centres, where num_c is the number of trajectory clusters. Third, the number of trajectories within each trajectory cluster is approximately consistent, the value of “k” is consequently determined. This setting can also be applied to other applications such as trajectory privacy preservation.

The proposed trajectory clustering algorithm, denoted as TC_MFTSM, implements trajectory clustering based on MFTSM algorithm. The algorithm TC_MFTSM considers both temporal and spatial attributes of trajectories, it can be applied in areas such as congestion predicting and road-system planning.

The notations used in the TC_MFTSM algorithm are listed in Table 2.

Table 2 Notations used in the TC_MFTSM algorithm

There are mainly three steps in Algorithm 3. First, trajectory outliers are removed from TS according to Definition 7 in order to reduce their negative impact on clustering results (Line 1). Lines 2-4 initialize the related variables. Second, we calculate the time duration of each trajectory in TS (Lines 5-7), which are used for the selection of initial trajectory centers. As a result, the top num_c trajectories with the longest time duration are selected to initialize TCenters (Lines 8-9). Third, the trajectory clustering is completed based on the iteration process (Lines 10-33). Specifically, Lines 13-23 determine if each trajectory can be classified into a cluster or be discarded. Lines 24-31 calculate the new trajectory centers based on the last clustering result. The parameter MR is updated in Line 32. The clustering process is terminated when the end condition of the iteration process is met (Line 33). The output of Algorithm 3 is a set of trajectory clusters TClusters and a set of centers TCenters (Line 34).

The pseudo code of the TC_MFTSM algorithm is given as follows:

Each iteration of Algorithm 3 contains three main steps. 1) The determination of trajectory centers. 2) The classification of each trajectory. For each trajectory T_i, we find the central trajectory closest to T_i and determine if the distance between them is less than the threshold MR. If so, T_i is added into the cluster where the central trajectory is located. 3) The updation of the parameter MR.

Note that the improved k-means clustering method adopted here is based on relatively uniform division. The k value is adjusted in the experiments to verify the effect of TC_MFTSM algorithm. It is different from density-based clustering methods, such as the Quality Threshold (QT) algorithm mentioned in Section 1. QT clustering algorithm depends on the value of diameter threshold, which is mainly set according to the observations and empirical values. And the time complexity of QT clustering algorithm is relatively high, because only one cluster can be obtained after one iteration.

The reason that we use an improved k-means clustering method lies in two aspects. On the one hand, k-means is one of the most famous and most popular clustering methods. It is available in many applications. Moreover, k-means method belongs to the category of partitioning methods, which are the simplest and most basic version of clustering analysis. On the other hand, our proposed algorithm TC_MFTSM is mainly compared with the existing algorithms MDAV [28] and GC_DM [29], where the idea of k-means method is used in trajectory clustering. In order to obtain better comparison results on these three algorithms, we implement the trajectory clustering based on the improved k-means algorithm. In fact, we have improved trajectory k-means clustering method in terms of the selection of initial central trajectories, the selection of k value and the updation of trajectory centers.

In addition, the trajectory outliers as defined in Definition 7 are removed in the first step of Algorithm 3. The implementation of this step has two advantages: one is to reduce the running time, and the other is to reduce the interference of outlying trajectories on clustering results. Table 3 shows the execution time comparison of two schemes run on the synthetic dataset, which will be introduced in Section 7.1. Scheme 1 refers to the scheme implemented according to Algorithm 3, that is the TC_MFTSM algorithm. Scheme 2 does not perform the step of removing trajectory outliers in Algorithm 3, and the other steps in Scheme 2 are the same as those in Scheme 1.

Table 3 Execution time comparison of two schemes run on the synthetic dataset [sec]

As can be seen from Table 3, in the vast majority of cases, the execution time of Scheme 1 is less than that of Scheme 2 with the same k. It shows that the removal of trajectory outliers can effectively improve the efficiency of the algorithm. The accuracy verification can be seen from Section 7.

The time complexity of Algorithm 3 depends on the following four aspects:

(a) Line 1: the time for removing the trajectory outliers from TS, whose time complexity is O(p), where p = |TS|. (b) Lines 5-7: the time for calculating the vector tra_tp based on TIME, the time complexity is O(p). (c) Line 8: it is used to sort the vector tra_tp, whose time complexity is $O(p\log p)$. (d) Lines 10-33: First, from Lines 13-23 in Algorithm 3, we know that an iterative process of clustering must be executed num_c⋅p times. Hence, the time complexity of this sub-part is O(num_c⋅p). Second, from Lines 26-31, we know that the function of this sub-part is to calculate the new Tcenters, whose time complexity is O(num_c⋅lenclz). Therefore, the time complexity of the two sub-parts is O(num_c⋅p) + O(num_c⋅lenclz). Because $lenclz\doteq p/num_{c}$, p ≥ lenclz, the executive times do not exceed 2⋅num_c⋅p. The time complexity of Lines 13-31 is O(num_c⋅p). Further, Lines 11-32 are repeated max(MI,MD) times according to the repeat conditions (as shown in Line 33). In general, max(MI,MD) ≪ p, so the maximum time complexity of this part (Lines 10-33) is O(num_c⋅p²).

The time complexity of the other lines is O(1). So the total approximate time complexity of Algorithm 3 is $O(p)+O(p)+O(p\log p)+O(num_{c}{{\cdot }}p^{2})$. In conclusion, its overall time complexity is O(num_c⋅p²).

The space complexity of Algorithm 3 is O(p²), which is mainly due to storing the distance matrix. TC_MFTSM also needs space to store TClusters and TCenters, but the space complexity of TC_MFTSM does not exceed O(p²) because the space required by them are respectively num_c⋅lenclz and num_c. Both num_c (the number of trajectory clusters) and lenclz (the number of trajectories within each cluster) are much smaller than p. So the space complexity of Algorithm 3 is O(p²).

7 Experiments

We perform experiments to evaluate the accuracy and efficiency of the proposed algorithm. The experiments are conducted with Matlab 8.3 (64-bit) on a PC with Intel (R) Core (TM) 2 Duo CPU 2.6 GHz and 8 GB of RAM. The operating system is Microsoft Windows 7.

Three datasets (Section 7.1) are used to verify the performance of TC_MFTSM algorithm. On the one hand, we compare TC_MFTSM with the prior work of GC_DM [29] and MDAV [28]. Trajectory clustering methods adopted in these two algorithms are used as benchmarks for evaluating the relative performance of TC_MFTSM in all of the following experiments. On the other hand, in Section 7.3.3, we also conduct several experiments for comparing TC_MFTSM with a new algorithm using the distance calculation method proposed in Literature [34], where the trajectory clustering method is improved based on Traclus algorithm [12]. For ease of description, the new algorithm is denoted as IMDTraclus later.

The four algorithms have certain comparability. They use different trajectory similarity measurement algorithms, but similar trajectory clustering methods, which are all based on greedy clustering. The proposed algorithm adopts a new trajectory similarity measurement method and makes some improvements in the trajectory clustering process. The parameters allocation is presented in Section 7.3.

According to Algorithms 1, 2 and 3, for each dataset, our experimental process is specifically arranged as follows:

1):

Pre-processing the experimental dataset based on our proposed trajectory model.

2):

Calculating the matrixes PT and TIME by implementing Algorithm 1, and the distance matrix based on Algorithm 2.

3):

Implementing the distance calculation function between any two trajectories according to Algorithm 2.

4):

Completing the trajectory clustering using Algorithm 3.

5):

Achieving the experimental results comparison based on various evaluation metrics.

7.1 Dataset

1):

Synthetic dataset

The Brinkhoff generator [36] is used to generate 1000 synthetic trajectories, containing 46906 locations in the Oldenburg city of German. The parameters used are as follows: the number of timestamps is 100, the number of moving objects classes is 6, the number of external objects classes is 1, the number of moving objects generated per timestamp is 10, the number of external objects generated per timestamp is 1, the speed of the moving objects is 250, the value of “report probability (0-1000)” is 1000, which means that a moving object is reported at every timestamp during its moving. There are at most 100 locations in each trajectory, and 45.5 locations per trajectory on average.

2):

Real-life dataset

We also use the dataset of taxi moving trajectories collected from San Francisco in the United States [37, 38] as the real-life dataset in our experiments. It contains GPS coordinates of approximately 500 taxis collected in the San Francisco Bay Area during May 2008. The locations in this dataset are very fine-grained because the average time interval between two consecutive locations is less than 10 seconds [38]. The format of each mobility trajectory file is as follows. Each line contains latitude, longitude, occupancy and time, where the occupancy is ignored in our experiments. Since the trajectory of a cab during an entire month can hardly be considered a single trajectory, we use the method in the literature [28] to pre-process this dataset. In particular, the trajectory data of the day between May 25 at 12:04 and May 26 at 12:04 is extracted because during this period there was the highest concentration of locations in the dataset [28]. After a trajectory filtering and location interpolation process, we obtained 480 trajectories and 244 locations per trajectory on average.

3):

Clustered reference dataset

In order to calculate the (Adjusted) Rand Index value (will be introduced in Section 7.2), a trajectory dataset with reference classes is required. Therefore, we generate a dataset of clustered synthetic trajectories using the publicly available trajectory generator program written by Piciarelli¹.

A set of 1000 normal trajectories from 10 different trajectory clusters and another set of 50 abnormal trajectories from 50 different clusters are created with the randomness parameter set to the default value 0.7, which is set referring to Literature [39]. After being added time dimension, the dataset contains 1050 random three-dimensional trajectories of length 10. This dataset is used as one reference dataset in our experiments. Moreover, another two datasets derived from it will also be used (Section 7.3.3).

7.2 Evaluation metrics

The evaluation metrics in our experiments are described in this section.

1):

The intra-cluster and inter-cluster distances

Four types of distances are calculated to evaluate the clustering effect. Their calculation methods are provided in Table 4, where $indave\_c_{i}$ and $indmax\_c_{i}$ respectively refer to the average distance and the maximum distance between central trajectory and other trajectories inside the i-th cluster, $outdave\_c_{i}$ and $outdmin\_c_{i}$ respectively refer to the average distance and the minimum distance between the central trajectory of the i-th cluster and trajectories in other clusters.

Table 4 Four types of distances

The smaller the intra-cluster distance is, or the greater the inter-cluster distance is, the higher the similarity degree within each cluster is.

2):

The coupling degree

The coupling degree, denoted as cp_dg, can be used to reflect the degree of closeness within a cluster. This metric is based on the distances presented in Table 4. The smaller the coupling degree is, the better the clustering effect is. The coupling degree can be calculated as follows:

$$ cp\_dg=\frac{1}{num_{c}}\sum\limits_{i = 1}^{num_{c}}\frac{indave\_c_{i}}{outdave\_c_{i}} $$

(20)

3):

The Total Sum of Squared Error

We use the Sum of Squared Error (SSE) [40] to measure the clustering quality. The total SSE, denoted as TSSE, can be calculated as follows:

$$ TSSE=\sum\limits_{i = 1}^{num_{c}}(\frac{1}{2{{\cdot}}|C_{i}|}{{\cdot}}\sum\limits_{T_{x}\in C_{i}}\sum\limits_{T_{y}\in C_{i}}dist(T_{x},T_{y})^{2}) $$

(21)

where C_i represents the i-th trajectory cluster, and dist(T_x, T_y) is the distance between trajectories T_x and T_y. The smaller the TSSE is, the better the clustering effect is.

4):

The Silhouette Index

The silhouette value is here used as a measure of how similar a trajectory T_x is to its own cluster C_i (cohesion) compared to other clusters (separation), denoted as S(T_x):

$$ S(T_{x})=\frac{b(T_{x})-a(T_{x})}{max\{a(T_{x}),b(T_{x})\}} $$

(22)

where a(T_x) is the average dissimilarity of T_x to all T_y (T_x, T_y ∈ C_i, T_y ≠ T_x), b(T_x) is the minimum dissimilarity over all clusters C_j (j ≠ i), of the average dissimilarities to T_y ∈ C_j [41]. The calculation equations are:

$$ a(T_{x})=\frac{1}{|C_{i}|-1}\sum\limits_{T_{x},T_{y}\in C_{i}, T_{y}\ne T_{x}}dist(T_{x},T_{y}) $$

(23)

$$ b(T_{x})=min_{C_{i},C_{j}\in TClusters,j\ne i}\{\frac{1}{|C_{j}|}\sum\limits_{T_{y}\in C_{j}}dist(T_{x},T_{y})\} $$

(24)

We can then quantify the validity of the trajectory clustering by the Silhouette Index (SI), defined as follows:

$$ SI=\frac{1}{num_{c}}\sum\limits_{i = 1}^{num_{c}}\{\frac{1}{|C_{i}|}\sum\limits_{T_{x}\in C_{i}}S(T_{x})\} $$

(25)

The silhouette value S(T_x) ranges from -1 to 1, where a high value indicates that the trajectory T_x is well matched to its own cluster and poorly matched to neighboring clusters. If most trajectories have high values, then the trajectory clustering result is appropriate.

5):

The Rand Index and Adjusted Rand Index

Given a set of n elements $S=\{o_{1},\dots ,o_{n}\}$ and two partitions of S to compare, $X=\{X_{1},\dots ,X_{r}\}$, a partition of S into r subsets, and $Y=\{Y_{1},\dots ,Y_{s}\}$, a partition of S into s subsets.

First, we evaluate the performance of the proposed trajectory clustering algorithm using Rand Index (RI) [42]. The RI value is calculated as follows [43]:

$$ RI(X,Y)=\frac{a+b}{a+b+c+d}=\frac{a+b}{\tbinom{n}{2}} $$

(26)

where each element is a trajectory object, a represents the number of pairs of elements in S that are in the same subset in X and in the same subset in Y, b represents the number of pairs of elements in S that are in the different subsets in X and in the different subsets in Y, c represents the number of pairs of elements in S that are in the same subset in X and in the different subsets in Y, d represents the number of pairs of elements in S that are in the different subsets in X and in the same subset in Y.

The Rand Index has a value between 0 and 1, with 0 indicating that the two clusterings do not agree on any pair of objects and 1 indicating that the two clusterings are identical. The larger the RI value the better is the clustering.

Second, the Adjusted Rand Index (ARI) [42, 43] is also used in measuring the quality of trajectory clustering. ARI is the corrected-for-chance version of the Rand Index. The overlap between X and Y can be summarized in a contingency table [n_ij] where each entry $n_{ij} (i = 1,\dots ,r; j = 1,\dots ,s)$ refers to the number of objects in common between X_i and Y_j, that is, n_ij = |X_i ∩ Y_j|. No more expatiation about the contingency table here as it can be obtained from Literature [43].

The ARI value is calculated as follows:

$$ \mathit{ARI}(X,Y)=\frac{{\sum}_{ij}\tbinom{n_{ij}}{2} - [{\sum}_{i}\tbinom{a_{i}}{2}{\sum}_{j}\tbinom{b_{j}}{2}]/\tbinom{n}{2}} {\frac{1}{2}[{\sum}_{i}\tbinom{a_{i}}{2} + {\sum}_{j}\tbinom{b_{j}}{2}] - [{\sum}_{i}\tbinom{a_{i}}{2}{\sum}_{j}\tbinom{b_{j}}{2}]/\tbinom{n}{2}} $$

(27)

where $a_{i}={\sum }_{j = 1}^{s}n_{ij}$, $b_{j}={\sum }_{i = 1}^{r}n_{ij}$. In essence, (27) calculates the value of $\frac {Index-ExpectedIndex}{MaxIndex-ExpectedIndex}$. The ARI value ranges from -1 to 1 and takes on the value 0 when the Index is equal to its expected value (under the generalized hypergeometric distribution assumption for randomness). The greater the ARI value is, the higher the clustering quality is.

7.3 Experimental results

Experimental results and the related analysis are given in this section, in order to verify the accuracy and efficiency of the proposed trajectory clustering method based on multi-feature distance measurement. Specifically, we have conducted a set of experiments in which we executed TC_MFTSM, GC_DM, MDAV and IMDTraclus algorithms on the synthetic and real datasets.

The parameters used in our algorithms include η_o, η_s, k, MR, MD, MI.

MD and MI respectively represent the threshold of the number of discarded trajectories and the threshold of iteration times. MR represents the threshold of distance radius within any trajectory cluster. The value of MD depends on the size of a dataset. As a rule of thumb, we choose MD so that the number of discarded trajectories is between 2% and 5% of the total number of trajectories. The three datasets used in the experiments are respectively with size of 1000, 480 and 1050, so it is appropriate to set MD as 20. It is not necessary to assign a large value to the parameter MI for multiple iterations, because the iteration terminates when one of the three conditions (Line 33 of Algorithm 3) is met. It is enough to set the number of iterations to 100. According to the experimental methods in Refs. [28, 29], the initial value of MR is set based on the map size and is increased by 5% for each iteration.

Therefore, the parameters are set as follows: MD = 20, MI = 100, η_o and η_s are equal to 0.3 to give the same importance to the orientation and speed distance. The selection of k values is presented in Sections 7.3.1 and 7.3.2.

7.3.1 Synthetic dataset

1):

Visual display of the clustering results

To intuitively demonstrate the effect of clustering, without loss of generality, we set the parameter k = 100, and accordingly, the number of clusters is 9 in each algorithm. Figures 5, 6 and 7 respectively illustrate the clustering results of TC_MFTSM, GC_DM and MDAV on the synthetic dataset. The trajectories in 3-dimensional space are depicted with black lines, and their corresponding projections in the 2D-plane are marked in red.

Fig. 5

Clustering results of TC_MFTSM algorithm on the synthetic dataset

Fig. 6

Clustering results of GC_DM algorithm on the synthetic dataset

Fig. 7

Clustering results of MDAV algorithm on the synthetic dataset

In Figs. 5–7, each sub-figure represents a cluster. In each figure, there are 9 clusters that are respectively shown in 9 sub-figures. In Fig. 5, all the clusters are highly gathered except the first one. The aggregation effect in Fig. 5 is superior to the other two figures in terms of time dimension, spatial dimension and trajectory direction. For example, in the second sub-figure (Row 1, Col 2) of Fig. 5, all the trajectories in this cluster have highly similar time intervals, centralized geographical locations, and consistent directions. Other sub-figures in Fig. 5 are the same.

From the results of the latter two algorithms, there are obvious trajectory outliers in some clusters. For example, in the fifth sub-figure (Row 2, Col 2) of Fig. 6 and in the seventh sub-figure (Row 3, Col 1) of Fig. 7, the trajectories in the corresponding cluster are very different with each other regardless of the time, location or direction. The same goes for the other clusters in Figs. 6–7. The reason is that some characteristics are ignored in measuring trajectory similarity. As is seen from Figs. 5–7, the clustering effect of the TC_MFTSM algorithm outperforms that of the other two algorithms GC_DM and MDAV.

In the following experiments, we vary the value k between 20 and 140.

2):

Execution time

Execution time is the time it takes an algorithm to complete trajectory clustering. The Execution time comparison of 3 algorithms executed on the synthetic dataset is shown in Fig. 8.

Fig. 8

Execution time comparison of 3 algorithms run on the synthetic dataset

As can be seen from Fig. 8, in the vast majority of cases, the execution time of TC_MFTSM algorithm is less than that of the other two algorithms GC_DM and MDAV with the same k. The reason is that in our algorithm the trajectory outliers have been removed from the dataset before clustering. The general trend is, the larger the value of k, the fewer the number of clusters, and the faster the clustering speed.

3):

The intra-cluster and inter-cluster distances

According to the calculation methods described in Table 4, the four types of distances in the experimental results on the synthetic dataset are provided in Table 5 and Fig. 9.

Table 5 The distances comparison of clustering results of 3 algorithms on the synthetic dataset

Fig. 9

The four types of distances comparison of clustering results on the synthetic dataset

Table 5 and Fig. 9 show that the average intra-cluster distance (indave) of three algorithms is far less than the average inter-cluster distance (outdave), which indicates the good clustering effect. And all the four distances of TC_MFTSM algorithm are less than that of the other two algorithms. This depends on the different distance measure metric. In addition, for the three algorithms at the same k, it is normal that the minimum inter-cluster distance (outdmin) is smaller than the maximum intra-cluster distance (indmax) because the distance between some trajectories and trajectory centers in other clusters is less than the maximum distance radius in those clusters.

4):

The coupling degree

Based on (20), the coupling degree comparison of 3 algorithms run on the synthetic dataset is shown in Fig. 10. The coupling degree (cp_dg) of TC_MFTSM is substantially less than that of the algorithms GC_DM and MDAV at the same k in the interval [60,140]. For the dataset containing more than 1000 trajectories, it is proper to set the presupposed size of each trajectory cluster (k) within this interval. As described in Section 7.2, the coupling degree represents the degree of closeness within a cluster. Therefore, Fig. 10 shows that our algorithm outperforms the existing algorithms.

Fig. 10

Coupling degree comparison of 3 algorithms run on the synthetic dataset

5):

The Total Sum of Squared Error

Based on (21), we calculate TSSE values of the three algorithms on the synthetic dataset. Table 6 shows the comparison results. Obviously, the TSSE value of our algorithm is smaller than that of the other two algorithms at the same k.

Table 6 The TSSE comparison of 3 algorithms on the synthetic dataset (× 10⁷)

6):

The Silhouette Index

Based on (22)–(25), we calculate SI values of the three algorithms on the synthetic dataset. Table 7 shows the comparison results. As is described in Section 7.2, higher SI value indicates higher quality of trajectory clustering. Obviously, the SI value of our algorithm is higher than that of the other two algorithms at the same k.

Table 7 The SI comparison of 3 algorithms on the synthetic dataset

7.3.2 Real-life dataset

Because the number of trajectories in the real-life dataset is 480, which is less than the number of trajectories in the above synthetic dataset, in the following experiments, we change the value k, varying it between 10 and 100.

1):

Execution time

The Execution time comparison of 3 algorithms run on the real-life dataset is shown in Fig. 11.

Fig. 11

Execution time comparison of 3 algorithms run on the real-life dataset

As can be seen from Fig. 11, in the vast majority of cases, the execution time of TC_MFTSM algorithm is less than that of the other two algorithms GC_DM and MDAV with the same k. And the time curve of TC_MFTSM algorithm is much smoother with different k. Because in our algorithm the selection of initial trajectory centers is also optimized except for the outliers elimination.

2):

The intra-cluster and inter-cluster distances

The four types of distances in the experimental results on the real-life dataset are provided in Table 8 and Fig. 12.

Table 8 The distances comparison of clustering results of 3 algorithms on the real-life dataset (× 10^− 2)

Fig. 12

The four types of distances comparison of clustering results on the real-life dataset

Table 8 and Fig. 12 show that, for this real-life cab dataset, all of the four distances are very small, and thus the difference among the 3 algorithms is not very significant. The results of our algorithm do not outperform the algorithm MDAV, but the difference is controlled in a small range. More features are considered in our algorithm, so the absolute values are bigger than the ones of MDAV.

3):

The coupling degree

Based on (20), the coupling degree comparison of 3 algorithms run on the real-life dataset is shown in Fig. 13. The coupling degree of TC_MFTSM is substantially less than that of GC_DM algorithm and a little greater than that of MDAV algorithm at the same k in the interval [10,100]. For the dataset containing 480 trajectories, it is proper to set the presupposed size of each trajectory cluster (k) within this interval. As described in Section 7.2, the coupling degree represents the degree of closeness within a cluster. Therefore, Fig. 13 shows that our algorithm is effective in terms of this metric, it outperforms GC_DM algorithm and is similar to the result of MDAV algorithm. Moreover, the curve of our algorithm with different parameter is smoother than those of the others.

Fig. 13

Coupling degree comparison of 3 algorithms run on the real-life dataset

4):

The Total Sum of Squared Error

Based on (21), we calculate TSSE values of the three algorithms on the real-life cab dataset. Table 9 shows the comparison results. Obviously, the TSSE value of our algorithm is far smaller than that of the other two algorithms at the same k. It represents the priority of our algorithm in effect and accuracy of clustering.

Table 9 The TSSE comparison of 3 algorithms on the real-life dataset

5):

The Silhouette Index

Based on (22)–(25), we calculate SI values of the three algorithms on the real-life dataset. Table 10 shows the comparison results. The SI value of TC_MFTSM algorithm is obviously higher than that of GC_DM algorithm at the same k. Moreover, TC_MFTSM outperforms MDAV algorithm in the vast majority of cases.

Table 10 The SI comparison of 3 algorithms on the real-life dataset

In summary, based on most evaluation metrics, experimental results on the synthetic and real-life datasets show that the proposed TC_MFTSM algorithm outperforms the existing algorithms GC_DM and MDAV in terms of execution efficiency and clustering utility, and can better reflect the multiple internal and external characteristics of the trajectory itself. Therefore, the TC_MFTSM algorithm is feasible and effective.

7.3.3 Clustered reference dataset

In this section, we evaluate the clustering performance of TC_MFTSM vs. GC_DM, MDAV and IMDTraclus based on the calculation of Rand Index (RI) and Adjusted Rand Index (ARI) values. These two metrics are very popular for testing the performance of clustering algorithms. The RI (ARI) measurement result is representative in measuring the effect of clustering, so we choose to add a set of experiments comparing the proposed algorithm TC_MFTSM with the new algorithm IMDTraclus to this section. To calculate RI and ARI, a clustered dataset is needed as a reference standard. Therefore, a clustered reference dataset (denoted as ClusDS) is generated by a trajectory generator, as described in Seciton 7.1.

We conduct a set of experiments based on the following 3 reference datasets, which are all derived from ClusDS:

(a):

ClusDS itself. That is, a generated dataset of all the normal and abnormal trajectories without any processing. There are 1000 normal trajectories and 50 abnormal trajectories, where the normal trajectories are grouped into 10 clusters and there are 100 trajectories in each cluster, all the abnormal trajectories are treated as 1 cluster. In order to unify the numbering of 3 datasets and to facilitate the later description, ClusDS is also denoted as ClusDS1. It is shown in Fig. 14. The 3-dimensional effects of these synthetic trajectories are shown in Fig. 14a, while their projections in the 2D-plane are shown in Fig. 14b. Note that for clarity, different trajectory clusters are represented with different colors in Fig. 14. The trajectories marked with solid lines are labelled normal and the trajectories marked with blue dotted lines are labelled abnormal.

(b):

A dataset of all the normal trajectories without any locations deletion, denoted as ClusDS2, it is a subset of ClusDS1. There are 10 clusters and 100 trajectories in each cluster. As is shown in Fig. 14, the trajectories within ClusDS2 are those marked with solid lines. That is, after the trajectories marked with dotted lines are excluded from Fig. 14, the dataset of remaining trajectories is ClusDS2.

(c):

A dataset of all the normal trajectories with random deletion of some locations, denoted as ClusDS3. It is shown in Fig. 15. The number of trajectories in ClusDS3 is the same as the number of trajectories in ClusDS2, but the number of locations in ClusDS3 is less than the number of locations in ClusDS2. For each trajectory, several locations have been randomly deleted. This is a dataset that is not synchronized in time. It can be used to better verify the performance of our algorithm because both temporal and spatial factors should be considered in trajectory distance measurement.

Fig. 14

The reference dataset without locations deletion (ClusDS1)

Fig. 15

The reference dataset with random deletion of some locations (ClusDS3)

As can be seen from Figs. 14 and 15, the clustering results in trajectory datasets ClusDS1-ClusDS3 are perfect for its high similarity within each cluster. It is appropriate that we use one of these datasets as a reference/standard to calculate the (Adjusted) Rand Index values. In order to make comparisons on the RI and ARI values with different parameters, in the following experiments, we change the value num_c (the number of trajectory clusters), varying it between 5 and 40.

The experiments in this section are conducted based on three labelled trajectory datasets with reference significance. In order to make the proposed algorithm more convincing, we add a new algorithm IMDTraclus to the following comparison experiments in addition to the above two algorithms GC_DM and MDAV. The reason for selecting IMDTraclus here is as follows. This algorithm is also implemented in two steps. First, trajectory similarity measurement method proposed in Literature [34] is adopted to calculate the distance between two trajectories. Second, being similar with the other two algorithms MDAV and GC_DM, a greedy clustering method is used to complete the trajectory clustering process. All of the four algorithms are two-stage methods mentioned in Section 2. So it is reasonable to conduct the comparison among these algorithms.

1):

The Rand Index

Based on (26), we respectively calculate RI values of the four algorithms on datasets ClusDS1-ClusDS3. In calculation of RI(X,Y ), the clustering of a reference dataset is acted as X and the clustering result of an algorithm is acted as Y. For example, the clustering results of TC_MFTSM, GC_DM, MDAV and IMDTraclus are respectively acted as Y to calculate RI(X,Y ).

Figure 16 shows the comparison of the four algorithms on the RI value, where Fig. 16a and c respectively represent the running results on the trajectory datasets ClusDS1-ClusDS3.

Fig. 16

The RI comparison of 4 algorithms on datasets ClusDS1-ClusDS3

As can be seen from Fig. 16, the results of TC_MFTSM algorithm are slightly better than that of the other three algorithms with different values of parameter num_c. With different values of num_c, the average RI values of TC_MFTSM, GC_DM, MDAV and IMDTraclus are respectively 0.935, 0.940, 0.939, 0.894 for ClusDS1. They are respectively 0.940, 0.938, 0.939, 0.888 for ClusDS2, and 0.900, 0.898, 0.891, 0.852 for ClusDS3. The RI values of TC_MFTSM algorithm are higher than that of IMDTraclus algorithm in all cases. Taken together, the TC_MFTSM algorithm has higher accuracy. One of the advantages of our algorithm is that multiple features are considered in trajectory distance measurement. For a dataset consisting of trajectories with standard length, the superiority of our algorithm is not very notable. But if a dataset consisting of trajectories with different lengths and shapes is used, it is clear that TC_MFTSM algorithm is better than the others. As described above, ClusDS1 is a complete dataset including all the normal and abnormal trajectories. ClusDS2 is a subset of ClusDS1, it includes all the normal trajectories. For each trajectory in ClusDS1 or ClusDS2, there are 10 locations without any deletion. On the other hand, ClusDS3 is a dataset consisting of trajectories with different lengths. As is shown in Fig. 16c, the TC_MFTSM algorithm outperforms the other algorithms in the vast majority of cases. The reason is that the initial trajectory centers are optimized in TC_MFTSM algorithm, which is applicable to irregular datasets. In real life, the trajectories collected from various devices are heterogeneous, so the TC_MFTSM algorithm is more applicable. In general, we can see the priority of our algorithm in accuracy of clustering from Fig. 16.

2):

The Adjusted Rand Index

Based on (27), we respectively calculate ARI values of the four algorithms on datasets ClusDS1-ClusDS3. In calculation of ARI(X,Y ), the clustering of a reference dataset is acted as X and the clustering result of an algorithm is acted as Y. For example, the clustering results of TC_MFTSM, GC_DM, MDAV and IMDTraclus are respectively acted as Y to calculate ARI(X,Y ).

Figure 17 shows the comparison of the four algorithms on the ARI value, where Fig. 17a and c respectively represent the running results on the trajectory datasets ClusDS1-ClusDS3.

Fig. 17

The ARI comparison of 4 algorithms on datasets ClusDS1-ClusDS3

As can be seen from Fig. 17, with different values of parameter num_c, the results of TC_MFTSM algorithm are better than that of GC_DM and MDAV algorithms in the vast majority of cases, and are better than that of IMDTraclus algorithm in all cases. Just as reviewed in Section 2, the existing similarity measurement methods cannot fully utilize the specific features of trajectory itself when measuring the distance between trajectories. Another factor is that the selection method of initial trajectory centers is optimized in our algorithm. The comparison results indicate the effectiveness and superiority of the proposed algorithm.

Additionally, one can observe that the ARI values in Fig. 17c are relatively smaller than the ARI values in Fig. 17a and b. The reason is that, as described above, ClusDS3 is a dataset of all the normal trajectories with random deletion of some locations. In the case of clustering results being randomly generated, the ARI value is close to zero.

Based on various evaluation metrics, the proposed algorithm has been verified on 3 different datasets mentioned in Section 7.1. According to the analysis of algorithm complexity and experimental results, TC_MFTSM algorithm is stable, reasonable and effective.

8 Conclusion

In this paper, we introduce the problem of trajectory similarity clustering and its applications. We propose a trajectory clustering algorithm based on multi-feature distance measurement. The proposed trajectory clustering algorithm TC_MFTSM uses the characteristics of orientation, speed, shape, location and continuity of each trajectory to achieve more accurate clustering results. In addition, the initial centers of trajectory clusters are optimized based on the time interval of each trajectory. Both the intuitive visualization presentation and the experimental results show that the proposed algorithm achieves high accuracy and efficiency. Compared to the GC_DM, MDAV and IMDTraclus algorithms, the TC_MFTSM algorithm reduces the negative impact of outlying trajectories when selecting the initial centers. Furthermore, it improves accuracy and stability in clustering results. The proposed algorithm can be used in many geographical research fields. In future research, we first plan to develop a trajectory privacy preserving method based on the proposed trajectory clustering algorithm to achieve trajectory k-anonymity within each cluster while maintaining higher utility of published trajectory data. Second, we will explore further applications for the TC_MFTSM method, such as tourist routes recommendation and congestion prediction. Third, in order to facilitate further research and application, we will develop a trajectory data analysis and visualization application system that integrates the functions of trajectory input, query, processing, analysis, output and display. The program that implements the proposed method will be used as a background part of the system.