A novel methodology to describe neuronal networks activity reveals spatiotemporal recruitment dynamics of synchronous bursting states

Abstract

We propose a novel phase based analysis with the purpose of quantifying the periodic bursts of activity observed in various neuronal systems. The way bursts are intiated and propagate in a spatial network is still insufficiently characterized. In particular, we investigate here how these spatiotemporal dynamics depend on the mean connection length. We use a simplified description of a neuron’s state as a time varying phase between firings. This leads to a definition of network bursts, that does not depend on the practitioner’s individual judgment as the usage of subjective thresholds and time scales. This allows both an easy and objective characterization of the bursting dynamics, only depending on system’s proper scales. Our approach thus ensures more reliable and reproducible measurements. We here use it to describe the spatiotemporal processes in networks of intrinsically oscillating neurons. The analysis rigorously reveals the role of the mean connectivity length in spatially embedded networks in determining the existence of “leader” neurons during burst initiation, a feature incompletely understood observed in several neuronal cultures experiments. The precise definition of a burst with our method allowed us to rigorously characterize the initiation dynamics of bursts and show how it depends on the mean connectivity length. Although presented with simulations, the methodology can be applied to other forms of neuronal spatiotemporal data. As shown in a preliminary study with MEA recordings, it is not limited to in silico modeling.

1 Introduction

With experimental recordings or numerical simulations from the whole brain (Olmi et al., 2019; Massimini et al., 2004) to neuronal cultures (Paraskevov & Zendrikov, 2017; Orlandi et al., 2013) scientists try to understand the information processing (Kirst et al., 2016) underlying propagating activities in complex neuronal networks. Phenomena of rhythmic actvivity coupled to propagation are extensively studied in complex neuronal systems. In a bottom up approach, exploring the variety of activity patterns that exists is a relevant path in order to understand higher brain functions, or diseases. As an example, propagating waves have been identified as the default activity of cortical structures (Sanchez-Vives et al., 2017; Sanchez-Vives, 2015). They are observed in various conditions, during sleep in the healthy brain, or during epileptic epochs, and at different scales: from thousands of neurons in less than a millimeter in culture, to billions of neurons through the whole cortical layer. In order to go even deeper in the understanding of neuronal wave activity, one needs reproducible and unbiased quantitative measurements adapted to the considered phenomena.

We propose here a methodological approach of such phenomena motivated by studies on neuronal culture activity (Renault et al., 2015; Renault et al., 2016; Yamamoto et al., 2018; Tibau et al., 2018). Although recorded at different scales, activity observed in vitro are thought to be a well suited model for propagating phenomenon in the brain either similar to slow wave sleep (Sanchez-Vives & McCormick, 2000) or to epileptic activity (Derchansky et al., 2008; McCormick and Contreras, 2001). Indeed, recent studies on young 2D neuronal cultures have forwarded evidences that specific regions are able to initiate a propagating front of activity going through the whole network during what is now called a network burst (Orlandi et al., 2013; Lonardoni et al., 2017; Paraskevov & Zendrikov, 2017). A rhythmic activity takes place within the culture, formed by long periods of silence and shorter epochs of intense firing at the culture scale, that constitute a burst. Although morphological properties of neurons grown in culture may vary from healthy brain tissues, this process of localised initiation and/or propagation has been observed during many activity routing in the brain: during epileptic seizures (McCormick and Contreras, 2001), slow wave sleep (Massimini et al., 2004), retinal development (Butts et al., 1999; Maccione et al., 2014) or in cortical areas in anesthetized and awake conditions (Muller & Destexhe, 2012),

1.1 Motivations

Spatiotemporal analysis of collective rythms and waves is not straightforward, as shown by the multiple number of methods used in the literature. How to faithfully quantify neuronal network activity in time and space is still an open question. The most common approach uses a binning strategy: neurons’ activity is considered to be a series of consecutive discrete events in time and space thus easy to count within specific time bin of size $\Delta t$. The obtained function can afterwards be used to compute a firing rate as a function of time (Penn et al., 2016; Gritsun et al., 2012; Bologna et al., 2010; Eckmann et al., 2008; Eytan & Marom, 2006), a degree of synchrony with cross/auto-correlations (Penn et al., 2016; Stegenga et al., 2008; Chiappalone et al., 2006; Salinas & Sejnowski, 2001; Wand & Buzski, 1996), a global network activation (percentage of active units within a time bin) (Yamamoto et al., 2018), spatial properties of information transfer with avalanches (Yaghoubi et al., 2018; Zierenberg et al., 2018; Levina & Herrmann, 2006; Beggs & Plenz, 2003), a center of activity and trajectory (Chao et al., 2005), or even very persuasive snapshots displaying the activity in space (Paraskevov & Zendrikov, 2017; Gritsun et al., 2012; Kitano and Fukai, 2007). However, all those tools are known to display time binning and/or thresholds biases (Tsai et al., 2017; Touboul & Destexhe, 2010). These are example of analytical biases. We call here biased, any computation that uses arbitrary parameters that may modify the result. For example, the avalanches size distribution may or may not resemble a critical-like power law distribution depending on $\Delta t$ (Beggs & Plenz, 2003). Moreover, the discrete nature of neuron communicating system as action potential should not be taken as the characteristic of a two state dynamical system: either active of inactive. Action potentials are simple hallmarks of a much complex dynamics. However, a binning strategy represents the idea that neurons are either active or silent and thus neglects their dynamical properties.

Let us also note that the very nature of the observed periodic activity in culture is ill-defined, and different definitions of a network burst are found in the literature (Lonardoni et al., 2017; Eckmann et al., 2008; Mazzoni et al., 2007). Along with different definitions (and namings), various methods exist to detect bursting states. At a single unit level, Cotterill et al. (2016) concluded, after analyzing 8 representatives algorithms, that there is still need for an accurate burst detection method to be adopted. The variety of methods and definitions (Lonardoni et al., 2017; Eckmann et al., 2008; Eytan & Marom, 2006; Chiappalone et al., 2006) used at the network level is an impediment to a reproducible description of a neuronal synchronized state independent of any arbitrary parameters.

1.2 Objectives

The main focus of this article is to show that there exists an unbiased, parameter free quantity that can define and identify bursts in neuronal culture (Section 2.2.2). Along with a clear definition of a network burst (Section 2.2.3), we present, on simulated data, the dynamical process involved in the recruitment of the network during the bursts initiation. The key concept we introduce to properly define network bursts is the network phase function. We illustrate the potential of this definition on a theoretical model of neuronal culture made of oscillatory units and reveal the bursts initiation involved. Rigourosly, the firing rate is the single-spike probability density (Dayan & Abbott, 2001), although it is always represented as the spike-count firing rate. Coming back to the original definition of the firing rate, as a probability density, we show that our burst definition reveals the initiation time scale of nework bursts (Section 3.1). We conclude on the activity in the 2 dimensional real space and discuss the role of the network connectivity length in the burst initiation (Section 3.3).

2 Materials and methods

2.1 Simulations of neuronal networks

2.1.1 Neurons activity

The methods described in the following sections are studied on simulations of neuronal networks (see Appendix 2 for more details). Neuronal activity is modeled via the adaptive exponential integrate and fire model (Brette & Gerstner, 2005) for its computational efficiency and biological relevance.

By controlling both pre and post synaptic mechanisms Penn et al. (2016) found that over two thirds of dissociated hippocampal and cortical neurons are pacemaker neurons. Neurons are said to be pacemakers when they regularly spike even when pull apart from any other neurons. They are oscillators. In neuronal cultures, such behavior may come from persistent sodium current $I_{Na,P}$ (Tazerart et al., 2008; Sipil et al., 2006), gap junctions (Draguhn et al., 1998; Rouach et al., 2003) or even glial cells. Following these results, we use 3 different parameter sets corresponding to self-sustained oscillating neurons independently of their connectivity. They will be referred to as ’Noise Driven’, ’Regular Spiking’ and ’Intrinsically Bursting’ depending on their spiking patterns (see Appendix 2 for further details). We want to raise awareness on the Noise Driven type. Although the name might be misleading, ND neurons are regularly spiking, however the spike interval depends highly on the number and intensity of inputs received (for example noise). Looking at pacemaker neurons comes with significant consequences. Those neurons intrinsically follow their inner dynamics, and pushing them away from their stable cycle demands specific conditions. For instance, the required input to make a pacemaker spike in a small time window, depends on this neuron inner state when the input is received and not only on its strength. The examples illustrating this paper investigate a novel perspective on bursting phenomena with pacemaker neurons.

2.1.2 Network model

Metric correlations of the network have been shown to shape network global activation (Hernandez-Navarro et al., 2017). We take this into account by choosing an Exponential Distance Rule (EDR) model (Fardet, 2018) for the neuronal connectivity. This is an Erdös-Rényi like network, where the connection probability depends on the Euclidean distance, with an exponential decrease. The exponential characteristic length $\lambda$ is later called, the network spatial scale and is equal to the mean connectivity length. The network is built under the condition of fixed mean degree, from a random selection of somata positions in a 800 $\mu m$ radius circular culture with strict border conditions (more details in the Appendix 2). Each pair of somata separated by a distance (d) is connected with the probability $p(d)=p_0e^{-d/\lambda }$, with $p_0$ a normalization factor. It is to be noted that the proposed analysis is not limited to those specific parameters and model. As an example, a different model is analyzed in detail in Appendix 3.

2.2 Temporal spikes analysis

2.2.1 Spike count rate

We consider spikes as identical, discrete events, varying only in their time of emission and emitter position. In other words, we neglect the information that may exist in the spike shapes and sub-threshold membrane oscillations. Usually, the firing rate is approximated with a convolution of the neural response function with a chosen kernel (rectangular, gaussian, exponential, alpha etc...). Although this spike-count rate has been shown to correlate with specific stimuli in neuroscience studies (Dayan & Abbott, 2001), this approach entails huge variability and may not be reproducible depending on the choice of kernel, and its characteristic time scale. In an attempt to provide unbiased estimators of neurons activity, we suggest a different method in order to rid activity analysis of time binning strategies. We use in this paper individual spike times. While our method is specially appropriate for simulations, the required high spatiotemporal resolution necessary to discriminate single spikes is increasingly available through MEA (Grewe et al., 2010) and even fast calcium imaging that reaches the millisecond range with Oregon Green BAPTA-1 calcium indicator (Tsai et al., 2017).

2.2.2 The network phase

Pikovsky et al. (2001) defined the phase of an oscillatory signal with discrete events as a piecewise continuous function in between two events. Thus, concurrently to single spike times, we will use $\phi _i(t)$ for neuron i, and any time t in between two spikes $t_{i,k}$ and $t_{i,k+1}$:

$$\begin{aligned} \phi _i(t) = \frac{t - t_{i,k}}{t_{i,k+1} - t_{i,k}}, ~ t \in [t_{i,k} , t_{i,k+1}[ \end{aligned}$$

(1)

Fig. 1

Bursting events acting as an epoch of synchronous spiking is visible with large oscillations of the network phase. The middle panel represents the maximum (red) and minimum (green) values of the phase extrema averaged over 50s simulations. In each simulation a proportion p of Intrinsically Bursting neurons, in a synchronous state, have been substituted for a Poisson spiking neuron of rate 10 Hz in order to mimick non-synchronous neurons. As expected (see Eq. (4)), the proportion of synchronous neurons correlates with the network phase peak values. Left and right panels show the network phase and a raster plot of 50 randomly chosen neurons (in a population of 2000 neurons) as functions of time for two different proportion $p = 0.14$ (left) $p = 0.78$ (right). One can see the two peaks that surround the bursts

where $t_{i,k}$ is the time of the $k^{th}$ spike of neuron i, in the ordered sequence of spike times. The phase function of a discrete set of events is computed after the recording of the sequence of firing times; its value at some time $t>t_{i,k}$ depending on the knowledge of the following firing time $t_{i,k+1}$. The phase $\phi _i(t)$ is the difference between time t and the closest spike in the past, divided by the instantaneous interspike interval at this time t. An oscillatory neuron state can thus be defined by this bounded variable, that embodies both frequency and spike timing. It is the simplest step to estimate a neuron dynamical state, without constraining it to a two state dynamics. We define the network phase as the mean phase:

$$\begin{aligned} \Phi (t) = \frac{1}{N} \sum _{i=1}^N \phi _i(t) \end{aligned}$$

(2)

with N the total number of neurons. After each spike, the phase of a neuron decreases from 1 to 0 in a discontinuous way. Accordingly, the network phase decreases by an amount in the range of $\frac{1}{N}$. Because of this reset, the network phase decreases more significantly whenever several neurons spike simultaneously, allowing us to detect and define a synchronized bursting regime. The network phase typically increases slowly in between bursts because few neurons spike, and rather irregularly, and it decreases down, and/or oscillates around 0.5, during bursts because of high firing rate (see Fig. 1). Let us stress that the network phase we use here is a simple way to access the complexity of the spike times’ sequence from experimental or simulated data and not a novel modeling of the dynamics.

2.2.3 Burst definition

Using the network phase, we develop now a mathematical characterization of synchronous bursting states. The network phase $\Phi (t)$ specific behavior in bursting activities (see Fig. 1) guides us towards a definition: bursts are global events observed in between a maximum and minimum of the network phase. Let us show that, a local maximum of the network phase is associated with the synchronization of at least some neurons in the culture. Let us call q the proportion of synchronized neurons that spike in a specific time window, let’s call it $\Delta t$, around time t. This proportion q of coactivated neurons might not represent the whole network, thus a proportion $p = 1 - q$ does not spike in this time window but at a latter time in the burst. Because the phase between two spikes has a linear evolution, (with the slope being the inverse of the interspike) the network phase variation due to non-synchronous neurons is easily determined. On the contrary, the phase of the spiking neurons goes through the hard reset from 1 to 0 which forces the network phase to decrease by a certain amount $|\Delta \Phi |$. We note $N_1$ and $N_2$ the number of synchronous, and non-synchronous neurons (respectively). The synchronous neurons represent the first one to fire in a burst, whereas the non-synchronous neurons represent those who will spike at a latter time, not at all or with an irregular pattern. We can write the quantity $\Delta \Phi$ being equal to:

$$\begin{aligned} \Delta \Phi = \Phi (t+\frac{\Delta t}{2}) - \Phi (t-\frac{\Delta t}{2}) \end{aligned}$$

And, given the definition of the network phase (Equation (1)), the most general form is:

$$\begin{aligned} \Delta \Phi = \frac{1}{N} \bigg (&\sum _{i=1}^{N_2} \frac{t + \frac{\Delta t}{2} - t_{i,k+1}}{t_{i,k+2} - t_{i,k+1}} - \frac{t - \frac{\Delta t}{2} - t_{i,k}}{t_{i,k+1} - t_{i,k}} \\&+ \sum _{i=N_1+1}^{N_2} \frac{ \Delta t}{t_{i,k+1} - t_{i,k}} \bigg ) \end{aligned}$$

As explained before, because of synchronous spiking neurons, the network phase will decrease when a burst starts. We are looking for the condition for $\Delta \phi$ to be negative. In order to continue the computation without to much complexity, we assume that the instantaneous interspike interval, noted ISI, is the same for both synchronous and non-synchronous populations. This is sufficient to capture the important parameters at play, and reflects data recorded with calcium imaging, where only the first spikes of a burst are accessible with high resolution. For synchronized neurons the ISI corresponds to the interburst interval, while for non-synchronized neurons the ISI represents the interval between irregular firings. We can write:

$$\begin{aligned} \Delta \Phi = q \left( \frac{\Delta t}{2 ISI} - ( 1 - \frac{\Delta t}{2 ISI}) \right) + p \frac{\Delta t}{ISI} \end{aligned}$$

(3)

The first and second terms describe respectively, the decrease of the network phase due to the synchronous neurons and the increase due to the non-synchronous ones. Thus, the characterization of a synchronous event as we defined it above implies :

$$\begin{aligned} \frac{\Delta t}{ISI} - q < 0 \end{aligned}$$

(4)

This means that a decrease of the network phase happens if a proportion q of the population spikes in a time scale smaller than $q \times ISI$. This coactivation is associated with a decrease of the network phase by an amount proportional to the size q. A bursting state can thus be detected without any arbitrary parameters and happens in between a maximum and a minimum of the network phase. The amplitude $|\Delta \Phi |$ is related to the proportion of bursting neurons.

With less restrictive assumptions, one can understand that the network phase decreases whenever some neurons are coactivated in a time interval $\Delta t$ . The network phase decreases by an amount proportional to q, as long as this group phase does not increase back to 1 in this $\Delta t$ time window. This increase is represented by the last term in Equation (3): $(1 - \frac{\Delta t}{2ISI})$. Hence, the time scale of the synchronization $\Delta t$ has to be smaller than the fast time scale $q \times ISI_{in\_burst}$.

With this definition, the network phase $\Phi (t)$ offers, independantly of any arbitrary parameters, a burst starting time reference as a maximum, and an ending time reference as a minimum. Moreover, as Eq. (4) demonstrates it, the difference between the maximum and minimum values of the network phase is a measure of the proportion of synchronous neurons. As Fig. 1 represents it, the minimum and maximum values are linearly correlated with the proportion of synchronous neurons, or equivalently non-synchronous neurons.

2.2.4 The network phase with experimental recording

Fig. 2

Raster plot of 50 electrodes and the network phase as a function of time of experimental recordings from Lonardoni et al. (2017). The burst can clearly be identified. The different sizes of synchronized neurons’ groups in the high frequency regime of the bursts is clearly visible with the phase oscillations

Fig. 3

Search for initiation area in a bursting activity of Intrinsically Bursting neurons. Bottom panel is a raster plot of the burst, each line is one out of 800 neurons randomly pick in the 2000 neurons simulation. The black line represents the network phase. Top panels represent in space 4 different time points with colored neurons as neurons that have spiked up to the considered time (dashed lines in the raster plot). Neurons that have not yet spiked are plotted in grey. Shadows represent the elliptic initiation area. One can observe that at first, the activity is dispersed and no specific region is detected. Some time after, a region has been sufficiently active to be detected then at a later time an other one appears on the right (last panel) These two regions latter grow up to the size of the culture when all neurons have started spiking

Large oscillations of the phase, showing bursting regime and different degree of synchronization can also be seen in experimental recordings. Data publicly available, from Lonardoni et al. (2017) is represented in Fig. 2. It is a recording of hippocampal cell cultures made with a 64x64 micro-electrode array. Each electrode is considered as an individual unit to compute the phase with, and the network phase is the mean average over the 4096 electrodes.

2.2.5 First spike probability distribution

Eytan and Marom (2006) have introduced the idea that some neurons in a culture are consistently the first ones to fire over consecutive bursts. Their analysis however depended on an arbitrary threshold on the activity in order to define the sequence of precursors in neuron firing. Our approach allows an unbiased characterization of these. We are going to compute the probability density for the occurrence of a spike close to the burst beginning. Thanks to the time reference for each burst given by its phase’s maximum (see Section 2.2.3), we can derive the probability for a neuron to emit its first spike during the burst at time $\tau = t - t_b$ where $t_b$ is the detected burst starting time (see Fig. 1). Note that $\tau$ can be above or below zero. This probability is the rigorous definition of the firing rate. Indeed, according to Dayan and Abbott (2001) “The probability density for the occurrence of a spike is, by definition, the firing rate [...]”. Here, each trial is an individual burst, and in order to look for the burst initiation, we only take into consideration the first recorded spike of each neuron. Let us note however that in many publications, possibly due to finite number of recordings, the term “firing rate” is more commonly associated with its approximation, the spike count rate. To avoid confusion we will speak in the paper of “spike probability distribution”.

Although we modeled neurons as pacemaker, the noise added as miniature post synaptic events (see Appendix 2 for more details) creates some variability and the sequence of action potentials may vary from burst to burst. Hence the need to investigate the initiation in a probabilistic manner. In order to carry out this analysis one needs a time reference coherent over consecutive bursts/trials with the spike sequence probability density.

To compute this quantity, one first detects for each neuron the first spike in a burst and then compute the cumulative activity: $C_b(\tau ) = \frac{1}{N} \sum _{n=1}^{N} \Theta (\tau -\tau _{n,b})$, where N is the number of neurons, and $\tau _{n,b}$ is their first spiking time in burst b and $\Theta$ the Heaviside function. The cumulative activity is then averaged over multiple bursts of the same simulation. Then the numerical derivative F is the first spike time probability density, computed with the time resolution r:

$$\begin{aligned} F(\tau ) = \dfrac{<C_b>(\tau + r) - <C_b>(\tau )}{r} \end{aligned}$$

(5)

2.3 Spatial spike analysis

This section focuses on the initiation in space of bursting dynamics. Many studies (Orlandi et al., 2013; Lonardoni et al., 2017; Paraskevov & Zendrikov, 2017) either from numerical simulations or experimental recordings in cultures, have reported that bursts start repeatedly in one or several localised regions of the culture. We propose here a method to detect such regions based on a clustering algorithm of spiking neurons. Although we know the in-burst spike times because of the high resolution used in simulations, we will use only the first spike of each neuron in order to look at how does the bursting regime starts.

2.3.1 A specific region of the culture starts spiking before the whole population

Fig. 4

Estimation of the parameter $\epsilon$. Each panel shows the number of detected cluster (red) and the number of neurons in it normalized by the total number of neurons (blue) as function of $\epsilon$. Top row: circular culture of radius 800 $\mu$m. Bottom row: Triangular culture, with aspect ratio 1:10. Scale bar in the inset of the right panel shows 400 $\mu$m. Both geometries present similar total densities. Each inset presents the result for $\epsilon = 35 \mu$m: orange dots are neurons in a cluster and black dots are visible neurons not in a cluster. Column A: All neurons are visible for the DBSCAN algorithm, and although a first cluster is detected at $\epsilon = 10 \mu$m, each neuron belongs to this cluster above 25 $\mu$m. This sets the minimum value possible. Column B: Same cultures, with only $20\%$ randomly chosen neurons visible. We observe that for large $\epsilon$ the density of visible neurons is too low for any cluster to be detected: because of Equation (6), the threshold number of neighbors cannot be reached. Column C: Same cultures, with two separate regions and a total of $10\%$ visible neurons. In the two examples (circular and triangular) the activated regions are the same size, with the same number of neurons

As a first hypothesis, one considers that the culture is homogeneously and randomly seeded with neurons. Thus, if one region is to start the activity, it should have a density of spiking neurons close to the density of the culture. This is how we will detect the initiation area. The algorithm DBSCAN (Ester et al., 1996) from the Scikit Library (Pedragosa et al., 2011), is a density based algorithm for cluster detection that only requires two parameters and does not need a priori guess of the number of clusters. The two parameters are, a radius of search $\epsilon$ to look for nearest neighbors, and threshold for the minimum number of neighbors $N_{th}$ required to belong in a cluster. We introduce later an approach to avoid these two arbitrary parameters. Overall, the algorithm can be used at any time point and works as follow:

• 1. Each burst is identified with the extrema of the network phase

• 2. For each burst, one looks at the first spike of each neuron. At the considered time point, if a neuron has not spiked yet, it is invisible to the DBSCAN search, if a neuron has spiked, one turns it into a visible state. Visible neurons are neurons that have spiked at least once before the considered time point.

• 3. The DBSCAN algorithm proceeds as the following:

  • For each visible neuron i, one counts the number of visible neurons in a radius $\epsilon$, noted $n_i$

  • If $n_i$ is larger than or equal to $N_{th}$, neuron i is said to belong to a cluster

  • If two neurons detected in a cluster are closer than $\epsilon$, they are in the same cluster.

• 4. Initiation areas are approximated with an ellipse overlapping each neuron in a cluster. There can be several regions, and they can overlap too.

The underlying hypothesis for what is here called a visible neuron, is that a spike may have causal influence over very long period of time. One needs to consider here first the propagation delay and second the integration processes in the post-synaptic neuron, which theoretically speaking can be as long as the interspike interval for pacemaker neurons as shown by Izhikevich (Izhikevich, 2007) with the description of the phase response curve.

The algorithm output is a region of the two dimensional culture -sometimes several regions- of high activity, in the sense that this region is not necessarily fast spiking at the moment or near the moment of the computation but most of its neurons have been active up to the point of computation. Figure 3 represents this search and the corresponding areas.

2.3.2 Parameters estimation

Fig. 5

Probability density function for any neuron to emit its first spike at time $\tau = t - t_b$, where $t_b$ is the time of the network phase maximum (see Burst definition 2.2.3). The right panel represents the probability function for Noise Driven neurons, and the left panel represents Regular Spiking neurons. Both panels include a zoom-in of the region of interest: first-to-fire neurons for $\tau < 0$. Networks with an EDR scale 1000 (lightgray) and 50 (black) $\mu$m are considered

In order to reduce the number of arbitrary parameters we propose to modify the original DBSCAN algorithm. We first choose to relate the minimum number of neighbors threshold $N_{th}$ and the radius of search $\epsilon$ to one another. To be identified as the initiation region, almost each neuron in it has to be activated. Thus, the threshold $N_{th}$ has to be the mean number of neuron in a disk of radius $\epsilon$. Given the density d of the culture, we could set $N_{th} = d \times \pi \epsilon ^2$. However, doing so, one does not account for the different local densities that arise from the strict condition on the culture boundary. Neurons in the center have necessarily a higher number of neighbors. Thus, we set $N_{th}$ to be the mean number of neurons in a disk, corrected by one standard deviation. In this way, neurons at the border can contribute to a cluster more easily. Under the assumption that the standard deviation scales as the square root of the mean, we set:

$$\begin{aligned} N_{th} = d \times \pi \epsilon ^2 - \sqrt{d \times \pi \epsilon ^2} \end{aligned}$$

(6)

To estimate $\epsilon$ let us first quote that for small values, some neurons may not be able to reach the threshold $N_{th}$ because there are to few neighbors at this distance. For large $\epsilon$ values, because of Equation (6), the threshold will be high and some neurons may not be able to reach it. This comes from the fact that, locally, the number of neighbors may not scale as fast as $N_{th}$ with $\epsilon$. Thus, there exists a suitable range of values that we are going to look for. Figure 4 presents an estimation of $\epsilon$ for 2 culture geometries based on running the DBSCAN program with different visible neurons. The goals are the following:

• If each neuron of the culture is visible, the algorithm should detect only one cluster with each neuron in it.

• If a large percentage of the population (at least more than half) is uniformly spiking in the culture, the algorithm should also detect 1 cluster with most of the spiking neurons in it.

• It can detect separate regions of activity.

Figure 4 presents the number of neurons in the initiation area as function of $\epsilon$ for different scenarii. One can observe that the 3 goals are to some extend achieved. As predicted, small values of $\epsilon$ are not suitable, and large values also miss the clusters. One can observe that the number of neurons in a cluster slightly depends on the culture geometry and density of activity. Sharp edges, with few neurons will be detected in a cluster for larger values of epsilon than culture with aspect ratio 1:1. However, for a relatively broad range of values the resulting number of neurons in a cluster does not depend on $\epsilon$. This is the range we are interested in. What is important for the following analysis is that the algorithm can localise high densities and treats each neurons equally in order to detect activity near the border as well as in the center. Moreover, it does not necessarily depend on the culture aspect ratio because the most suitable value of $\epsilon$ can be adapted to individual cultures.

Also, it is important to note that we only used here the first spike of a burst, making this analysis suitable for calcium imaging. The better the resolution on the first spike, the better one will be able to study the cluster growth.

3 Results

The results presented in this section demonstrate the valuable contribution of the maximum of the phase we introduced before to unambiguously unravel the network dynamics during bursts initiation. Indeed, this extremum defines a specific time point in the dynamics of a burst, coherent over consecutive bursts. With simulated neuronal populations in cultures we illustrate the spatio-temporal dynamics of initiation, uncharacterised until now. Then, with publicly available MEA data from (Lonardoni et al., 2017) we discuss on the practical use of our methods with experimental data.

3.1 Burst initiation

We now make use of the probability distribution to reveal different dynamical regimes during bursts. Figure 5 displays the temporal dynamics of burst initiation for a set of simulations with different connectivity spatial scales and neuron models. One can observe that the detected time of burst, at $\tau = 0$, appears to be a critical value that separates different behaviors. The probability density for $\tau < 0$ can be used to define a temporal scale for the initiation. With an estimation of the width of the probability density function, we find an initiation duration in the order of 10 ms for regular spiking neurons, and 100 ms for noise driven ones.

Surprisingly enough, the probability distribution for $\tau < 0$ seems independent of the connectivity spatial scale of the EDR model but depends on the neurons inner dynamics (here modeled through different sets of parameters). This time scale comes from the inner neurons dynamics, and not from the spatial correlation of the network model. On the contrary, for $\tau > 0$ the overall neuronal population is largely characterized by an uni-modal distribution that depends on the network spatial scale. The importance of the spatial correlation emerges in the second regime, ($\tau > 0$) where the curves for two different EDR scale differ from one another.

3.2 Spatial initiation: cluster algorithm performance

Fig. 6

Performance as a function of the detected cluster(s) surface. Top panels represent burst initiation in simulations with a network of Regular Spiking neuron and EDR scale of 50 $\mu$m. Snapshots are separated by 20 ms and red dots represent visible neurons (see Section 2.3.1). The activity is manifestly localised. Bottom panels represent burst initiation in simulations with the same neuron parameters, but a network with EDR scale of 1000 $\mu$m. Snapshots are separated by 20 ms and red dots represent visible neurons (see Section 2.3.1). The activity is seemingly not-localised. Middle panel shows the corresponding performance: the last fifty bursts have been analyzed through the clustering algorithm with a time step smaller than a millisecond. Each data point is here represented, and the red line is a mean average with linear extrapolation in between points. Straight lines represent the maximum of $P_c - \frac{A_c}{A_{tot}}$. They correspond to top second image and bottom last image

In order to quantify the localised initiation, we propose to measure the nucleation site identification performance of our cluster detection algorithm, more simply called performance. As presented before (see Section 2.3), the clustering algorithm is able to target regions of activity initiation. We define the performance of the detected cluster(s) $P_c$ as the number of visible (meaning active) neurons (see Section 2.3.1) in the detected region divided by the total number of visible neurons in the population at the calculation time point. As time evolves, one can run the algorithm and compute the performance as function of the estimated region’s surface (estimated as the smallest ellipse that encompass each point in it). When the activity starts, it may be sparse and the detected region will probably be of low performance. However, if the activity is indeed localised, in the sense that it is confined into a small region and extends from it, the performance should increase faster than the cluster(s) area and then stay relatively constant as the activity extends to the whole culture.

Moreover, one can estimate the smallest region with the maximum performance looking at the maximum of $P_c - \frac{A_c}{A_{tot}}$, with $P_c$ the performance of the detected cluster(s), and $A_c$, $A_{tot}$ respectively, the cluster(s) and culture area. The allows us to define consistently what we call “the initiation region”. Figure 6 represents the performance for two EDR networks with different connectivity scale. One can easily notice that (also reported earlier by Paraskevov and Zendrikov (2017)), long range connectivity does not exhibit localised initiation. This is noticeable both with the initiation region area being larger than 25% of the culture and the shape of the performance: growing slowly towards 1.

3.3 Looking for leaders

A debated topic is whether some neurons behave as “leaders” that display consistently a precursor activity, and what are there characteristics (Faci-Lázaro et al., 2019; Eckmann et al., 2008). In order to show the existence of leader neurons in simulations with pacemaker neurons, we focus on the first spike probability density before the burst onset time defined by the maximum of the network phase (see Fig. 5). Neurons that spike in the time lapse described here by $\tau < 0$ display a significantly different dynamics than the rest of the network. The main reason being that this is the only period of time where the probability density does not depend on the network spatial scale but on neurons’ inner dynamics. With noise driven neurons, the integral of the curve indicates that there are 20 first-to-fire neurons per bursts. However, they may not always be the same ones. In order to identify leadership in bursting dynamics, we look for first-to-fire statistics. If some neurons are repeatedly first-to-fire, we will call them leaders.

Figure 7 displays the first-to-fire statistics for two networks of different EDR scale. Although the distribution probability, Fig. 5 was similar for both of these networks, the first-to-fire statistics is notably different. By using an exponential fit of the distributions of Fig. 7 we estimate the total number of neurons acting as first-to-fire to be 24 and 95 for networks of connectivity scales respectively, 50 and 1000 $\mu$m. Thus, in our simulations, with a small EDR scale, the total number of first-to-fire is in the same range as the number of first-to-fire per burst. These short range networks contain leaders: around 20 neurons repeatedly drive the network to a bursting state in simulations with noise driven neurons. On the contrary with large EDR scale, the total number of neurons that act as first-to-fire is much larger than the number of first-to-fire per bursts. Thus, an established group of regular leader neurons does not exist in a network with long range connectivity.

For the culture sizes we simulated, we note a common growth dynamics that requires approximately 20 neurons to initiate a burst for long and short connectivity spatial scales. For short EDR scales, leader neurons exists, they are repeatedly in the burst initiation sequence among other rarely initiation neurons. For lager EDR scales, the variation in the composition of the burst precursor group is much larger and leaders rarefy.

Fig. 7

Statistics for each neuron to be a first-to-fire over 50 bursts in a simulation with Noise Driven neurons. X-axis has been sorted out to display a decreasing statistic. Black and grey refers to networks where the EDR scale was respectively 50 and 1000 $\mu$m (grey is sltihly transparent for better visualisation). There are 10 first-to-fire neurons present in more than 50$\%$ of the considered bursts for the small EDR scale, and most of the culture is never first-to-fire. On the contrary, long conectivity length increase the number of possible first-to-fire up to a third of the culture

4 Discussion

4.1 Dynamical regimes

The separation of behavior at $\tau = 0$ in the spike time probability distribution reveals the specific dynamics of what has been reported earlier as leader electrodes. (Eckmann et al., 2008; Eytan & Marom, 2006). Using a complex sorting algorithm, Eckmann et al. reported the existence of leader electrodes in neuronal cultures. They used an arbitrary threshold between the probability to spike during a pre-burst period (see Eckmann et al. (2008) for definition of a pre-burst) and the probability to spike at any time during silent periods (low firing rate) to identify leader electrodes.

Here, thanks to the first spike probability distribution, we distinguish naturally the very dynamics of first-to-fire neurons during what (Eckmann et al., 2008) called the pre-burst. This allowed us to show that the very beginning of these neurons activity is independent of the network spatial correlations. This property is clearly revealed thanks to our method unique feature to align bursts initiation through the maximum of the phase. The key element of this characterization is that the maximum of the phase is a coherent time point in the synchronization process over consecutive bursts. Because of this, the firing time sequences are properly aligned allowing to compute the first spike time probability distribution and reveal the initiation dynamics time scale. Previous methods making use of arbitrary reference time are not able to separate the spatial scale independent dynamics ($\tau < 0$) from the spatial scale dependent one ($\tau > 0$). This is illustrated in Appendix 4 where the first spike time probability distribution is evaluated through a conventional method. There, the burst initiation dynamics is blurred because of the arbitrary time reference.

Fig. 8

Performance computed with a recording on 64x64 MEA from Lonardoni et al. (2017), as function of the detected cluster(s) area. The same process is used as in Fig. 6. Black dots are data points, and the red curve is the average curve. The black line shows the minimum area for the maximum performance. It corresponds to 14% of the 5.12x5.12 mm$^2$ MEA. The activity recorded by the MEA appears to start in a region of 3.5 mm$^2$ representing more than 80% of the overall activity during the bursts nucleation. The activity is not uniformly distributed, but is initiated in the identified region

Our burst initiation alignment method allows us to highlight, on simulations, different regimes during a burst and the role of spatial correlations during initiation and propagation. Indeed, the spike time distributions in Fig. 5 show distinct initiation and spreading stages. The initiation stage appears insensitive to spatial correlations, while the burst propagation is strongly affected by it.

In addition, the spatial connectivity scale plays a role for the initiation localisation and the existence of leader neurons. Both properties have been found only in networks with small connectivity spatial scale. In order to understand this, we discuss the assumption that neuronal networks activity is made of avalanches. Neuronal avalanches are understood as the spreading of neuronal firings by a cascading process during which neurons that fire at some time t trigger other neuron firing at a later time. The activation of neurons at some time point is predominately determined by the inputs they receive from other neurons of the population just before. Let us first call “causal time”, the time duration between a neuron spike and the last input that may have influenced it. Because of the time delay due to spike propagation or other inner dynamics, a pre-synaptic neuron spike may not influence a post-synaptic neuron future spiking. Thus, there is a causal time below which neurons appearing co-activated are in fact, unrelated with one another, even if they are synaptically connected. Hence, the assumption that neuronal networks activity is made of avalanches tells us that multiple spikes with a time shift smaller than the causal time must have common predecessors that spiked during the avalanche: there is a path in the network (with inverted direction of connections) from those co-activated neurons to the first-to-fire that started the avalanche.

Although we have not reported it here, bursts of activity, when initiated locally, grow with a synchronous propagating front (Paraskevov & Zendrikov, 2017) (it can be seen in the activity snapshots in Appendix 6). These fast synchronous propagating fronts are an example of co-activations in time scale smaller than this causal time. They are synchronous because of the activity of their predecessors, their predecessors were synchronous because of their predecessors, and so on and so forth. The first ones being the first-to-fire in the burst, which spike at their own pace, according to their own dynamics dimly influenced by the network structural characteristics. Hence, the common temporal dynamics observed for different network spatial scale. Then, these first-to-fire neurons project to, and activate the propagating front starting at the phase maximum. The phase maximum corresponds to the time point of the first co-activated neurons in the avalanche: the beginning of the propagating dynamics. This regime depends highly on the network spatial correlations, and corresponds to an avalanche. Because of this avalanche dynamics, first-to-fire neurons can activate a synchronous propagating front if they share common successors. Neurons spatially localised with common successors are numerous in networks with small connectivity spatial scale, and are not likely to exist in networks with long range connections. Hence, the initiation is localised and a synchronous propagating front exists only in network with small connectivity spatial scale.

This scenario is revealed because the maximum of the phase is the time point that separates the leaders’ dynamics and the avalanche dynamics. Although, in simulations with pacemaker neurons, the network spatial correlations do not shape the leaders’ dynamics, the choice of leaders emerges as a result of the interaction between the network complex stucture and the neurons dynamics. Then, the second stage of the burst, dominated by an avalanche dynamics, coupled with a small connectivity spatial scale appears to be the key elements for a propagating front to exist.

4.2 Experimental data

Although our methods were developed alongside simulated data, we were concerned about their applicability on experimental data. The application of our analysis on experimental data is mainly dependent on the temporal resolution of the recordings. The decrease of calcium indicators fluorescence signal is too slow in many cases to reach the resolution needed to investigate in-bursts dynamics. However, the increase of the fluorescence signal during the action potential can be sufficiently fast to solve with high resolution the first spike of each burst. The methods presented in this paper can be applied when only the first spike in a burst is known. The computation of the network phase does not require high precision in the burst to pinpoint the starting point. Finally, all the analysis on space and temporal dynamics require only the first spike in each burst. Thus we believe that our methods are also suited for high resolution calcium recordings.

Matrix Electrode Arrays (MEA) provide high temporal resolution sufficient to resolve single spikes. We have looked at recordings from 64x64 MEA, in order to show that spatial resolution is not an issue with modern tools. The sample rate is 7 kHz and the spatial resolution 80 $\mu$m. The fast increase of the performance as function of the increasing area of activity, in Fig. 8 prooves that the bursts start locally. Like in our simulations, we were able to identify a specific region of the network, representing 14% of the MEA surface that initiates the bursting regime.

With a threshold based burst detection method, Lonardoni et al. (2017) were able to show that the bursts initiation sites are related to spatially segregated functionnal communities. We here find that the surface of initiation, unambiguously identified with our method, represents 14% of the MEA, similar to the size of the functionnal communities (see Fig. 4 of their paper). This links activity cross-correlation results from a full recording, with individual bursts initiation.

5 Conclusion

This study presents a novel methodology for characterizing synchronous bursting and propagating events in neuronal cultures. In particular we present the network phase, a natural measure for studying synchronous events. It enables us to propose a simple definition and detection criterion for a network burst starting time. This time reference is the basic component in order to determine the first spike time probability distribution which describes the burst initiation dynamics and indicates the existence of leader neurons in networks of naturally oscillating units. It also shows the characteristic time scale of the neuronal population dynamics during what Eckmann et al. (2008) called a pre-burst.

We use a modified clustering algorithm in order to detect whether the growing activity is confined in space. To do this, we compute a quantity we call performance which evaluate the location of activity. Its time evolution can highlight localised burst initiation, and pinpoint the area of initiation.

Finally, the presented methods are used to describe the burst initiation dynamics. The time reference we introduce with the network phase, allows us separate the first-to-fire inner dynamics from the regime where avalanches dominate. It shows a separation of behavior both in time and space. Our simulations with spatial networks of pacemaker neurons show that localised initiation happens only with a small connectivity spatial scale breaking the cylindrical symmetry of the simulated culture. Networks with a long connectivity scale display the same pre-burst initiation dynamics as short scale ones. However they do not display a localised initiation.

The methodology developed here makes possible a systemic analysis of bursting states, and the initiation dynamics still under many questionings. The network structural properties that drive specific neurons to be leader of bursting activities is still unknown but is now easier to address. Moreover, thanks to the linear correlation between the network phase and the number of synchronous events, it may become a powerful tool to further the discussion on the keenly debated topic of criticality in neuronal cultures.

In future work we would like to set up similar analysis on high temporal resolution calcium imaging in order to verify the applicability of the methods introduced here, and investigate with precision biological neuronal networks dynamics during bursting regime.

Fig. 9

Phase space and activity of the considered parameter sets. Each line describes one set of parameters, namely (from top to bottom) Intrinsically Bursting, Noise Driven and Regular Spiking neurons. The ($V_m$,w) phase plane (left column) is represented with a couple of cycle represented in dark dots. Blue line is the membrane potential nullcline (set of points where $\frac{dV_m}{dt} = 0$) and green line is the adaptation current nullcline (set of points where $\frac{dw}{dt} = 0$). The middle column represents the corresponding menbrane potential and adaptive current traces as functions of time. The left column is an histogram of interspike intervals with a poissonian input of rate 15 s$^{-1}$ and increasing weights: from zero noise in black to the highest in brown in pA

Appendices

Appendix

Simulation of neuronal network

1.1 Simulate neuronal activity

Simulations are carried out with the adaptive Exponential Integrate and Fire model (aEIF) (Brette & Gerstner, 2005) via the NNGT python library (Fardet, 2019) and NEST simulator (Gewaltig & Diesmann, 2007). This model is computationally reasonable and provide a large variety of activity patterns (Naud et al., 2008). Each neuron is described as a two dimensional system with the menbrane potential variable $V_m$ (as in the Integrate-and-Fire model) and an adaptation current w which modulate neurons’ excitability (as in the Izhikevich (2003) model).

Table 1 Parameters Values

$$\begin{aligned} \begin{aligned}&V_m < V_{peak} \left\{ \begin{array}{ll} C_m \dfrac{dV_m}{dt}&{}= - g_L (V_m - E_L) + g_L \Delta _T e^{\dfrac{V_m - V_{th}}{\Delta _T}}\\& \quad \; - w + I_e + I_s \\ \tau _w \dfrac{dw}{dt}&{}= a(V_m - E_L) - w \end{array} \right. \\&V_m > V_{peak} \left\{ \begin{array}{ll} V_m &{}\xleftarrow {} V_r \\ w &{}\xleftarrow {} w + b \end{array} \right. \\ \end{aligned} \end{aligned}$$

(7)

Where $C_m$ is the membrane capacitance, $E_L$ is the resting potential, $g_L$ is the leak conductance, $\Delta _T$ is a potential normalization constant that affect the spiking current, $V_{th}$ is the soft threshold, $\tau _w$ is the adaptation time scale, a relates to the sub-threshold adaptation, whereas b gives the spike-triggered adaptation strength and $V_r$ is the reset potential after the potential $V_m$ reaches $V_{peak}$. $I_e ~\text {and}~ I_s$ are currents that come from respectively external sources or neighboring spikes. The exponential non-linearity model the pre-spike membrane potential sharp increase and is needed to describe in-burst fast dynamics. In the end, we choose this model because it is more biologically relevant than the Izhikevich model (Izhikevich, 2003), and much less complex than the Hodgkin-Huxley model.

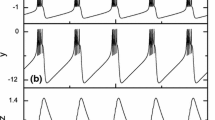
To follow indications of neurons in cultures being oscillators even when uncoupled, reported by Penn et al. (2016), we simulate the activity with three sets of parameters that display pacemaker neurons: Intrinsically Bursting (IB), Regular Spiking (RS) and Noise Driven neurons (ND) whose behavior is detailed in Fig. 9. A neuron said Regular Spiking has a very periodic activity even when submitted to noisy input. Its interspike interval varies by 3% when submitted to a 15 s$^{-1}$ poisson spike train. A Noise Driven neuron, on the other hand, is much more dependant on the input it receives: its interspike interval varies by 50 % under the same conditions. Intrinsically Bursting neurons present a more complex frequency pattern: high frequencies are super-imposed over a natural small one. This can be seen in the resetting point after a spike: it is below the $V_m$ nullcline (see Fig. 9). We use in the paper those 3 sets of parameters to show that the presented methods does not depend on specific values.

1.1.1 Model parameters

Table 1 lists all parameters with their values used in the paper.

1.2 Spatial network

To account for the spatial correlations that exist in cultures and shape its activity (Hernandez-Navarro et al., 2017), we use an Exponential Distance Rule (EDR) to connect all neurons. A population of 2000 excitatory neurons is randomly drawn in a circular culture of radius 800 $\mu$m. Then, with the same process as an Erdös-Renyi network generation, one connect node i to j with probability: $p_{ij} = p_0 e^{d_{ij}/\lambda }$, where $d_{ij}$ is the Euclidean distance between them. This results in a directional network, whose topological properties are predetermined by the magnitude of $\lambda$, the EDR scale and a sharp border condition: neurons can connect only inside the circular culture.

1.2.1 Post synaptic current

Interactions are modeled as fast current injection into the post-synaptic neuron, following a pre-synaptic spike and a space dependent delay. The delay is set as a 3.0 ms constant plus a spike propagation of velocity 0.1 m.s$^{-1}$, similar to what has been experimentaly observed in cultures (Barral and Reyes, 2016). Overall, it follows a log-normal distribution of mean 5. to 15. ms for every network. The network metric properties set up both specific connectivity patterns, and the delay in spike propagation with different connection spatial length. Miniature events are also set as a Poisson noise of rate 15 s$^{-1}$ for each synapses and with a post synaptic current (PSC) of half the amplitude of a spike-triggered PSC.

Synaptic weights that determine the post synaptic current amplitude are set such that the rhythmic activity is observed and stable. Stability of this state is estimated with the mean average interspike interval and network phase.

Analysis with the Izhikevich model, synaptic depression and stochastic inputs

Fig. 10

Analysis with the Izhikevich model. Top panel is a raster plot of 100 randomly selected neurons. Middle panel is a trace of the corresponding network phase. Bursts appear as in the paper, between 2 consecutive maxima and minima, however inter burst activity is always high thus the phase stays close to 0.5. Bottom left panel shows the first spike time probability distribution. This distribution shows the lack of first-to-fire dynamics neurons in this example. Middle bottom panel shows the clustering algorithm in space for 3 consecutive time step: visible neurons are represented as red dots, and all other as black dots. The corresponding performance is plotted in the bottom left panel. It shows the characteristic curve of localised growth with a region of initiation representing 14$\%$ of the total culture

Fig. 11

Representation in space of 2 bursts with neurons’ phases in color scale. Culture radius is 2.5mm. Time goes from left to right, then top to bottom. The starting point of the bursts is in between snapshot 3 and 4

We want to show that our methods can be used to analyze simulations with different models. For examples, previous studies (Orlandi et al., 2013; Levina & Herrmann, 2006; Levina et al., 2007) described the neuronal activity with dynamical synapses and stochastic inputs. More specifically we want to bring together various point of view in the understanding of bursting networks. Orlandi et al proposed a mechanism called noise focusing, based on simulations and experimental recordings, in order to interpret activity during burst initiation. On the other hand, we based our simulations under the assumption that bursting states are an example of oscillator synchronization (Dhamala et al., 2004; Penn et al., 2016).

Inspired by in silico networks in Orlandi et al. (2013), the following simulations are done with an EDR network with mean in-degree 70 and scale 100 $\mu$m in a culture of radius 2.5 mm with 5000 neurons, so that the density is 250 mm$^{-2}$. Following Izhikevich (2003) we look for parameters that display regular spiking neurons, who are not intrinsically spiking (synaptic connection and noise create the activity). This model is represented in its reduced form with the following equation

$$\begin{aligned} \begin{aligned} \text {if} ~&V < 30 mV \left\{ \begin{array}{ll} \dfrac{dv}{dt}&{}= 0.04v^2 + 5v + 140 - u + I_s(t) + \eta (t) \\ \dfrac{du}{dt}&{}= a(bv - u) \end{array} \right. \\ \text {else} ~&V \ge 30 mV \left\{ \begin{array}{ll} v &{}\xleftarrow {} c \\ u &{}\xleftarrow {} u + d \end{array} \right. \\ \end{aligned} \end{aligned}$$

(8)

where v represents the membrane potential and u a membrane recovery variable, which accounts for ionic currents. The parameter a represents the recovery variable time scale, b represents the sub-threshold adaptation, c describes the after-spike polarisation, d the spike-triggered adaptation strenght, and $I_s(t)$ is the post synaptic current. $\eta$ is a Gaussian White Noise current of mean value 0 and standard deviation 10 pA. It stays constant for a duration of 5 times the simulation time step, then changes values etc... Miniature events are also set as a Poisson noise of rate 50 s$^{-1}$. We set the following values: $a = 0.02$, $b = 0.25$, $c = -65$ and $d = 8$.

Following previous work, (Orlandi et al., 2013; Levina et al., 2007) we consider dynamical synapses with the Tsodyks et al. (2000) model described by the following equations:

$$\begin{aligned} \begin{array}{lll} \dfrac{dx}{dt}&{}= \dfrac{z}{\tau _{rec}} - U x \delta (t - t_{spk}) \\ \dfrac{dy}{dt}&{}= -\dfrac{y}{\tau _{PSC}} + U x \delta (t - t_{spk}) \\ \dfrac{dz}{dt}&{}= \dfrac{y}{\tau _{PSC}} - \dfrac{z}{\tau _{rec}} \\ \end{array} \end{aligned}$$

(9)

where x, y and z are the fractions of synaptic ressources in a (respectively) recovered (ready), active, and inactive state ; $\tau _{rec}$ is the recovery time scale for synaptic depression and is set to 1.2 s and U determines the decrease of available ressources used by each presynaptic spike and is set to 0.2; $\tau _{PSC}$ is the post synaptic current time scale and is set to 10 ms. Facilitation has been taken away by setting $\tau _{facil} = 0$ms.

It results in a synaptic current for neuron i given by $I_i = \sum _{j}^{k_i} g_{ij} y_{ij}(t)$, where $g_{ij}$ is the absolute synaptic strength between i and j. The sum runs over all pre-synaptic neurons of i.

Figures 10 and 11 represent the overall analysis from the network phase maximum detection to the spatial representation of the activity with the neuron’s individual phase. The proposed methodology is here able to pinpoint that this model displays a different spatiotemporal dynamics, not seen with simulations of pacemaker neurons presented in the paper. The spike probability distribution does not display the hallmarks of first-to-fire specific dynamic. Since the global activity is high in between burst a co-activation structured in space as a propagation front can be created without specific initiation. Spatial initiation is still both localised, and structured into a propagation front.

Firing rate and first spike probability distribution

Fig. 12

Spike time probability density for two different time references. Right panels show the spike count rate of 4 consecutive bursts aligned on their maximum (bottom) and on an arbitrary 20 Hz threshold crossing time (top). Left panels show the probability distributions with the corresponding time reference. The simulations correspond to Noise Driven neurons, used in the paper in Fig. 5. One can observe that changing the time reference does not strongly change the distribution shape, however here, we cannot observe first to fire behavior anymore

In order to show that the maximum of the phase represents a specific point in the bursting dynamics, we look at a time reference computed with the spike count rate. This firing rate was computed with a convolution with an exponential kernel first (with temporal scale 3 ms), then gaussian kernel (with temporal standard deviation 3 ms). The resulting function was searched for maximum above a certain threshold to detect bursting events. This maximum and a 20 Hz threshold value was then used as time references to compute the first spike probability distribution. Figure 12 shows an example of firing rate and spike time probability distribution for the same simulations as in the paper (Fig. 5) with two time references. The burst definition presented in the paper is specifically designed to look at the spiking pattern during initiation. It gives a time reference related to the network state with information about previous and future spikes and not only spikes in a couple of milliseconds time window. Hence, this time reference stays coherent over consecutive burst in the spike time probability distribution. The arbitrariness in the firing rate threshold method cannot achieve such coherence.

Data and code

Data and code are available in the a github repository:MalloryDazza/NN_Burst_Dynamics.

Activity snapshots

The following figures shows snapshots of the in-burst activity pattern, displayed with neurons individual phases. They correspond to the examples used in the paper (see Figs. 13, 14, 15, and 16).

Fig. 13

Representation in space of the burst used for presenting the spatial cluster detection (Fig. 2) in the paper. Neurons’ phases are plot at the soma location. Each frame are separated by 22 milliseconds

Fig. 14

Representation in space of the burst used for performance computation (Fig. 5) in the paper (top activity). Neurons’ phases are plot at the soma location. Each frame are separated by 5 milliseconds

Fig. 15

Representation in space of the burst used for performance computation (Fig. 5) in the paper (bottom activity). Neurons’ phases are plot at the soma location. Each frame are separated by 4 milliseconds

Fig. 16

Representation in space of the burst used for velocity computation (Fig. 6) in the paper (left panel). Neurons’ phases are plot at the soma location. Each frame are separated by 12 milliseconds