Spike timing precision of neuronal circuits

Abstract

Spike timing is believed to be a key factor in sensory information encoding and computations performed by the neurons and neuronal circuits. However, the considerable noise and variability, arising from the inherently stochastic mechanisms that exist in the neurons and the synapses, degrade spike timing precision. Computational modeling can help decipher the mechanisms utilized by the neuronal circuits in order to regulate timing precision. In this paper, we utilize semi-analytical techniques, which were adapted from previously developed methods for electronic circuits, for the stochastic characterization of neuronal circuits. These techniques, which are orders of magnitude faster than traditional Monte Carlo type simulations, can be used to directly compute the spike timing jitter variance, power spectral densities, correlation functions, and other stochastic characterizations of neuronal circuit operation. We consider three distinct neuronal circuit motifs: Feedback inhibition, synaptic integration, and synaptic coupling. First, we show that both the spike timing precision and the energy efficiency of a spiking neuron are improved with feedback inhibition. We unveil the underlying mechanism through which this is achieved. Then, we demonstrate that a neuron can improve on the timing precision of its synaptic inputs, coming from multiple sources, via synaptic integration: The phase of the output spikes of the integrator neuron has the same variance as that of the sample average of the phases of its inputs. Finally, we reveal that weak synaptic coupling among neurons, in a fully connected network, enables them to behave like a single neuron with a larger membrane area, resulting in an improvement in the timing precision through cooperation.

1 Introduction

The neurons and the synapses exhibit considerable variability and noise due to the inherent stochastic behavior of the ion channels and the neurotransmitter release processes. This makes them noisy, unreliable analog devices that process electro-chemical signals (White et al. 2000; Faisal et al. 2008). On the other hand, neuronal circuits in the brain, composed of neurons interconnected via synapses, are extremely robust in processing sensory data and in performing the subsequent computations that are crucial for behavioral and cognitive functions (Sharpeshkar 2010; Lennie 2003; Attwell and Laughlin 2001; Tank and Hopfield 1987).

A sensory neuron transmits information to multiple neurons via its axon terminals. The sensory information is ultimately delivered to the cortical neurons and integrated via their dendrites. The spike timing precision of the neurons in the cerebral cortex receiving multiple synaptic inputs is a key factor for accurate sensory data encoding, especially for the auditory and visual systems (Mainen and Sejnowski 1995; VanRullen et al. 2005; Grothe and Klump 2000). Experimental studies have revealed that cortical neuronal circuits possess several mechanisms that enable them to modulate and improve their spike timing precision. For example, the results presented in Mainen and Sejnowski (1995) and Nowak et al. (1997) show that neocortical neurons generate spikes with better timing precision when they receive a fluctuating stimulus as opposed to an unnatural constant input. The spiking mechanism in neurons is naturally designed to respond more reliably to fluctuating inputs. Another phenomenon observed in Hasenstaub et al. (2005) and Bacci and Huguenard (2006) is that the timing reliability of neocortical spiking neurons is improved when they receive feedback inhibition via recurrent networks of local GABAergic (GABA-releasing) inhibitory neurons. Feedforward inhibition is another mechanism utilized in the cortex in order to enhance spike timing reliability of neurons (Isaacson and Scanziani 2011; Pouille and Scanziani 2001). However, the underlying mechanisms for these phenomena have not been completely deciphered yet.

The rhythmic spiking of neuronal circuits in the neocortex has been observed experimentally (Buzsáki and Draguhn 2004; Destexhe et al. 1998a). Neurons are synchronized with each other due to the synaptic inputs from the other neurons so that the neuronal circuit overall generates robust rhythmic oscillations. In Esfahani et al. (2016), the authors show that the synaptic coupling delay between the neurons plays a crucial role in the transition between the synchronous and asynchronous states of a neuronal circuit. The spike timing precision of the neurons may play an important role in the synchronization of the neuronal circuits that generate persistent rhythms in the brain, which has not been investigated yet.

Computational modeling and simulation is a powerful tool that can help us gain insight into the spike timing regulation mechanisms of neuronal circuits in the brain. A deep understanding and computational models can help in the investigation, diagnosis and treatment of nervous system diseases arising from the deficient control and modulation of spike timing precision. In our recent work (Kilinc and Demir 2015, 2017), we have developed a general modeling framework for biological neuronal circuits that systematically captures the nonstationary stochastic behavior of the ion channels and the synaptic processes. In this framework, fine-grained, discrete-state, continuous-time Markov Chain (MC) models of both ion channels and synaptic processes are employed in a unified manner. Our modeling framework can automatically generate the corresponding coarse-grained, continuous-state, continuous-time Stochastic Differential Equation (SDE) models. In the computational neuroscience literature, both MC and SDE models have been used only in Monte Carlo type stochastic simulations for noise analysis, where an ensemble of sample paths are generated by simulating the neuronal circuit many times. This makes Monte Carlo based simulation techniques computationally expensive. In Kilinc and Demir (2017), for the stochastic characterization of neuronal variability and noise, we have adapted and repurposed semi-analytical analysis techniques that work both in time and frequency domains, which were previously developed for analog electronic circuits. In these semi-analytical noise evaluation schemes, (differential) equations that directly govern probabilistic characterizations in the form of correlation functions (time domain) or spectral densities (frequency domain) are first derived analytically, starting from the SDEs that model the noisy dynamics of the system. However, these derived equations for the probabilistic characteristics still need to be solved numerically. This numerical computation directly produces the stochastic characterizations needed, without the use of random number generators, and without the need to compute ensemble averages or perform spectral estimation from time series data as in Monte Carlo techniques. Therefore, these semi-analytical methods are regarded as non Monte Carlo analysis techniques, which are orders of magnitude faster than Monte Carlo type simulations. In Kilinc and Demir (2017), we have verified that these semi-analytical noise analysis techniques correctly and accurately capture the second order statistics (mean, variance, autocorrelation, and power spectral density) of the underlying neuronal processes as compared with Monte Carlo simulations. In particular, the spike timing jitter of noisy, spiking neuronal circuits can be accurately characterized based on these semi-analytical methods (Kilinc and Demir 2017; Demir et al. 2000). Thus, we can avoid costly repeated and long duration simulations of neuronal circuits in a Monte Carlo manner. In this paper, we utilize these efficient and robust techniques in order to investigate the timing reliability of various neuronal circuit architectures.

The paper is organized as follows. In Section 2, we provide a brief background on neurons and neuronal circuits and summarize our general modeling framework, leading to the facilitation of the semi-analytical techniques. In Section 3, we present a review of the semi-analytical noise evaluation methods that are used for the computation of the timing jitter variance of spiking neuronal circuits. In Section 4, we consider a spiking neuron with feedback inhibition. We use the timing jitter variance of the neuron in order to quantify its spike timing precision. We quantitatively investigate the effect of feedback inhibition on the energy efficiency and the spike timing precision of a neuron. We elucidate the underlying mechanism through which feedback inhibition improves spike timing precision. In Section 5, we consider a neuron with multiple excitatory synaptic inputs coming from spiking neurons. We analyze the effect of the integration of multiple afferent synaptic inputs, originating from the same sensory source, on the timing precision of the output neuron. In Section 6, we consider fully connected neuronal circuits where neurons are coupled with each other via synapses. We investigate the effect of the excitatory and inhibitory synapses on the synchronization time and the timing precision of the neuronal circuit.

2 Stochastic modeling framework

In a neuronal circuit, information is represented by sequences of membrane potential spikes, i.e., action potentials, of neurons in various temporal patterns (Dayan and Abbott 2001). Ion channels located in the membrane of a neuron play a fundamental role in the generation and propagation of action potentials. More specifically, ion channels allow or inhibit the passage of ions through the membrane. This causes depolarization and repolarization of the membrane, which eventually enables the generation of an action potential. The potential difference across the membrane, V (t), satisfies the following current-balance equation

$$ C_{m}\frac{dV(t)}{dt}=-{\sum}_{i}G_{\text{ion},i}[V(t)-E_{\text{ion},i}] +I_{\text{ext}}(t) $$

(1)

where C _m is the membrane capacitance, G_ion,i and E_ion,i are the total conductance and the reversal potential of the collection of type i ion channels, respectively, and I_ext(t) is an externally applied current (Dayan and Abbott 2001). The total ion channel conductances are given by $G_{\text {ion},i}=g_{\text {ion},i}N^{O}_{\text {ion},i}$ where g_ion,i is the conductance of a single type i channel, and $N^{O}_{\text {ion},i}$ is the number of type i channels in the open state.

There are two main types of ion channels: Voltage-Gated (VG) and Ligand-Gated (LG), for which the opening and closure rates depend on the membrane potential and the concentration of the ligand molecules, respectively. The random behavior of the ion channels causes variability and noise in the ion channel conductance and hence the membrane voltage. Moreover, since membrane potential and molecule concentrations naturally vary with time in neuronal computing, the opening and closure rates of ion channels are also time-varying. The details of the kinetic models of the ion channels used in the analysis of neuronal circuits in this work are presented in the Appendix.

In order to describe and present the flow of the modeling framework, a simplified illustration of the neuronal interaction through a synapse is shown in Fig. 1a. Neurotransmitters are stored in the synaptic vesicles of the presynaptic neuron, and released into the synaptic cleft upon the arrival of an action potential. Subsequently, they are captured by the receptor sites of the LG ion channels located on the postsynaptic neuron. The schematic representation of these neuronal processes is given in Fig. 1b. The membrane potential of presynaptic and postsynaptic neurons are coupled with the dynamics of the VG ion channels. During the neurotransmitter release process in the synapse, a set of chemical reactions take place. These reactions are coupled with the dynamics of the LG ion channels. Finally, all of these are coupled with each other due to the synaptic connection between the two neurons.

Fig. 1

a A simplified illustration of presynaptic and postsynaptic neurons, VG and LG ion channels, synapse, and neurotransmitter release mechanism. b A schematic representation of the interactions between the neuronal circuit components shown in a. Figure adapted from Kilinc and Demir (2017)

Fairly general and accurate models that were proposed for capturing the stochastic behavior of ion channels are based on fine-grained, discrete-state, continuous-time, inhomogeneous MC models, where the states of the MC model directly correspond to the distinct forms of these special protein molecules (Dayan and Abbott 2001; Fitzhugh 1965; Fox and Lu 1994). The chemical processes that take place in the synaptic connections are also modeled by Markovian kinetic schemes (Destexhe et al. 1994). For the computation of the time-varying membrane voltages of the neurons in a neuronal circuit, the membrane current-balance equations, which are coupled with the MC models of ion channels and synapses, need to be solved (Kilinc and Demir 2017; Gillespie 2007; Higham 2008). In this modeling paradigm, the noise sources are captured in an implicit manner, since their dynamics are intertwined with the dynamics of the neuronal circuit. Therefore, it is necessary to use special Monte Carlo type stochastic simulation techniques involving random number generators, which can be computationally prohibitive for a neuronal circuit with a large number of neurons. In order to reduce the computational cost of the analysis, approximate models for the stochastic simulation of ion channels based on coarse-grained, continuous-state, continuous-time SDE models, i.e., Langevin equations, have been proposed (Kilinc and Demir 2017; Goldwyn et al. 2011; Linaro et al. 2011; Orio and Soudry 2012). A unified SDE model for neuronal circuits, with both ion channels and synaptic connections, can be constructed directly, in an automated manner, from the corresponding discrete-state MC and chemical reaction models (Kilinc and Demir 2017). Although both MC and SDE models have been used in Monte Carlo type stochastic simulations in the computational neuroscience literature, we exploit the special mathematical structure of the SDE formalism in order to enable semi-analytical stochastic characterizations of neuronal circuits (Kilinc and Demir 2017). These methods are reviewed in the next section.

3 Methods

With the semi-analytical (non Monte Carlo) techniques presented in Kilinc and Demir (2017), stochastic characterizations of neuronal circuits can be directly computed, without the need to generate a large ensemble of simulated sample paths for the membrane voltages. Even though these techniques still require carefully devised numerical computations, they do not require computationally expensive, repeated simulations using random number generators. A consistent, reproducible and detailed stochastic characterization of neuronal circuits can be obtained efficiently. In this paper, we utilize these semi-analytical methods in order to compute nonstationary stochastic characterizations, which are then processed and distilled in order to arrive at succinct conclusions regarding the timing precision of spiking neuronal circuits.

The unified SDE model for a neuronal circuit consists of the collection of the current-balance equations for the membranes of the neurons coupled with the system of Itô SDEs for the ion channels and the chemical reactions, as given below

$$ \begin{array}{llllllllll} &\frac{\partial}{\partial t}\mathbf{q}(\mathbf{v}(t),\mathbf{N}^{c}_{t}) + \mathbf{f}(\mathbf{v}(t),\mathbf{N}^{c}_{t}) + \mathbf{b}(t) = 0\\ &d\mathbf{N}^{c}_{t} = \boldsymbol{\mu}(\mathbf{v}(t),\mathbf{N}^{c}_{t})dt + \boldsymbol{\sigma}(\mathbf{v}(t),\mathbf{N}^{c}_{t})\;d\mathbf{W}_{t} \end{array} $$

(2)

where $\mathbf {v}\in \mathbb {R}^{M}$ is the vector of the membrane voltages of M neurons, the nonlinear vector functions q and $\mathbf {f}\in \mathbb {R}^{M}$ represent the charge storage (in the membrane capacitance) and the ion channel currents, respectively, $\mathbf {b}(t)\in \mathbb {R}^{M}$ captures any external stimulus applied to the neuronal circuit. That is, v(t) = [V₁(t),…,V _M (t)]^T and

$$ \begin{array}{llllllllll} &\mathbf{q}(\mathbf{v}(t),\mathbf{N}^{c}_{t})=\left[\begin{array}{llllllllll} C_{m,1}V_{1}(t)\\ \vdots\\ C_{m,M}V_{M}(t) \end{array}\right],\;\; \mathbf{b}(t)=\left[\begin{array}{llllllllll} I_{\text{ext},1}(t)\\ \vdots\\ I_{\text{ext},M}(t) \end{array}\right],\\[1ex] &\mathbf{f}(\mathbf{v}(t),\mathbf{N}^{c}_{t})=\left[\begin{array}{llllllllll} -{\sum}_{i}G_{\text{ion},i}[V_{1}(t)-E_{\text{ion},i,1}]\\ \vdots\\ -{\sum}_{i}G_{\text{ion},i}[V_{M}(t)-E_{\text{ion},i,M}] \end{array}\right], \end{array} $$

(3)

where the current balance equations of the neurons defined by Eq. (1) are concatenated. $\boldsymbol {\mu }(\mathbf {v}(t), \mathbf {N}^{c}_{t})$ and $\boldsymbol {\sigma }(\mathbf {v}(t),\mathbf {N}^{c}_{t})$ in Eq. (2) are the drift and diffusion parts of the system of SDEs, respectively, obtained from the MC models of the ion channels, as described in the Appendix and in Kilinc and Demir (2017). $\mathbf {N}^{c}_{t}\in \mathbb {R}^{P}$ represents the concatenated state vectors of the ion channels and the synaptic chemical reactions, where P is the total number of ion channel state variables and chemical species. The subscript t and the superscript c are used to signify that $\mathbf {N}^{c}_{t}$ is a continuous-time and continuous-state stochastic process, respectively. $\mathbf {W}_{t}\in \mathbb {R}^{T}$ is a vector of independent Wiener processes, where T is the total number of state transitions in the MC models of the ion channels and the synaptic chemical reactions. We note that both q and f depend on the state variable vector $\mathbf {N}^{c}_{t}$, since the conductances and hence other electrical characteristics of the neurons depend on the states of the ion channels and the concentration of the ligand molecules.

The combination of the two coupled equations in Eq. (2) as a single set of nonlinear SDEs is given by

$$ \frac{\partial}{\partial t}\mathcal{Q}(\mathbf{x}(t)) + \mathcal{F}(\mathbf{x}(t)) + \mathcal{B}(t) + \mathcal{D}(\mathbf{x}(t))\boldsymbol{\eta}_{t} = 0 $$

(4)

where $\mathbf {x}(t) = [\mathbf {v}(t),\;\; \mathbf {N}^{c}_{t}]^{\mathrm {T}}$, and $\mathcal {Q}, \mathcal {F}, \mathcal {B}\in \mathbb {R}^{M+P}$ and $\mathcal {D}\in \mathbb {R}^{(M+P)\times T}$ with entries given by

$$\begin{array}{@{}rcl@{}} \mathcal{Q}(\mathbf{x}(t)) \!&=& \left[\begin{array}{llllllllll} \mathbf{q}(\mathbf{v}(t),\mathbf{N}^{c}_{t})\\ {\kern16pt}\mathbf{N}^{c}_{t} \end{array}\right]\!, \;\; \mathcal{F}(\mathbf{x}(t)) = \left[\begin{array}{llllllllll} \mathbf{f}(\mathbf{v}(t),\mathbf{N}^{c}_{t})\\ -\boldsymbol{\mu}(\mathbf{v}(t),\mathbf{N}^{c}_{t}) \end{array}\right],\\ \mathcal{B}(t) &=& \left[\begin{array}{llllllllll} \mathbf{b}(t)\\ \mathbf{0}_{R} \end{array}\right], \;\; \mathcal{D}(\mathbf{x}(t)) = \left[\begin{array}{llllllllll} {\kern15pt}\mathbf{0}_{M\times T}\\ -\boldsymbol{\sigma}(\mathbf{v}(t),\mathbf{N}^{c}_{t}) \end{array}\right], \end{array} $$

(5)

and η _t is a column vector of T independent standard white Gaussian noise processes.

All of the neuronal circuit setups we consider in this paper spike periodically, i.e., possess periodic steady-state solutions. In order to represent spike timing jitter for the spiking neurons, we express the solution of Eq. (4) as (Demir et al. 2000)

$$ \mathbf{x}(t) = \mathbf{x}_{s}(t+\alpha(t)) + \mathbf{x}_{n}(t) $$

(6)

where x _s (t) is the periodic, deterministic neuronal circuit response. x _s (t) is the steady-state solution of the set of differential equations obtained by removing the diffusion (noise) part of the original SDE model in Eq. (4) as below

$$ \frac{\partial}{\partial t}\mathcal{Q}(\mathbf{x}_{s}(t)) + \mathcal{F}(\mathbf{x}_{s}(t)) + \mathcal{B}(t) = 0. $$

(7)

The noiseless x _s (t) is deterministic and it captures the mean but time-varying behavior of the membrane voltages, ion channels and the synapses. In Eq. (6), α(t) is the stochastic timing jitter (phase deviation) in x _s (t + α(t)), and x _n (t) represents the stochastic amplitude deviation added to x _s (t + α(t)), both arising from noise. Since x _s (t) is periodic with a period T _c , it defines a limit cycle (a closed orbit that is parametrized by t) in the state-space of the neuronal variables. x _s (t + α(t)) traces exactly the same limit cycle (orbit) that corresponds to x _s (t), but with a random time deviation. On the other hand, x _n (t) represents an orbital deviation, i.e., an additive noise component. That is, the trajectory traced by x _s (t + α(t)) + x _n (t) (in the state-space of the neuronal variables) deviates from the limit cycle defined by x _s (t) or x _s (t + α(t)), due to the additive noise component x _n (t) (Demir et al. 2000). To sum up, α(t) represents the timing noise or timing jitter for a spiking neuronal circuit, whereas, x _n (t) captures the additive amplitude noise in the neuronal circuit response. The decomposition of the noisy neuronal circuit variable into the time-shifted x _s (t + α(t)) and the additive x _n (t) is performed in such a way so that x _n (t) stays small and bounded, whereas the time deviation α(t) may grow large (Demir et al. 2000), to values possibly exceeding the spiking period T _c .

Autonomously oscillating systems, that determine their own rhythm based on their internal dynamics, posses a timing noise α(t) that freely diffuses due to lack of a perfect timing reference. This behavior is unlike that of systems that are forced to oscillate at a frequency imposed by an external periodic stimulus. Thus, the variance of α(t), in general, increases with time even if the noise sources, η _t , in Eq. (4) are always small. On the other hand, the orbital deviation x _n (t) remains small as compared to x _s (t + α(t)). In Demir et al. (2000), the stochastic characterization of the timing jitter (noise) α(t) was rigorously derived. It was shown that, asymptotically with time, α(t) becomes a Gaussian random process with zero-mean and a variance given by Var[α(t)] = E[α(t)²] = c _{s s} t. The asymptotic (steady-state) slope of the timing jitter variance is constant and represented by c _{s s} . It is important to note that α(t) represents the total accumulated timing noise of the noisy output x _s (t + α(t)) at time t with respect to the noiseless output x _s (t). That is, Var[α(kT _c )] is the timing jitter variance of the k th spike, where T _c is the spiking period, with respect to a trigger (reference) set at the first spike. On the other hand, spike-to-spike accumulated jitter (for the timing of the k + 1th spike, with the trigger set at the previous k th spike) is constant and given by c _{s s} T _c , that is, it is independent of k. Therefore, the slope of the timing jitter variance c _{s s} and the spiking period T _c are two important parameters that can be used to characterize the timing precision of a spiking neuronal circuit. The period T _c and the noiseless response x _s (t) for an autonomously oscillating neuronal circuit can be computed by finding the periodic steady-state solution of Eq. (7) via well-established numerical methods, e.g., time-domain shooting methods and frequency-domain Fourier spectral collocation based methods (Kundert et al. 1990). Then, the asymptotic timing jitter variance slope c _{s s} can be directly computed based on a specialized perturbation analysis. On the other hand, the time it takes for the timing jitter variance to settle to its asymptotic linear form, i.e., Var[α(t)] = c _{s s} t, is also an important parameter in characterizing the timing noise performance of oscillatory systems. We next review both a direct (steady-state) technique (Demir et al. 2000) that produces the asymptotic timing jitter variance slope, as well as a transient, time-domain technique (Demir and Sangiovanni-Vincentelli 1998) which enables also the computation of the settling time.

In order to formulate the perturbation analysis for noise, we linearize (4) around x _s (t) to obtain

$$ \frac{d}{dt}(\mathbf{C}(t)\mathbf{x}_{n}(t)) + \mathbf{G}(t)\mathbf{x}_{n}(t) + \mathbf{H}(t)\boldsymbol{\eta}_{t} = 0 $$

(8)

where $\mathbf {H}(t) = \mathcal {D}(\mathbf {x}_{s}(t))$ and the Jacobian matrices $\mathbf {C}, \mathbf {G}, \in \mathbb {R}^{(M+P)\times (M+P)}$ have the block forms given by

$$\begin{array}{@{}rcl@{}} \mathbf{C}(t) &=& \frac{\partial}{\partial \mathbf{x}}\mathcal{Q}(\mathbf{x}) \rvert_{\mathbf{x}\vphantom{\frac{1}{2}} = \mathbf{x}_{s}(t)} = \left[\begin{array}{llllllllll} \frac{\partial\mathbf{q}}{\partial \mathbf{v}}&\frac{\partial\mathbf{q}}{\partial \mathbf{N}^{c}_{t}}\\ \mathbf{0}_{P\times M}&\mathbf{I}_{P} \end{array}\right]_{\mathbf{x} = \mathbf{x}_{s}(t)},\\ \mathbf{G}(t) &=& \frac{\partial}{\partial \mathbf{x}}\mathcal{F}(\mathbf{x}) \rvert_{\mathbf{x} \vphantom{\frac{1}{2}}= \mathbf{x}_{s}(t)} = \left[\begin{array}{llllllllll} \;\frac{\partial\mathbf{f}}{\partial \mathbf{v}}\;\;\;\; &\frac{\partial\mathbf{f}}{\partial \mathbf{N}^{c}_{t}}\\ -\frac{\partial\boldsymbol{\mu}}{\partial \mathbf{v}}\;\;\;\; &-\frac{\partial\boldsymbol{\mu}}{\partial \mathbf{N}^{c}_{t}} \end{array}\right]_{\mathbf{x} = \mathbf{x}_{s}(t)},\\ \end{array} $$

(9)

where 0_P×M is the P × M matrix with all zero entries and I _P is the P × P identity matrix. Equation (8) is a system of linear (but with time-varying coefficients) SDEs. As a result, in this perturbation analysis, the computation of the “noiseless” solution x _s (t) via (7) and the characterization of noise x _n (t) via (8) are separated. However, x _s (t) needs to be computed first, or concurrently with x _n (t), since the Jacobian and the diffusion matrices in Eq. (8) depend on it.

The transient, time-domain analysis technique (Demir and Sangiovanni-Vincentelli 1998) to be outlined next is not restricted to neuronal circuits operating in some sort of steady-state (e.g., tonic firing). It can be applied in more general time-varying scenarios, e.g., for transient bursting conditions. In this technique, differential equations for the auto- and cross-correlation functions of the noisy neuronal circuit are first derived analytically and then solved with specialized numerical methods. More specifically, the solution of the system of linear SDEs in Eq. (8), i.e., x _n (t), is known as a multivariate Ornstein-Uhlenbeck process, which in fact is a nonstationary, multivariate Gaussian process (Demir and Sangiovanni-Vincentelli 1998; Gardiner 1983). Since x _n (t) is Gaussian, it can be completely characterized by its mean and correlation function. The mean of x _n (t) is given by E[x _n (t)] = 0. The correlation matrix of the components of x _n (t) as a function of t is defined by

$$ \mathbf{K}(t) = \mathrm{E}[\mathbf{x}_{n}(t)\mathbf{x}_{n}(t)^{\mathrm{T}}] $$

(10)

where $\mathbf {K}\in \mathbb {R}^{(M+P)\times (M+P)}$. In Demir and Sangiovanni-Vincentelli (1998), it was shown that K(t) satisfies the following system of ODEs

$$ \frac{d}{dt}\mathbf{K}(t) = \mathbf{E}(t)\mathbf{K}(t) + \mathbf{K}(t)\mathbf{E}(t)^{\mathrm{T}} + \mathbf{F}(t)\mathbf{F}(t)^{\mathrm{T}} $$

(11)

where

$$\begin{array}{@{}rcl@{}} &&\mathbf{E}(t) = -\mathbf{C}(t)^{-1}\left[\frac{d}{dt}\mathbf{C}(t) + \mathbf{G}(t)\right] \\ &&\mathbf{F}(t) = -\mathbf{C}(t)^{-1}\mathbf{H}(t). \end{array} $$

(12)

E(t) and F(t) are computed by using x _s (t), which is the solution of Eq. (7). Equation (11) is known as the differential Lyapunov matrix equation (Gajic and Qureshi 2008). In order to compute K(t), we solve (11) by using a specialized numerical method (Subrahmanyam 1986). K(t) represents the noise correlation matrix of the neuronal circuit variables as a function of time. The time-varying noise variances of the neuronal circuit variables, or the noise correlations between these variables at a given time point are captured by K(t). The spike timing jitter variance of noisy neurons at spike times kT _c (coinciding with the rising or falling edge of the k th action potential where the slope is the highest) can be directly computed by

$$ \text{Var}[\alpha(k T_{c})] = \cfrac{\mathbf{K}_{ii}(k T_{c})}{\left.\left( \cfrac{d\mathbf{x}_{s,i}(t)}{dt}\right)^{2}\right|_{t=k T_{c}}} $$

(13)

as discussed in Demir and Sangiovanni-Vincentelli (1998), where i selects the membrane voltage of one of the spiking neurons in the circuit. It was shown in Demir and Sangiovanni-Vincentelli (1998) that Var[α(kT _c )] is the same for all of the neurons in the circuit if they oscillate in a locked manner. By computing Var[α(kT _c )] via (11) and (13), one can reveal its transient behavior before and as it settles to the asymptotic linear form given by Var[α(kT _c )] = c _{s s} kT _c .

The steady-state method, to be reviewed next, can be used for neuronal circuits that are in periodic steady-state operation, e.g., for tonic firing conditions (Kilinc and Demir 2017; Demir et al. 2000; Mahmutoglu and Demir 2014). In this case, the slope c _{s s} of the asymptotic form of the timing jitter variance, i.e., Var[α(t)] = c _{s s} t, can be computed directly with a very efficient numerical technique. It was shown in Demir et al. (2000) that

$$ c_{ss}=\frac{1}{T_{c}}{\int}_{0}^{T_{c}} \mathbf{v}^{\mathrm{T}}(\tau)\mathbf{H}(\tau)\mathbf{H}^{\mathrm{T}}(\tau)\mathbf{v}(\tau)d\tau $$

(14)

where v(t) is the periodic steady-state solution of the so-called adjoint equation given below

$$ \mathbf{C}^{\mathrm{T}}(t)\frac{d}{dt} \mathbf{v}(t) - \mathbf{G}^{\mathrm{T}}(t)\mathbf{v}(\tau) = 0 $$

(15)

with the following normalization condition

$$ \mathbf{v}^{\mathrm{T}}(t)\:\mathbf{C}^{\mathrm{T}}(t)\: \frac{d}{dt}\mathbf{x}_{s}(t) = 1 $$

(16)

v(t) and the integral in Eq. (14) can be computed with efficient numerical techniques (Demir 2000; Demir and Roychowdhury 2003). v(t) is known as the Perturbation Projection Vector (PPV) (Demir and Roychowdhury 2003), entries of which are the infinitesimal Phase Response Curves (PRCs) (Izhikevich 2007). Phase models for oscillators have been studied extensively in several disciplines, such as electronics (Demir et al. 2000), mathematical biology (Winfree 2001) and neuroscience (Brown et al. 2004; Izhikevich 2007). A review on the topic, encompassing several disciplines, can be found in Demir et al. (2010) and Suvak and Demir (2011).

In this paper, we use the semi-analytical noise analysis techniques outlined above, via our unified modeling framework, in order to investigate the timing reliability of various neuronal circuit structures. We have verified and confirmed all of the results presented in this paper, that were obtained with the semi-analytical techniques described above, against straightforward Monte Carlo simulations of the SDEs of the neuronal circuits. However, we do not further discuss the verification of our semi-analytical, non Monte Carlo methods in this paper, which has already been carried out in detail in Kilinc and Demir (2017). A summary of the results presented in our recent previous work (Kilinc and Demir 2017), and the new results we obtain in this paper, is given in Table 1. In the subsequent sections, we discuss the details of these findings. The numerical simulation files are available for public download under the ModelDB section (with accession number 239146) of the Senselab database (http://senselab.med.yale.edu).

Table 1 Summary of the results obtained for various neuronal circuit architectures

4 Feedback inhibition

Experimental findings suggest that the timing precision of the firing of neurons is an important factor in accurate sensory information representation, especially for the auditory and visual systems (Mainen and Sejnowski 1995; VanRullen et al. 2005; Grothe and Klump 2000). It has been observed experimentally that the timing reliability of spiking neurons is improved when they receive feedback inhibition (Hasenstaub et al. 2005; Bacci and Huguenard 2006). In the literature, there are numerous experimental studies investigating feedback inhibition from this perspective (Deleuze et al. 2014; Isaacson and Scanziani 2011). However, the underlying mechanisms have not been completely unveiled yet. We investigate this phenomenon from a computational modeling and simulation perspective based on the framework summarized in Section 2, via the methods presented in Section 3.

4.1 Spike timing precision vs feedback inhibition

We use the setup shown in Fig. 2 in order to investigate the effects of feedback inhibition on the spike timing precision and try to gain some insight into the underlying mechanism. A constant suprathreshold current stimulus is injected into neuron $\mathcal {N}_{1}$. In this case, the neuron $\mathcal {N}_{1}$ is oscillating, i.e., it is under tonic spiking conditions. The neurons $\mathcal {N}_{1}$ and $\mathcal {N}_{2}$ are connected via synapses, where filled and empty circles represent excitatory and inhibitory synapses, respectively. More specifically, $\mathcal {N}_{1}$ makes an excitatory synapse on $\mathcal {N}_{2}$, whereas $\mathcal {N}_{2}$ makes an inhibitory synapse on $\mathcal {N}_{1}$. Therefore, each spike generated by $\mathcal {N}_{1}$ initiates another spike in the membrane of $\mathcal {N}_{2}$, which eventually inhibits $\mathcal {N}_{1}$. This constitutes feedback inhibition for $\mathcal {N}_{1}$.

Fig. 2

Feedback inhibition of neuron $\mathcal {N}_{1}$ by neuron $\mathcal {N}_{2}$. Neuron $\mathcal {N}_{1}$ is under tonic spiking conditions with a constant, suprathreshold current stimulus

Fig. 3

a 20 sample paths, generated for the membrane voltage of neuron $\mathcal {N}_{1}$ in Fig. 2, are drawn on top of each other. The timing jitters α(T _c ) and α(2T _c ) are indicated for the first two output action potentials, where increasing timing jitter variance can be easily observed. b The timing jitter variance of the output spikes of neuron $\mathcal {N}_{1}$ in Fig. 2. The amplitude of the external suprathreshold current input to neuron $\mathcal {N}_{1}$ is held constant at I_ext = 0.25 A/m². The membrane area of each neuron in Fig. 2 is fixed at $A_{m}= 1000 \mu \textit {m}^{2}$. The numbers of receptor ion channels in the synapses between $\mathcal {N}_{1}$ and $\mathcal {N}_{2}$ are N_ext = 3 × 10⁴ excitatory AMPA/kainate receptor channels (in $\mathcal {N}_{2}$) and N_inh = 1 × 10⁴ inhibitory GABA _A receptor channels (in $\mathcal {N}_{1}$). The timing jitter variance increases linearly with time as expected

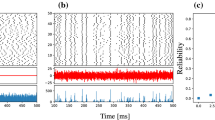
The phase fluctuations with an increasing variance can be easily observed in Fig. 3a, where only 20 membrane voltage waveforms (for neuron $\mathcal {N}_{1}$) generated by Monte Carlo simulations are plotted on top of each other. At steady-state, the timing jitter variance evaluated at each multiple of the oscillation period T _c is given by Var[α(kT _c )] = c _{s s} kT _c . If we normalize Var[α(kT _c )] with kT _c , we get the slope c _{s s} , which is the accumulation rate of the timing jitter variance. We use the timing jitter variance slope c _{s s} of a spiking neuron to quantify its spike timing precision. Hence, we can compare the timing precision performance of spiking neurons with different spiking periods at the end of a given duration.

For the analysis in this section, the amplitude of the external suprathreshold current input to neuron $\mathcal {N}_{1}$ is held constant at I_ext = 0.25 A/m². The membrane area of each neuron is fixed at A _m = 1000μm² with the VG ion channel densities equal to 60 Na⁺ channels/μm² and 18 K⁺ channels/μm². The number of the excitatory receptor ion channels in the synapse between $\mathcal {N}_{1}$ and (on) $\mathcal {N}_{2}$ is also kept constant at 3 × 10⁴ AMPA/kainate receptor channels. In Fig. 3b, the timing jitter variance, Var[α(t)], for N_inh = 1 × 10⁴ inhibitory GABA _A receptor ion channels (for the synapse from $\mathcal {N}_{2}$ to $\mathcal {N}_{1}$), is shown. For each point in Fig. 3b, the timing jitter variance at a multiple of the oscillation period T _c , i.e., Var[α(kT _c )], was computed using the transient semi-analytical method reviewed in Section 3. The timing jitter variance increases linearly with time as expected, without any transient settling behavior in this case.

In order to asses the effect of the inhibitory feedback synapse, the number of the inhibitory GABA _A receptor ion channels N_inh in the membrane of $\mathcal {N}_{1}$ is varied. For each value of N_inh, the asymptotic timing jitter variance slope of the neuronal circuit in Fig. 2 is computed via the steady-state semi-analytical method reviewed in Section 3. The results in Fig. 4a show that as the feedback inhibition strength is increased, the timing jitter variance decreases. These results are consistent with experimental findings which have shown that the spike timing precision of neurons is improved when they receive feedback inhibition (Bacci and Huguenard 2006). In addition, an increase in the feedback inhibition strength results in an increase in the spiking period, as shown in Fig. 4b. This behavior suggests that feedback inhibition prolongs the refractory period of neuron $\mathcal {N}_{1}$.

Fig. 4

a The timing jitter variance slope, b the spiking period, and c the spike timing information content of the output action potentials of neuron $\mathcal {N}_{1}$ in Fig. 2 with respect to the number of the inhibitory synaptic channels (in $\mathcal {N}_{1}$) for I_ext = 0.25 A/m$^{2}, A_{m}= 1000 \mu \textit {m}^{2}$, and N_ext = 3 × 10⁴ AMPA/kainate receptor channels (in $\mathcal {N}_{2}$)

In order to more clearly elucidate the spike timing precision improvement brought about by feedback inhibition, we consider the amount of information that can be coded by the timing of a spike. Given the timing of the k th spike, the timing of the (k + 1)th spike is a Gaussian random variable with a variance of c _{s s} T _c , which indicates an uncertainty in the timing of the (k + 1)th spike. Due to this uncertainty, the amount of information that can be encoded by the timing of the (k + 1)th spike within one oscillation period T _c is limited. More precisely, the timing of the (k + 1)th spike within one period T _c cannot be determined with a resolution that is better (less) than the standard deviation of timing jitter, i.e., $\sqrt {c_{ss}T_{c}}$. The information encoded by the spike can be reliably decoded only when the timing needs to be resolved within $\sqrt {c_{ss}T_{c}}$. If the amount of information encoded dictates a finer resolution requirement for reliable detection, then the information may be lost as a result of the uncertainty due to timing jitter. Thus, the count of possible timing intervals that can be resolved and used to encode information by the (k + 1)th spike is limited and given by

$$ \mathcal{L}_{\text{spike}} = \frac{T_{c}}{ \sqrt{c_{ss}\,T_{c}}} = \sqrt{\frac{T_{c}}{c_{ss}}}. $$

(17)

The information content, $\mathcal {I}_{\text {spike}}$, per spike measured as the number of binary bits that can be represented by the timing of the spike is then given by

$$ \mathcal{I}_{\text{spike}} = \log_{2}\left( \mathcal{L}_{\text{spike}}\right) = \frac{1}{2}\log_{2}{\left( \frac{T_{c}}{c_{ss}}\right)}, $$

(18)

where T _c /c _{s s} can be considered as the signal-to-noise ratio (SNR). In particular, as T _c is increased or c _{s s} is decreased, the SNR increases, which results in an increase in the spike timing information content. The information content for the two-neuron circuit in Fig. 2 is shown in Fig. 1a as a function of the number of inhibitory synaptic channels (in neuron $\mathcal {N}_{1}$), which indicates that feedback inhibition improves the information content that can be encoded in the spike timings.

The justification and basis for the discussion and derivation above originate in well established concepts and results in information theory. The information content relation in Eq. (18) is very similar to the information capacity of an additive white Gaussian communication channel (Cover and Thomas 2012).

With zero jitter, the spikes are separated from each other with exactly T _c . In this case, other than being a perfect time reference, the spike timings do not indeed contain any information. This may suggest that it would be better if the spike timings were completely randomized from an information content point of view. However, this situation will change when the frequency/period of spiking is modulated, for instance, with signals from sensory receptors. In this case, the spike timings will not be separated from each other with a fixed T _c , but with a time-varying T _c (t) that encodes sensory information. Then, lower jitter in spike timings will allow the detection and determination of the spike timings with a higher resolution, resulting in a higher information content that can be encoded in the timings.

4.2 Spike timing precision vs synaptic channel noise

The results above on feedback inhibition were obtained with SDE models of the ion channels and the synapses. The noise (diffusion) part of these SDE models depend on the noiseless mean (drift) component. The diffusion parts were not added to the model in a phenomenological manner. Their form is directly linked to the noiseless drift component and are both derived from the Markovian models of the ion channels (Kilinc and Demir 2017). Thus, with an SDE model, when the number of the synaptic LG channels is varied, both the mean synaptic current and also the synaptic channel noise levels change. This is indeed what happens in a real neuron. In order to dig deeper into this, we observe that the noise, relative to the mean, contributed by the synaptic channels decreases with increasing number of LG receptor channels. This is so because the drift (mean) component of the SDE that governs channel behavior is proportional to the number of channels, whereas the diffusion (noise) component is proportional to the square root of the number of channels. Then, the following question may arise: Is the spike timing precision improvement observed with increasing number of feedback inhibitory synaptic channels due to (i) increased mean inhibitory feedback current, i.e., stronger feedback inhibition, or (ii) reduced synaptic current noise relative to the mean? In order to shed light onto this matter, we need to separately analyze the effects of the mean and noise of the synaptic current. For this, we keep the mean inhibitory synaptic current entering into neuron $\mathcal {N}_{1}$ fixed by keeping the total maximal receptor channel conductance constant, given by the product $N_{\text {inh}}\cdot g_{\text {GABA}_{A}}$, where $g_{\text {GABA}_{A}}$ is the conductance of a single inhibitory GABA _A receptor channel. That is, as N_inh is varied, we also vary $g_{\text {GABA}_{A}}$ accordingly in order to keep their product constant. Although doing this does not have a physiological basis, it can help answer the question posed above. When the number of inhibitory synaptic channels is increased in this setup, the noise contributed by the synaptic channels decreases while the mean synaptic current is held constant. This is so because while both the drift and diffusion components of the SDE that governs the synaptic current are proportional to $g_{\text {GABA}_{A}}$, the drift part is proportional to N_inh and the diffusion part is proportional to $\sqrt {N_{\text {inh}}}$.

In Fig. 5, the timing jitter variance slope of the output action potentials of neuron $\mathcal {N}_{1}$ in Fig. 2 for constant mean synaptic current (i.e., for constant $N_{\text {inh}}\cdot ~g_{\text {GABA}_{A}}= 2\times 10^{5}$ pS) is shown with red dashed curve (square markers) for varying values of N_inh (on lower x-axis) and $g_{\text {GABA}_{A}}$ (on upper x-axis). The curve in Fig. 4a is also included in Fig. 5 with a blue solid curve (circle markers), which shows the timing jitter variance slope of the output action potentials of neuron $\mathcal {N}_{1}$ for constant $g_{\text {GABA}_{A}}= 20$ pS with respect to the number of the inhibitory synaptic channels (in $\mathcal {N}_{1}$) (on lower x-axis).

Fig. 5

The timing jitter variance slope of the output action potentials of neuron $\mathcal {N}_{1}$ in Fig. 2 for constant $\protect N_{\text {inh}}\cdot ~g_{\text {GABA}_{A}}= 2\times 10^{5}$ pS is plotted with red dashed curve (square markers) with respect to the number of the inhibitory synaptic channels (in $\mathcal {N}_{1}$) on the lower x-axis and the conductance of a single inhibitory synaptic channel (in $\mathcal {N}_{1}$) on the upper x-axis. The blue solid curve (circle markers) is the same curve as the one in Fig. 4a, which shows the timing jitter variance slope of the output action potentials of neuron $\mathcal {N}_{1}$ for constant $\protect g_{\text {GABA}_{A}}= 20$ pS with respect to the number of the inhibitory synaptic channels (in $\mathcal {N}_{1}$) on the lower x-axis. For both cases, the amplitude of the external suprathreshold current input to neuron $\mathcal {N}_{1}$ is I_ext = 0.25 A/m², the membrane area of each neuron is $A_{m}= 1000 \mu \textit {m}^{2}$, and the number of excitatory AMPA/kainate receptor channels is N_ext = 3 × 10⁴ channels (in $\mathcal {N}_{2}$). The product $\protect N_{\text {inh}}\cdot ~g_{\text {GABA}_{A}}$ is kept constant at each point of the red dashed curve (square markers). Thus, as the number of inhibitory synaptic channels is increased, although the mean inhibitory synaptic current does not change, the inhibitory synaptic current noise decreases. As the noise level decreases, the timing jitter variance first decreases and then becomes constant. On the other hand, for the blue solid curve (circle markers), as the number of inhibitory synaptic channels is increased, the mean inhibitory synaptic current increases and the noise relative to the mean current decreases. In this case, the timing jitter variance monotonically decreases with increasing number of inhibitory synaptic channels

As the number of inhibitory synaptic LG channels is increased while the mean inhibitory synaptic current is held constant as discussed above, the channel noise of these inhibitory LG channels decreases and eventually becomes negligible compared with the channel noise of the VG ion channels in neuron $\mathcal {N}_{1}$. Since the number of VG ion channels, as well as the mean inhibitory current, is constant in this scenario, the contribution of the VG channels to noise and timing jitter does not change. Thus, as the number of inhibitory synaptic channels is increased, the timing jitter variance of neuron $\mathcal {N}_{1}$ first decreases due to the reduction in LG channel noise, but then becomes constant mainly arising from VG channel noise. This behavior can be clearly observed on the red dashed curve (square markers) in Fig. 5. On the other hand, as the number of inhibitory synaptic LG channels is reduced while the mean inhibitory synaptic current is held constant, the channel noise of the inhibitory LG ion channels becomes more prominent and eventually becomes comparable to the noise of the VG ion channels in neuron $\mathcal {N}_{1}$. Hence, the increase in LG channel noise results in an increased timing jitter variance.

Table 2 Spike timing precision and energy consumption analysis of neuronal circuits with and without feedback inhibition

Table 3 Spike timing precision and energy consumption analysis of neuronal circuits with feedback inhibition

In Fig. 5, the two curves intersect at the point where $g_{\text {GABA}_{A}}$ is set to its nominal value of 20 pS with N_inh = 10⁴ for the red dashed curve (square markers) with constant $N_{\text {inh}}\cdot ~g_{\text {GABA}_{A}}$, i.e., with constant mean inhibitory synaptic current. The points on the blue solid curve (circle markers) with constant $g_{\text {GABA}_{A}}= 20$ pS correspond to larger mean inhibitory synaptic currents compared with the points on red dashed curve (square markers) for $g_{\text {GABA}_{A}}<20$ pS, i.e., to the right of the intersection point, with the difference increasing as one moves further right from the intersection point. Furthermore, for both curves, the inhibitory synaptic channel noise relative to the mean synaptic current decreases with increasing N_inh. In particular, for N_inh > 10⁵, the noise of the inhibitory LG channels is negligible in both scenarios. That is why, the curve with constant mean inhibitory synaptic current (red dashed curve, square markers) is flat. However, in the case with constant $g_{\text {GABA}_{A}}$ (blue solid curve, circle markers), the timing jitter is further reduced with increasing mean synaptic current for N_inh > 10⁵, where the dominant noise sources are the VG ion channels whose count is held constant. This shows that the improvement of timing precision with increased inhibitory synaptic strength (and hence with stronger feedback inhibition) can not be attributed to only the reduction of the relative synaptic noise due to larger number of synaptic channels. Thus, the answer to the question posed above is as follows: The spike timing precision improvement observed with increasing number of feedback inhibitory synaptic channels is due to a combined effect of both stronger feedback inhibition and also reduced synaptic current noise relative to the mean.

The behavior to the left of the intersection point in Fig. 5 also requires a comment. For N_inh < 5 × 10³, the noise of the inhibitory LG channels dominates when compared with the noise from the VG channels. This results in worse spike timing precision in both cases. On the other hand, for the curve with constant $\protect N_{\text {inh}}\cdot ~g_{\text {GABA}_{A}}$ (red dashed curve, square markers), LG channel noise level is even higher due to larger $g_{\text {GABA}_{A}}$ values as N_inh is further reduced. This results in worse timing precision when compared with the case (blue solid curve, circle markers) with constant $g_{\text {GABA}_{A}}$, even though the mean synaptic current is higher in the former.

4.3 Energy consumption vs feedback inhibition

We consider the current balance equation of the neuron membrane in Eq. (1) for the energy consumption analysis. The power, i.e., energy consumption rate, of a neuron due to the ion currents passing through its membrane and the power supplied by an external stimulus are given by

$$ \begin{array}{llllllllll} P_{\text{ion}}(t)&={\sum}_{i}G_{\text{ion},i}[V(t)-E_{\text{ion},i}]^{2},\\ P_{\text{ext}}(t)&= V(t)I_{\text{ext}}(t). \end{array} $$

(19)

The energy consumption for an action potential can be computed by integrating P_ion(t) and P_ext(t) over the duration of the action potential (Moujahid et al. 2011). In neurons, energy is consumed by ion pumps, which are transmembrane proteins. Ion pumps expel ions through the membrane against their concentration gradient by consuming energy in the form of adenosine triphosphate (ATP) molecules (Dayan and Abbott 2001). Hence, ion pumps play a fundamental role in keeping the ion concentration difference between the inside and the outside of the neuron at a certain value so that the neuron can maintain its activity after an action potential. The ion concentration differences maintained by the ion pumps are captured by the constant reversal potentials E_ion,i in Eq. (1), as voltage sources connected in series to the ion channel conductances. The total energy consumed in order for a neuronal circuit to spike is computed as the sum of the energy consumed by the ion pumps and the energy supplied by the external current injection. We compute the average energy consumed by a neuronal circuit in generating an action potential, denoted by E_AP, by averaging over 100 action potential cycles.

In order to assess the effect of feedback inhibition from a timing jitter and energy consumption perspective, we consider a standalone neuron excited by a constant suprathreshold current stimulus, I_ext, and compare its jitter, c _{s s} , and energy consumption, E_AP, to that of the neuronal circuit with feedback inhibition in Fig. 2. We set the parameters of the standalone neuron circuit in such a way so that its firing frequency, f _c = 1/T _c , is the same as that of the one with feedback inhibition. If the standalone neuron has the same energy consumption per spike (timing jitter variance slope) as that of the neuronal circuit with feedback inhibition, its timing jitter variance slope (energy consumption) is roughly twice the one obtained for the neuronal circuit with feedback inhibition. Thus, feedback inhibition of a spiking neuron improves its energy efficiency for a given spike timing precision, or alternatively, feedback inhibition yields better spike timing precision for a given energy consumption, as summarized and quantified in Table 2.

Fig. 6

Feedback inhibition of neuron $\mathcal {N}_{1}$ by neuron $\mathcal {N}_{2}$. Neuron $\mathcal {N}_{1}$ is stimulated by a single suprathreshold current pulse with a duration of 2 msec

We next consider the neuron with feedback inhibition in Fig. 2 with a larger inhibition strength, obtained by increasing the number of the inhibitory GABA _A receptor ion channels (in $\mathcal {N}_{1}$) tenfold, and compare its performance to the case with weaker feedback inhibition. We again make sure that the firing frequencies of the two cases are the same by choosing the relevant parameters appropriately. If the energy consumption (timing jitter variance slope) of the high inhibition strength case is the same as that of the low inhibition case, its timing jitter variance slope (energy consumption) is approximately 3.5 times better. Thus, as the strength of feedback inhibition is enhanced, both the timing precision and the energy efficiency of the neuronal circuit are improved, as summarized and quantified in Table 3.

4.4 Membrane voltage variance vs feedback inhibition

We next analyze the transient dynamics of feedback inhibition. We use the same setup described above. However, in this case, at t = 10 msec, a transient suprathreshold current stimulus with an amplitude I_ext = 0.25 A/m² and a duration of 2 msec is injected into neuron $\mathcal {N}_{1}$, as opposed to a constant current stimulus. The updated setup is shown in Fig. 6. With the transient stimulus applied to $\mathcal {N}_{1}$, a single action potential is generated in its membrane, which initiates another action potential in the membrane of $\mathcal {N}_{2}$ as shown in Fig. 7a. We compute the membrane voltage variance of $\mathcal {N}_{1}$ via the transient semi-analytical method summarized in Section 3. In our previous work (Kilinc and Demir 2017), we have shown that the second order stochastic characterization of neuronal circuits can be accurately computed by using this technique.

Fig. 7

a The mean membrane voltages of the neurons $\mathcal {N}_{1}$ and $\mathcal {N}_{2}$ shown in Fig. 6, where $\mathcal {N}_{1}$ (with membrane area $A_{m}= 1000 \mu \textit {m}^{2}$) is stimulated by a single suprathreshold current pulse with an amplitude I_ext = 0.25 A/m² and a duration of 2 msec. The numbers of the receptor ion channels in the synapses between $\mathcal {N}_{1}$ and $\mathcal {N}_{2}$ are N_ext = 3 × 10⁴ excitatory AMPA/kainate receptor channels (in $\mathcal {N}_{2}$), and N_inh = 2 × 10⁴ inhibitory GABA _A receptor channels (in $\mathcal {N}_{1}$). b The variance of the membrane voltage of neuron $\mathcal {N}_{1}$ shown in Fig. 6 evaluated for varying number of inhibitory synaptic channels N_inh (in $\mathcal {N}_{1}$). Feedback inhibition significantly decreases the membrane voltage variance during the refractory period. The membrane voltage fluctuations become depressed for a longer duration, which prevents the excessive accumulation of timing jitter until the next spike

The membrane voltage variance of $\mathcal {N}_{1}$ for varying feedback inhibition strengths can be seen in Fig. 7b. Let us first consider the case without feedback inhibition. Without an external stimulus, the neuron membrane voltage fluctuates, with a constant variance around its mean resting potential of − 65 mV, until t = 10 msec. Due to the action potential generated with the injection of the current pulse at t = 10 msec, the membrane voltage and hence the transition rates of the ion channels undergo a fast variation. Thus, the membrane voltage noise variance exhibits peaks at the rising and falling edges of the action potential, i.e., during the depolarization and repolarization phases, as observed in Fig. 7b. During the refractory period, the membrane voltage reaches its minimum value, which is around − 75 mV. At this point, most of the ion channels are closed (Dayan and Abbott 2001; Goldwyn et al. 2011). As a result, the fluctuations in the membrane voltage become subdued. The dip value in the membrane voltage variance in Fig. 7b coincides in time with the minimum value of the mean membrane voltage of $\mathcal {N}_{1}$ shown in Fig. 7a, in the beginning of the refractory period, as expected. When the refractory period ends, the variance of the membrane voltage returns to its steady-state value, corresponding to the resting membrane potential.

According to the results in Fig. 7b, feedback inhibition results in a significant reduction in the membrane voltage variance during the refractory period. The inhibition of $\mathcal {N}_{1}$ by $\mathcal {N}_{2}$ prolongs the refractory period of neuron $\mathcal {N}_{1}$, during which most of the ion channels remain closed. As a result, the membrane voltage fluctuations become depressed for a longer duration, which prevents the excessive accumulation of timing jitter until the next spike. This may be the key mechanism through which feedback inhibition enhances spike timing precision.

5 Synaptic integration

In the mammalian brain, the sensory information is transmitted to the neocortex, where it is processed for behavioral and cognitive functions (Miller 2000; Ghazanfar and Schroeder 2006). The processing in the cortical neurons involves the integration of their synaptic inputs and the generation of trains of action potentials in various temporal patterns. For a cortical neuron receiving multiple synaptic inputs, its spike timing precision is important in producing a coherent output in response to sensory stimuli.

A sensory neuron transmits information to multiple neurons with an axonal divergence of its output. On the other hand, a neuron can receive multiple synaptic inputs through dendritic convergence. These motifs are prevalent in the nervous system. For example, cortical neurons receive multiple afferent synaptic inputs originating from sensory sources (Varga et al. 2011). For example, the information about head and body motion is transmitted to the vestibular system through multiple sensory pathways (DiGiovanna et al. 2016).

We consider dendritic convergence in a neuron, which receives multiple excitatory synaptic inputs from spiking neurons, as shown in Fig. 8. We analyze the effect of the synaptic inputs on the timing precision of the output neuron. Each input neuron is excited by a constant suprathreshold current stimulus with an amplitude I_ext = 0.25 A/m². The membrane area of each neuron in the setup is fixed at A _m = 1000μm² with the VG ion channel densities set to 60 Na⁺ channels/μm² and 18 K⁺ channels/μm². The output neuron includes 2 × 10⁴ excitatory AMPA/kainate receptor channels per synapse. Each input neuron is spiking at the same frequency due to the same constant suprathreshold current excitation, while the output neuron generates an action potential upon the arrival of an excitatory synaptic input. The strength of a single excitatory synapse is sufficient to induce an action potential in the membrane of the output neuron. In the absence of variability and noise, the input neurons generate spikes at the same time, even though they are not coupled with each other. This setup, in a simplistic manner, represents the situation in which the sensory information relayed by each of the input neurons comes from the same source.

We use the transient semi-analytical method in order to compute the asymptotic timing jitter variance slope of the output neuron shown in Fig. 8. The results in Fig. 9 reveal that as the number of excitatory synaptic inputs M_input is increased, the timing precision of the output neuron is improved. It is indeed interesting to note that the timing jitter variance of the output neuron, c_ss,out, is equal to that of a single input neuron, $\bar {c}_{ss}$, scaled by 1/M_input. That is, the timing jitter variance of the output neuron is $\bar {c}_{ss}\,t/M_{\text {input}}$.

Fig. 8

The synaptic integration of excitatory inputs. Each input neuron is under tonic spiking conditions with a constant, suprathreshold current stimulus and has an excitatory synaptic connection to the output neuron

Fig. 9

The timing jitter variance slope of the action potentials of the output neuron shown in Fig. 8 with respect to the number of input neurons. Each input neuron is excited by a suprathreshold current stimulus with an amplitude I_ext = 0.25 A/m². The membrane area of each neuron is $A_{m}= 1000 \mu \textit {m}^{2}$. The output neuron includes 2 × 10⁴ excitatory AMPA/kainate receptor channels per synapse. The timing jitter variance of the output neuron c_ss,out is the same as the timing jitter variance of a single input neuron $\bar {c}_{ss}$ scaled by 1/M_input

We next consider multiple independent spiking input neurons with different membrane areas. Hence, each input neuron has a distinct timing jitter variance $\bar {c}_{ss,i}$. Since the excitation current per unit membrane area, I_ext = 0.25 A/m², is set to the same value for all of the input neurons, their spiking frequencies are all equal. Based on running extensive analyses using the transient semi-analytical technique, we arrive at the following result: The timing jitter variance slope of the output neuron is given by

$$ c_{ss,\text{out}}=\frac{1}{M_{\text{input}}^{2}}{\sum}_{i = 1}^{M_{\text{input}}}\bar{c}_{ss,i}. $$

(20)

The above result is consistent with the one we have obtained for the case of input neurons with identical membrane areas. It can be explained as follows: The output neuron is in effect estimating the unperturbed timing of the input spikes denoted by t (which represents the same sensory information encoded by the spike timings of all of the input neurons), given M_input independent sample observations for their perturbed timings, i.e., t + α _i (t), corresponding to the spikes of the input neurons with a timing uncertainty. The timing deviation of the i th input neuron is α _i (t) and becomes an additive Gaussian random variable $\mathcal {N}(0,\bar {c}_{ss,i}\:t)$ asymptotically with time, as discussed in Section 3. Furthermore, α _i (t)’s are independent since they arise from independent noise sources contained in different neurons. The estimate for the timing, denoted by t_estimate, can be computed by the sample average of the M_input observations, i.e.,

$$ t_{\text{estimate}} = \frac{1}{M_{\text{input}}} {\sum}_{i = 1}^{M_{\text{input}}}(t+\alpha_{i}(t)). $$

(21)

Then, the variance of the timing estimate (spike timing uncertainty at the output) is given by

$$ \text{Var}[t_{\text{estimate}}] = \frac{1}{M_{\text{input}}^{2}} {\sum}_{i = 1}^{M_{\text{input}}}\bar{c}_{ss,i}\:t $$

(22)

where the slope of the variance is the same as the timing jitter variance slope in Eq. (20) that was distilled from the simulation data. Thus, the sample average operation above is effectively implemented by the synaptic integration of the input spikes.

Our results suggest that the synaptic integration of multiple afferent synaptic inputs originating from the same sensory source may be an important mechanism that is utilized by the cortical neurons in regulating spike timing precision. The sensory data is first transmitted to multiple neurons via axonal divergence of the sensory neuron. The information is transmitted through different neural pathways. Finally, dendritic convergence in an intermediate or a cortical neuron improves spike timing precision and hence the reliability of the information received.

Feedforward inhibition is considered to be another mechanism utilized in the cortex in order to enhance the spike timing reliability of neurons (Isaacson and Scanziani 2011; Pouille and Scanziani 2001). For example, feedforward inhibition of $\mathcal {N}^{\text {out}}$ in Fig. 8 would narrow its integration window, which reduces the effective number of the received input spikes. However, according to our results, integrating more inputs from multiple neurons enhances spike timing precision. At first thought, this seems to contradict with the enhancement of timing reliability via feedforward inhibition. However, there is in fact no contradiction. Feedforward inhibition acts so as to establish coincidence detection for the received spikes in $\mathcal {N}^{\text {out}}$, which can reduce the jitter due to the spontaneous spikes generated by the input neurons without any sensory cause (Isaacson and Scanziani 2011; Pouille and Scanziani 2001). That is, with feedforward inhibition, a spontaneous action potential generated in an input neuron is prevented from inducing a subsequent action potential in $\mathcal {N}^{\text {out}}$, unless other input neurons fire at the same time. Feedforward inhibition ensures that $\mathcal {N}^{\text {out}}$ fires if it receives multiple input spikes with coincident timing. On the other hand, in the scenario we have considered above, all of the input neurons receive the same sensory stimulus and generate spikes that are coincident within a deviation due to noise. Furthermore, an action potential generated in an input neuron is able to induce another action potential in $\mathcal {N}^{\text {out}}$ on its own. In summary, these two motifs, i.e., (i) feedforward inhibition that effectively subdues spontaneous spikes with no sensory cause, and (ii) synaptic integration of multiple inputs that encode the same sensory stimulus, may represent different mechanisms utilized by the neurons in the cortex in order to enhance spike timing reliability.

6 Synaptic coupling

Rhythmic collective oscillations are commonly seen in the operation of neural circuits. The neurons in these circuits are synchronized with each other through their synaptic connections so that the circuit overall spikes in a robust manner. The nature of these rhythmic oscillations are determined by the particular neuronal circuit organization. In Esfahani et al. (2016), the authors argue that the synaptic coupling delay between the neurons determines the transition between synchronous and asynchronous states of a neuronal circuit. The spike timing precision of the neurons directly relates to the synaptic delay between them, and may be an important factor in the synchronization of the neuronal circuits that generate robust rhythms in the brain.

The synchronization of coupled oscillators is ubiquitous, e.g., synchronized pendulum clocks that are placed on the same wall and the synchronous flashing of fireflies (De Smedt et al. 2015). The synchronization in these systems is facilitated mainly through a mechanism called injection locking (Adler 1973). The timing jitter variance of autonomously oscillating electrical circuits can be reduced by injection locking (Razavi 2004). A similar mechanism is possibly exploited by the circuits in the brain in order to reduce the timing noise and enhance the timing reliability of the generated spikes. Next, we investigate the effect of the nature and the strength of the synaptic coupling among neurons on the timing precision of a neural circuit. Here, we define the synaptic coupling strength to be synonymous to the number of LG synaptic receptor channels per synapse.

Oscillatory neuronal circuits in the brain can have complex organizations. For simplicity, we consider fully connected neuronal circuits. That is, each neuron is connected to all of the other neurons in the circuit via synapses, as shown in Fig. 10 for a five-neuron network. Similar network topologies with various connection scenarios have been considered in the literature (Esfahani et al. 2016; Gu et al. 2015) in order to investigate the mechanisms of synchronous oscillations in the brain.

Fig. 10

Fully connected neuronal oscillator circuit with five neurons. Each neuron is under tonic spiking conditions with a constant, suprathreshold current stimulus

Fig. 11

a The timing jitter variance of the output action potentials of a neuron in the five-neuron E network in Fig. 10, for N_ex = 750 and 3000 excitatory AMPA/kainate receptor channels per synapse. The amplitude of the external suprathreshold current input to each neuron is I_ext = 0.25 A/m² and the membrane area of each neuron is $A_{m}= 1000 \mu \textit {m}^{2}$. The timing jitter variance of a standalone neuron excited by the same suprathreshold current stimulus I_ext = 0.25 A/m², with a membrane area $A_{m}= 1000 \mu \textit {m}^{2}$, is also shown. The synchronization times T_sync,1 (for N_ex = 3000) and T_sync,2 (for N_ex = 750) for the E networks are indicated on the graph. b The synchronization times of the five-neuron E, I, and EI networks as a function of the number of receptor channels per synapse. The amplitude of the total external suprathreshold current input to each neuron is I_ext = 0.25 A/m². The membrane area of each neuron is $A_{m}= 1000 \mu \textit {m}^{2}$. For the EI network, N indicates the total number of excitatory (N/2) and inhibitory (N/2) channels per synapse. For the E and I networks, N is the number of excitatory and inhibitory channels per synapse, respectively

For the five-neuron network in Fig. 10, we consider three different cases: (i) an excitatory (E) network with only excitatory synapses , (ii) an inhibitory (I) network with only inhibitory synapses, and (iii) a balanced excitatory and inhibitory (EI) network with both excitatory and inhibitory synapses. For the EI network, the numbers of the excitatory and inhibitory synaptic receptor channels per synapse is set to the same value. We denote the total number of LG receptor channels per synapse with N. Each neuron in the network shown in Fig. 10 is excited by a constant suprathreshold current stimulus with an amplitude I_ext = 0.25 A/m². The membrane area of each neuron is fixed at A _m = 1000μm², with the VG ion channel densities equal to 60 Na⁺ channels/μm² and 18 K⁺ channels/μm². For the three cases stated above, the numbers of the excitatory AMPA/kainate receptor channels and the inhibitory GABA _A receptor channels per synapse are varied in order to observe their effect on the timing reliability of the neuronal circuit.

6.1 Synchronization time vs synaptic coupling strength

The instantaneous timing jitter variance of the output action potentials of a neuron in the five-neuron E network is shown in Fig. 11a, for both N_ex = 750 and 3000 excitatory channels per synapse. In addition, the timing jitter variance of a single, standalone neuron excited by the same suprathreshold current stimulus density is also shown in Fig. 11a. The firing rates for these three cases (i.e., (i) standalone neuron, (ii) and (iii) 5-neuron network with N_ex = 750 and 3000) are roughly the same and equal to f _c = 1/T _c = 92.0 Hz. The data for the plots in Fig. 11a was computed via the transient semi-analytical method for the jitter variance of a number of consecutive spikes occurring at t = kT _c , i.e., Var[α(kT _c )].

The results in Fig. 11a show that the timing jitter variances, for all of the cases considered, increase linearly asymptotically with time, as predicted by the theory presented in Demir et al. (2000). Although the timing jitter variance of the standalone neuron reaches its asymptotic form immediately, the five-neuron network exhibits transient behavior before settling to its asymptotic linear form. In an oscillating neuronal circuit, there are multiple oscillating units (i.e., individual neurons) coupled with each other. When these coupled oscillators reach a steady-state, they may become synchronized, i.e., they lock with each other and the whole circuit behaves as one oscillating unit. Here, synchronization is used to refer to this condition of lock. However, the fact that the oscillators are locked with each other does not mean that they become noiseless. The stochasticity that arises from the ion channels and the synapses is still there, even with synchronization. The overall neuronal circuit oscillator is still noisy and has an increasing timing jitter variance with time even after synchronization. For any oscillator (whether it is composed of a single oscillating unit, or multiple units that are locked with each other) without an embedded perfect time reference, the timing jitter variance increases asymptotically linearly with time, as shown in Demir et al. (2000). For oscillators composed of multiple, locked oscillating units, the asymptotic timing jitter variance may be different (usually less) than that of the individual units if they were operating alone. The jitter variance of the composite oscillator is reduced through a sort of cooperation of the individual neurons in the network. On the other hand, the synchronization mechanism (injection locking via coupling) that eventually locks the individual units with each other has a time constant that is usually (much) larger than the oscillation period. The effect of this time constant can be observed if the timing jitter of the spikes generated by the neurons are computed with respect to the timing of an initial trigger (reference) spike (Demir 2006). In the short time scale (for the spikes that immediately follow the reference spike), the timing jitter variance slope (i.e., jitter accumulation rate) observed is equal to the slope one would obtain if the neuron under consideration was operating alone as an independent unit. In the longer time scale, when the observed spike and the reference spike are separated from each other by more than the synchronization time constant, the jitter variance accumulation rate becomes smaller. This behavior is very similar to the operation of phase locked loops (PLLs) used in electronic circuits, where the phase of a noisy oscillator is locked to the phase of a cleaner reference signal with more precise timing (Gupta 1975; Demir 2006). The synchronization time in the case of PLLs is determined by the loop bandwidth. For neuronal circuits, we define synchronization timeT_sync to be the time duration (measured from the reference spike) that is needed for the timing jitter slope to settle to its reduced, locked value from the larger value that corresponds to the standalone state of the neuron. The jitter characteristics discussed above can be observed in the results presented in Fig. 11a.

It is important to note that, when the neurons in the network are locked, that is, when they operate as one oscillation unit, the timing jitter variances of all of the neurons in the network are the same. In fact, the timing jitter variance that is computed for a neuronal circuit is a network property shared by all of the neurons that are locked to each other. This is also apparent in the representation of the timing jitter as a common time deviation α(t) in x _s (t + α(t)), that is shared by all of the membrane voltages in the state vector x _s . The technique we use for computing the periodic x _s (t) (based on Fourier spectral collocation, mentioned in Section 3), with noise removed, reveals whether the neurons are indeed locked to each other operating as one oscillation unit, or oscillating independently.

For various number of synaptic channels per synapse, the synchronization times for the five-neuron E, I, and EI networks were computed, shown in Fig. 11b. As the number of LG receptor channels per synapse is increased, the synchronization time decreases for all network types. The effect of the synaptic inputs of a neuron from other neurons in the circuit is enhanced when the coupling strength is increased due to larger number of synaptic receptor channels. As a result, the time constant of the synchronization mechanism becomes smaller. According to our results, the EI network synchronizes roughly one order of magnitude faster than the E network for the same total number of excitatory and inhibitory receptor channels per synapse, as observed in Fig. 11b. In addition, the synchronization time of the I network is almost half of that of the EI network. As we increase the proportion of the inhibitory channels, for a given total number of (excitatory and inhibitory) receptor channels per synapse, the synchronization time of the EI network decreases. In the light of the results obtained for the feedback inhibition mechanism in Section 4, the inhibitory synapses possibly help speed up the synchronization of the network by preventing the excessive accumulation of timing jitter until the next spike. In the next subsection, we analyze the effect of the coupling strength on the asymptotic timing jitter variance of the fully connected five-neuron networks.

6.2 Spike timing precision and spiking period vs synaptic coupling strength

We now consider the asymptotic (beyond the synchronization time) timing jitter variance slopes and the spiking periods for the five-neuron E, I, and EI neuronal circuits. The steady-state jitter variance slopes are computed via the steady-state semi-analytical method reviewed in Section 3. The obtained results are presented in Fig. 12, which also includes results on the timing jitter variances and the spiking periods of single, standalone neurons with membrane areas A _m and 5A _m stimulated by the same suprathreshold stimulus current density.

Fig. 12

a The timing jitter variance slope and b the spiking period of a neuron in the five-neuron E, I, and EI networks in Fig. 10 as a function of the number of receptor channels per synapse. The amplitude of the external suprathreshold current input to each neuron is I_ext = 0.25 A/m². The membrane area of each neuron is $A_{m}= 1000 \mu \textit {m}^{2}$. For the EI network, N is the total number of excitatory (N/2) and inhibitory (N/2) channels per synapse. For E and I networks, N is the number of excitatory and inhibitory channels per synapse, respectively. In a, the timing jitter variance slopes of single, standalone neurons with membrane areas $A_{m}= 1000 \mu \textit {m}^{2}$ and $5A_{m}= 5000 \mu \textit {m}^{2}$, excited by the same suprathreshold current stimulus I_ext = 0.25 A/m², are also shown. If the number of synaptic receptor channels is lower than a certain value, the timing jitter variances of the five-neuron E, I, and EI networks are the same as that of an autonomously oscillating standalone neuron with a membrane area of 5A _m excited by the same constant suprathreshold current stimulus. In b, the spiking period for a single, standalone neuron (with membrane area $A_{m}= 1000 \mu \textit {m}^{2}$ or $5A_{m}= 5000 \mu \textit {m}^{2}$, the period is the same) excited by the same suprathreshold current stimulus I_ext = 0.25 A/m² is also presented. If the number of synaptic receptor channels is lower than a certain value, the spiking periods of the five-neuron E, I, and EI networks are the same as that of an autonomously oscillating standalone neuron excited by the same constant suprathreshold current stimulus. We note that the spiking period of a standalone neuron is independent of its membrane area if the current stimulus density is kept constant. The reason for the gaps in the data (due to instability of the circuit) is explained in the main text

Fig. 13

Sample paths for the membrane voltages of the neurons in the EI network in Fig. 10. a The EI network is stable and synchronized with cooperation for N_ex = 2 and N_in = 2 channels per synapse. All of the neurons in the network generate spikes periodically. b The EI network exhibits unstable behavior. Initially, the network behavior is dominated by neuron $\mathcal {N}_{3}$. However, after a perturbation due to noise in the neuronal circuit, neuron $\mathcal {N}_{4}$ starts to dominate the network behavior and the spiking neuron $\mathcal {N}_{3}$ is inhibited. We note that neuron $\mathcal {N}_{5}$ also tries to spike but cannot maintain its spiking state. The numbers of excitatory and inhibitory receptor channels per synapse are N_ex = 2000 and N_in = 2000, respectively. c The EI network is stable and desynchronized with the domination of neuron $\mathcal {N}_{4}$ in the network for N_ex = 20000 and N_in = 20000 channels per synapse. For each case, the amplitude of the external suprathreshold current input to each neuron is I_ext = 0.25 A/m². The membrane area of each neuron is $A_{m}= 1000 \mu \textit {m}^{2}$

The results in Fig. 12, show that the behaviors of the I and EI networks are substantially different from that of the E network, due to the presence of the inhibitory synapses. According to these results, the response of the E network continuously varies as the coupling strength is increased. However, the I and EI networks exhibit a three-phase discontinuous response as a function of the coupling strength: (i) stable and synchronized with cooperation, (ii) unstable, (iii) stable and desynchronized with the domination of one neuron in the network. These three phases for the EI network are illustrated in Fig. 13, where sample paths for the membrane voltages of the neurons in the network are presented. We note that, in the unstable case, the timing jitter variance and the spiking period become meaningless. That is why there are gaps in the graphs for the I and EI networks in Fig. 12a and b. Next, we discuss in detail the behavior of the fully connected E, I and EI networks as the coupling strength is changed.

According to the results in Fig. 12a, if the number of the synaptic receptor channels is lower than a certain value, i.e., with weak coupling, the asymptotic timing jitter variance slopes, c _{s s} ’s, of M_sync-neuron E, I, and EI networks are the same as that of an autonomously oscillating standalone neuron with a membrane area of M_syncA _m , excited by the same constant suprathreshold current stimulus. In Kilinc and Demir (2017), we have shown that the asymptotic timing jitter variance slope for a neuron with a constant suprathreshold current is inversely proportional to its membrane area. Indeed, if a neuron with a membrane area of A _m has a timing jitter variance slope $\bar {c}_{ss}$, then for a neuron with a membrane area of M_syncA _m , the slope becomes $c_{ss}=\bar {c}_{ss}/M_{\text {sync}}$. It can be concluded that weak synaptic coupling between neurons in the E, I, and EI networks enables them to behave like a single neuron with a larger membrane area, i.e., the timing precision of these networks is improved by cooperation. In fact, we have found out that this improvement is realized even with very weak coupling, all the way down to 1 channel/synapse. This manifests itself as a reduction in the timing jitter slope beyond the synchronization time T_sync, when computed with the transient semi-analytical technique, albeit with larger synchronization times for weaker coupling. We note that when the synaptic connections between the neurons are completely removed, each neuron indeed operates in a standalone manner. Then, the timing jitter variances of the neurons become equal to that of a standalone neuron with membrane area A _m , without any reduction.

The results in Fig. 12b show that, if the number of synaptic receptor channels is lower than a certain value, the spiking period of the E, I, and EI networks are the same as that of an autonomously oscillating standalone neuron excited by the same constant suprathreshold stimulus current density. This result is consistent with the timing jitter variance of the E, I, and EI networks for weak coupling, i.e., they behave like a single neuron oscillator with a membrane area of 5A _m .

As we further increase the number of the synaptic receptor channels per synapse, the ion currents passing through these LG channels start to dominate the currents passing through the VG K⁺ and Na⁺ channels in the neuron. Thus, strong synaptic coupling among the neurons emerges as a disruption to the internal spiking dynamics. This results in an increase in both the timing jitter variance slope and the spiking period as observed in Fig. 12a and b, respectively. In other words, the timing reliabilities of the fully connected E, I, and EI networks start to deteriorate for coupling strengths that are above a certain value. The increase in the timing jitter slope c _{s s} of the networks may be due to the prolonged oscillation periods T _c . We have observed a similar relationship between c _{s s} and T _c for the single, standalone neuron oscillator in Kilinc and Demir (2017). We also note that, as the number of receptor channels per synapse is increased, the spiking periods of the I and EI networks increase more than that of the E network. In addition, the increase in the spiking period of the I network is higher than that of the EI network. That is, as we increase the proportion of the inhibitory channels for a given total number of (excitatory and inhibitory) channels per synapse, the spiking period of the network increases. This behavior may be due to the fact that the inhibitory synapses try to depress the spiking behavior of the network, opposing the suprathreshold external current stimulus. This may then result in an increase in the spiking period, as observed in Fig. 12b.

If the number of the receptor channels per synapse in the I and EI networks exceed 600 and 1200 channels/synapse, respectively, these networks become unstable. The inhibitory synapses in both the I and EI networks try to shut down the spiking of the neurons. However, at the same time, each neuron is being forced to oscillate by the suprathreshold current stimulus, and in the EI network also by the excitatory synapses. Due to the imbalance between these two driving forces, the behavior of the I and EI networks becomes unstable. The unstable behavior of the EI network is illustrated in Fig. 13b. Initially, the network behavior is dominated by a spiking neuron. However, after a perturbation due to noise in the neuronal circuit, another neuron starts to dominate the network behavior and then inhibits the initially spiking neuron. That is, the oscillation of the network is not stable, and noise causes the behavior of the network to change randomly. In contrast, the stability of the E network is maintained as the number of excitatory receptor channels per synapse is increased. In the E network, all of the driving forces, i.e., the synapses and the current stimulus, are excitatory, which do not result in instability even for stronger synaptic coupling. As the number of synaptic receptor channels in both the I and EI networks is further increased beyond 8000 and 16000 channels/synapse, respectively, one of the neurons in these networks shuts down the other neurons completely, which re-stabilizes the overall network activity as illustrated in Fig. 13c. That is, the inhibitory synapses of that neuron become dominant when compared with the excitatory driving forces and remains dominant even in the presence of disturbances due to noise. However, in this case, the overall neuronal circuit behaves like a single, standalone neuron with a membrane area A _m . This is the expected behavior, because the activity of the network at this point is dominated by a single neuron. That is, the spiking period and the timing jitter variance slope of the I and EI networks become same as those of a single neuron oscillator with a membrane area of A _m excited by the same stimulus current density.

6.3 Spike timing precision of weakly coupled heterogeneous neuronal networks

We can conclude based on the above results is that weak synaptic coupling among the neurons in E, I, and EI networks is a key mechanism that improves the timing precision of neuronal circuits through cooperation. A weakly connected M_sync-neuron circuit behaves like a single neuron with a membrane area equal to the total membrane area of the neurons in the network, i.e., M_syncA _m , assuming that the neurons in the network have equal membrane areas.

Now, we consider a heterogeneous, fully connected network, where each neuron has a different membrane area A_m,i, but excited by the same stimulus current density I_ext = 0.25 A/m². Here, we would like to clarify that heterogeneity to the network is introduced only through different membrane areas, which results in different noise levels for each neuron. We have performed extensive characterizations for the timing jitter performances of various heterogeneous, fully connected E, I, and EI neuronal circuits with varying number of neurons and varying membrane areas. By carefully analyzing these extensive set of results, we arrive at the following conclusion: The asymptotic timing jitter variance slope c _{s s} of a weakly coupled, heterogeneous network with M_sync neurons is the same as that of a standalone, single neuron with a membrane area of M_sync A _{H M} , excited by the same (per neuron) current density. Here, A _{H M} is the harmonic mean of the membrane areas of M_sync neurons, given by

$$ A_{HM} = M_{\text{sync}}\left[{\sum}_{i = 1}^{M_{\text{sync}}}\frac{1}{A_{m,i}}\right]^{-1}. $$

(23)

This conclusion applies to all of E, I, and EI heterogeneous networks. This result is consistent with the one for the case when the neurons in the network have equal membrane areas, i.e., A _{H M} = A _m with A_m,i = A _m . Since the harmonic mean is limited by the value of the minimum element as expressed by A _{H M} ≤ M_syncmin{A_m,i}, the performances of the E, I, and EI networks in terms of their timing jitter variance slopes are limited by the performance of the smallest neuron in the network. The smallest neuron has the worst timing jitter performance. Therefore, in order to improve the performance of the network, either the membrane area for the neuron with the smallest area should be increased or it should be removed from the network. We can conclude that, given a total membrane area budget, the optimal weakly coupled network (E, I or EI), with respect to the timing jitter performance, is the one where the neurons are similarly sized.

In order to investigate the main mechanism behind the above result, let standalone neurons with membrane areas of A _m and A_m,i have timing jitter variance slopes of $\bar {c}_{ss}$ and $\bar {c}_{ss,i}$, respectively. As mentioned previously, the asymptotic timing jitter variance slope is inversely proportional to the membrane area, i.e., $\bar {c}_{ss}A_{m} = \bar {c}_{ss,i}A_{m,i} = \text {constant}$. Then, for a neuron with a membrane area of M_syncA _{H M} , the jitter variance slope is given by

$$ \begin{array}{llllllllll} c_{ss} = \frac{\bar{c}_{ss}A_{m}}{M_{\text{sync}}A_{HM}} &= \frac{1}{M_{\text{sync}}^{2}}{\sum}_{i = 1}^{M_{\text{sync}}}\frac{\bar{c}_{ss}A_{m}}{A_{m,i}} \\&= \frac{1}{M_{\text{sync}}^{2}}{\sum}_{i = 1}^{M_{\text{sync}}}\bar{c}_{ss,i}. \end{array} $$

(24)

This result is very similar to the timing jitter variance slope of a neuron integrating M_sync synaptic inputs from multiple independent standalone neurons with timing jitter variance slopes of $\bar {c}_{ss,i}$ and membrane areas of A_m,i, given by Eq. (22) in Section 5. However, in an M_sync-neuron fully connected network, each neuron receives synaptic inputs from the other (M_sync − 1) neurons. We note that, in such a network, each neuron itself also behaves like an oscillating standalone neuron due to the suprathreshold current stimulus. Then, each neuron in the fully connected network integrates the timing information of M_sync neurons (including itself), with area A_m,i and jitter slope $\bar {c}_{ss,i}$ for the i th neuron. Thus, the above results are indeed consistent with the results presented in Section 5. In conclusion, it can be said that the fully connected E, I, and EI networks also loosely implement the sample average mechanism (as in synaptic integration considered in Section 5) on the spike timings of the neurons in the network, provided that they are weakly coupled. If the number of the LG receptor channels are increased beyond a certain threshold value, the behaviors of the heterogeneous networks are similar to those of the homogeneous networks discussed above.

7 Conclusion

We utilized semi-analytical techniques, which were adapted from previously developed techniques for electronic circuits, for the stochastic characterization of the timing jitter and noisy membrane voltages of spiking neuronal circuits. These semi-analytical methods helped us gain insight into three common neuronal circuit motifs from a spike timing precision perspective: (i) feedback inhibition, (ii) synaptic integration, and (iii) excitatory and inhibitory synaptic coupling. First, we showed that feedback inhibition improves the timing precision and energy efficiency of a spiking neuron. In addition, we have elucidated that this improvement is due to the fact that feedback inhibition prolongs the refractory period of a neuron. Since most of the ion channels remain closed in the refractory period, the membrane voltage fluctuations become subdued for a longer duration. Thus, feedback inhibition prevents the excessive accumulation of timing jitter until the next spike and enhances spike timing precision. Second, we have considered dendritic convergence of multiple excitatory synaptic inputs originating from the same sensory source. We showed that a neuron can improve on the timing jitter of its inputs by synaptic integration. Furthermore, our results suggest that a neuron in effect performs a sample average of the timings of the input spikes, which improves the timing precision of its output spikes. Finally, our results revealed that weak excitatory or inhibitory coupling among neurons in a fully connected network enables them to behave like a single neuron with a larger membrane area in such a way so that the timing precision of the network is improved by cooperation. This improvement is maximized, with a total membrane area budget, if the neurons in the network are similarly sized.

Appendix: : ion channel models

Neurons used in our numerical analyses include 18 K⁺ channels/μm² and 60 Na⁺ VG channels/μm² (Dayan and Abbott 2001). In analyzing various neuronal architectures, the number of excitatory and inhibitory synaptic receptor LG channels per synapse are varied, in accordance with the physiologically plausible values for the receptor channel densities, the number of synapses, and the membrane areas of the neurons (Masugi-Tokita et al. 2007; Chiu et al. 2002). We utilize well established kinetic schemes for K⁺ and Na⁺ channels, as shown in Fig. 14a and b (Dayan and Abbott 2001). Excitatory synapses include AMPA/kainate receptor channels with a kinetic scheme shown in Fig. 14c (Destexhe et al. 1998b). Inhibitory synapses include GABA _A receptor channels having a kinetic scheme illustrated in Fig. 14d (Destexhe et al. 1998b).

Fig. 14

MC models for a K⁺, b Na⁺, c excitatory AMPA/kainate receptor, and d inhibitory GABA _A receptor ion channels

The transition rates we use for the kinetic models of K⁺ and Na⁺ channels are given by

$$ \begin{array}{llllllllll} &\alpha_{n}(V(t))=\frac{0.01(V(t)+ 55)}{1-\exp[-(V(t)+ 55)/10]},\\ &\beta_{n}(V(t))= 0.125\exp[-(V(t)+ 65)/80],\\ &\alpha_{m}(V(t))=\frac{0.1(V(t)+ 40)}{1-\exp[-(V(t)+ 40)/10]},\\ &\beta_{m}(V(t))= 4\exp[-(V(t)+ 65)/18],\\ &\alpha_{h}(V(t))= 0.07\exp[-(V(t)+ 65)/20],\\ &\beta_{h}(V(t))=\frac{1}{1+\exp[-(V(t)+ 35)/10]}, \end{array} $$

(25)

where V (t) is the membrane potential of the neuron as described by Eq. (1) and expressed in mV, α _i ’s and β _i ’s are expressed in msec^− 1 (Dayan and Abbott 2001). The ionic K⁺ and Na⁺ currents are given by

$$ \begin{array}{llllllllll} &I_{\mathrm{K}^{+}}=g_{\mathrm{K}^{+}}N_{n^{4}}[V(t)-E_{\mathrm{K}^{+}}],\\ &I_{\text{Na}^{+}}=g_{\text{Na}^{+}}N_{m^{3}h^{1}}[V(t)-E_{\text{Na}^{+}}], \end{array} $$

(26)

where $g_{\mathrm {K}^{+}}=g_{\text {Na}^{+}}= 20$ pS, $E_{\mathrm {K}^{+}}=-77$ mV, $E_{\text {Na}^{+}}= 50$ mV, $N_{n^{4}}$ and $N_{m^{3}h^{1}}$ are the total number of open K⁺ and Na⁺ channels, respectively (Dayan and Abbott 2001).

Nominal values for the transition rates in the kinetic model of the AMPA/kainate receptor channel, i.e., $R_{b}([L(t)])= 1.3\times 10^{7}[L(t)], R_{u_{1}}= 5.9\times 10^{0}, R_{u_{2}}= 8.6\times 10^{4}, R_{r}= 6.4\times 10^{1}, R_{d}= 9.0\times 10^{2},R_{c}= 2.0\times 10^{2}$, and R _o = 2.7 × 10³ (all in units of s^− 1), are given in (Destexhe et al. 1998b). The results presented in Section 5 were obtained based on these transition rates for the AMPA/kainate receptor channel. With these values, the synaptic delay is approximately 1 msec. In order to increase the synaptic delay (between the spikes generated in the presynaptic and postsynaptic neuron connected via an excitatory synapse) by ∼1 msec to 2 msec, we also use updated transition rates for the AMPA/kainate receptor channels, given by $R_{b}([L(t)])= 1.0\times 10^{6}[L(t)], R_{u_{1}}= 3.0\times 10^{1}, R_{u_{2}}= 1.6\times 10^{5}, R_{r}= 3.4\times 10^{1}, R_{d}= 8.4\times 10^{2}, R_{c}= 3.7\times 10^{2}$, and R _o = 0.9 × 10³ (all in units of s^− 1). The results presented in Sections 4 and 6 were obtained based on these updated transition rates for the AMPA/kainate receptor channel. These updated values are justified based on the diversity of activation and desensitization properties of AMPA/kainate receptor channels that is described in Pinheiro and Mulle (2006) and Perrais et al. (2010). For neurons that are reciprocally connected by excitatory and inhibitory synapses, a synaptic delay that is shorter than the depolarization duration of an action potential would result in a premature inhibition of the action potential. Thus, a ∼1 msec increase in the synaptic delay makes the neuronal dynamics more physiologically meaningful. Prolonged synaptic delays can alternatively be modeled via distributed multi-compartment synapse or neuron models.

The transition rates in the kinetic model of the GABA _A receptor channel are set to $R_{b_{1}}([L(t)])= 2.0\times 10^{7}[L(t)], R_{b_{2}}([L(t)])= 1.0\times 10^{7}[L(t)], R_{u_{1}}= 4.6\times 10^{3}, R_{u_{2}}= 9.2\times 10^{3}, R_{c_{1}}= 9.8\times 10^{3}, R_{c_{2}}= 4.1\times 10^{2}, R_{o_{1}}= 3.3\times 10^{3}$, and $R_{o_{2}}= 1.1\times 10^{4}$ (all in units of s^− 1), as given in Destexhe et al. (1998b).

[L(t)] is the concentration of neurotransmitter molecules in the synaptic cleft, given by

$$ [L(t)]=\frac{L_{\max}}{1+\exp[-(V_{\text{pre}}(t)-V_{p})/K_{p}]} $$

(27)

where L_max = 2.84 × 10^− 3 M is the maximal concentration, V_pre(t) is the membrane potential of the presynaptic neuron expressed in mV, K _p = 5 mV is the steepness parameter and V _p = 2 mV determines the value at which the concentration is half of the maximum value (Destexhe et al. 1994). The ionic AMPA and GABA _A currents are given by

$$ \begin{array}{llllllllll} &I_{\text{AMPA}}=g_{\text{AMPA}}N_{O}[V(t)-E_{\text{AMPA}}],\\ &I_{\text{GABA}_{A}}=g_{\text{GABA}_{A}}[N_{O_{1}}+N_{O_{2}}][V(t)-E_{\text{GABA}_{A}}], \end{array} $$

(28)

where g_AMPA = g_GABA = 20 pS, E_AMPA = 0 mV, $E_{\text {GABA}_{A}}=-70$ mV, N _O and $N_{O_{1}}+N_{O_{2}}$ are the total number of open AMPA and GABA _A receptor channels, respectively (Destexhe et al. 1998b).