1 Introduction

For many years, optical fiber Fabry–Perot (FP) interferometric sensors have found extensive application, as they can offer many important advantages over conventional sensors, including electromagnetic interference, high sensitivity, instant response, and small size. Also, these sensors provide high sensitivity and low noise, with easy optical multiplexing to arrays. The high sensitivity results from the high compatibility of the diaphragm, which can be measured interferometrically even under very low pressure. Because of these unique features, they are studied and developed for use in applications such as MRI-compatible microphones [1], small force measurements [2], large structure monitoring [3], underwater surveillance [4], seismic research [5], biochemical sensors [6], atomic force microscopy [7], and photo-acoustic imaging [8].

The FP interferometer-based sensor tip consists of two parallel interfaces, fiber and diaphragm. Therefore, the diaphragm is an important factor in the practical application of extrinsic Fabry–Perot interferometric (EFPI) sensors. Various diaphragm materials have been used in the design, including silicon [9], silica [10], metallic [11,12,13], two-dimensional (2D) [14], and polymer [15,16,17] materials. The geometric properties and material used for the diaphragm are important parameters that determine the sensitivity and frequency response of the EFPI sensor [18]. Sensor parameters such as bandwidth, linearity, and sensitivity must be determined for the efficient operation of the diaphragm. Analysis of multiple factors is required to determine these parameters.

Many theoretical studies regarding the effects of the medium on the resonance frequency have provided valuable information. The Poisson–Kirchhoff vibration theory of circular plates was investigated by several authors, and the free edge condition was studied by Kirchhoff [19], Lamb [20], and Rayleigh [21]. Timoshenko [22] used the energy method to solve the clamped edge plate condition. Amabili and Kwak [23, 24] investigated the effect of free surface waves on the free vibrations of circular plates based on the free surface of an infinite liquid area. Kozlovsky [25] studied Lamb’s work for viscous liquid, and Olfatnia [26] experimentally confirmed Lamb’s theoretical results. However, in his studies, residual stress was not studied in the membrane. Yu et al. and Wu et al. [27, 28] studied the effects of residual stress on the dynamic behavior of a sensor diaphragm. In diaphragm-based biosensors, the mass microbalance technique uses a dynamic mode to measure the shift in resonance frequency that reflects the change in mass [29]. Since the sensor dimensions can be reduced, it can be designed with large natural frequencies. In this case, a dynamic mode provides higher sensitivity than a static mode [29]. In the literature, diaphragm analysis of acoustic sensors has typically been carried out using static deflection and frequency analysis, where the diaphragms did not have vibration damping. In practice, the operating medium (OM) of the sensor usually has dynamic properties such as acoustic damping and variable frequency. Three types are used in mechanical sensors: cantilever, bridge, and diaphragm. The diaphragm has advantages because the effect of medium damping on the quality of the diaphragm is less than with other structures [30], and the diaphragm is also resistant to viscous damping [31]. Thanks to these superior features, the diaphragm has become an effective element for mechanical sensors.

On the other hand, the dynamic response of the diaphragm is often greatly affected by acoustic radiation losses [32]. As a result, it is important to clearly understand the relationship between structure and medium damping for the design of a high-performance diaphragm-based static/dynamic pressure sensor (DB-S/DPS). Therefore, the effect of dynamic mode performance of diaphragm materials on sensor parameters (sensitivity, bandwidth, linearity) in a dynamic OM becomes even more important. Since sensors are designed to detect dynamic pressure, it is necessary to determine the natural frequency and flexural properties, and this is only possible with a dynamic analysis of the diaphragm. Thus, it is possible to design sensors with desired operating frequency, sensitivity, and bandwidth. The development of high performance requires investigating the dynamic properties of the diaphragm and OM.

In this study, the effects of diaphragm materials and OM parameters on sensor performance were investigated for a DB-S/DPS. Simulation following theoretical analysis studies was performed with different diaphragm materials (silica, silicon, graphene, gold, aluminum, cellulose triacetate [CTA]) and in different operating media (air, water, oil). Theoretically, analysis of multiple parameters by MATLAB software was carried out considering the diaphragm vibration-damping values and forced oscillations which were not generally examined in the literature. Also, thanks to these analyses, the effects of the mechanical properties and geometric dimensions of the diaphragm on the dynamic pressure sensitivity and natural frequency were determined for DB-S/DPS design. This very comprehensive and impressive study will shed light on the optimization of the diaphragm material and geometric dimensions according to the sensor OM in determining the DB-S/DPS design parameters.

1.1 Dynamic pressure response of the circular diaphragm

Descriptions of the symbols used in Sect. 2 are given in Table 1.

Table 1 Definition of variables
Full size table

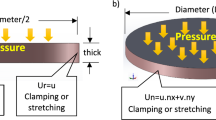
When the sound wave impacts the diaphragm, the actuating force in the unit area is the pressure P(r,θ,t). If the wavelength of the sound is not smaller than the diaphragm size (occurs only at frequencies higher than 20 kHz), the pressure effect can be assumed to be equal on the surface of the diaphragm [33]. The dynamic response of the diaphragm for forced oscillations is governed by Eq. (1). For vibration analysis of the circular diaphragm in a vacuum, transverse deflection is admitted, being w.

$${D\nabla }^{4}w+\rho h\frac{{\partial }^{2}w}{\partial {t}^{2}}+2\xi \frac{\partial w}{\partial t}=P\left(r,\theta ,t\right)$$
(1)

where ∇4 = ∇2∇2, D = Eh3/12(1 −v2) is the diaphragm’s bending strength, v is the material’s Poisson ratio, and E is the material’s Young’s modulus. The right side of Eq. (1) is taken as zero when pressure is not applied. Since we focus on applying a forced pressure to the diaphragm, the value of P(r,θ,t) is written. The Laplacian operator in polar coordinates is given in Eq. (2):

$${\nabla }^{2}=\frac{{\partial }^{2}}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{{r}^{2}}\frac{{\partial }^{2}}{\partial {\theta }^{2}}$$
(2)

However, analyzing Eq. (1) analytically is very troublesome. For convenience, the following quadratic differential equation, known as the single-degree-freedom system [34], has been added to obtain the output response.

$$m\ddot{d}+c\dot{d}+kd={F}_{0}\mathrm{cos}\omega t$$
(3)

where, m, c, and k respectively indicate mass, damping coefficient, and spring constant, and d = d(t) indicates the system’s stretching. Also, F0cosωt represents the harmonic oscillatory excitation acting on the diaphragm. Equation (4) is written by editing Eq. (3).

$$\ddot{d}+2\gamma \dot{d}+{\delta }^{2}d={d}_{c}\mathrm{cos}\omega t$$
(4)

Here, γ = c/2 m, δ = √(k/m), and dc = F0/m are given. The solution of Eq. (3), which expresses the steady-state response of its system, is given in Eq. (5) [34].

$$\begin{aligned}d(t)&=\frac{{d}_{c}}{\sqrt{{\left[1-{\left(\omega /{\omega }_{mn}\right)}^{2}\right]}^{2}+{\left(2\xi \omega /{\omega }_{mn}\right)}^{2}}}\\&\quad\times\left\{\left(2\xi \omega /{\omega }_{mn}\right)\mathrm{sin}\omega t+\left[1-{\left(\omega /{\omega }_{mn}\right)}^{2}\right]\mathrm{cos}\omega t\right\}\end{aligned}$$
(5)

Thus, the harmonic response can be written compactly as in Eq. (6).

$$d(t)= A\mathrm{cos}\left(\omega t-\varnothing \right)$$
(6)
$$A=d(\omega )= \frac{{d}_{c}}{\sqrt{{\left[1-{\left(\omega /{\omega }_{mn}\right)}^{2}\right]}^{2}+{\left(2\xi \omega /{\omega }_{mn}\right)}^{2}}}$$
(7)
$$\varnothing =\varnothing (\omega )={\mathrm{tan}}^{-1}\left(\frac{2\xi \omega /{\omega }_{mn}}{1-{\left(\omega /{\omega }_{mn}\right)}^{2}}\right)$$
(8)

d(ω) determines the dynamic deflection response of the system, while ∅(ω) determines the phase angle of the steady-state response. Also, dc is the static-state response of the system and is determined as follows [35]:

$${d}_{c}=\frac{3\left(1-{v}^{2}\right)P{r}^{4}}{16E{t}^{3}}$$
(9)

Equation (7) is arranged according to the dynamic frequency applied to the diaphragm, and Eq. (10) is obtained. Dynamic sensitivity, S, is given in Eq. (11).

$$d(f)= \frac{{d}_{c}}{\sqrt{{\left[1-{\left(f/{f}_{mn}\right)}^{2}\right]}^{2}+{\left(2\xi f/{f}_{mn}\right)}^{2}}}$$
(10)

Throughout the study, the terms sensitivity and dynamic sensitivity are used interchangeably.

$$S=\frac{d(f)}{P}$$
(11)

The natural resonance frequency of the diaphragm is fmn, given by Eq. (12) [36]. The deflections of a smooth thick flexible circular diaphragm fixed to a rigid circular frame are solutions of the two-dimensional wave equation. The natural modes of vibration and mode shapes are defined by (m,n). The index m = 0, 1, 2 corresponds to the number of diameter lines with zero displacements on the diaphragm, while n = 1, 2, 3 corresponds to the number of circumferential lines with zero displacements. In other words, m and n relate to the node diameters and number of knot circles, respectively [36]. Since the frequency mode with the highest sensitivity is f01, this study focused on the frequency of f01. The natural resonance frequency value expressed in the article is f01.

$${f}_{mn}=\frac{{\varphi }_{mn}^{2}}{{2\pi r}^{2}}\sqrt{\frac{E{t}^{2}}{12\rho (1-{v}^{2})}}$$
(12)

For a diaphragm that is in contact with an inviscid and incompressible fluid with density ρ' on one side, the presence of the fluid causes the vibration to be dampened due to the energy driven by lowering frequency and sound waves due to increased inertia. Therefore, this type of damping is known as acoustic radiation or additional mass effect. The kinetic energy of the liquid in contact with the diaphragm is expressed following Lamb [37]:

$${T}_{f}=0.0102{\rho }^{^{\prime}}r{d}_{c}$$
(13)

The resonance frequency of the diaphragm inside the fluid is reduced by an added virtual mass incremental (AVMI) factor β [26].

$$\frac{{T}_{f}+{T}_{d}}{{T}_{d}}=1+\beta$$
(14)
$$\beta =0.6689\frac{{\rho }^{^{\prime}}}{\rho }\frac{r}{t}$$
(15)
$${f}_{f}=\frac{{f}_{mn}}{\sqrt{1+\beta }}$$
(16)

2 Results and discussion

In this study, circular diaphragms with a clamped edge are modeled and analyzed using MATLAB. In the program, with Eq. (11) for dynamic sensitivity, Eq. (12) for diaphragm air natural resonance frequency, and Eq. (16) for water, the natural resonance frequency is used. In the multiple parameter implementation (MPI) with MATLAB software of modeled structures, the effects of factors such as different diaphragm materials, damping values, media, geometric dimensions on the dynamic sensitivity, and frequency were investigated. In this way, sensor parameters such as bandwidth, sensitivity, and linearity were determined for a DB-S/DPS. Although there are many theoretical and experimental studies for diaphragms, the formulas applied in these studies are generally carried out in static and non-damped media, but all experiments are carried out in opposite conditions. The effects of dynamic parameters on sensor parameters cannot be seen. This situation reveals a contradiction between theoretical and experimental studies, and for this reason, the importance of the diaphragm dynamic response is increased. For this purpose, a comprehensive analysis is carried out. In the analyses, silica, silicon, graphene, gold, aluminum, and CTA were used as diaphragm materials and in geometric dimensions r = 0–8 mm, t = 0–50 µm. As the OM, air for the microphone applications, water for hydroponics applications, and mineral oil for partial discharge applications were selected. The mechanical properties of the materials used in the study are given in Table 2.

Table 2 Mechanical properties of materials
Full size table

2.1 The effect of damping ratio, AVMI factor, and frequency on dynamic sensitivity

In this study, we first focused on the vibration damping ratio of the diaphragm, which we think has an important effect on the sensor parameters mentioned above [38]. In general, damping can be caused by energy distributed internally in the diaphragm material and energy flow to the surrounding fluid. This physical condition is more effective than the other and is commonly used to determine the damping coefficient in the design of pressure sensors. An example of this is the inclusion of a perforated backplate in many condenser microphones to increase damping [39]. Studies have demonstrated that damping is an important factor in sensor design [40, 41]. The inclusion of damping by nonlinear and linear analysis to increase bandwidth and reduce the nonlinear effect further flattens the sensor diaphragm frequency response. In Fig. 1, dynamic sensitivity versus frequency is given at different damping values for different diaphragm materials in an air medium. As noted by Yu and Balachandran, as the ξ value increases, the behavior of the dynamic sensitivity evolves from a sharp resonance peak to a flatter response. In this case, the diaphragm causes an increase in bandwidth of full width at half maximum (FWHM). Moreover, as the ξ value increases, the frequency sensitivity decreases, thus reducing the dynamic sensitivity. In partial discharge determination in transformers, it is generally preferred that the sensor be a flat response since the resonance frequency (partial discharge formation band at 20–200 kHz) of discharge is not fully known. Similarly, in optical microphone applications, a flat response sensor is preferred because detection is performed on a certain sound band (1–10 kHz). In a special case such as a non-damped system, where ξ = 0, the graph shows a discontinuity at Eq. (10) for f/fmn = 1, at which point the flexural amplitude becomes infinite, which is called resonance. Since it is not possible to have infinite displacement of the diaphragm in physical systems, the deflection should be limited by not stimulating at the resonance frequency. The solution of the system is made by assuming that the displacements are small enough to remain in the linear range. Therefore, a separate solution must be produced for a system without damping in resonance. However, the graph of the frequency response corresponding to ξ = 0 serves as a warning that the system may experience severe vibration when the excitation frequency passes through resonance. At the same time, if excitation is made at a frequency close to the natural resonance frequency of the diaphragm, the deflection response of the diaphragm also behaves as a nonlinear response. Therefore, it is not possible to operate the sensor in the linear region. In a sensor design, the nonlinear effect is not desired. Therefore, if the sensor remains in the linear region, excitation should be made at values less than one-third of the natural resonance frequency value [42].

Fig. 1
figure 1

Dynamic sensitivity versus frequency at different ξ values with various diaphragm materials in air

Full size image

When the OM changes, that is, when the AVMI factor is included in the calculation, MPI has been carried out in media such as water and mineral oil outside the air to investigate how the sensor affects its dynamic sensitivity. Since water and mineral oil showed very similar results in the analyses, the analyses were continued with water instead of oil. The natural frequency of a vibrating diaphragm decreases when it comes into contact with a fluid [37], a special case caused by the induced vibration of the fluid. While the vibration continues through the fluid, it can be considered as a layer of fluid that is coupled to the diaphragm and vibrates with the diaphragm. Assuming that it exists, the diaphragm vibrates as if its mass has grown by the mass of fluid that vibrates virtually, resulting in the natural resonance frequency decreasing. This special case is called an additional virtual mass effect. The original classical analysis of the problem by Lamb [37] is important in this regard and proceeds according to the stages specified below. The analysis content is the stretching of a thin circular deflectable diaphragm, which is clamped against a hard wall. Its natural mode in a vacuum is explained by the theory of flexibility [22]. It is estimated that the vibration mode remains unchanged when the plate contacts a liquid. To determine the vibration of the fluid, the fluid is considered incompressible and invisible, and therefore its speed is derived from a speed potential. The speed of the fluid must match the overall speed of the diaphragm at the diaphragm boundary. Besides, the kinetic energies of the diaphragm and fluid are determined, and the ratio of the fluid to that of the diaphragm determines the added virtual mass. The difference between Figs. 1 and 2 is the transition of the OM from air to water, respectively. As noted above, although there is no change in the behavior of the materials in the measurements in water, consistent with Eq. (16), a significant decrease in their natural frequency in the liquid was noticed. While ξ reduces the dynamic sensitivity, it is seen that the AVMI factor β decreases the natural frequency.

Fig. 2
figure 2

Dynamic sensitivity versus frequency at different ξ values with various diaphragm materials in water

Full size image

In Fig. 3, sensitivity versus frequency behaviors of different diaphragm materials are given in air and water. The figure shows the effects of different ξ (0.01, 0.05, 0.07) values. The results obtained by increasing the ξ values in Fig. 3 are given in Fig. 4. In Fig. 5, the dynamic responses of the diaphragms in the MHz band are shown. As seen in Figs. 3, 4, and 5, although the dynamic sensitivity of graphene is low, natural frequencies are much higher than other materials. Since graphene was first isolated by Stankovich et al. [43], it has aroused great curiosity due to its remarkable properties. Graphene also has very high mechanical strength and can be stretched up to 20% [44]. It is the thinnest natural diaphragm, with a thickness of approximately 0.335 nm, which enables it to oscillate at high frequencies. In this respect, it is a very suitable material for biomedical imaging [45] and photoacoustic detection [46] applications performed in the megahertz frequency band. CTA differs markedly from other materials such as graphene, and demonstrates very high dynamic sensitivity in the audible frequency range. It is an important cellulose derived from an organic acid-based natural polymer. The CTA film surface is smooth and has good optical and mechanical properties. It is also resistant to water and oil, and even solvents such as acetone [15]. With its low density and a satisfactory Poisson ratio, its dynamic sensitivity is higher than that of other materials. With these features, the optical microphone is very suitable for sound and pressure sensing applications at very low amplitudes. Although silica is a glass derivative and aluminum is a metallic material, the sensitivity and frequency response are both very similar when the geometric dimensions and selected OM are taken into consideration. While gold has a lower value than the frequency values of silica and Al in air, it gives the same frequency values in water. Because, as seen in Table 2, the density value of Au is much higher than the medium densities, in Eq. (15) the effect of the AVMI factor decreases. For this reason, there is very little change in the frequency value in water in Eq. (16). Since the opposite situation is seen in the case of other materials, the frequency shifts were higher. Detailed analyses are available in our previous study [47].

Fig. 3
figure 3

Dynamic sensitivity versus frequency at low ξ values with various diaphragm materials in air and water

Full size image
Fig. 4
figure 4

Dynamic sensitivity versus frequency (in the kHz band) at high ξ values with various diaphragm materials in air and water

Full size image
Fig. 5
figure 5

Dynamic sensitivity versus frequency (in the MHz band) at high ξ values with various diaphragm materials in air and water

Full size image

2.2 The effect of diaphragm radius on dynamic sensitivity

We have already mentioned that when designing a pressure sensor, the diaphragm should be smaller than the first natural frequency to ensure sensor linearity. In determining this situation, besides the mechanical properties of the diaphragm and whether the medium is damped, the geometric size of the diaphragm is an important parameter. The effects of circular diaphragm sizes are vital for micromachined pressure sensors [48]. By reducing the radius, increasing the thickness, or increasing the tension parameter, the first natural frequency of the diaphragm can be increased, which increases the sensor bandwidth. However, the exchanges between bandwidth and sensitivity should be carefully studied. High sensitivity does not always mean broad bandwidth, or it can sometimes happen in a contrasting situation. Considering that the sensing event is based on a pressure-dependent diaphragm deflection measurement, precision is related to the displacement of the diaphragm center for unit pressure. Within these comments, it may be thought that it is possible to design a sensor with both wide bandwidth and high sensitivity by applying the tension determined by establishing the best relationship between bandwidth and sensitivity and reducing the diaphragm thickness or increasing the radius. In the graphs from Figs. 6, 7, 8, and 9, the changes in dynamic sensitivity according to the radius of the diaphragm are shown for different media, frequency, and ξ. Figure 6 was performed with signal excitation ranging from 1 to 10 kHz by selecting ξ = 0.3 and t = 30 µm in air. As can be seen from the graphs, the dynamic sensitivity increases as the excitation frequency decreases, and the radius increases. While the sensitivity is expected to increase continuously with increasing radius in Fig. 6, it is determined that the sensitivity decreases and then remains constant after a certain radius value. Of course, this can be determined by the spectral content of dynamic sensitivity. This constant sensitivity is lower in water, and as can be seen from Fig. 7, the behavior varied within a narrower radius range. In Fig. 7, there are serious decreases in dynamic sensitivities due to the increased weight effect with the inclusion of the AVMI factor. Additionally, due to the natural frequency of the diaphragm falling due to the AVMI factor effect, the radius in which the maximum sensitivity in the frequency in air was obtained in smaller radii in water. In DB-S/DPS designs, it is desirable to have sensor sizes as small as possible. As an example of this situation, in Fig. 6, from the point of obtaining both a small and sensitive sensor, it is observed that CTA provides high dynamic sensitivity using small radii.

Fig. 6
figure 6

Dynamic sensitivity versus radius at different frequencies with various diaphragm materials in air (ξ = 0.3)

Full size image
Fig. 7
figure 7

Dynamic sensitivity versus radius at different frequencies with various diaphragm materials in water (ξ = 0.3)

Full size image

Figure 8 was performed with signal excitation of 1 to 10 kHz in air by selecting ξ = 0.7 and t = 30 µm, while Fig. 9 was performed with signal excitation of 1 to 10 kHz by selecting ξ = 0.7 and t = 30 µm in water. Figure 8 refers to the behavior that shows the typical radius-static sensitivity relationship in the literature. But this behavior corresponds to one of the four different situations examined in this study. These four states are low damped air, high damped air, low damped water, and high damped water. With increasing ξ, according to Fig. 6, the radius at which the maximum precision was achieved in Fig. 8 has grown, and after this value, the sensitivity has not decreased and remained constant. It is seen that as the damping increases, the radius should be increased to increase the sensitivity, but after a certain value, the sensitivity of the diaphragm becomes independent from the radius. This situation reveals how important the dynamic field effect is again. Because as the radius increases, d(c) will increase, but the falling frequency and the spectral content of ξ and d(f) stabilized it by balancing it.

Fig. 8
figure 8

Dynamic sensitivity versus radius at different frequencies with various diaphragm materials in air (ξ = 0.7)

Full size image
Fig. 9
figure 9

Dynamic sensitivity versus radius at different frequencies with various diaphragm materials in water (ξ = 0.7)

Full size image

2.3 The effect of diaphragm thickness on dynamic sensitivity

Data related to another diaphragm parameter, thickness, are given in Figs. 10, 11, 12, and 13. As mentioned above, when the radius is increased (Figs. 6, 7, 8, 9) and the thickness is reduced (Figs. 10, 11, 12, 13), the displacement amplitude of a diaphragm center will increase. In this way, the first natural frequency will decrease, and a smaller sensor bandwidth will be obtained. This raises another problem between sensor bandwidth and sensitivity which must be dealt with in designing a sensor. Thin diaphragms exhibit higher sensitivity with greater deflection. However, thinning in the diaphragm causes an increase in the nonlinearity. Thus, it is necessary to establish a balance between sensitivity and linearity [49]. In Fig. 10, a decrease in the dynamic sensitivity is observed with increasing radius. However, after this decrease, the dynamic sensitivity increases with increasing frequency which is approaching the natural frequency of the diaphragm. Along with the changing thickness, the natural resonance frequency of the diaphragm changes, and where this value equals the excitation frequency, maximum dynamic sensitivity occurs. Therefore, the effect of both thickness and frequency can be interpreted simultaneously. As can be seen from the graphs, sensitivity decreases with increasing thickness and reaches a minimum value at a certain thickness. With a further increase in thickness, sensitivity starts to increase until the thickness corresponding to the resonance frequency value. At this point, increased dynamic sensitivity is not expected. This situation, which is ignored in the literature, is a result of the dynamic content of sensitivity.

Fig. 10
figure 10

Dynamic sensitivity versus thickness at different frequencies with various diaphragm materials in air (ξ = 0.1)

Full size image

In Fig. 11, only the medium was determined as water without changing the other parameters. With the increase in thickness in Fig. 11, the dynamic sensitivity did not decrease very quickly as in Fig. 10. Increasing thickness with the effect of the AVMI factor could not increase the natural frequency; therefore, the sensitivity remained constant and then increased in thickness values close to resonance. As seen in Fig. 11, the sensitivity of aluminum in air is two to eight times that of other materials, and it reaches the same level in water as the other materials. Considering the thicknesses between 0 and 50 µm, depending on the radius values used in the analyses, the resonance frequency effect seen in the other five materials is not seen in the CTA. If higher thicknesses are chosen, the CTA will respond similarly.

Fig. 11
figure 11

Dynamic sensitivity versus thickness at different frequencies with various diaphragm materials in water (ξ = 0.1)

Full size image

In Fig. 12, taking ξ = 0.7, the change in sensitivity according to the diaphragm thickness at different frequency values and air media is shown for different diaphragm materials. Figure 12 shows the typical thickness–static sensitivity relationship reported in the literature. But this behavior corresponds to one of the four different situations examined in this study. In this way, the effect of the increased damping of the diaphragm was observed clearly. Even a small increase in thickness reduced the dynamic sensitivity very quickly, and the sensitivity could not be increased again. High damping suppressed the effect of the frequency increase, preventing the diaphragm from oscillating. Figure 13 was performed with signal excitation of 1 kHz to 10 kHz by selecting ξ = 0.7 and t = 30 µm in water. In this graph, the dynamic sensitivity is first unresponsive to the increase in thickness and then decreases as expected. Increased thickness could not increase the fmn much due to the effect of the AVMI factor. Although the decrease in static sensitivity decreases the numerator of Eq. (10), the decrease in dynamic sensitivity is very slow, as the increase in the denominator remains limited. At resonance frequency and subsequent thicknesses, the value of the denominator increases, and the dynamic sensitivity decreases very rapidly.

Fig. 12
figure 12

Dynamic sensitivity versus thickness at different frequencies with various diaphragm materials in air (ξ = 0.7)

Full size image
Fig. 13
figure 13

Dynamic sensitivity versus thickness at different frequencies with various diaphragm materials in water (ξ = 0.7)

Full size image

3 Conclusion

In the present work, the dynamic pressure performance of diaphragms in a DB-S/DPS design was investigated, and the effects of different diaphragm materials (silica, silicon, graphene, gold, aluminum, CTA) and different media (air, water, oil) on the sensor parameters were determined. Following a theoretical study, multiple parameter analyses were performed. With the study, forced oscillations are considered for the dynamic deflection value of the diaphragm, which is not mentioned in the literature. In these analyses, the changes of the diaphragm vibration-damping values according to the OM and materials and as a result, the effects on dynamic sensitivity are shown. Besides, thanks to these analyses, the necessary mechanical properties and geometric dimensions of the sensor diaphragm were determined under the desired working conditions. The effects of many possible parameters on the dynamic sensitivity of the diaphragm at the same time are revealed through the graphs obtained from the theoretical results. With this study, very extensive and impressive research was carried out to shed light on the process of determining DB-S/DPS design parameters.