1 Introduction

Organic thin-film transistors (OTFTs) have emerged as a subject of intensive research owing to their applications in low-cost electronic circuits such as large area flexible displays, electronic paper (e-paper), radio frequency identification tags (RFIDs), bio-medical applications such as electronic skin (e-skin), electronic nose (e-nose) and smart fabrics [1, 2]. OTFTs are also finding applications in various analog and digital electronic circuits, and new techniques are being devised in improving the performance of organic-based electronic circuits [3, 4]. The idea of introducing plastic logic is not that of attaining the performance of silicon but of replacing silicon with low-cost organic circuits for low-end applications. The development of organic electronics into a commercial technology requires the design and testing of OTFT-based circuits in electronic design automation (EDA) software. This necessitates the design and development of analytical models and processes generic to organic materials. Till now the MOSFET models have used for the design and simulation of OTFTs. But the MOSFET models have been developed for the inversion mode operation and the mobility behavior of the inorganic materials. The application of MOSFET models for the design and simulation of OTFTs have been proved as a viable option in predicting the performance of these devices. But the current–voltage and other characteristics of OTFTs show some significant deviations from the behavior as predicted by MOSFET theory [5]. Thus, the MOSFET models generic to inorganic materials are not reliable in accurately predicting the performance of OTFTs as the charge transport mechanism and operation in OTFTs is different than in silicon-based transistors. The non-reliability of MOSFET models to OTFTs becomes more pronounced as new techniques are devised towards the performance improvement of OTFTs, such as channel length scaling, mobility enhancement techniques and use of high-k dielectric materials [6]. The trap states which are inevitable in disordered organic semiconductors are not taken into account in MOS (metal-oxide semiconductor) models [7]. The effect of trap states on the OTFTs performance is simulated by incorporating traps specific parameters in device simulation. Thus, it becomes imperative to analyze and design the device models for OTFTs taking into account the material and behavioral parameters of organic materials.

The development of analytical models generic to organic thin-film transistors (OTFTs) has been a topic of great research interest since a decade, and significant amount of research work has been reported. In [8], a report on the modeling of direct current (DC) characteristics of organic pentacene thin-film transistors in the top-contact and bottom-contact configuration has been presented. The modeling work presented in [8] is based on the characteristic equations of the inorganic MOSFET transistors. The model incorporates a highly nonlinear drain and source contact series resistances. But the investigation and modeling of trap states and their effect on the DC characteristics of the device have not been studied. A TFT generic charge drift model has been derived in [9] based on threshold voltage model, and a Level 1 TFT compact DC model has been proposed. The paper has focused on redefining the current–voltage equations of OTFTs, but only the mobility enhancement factor because of vertical electric field has been considered. A parameter extraction methodology and the verification of a generic analytical model and a TFT compact DC model derived in [9] for the current–voltage characteristics of OTFTs have been presented in [10]. It has been found that the models proposed in [9] meet the requirements for compact modeling and that TFT generic model can be denoted as level 0 in SPICE and TFT compact model at level 1. The electrical characteristics of thin-film field-effect transistors based on organic materials have been modeled in [11]. However, the paper carries the modeling analysis of OTFTs as trap-free materials and is based on linear charge–voltage relation. In [12], the electrical characteristics of OTFTs have been modeled taking into account the effect of trap states and impurities. The supra-linear behavior of the observed current–voltage characteristics has been explained within the framework of trap states by assuming a field-assisted thermal excitation from trap states as proposed by Poole and Frenkel. Stallinga and Gomes [13] have presented an important interpretation of the distribution of trap states on the I–V characteristics. The work presented explains the bias and temperature dependence of the field-effect mobility. When the trap states are discrete in nature, the mobility is only temperature dependent, but when trap states are distributed exponentially in energy, the mobility also becomes bias dependent. A universal compact model for long and short-channel thin-film transistors has been presented in [14]. The authors have developed an eight-parameter universal TFT model making the parameter extraction easier. The work also presents the effect of a contact transistor between the source and the channel in order to model the nonlinear contact effects especially at short-channel lengths.

This paper presents a complete mathematical model of the OTFTs taking into account the influence of trap states. The trap states which are inevitable in organic semiconductors because of their irregular structure have been approximated by an exponential trap density function and the influence of change in the density of trap states and the characteristic decay rate on the electrical characteristics of OTFTs has been studied. An effective mobility model for OTFTs has been derived for the first time taking into account the Poole–Frenkel mobility behavior and also the surface mobility model. A capacitance model based on the unified charge control model (UCCM) of MOSFETs taking into account the trap capacitance has been reported for the first time, and the capacitive behavior of OTFTs has been explained in its context.

2 OTFT modeling

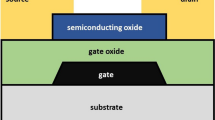
This section presents the derivation of mathematical equations for the analytical modeling of OTFTs. The surface charge equations, mobility model, current–voltage equations and the capacitance model of OTFTs have been derived. The schematic of the OTFT adopted in the bottom-contact configuration with pentacene as the active layer is shown in Fig. 1 [15].

Fig. 1
figure 1

Schematic of OTFT [15]

Full size image

The bottom-contact configuration of OTFTs is preferred over the top-contact as the metal electrodes are patterned first and the soft organic semiconductor is deposited on top and protected from the harsh chemicals [16]. Pentacene is a p-type semiconductor and exhibits grain-like structure, thus trap states are inevitable because of grain boundaries [16]. The effect of trap states on the device performance cannot be neglected and must be taken into account in device modeling. Traps can be neutral (N 0T ) or become positively charged (N +T ) by capturing free holes [12]. Trap states are distributed in energy between the HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) and can be deep or shallow [17]. The density of traps in deep states has been explained by the Gaussian distribution and the shallow states by an exponential distribution as shown in Fig. 2 [18, 19]. In this paper, we have considered the shallow trap states into modeling and analysis of OTFTs because these traps being close to the valence band edge will capture the holes at small values of applied bias compared to the deep traps. Both the trap states have an effect on the charge conduction in OTFTs resulting in performance deterioration, but the role of shallow trap states is more significant as they are subject to continuous trapping and detrapping of free carriers because of being near to the band edges. The movement of charge in an organic semiconductor with the trap states has been explained by the combined effect of multiple trap and release model (MTR) and Poole–Frenkel model using band theory [20].

Fig. 2
figure 2

A simplified model illustrating the trap density of states in an organic material [18]

Full size image

2.1 Surface charge modeling

At small values of gate-source voltages (VGS), the charge carriers induced are captured by the trap states and once all the trap states are filled with increasing VGS, the free charge carrier density increases resulting in the flow of current in the device [9]. Thus the gate charge must balance the free charge carriers induced in the channel and the trapped charge density. This results in an increase in the threshold voltage (VTH) [15].

The basic Poisson’s equation can then be modified to include the trap density of states

$$\frac{{{\text{d}}^{2} \psi }}{{{\text{d}}x^{2} }} = \frac{ - \rho }{{\varepsilon_{\text{s}} }} = \frac{ - q}{{\varepsilon_{\text{s}} }}(p - n + N_{\text{D}}^{ + } - N_{\text{A}}^{ - } + N_{\text{T}}^{ + } )$$
(1)

The pentacene is assumed to be intrinsic, N +D =0, N −A  = 0.

The density of holes has been approximated in [12] as:

$$p(x) = N_{\text{V}} \exp \left[ {\frac{{(E_{\text{V}} - E_{\text{F}} }}{kT}} \right]$$
(2)

The density of trap states shows dependence on the position of Fermi level as defined in [12]:

$$N_{\text{T}}^{ + } (E_{\text{F}} ) = N_{0} (T)\exp \left[ {\frac{{(E_{\text{V}} - E_{\text{F}} )}}{{kT_{2} }}} \right]$$
(3)

and

$$N_{0} (T) = \alpha (T)g_{T0} \frac{{k^{2} T_{2}^{2} }}{{kT_{2} - kT}}$$
(4)

N0 is a function of temperature but not of the position of Fermi level, α(T) is a slowly varying, dimensionless function depending only on the temperature and compensates for the error of integration, gT0 is the density of states at E = EV and T2 is the decay rate or characteristic energy. Numerical simulations show that α(T) oscillates between 1 and 0.8 [12].

Substituting Eqs. (2) and (3) in (1), the electric field perpendicular to the interface can be solved as

$$E(x) = \sqrt {\frac{{2kTN_{\text{V}} }}{{\varepsilon_{\text{S}} }}} \cdot F(\psi )$$
(5)

where F(ψ) is the potential and is given by

$$F(\psi ) = \sqrt {\left( {{\text{e}}^{{\frac{ - q\psi (x)}{kT}}} + \frac{q\psi }{kT} - 1} \right) + \frac{{n_{i}^{2} }}{{N_{V}^{2} }}\left( {{\text{e}}^{{\frac{q\psi (x)}{kT}}} - \frac{q\psi }{kT} - 1} \right) + \frac{{N_{0} (T) \cdot T_{2} }}{{N_{V} \cdot T}}\left( {{\text{e}}^{{\frac{ - q\psi (x)}{{kT_{2} }}}} - 1} \right)}$$
(6)

The potential F(ψ) given by Eq. (6) is the same as the potential equation of MOS transistors except for the last term in the brackets which takes into account the effect of trap states for analysis of OTFTs.

For the accumulation mode operation, \({\text{e}}^{{\frac{ - q\psi \left( x \right)}{kT}}}\) term dominates in Eq. (6) and other terms can be neglected. At x = 0, ψ(0) = ψs is the surface potential then:

$$F(\psi_{\text{s}} ) = \sqrt {\left( {{\text{e}}^{{\frac{ - q\psi (x)}{kT}}} } \right) + \frac{{N_{0} (T) \cdot T_{2} }}{{N_{V} \cdot T}}\left( {{\text{e}}^{{\frac{ - q\psi (x)}{{kT_{2} }}}} } \right)}$$
(7)

The surface electric field is then given by

$$E_{\text{s}} = \sqrt {\frac{{2kTN_{\text{V}} }}{{\varepsilon_{\text{S}} }}} \cdot F(\psi_{\text{s}} )$$
(8)

The total charge in semiconductor can be found as per Gauss’s law [20]:

$$Q_{\text{s}} (\psi_{\text{s}} ) = \varepsilon_{\text{s}} \cdot E_{\text{s}}$$
(9)
$$Q_{\text{s}} = \sqrt {2kTN_{\text{V}} \varepsilon_{\text{s}} } \cdot F(\psi_{\text{S}} )$$
(10)

Equation (10) gives us a simple way of estimating the surface charge induced in the channel taking into account the trap states. Qs is used to represent the total charge density in different modes of device operation.

The surface potential can be estimated from Eq. (10) using the following relation [21]

$$V_{\text{GS}} - V_{\text{FB}} - \psi_{\text{s}} = \frac{{ - Q_{\text{S}} }}{{C_{\text{OX}} }}$$
(11)

where VFB is the flat-band voltage incorporating the workfunction difference between the metal gate and semiconductor contact.

2.2 Mobility modeling

The mobility behavior of OTFTs is far more complex compared to the inorganic transistors. The supra-linear increase in the drain current observed at low values of drain-source voltage (VDS) has been attributed to the field-induced enhancement in mobility and is defined by the Poole–Frenkel (PF) mobility model [22]. The carrier mobility defined by Poole–Frenkel mobility model is expressed in Eq. (12) [4, 23]:

$$\mu_{\text{PF}} \left( E \right) = \mu_{0} \exp \left[ { - \frac{\Delta }{kT} + \left( {\frac{\beta }{kT} - \delta } \right)\sqrt E } \right]$$
(12)

where \(\mu_{\text{PF}} \left( E \right)\) is the field-dependent mobility, µ0 is the zero field mobility, Δ is the zero field activation energy, β is the electron Poole–Frenkel factor, γ is the fitting parameter, k is the Boltzmann constant, and T is the temperature. PF mobility model explains both the temperature and field dependence of carrier mobility in OTFTs.

However, it has been reported from the simulation studies that OTFTs show a field-induced mobility degradation which gets enhanced at short-channel lengths [23, 24]. This mobility degradation is attributed to the surface roughness and scattering of charge carriers due to grain structure of pentacene and interface traps [25, 26]. Simulation results carried on OTFTs in ATLAS have shown that the surface mobility model (SURFMOB) derived by Watt is compatible for predicting this mobility degradation behavior in OTFTs [25]. Thus, a mobility model which is valid at all channel lengths can be derived from PF mobility model and the SURFMOB model.

The effective hole mobility in the Watt model is given by [27]:

$$\begin{aligned} \frac{1}{{\mu_{\text{eff,p}} }} = \frac{1}{{{\text{MREF1P}} . {\text{WATT}}}}\left( {\frac{{10^{6} }}{{E_{\text{eff,p}} }}} \right)^{ - 0.29} + \frac{1}{{{\text{MREF2P}} . {\text{WATT}}}}\left( {\frac{{10^{6} }}{{E_{\text{eff,p}} }}} \right)^{ - 1.62} \\ + \frac{1}{{{\text{MREF3P}} . {\text{WATT}}}}\left( {\frac{{10^{18} }}{{N_{\text{B}} }}} \right)^{ - 1} \left( {\frac{{10^{12} }}{{N_{i} }}} \right)^{ - 1} \\ \end{aligned}$$
(13)
$$E_{\text{eff,p}} = E_{ \bot } + {\text{ETAP}} . {\text{WATT}}(E_{0} - E_{ \bot } )$$
(14)

where \(E_{\text{eff,p}}\) is the effective electric field given by Eq. (14), NB is the surface trapped charge density, and Ni is the inversion layer charge density. Equation (13) gives the effective hole mobility in terms of three scattering mechanism, where the first term corresponds to phonon scattering, the second term corresponds to surface roughness, and third term corresponds to charged impurity scattering. The first two terms take into account the electric field effects and are important for modeling mobility behavior in organic semiconductors. These two terms correspond to universal field-mobility relation. ETAP.WATT in Eq. (14) is a fitting parameter of value 0.33, E⊥ is the electric field perpendicular to the current flow, and E0 is the field perpendicular at insulator–semiconductor interface. The pre-exponents in the three terms of Eq. (13) are constants, and their values are given in the WATT model at T = 300 K.

The trapped charge density in the OTFTs is proportional to the density of trap states. Therefore, replacing the NB in Eq. (13) by NV and neglecting Ni term gives

$$\begin{aligned} \frac{1}{{\mu_{\text{eff,p}} }} & = \frac{1}{{{\text{MREF1P}} . {\text{WATT}}}}\left( {\frac{{10^{6} }}{{E_{\text{eff,p}} }}} \right)^{ - 0.29} + \frac{1}{{{\text{MREF2P}} . {\text{WATT}}}}\left( {\frac{{10^{6} }}{{E_{\text{eff,p}} }}} \right)^{ - 1.62} \\ & \quad + \frac{1}{{{\text{MREF3P}} . {\text{WATT}}}}\left( {\frac{{10^{18} }}{{N_{\text{V}} }}} \right)^{ - 1} \\ \end{aligned}$$
(15)

The resultant carrier mobility of OTFTs can be modeled from Eqs. (12) and (15) and combined using Matthiessen’s rule for mobility [9]. The rule states that the different functions independent of each other but having an effect on some resulting parameter can be combined using equation:

$$\frac{1}{U} = \frac{{a_{x} }}{X} + \frac{{b_{x} }}{Y} - \frac{{a_{z} }}{Z}\left( { \pm \frac{{a_{v} }}{V} \ldots .} \right)$$

where X, Y, Z (, V..) are different functions for one quantity, e.g., mobility or current; U is the resulting value for the same quantity; ax, ay, az… are weighting parameters, usually taken as unity; and the sign (+) is used to limit, whereas the sign (−) is used to enhance the value of U.

The resultant mobility of OTFTs is given by

$$\frac{1}{{\mu_{\text{OTFT}} }} = \frac{1}{{\mu_{0} }} + \frac{1}{{\mu_{\text{PF}} }} + \frac{1}{{\mu_{\text{eff,P}} }}$$
(16)

where µ0 is the zero field carrier mobility, µPF is given by Eq. (12), and µeff,P is given by Eq. (15), respectively.

2.3 Current–voltage relation

Considering the device shown in Fig. 1 with channel length L and width W, p as the concentration of holes and N +T as the concentration of ionized traps, the charge–voltage equation can be written as

$$Q_{\text{p}} (x) = p + N_{T}^{ + } = - C_{\text{OX}} (V_{\text{GS}} - V_{\text{TH}} - V_{\text{X}} )$$
(17)

where Qp(x) represents the positive charge at a point x along the channel, i.e., holes in the organic semiconductor; VX is the voltage with respect to source at the coordinate x.

Using gradual channel approximation (i.e., magnitude of change in electric field along x is negligible with respect to that along y), the current can be given by [13, 28]:

$$I(x) = - \mu_{\text{p}} WQ_{\text{p}} (x) \cdot \frac{{{\text{d}}V}}{{{\text{d}}x}}$$
(18)

Substituting expressions for p and N +T from Eqs. (2) and (3) in (17) and simplifying, we get

$$p + p^{{{\raise0.7ex\hbox{$T$} \!\mathord{\left/ {\vphantom {T {T_{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T_{2} }$}}}} \left( {\frac{{N_{o} (T)}}{{N_{V}^{{{\raise0.7ex\hbox{$T$} \!\mathord{\left/ {\vphantom {T {T_{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T_{2} }$}}}} }}} \right) = - C_{\text{OX}} (V_{\text{GS}} - V_{\text{TH}} - V_{\text{X}} )$$
(19)

For high density of trap states, the first term on L.H.S. of Eq. (19) is negligible. Upon simplifying we get

$$p(V_{\text{GS}} ) = N_{\text{V}} \left( {\frac{{ - C_{\text{OX}} (V_{\text{GS}} - V_{\text{TH}} - V_{\text{X}} )}}{{N_{\text{o}} (T)}}} \right)^{{{\raise0.7ex\hbox{${T_{2} }$} \!\mathord{\left/ {\vphantom {{T_{2} } T}}\right.\kern-0pt} \!\lower0.7ex\hbox{$T$}}}}$$
(20)

Substituting Eq. (20) into Eq. (18) and integrating the current from 0 to L.

Assuming linear mode of device operation, i.e., VDS ≤ (VGS − VTH) and let \(\gamma = \frac{{T_{2} }}{T}\)

$$\int\limits_{0}^{L} {I_{\text{D}} (x) \cdot {\text{d}}x = - \frac{{\mu_{\text{p}} WN_{\text{V}} \cdot C_{\text{OX}}^{(\gamma + 1)} }}{{N_{\text{o}} (T)^{\gamma } }}} \int\limits_{0}^{{V_{\text{DS}} }} {(V_{\text{GS}} - V_{\text{TH}} - V_{\text{X}} } )^{\gamma } \cdot {\text{d}}V$$
(21)

Equation (21) can be solved to obtain the drain current as

$$I_{\text{D}} = - \frac{{\mu_{\text{p}} WN_{V} \cdot C_{\text{OX}}^{(\gamma + 1)} }}{{LN_{\text{o}} (T)^{\gamma } }}\left( {(V_{\text{GS}} - V_{\text{TH}} )^{\gamma + 1} \cdot V_{\text{DS}} - \frac{{V_{\text{DS}}^{\gamma + 2} }}{\gamma + 2}} \right)$$
(22)

The drain current in saturation for VDS ≥ (VGS − VTH) can be obtained as

$$I_{\text{DSAT}} = - \frac{{\mu_{\text{p}} WN_{\text{V}} \cdot C_{\text{OX}}^{(\gamma + 1)} }}{{(\gamma + 2)LN_{\text{o}} (T)^{\gamma } }}\left( {(\gamma + 1)(V_{\text{GS}} - V_{\text{TH}} )^{\gamma + 2} } \right)$$
(23)

It can be easily shown that for a trap-free situation, the charge contributing to current is only free holes. Therefore, for a trap-free situation γ = 0 and Eq. (22) can be written as

$$I_{\text{D}} = - \frac{{\mu_{\text{p}} WN_{\text{V}} \cdot C_{\text{OX}}^{{}} }}{L}\left( {(V_{\text{GS}} - V_{\text{TH}} ) \cdot V_{\text{DS}} - \frac{{V_{\text{DS}}^{{}} }}{2}} \right)$$
(24)

For short-channel devices, channel length modulation cannot be neglected and the drain current can be rewritten as

$$I_{\text{D}} = I_{\text{DSAT}} (1 + \lambda V_{\text{DS}} )$$
(25)

2.4 Unified charge control model and capacitance modeling

The unified charge control model developed for MOSFETs can be extended to OTFTs [29].

The charge balance equation for OTFTs is given by

$$Q_{\text{G}} = Q_{\text{C}} + \Delta Q_{\text{T}} = Q_{\text{S}}$$
(26)

where QC is the channel charge (accumulation charge density, i.e., holes), ΔQT refers to the charge trapped in the acceptor trap states, QG is the gate charge, and QS is the total charge per unit area.

As the trap states are filled in response to the changes in surface potential, they give rise to trap capacitance per unit area, CT, defined by

$$C_{\text{T}} (\psi_{\text{S}} ) = \frac{{{\text{d}}Q_{\text{T}} (\psi_{\text{s}} )}}{{{\text{d}}\psi_{\text{S}} }}$$
(27)

The potential balance relation given in Eq. (11) can be differentiated with respect to QS;

$$\frac{{{\text{d}}V_{\text{G}} }}{{{\text{d}}Q_{\text{S}} }} = \frac{1}{{C_{\text{OX}} }} + \frac{{{\text{d}}\psi_{\text{S}} }}{{{\text{d}}(Q_{\text{C}} + Q_{\text{T}} )}}$$
(28)
$$\frac{1}{{C_{\text{GB}} }} = \frac{1}{{C_{\text{OX}} }} + \frac{1}{{(C_{\text{C}} + C_{\text{T}} )}}$$
(29)

Equation (30) shows that the traps contribute a capacitance in parallel to the channel capacitance.

The MOS three terminal charge balance equation can be applied to OTFTs to obtain [30];

$$\frac{{{\text{d}}V_{\text{G}} }}{{{\text{d}}\psi_{\text{S}} }} = 1 + \frac{1}{{C_{\text{OX}} }}\frac{\text{d}}{{{\text{d}}\psi_{\text{S}} }}\left( {Q_{\text{C}} (\psi_{\text{S}} ) + Q_{\text{T}} (\psi_{\text{S}} )} \right)$$
(30)

The surface charge density from the MOS unified charge theory can be approximated as [30, 31]:

$${\text{d}}Q_{\text{S}} = (C_{\text{C}} + C_{\text{T}} ){\text{d}}\psi_{\text{S}}$$
(31)

Substituting Eq. (31) into Eq. (30) gives

$$\frac{{{\text{d}}Q_{\text{S}} }}{{{\text{d}}V_{\text{G}} }} = \frac{{\left( {C_{\text{c}} + C_{\text{T}} } \right) \cdot C_{\text{OX}} }}{{C_{\text{C}} + C_{\text{T}} + C_{\text{OX}} }}$$
(32)

Equation (32) is equivalent to the small signal capacitance model shown in Fig. 3.

Fig. 3
figure 3

Equivalent capacitance model of OTFT

Full size image

Since OTFTs operate in accumulation, therefore channel capacitance Cc = Cox, and thus Eq. (31) can be rewritten as;

$${\text{d}}Q_{\text{S}} = (C_{\text{ox}} + C_{\text{T}} ){\text{d}}\psi_{\text{S}} = \eta C_{\text{ox}} {\text{d}}\psi_{\text{S}}$$
(33)

where \(\eta = 1 + \frac{{C_{\text{T}} }}{{C_{\text{ox}} }}\) is the slope factor.

3 Results and discussion

In this section, the mathematical modeling equations derived in section II for OTFTs are plotted to evaluate the validity of the model. Table 1 lists the values of device parameters used in modeling results and has been adopted from the literature [23, 27]. The variation of charge density as a function of surface potential for different values of trap states is plotted in Fig. 4. The OTFTs being accumulation devices, thus for negative values of ψs the first and third terms of Eq. (10) dominate and the charge density increases exponentially. At flat-band condition, ψs = 0 and hence Qs = 0. For positive values of ψs, QS starts to increase but shows an exponential rise only when ψs is sufficiently positive to induce inversion. Further as the value of trap states is increased, the total charge density shows an increase as predicted by Eq. (10).

Table 1 Model parameters used in mathematical equations
Full size table
Fig. 4
figure 4

Variation of total charge density as a function of surface potential for different values of trap states

Full size image

Figure 5 shows the variation of surface potential with respect to gate voltage approximated from Eq. (11). Results show that the surface potential varies linearly with gate voltage and saturates for high values of gate voltage indicating strong accumulation operation. Thus, the results presented in Fig. 5 provide a good approximation for weak, moderate and strong accumulation operation of OTFTs with gate voltage.

Fig. 5
figure 5

Surface potential versus gate voltage for OTFTs with flat-band voltage, VFB = 0 V

Full size image

Figure 6 shows the variation of electric field at the surface of the pentacene semiconductor given by Eq. (8). As predicted by the modeled equation, the surface electric field increases to a high value either in the accumulation mode or on the onset of inversion. The surface electric field remains at a low value for the low density of charge carriers in weak accumulation and depletion regimes. The result further validates the variation of surface electric field with the surface potential.

Fig. 6
figure 6

Electric field variation as a function of surface potential across the organic semiconductor

Full size image

Figure 7 shows the effective mobility calculated from Eq. (16) as a function of the effective electric field. It can be observed from the results that the effective mobility of holes in pentacene increases linearly with increase in the electric field. But the carrier mobility peaks for some value of electric field and then decreases. This result is consistent with the observed degradation of channel mobility in simulation results of OTFTs with the vertical electric field [25]. It is further observed that the trap states play an important role in mobility modeling. As the density of trap states increases, the mobility decreases. This result is proved by the fact that as the density of trap states increases, more number of charge carriers are trapped and the density of free charge carriers decreases leading to decrease in mobility. Thus, the mobility equations provide a complete mathematical mobility model for OTFTs.

Fig. 7
figure 7

Resultant mobility variation with the effective electric field for different values of N0(T)

Full size image

Figure 8 shows the variation of drain current (Idrain) with the gate voltage for VTH = −9.09 V. Idrain is plotted for different values of NTA, and it has been found that the drain current decreases as the value of NTA increases. The decrease in Idrain at high values of NTA is because an increase in the density of traps leads to the increase in trapped charge density per unit area reducing mobile charge carriers, i.e., holes and thus the current decreases.

Fig. 8
figure 8

Drain current variation with gate-source voltage, VGS for different values of N0(T) and γ = 1

Full size image

Further the variation of drain current with the gate voltage is very well predicted by the modeled equation given in (23). Idrain shows an increase only when VGS increases to VTH.

Figure 9 shows the variation of Idrain with gate-source voltage (VGS) for different values of γ plotted on log scale. It has been observed from the results presented in Fig. 9 that as the value of γ, which stands for the characteristic decay energy of trap states changes, Idrain also changes. Idrain decreases for increase in value of γ because of increase in characteristic energy of trap states and increases at low values of γ. Thus, the mathematical model of Idrain presented in section II effectively describes the conduction behavior of OTFTs taking into account both the density of trap states and their characteristic energy. Idrain variation with drain-source voltage (VDS) is plotted in Fig. 10 for different values of N0(T). It has been observed Idrain has the highest value for N0(T) = 1018 cm−3 and decreases as the value of N0(T) increases.

Fig. 9
figure 9

Drain current variation with gate-source voltage, VGS for different values of γ (N0(T) = 1018 cm−3, VDS = −1 V)

Full size image
Fig. 10
figure 10

Drain current variation with drain-source voltage, VDS for different values of NT (VGS = −15 V, γ = 1, T = 300 K)

Full size image

It can be seen that for VDS < (VGS − VTH), the drain current increases linearly and once VDS > (VGS–VTH), the drain current saturates. This proves that the linear and saturation behavior of Idrain with VDS and the inclusion of trap states have been very well modeled in Eqs. (22) and (23), respectively. Figure 11 shows the Idrain variation with VDS for different values of γ. At constant value of N0(T), Idrain decreases as the characteristic energy of trap states increases and hence γ increases. Idrain shows a fourfold increase as γ changes from 1.0 to 0.9. Thus, the predicted results are as expected with increasing energy of trap states; less number of charge carriers are available for conduction, and hence Idrain must reduce. Figure 12 shows the total capacitance of pentacene-based OTFT versus the surface potential. The channel capacitance (CC + CT) is found from the derivative of Fig. 3 according to Eq. (33) and then substituted in Eq. (29) to find the total capacitance. It is shown in Fig. 12 that for ψs < 0, in device accumulation, the channel capacitance is very high and the total capacitance is equal to the gate oxide capacitance in accordance with Eq. (29). But as ψs > 0 V, the channel capacitance decreases, thereby decreasing the total capacitance. For values of ψs sufficiently positive to induce inversion, the channel capacitance again increases and saturates at COX.

Fig. 11
figure 11

Drain current variation with drain-source voltage, VDS for different values of γ (VGS = −15 V, N0(T) = 1018 cm−3, T = 300 K)

Full size image
Fig. 12
figure 12

Total capacitance variation of OTFTs with surface potential (N0(T) = 1018 cm−3, T = 300 K)

Full size image

The slope factor, η given in Eq. (33), has been estimated from Fig. 12 and is almost equal to 0.17. It can be used to find the value of trap capacitance contributed to the total device capacitance. The effect of the variation of trap states on the gate-body capacitance (Cgb) has been plotted in Fig. 13. Results obtained in Fig. 13 show that for N0(T) < NV, the device capacitance is similar to that of trap-free situation. But for values of N0(T) > NV, the C–V curves exhibit a sharp bump. This momentary bump in the C–V characteristics has been attributed to the charging and discharging of trap states with charge carriers. Traps act as generation/recombination centers. The exponential distribution assumed in this paper has most trap states close to the band edge. The trap states can be even filled and unfilled at just flat-band conditions, and as VGS becomes negative, the Fermi level moves down and gets pinned near HOMO (highest occupied molecular orbital) at the oxide–semiconductor interface. The traps being dynamic in nature cause trapping and detrapping leading to presence of hump in the C–V curves. The capacitance has a value equal to COX for VGS > 0 V, i.e., inversion mode and again reaches to COX in the accumulation. Only at the onset of accumulation the C–V shows a bump which is because of additional trap capacitance (trap states getting filled). The inset graph shown in Fig. 13 is a plot of Cgb normalized with respect to COX. The normalized values of capacitance are equal to 1 in both inversion and accumulation mode of device operation. Only at the onset of accumulation the normalized capacitance value jumps to 1.1, i.e., trap capacitance adds 0.1 µF/cm2 of capacitance to Cox for a change of NTA from 1018 to 1020 cm−3 (i.e., for 102 cm−3 change in NTA momentary capacitance increase is just 0.1 which is not a substantial change). The simulation studies on the C–V characteristics of the bottom-contact OTFTs show similar trends as shown in Fig. 13 [23].The appearance of bump in the C–V characteristics has also been reported in MOS devices in the presence of trap states [32]. Further, the capacitance is a dynamic quantity which can change with applied frequency, semiconductor doping, density of trap states, temperature and time. Thus, the modeling results presented in Fig. 13 show that the proposed model can be used to analyze the capacitive behavior of OTFT’s in presence of trap states.

Fig. 13
figure 13

Capacitance variation with VGS for different values of trap states (inset graph shows normalized capacitance)

Full size image

4 Conclusion

In this paper, an analytical solution for the electrical behavior of organic thin-film transistors has been presented. The density of trap states along with the characteristic decay rate has been incorporated in the analytical model. The surface potential, charge density and the current–voltage characteristics of OTFTs have been obtained from the developed model. The results obtained from modeling equations are very well consistent with the electrical characteristics presented on the simulation of OTFTs. The device performance parameters show significant variation with the change in trap parameters and the modeling of transistors based on organic semiconductors cannot be complete if trap states are not accounted for. Further, an effective mobility model has been developed taking PF mobility model and surface mobility model together. The mobility model developed can be used for even short-channel length transistors which show significant mobility degradation. The capacitance model for OTFTs has been presented, and the capacitance characteristics of OTFTs obtained from the proposed model show similar trends with the simulation results. The analytical model presented can be extended to incorporate sub-threshold behavior and effect of contact resistances in future. The proposed model can therefore provide a complete solution to the compact modeling and simulation of OTFTs without relying on the MOSFET models for the design and development of organic-based circuits into a commercial platform.