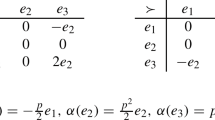Anti-dendriform algebras, new splitting of operations and Novikov-type algebras

Abstract

We introduce the notion of an anti-dendriform algebra as a new approach of splitting the associativity. It is characterized as the algebra with two multiplications giving their left and right multiplication operators, respectively, such that the opposites of these operators define a bimodule structure on the sum of these two multiplications, which is associative. This justifies the terminology due to a closely analogous characterization of a dendriform algebra. The notions of anti-${\mathcal {O}}$-operators and anti-Rota–Baxter operators on associative algebras are introduced to interpret anti-dendriform algebras. In particular, there are compatible anti-dendriform algebra structures on associative algebras with nondegenerate commutative Connes cocycles. There is an important observation that there are correspondences between certain subclasses of dendriform and anti-dendriform algebras in terms of q-algebras. As a direct consequence, we give the notion of Novikov-type dendriform algebras as an analogue of Novikov algebras for dendriform algebras, whose relationship with Novikov algebras is consistent with the one between dendriform and pre-Lie algebras. Finally, we extend to provide a general framework of introducing the notions of analogues of anti-dendriform algebras, which interprets a new splitting of operations.

1 Introduction

The aim of this paper is to introduce the notion of anti-dendriform algebras illustrating a new splitting of operations and study the relationships between them and the related structures such as anti-${\mathcal {O}}$-operators, commutative Connes cocycles on associative algebras, dendriform algebras and Novikov algebras.

Recall that a dendriform algebra is a vector space A over a field ${\mathbb {F}}$ with two binary operations $\succ ,\prec$ satisfying

$$\begin{aligned} x\succ (y\succ z)&=(x\cdot y)\succ z,\ \ (x\prec y)\prec z=x\prec (y\cdot z),\nonumber \\ (x\succ y)\prec z&=x\succ (y\prec z), \end{aligned}$$

(1)

where

$$\begin{aligned} x\cdot y=x\succ y+x\prec y, \end{aligned}$$

(2)

for all $x,y,z\in A$. The notion of dendriform algebras was introduced by Loday in the study of algebraic K-theory [28]. They appear in a lot of fields in mathematics and physics, such as arithmetic [29], combinatorics [32], Hopf algebras [13, 23, 24, 31, 34], homology [18, 19], operads [30], Lie and Leibniz algebras [19] and quantum field theory [17]. The fact that the sum of the two binary operations in a dendriform algebra $(A,\succ ,\prec )$ gives an associative algebra $(A,\cdot )$ expresses a kind of “splitting the associativity.” Moreover, dendriform algebras are closely related to pre-Lie algebras which are a class of Lie-admissible algebras whose commutators are Lie algebras, also appearing in many fields in mathematics and physics (see [3, 11] and the references therein), in the sense that for a dendriform algebra $(A,\succ ,\prec )$, the binary operation

$$\begin{aligned} x*y=x\succ y-y\prec x,\;\;\forall x,y\in A, \end{aligned}$$

(3)

defines a pre-Lie algebra $(A,*)$, which is called the associated pre-Lie algebra of $(A,\succ ,\prec )$. Therefore, there is the following relationship among Lie algebras, associative algebras, pre-Lie algebras and dendriform algebras in the sense of commutative diagram of categories [12]:

$$\begin{aligned} \begin{matrix} {\textrm{dendriform}}\quad {\textrm{algebras}} &{} \longrightarrow &{} \hbox {pre-Lie algebras} \\ \downarrow &{} &{}\downarrow \\ {\textrm{associative}}\quad {\textrm{algebras}} &{} \longrightarrow &{} {\textrm{Lie}} \quad {\textrm{algebras}} \\ \end{matrix}\end{aligned}$$

(4)

On the other hand, there is an “anti-structure” for pre-Lie algebras, namely anti-pre-Lie algebras, introduced in [27], which are characterized as the Lie-admissible algebras whose negative left multiplication operators give representations of the commutator Lie algebras, justifying the terminology since pre-Lie algebras are the Lie-admissible algebras whose left multiplication operators give representations of the commutator Lie algebras.

We give a new approach of splitting operations, motivated by the study of anti-pre-Lie algebras. We introduce the notion of anti-dendriform algebras, still keeping the property of having two multiplications splitting the associativity, but it is the opposites of the left and right multiplication operators defined by the two multiplications, respectively, that compose the bimodules over the sum associative algebras, instead of the left and right multiplication operators for dendriform algebras. Such a characterization justifies the terminology, and moreover, the following commutative diagram holds, which is the diagram (4) with replacing dendriform and pre-Lie algebras by anti-dendriform and anti-pre-Lie algebras, respectively.

$$\begin{aligned} \begin{matrix} \hbox { anti-dendriform algebras} &{} \longrightarrow &{} \hbox {anti-pre-Lie algebras} \\ \downarrow &{} &{}\downarrow \\ {\textrm{associative}}\quad {\textrm{algebras}} &{} \longrightarrow &{} {\textrm{Lie}}\quad {\textrm{algebras}}\\ \end{matrix}\end{aligned}$$

(5)

As ${\mathcal {O}}$-operators and Rota–Baxter operators on associative algebras interpreting dendriform algebras [6], we introduce the notions of anti-${\mathcal {O}}$-operators and anti-Rota–Baxter operators on associative algebras to interpret anti-dendriform algebras. In particular, there are compatible anti-dendriform algebra structures on associative algebras with nondegenerate commutative Connes cocycles.

In [27], there is an important observation that there is a correspondence between Novikov algebras as a subclass of pre-Lie algebras and admissible Novikov algebras as a subclass of anti-pre-Lie algebras in terms of q-algebras (q is in the base field $\mathbb {F}$, see [15]). That is, the 2-algebra over a Novikov algebra is an admissible Novikov algebra, whereas the $-2$-algebra over an admissible Novikov algebra is a Novikov algebra. We also find that there is a similar correspondence between some subclasses of dendriform algebras and anti-dendriform algebras in terms of q-algebras. Note that such a correspondence is available for any $q\ne 0, \pm 1$, not for only a special value of q in [27], which in fact corresponds to $q=-2$ in this paper. We also extend the correspondence between the subclasses of pre-Lie algebras and anti-pre-Lie algebras for these qs and in particular, for a fixed $q\ne 0,\pm 1$, the relationship between the corresponding subclasses of dendriform algebras and pre-Lie algebras as well as anti-dendriform algebras and anti-pre-Lie algebras is still kept as the one given by Eq. (3).

Moreover, there is an interesting by-product. As a subclass of pre-Lie algebras, Novikov algebras were introduced in connection with Hamiltonian operators in the formal variational calculus [20] and Poisson brackets of hydrodynamic type [8]. On the other hand, the notion of successors was introduced to interpret the splitting of operations in terms of operads in [4]. In this sense, both pre-Lie algebras and dendriform algebras are examples of splitting operations and their operads are the successors of the operads of Lie and associative algebras, respectively. So it is natural to ask whether and how one can give a reasonable notion of analogues of Novikov algebras for the successors’ algebras, in particular, for dendriform algebras? In fact, the above approach answers this problem. Due to the introduction of the notion of anti-dendriform algebras and the above correspondence, one might introduce the notion of Novikov-type dendriform algebras as the aforementioned subclass of dendriform algebras for $q=-2$. The speciality of $q=-2$ also can be seen from the identity involving q (Proposition 3.4). Moreover, it is consistent with the diagram (4) in the following sense:

(6)

We would like to point out that this “rule” of constructing analogues of Novikov algebras for dendriform algebras is due to the introduction of the notion of anti-dendriform algebras and hence it is regarded as an application of the latter.

The paper is organized as follows. In Section 2, we introduce the notion of anti-dendriform algebras as a new approach of splitting the associativity. The notions of anti-${\mathcal {O}}$-operators and anti-Rota–Baxter operators on associative algebras are introduced to interpret anti-dendriform algebras. The relationships between anti-dendriform algebras and commutative Connes cocycles on associative algebras are given. In Section 3, we investigate the correspondences of some subclasses of dendriform algebras and anti-dendriform algebras as well as pre-Lie algebras and anti-pre-Lie algebras in terms of q-algebras. The relationships among these subclasses are given. In particular, in the case that $q=-2$, we introduce the notions of Novikov-type dendriform algebras and admissible Novikov-type dendriform algebras with their correspondences. In Section 4, we provide a general framework of introducing the notions of analogues of anti-dendriform algebras to interpret a new splitting of operations. They are characterized in terms of double spaces, where a double space of an algebra A refers to the direct sum $A\oplus A$ of the underlying vector spaces of A.

Throughout this paper, all vector spaces are assumed to be finite-dimensional over a field $\mathbb {F}$ of characteristic 0, although many results are still available in the infinite-dimensional case. All operations are assumed to be binary.

2 Anti-dendriform algebras

We introduce the notion of anti-dendriform algebras as a new approach of splitting the associativity, characterized as the associative admissible algebras in which the opposites of the left and right multiplication operators defined, respectively, by the two operations compose the bimodules over the associated associative algebras. We introduce the notions of anti-${\mathcal {O}}$-operators and anti-Rota–Baxter operators on associative algebras to interpret anti-dendriform algebras. There is a compatible anti-dendriform algebra structure on an associative algebra if and only if there exists an invertible anti-${\mathcal {O}}$-operator of the associative algebra. In particular, there are compatible anti-dendriform algebra structures on associative algebras with nondegenerate commutative Connes cocycles.

2.1 Anti-dendriform algebras

Definition 2.1

Let A be a vector space with two binary operations

$$\begin{aligned} \vartriangleright : A\otimes A\rightarrow A,\quad \vartriangleleft : A\otimes A\rightarrow A. \end{aligned}$$

Define a binary operation $\cdot$ as

$$\begin{aligned} x\cdot y=x\vartriangleright y+x\vartriangleleft y,\;\;\forall x,y\in A. \end{aligned}$$

(7)

The triple $(A,\vartriangleright ,\vartriangleleft )$ is called an associative admissible algebra if $(A, \cdot )$ is an associative algebra. In this case, $(A,\cdot )$ is called the associated associative algebra of $(A,\vartriangleright ,\vartriangleleft )$.

Remark 2.2

The triple $(A,\vartriangleright ,\vartriangleleft )$ is an associative admissible algebra if and only if the following equation holds:

$$\begin{aligned}&(x\vartriangleright y)\vartriangleright z+(x\vartriangleleft y)\vartriangleright z+(x\vartriangleright y)\vartriangleleft z+(x\vartriangleleft y)\vartriangleleft z\nonumber \\&=x\vartriangleright (y\vartriangleright z)+x\vartriangleright (y\vartriangleleft z)+x\vartriangleleft (y\vartriangleright z)+x\vartriangleleft (y\vartriangleleft z),\;\;\forall x,y,z\in A. \end{aligned}$$

(8)

It is known [28] that dendriform algebras are associative admissible algebras.

Let $(A,\cdot )$ be an associative algebra. Recall that a bimodule over $(A,\cdot )$ is a triple (V, l, r) consisting of a vector space V and linear maps $l,r: A\rightarrow \textrm{End}_\mathbb {F}(V)$ such that

$$\begin{aligned}{} & {} l(x\cdot y)v=l(x)(l(y)v), \ \ r(x\cdot y)v=r(y)(r(x)v), \ \ l(x)(r(y)v)=r(y)(l(x)v),\ \\{} & {} \quad \forall x,y\in A, v\in V. \end{aligned}$$

In particular, $(A, L_\cdot , R_\cdot )$ is a bimodule over $(A,\cdot )$, where $L_\cdot ,R_\cdot :A\rightarrow \textrm{End}_\mathbb {F}(A)$ are two linear maps defined by $L_\cdot (x)(y)=R_\cdot (y)(x)=x\cdot y$ for all $x,y\in A$, respectively.

Let $(A, \vartriangleright , \vartriangleleft )$ be an associative admissible algebra. Define two linear maps $L_\vartriangleright ,R_\vartriangleleft :A\rightarrow \textrm{End}_\mathbb {F}(A)$, respectively, by

$$\begin{aligned} L_\vartriangleright (x)(y)=x\vartriangleright y,\quad R_\vartriangleleft (x)(y)=y\vartriangleleft x,\quad \forall x,y\in A. \end{aligned}$$

Proposition 2.3

Let A be a vector space with two binary operations $\vartriangleright$ and $\vartriangleleft$. Define a binary operation $\cdot$ by Eq. (7). Then for any nonzero $\lambda \in \mathbb {F}$, the following conditions are equivalent.

• (1) $(A,\cdot )$ is an associative algebra and $(A, \lambda L_\vartriangleright , \lambda R_\vartriangleleft )$ is a bimodule over $(A,\cdot )$.

• (2) $(A,\cdot )$ is an associative algebra and for all $x,y,z\in A$, the following equations hold:

  $$\begin{aligned} \lambda x\vartriangleright (y\vartriangleright z)= & {} (x\cdot y)\vartriangleright z,\ \lambda (x\vartriangleleft y)\vartriangleleft z= x\vartriangleleft (y\cdot z),\nonumber \\ (x\vartriangleright y)\vartriangleleft z= & {} x\vartriangleright (y\vartriangleleft z). \end{aligned}$$

  (9)

• (3) Eq. (9) and the following equation hold:

  $$\begin{aligned} (\lambda -1)x\vartriangleright (y\vartriangleright z)=(\lambda -1)(x\vartriangleleft y)\vartriangleleft z,\;\; \forall x,y,z\in A. \end{aligned}$$

  (10)

Proof

(1) $\Longleftrightarrow$ (2). Let $x,y,z\in A$. Then, we have

$$\begin{aligned} \lambda L_\vartriangleright (x)(\lambda L_\vartriangleright (y)z)=(\lambda L_\vartriangleright )(x\cdot y)(z)\ \ {}&\Longleftrightarrow \ \ \lambda x\vartriangleright (y\vartriangleright z)=(x\cdot y)\vartriangleright z, \\ \lambda R_\vartriangleleft (y)(\lambda R_\vartriangleleft (x)z)= (\lambda R_\vartriangleleft )(x\cdot y)(z)\ \ {}&\Longleftrightarrow \ \ \lambda (z\vartriangleleft x)\vartriangleleft y=z\vartriangleleft (x\cdot y), \\ (\lambda L_\vartriangleright )(x)(\lambda R_\vartriangleleft (y)z)=(\lambda R_\vartriangleleft (y))(\lambda L_\vartriangleright (x)z) \ \ {}&\Longleftrightarrow \ \ x\vartriangleright (z\vartriangleleft y)=(x\vartriangleright z)\vartriangleleft y. \end{aligned}$$

Hence, Item (1) holds if and only if Item (2) holds.

(2) $\Longleftrightarrow$ (3). Suppose that Eq. (9) holds. Then, it is straightforward to show that Eq. (8) holds if and only if Eq. (10) holds. Hence, Item (2) holds if and only if Item (3) holds. $\square$

Note that in the case that $\lambda =1$, it is particular that Eq. (10) holds automatically and at this time, $(A,\vartriangleright , \vartriangleleft )$ is exactly a dendriform algebra. On the other hand, for the case that $\lambda =-1$, we give the following notion.

Definition 2.4

Let A be a vector space with two binary operations $\vartriangleright$ and $\vartriangleleft$. The triple $(A,\vartriangleright ,\vartriangleleft )$ is called an anti-dendriform algebra if the following equations hold:

$$\begin{aligned} x\vartriangleright (y\vartriangleright z)=-(x\cdot y)\vartriangleright z=-x\vartriangleleft (y\cdot z)=(x\vartriangleleft y)\vartriangleleft z, \end{aligned}$$

(11)

$$\begin{aligned} (x\vartriangleright y)\vartriangleleft z=x\vartriangleright (y\vartriangleleft z),\;\;\forall x,y,z \in A, \end{aligned}$$

(12)

where the binary operation $\cdot$ is defined by Eq. (7).

Corollary 2.5

Let A be a vector space with two binary operations $\vartriangleright$ and $\vartriangleleft$. Define a binary operation $\cdot$ by Eq. (7). Then, the following conditions are equivalent.

• (1) $(A, \vartriangleright , \vartriangleleft )$ is an anti-dendriform algebra.

• (2) $(A,\cdot )$ is an associative algebra and for all $x, y, z\in A$, the following equations hold:

  $$\begin{aligned}{} & {} x\vartriangleright (y\vartriangleright z)=-(x\cdot y)\vartriangleright z,\ (x\vartriangleleft y)\vartriangleleft z=-x\vartriangleleft (y\cdot z), \nonumber \\{} & {} (x\vartriangleright y)\vartriangleleft z=x\vartriangleright (y\vartriangleleft z). \end{aligned}$$

  (13)

• (3) $(A,\cdot )$ is an associative algebra and $(A, -L_\vartriangleright , -R_\vartriangleleft )$ is a bimodule over $(A,\cdot )$.

Proof

It follows from Proposition 2.3 in the case that $\lambda =-1$. Note that in this case, Eq. (11) holds if and only if Eq. (10) and the first two equations in Eq. (13) hold. $\square$

Remark 2.6

As Proposition 2.3 shows, a dendriform algebra $(A,\succ ,\prec )$ corresponding to the case that $\lambda =1$ is an associative admissible algebra such that $(A, L_\succ , R_\prec )$ is a bimodule over the associated associative algebra $(A,\cdot )$ (also see [2]). Therefore, the notion of anti-dendriform algebras is justified due to the equivalent characterization (3) above. Note that Proposition 2.3 also explains why the case that $\lambda =-1$ corresponding to an anti-dendriform algebra needs an extra equality.

Definition 2.7

Let $(A, \vartriangleright , \vartriangleleft )$ be an anti-dendriform algebra. Define a binary operation $\cdot$ by Eq. (7). Then, the resulting associative algebra $(A,\cdot )$ is called the associated associative algebra of $(A, \vartriangleright , \vartriangleleft )$. On the other hand, $(A, \vartriangleright , \vartriangleleft )$ is called a compatible anti-dendriform algebra structure on $(A,\cdot ).$

Suppose that $(A,\cdot )$ is an associative algebra. Let V be a vector space and $l,r: A\rightarrow \textrm{End}_{{\mathbb {F}}}(V)$ be linear maps. Then, (V, l, r) is a bimodule over $(A,\cdot )$ if and only if there is an associative algebra structure on the direct sum $A\oplus V$ of vector spaces with the following binary operation, still denoted by $\cdot$:

$$\begin{aligned} (x,u)\cdot (y,v)=(x\cdot y,l(x)v+r(y)u),\quad \forall x,y\in A,u,v\in V. \end{aligned}$$

We denote this associative algebra by $A\ltimes _{l,r}V$.

Corollary 2.8

Let A be a vector space with two binary operations $\vartriangleright ,\vartriangleleft : A\otimes A\rightarrow A$. Then, on the direct sum ${\hat{A}}:=A\oplus A$ of vector spaces, the following binary operation

$$\begin{aligned} (x,a)\cdot (y,b)=(x\vartriangleright y+x\vartriangleleft y, -x\vartriangleright b-a\vartriangleleft y),\;\;\forall x,y,a,b\in A, \end{aligned}$$

(14)

makes an associative algebra $({\hat{A}},\cdot )$ if and only if $(A,\vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra.

Proof

It is clear that $({\hat{A}},\cdot )$ is an associative algebra if and only if $(A, \vartriangleright , \vartriangleleft )$ is an associative admissible algebra, and $(A, -L_\vartriangleright , -R_\vartriangleleft )$ is a bimodule over the associated associative algebra, which is equivalent to the fact that $(A, \vartriangleright , \vartriangleleft )$ is an anti-dendriform algebra by Corollary 2.5. $\square$

Example 2.9

Let $(A,\vartriangleright ,\vartriangleleft )$ be a 1-dimensional anti-dendriform algebra with a basis $\{e\}$. Assume that

$$\begin{aligned} e\vartriangleright e=\alpha e,\quad e\vartriangleleft e=\beta e, \end{aligned}$$

where $\alpha ,\beta \in \mathbb {F}$. Then by Eq. (11), we have

$$\begin{aligned} \alpha ^2e=(-\alpha ^2-\alpha \beta ) e=(-\beta ^2-\alpha \beta ) e=\beta ^2e. \end{aligned}$$

Hence, $\alpha =\beta =0$; that is, any 1-dimensional anti-dendriform algebra is trivial.

Let A be a vector space with a binary operation $\circ : A\otimes A\rightarrow A$. Then, $(A,\circ )$ is called a Lie-admissible algebra, if the binary operation $[,\,]:A\otimes A\rightarrow A$ defined by

$$\begin{aligned}{}[x,y]=x\circ y-y\circ x,\;\; \forall x,y\in A, \end{aligned}$$

(15)

makes $(A,[,\,])$ a Lie algebra. In this case, $(A,[,\,])$ is called the sub-adjacent Lie algebra of $(A,\circ )$ and denoted by $(\mathfrak {g}(A),[,\,])$. Obviously, an associative algebra is a Lie-admissible algebra.

An anti-pre-Lie algebra [27] is a vector space A with a binary operation $\circ$ satisfying

$$\begin{aligned}&x\circ (y\circ z)-y\circ (x\circ z)=[y,x]\circ z, \end{aligned}$$

(16)

$$\begin{aligned}&[x,y]\circ z+[y,z]\circ x+[z,x]\circ y=0, \;\;\forall x,y,z\in A, \end{aligned}$$

(17)

where the binary operation $[,\,]$ is defined by Eq. (15). Equivalently, an anti-pre-Lie algebra $(A,\circ )$ is a Lie-admissible algebra satisfying Eq. (16).

Proposition 2.10

Let $(A, \vartriangleright , \vartriangleleft )$ be an anti-dendriform algebra.

• (1) The binary operation $\circ :A\otimes A\rightarrow A$ given by

  $$\begin{aligned} x\circ y=x\vartriangleright y-y\vartriangleleft x,\ \ \forall x,y\in A,\end{aligned}$$

  (18)

  defines an anti-pre-Lie algebra, called the associated anti-pre-Lie algebra of $(A, \vartriangleright , \vartriangleleft ).$

• (2) Let $(A,\cdot )$ be the associated associative algebra of $(A, \vartriangleright , \vartriangleleft )$, where the binary operation $\cdot$ is defined by Eq. (7). Then, both $(A, \cdot )$ and $(A, \circ )$ have the same sub-adjacent Lie algebra $(\mathfrak {g}(A),[,\,])$ defined by

  $$\begin{aligned} =x\vartriangleright y+x\vartriangleleft y-y\vartriangleright x-y\vartriangleleft x,\quad \forall x,y\in A.\end{aligned}$$

  (19)

Proof

(1). Let $x,y,z\in A$. Then, we have

$$\begin{aligned} x\circ (y\circ z)= & {} x\vartriangleright (y\vartriangleright z-z\vartriangleleft y)-(y\vartriangleright z-z\vartriangleleft y)\vartriangleleft x \\= & {} x\vartriangleright (y\vartriangleright z)-x\vartriangleright (z\vartriangleleft y)-(y\vartriangleright z)\vartriangleleft x+(z\vartriangleleft y)\vartriangleleft x,\\ (y\circ x)\circ z= & {} (y\vartriangleright x-x\vartriangleleft y)\vartriangleright z-z\vartriangleleft (y\vartriangleright x-x\vartriangleleft y) \\= & {} (y\vartriangleright x)\vartriangleright z-(x\vartriangleleft y)\vartriangleright z-z\vartriangleleft (y\vartriangleright x)+z\vartriangleleft (x\vartriangleleft y). \end{aligned}$$

By swapping x and y,  we have

$$\begin{aligned} y\circ (x\circ z)&=y\vartriangleright (x\vartriangleright z)-y\vartriangleright (z\vartriangleleft x)-(x\vartriangleright z)\vartriangleleft y+(z\vartriangleleft x)\vartriangleleft y,\\ (x\circ y)\circ z&=(x\vartriangleright y)\vartriangleright z-(y\vartriangleleft x)\vartriangleright z-z\vartriangleleft (x\vartriangleright y)+z\vartriangleleft (y\vartriangleleft x). \end{aligned}$$

Using Eqs. (11) and (12), we obtain

$$\begin{aligned} x\circ (y\circ z)-y\circ (x\circ z)=&x\vartriangleright (y\vartriangleright z)+(z\vartriangleleft y)\vartriangleleft x-y\vartriangleright (x\vartriangleright z)-(z\vartriangleleft x)\vartriangleleft y\\ =&(y\vartriangleright x+y\vartriangleleft x)\vartriangleright z-(x\vartriangleright y+x\vartriangleleft y)\vartriangleright z\\&-z\vartriangleleft (y\vartriangleright x+y\vartriangleleft x)+z\vartriangleleft (x\vartriangleright y+x\vartriangleleft y) \\ =&(y\circ x)\circ z-(x\circ y)\circ z\nonumber =[y, x]\circ z. \end{aligned}$$

Moreover, we have

$$\begin{aligned} x\circ y-y\circ x=x\vartriangleright y-y\vartriangleleft x-y\vartriangleright x+x\vartriangleleft y=x\cdot y-y\cdot x,\;\;\forall x,y\in A. \end{aligned}$$

Thus, $(A,\circ )$ is a Lie-admissible algebra and hence an anti-pre-Lie algebra.

(2). It is straightforward. Note that it also appears in the proof of Item (1). $\square$

As a direct consequence, we have the following conclusion.

Corollary 2.11

The commutative diagram  (5) holds.

Recall that an associative algebra $(A,\cdot )$ is 2-nilpotent if $(x\cdot y)\cdot z=x\cdot (y\cdot z)=0$ for all $x,y,z\in A$. Furthermore, two binary operations $\vartriangleright , \vartriangleleft$ on a vector space A are called colinear if there exists $\lambda \in {\mathbb {F}}$ such that $\vartriangleright =\lambda \vartriangleleft$ or $\vartriangleleft =\lambda \vartriangleright$. Obviously, any binary operation and the zero operation are colinear.

Proposition 2.12

Let A be a vector space with two binary operations $\vartriangleright , \vartriangleleft :A\otimes A\rightarrow A$. Define a binary operation $\cdot$ by Eq. (7). Suppose $\vartriangleright , \vartriangleleft$ are colinear and $\vartriangleright \ne -\vartriangleleft$. Then, $(A, \vartriangleright , \vartriangleleft )$ is an anti-dendriform algebra if and only if $(A,\cdot )$ is a 2-nilpotent associative algebra. In particular, if $(A,\cdot )$ is a 2-nilpotent associative algebra, then $(A, \vartriangleright , \vartriangleleft )$ with $\vartriangleright =\cdot , \vartriangleleft =0$ or $\vartriangleright =0, \vartriangleleft =\cdot$ is a compatible anti-dendriform algebra. And conversely, if $(A, \vartriangleright , \vartriangleleft )$ with $\vartriangleleft =0$ or $\vartriangleright =0$ is an anti-dendriform algebra, then the associated associative algebra $(A,\cdot )$ is 2-nilpotent.

Proof

By the assumption without loss of generality, we suppose that $\vartriangleright =\lambda \vartriangleleft$, where $\lambda \in {\mathbb {F}}$ and $\lambda \ne -1$. Then, $\cdot =(\lambda +1) \vartriangleleft$. If $(A, \vartriangleright , \vartriangleleft )$ is an anti-dendriform algebra and assume that $(A,\cdot )$ is not a 2-nilpotent associative algebra, then by Eq. (11), we get

$$\begin{aligned} \lambda ^2=-\lambda (\lambda +1)=-(\lambda +1)=1. \end{aligned}$$

However, obviously there does not exist a $\lambda \in {\mathbb {F}}$ satisfying the above equations, which is a contradiction. So $(A,\cdot )$ is a 2-nilpotent associative algebra. Conversely, suppose that $(A,\cdot )$ is a 2-nilpotent associative algebra. Since $\vartriangleleft =\frac{1}{\lambda +1}\;\cdot$ and $\vartriangleright =\lambda \vartriangleleft =\frac{\lambda }{\lambda +1}\;\cdot$, all products for $\vartriangleleft$ and $\vartriangleright$ involving three elements such as $(x\vartriangleright y)\vartriangleright z$ and $x\vartriangleleft (y\vartriangleright z)$ are zero. Hence, $(A, \vartriangleright , \vartriangleleft )$ is an anti-dendriform algebra. The remaining conclusions follow immediately from the special case that any binary operation and the zero operation are colinear. $\square$

Remark 2.13

Suppose that $\vartriangleright = -\vartriangleleft$. Then, $(A,\cdot )$ is trivial in the sense that all products are zero, which is a 2-nilpotent associative algebra automatically. On the other hand, in this case, $(A, \vartriangleright , \vartriangleleft )$ is an anti-dendriform algebra if and only if $(A,\vartriangleright )$ is a 2-nilpotent associative algebra.

Proposition 2.14

Let $(A,\cdot )$ be an associative algebra with a nonzero idempotent e, that is, $e\cdot e=e$. Then, there does not exist a compatible anti-dendriform algebra structure on $(A,\cdot )$.

Proof

Assume that $(A, \vartriangleright , \vartriangleleft )$ is a compatible anti-dendriform algebra structure on $(A,\cdot )$. Then by Eq. (11) for e, e, e, we have

$$\begin{aligned} e\vartriangleright e=(e\cdot e)\vartriangleright e=e\vartriangleleft (e\cdot e)=e\vartriangleleft e. \end{aligned}$$

On the other hand, note that $e=e\cdot e= e\vartriangleright e+e\vartriangleleft e$. Hence, $e\vartriangleright e=e\vartriangleleft e=\frac{1}{2}e$. Then by Eq. (11) for e, e, e again, we have

$$\begin{aligned} \frac{1}{4}e=e\vartriangleright (e\vartriangleright e)=-(e\cdot e)\vartriangleright e=-\frac{1}{2}e, \end{aligned}$$

(20)

which is a contradiction. Hence, the conclusion holds. $\square$

It is known that any finite-dimensional associative algebra without a nonzero idempotent element is nilpotent. Therefore, we have the following conclusion.

Corollary 2.15

The associated associative algebra of any finite-dimensional anti-dendriform algebra is nilpotent.

Suppose that $(A,\cdot )$ is a 2-dimensional nilpotent associative algebra over the field ${\mathbb {C}}$ of complex numbers with a basis $\{e_1,e_2\}$. Then, it is known (for example, see [7] or [10]) that $(A,\cdot )$ is isomorphic to one of the following two cases (only nonzero products are given):

$(A1)_{ }$:

$(A,\cdot )$ is trivial, that is, all products are zero;

$(A2)_{ }$:

$e_1\cdot e_1=e_2$.

Obviously, both of them are 2-nilpotent associative algebras.

Proposition 2.16

Let $(A,\cdot )$ be a 2-dimensional nilpotent associative algebra over ${\mathbb {C}}$ with a basis $\{e_1,e_2\}$.

• (I) If $(A,\cdot )$ is (A1), then any compatible anti-dendriform algebra $(A, \vartriangleright , \vartriangleleft )$ on $(A,\cdot )$ is one of the following two cases up to isomorphism (only nonzero products are given):

  $(A1)_1$:

  $(A,\vartriangleright ,\vartriangleleft )$ is trivial;

  $(A1)_2$:

  $e_1\vartriangleright e_1=e_2,\ \ e_1\vartriangleleft e_1=-e_2$.

• (II) If $(A,\cdot )$ is (A2), then any compatible anti-dendriform algebra $(A, \vartriangleright , \vartriangleleft )$ on $(A,\cdot )$ is one of the following two cases up to isomorphism (only nonzero products are given):

  $(A2)_{1\;\;\ }$:

  $e_1\vartriangleleft e_1=e_2$;

  $(A2)_{2,\lambda }$:

  $e_1\vartriangleright e_1=e_2,\ \ e_1\vartriangleleft e_1=\lambda e_2$, where $\lambda \in \mathbb {C}$ with $\lambda \ne -1$.

Consequently, any 2-dimensional complex anti-dendriform algebra $(A,\vartriangleright ,\vartriangleleft )$ is isomorphic to one of the following mutually non-isomorphic cases (only nonzero products are given):

$(B1)_{ }$:

$(A,\vartriangleright ,\vartriangleleft )$ is trivial;

$(B2)_{ }$:

$e_1\vartriangleleft e_1=e_2$;

$(B3)_{\lambda }$:

$e_1\vartriangleright e_1=e_2,\ \ e_1\vartriangleleft e_1=\lambda e_2$, where $\lambda \in \mathbb {C}$.

Obviously, these anti-dendriform algebras are “2-nilpotent” in the sense that all products involving three elements such as $(x\vartriangleright y)\vartriangleright z$ and $x\vartriangleleft ( y\vartriangleright z)$ are zero. Moreover, for any 2-dimensional complex anti-dendriform algebra $(A, \vartriangleright , \vartriangleleft )$, the two binary operations $\vartriangleright$ and $\vartriangleleft$ are colinear.

Proof

Assume that $(A, \vartriangleright , \vartriangleleft )$ is a compatible anti-dendriform algebra structure on $(A,\cdot )$. Set

$$\begin{aligned} e_i \vartriangleright e_j=\alpha _{ij}e_1+\beta _{ij}e_2,\;\;\alpha _{ij},\beta _{ij}\in \mathbb {C},\;\; 1\le i,j\le 2. \end{aligned}$$

(I) If $(A,\cdot )$ is (A1), then it is clear that

$$\begin{aligned} e_i \vartriangleleft e_j=-\alpha _{ij}e_1-\beta _{ij}e_2,\;\; 1\le i,j\le 2. \end{aligned}$$

Next, we consider the following three cases.

• Case (1) $\alpha _{22}=0$. Then, $\mathbb {C}e_2$ is an 1-dimensional subalgebra of $(A, \vartriangleright , \vartriangleleft )$. By Example 2.9, we have $\beta _{22}=0$. By Eq. (11) for $e_1,e_2,e_2$ and $e_2,e_2,e_1$, respectively, we have

  $$\begin{aligned} \alpha _{12}^2 e_1+\alpha _{12}\beta _{12}e_2=\alpha _{21}^2 e_1+\alpha _{21}\beta _{21}e_2=0. \end{aligned}$$

  Thus, $\alpha _{12}=\alpha _{21}=0$. By Eq. (11) for $e_1,e_1,e_2$ and $e_2,e_1,e_1$, respectively, we have $\beta _{12}=\beta _{21}=0$. By Eq. (11) for $e_1,e_1,e_1$, we have $\alpha _{11}=0$.

• Case (2) $\beta _{11}=0$. Then by the linear transformation $e_1\rightarrow e_2, e_2\rightarrow e_1$, we get Case (1).

• Case (3) $\beta _{11}\ne 0, \alpha _{22}\ne 0$. By Eq. (12) for $e_1,e_1,e_2$, we have

  $$\begin{aligned}&\alpha _{11}\alpha _{12}+\beta _{11}\alpha _{22}=\alpha _{11}\alpha _{12}+\beta _{12}\alpha _{12},\ \ \alpha _{11}\beta _{12}+\beta _{11}\beta _{22}=\alpha _{12}\beta _{11}+\beta _{12}^2. \end{aligned}$$

  Hence, $\alpha _{12}\ne 0, \beta _{12}\ne 0$. By Eq. (11) for $e_1,e_1,e_1$ and $e_2,e_2,e_2$, respectively, we have

  $$\begin{aligned} \alpha _{11}^2+\beta _{11}\alpha _{12}= & {} \alpha _{11}^2+\beta _{11}\alpha _{21}=\beta _{11}(\alpha _{11}+\beta _{12})=\beta _{11}(\alpha _{11}+\beta _{21})=0, \\ (\alpha _{21}+\beta _{22})\alpha _{22}= & {} (\alpha _{12}+\beta _{22})\alpha _{22}=\beta _{21}\alpha _{22}+\beta _{22}^2=\alpha _{22}\beta _{12}+\beta _{22}^2=0. \end{aligned}$$

  Therefore, we have

  $$\begin{aligned} \alpha _{12}=\alpha _{21}=-\beta _{22}=-\frac{\alpha _{11}^2}{\beta _{11}}\ne 0,\ \ \beta _{12}=\beta _{21}=-\alpha _{11},\ \ \alpha _{22}=\frac{\alpha _{11}^3}{\beta _{11}^2}. \end{aligned}$$

  Hence by a straightforward computation, we have

  $$\begin{aligned} (\frac{\alpha _{11}}{\beta _{11}}e_1+e_2)\vartriangleright (\frac{\alpha _{11}}{\beta _{11}}e_1+e_2)=(\frac{\alpha _{11}}{\beta _{11}}e_1+e_2)\vartriangleleft (\frac{\alpha _{11}}{\beta _{11}}e_1+e_2)=0. \end{aligned}$$

  Thus by the linear transformation $e_1\rightarrow e_1, e_2\rightarrow \frac{\alpha _{11}}{\beta _{11}}e_1+e_2$, we get Case (1).

Obviously, $(A, \vartriangleright , \vartriangleleft )$ with the nonzero products given by

$$\begin{aligned} e_1\vartriangleright e_1=\gamma e_2,\ \ e_1\vartriangleleft e_1=-\gamma e_2,\;\;\gamma \in {\mathbb {C}}, \end{aligned}$$

is an anti-dendriform algebra, corresponding to the above Case (1) with $\beta _{11}=\gamma$. Furthermore, it is straightforward to show that if $\gamma =0$, then $(A,\vartriangleright ,\vartriangleleft )$ is isomorphic to $(A1)_1$; otherwise, $(A,\vartriangleright ,\vartriangleleft )$ is isomorphic to $(A1)_2$.

(II) If $(A,\cdot )$ is (A2), then we have

$$\begin{aligned}&e_1\vartriangleleft e_1=-\alpha _{11} e_1-(\beta _{11}-1) e_2,\ \ e_1\vartriangleleft e_2=-\alpha _{12} e_1-\beta _{12} e_2,\\&e_2\vartriangleleft e_1=-\alpha _{21} e_1-\beta _{21} e_2,\ \ e_2\vartriangleleft e_2=-\alpha _{22} e_1-\beta _{22} e_2. \end{aligned}$$

Next, we consider the following two cases.

• Case (1) $\alpha _{22}=0$. Then by a similar discussion as for Case (1) of (I), we have

  $$\begin{aligned} \alpha _{11}=\alpha _{12}=\alpha _{21}=\beta _{12}=\beta _{21}=\beta _{22}=0. \end{aligned}$$

• Case (2) $\alpha _{22}\ne 0$. By Eq. (11) for $e_2,e_2,e_2$, we have

  $$\begin{aligned} \beta _{22}^2+\alpha _{22}\beta _{21}=\beta _{22}^2+\beta _{12}\alpha _{22}=\alpha _{22}(\alpha _{21}+\beta _{22})=\alpha _{22}(\alpha _{12}+\beta _{22})=0. \end{aligned}$$

  Thus, we have

  $$\begin{aligned} \beta _{22}^2+\alpha _{22}\beta _{21}=0, \ \ \alpha _{12}=\alpha _{21}=-\beta _{22},\ \ \beta _{12}=\beta _{21}. \end{aligned}$$

  By Eq. (11) for $e_1,e_1,e_1$, we have

  $$\begin{aligned} \alpha _{21}=-\alpha _{12},\;\;\beta _{21}=-\beta _{12}. \end{aligned}$$

  Therefore, we have

  $$\begin{aligned} \alpha _{12}=\alpha _{21}=\beta _{12}=\beta _{21}=\beta _{22}=0. \end{aligned}$$

  (21)

  Hence by Eq. (11) for $e_1,e_1,e_2$, we have

  $$\begin{aligned} -e_1\vartriangleright (e_1\vartriangleright e_2)=(e_1\vartriangleright e_1+e_1\vartriangleleft e_1)\vartriangleright e_2=\alpha _{22}e_1+\beta _{22}e_2=0. \end{aligned}$$

  Thus, $\alpha _{22}=0$, which is a contradiction.

Obviously, $(A, \vartriangleright , \vartriangleleft )$ with the nonzero products given by

$$\begin{aligned} e_1\vartriangleright e_1=\gamma e_2,\ \ e_1\vartriangleleft e_1=(1-\gamma ) e_2,\;\;\gamma \in {\mathbb {C}}, \end{aligned}$$

is an anti-dendriform algebra, corresponding to the above Case (1) with $\beta _{11}=\gamma$. Furthermore, it is straightforward to show that these anti-dendriform algebras are classified up to isomorphism into the cases $(A2)_1$ and $(A2)_{2,\lambda }$. More explicitly, if $\gamma =0$, then $(A,\vartriangleright ,\vartriangleleft )$ is isomorphic to $(A2)_1$; otherwise, $(A,\vartriangleright ,\vartriangleleft )$ is isomorphic to $(A2)_{2,\frac{1-\gamma }{\gamma }}$.

The rest of the proof follows straightforwardly. $\square$

Example 2.17

Let $(A,\cdot )$ be the 3-dimensional associative algebra with a basis $\{e_1,e_2,e_3\}$ whose nonzero products are given by

$$\begin{aligned} e_1\cdot e_1=e_2,\quad e_1\cdot e_2=e_2\cdot e_1=e_3. \end{aligned}$$

By a straightforward computation, $(A,\vartriangleright ,\vartriangleleft )$ is a compatible anti-dendriform algebra structure on $(A,\cdot )$ with the following nonzero products:

$$\begin{aligned}{} & {} e_1\vartriangleright e_1=\frac{1}{2}e_2+\gamma e_3,\;\; e_1\vartriangleleft e_1=\frac{1}{2}e_2-\gamma e_3,\;\; \\{} & {} e_1\vartriangleright e_2=e_2\vartriangleleft e_1=2e_3, \; \; e_2\vartriangleright e_1=e_1\vartriangleleft e_2=-e_3. \end{aligned}$$

for any $\gamma \in \mathbb {F}$. Note that $(A,\vartriangleright ,\vartriangleleft )$ is not “2-nilpotent” since $(e_1\vartriangleright e_1)\vartriangleleft e_1=e_3$.

2.2 Anti-${\mathcal {O}}$-operators and anti-Rota–Baxter operators

Definition 2.18

Let $(A,\cdot )$ be an associative algebra and (V, l, r) be a bimodule. A linear map $T: V\rightarrow A$ is called an anti-${\mathcal {O}}$-operator of $(A,\cdot )$ associated with (V, l, r) if the following equation holds:

$$\begin{aligned} T(u)\cdot T(v)=-T\big (l(T(u))v+r(T(v))u\big ), \quad \forall u,v\in V.\end{aligned}$$

(22)

Furthermore, T is called strong if

$$\begin{aligned} l(T(u)\cdot T(v))w=r(T(v)\cdot T(w))u, \quad \forall u, v, w\in V.\end{aligned}$$

(23)

In particular, an anti-${\mathcal {O}}$-operator T of $(A,\cdot )$ associated with the bimodule $(A,L_\cdot ,R_\cdot )$ is called an anti-Rota–Baxter operator; that is, $T:A\rightarrow A$ is a linear map satisfying

$$\begin{aligned} T(x)\cdot T(y)=-T\big (T(x)\cdot y+x\cdot T(y)\big ), \quad \forall x,y\in A.\end{aligned}$$

(24)

An anti-Rota–Baxter operator T is called strong if T satisfies

$$\begin{aligned} T(x)\cdot T(y)\cdot z=x\cdot T(y)\cdot T(z), \quad \forall x, y, z\in A.\end{aligned}$$

(25)

In these cases, we also call (A, T) an anti-Rota–Baxter algebra and a strong anti-Rota–Baxter algebra, respectively.

Remark 2.19

Let $(A,\cdot )$ be an associative algebra and (V, l, r) be a bimodule. Recall that a linear map $T:V\rightarrow A$ is called an ${\mathcal {O}}$-operator of $(A,\cdot )$ associated with the bimodule (V, l, r) if T satisfies

$$\begin{aligned} T(u)\cdot T(v)=T\big (l(T(u))v+r(T(v))u\big ), \quad \forall u,v\in V. \end{aligned}$$

In particular, an ${\mathcal {O}}$-operator T of $(A,\cdot )$ associated with the bimodule $(A,L_\cdot ,R_\cdot )$ is called a Rota–Baxter operator (of weight zero); that is, $T:A\rightarrow A$ is a linear map satisfying

$$\begin{aligned}T(x)\cdot T(y)=T\big (T(x)\cdot y+x\cdot T(y)\big ), \quad \forall x,y\in A.\end{aligned}$$

Rota–Baxter operators were introduced by G. Baxter to solve an analytic formula in probability [9] and then appeared in many areas in mathematics and physics [22, 35]. The notion of ${\mathcal {O}}$-operators was introduced in [5] (also appeared independently in [36] as a natural generalization of Rota–Baxter operators, which correspond to the solutions of associative Yang–Baxter equations in $(A,\cdot )$ under certain conditions. The notion of anti-${\mathcal {O}}$-operators as well as anti-Rota–Baxter operators is justified due to the comparison between them. Furthermore, it will be interesting to study the relationships between certain algebraic equations and anti-dendriform algebras as well as anti-${\mathcal {O}}$-operators, inspired by the relationships between the associative Yang–Baxter equation and dendriform algebras as well as ${\mathcal {O}}$-operators.

Proposition 2.20

Let $(A,\cdot )$ be an associative algebra and (V, l, r) be a bimodule. Suppose that $T: V\rightarrow A$ is an anti-${\mathcal {O}}$-operator of $(A,\cdot )$ associated with (V, l, r). Define two binary operations $\vartriangleright ,\vartriangleleft$ on V, respectively, as

$$\begin{aligned} u\vartriangleright v=-l(T(u))v,\quad u\vartriangleleft v=-r(T(v))u,\quad \forall u,v\in V. \end{aligned}$$

(26)

Then, the following conclusions hold.

• (1) For all $u,v,w\in V$, the following equations hold:

  $$\begin{aligned}{} & {} u\vartriangleright (v\vartriangleright w)=-(u\cdot v)\vartriangleright w,\ (u\vartriangleleft v)\vartriangleleft w=-u\vartriangleleft (v\cdot w), \nonumber \\{} & {} \ (u\vartriangleright v)\vartriangleleft w=u\vartriangleright (v\vartriangleleft w), \end{aligned}$$

  (27)

  where $u \cdot v=u\vartriangleright v +u\vartriangleleft v$.

• (2) $(V, \vartriangleright , \vartriangleleft )$ is an anti-dendriform algebra if and only if T is strong. In this case, T is a homomorphism of associative algebras from the associated associative algebra $(V,\cdot )$ to $(A,\cdot )$. Furthermore, there is an induced anti-dendriform algebra structure on $T(V)=\{T(u)~|~u\in V\}\subseteq A$ given by

  $$\begin{aligned} T(u)\vartriangleright T(v)=T(u\vartriangleright v),\quad T(u)\vartriangleleft T(v)=T(u\vartriangleleft v),\quad \forall u,v\in V, \end{aligned}$$

  (28)

  and T is a homomorphism of anti-dendriform algebras.

Proof

(1). Let $u,v,w\in V$. Then, we have

$$\begin{aligned} -u\vartriangleleft (v\cdot w)= & {} -u\vartriangleleft (v\vartriangleright w+v\vartriangleleft w)\\ {}= & {} -r\bigg (T\big (l(T(v))w\big )\bigg )u-r\bigg (T\big (r(T(w))v\big )\bigg )u \\= & {} r\big (T(v)\cdot T(w)\big )u=r(T(w))(r(T(v))u)=(u\vartriangleleft v)\vartriangleleft w. \end{aligned}$$

Similarly, we have

$$\begin{aligned} u\vartriangleright (v\vartriangleright w)=-(u\cdot v)\vartriangleright w,\quad (u\vartriangleright v)\vartriangleleft w=u\vartriangleright (v\vartriangleleft w). \end{aligned}$$

Thus, Eq. (27) holds.

(2). From Item (1) and Definition 2.4, $(V, \vartriangleright , \vartriangleleft )$ is an anti-dendriform algebra if and only if the following equation holds:

$$\begin{aligned} l\big (T(u)\cdot T(v)\big )w= & {} u\vartriangleright (v\vartriangleright w)=(u\vartriangleleft v)\vartriangleleft w\\ {}= & {} r\big (T(v)\cdot T(w)\big )u,\quad \forall u,v,w\in V; \end{aligned}$$

that is, T is a strong anti-${\mathcal {O}}$-operator. The other results follow immediately. $\square$

Corollary 2.21

Let $(A,\cdot )$ be an associative algebra and P be a strong anti-Rota–Baxter operator. Then, the triple $(A,\vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra, where

$$\begin{aligned} x\vartriangleright y=-P(x)\cdot y,\ \ x\vartriangleleft y=-x\cdot P(y), \ \ \forall x,y\in A.\end{aligned}$$

(29)

Conversely, if $P:A\rightarrow A$ is a linear transformation on an associative algebra $(A,\cdot )$ such that Eq. (29) defines an anti-dendriform algebra, then P satisfies

$$\begin{aligned} P(x)\cdot P(y)\cdot z= & {} -P\big (P(x)\cdot y+x\cdot P(y)\big )\cdot z=-x\cdot P\big (P(y)\cdot z+y\cdot P(z)\big )\nonumber \\ {}= & {} x\cdot P(y)\cdot P(z), \end{aligned}$$

(30)

for all $x,y,z\in A$. In particular, if

$$\begin{aligned} \textrm{Ann}^L_A(A)= & {} \{x\in A~|~x\cdot y=0,\forall y\in A\}=0,\;\;{or}\\ \textrm{Ann}^R_A(A)= & {} \{x\in A~|~y\cdot x=0,\forall y\in A\}=0, \end{aligned}$$

then P is a strong anti-Rota–Baxter operator.

Proof

The first part follows from Proposition 2.20 by letting $(V,l,r)=(A,L_{\cdot },R_{\cdot })$. The second part follows from Definition 2.4. $\square$

Example 2.22

Let $(A,\cdot )$ be a complex associative algebra with a basis $\{e_1,e_2\}$ whose nonzero products are given by

$$\begin{aligned} e_1\cdot e_1=e_1,\ \ e_1\cdot e_2=e_2. \end{aligned}$$

Suppose that $P:A\rightarrow A$ is a linear map whose corresponding matrix is given by $\left( \begin{matrix}\alpha _{11} &{}\alpha _{12}\\ \alpha _{21}&{}\alpha _{22}\\ \end{matrix}\right)$ under the basis $\{e_1,e_2\}$. Then by Eq. (24), P is an anti-Rota–Baxter operator on $(A,\cdot )$ if and only if

$$\begin{aligned} \alpha _{11}=\alpha _{12}=\alpha _{22}=0. \end{aligned}$$

Therefore, the set of all anti-Rota–Baxter operators on $(A,\cdot )$ is $\{ P=\left( \begin{matrix}0 &{}0 \\ \gamma &{}0\\ \end{matrix}\right) |\gamma \in {\mathbb {C}}\}$. Moreover, any anti-Rota–Baxter operator on $(A,\cdot )$ is strong. Hence by Eq. (29), we obtain the following anti-dendriform algebras whose nonzero products are given by

$$\begin{aligned} e_1\vartriangleleft e_1=-\gamma e_2,\;\; \gamma \in {\mathbb {C}}. \end{aligned}$$

It is straightforward to show that if $\gamma =0$, then it is isomorphic to (B1) and if $\gamma \ne 0$, then it is isomorphic to (B2), where the notations are given in Proposition 2.16.

Lemma 2.23

An invertible anti-${\mathcal {O}}$-operator of an associative algebra is automatically strong.

Proof

Let $T:V\rightarrow A$ be an invertible anti-${\mathcal {O}}$-operator of an associative algebra $(A,\cdot _A)$ associated with a bimodule (V, l, r). Define two binary operations $\vartriangleright ,\vartriangleleft$ on V, respectively, by Eq. (26). Define a binary operation $\cdot _V$ on V by

$$\begin{aligned} u\cdot _V v=u\vartriangleright v+u\vartriangleleft v,\;\;\forall u,v\in V. \end{aligned}$$

Let $u,v,w\in V$. Then, we have

$$\begin{aligned}&\big (T(u)\cdot _A T(v)\big )\cdot _A T(w)\nonumber \\ {}&\quad =-T\big (l(T(u))v+r(T(v))u\big )\cdot _A T(w) \\&\quad =T\bigg (l\big (T(l(T(u))v+r(T(v))u)\big )w+r(T(w))(l(T(u))v+r(T(v))u)\bigg ) \\&\quad =-T\big ((l(T(u))v+r(T(v))u)\vartriangleright w+(l(T(u))v+r(T(v))u)\vartriangleleft w\big )\\&\quad =T\bigg ((u\cdot _V v)\vartriangleright w+(u\vartriangleright v)\vartriangleleft w+(u\vartriangleleft v)\vartriangleleft w\bigg ). \end{aligned}$$

Similarly, we have

$$\begin{aligned}{} & {} T(u)\cdot _A \big (T(v)\cdot _A T(w)\big )=T\bigg (u\vartriangleright (v\vartriangleright w)+u\vartriangleright (v\vartriangleleft w)+u\vartriangleleft (v\cdot _V w)\bigg ). \end{aligned}$$

Since $(A,\cdot _A)$ is an associative algebra and T is invertible, we have

$$\begin{aligned}{} & {} (u\cdot _V v)\vartriangleright w+(u\vartriangleright v)\vartriangleleft w+(u\vartriangleleft v)\vartriangleleft w\\ {}{} & {} \quad =u\vartriangleright (v\vartriangleright w)+u\vartriangleright (v\vartriangleleft w)+u\vartriangleleft (v\cdot _V w). \end{aligned}$$

By Proposition 2.20, Eq. (27) holds and hence $u\vartriangleright (v\vartriangleright w)=(u\vartriangleleft v)\vartriangleleft w$. Therefore, $(V, \vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra and thus by Proposition 2.20 again, T is strong. $\square$

Theorem 2.24

Let $(A,\cdot )$ be an associative algebra. Then, there is a compatible anti-dendriform algebra structure on $(A,\cdot )$ if and only if there exists an invertible anti-${\mathcal {O}}$-operator of $(A,\cdot )$.

Proof

Suppose that $(A,\vartriangleright ,\vartriangleleft )$ is a compatible anti-dendriform algebra structure on $(A,\cdot )$. Then,

$$\begin{aligned} x\cdot y=x\vartriangleright y+x\vartriangleleft y=-(-L_\vartriangleright (x) y-R_\vartriangleleft (y)x),\;\;\forall x,y\in A. \end{aligned}$$

Hence, the identity map $\textrm{Id}:A\rightarrow A$ is an invertible anti-${\mathcal {O}}$-operator of $(A,\cdot )$ associated with the bimodule $(A,-L_\vartriangleright ,-R_\vartriangleleft )$.

Conversely, suppose that $T:V\rightarrow A$ is an invertible anti-${\mathcal {O}}$-operator of $(A,\cdot )$ associated with a bimodule (V, l, r) over $(A,\cdot )$. Then by Lemma 2.23 and Proposition 2.20, there exist anti-dendriform algebra structures on V and $T(V)=A$ defined by Eqs. (26) and  (28), respectively. Let $x,y\in A$. Then, there exist $u,v\in V$ such that $x=T(u),y=T(v)$. Hence, we have

$$\begin{aligned} x\cdot y&=T(u)\cdot T(v)=-T(l(T(u))v+r(T(v))u)=T(u\vartriangleright v+u\vartriangleleft v)\\&=T(u)\vartriangleright T(v)+T(u)\vartriangleleft T(v)=x\vartriangleright y+x\vartriangleleft y. \end{aligned}$$

So $(A,\vartriangleright ,\vartriangleleft )$ is a compatible anti-dendriform algebra structure on $(A,\cdot )$. $\square$

Proposition 2.25

Let $(A,\cdot )$ be an associative algebra and (V, l, r) be a bimodule. Suppose that $T:V\longrightarrow A$ is a linear map. Then, T is an anti-${\mathcal {O}}$-operator of $(A,\cdot )$ associated with (V, l, r) if and only if the linear map

$$\begin{aligned} {\hat{T}}: A\ltimes _{l,r} V\longrightarrow A\ltimes _{l,r} V,\quad (x,u)\longmapsto (T(u),0), \end{aligned}$$

is an anti-Rota–Baxter operator on the associative algebra $A\ltimes _{l,r}V$.

Proof

Let $x,y\in A,u,v\in V$. Then, we have

$$\begin{aligned} {\hat{T}}((x,u))\cdot {\hat{T}}((y,v))= & {} (T(u),0)\cdot (T(v),0)=(T(u)\cdot T(v),0),\\ {\hat{T}}((x,u))\cdot (y,v)= & {} (T(u),0)\cdot (y,v)=(T(u)\cdot y, l(T(u))v),\\ (x,u)\cdot {\hat{T}} ((y,v))= & {} (x,u)\cdot (T(v),0)=(x\cdot T(v), r(T(v))u). \end{aligned}$$

Hence, ${\hat{T}}$ is an anti-Rota–Baxter operator on the associative algebra $A\ltimes _{l,r}V$ if and only if

$$\begin{aligned} (T(u)\cdot T(v),0)=-\bigg (T\big (l(T(u))v+r(T(v))u\big ),0\bigg ); \end{aligned}$$

that is, T is an anti-${\mathcal {O}}$-operator of $(A,\cdot )$ associated with (V, l, r). $\square$

Corollary 2.26

Let $(A,\vartriangleright ,\vartriangleleft )$ be an anti-dendriform algebra and $(A,\cdot )$ be the associated associative algebra. Set ${\hat{A}}=A\oplus A$ as the direct sum of vector spaces. Define a binary operation $\cdot$ on ${\hat{A}}$ by Eq. (14) and a linear map $\widehat{\textrm{Id}}:{\hat{A}}\rightarrow {\hat{A}}$ by

$$\begin{aligned} \widehat{\textrm{Id}}((x,y))=(y,0),\;\;\forall x,y\in A. \end{aligned}$$

Then, $\widehat{\textrm{Id}}$ is an anti-Rota–Baxter operator on the associative algebra $({\hat{A}},\cdot )$; that is, $({\hat{A}}, \widehat{\textrm{Id}})$ is an anti-Rota–Baxter algebra.

Proof

By Corollary 2.8, $({\hat{A}},\cdot )$ is an associative algebra, which is exactly $A\ltimes _{-L_\vartriangleright ,-R_\vartriangleleft } A$. Since $\textrm{Id}:A\rightarrow A$ is an anti-${\mathcal {O}}$-operator of $(A,\cdot )$ associated with the bimodule $(A,-L_\vartriangleright ,-R_\vartriangleleft )$, by Proposition 2.25, $\widehat{\textrm{Id}}$ is an anti-Rota–Baxter operator on the associative algebra $({\hat{A}},\cdot )$. $\square$

Remark 2.27

In general, $\widehat{\textrm{Id}}$ is not a strong anti-Rota–Baxter operator on the associative algebra $({\hat{A}},\cdot )$ and hence one shows that there is not an anti-dendriform algebra structure on ${\hat{A}}$ defined by Eq. (29). On the other hand, we still define two binary operations $\vartriangleright ,\vartriangleleft$ on the vector subspace $A'=\{(0,x)|x\in A\}\subset {\hat{A}}$ by

$$\begin{aligned}{} & {} (0,x)\vartriangleright (0,y)=-\widehat{\textrm{Id}}((0,x))\cdot (0,y)=(0, x\vartriangleright y),\;\;\\ {}{} & {} (0,x)\vartriangleleft (0,y)=-(0,x)\cdot \widehat{\textrm{Id}}((0,y))=(0, x\vartriangleleft y), \end{aligned}$$

for all $x,y\in A$. Then, it is straightforward to show that $(A',\vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra. That is, there is still an anti-dendriform algebra structure on the subspace $A'$ of ${\hat{A}}$ defined by the anti-Rota–Baxter operator $\widehat{\textrm{Id}}$ through Eq. (29). Let $F:A\rightarrow A'$ be a linear map defined by

$$\begin{aligned} F(x)=(0,x),\;\;\forall x\in A. \end{aligned}$$

Then, F is an isomorphism of anti-dendriform algebras from $(A,\vartriangleright ,\vartriangleleft )$ to $(A',\vartriangleright ,\vartriangleleft )$. Hence in the sense above, the anti-dendriform algebra $(A,\vartriangleright ,\vartriangleleft )$ is “embedded” into the anti-Rota–Baxter algebra $({\hat{A}}, \widehat{\textrm{Id}})$. Note that it is a little different from the case of dendriform algebras and Rota–Baxter algebras given in [21], where there is a dendriform algebra structure on the whole space ${\hat{A}}$ defined by the Rota–Baxter operator $\widehat{\textrm{Id}}$.

2.3 Commutative Connes cocycles

A Connes cocycle on an associative algebra $(A,\cdot )$ is an antisymmetric bilinear form ${\mathcal {B}}$ satisfying

$$\begin{aligned} {\mathcal {B}}(x\cdot y, z)+{\mathcal {B}}(y\cdot z, x)+{\mathcal {B}}(z\cdot x, y)=0,\quad \forall x,y,z\in A. \end{aligned}$$

(31)

It corresponds to the original definition of cyclic cohomology by Connes [14]. Recall [2] that for a nondegenerate Connes cocycle ${\mathcal {B}}$ on an associative algebra $(A,\cdot )$, there exists a dendriform algebra structure (A, $\succ$, $\prec )$ on $(A,\cdot )$ defined by

$$\begin{aligned} {\mathcal {B}}(x\succ y, z)={\mathcal {B}}(y,z\cdot x),\ \ {\mathcal {B}}(x\prec y, z)={\mathcal {B}}(x,y\cdot z),\ \ \forall x,y,z\in A, \end{aligned}$$

(32)

such that the associated associative algebra of (A, $\succ$, $\prec )$ is $(A,\cdot )$.

Next we consider the “symmetric” version of a Connes cocycle.

Definition 2.28

Let $(A,\cdot )$ be an associative algebra and ${\mathcal {B}}$ be a bilinear form on $(A,\cdot )$. If ${\mathcal {B}}$ is symmetric and satisfies Eq. (31), then ${\mathcal {B}}$ is called a commutative Connes cocycle.

Let (V, l, r) be a bimodule over an associative algebra $(A,\cdot )$. Then, $(V^*, r^*, l^*)$ is also a bimodule over $(A,\cdot )$, where $V^*$ is the dual space of V and the linear maps $r^*,l^*:A\rightarrow \textrm{End}_{{\mathbb {F}}}(V^*)$ are defined, respectively, by

$$\begin{aligned} \langle r^*(x)u^*, v\rangle =\langle u^*, r(x)v\rangle , \quad \langle l^*(x)u^*, v\rangle =\langle u^*, l(x)v\rangle ,\quad \forall x\in A, u^*\in V^*, v\in V. \end{aligned}$$

In particular, $(A^*, R.^*, L.^*)$ is a bimodule over $(A,\cdot )$.

Theorem 2.29

Let $(A,\cdot )$ be a finite-dimensional associative algebra and ${\mathcal {B}}$ be a nondegenerate commutative Connes cocycle on $(A,\cdot )$. Then, there exists a compatible anti-dendriform algebra structure (A, $\vartriangleright$, $\vartriangleleft )$ on $(A,\cdot )$ defined by

$$\begin{aligned} {\mathcal {B}}(x\vartriangleright y, z)=-{\mathcal {B}}(y,z\cdot x),\ \ {\mathcal {B}}(x\vartriangleleft y, z)=-{\mathcal {B}}(x,y\cdot z),\ \ \forall x,y,z\in A. \end{aligned}$$

(33)

Proof

Define a linear map $T: A\rightarrow A^*$ by

$$\begin{aligned} \langle T(x), y\rangle ={\mathcal {B}}(x,y),\ \ \forall x,y\in A. \end{aligned}$$

Then, T is invertible since ${\mathcal {B}}$ is nondegenerate. For all $a^*,b^*\in A^*, z\in A$, we have

$$\begin{aligned}&{\mathcal {B}}(-T^{-1}\big (R.^*(T^{-1}(a^*))(b^*)+L.^*(T^{-1}(b^*))(a^*)\big ),z)\\ =&-\langle R.^*(T^{-1}(a^*))(b^*)+L.^*(T^{-1}(b^*))(a^*),z \rangle \\ =&-\langle b^*, z\cdot T^{-1}(a^*)\rangle -\langle a^*, T^{-1}(b^*)\cdot z\rangle \\ =&-{\mathcal {B}}(T^{-1}(b^*), z\cdot T^{-1}(a^*))-{\mathcal {B}}(T^{-1}(a^*), T^{-1}(b^*)\cdot z)\\ =&{\mathcal {B}}(T^{-1}(a^*)\cdot T^{-1}(b^*), z), \end{aligned}$$

which implies that $T^{-1}: A^*\rightarrow A$ is an anti-${\mathcal {O}}$-operator of $(A,\cdot )$ associated with $(A^*, R.^*, L.^*)$.

Note that for any $x,y\in A,$ there exist $a^*,b^*\in A^*$ such that $x=T^{-1}(a^*), y=T^{-1}(b^*)$. By Theorem 2.24, there is a compatible anti-dendriform algebra structure on $(A,\cdot )$ defined by

$$\begin{aligned} x\vartriangleright y:&=T^{-1}(a^*\vartriangleright b^*)=-T^{-1}\big (R.^*(T^{-1}(a^*))b^*\big )=-T^{-1}\big (R.^*(x)T(y)\big ),\\ x\vartriangleleft y:&=T^{-1}(a^*\vartriangleleft b^*)=-T^{-1}\big (L.^*(T^{-1}(b^*))a^*\big )=-T^{-1}\big (L.^*(y)T(x)\big ). \end{aligned}$$

Therefore, for all $x,y,z\in A$, we have

$$\begin{aligned} {\mathcal {B}}(x\vartriangleright y, z)&= -\langle R.^*(x)T(y), z\rangle =-\langle T(y),z\cdot x\rangle =-{\mathcal {B}}(y, z\cdot x),\\ {\mathcal {B}}(x\vartriangleleft y, z)&= -\langle L.^*(y)T(x), z\rangle =-\langle T(x),y\cdot z\rangle =-{\mathcal {B}}(x, y\cdot z). \end{aligned}$$

Thus, the conclusion holds. $\square$

Corollary 2.30

Let $(A,\vartriangleright ,\vartriangleleft )$ be an anti-dendriform algebra and $(A,\cdot )$ be the associated associative algebra. Define a bilinear form ${\mathcal {B}}$ on $A\oplus A^{*}$ by

$$\begin{aligned} {\mathcal {B}}(x+a^{*},y+b^{*})=\langle x,b^{*}\rangle +\langle a^{*},y\rangle ,\ \ \forall x,y\in A, a^{*},b^{*}\in A^{*}. \end{aligned}$$

(34)

Then, ${\mathcal {B}}$ is a nondegenerate commutative Connes cocycle on the associative algebra $A\ltimes _{-R^{*}_{\vartriangleleft },-L^{*}_{\vartriangleright }}A^*$. Conversely, let $(A,\cdot )$ be an associative algebra and $(A^*,l,r)$ be a bimodule over $(A,\cdot )$. Suppose that the bilinear form given by Eq. (34) is a commutative Connes cocycle on $A\ltimes _{l,r}A^*$. Then, there is a compatible anti-dendriform algebra structure $(A,\vartriangleright ,\vartriangleleft )$ on $(A,\cdot )$ such that $l=-R^{*}_{\vartriangleleft }, r=-L^{*}_{\vartriangleright }$.

Proof

It is straightforward to show that ${\mathcal {B}}$ is a nondegenerate commutative Connes cocycle on $A\ltimes _{-R^{*}_{\vartriangleleft },-L^{*}_{\vartriangleright }}A^*$. Conversely, by Theorem 2.29, there is a compatible anti-dendriform algebra structure $\vartriangleright ,\vartriangleleft$ given by Eq. (33) on $A\ltimes _{l,r}A^*.$ In particular, we have

$$\begin{aligned} {\mathcal {B}}(x\vartriangleright y, z)=-{\mathcal {B}}(y,z\cdot x)=0,\ \ {\mathcal {B}}(x\vartriangleleft y, z)=-{\mathcal {B}}(x,y\cdot z)=0,\ \ \forall x,y,z\in A. \end{aligned}$$

Thus, $x\vartriangleright y,x\vartriangleleft y\in A$ for all $x,y\in A$ and hence $(A, \vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra. Furthermore, for all $x,y\in A, a^*\in A^*,$ we have

$$\begin{aligned}&\langle -R_{\vartriangleleft }^*(x)a^*, y\rangle =-\langle a^*, y\vartriangleleft x\rangle =-{\mathcal {B}}( y\vartriangleleft x, a^*) ={\mathcal {B}}( y, l(x) a^*)=\langle l(x) a^*, y\rangle ,\\&\langle -L_{\vartriangleright }^*(x)a^*, y\rangle =-\langle a^*, x\vartriangleright y\rangle =-{\mathcal {B}}( x\vartriangleright y, a^*) ={\mathcal {B}}(y, r(x) a^*)=\langle r(x) a^*,y\rangle . \end{aligned}$$

So $l=-R^{*}_{\vartriangleleft }, r=-L^{*}_{\vartriangleright }$. $\square$

Definition 2.31

Let $(A, \vartriangleright ,\vartriangleleft )$ be an anti-dendriform algebra. A bilinear form ${\mathcal {B}}$ on $(A, \vartriangleright ,\vartriangleleft )$ is called invariant if

$$\begin{aligned} {\mathcal {B}}(x\vartriangleright y, z)=-{\mathcal {B}}(y,z\cdot x),\ \ {\mathcal {B}}(x\vartriangleleft y, z)=-{\mathcal {B}}(x,y\cdot z),\ \ \forall x,y,z\in A, \end{aligned}$$

where the binary operation $\cdot$ is defined by Eq. (7).

The following conclusion is obvious.

Lemma 2.32

Let ${\mathcal {B}}$ be an invariant bilinear form on an anti-dendriform algebra (A, $\vartriangleright$, $\vartriangleleft )$. Then, ${\mathcal {B}}$ satisfies

$$\begin{aligned} {\mathcal {B}}(x\vartriangleleft y,z)={\mathcal {B}}(z\vartriangleright x, y),\;\;\forall x,y,z\in A. \end{aligned}$$

Proposition 2.33

Let $(A,\vartriangleright ,\vartriangleleft )$ be an anti-dendriform algebra and ${\mathcal {B}}$ be a symmetric invariant bilinear form on $(A,\vartriangleright ,\vartriangleleft ).$ Then, ${\mathcal {B}}$ is a commutative Connes cocycle on the associated associative algebra $(A,\cdot )$. Conversely, suppose that $(A,\cdot )$ is an associative algebra and ${\mathcal {B}}$ is a nondegenerate commutative Connes cocycle on $(A,\cdot ).$ Then, ${\mathcal {B}}$ is invariant on the compatible anti-dendriform algebra $(A,\vartriangleright ,\vartriangleleft )$ defined by Eq. (33).

Proof

For the first part, we have

$$\begin{aligned}{} & {} {\mathcal {B}}(x\cdot y,z)+{\mathcal {B}}(y\cdot z,x)+{\mathcal {B}}(z\cdot x,y)\\ {}{} & {} \quad ={\mathcal {B}}(x\cdot y,z)-{\mathcal {B}}(x\vartriangleleft y, z)-{\mathcal {B}}(x\vartriangleright y, z)=0, \end{aligned}$$

for all $x,y,z\in A$. So ${\mathcal {B}}$ is a commutative Connes cocycle on $(A,\cdot )$. The second part follows from Theorem 2.29 immediately. $\square$

Recall that two bimodules $(V_1,l_1,r_1)$ and $(V_2,l_2,r_2)$ over an associative algebra $(A,\cdot )$ are called equivalent if there is a linear isomorphism $\varphi :V_1\rightarrow V_2$ such that

$$\begin{aligned} \varphi (l_1(x)v_1)=l_2(x)\varphi (v_1),\ \ \varphi (r_1(x)v_1)=r_2(x)\varphi (v_1),\ \ \forall x\in A, v_1\in V_1. \end{aligned}$$

Proposition 2.34

Let $(A, \vartriangleright ,\vartriangleleft )$ be an anti-dendriform algebra. Then, there is a nondegenerate invariant bilinear form on $(A, \vartriangleright ,\vartriangleleft )$ if and only if $(A, -L_\vartriangleright ,-R_\vartriangleleft )$ and $(A^*, R.^*, L.^*)$ are equivalent as bimodules over the associated associative algebra $(A,\cdot )$.

Proof

Suppose that $(A, -L_\vartriangleright ,-R_\vartriangleleft )$ and $(A^*, R.^*, L.^*)$ are equivalent as bimodules over $(A,\cdot )$. Then, there exists a linear isomorphism $\psi : A\rightarrow A^*$ such that

$$\begin{aligned} \psi (-L_\vartriangleright (x)y)=R.^*(x)\psi (y),\ \ \psi (-R_\vartriangleleft (x)y)=L.^*(x)\psi (y),\ \ \forall x,y\in A. \end{aligned}$$

Define a nondegenerate bilinear form ${\mathcal {B}}$ on A as

$$\begin{aligned} {\mathcal {B}}(x,y)=\langle \psi (x), y\rangle ,\quad \forall x,y\in A. \end{aligned}$$

(35)

For all $x,y,z\in A,$ we have

$$\begin{aligned} {\mathcal {B}}(x\vartriangleright y,z)&=-\langle \psi (-L_\vartriangleright (x)y),z\rangle =-\langle R.^*(x)\psi (y), z\rangle =-{\mathcal {B}}(y,z\cdot x),\\ {\mathcal {B}}(x\vartriangleleft y,z)&=-\langle \psi (-R_\vartriangleleft (y)x),z\rangle =-\langle L.^*(y)\psi (x),z\rangle =-{\mathcal {B}}(x,y\cdot z). \end{aligned}$$

So ${\mathcal {B}}$ is invariant.

Conversely, suppose that ${\mathcal {B}}$ is a nondegenerate invariant bilinear form on $(A, \vartriangleright ,\vartriangleleft ).$ Define a linear map $\psi :A\rightarrow A^*$ by Eq. (35). By a similar proof as above, we show that $\psi$ gives an equivalence between $(A, -L_\vartriangleright ,-R_\vartriangleleft )$ and $(A^*, R.^*, L.^*)$ as bimodules over $(A,\cdot )$.

This completes the proof. $\square$

Recall that a symmetric bilinear form ${\mathcal {B}}$ on a Lie algebra $(A,[,\,])$ is called a commutative 2-cocycle (see [16]) if the following equation holds:

$$\begin{aligned} {\mathcal {B}}([x,y],z)+{\mathcal {B}}([y,z],x)+{\mathcal {B}}([z,x],y)=0,\ \ \forall x,y,z\in A. \end{aligned}$$

By [27], there is a compatible anti-pre-Lie algebra structure $(A,\circ )$ on a Lie algebra $(A,[,\,])$ with a nondegenerate commutative 2-cocycle ${\mathcal {B}}$ defined by

$$\begin{aligned} {\mathcal {B}}(x\circ y,z)={\mathcal {B}}(y,[x,z]), \ \ \forall x,y,z\in A.\end{aligned}$$

(36)

A bilinear form ${\mathcal {B}}$ on an anti-pre-Lie algebra $(A,\circ )$ is called invariant if Eq. (36) holds.

Lemma 2.35

[27] Any symmetric invariant bilinear form on an anti-pre-Lie algebra $(A,\circ )$ is a commutative 2-cocycle on the sub-adjacent Lie algebra $(\mathfrak {g}(A),[,\,])$. Conversely, a nondegenerate commutative 2-cocycle on a Lie algebra $(A,[,\,])$ is invariant on the compatible anti-pre-Lie algebra $(A,\circ )$ defined by Eq. (36).

Lemma 2.36

• (1) Let $(A,\vartriangleright ,\vartriangleleft )$ be an anti-dendriform algebra with a symmetric invariant bilinear form ${\mathcal {B}}.$ Then, ${\mathcal {B}}$ is invariant on the associated anti-pre-Lie algebra $(A,\circ ).$

• (2) Let $(A,\cdot )$ be an associative algebra with a commutative Connes cocycle ${\mathcal {B}}.$ Then, ${\mathcal {B}}$ is a commutative 2-cocycle on the sub-adjacent Lie algebra $(\mathfrak {g}(A),[\,,\, ]).$

Proof

It is straightforward. $\square$

Proposition 2.37

Let $(A,\vartriangleright ,\vartriangleleft )$ be an anti-dendriform algebra with a symmetric invariant bilinear form ${\mathcal {B}}$. Then, the following conclusions hold:

• (1) ${\mathcal {B}}$ is a commutative Connes cocycle on the associated associative algebra $(A,\cdot )$;

• (2) ${\mathcal {B}}$ is invariant on the associated anti-pre-Lie algebra $(A,\circ )$;

• (3) ${\mathcal {B}}$ is a commutative 2-cocycle on the sub-adjacent Lie algebra $(\mathfrak {g}(A),[,\,])$ of both $(A,\cdot )$ and $(A,\circ )$.

That is, the following diagram by “putting” the symmetric bilinear forms into the diagram (5) is commutative.

(37)

Conversely, let $(A,\cdot )$ be an associative algebra with a nondegenerate commutative Connes cocycle ${\mathcal {B}}$. On the one hand, ${\mathcal {B}}$ is a nondegenerate commutative 2-cocycle on the sub-adjacent Lie algebra $(\mathfrak {g}(A),[\,,\, ])$ and hence there is a compatible anti-pre-Lie algebra $(A,\circ )$ defined by Eq. (36) and ${\mathcal {B}}$ is invariant on $(A,\circ )$. On the other hand, there is a compatible anti-dendriform algebra $(A,\vartriangleright ,\vartriangleleft )$ defined by Eq. (33) and ${\mathcal {B}}$ is invariant on $(A,\vartriangleright ,\vartriangleleft )$. Hence, ${\mathcal {B}}$ is invariant on the associated anti-pre-Lie algebra $(A,\circ ')$ defined by Eq. (18). Moreover, $(A,\circ )$ and $(A,\circ ')$ coincide; that is, the following diagram is commutative.

(38)

Proof

By the first parts of Proposition 2.33 and Lemma 2.35, respectively, and Lemma 2.36, the first part follows. For the second part, note that for all $x,y,z\in A$, we have

$$\begin{aligned}{} & {} {\mathcal {B}}(x\circ y, z)={\mathcal {B}}(y,[x,z])\\ {}{} & {} \quad ={\mathcal {B}}(y,x\cdot z-z\cdot x)={\mathcal {B}}(x\vartriangleright y, z)-\mathcal B(y\vartriangleleft x,z)={\mathcal {B}}(x\circ ' y,z). \end{aligned}$$

Hence, $x\circ y=x\circ 'y$. Then, the conclusion follows immediately from the second parts of Proposition 2.33 and Lemma 2.35, respectively, and Lemma 2.36. $\square$

3 Correspondences between some subclasses of dendriform and anti-dendriform algebras

We give the correspondence between some subclasses of dendriform algebras and anti-dendriform algebras in terms of q-algebras. We also generalize the correspondence between some subclasses of pre-Lie algebras and anti-pre-Lie algebras from $q=- 2$ in [27] to any $q\ne 0,\pm 1$, and hence, the relationships between dendriform algebras and the associated pre-Lie algebras as well as anti-dendriform algebras and the associated anti-pre-Lie algebras are still kept on these subclasses for a fixed q. Therefore in the case that $q=- 2$, the notions of Novikov-type dendriform algebras and admissible Novikov-type dendriform algebras are introduced as analogues of Novikov algebras and admissible Novikov algebras for dendriform algebras and anti-dendriform algebras, respectively.

Throughout this section, $q\in \mathbb {F}$ satisfies $q\ne 0, \pm 1.$

3.1 Correspondences between some subclasses of dendriform and anti-dendriform algebras

Definition 3.1

Let A be a vector space with two binary operations $\succ ,\prec .$ Define two binary operations $\vartriangleright ,\vartriangleleft :A\otimes A\rightarrow A$, respectively, by

$$\begin{aligned} x\vartriangleright y=x\succ y+qx\prec y, \quad x\vartriangleleft y=x\prec y+qx\succ y,\quad \forall x,y\in A. \end{aligned}$$

(39)

Then, the triple $(A,\vartriangleright ,\vartriangleleft )$ is called the q-algebra over $(A,\succ ,\prec )$.

Remark 3.2

There is an alternative choice of q-algebras for the triple $(A,\succ ,\prec )$. Let A be a vector space with two binary operations $\succ ,\prec .$ Define two binary operations $\vartriangleright ',\vartriangleleft ':A\otimes A\rightarrow A$, respectively, by

$$\begin{aligned} x\vartriangleright ' y=x\succ y+qy\succ x, \quad x\vartriangleleft ' y=x\prec y+qy\prec x,\quad \forall x,y\in A. \end{aligned}$$

(40)

However, such an approach is not “naturally available” for associative admissible algebras such as dendriform as well as anti-dendriform algebras. In fact, suppose that $(A,\succ ,\prec )$ is an associative admissible algebra. Then, we have the following conclusions.

• (1) By Eq. (39), $(A,\vartriangleright ,\vartriangleleft )$ is always an associative admissible algebra.

• (2) If $q\ne 0$, then from Eq. (40), $(A,\vartriangleright ',\vartriangleleft ')$ is an associative admissible algebra if and only if the q-algebra (see Definition 3.14) over the associated associative algebra $(A,\cdot )$ of $(A,\succ ,\prec )$, where $\cdot$ is defined by Eq. (2), is still an associative algebra. Note that the latter holds if and only if the sub-adjacent Lie algebra $(\mathfrak {g}(A),[,\,])$ of $(A,\cdot )$ is two-step nilpotent, that is, $[[x,y],z]=0$ for all $x,y,z\in A$.

Hence in the sense of keeping the property of splitting the associativity for both an associative admissible algebra $(A,\succ ,\prec )$ and its q-algebra, it is natural to use Eq. (39) (not Eq. (40)) to define the q-algebra over the associative admissible algebra $(A,\succ ,\prec )$.

Remark 3.3

When $q=0$, the 0-algebra over $(A,\succ ,\prec )$ is itself. Moreover, note that

$$\begin{aligned} x\vartriangleright y-qx\vartriangleleft y=(1-q^2)x\succ y,\ \ x\vartriangleleft y-qx\vartriangleright y=(1-q^2)x\prec y,\ \ \forall x,y\in A. \end{aligned}$$

Hence, we have the following conclusions.

• (1) When $q\ne \pm 1$, the binary operations $\succ ,\prec$ can be presented by $\vartriangleright ,\vartriangleleft$. Furthermore, the $(-q)$-algebra over $(A,\vartriangleright ,\vartriangleleft )$ has the same algebra structure as $(A,\succ ,\prec )$.

• (2) When $q=\pm 1$, the binary operations $\succ ,\prec$ cannot be presented by $\vartriangleright ,\vartriangleleft$. Furthermore, the $(-q)$-algebra over $(A,\vartriangleright ,\vartriangleleft )$ is trivial.

So in the sense that the triple $(A,\succ ,\prec )$ and its q-algebra can be non-trivially presented by each other, the cases that $q=0,\pm 1$ are excluded.

Proposition 3.4

Let $(A,\succ ,\prec )$ be a dendriform algebra. Denote by $(A, \vartriangleright ,\vartriangleleft )$ the q-algebra over $(A,\succ ,\prec ).$ Then, $(A,\vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra if and only if $(A,\succ ,\prec )$ satisfies the following equations:

$$\begin{aligned}{} & {} x\succ (y\succ z)=(x\prec y)\prec z, \end{aligned}$$

(41)

$$\begin{aligned}{} & {} (x\prec y)\succ z=x\prec (y\succ z), \end{aligned}$$

(42)

$$\begin{aligned}{} & {} (q+1)(q+2)(x\prec y)\prec z+q(q+2)x\succ (y\prec z)+q(q-1)x\prec (y\prec z)=0,\nonumber \\ \end{aligned}$$

(43)

for all $x,y,z\in A$.

Proof

Let $x,y,z\in A$. By Eq. (39) and the definition of dendriform algebras, we have

$$\begin{aligned}{} & {} x\vartriangleright (y\vartriangleright z)+(x\vartriangleright y)\vartriangleright z+(x\vartriangleleft y)\vartriangleright z\nonumber \\{} & {} =2x\succ (y\succ z)+q\big (2(x\succ y)\prec z+x\prec (y\succ z)+(x\prec y)\succ z\nonumber \\{} & {} \quad +(x\succ y)\succ z+(x\prec y)\prec z\big )\nonumber \\{} & {} \hspace{0.4cm} +q^2\big (x\prec (y\prec z)+(x\prec y)\prec z+(x\succ y)\prec z\big ), \end{aligned}$$

(44)

$$\begin{aligned}{} & {} (x\vartriangleleft y)\vartriangleleft z+ x\vartriangleleft (y\vartriangleright z)+ x\vartriangleleft (y\vartriangleleft z)\nonumber \\{} & {} =2(x\prec y)\prec z+q\big (2x\succ (y\prec z)+(x\prec y)\succ z+x\prec (y\prec z)\nonumber \\{} & {} \quad +x\succ (y\succ z)+x\prec (y\succ z)\big )\nonumber \\{} & {} \hspace{0.4cm}+q^2\big ((x\succ y)\succ z+x\succ (y\prec z)+x\succ (y\succ z)\big ), \end{aligned}$$

(45)

$$\begin{aligned}{} & {} x\vartriangleright (y\vartriangleright z)-(x\vartriangleleft y)\vartriangleleft z\nonumber \\{} & {} =x\succ (y\succ z)-(x\prec y)\prec z+q\big (x\prec (y\succ z)-(x\prec y)\succ z\big )\nonumber \\{} & {} \quad +q^2\big (x\prec (y\prec z)-(x\succ y)\succ z\big ), \end{aligned}$$

(46)

$$\begin{aligned}{} & {} (x\vartriangleright y)\vartriangleleft z-x\vartriangleright (y\vartriangleleft z)\nonumber \\{} & {} =q\big ((x\prec y)\prec z+(x\succ y)\succ z-x\succ (y\succ z)-x\prec (y\prec z)\big )\nonumber \\{} & {} \quad +q^2\big ((x\prec y)\succ z-x\prec (y\succ z)\big ). \end{aligned}$$

(47)

Therefore, $(A,\vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra if and only if the right-hand sides of Eqs. (44–47) are zero. Next we assume that the right-hand sides of Eqs. (44–47) are zero and we still denote them by Eqs. (44–47), respectively. Thus, we have the following interpretation.

• (1) The difference between Eqs. (44) and (45) is

  $$\begin{aligned}{} & {} 2x\succ (y\succ z)-2(x\prec y)\prec z+q\big ((x\succ y)\succ z\nonumber \\{} & {} \quad +(x\prec y)\prec z-x\prec (y\prec z)-x\succ (y\succ z)\big )\nonumber \\{} & {} \hspace{0.4cm}+q^2\big (x\prec (y\prec z)+(x\prec y)\prec z-(x\succ y)\succ z-x\succ (y\succ z)\big ) \nonumber \\{} & {} =(2-q-q^2)\big (x\succ (y\succ z)-(x\prec y)\prec z\big )\nonumber \\{} & {} \quad +(q-q^2)\big ((x\succ y)\succ z-x\prec (y\prec z)\big )=0. \end{aligned}$$

  (48)

• (2) The difference between Eqs. (48) and (47) is

  $$\begin{aligned}&(-2q^2+2)\big (x\succ (y\succ z)-(x\prec y)\prec z\big )=0. \end{aligned}$$

  (49)

  By the assumption of q, Eq. (49) holds if and only if Eq. (41) holds.

• (3) Suppose that Eqs. (48) and (41) hold. Then, Eq. (46) holds if and only if the following equation holds:

  $$\begin{aligned} x\prec (y \succ z)-(x\prec y)\succ z=0; \end{aligned}$$

  that is, Eq. (42) holds.

• (4) Suppose that Eqs. (41) and (42) hold. Then by the definition of dendriform algebras, we have

  • (a) Eq. (48) holds;

  • (b) Eq. (45) holds if and only if the following equation holds:

    $$\begin{aligned}&(q+1)(q+2)(x\prec y)\prec z+ q(q+2)x\succ (y\prec z)+ q(q-1)x\prec (y\prec z)\\ {}&\quad =0; \end{aligned}$$

    that is, Eq. (43) holds.

Therefore, $(A,\vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra if and only if the following equivalences hold:

$$\begin{aligned} \mathrm{Eqs.}~(44),~(45),~(46) \mathrm{\ and\ }(47) \mathrm{\ hold}.&\Longleftrightarrow \ {}&\mathrm{Eqs.}~(41),~(45),~(46)\mathrm{\ and\ }~(48)\mathrm{\ hold}.\\&\Longleftrightarrow \ {}&\mathrm{Eqs.}~(41),~(42)\mathrm{\ and\ } (43)\mathrm{\ hold}. \end{aligned}$$

Therefore, the conclusion holds. $\square$

Proposition 3.5

Suppose that $(A,\vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra. Denote by $(A,\succ ,\prec )$ the $(-q)$-algebra over $(A, \vartriangleright ,\vartriangleleft ).$ Then, $(A,\succ ,\prec )$ is a dendriform algebra if and only if $(A, \vartriangleright ,\vartriangleleft )$ satisfies the following equations:

$$\begin{aligned}{} & {} (x\vartriangleleft y)\vartriangleright z=x\vartriangleleft (y\vartriangleright z), \end{aligned}$$

(50)

$$\begin{aligned}{} & {} -(q-2)(q+1)(x\vartriangleleft y)\vartriangleleft z-q^2(x\vartriangleright y)\vartriangleleft z+q(q+1)x\vartriangleleft (y\vartriangleleft z)=0,\nonumber \\ \end{aligned}$$

(51)

for all $x,y,z\in A$.

Proof

Let $x,y,z\in A$. By the definitions of q-algebras and anti-dendriform algebras, we have

$$\begin{aligned}{} & {} x\succ (y\succ z)-(x\succ y)\succ z-(x\prec y)\succ z\nonumber \\{} & {} =2x\vartriangleright (y\vartriangleright z)+q\big (x\vartriangleleft (y\vartriangleright z)+(x\vartriangleright y)\vartriangleright \nonumber \\{} & {} \quad z+(x\vartriangleleft y)\vartriangleleft z-(x\vartriangleleft y)\vartriangleright z\big )\nonumber \\{} & {} \hspace{0.4cm} +q^2\big (x\vartriangleleft (y\vartriangleleft z)-(x\vartriangleleft y)\vartriangleleft z-(x\vartriangleright y)\vartriangleleft z\big ), \end{aligned}$$

(52)

$$\begin{aligned}{} & {} (x\prec y)\prec z-x\prec (y\prec z)-x\prec (y\succ z)\nonumber \\{} & {} =2(x\vartriangleleft y)\vartriangleleft z+q\big (x\vartriangleleft (y\vartriangleright z)+x\vartriangleleft (y\vartriangleleft z)+x\vartriangleright (y\vartriangleright z)-(x\vartriangleleft y)\vartriangleright z\big )\nonumber \\{} & {} \hspace{0.4cm} +q^2\big ((x\vartriangleright y)\vartriangleright z-x\vartriangleright (y\vartriangleright z)-x\vartriangleright (y\vartriangleleft z)\big ), \end{aligned}$$

(53)

$$\begin{aligned}{} & {} (x\succ y)\prec z-x\succ (y\prec z)=(q^2+q)\big ((x\vartriangleleft y)\vartriangleright z-x\vartriangleleft (y\vartriangleright z)\big ). \end{aligned}$$

(54)

So $(A,\succ ,\prec )$ is a dendriform algebra if and only if the right-hand sides of Eqs. (52–54) are zero. Now, we assume that the right-hand sides of Eqs. (52–54) are zero and we still denote them by Eqs. (52–54), respectively. Thus, we have the following interpretation.

• (1) By the assumption of q, Eq. (54) holds if and only if Eq. (50) holds.

• (2) By the definition of anti-dendriform algebras, the difference between Eqs. (52) and (53) is Eq. (54). Therefore after supposing that Eq. (50) holds, we show that Eq. (52) holds if and only if Eq. (53) holds.

• (3) Suppose that Eq. (50) holds. By the definition of anti-dendriform algebras again, Eq. (52) holds if and only if the following equation holds:

  $$\begin{aligned} -(q-2)(q+1)(x\vartriangleleft y)\vartriangleleft z-q^2(x\vartriangleright y)\vartriangleleft z+q(q+1)x\vartriangleleft (y\vartriangleleft z)=0; \end{aligned}$$

  that is, Eq. (51) holds.

Hence, $(A,\succ ,\prec )$ is a dendriform algebra if and only if the following equivalences hold:

$$\begin{aligned} \mathrm{Eqs.}~(52),~(53),\mathrm{\ and\ }(54)\mathrm{\ hold}.&\Longleftrightarrow \ {}&\mathrm{Eqs.}~(50)\mathrm{\ and\ } ~(52)\mathrm{\ hold}.\\&\Longleftrightarrow \ {}&\mathrm{Eqs.}~(50)\mathrm{\ and\ } ~(51)\mathrm{\ hold}. \end{aligned}$$

This completes the proof. $\square$

Theorem 3.6

Let A be a vector space with two binary operations ${\succ },{\prec }$. Then, $(A,{\succ },{\prec })$ is a dendriform algebra satisfying Eqs. (41–43) if and only if its q-algebra $(A,\vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra satisfying Eqs. (50–51).

Proof

Suppose that $(A,\succ ,\prec )$ is a dendriform algebra satisfying Eqs. (41–43). Then, it is clear that $(A,\vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra by Proposition 3.4. Furthermore, note that $(-q)$-algebra over $(A,\vartriangleright ,\vartriangleleft )$ is a dendriform algebra, thus Eqs. (50–51) hold by Proposition 3.5; that is, $(A,\vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra satisfying Eqs. (50–51). The converse is similar. $\square$

Remark 3.7

Theorem 3.6 is equivalent to the following statement. The triple $(A,\vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra satisfying Eqs. (50–51) if and only if its $(-q)$-algebra $(A,\succ ,\prec )$ is a dendriform algebra satisfying Eqs. (41–43).

Recall that a pre-Lie algebra is a vector space A with a binary operation $*$ satisfying

$$\begin{aligned} (x*y)*z-x*(y*z)=(y*x)*z-y*(x*z),\quad \forall x,y,z\in A.\end{aligned}$$

(55)

A Novikov algebra [8, 20]) is a pre-Lie algebra $(A,*)$ such that

$$\begin{aligned} (x*y)*z=(x*z)*y, \quad \forall x,y,z\in A. \end{aligned}$$

(56)

An admissible Novikov algebra is a vector space with a binary operation $\circ$ satisfying Eq. (16) and the following equation:

$$\begin{aligned} 2x\circ [y,z]=(x\circ y)\circ z-(x\circ z)\circ y, \;\; \forall x,y,z\in A. \end{aligned}$$

(57)

It is known that an admissible Novikov algebra is an anti-pre-Lie algebra [27].

On the other hand, for Eq. (43), $q=-2$ is a little “special” in the sense that only one monomial in x, y, z is left, giving the following notion.

Definition 3.8

Let $(A,\succ ,\prec )$ be a dendriform algebra. Then, $(A,\succ ,\prec )$ is called a Novikov-type dendriform algebra if Eqs. (41–42) and the following equation hold:

$$\begin{aligned} x\prec (y\prec z)=0,\quad \forall x,y,z\in A.\end{aligned}$$

(58)

Proposition 3.9

Let A be a vector space with two binary operations $\succ ,\prec$. Then, $(A,\succ ,\prec )$ is a Novikov-type dendriform algebra if and only if the following equations hold:

$$\begin{aligned}{} & {} x\succ (y\succ z)=(x\prec y)\prec z=x\prec (y\succ z)=(x\prec y)\succ z, \end{aligned}$$

(59)

$$\begin{aligned}{} & {} x\succ (y\prec z)=(x\succ y)\prec z, \end{aligned}$$

(60)

$$\begin{aligned}{} & {} (x\succ y)\succ z=x\prec (y\prec z)=0, \end{aligned}$$

(61)

for all $x,y,z\in A$.

Proof

Let $x,y,z\in A$. Then, we set all products involving x, y, z as variables; that is, there are the following 8 variables

$$\begin{aligned} (x\succ y)\succ z, x\succ (y\succ z), (x\prec y)\prec z, x\prec (y\prec z), (x \succ y)\prec z, x\succ (y\prec z), (x\prec y)\succ z, x\prec (y\succ z). \end{aligned}$$

Therefore, Eqs. (1), (41), (42) and (58) compose a set of linear equations in these variables. It is straightforward to show that the solution of these linear equations is given by Eqs. (59–61) with the two free variables $(x\prec y)\succ z$ and $(x\succ y)\prec z$; that is, the other variables are the linear combinations of $(x\prec y)\succ z$ and $(x\succ y)\prec z$, respectively. Thus, the conclusion holds. $\square$

For the corresponding case of anti-dendriform algebras, we give the following notion.

Definition 3.10

Let $(A,\vartriangleright ,\vartriangleleft )$ be an anti-dendriform algebra. Then, $(A,\vartriangleright ,\vartriangleleft )$ is called an admissible Novikov-type dendriform algebra if Eq. (50) and the following equation hold:

$$\begin{aligned} x\vartriangleleft (y\vartriangleleft z)=2(x\cdot y)\vartriangleleft z,\;\;\forall x,y,z\in A,\end{aligned}$$

(62)

where the binary operation $\cdot$ is defined by Eq. (7), that is, $x\cdot y=x\vartriangleright y+x\vartriangleleft y$ for all $x,y\in A$.

Proposition 3.11

Let A be a vector space with two binary operations $\vartriangleright ,\vartriangleleft$. Then, $(A,\vartriangleright ,\vartriangleleft )$ is an admissible Novikov-type dendriform algebra if and only if the following equations hold:

$$\begin{aligned}{} & {} (x\vartriangleright y)\vartriangleright z=x\vartriangleleft (y\vartriangleleft z) =\frac{2}{3}(x\vartriangleright y)\vartriangleleft z-\frac{2}{3}(x\vartriangleleft y)\vartriangleright z, \end{aligned}$$

(63)

$$\begin{aligned}{} & {} x\vartriangleright (y\vartriangleright z)=(x\vartriangleleft y)\vartriangleleft z =-\frac{2}{3}(x\vartriangleright y)\vartriangleleft z-\frac{1}{3}(x\vartriangleleft y)\vartriangleright z,\end{aligned}$$

(64)

$$\begin{aligned}{} & {} x\vartriangleright (y\vartriangleleft z)=(x\vartriangleright y)\vartriangleleft z,\end{aligned}$$

(65)

$$\begin{aligned}{} & {} x\vartriangleleft (y\vartriangleright z)=(x\vartriangleleft y)\vartriangleright z, \end{aligned}$$

(66)

for all $x,y,z\in A$.

Proof

It is similar to the proof of Proposition 3.9. $\square$

Corollary 3.12

Let A be a vector space with two binary operations $\succ ,\prec$. The triple $(A,\succ ,\prec )$ is a Novikov-type dendriform algebra if and only if its $-2$-algebra $(A,\vartriangleright ,\vartriangleleft )$ is an admissible Novikov-type dendriform algebra.

Proof

Note that when $q=-2$, Eq. (58) holds if and only if Eq. (43) holds, and Eq. (62) holds if and only if Eq. (51) holds. Hence, the conclusion follows from Theorem 3.6. $\square$

Example 3.13

It is obvious that all “2-nilpotent” dendriform algebras in the sense that all products involving three elements are zero (see Proposition 2.16) are Novikov-type dendriform algebras. In particular, any 2-nilpotent associative algebra $(A,\cdot )$ gives a Novikov-type dendriform algebra $(A,\succ , \prec )$ by letting $\succ =\lambda \cdot , \prec =\mu \cdot$, where $\lambda ,\mu \in {\mathbb {F}}$. Accordingly, all “2-nilpotent” anti-dendriform algebras are admissible Novikov-type dendriform algebras. In particular, all complex anti-dendriform algebras in dimensions 1 and 2 which are classified in Examples 2.9 and Proposition 2.16, respectively, are admissible Novikov-type dendriform algebras. Note that the 3-dimensional anti-dendriform algebras given in Example 2.17 are not admissible Novikov-type dendriform algebras.

3.2 More correspondences and their relationships

Definition 3.14

Let A be a vector space with a binary operation $\bullet .$ Define a binary operation $\diamond$ as

$$\begin{aligned} x\diamond y=x\bullet y+q y\bullet x,\quad \forall x,y\in A. \end{aligned}$$

(67)

Then, $(A,\diamond )$ is called the q -algebra over $(A,\bullet )$.

Proposition 3.15

Let $(A,*)$ be a pre-Lie algebra. Denote by $(A,\circ )$ the $(-q)$-algebra over $(A,*).$ Then, $(A,\circ )$ is an anti-pre-Lie algebra if and only if the following equation holds:

$$\begin{aligned}&(q+2)[x,y]*z -q(q+2)z*[x,y]+ q(q-1)((z*y)*x-(z*x)*y)=0,\ \ \nonumber \\ {}&\forall x,y,z\in A, \end{aligned}$$

(68)

where $[x,y]=x*y-y*x$.

Proof

Let $x,y,z\in A$ and $[\,\ ]_{\circ }$ be the commutator of $\circ$ defined by Eq. (15). By Eq. (67), we have

$$\begin{aligned}{}[x,y]_\circ =x\circ y-y\circ x=x*y-qy*x-y*x+qx*y=(q+1)[x,y]. \end{aligned}$$

So $(A,\circ )$ is a Lie-admissible algebra. Furthermore, by Eq. (67) and the definition of pre-Lie algebras, we have

$$\begin{aligned}{} & {} x\circ (y\circ z)-y\circ (x\circ z)-[y,x]_\circ \circ z\nonumber \\{} & {} =(q+2)[x,y]*z -q(q+2)z*[x,y]+ q(q-1)\big ((z*y)*x-(z*x)*y\big ).\nonumber \\ \end{aligned}$$

(69)

Therefore, $(A,\circ )$ is an anti-pre-Lie algebra if and only if the right-hand side of Eq. (69) is zero. Hence, the conclusion follows. $\square$

Remark 3.16

Note that when $q=-2$, Eq. (68) holds if and only if Eq. (56) holds; that is, in this case, a pre-Lie algebra satisfying Eq. (68) is exactly a Novikov algebra.

Proposition 3.17

Let $(A,\circ )$ be an anti-pre-Lie algebra. Denote by $(A,*)$ the q-algebra over $(A,\circ ).$ Then, $(A,*)$ is a pre-Lie algebra if and only if the following equation holds:

$$\begin{aligned}&(q+2)[x,y]_\circ \circ z-q^2z\circ [x,y]_\circ + q(q+1)\big ((z\circ x)\circ y-(z\circ y)\circ x\big )=0,\ \ \nonumber \\ {}&\forall x,y,z\in A, \end{aligned}$$

(70)

where $[x,y]_\circ =x\circ y-y\circ x$.

Proof

Let $x,y,z\in A$. By Eq. (67) and the definition of anti-pre-Lie algebras, we have

$$\begin{aligned}{} & {} (x*y)*z-x*(y*z)-(y*x)*z+y*(x*z)\nonumber \\{} & {} =(q+2)[x,y]_\circ \circ z-q^2z\circ [x,y]_\circ + q(q+1)((z\circ x)\circ y-(z\circ y)\circ x). \end{aligned}$$

(71)

Therefore, $(A,*)$ is a pre-Lie algebra if and only if the right-hand side of Eq. (71) is zero. This completes the proof. $\square$

Remark 3.18

Note that when $q=-2$, Eq. (70) holds if and only if Eq. (57) holds; that is, in this case, an anti-pre-Lie algebra satisfying Eq. (70) is exactly an admissible Novikov algebra.

Theorem 3.19

Let A be a vector space with a binary operation $*$. Then, $(A,*)$ is a pre-Lie algebra satisfying Eq. (68) if and only if its $(-q)$-algebra $(A,\circ )$ is an anti-pre-Lie algebra satisfying Eq. (70).

Proof

It is similar to the proof of Theorem 3.6. $\square$

In particular, when $q=-2$, the following conclusion has already been given in [27].

Corollary 3.20

Let A be a vector space with a binary operation $*$. Then, $(A,*)$ is a Novikov algebra if and only if its 2-algebra $(A,\circ )$ is an admissible Novikov algebra.

Corollary 3.21

• (1) Suppose that $(A,\succ ,\prec )$ is a dendriform algebra satisfying Eqs. (41–43). Then, its associated pre-Lie algebra $(A, *)$ defined by Eq. (3) satisfies Eq. (68). In particular, when $q=-2$, the associated pre-Lie algebra of a Novikov-type dendriform algebra is a Novikov algebra.

• (2) Suppose that $(A,\vartriangleright ,\vartriangleleft )$ is an anti-dendriform algebra satisfying Eqs. (50–51). Then, its associated anti-pre-Lie algebra $(A,\circ )$ satisfies Eq. (70). In particular, when $q=-2$, the associated anti-pre-Lie algebra of an admissible Novikov-type dendriform algebra is an admissible Novikov algebra.

Proof

(1). Note that the q-algebra over $(A,\succ ,\prec )$ is an anti-dendriform algebra $(A,\vartriangleright ,\vartriangleleft )$ by Proposition 3.4. Let $(A,\circ )$ be the associated anti-pre-Lie algebra of $(A,\vartriangleright ,\vartriangleleft )$. Then, we have

$$\begin{aligned} x\circ y= & {} x\vartriangleright y-y\vartriangleleft x=x\succ y +qx\prec y -y\prec x-qy\succ x\\ {}= & {} x*y-q y*x,\;\;\forall x,y\in A, \end{aligned}$$

that is, $(A,\circ )$ is the $(-q)$-algebra over $(A, *)$. By Proposition 3.15, $(A, *)$ satisfies Eq. (68). The conclusion for the special case that $q=-2$ follows straightforwardly.

(2). It is similar to the proof of Item (1). $\square$

Combining Theorems 3.6, 3.19 and Corollary 3.21 together, we have the following commutative diagram which is consistent with both the diagrams (4) and (5).

(72)

In particular, when $q=-2,$ we have the following commutative diagram:

(73)

The above commutative diagram illustrates that it is reasonable to regard Novikov-type dendriform and admissible Novikov-type dendriform algebras as “analogues” of Novikov and admissible Novikov algebras for dendriform and anti-dendriform algebras, respectively, justifying the notions of the former.

4 General framework: analogues of anti-dendriform algebras and a new splitting of operations

Moving further along the study of anti-dendriform algebras in the previous sections, we provide a general framework of introducing the notions of analogues of anti-dendriform algebras to interpret a new approach of splitting operations. We also characterize such a construction in terms of double spaces.

We commence by using associative algebras as an example to exhibit the new approach of splitting operations, which is interpreted by a general framework of introducing the notions of analogues of anti-dendriform algebras. At first, we consider “splitting the associativity,” that is, expressing the multiplication of an associative algebra as the sum of a string of binary operations. Explicitly, let $(A,\cdot )$ be an associative algebra and $(\cdot _i)_{1\le i\le N}:A\otimes A\rightarrow A$ be a family of binary operations on A. Then, the operation $\cdot$ splits into the N operations $\cdot _1,\cdots , \cdot _N$ if

$$\begin{aligned} x\cdot y=\sum _{i=1}^N x\cdot _iy,\;\;\forall x,y\in A. \end{aligned}$$

(74)

Example 4.1

The ordinary operations splitting the associativity give the following so-called Loday algebras.

• (1) $N=2$: dendriform algebra [28];

• (2) $N=3$: tridendriform algebra [33];

• (3) $N=4$: quadri-algebra [1];

• (4) $N=8$: octo-algebra [26];

• (5) $N=9$: ennea-algebra [25].

For the case that $N=2^n$, $n=0,1,2,\cdots$, there is the following “rule” of constructing Loday algebras: by induction, for the algebra $(A, \cdot _i)_{1\le i\le 2^n}$, besides the natural (regular) bimodule over A on the underlying vector space of A itself given by the left and right multiplication operators, one can introduce the $2^{n+1}$ operations $\{\cdot _{i_1}, \cdot _{i_2}\}_{1\le i\le 2^n}$ such that

$$\begin{aligned} x\cdot _i y=x\cdot _{i_1} y+x\cdot _{i_2}y,\;\;\forall x,y\in A, \; 1\le i\le 2^n,\end{aligned}$$

(75)

and the left and right multiplication operators in a certain way give a bimodule structure over $(A, \cdot _i)_{1\le i\le 2^n}$ by acting on the underlying vector space of A itself. In the sense of [4], these Loday algebras are the successors’ algebras starting from the associative algebras.

Now, we consider to construct analogues of anti-dendriform algebras by the following “rule” as another approach of splitting the associativity. Let $N=2^n$, $n=0,1,2,\cdots$. By induction, for the algebra $(A, \cdot _i)_{1\le i\le 2^n}$, one can introduce the $2^{n+1}$ operations $\{\cdot _{i_1}, \cdot _{i_2}\}_{1\le i\le 2^n}$ such that

$$\begin{aligned} x\cdot _i y=x\cdot _{i_1} y+x\cdot _{i_2}y,\;\;\forall x,y\in A, \; 1\le i\le 2^n,\end{aligned}$$

(76)

and the opposites of the left and right multiplication operators in the aforementioned way give a bimodule structure over $(A, \cdot _i)_{1\le i\le 2^n}$ by acting on the underlying vector space of A itself. Hence, these algebras can be regarded as the “anti-structures” for the successors’ algebras starting from the associative algebras.

Example 4.2

When $N=2$, that is, $n=1$, the corresponding algebra $(A,\cdot _i)_{1\le i\le 2}=(A,\cdot _1,\cdot _2)$ is an anti-dendriform algebra.

Similarly, we consider the following approach of splitting the Lie bracket of a Lie algebra in which anti-pre-Lie algebras are included.

Let $(X,[\,\ ])$ be a Lie algebra and $(\cdot _i)_{1\le i\le N}:X\otimes X\rightarrow X$ be a family of binary operations on X. Then, the Lie bracket $[\,\ ]$ splits into the commutator of N binary operations $\cdot _1,\cdots , \cdot _N$ if

$$\begin{aligned}{}[x,y]=\sum _{i=1}^N (x\cdot _iy-y\cdot _ix),\;\;\forall x,y\in X. \end{aligned}$$

(77)

For the case that $N=2^n$, $n=0,1,2,\cdots$, there is a “rule” of constructing the binary operations $\cdot _i$ as follows. By induction, for the algebra $(X, \cdot _i)_{1\le i\le 2^n}$, one can introduce the $2^{n+1}$ binary operations $\{\cdot _{i_1}, \cdot _{i_2}\}_{1\le i\le 2^n}$ such that

$$\begin{aligned} x\cdot _i y=x\cdot _{i_1} y-y\cdot _{i_2}x,\;\;\forall x,y\in A, \; 1\le i\le 2^n, \end{aligned}$$

(78)

and the opposites of the left or right multiplication operators which are in the way defining the successors’ algebras starting from the Lie algebras, give a representation of $(X, \cdot _i)_{1\le i\le 2^n}$ by acting on the underlying vector space of A itself. These algebras can be regarded as the “anti-structures” for the successors’ algebras starting from the Lie algebras.

Example 4.3

When $N=1$, that is, $n=0$, the corresponding algebra $(X,\cdot _1)$ is an anti-pre-Lie algebra.

In a summary, such “anti-structures” as the “counterparts” of the successors’ algebras, which are put into the above general framework as analogues of anti-dendriform algebras as well as anti-pre-Lie algebras, provide a new splitting of operations. The study on these structures such as the relationships with anti-${\mathcal {O}}$-operators and anti-Rota–Baxter operators, the correspondences between the subclasses of successors’ algebras and their anti-counterparts in terms of q-algebras, and the operadic interpretation is expected in the future works.

At the end of this section, we give the following characterization of these “anti-structures” in terms of double spaces, motivated by Corollary 2.8.

Let ${\mathcal {C}}$ denote the category of all algebras $(A,\cdot )$ which satisfy a given set of multilinear relations ${\mathcal {R}}_1=0$, $\cdots$, ${\mathcal {R}}_k=0$.

Definition 4.4

An algebra $(A,\vartriangleright ,\vartriangleleft )$ is called a ${\mathcal {C}}$-anti-dendriform algebra if $(A\oplus A, \cdot )\in {\mathcal {C}}$, where $\cdot$ is defined by Eq. (14).

Similarly, one can characterize the anti-structures for the algebras $(A,\cdot _i)_{1\le i\le N}$ with $N=2^n$, $n=0,1,2,\cdots$ as follows. By induction, for the algebra $(A, \cdot _i)_{1\le i\le 2^n}$ giving the category ${\mathcal {C}}_{2^n}$, one can introduce the $2^{n+1}$ operations $\{\cdot _{i_1}, \cdot _{i_2}\}_{1\le i\le 2^n}$ such that $(A\oplus A, \cdot _1,\cdots ,\cdot _{2^n})\in {\mathcal {C}}_{2^n}$, where $\cdot _i$ ($1\le i\le 2^n$) is defined by

$$\begin{aligned} (x,a)\cdot _i (y,b)=(x\cdot _{i1} y+x\cdot _{i2} y, -x\cdot _{i1} b-a\cdot _{i2} y),\;\;\forall x,y,a,b\in A. \end{aligned}$$

(79)