Vertex-minimal graphs with nonabelian ${\mathbf{2}}$-group symmetry

Abstract

A graph whose full automorphism group is isomorphic to a finite group G is called a G-graph, and we let $\alpha (G)$ denote the minimal number of vertices among all G-graphs. The value of $\alpha (G)$ has been established for numerous infinite families of groups. In this article, we expand upon the subject matter of vertex-minimal G-graphs by computing the value of $\alpha (G)$ when G is isomorphic to either a quasi-dihedral group or a quasi-abelian group. These results completely establish the value of $\alpha (G)$ when G is a member of one of the six infinite families of 2-groups that contain a cyclic subgroup of index 2.

1 Introduction

Throughout this article, all groups considered are finite and all graphs considered are simple and finite. In 1936, König [16] famously inquired about which abstract groups could be realized as the automorphism group of some graph. Three years later, Frucht [5] proved that for every group G, there exists a graph whose full automorphism group is isomorphic to G; such a graph is called a $\varvec{G}$-graph.

For a group G, let $\varvec{\alpha (G)}$ denote the minimal number of vertices among all G-graphs. In general, $\alpha (G) \le 3|G|$ and the cyclic groups of orders 3, 4, and 5 demonstrate that this bound is best possible (i.e., $\alpha (G) = 3|G|$ provided G is a cyclic group of orders 3, 4, or 5). Without sacrificing much generality, Babai improved this bound on the value of $\alpha (G)$.

Theorem 1

(Babai [2]) If G is a group different from the cyclic group of orders 3, 4, or 5, then $\alpha (G) \le 2|G|$.

The constant 2 in Theorem 1 is sharp. For example, Sabidussi [23] proved that $\alpha (G) = 2|G|$ for cyclic groups of prime order $p\ge 7$, and Graves et. al. [9] proved equality for generalized quaternion groups. However, this constant can be sharpened for most groups by considering a graphical regular representation. A graph $\Gamma$ is a graphical regular representation (GRR) of a group G if the automorphism group of $\Gamma$ is a regular permutation group that is isomorphic to G. In this case, G admits a GRR, and the GRR problem was to identify all groups that admit a GRR. It follows immediately from these definitions that if the group G admits a GRR, then $\alpha (G) \le |G|$.

The results of numerous authors provided partial solutions for the GRR problem (see [4, 14, 15, 20, 21, 24, 26,27,28]). A complete classification of groups that admit a GRR was found by Hetzel [13] and Godsil [6, 7], and we state their result below.

Theorem 2

(Hetzel [13], Godsil [6, 7]) The group G admits a GRR provided it is distinct from each of the following groups : 

• (a) an abelian group of exponent greater than 2; 

• (b) an elementary abelian group of orders 4, 8, or 16; 

• (c) a generalized dicyclic group;  and

• (d) one of ten exceptional groups whose orders are at most 32, two of which are nonabelian groups of order 16.

Theorem 2 implies that the bound $\alpha (G) \le |G|$ will hold for most groups G. We will establish an infinite family of groups that demonstrate this bound is best possible in Theorem 4.

In addition to the aforementioned bounds, the exact value of $\alpha (G)$ has been computed for some infinite families of groups G. In the following remark, we state all the groups G for which the exact value of $\alpha (G)$ is known.

Remark 3

The value of $\alpha (G)$ has been established for the following groups G:

• (a) cyclic groups (Meriwether [19], Sabidussi [23]);

• (b) noncyclic abelian groups (Arlinghaus [1]);

• (c) hyperoctahedral groups (Haggard et al. [12]);

• (d) symmetric groups (Quintas  [22]);

• (e) alternating groups of degree at least 13 (Liebeck [17]);

• (f) generalized quaternion groups (Graves et al. [9]); and

• (g) dihedral groups (Graves, Graves, Haggard, McCarthy [8, 10, 11, 18]).

In this article, we wish to further expand the results on the subject matter of vertex-minimal G-graphs. Burnside [3] proved that there are six infinite families of order-$2^m$ groups that each contain a cyclic subgroup of index 2: the cyclic group ${\mathbb {Z}}_{2^m}$, the noncyclic abelian group ${\mathbb {Z}}_{2^{m-1}} \times {\mathbb {Z}}_2$, the dihedral group $D_{2^m}$, the generalized quaternion group (or the dicyclic group) $Q_{2^m}$, the quasi-dihedral group (or the semi-dihedral group) $\hbox {QD}_{2^m}$, and the quasi-abelian group (or the modular group) $\hbox {QA}_{2^m}$. As shown in Remark 3, four of these six families have been considered in relation to the orders of vertex-minimal graphs with prescribed automorphism groups. In particular,

$$\begin{aligned} \alpha ({\mathbb {Z}}_{2^m}) = {\left\{ \begin{array}{ll} 2^m &{} \text {if } m=0,1\\ 2^{m}+6 &{} \text {if } m \ge 2 \end{array}\right. } \quad \text { and } \quad \alpha ({\mathbb {Z}}_{2^{m-1}} \times {\mathbb {Z}}_2) = {\left\{ \begin{array}{ll} 4 &{} \text {if } m=2\\ 2^{m-1}+8 &{} \text {if } m \ge 3, \end{array}\right. } \end{aligned}$$

and when $m \ge 3$, we have that $\alpha (D_{2^m})=2^{m-1}$ and $\alpha (Q_{2^m}) = 2^{m+1}$ (see [1, 9, 11, 23], respectively).

Here, we will consider the remaining two families of 2-groups that contain a cyclic subgroup of index 2. The quasi-dihedral group $\hbox {QD}_{2^m}$ and quasi-abelian group $\hbox {QA}_{2^m}$ only exist when $m \ge 4$, and their presentations are given in Sect. 2. The following two theorems contain our main results.

Theorem 4

Let $m \ge 4$ be an integer. The quasi-dihedral group $\hbox {QD}_{2^m}$ of order $2^m$ satisfies $\alpha (\hbox {QD}_{2^m})=2^m$.

Theorem 5

Let $m \ge 4$ be an integer. The quasi-abelian group $\hbox {QA}_{2^m}$ of order $2^m$ satisfies $\alpha (\hbox {QA}_{16}) = 18$ and $\alpha (\hbox {QA}_{2^m}) = 2^{m-1}+6$ when $m \ge 5$.

Fix $m\ge 5$, and let G be a group of order $2^m$ that contains a cyclic subgroup of index 2 (so that G belongs to one of the aforementioned six families of 2-groups). Theorems 4 and 5 completely establish the orders of vertex-minimal graphs whose automorphism groups are isomorphic to a 2-group that contains a cyclic subgroup of index 2. Although the groups in these families are similar (in the sense that they each have the same order and a large cyclic subgroup), the order of a vertex-minimal G-graph is distinct. Specifically,

$$\begin{aligned} \alpha (D_{2^m})< \alpha (\hbox {QA}_{2^m})<\alpha ({\mathbb {Z}}_{2^{m-1}} \times {\mathbb {Z}}_2)< \alpha (\hbox {QD}_{2^m})< \alpha ({\mathbb {Z}}_{2^m})<\alpha (Q_{2^m}), \end{aligned}$$

for a fixed integer $m\ge 5$.

This article is organized as follows. We first develop the background and notation that will be used to prove Theorems 4 and 5 in Sect. 2. In Sect. 3, we will consider quasi-dihedral groups and prove that a certain GRR admitted by $\hbox {QD}_{2^m}$ is vertex-minimal among all $\hbox {QD}_{2^m}$-graphs. As a result, $\alpha (\hbox {QD}_{2^m})=2^m$, which will establish Theorem 4. The group $\hbox {QA}_{16}$ is the only quasi-abelian group that does not admit a GRR; the results of Sect. 4 will focus on this special case. Finally, in Sect. 5, we will consider the quasi-abelian group $\hbox {QA}_{2^m}$ with $m \ge 5$ and prove Theorem 5.

2 Preliminaries

In this section, we will introduce the background and notation required to prove Theorems 4 and 5. When $m \ge 4$ is an integer, we will utilize the presentation

$$\begin{aligned} \hbox {QD}_{2^m}=\left\langle \sigma ,\tau : \sigma ^{2^{m-1}}=1=\tau ^2,\ \tau \sigma \tau =\sigma ^{2^{m-2}-1} \right\rangle \end{aligned}$$

(1)

for the quasi-dihedral group of order $2^m$ and the presentation

$$\begin{aligned} \hbox {QA}_{2^m}=\left\langle \sigma ,\tau : \sigma ^{2^{m-1}}=1=\tau ^2,\ \tau \sigma \tau =\sigma ^{2^{m-2}+1} \right\rangle \end{aligned}$$

(2)

for the quasi-abelian group of order $2^m$. Assume that G is isomorphic to either $\hbox {QD}_{2^m}$ or $\hbox {QA}_{2^m}$. To establish the value of $\alpha (G)$, we will consider G as a permutation group whose elements are permutations of the vertex set of some graph. In particular, we assume that G acts on a set S of n symbols for some permissible integer $n \ge 2^{m-1}$ and then focus on the cycle decomposition of the generator $\sigma$. We will implicitly assume that the cycle decomposition of every permutation in G is disjoint, and call a cycle of length r an $\varvec{r}$-cycle. Lastly, the support of a permutation $\rho \in G$ is

$$\begin{aligned} {{\,\mathrm{supp}\,}}(\rho )=\{s\in S:\rho (s)\ne s\}. \end{aligned}$$

Under these assumptions, we obtain the following property of the cycle decomposition of $\sigma \in G$.

Lemma 6

Assume that G is isomorphic to $\hbox {QD}_{2^m}$ or $\hbox {QA}_{2^m}$, where $m \ge 4$ is an integer. Consider G as a permutation group, and let $\sigma$ and $\tau$ be the generators of G as defined in Eq. (1) if $G\cong \hbox {QD}_{2^m}$ or in Eq. (2) if $G\cong \hbox {QA}_{2^m}$. If $\sigma _1$ and $\sigma _2$ are cycles in the cycle decomposition of $\sigma$, and $\tau$ transposes a symbol in ${{\,\mathrm{supp}\,}}(\sigma _1)$ with a symbol in ${{\,\mathrm{supp}\,}}(\sigma _2)$, then $\sigma _1$ and $\sigma _2$ have equal length.

Proof

After a possible relabeling, assume that $\sigma _1=(1,2,\ldots ,a)$ and $\sigma _2=(a+1,a+2,\ldots ,b)$ are cycles in the cycle decomposition of $\sigma$, where $a,b \in {\mathbb {Z}}^+$ with $a<b$. Assume that the permutation $\tau \in G$ exchanges the symbols 1 and $a+k$ for some $k \in \{1,2,\ldots ,b-a\}$. In this case, the relation $\tau \sigma \tau =\sigma ^\ell$ (with either $\ell =2^{m-2}-1$ or $\ell =2^{m-2}+1$) implies that $\tau \sigma _1\tau =\sigma _2^\ell$. Since the cycle $\tau \sigma _1\tau$ is an a-cycle and $\sigma _2^\ell$ has length $b-(a+1)+1$, we have that $a=b-(a+1)+1$. Therefore, $2a=b$ and the result now follows. $\square$

We will continue with a few more preliminaries to be used throughout the remainder of this article. The automorphism group of a graph $\Gamma$, denoted ${{\,\mathrm{Aut}\,}}\Gamma$, is the set of adjacency-preserving permutations of the vertices of $\Gamma$. Let $V(\Gamma )$ and $E(\Gamma )$ denote the vertex set of $\Gamma$ and the edge set of $\Gamma$, respectively. In many of the proofs that follow, we will use the Orbit-Stabilizer Theorem, which gives a relationship between the order of ${{\,\mathrm{Aut}\,}}\Gamma$, the size of the orbit of vertex v in ${{\,\mathrm{Aut}\,}}\Gamma$, and the order of the stabilizer of v in ${{\,\mathrm{Aut}\,}}\Gamma$. Specifically, for each $v \in V(\Gamma )$, the orbit of v is

$$\begin{aligned} {{\,\mathrm{{\mathcal {O}}}\,}}(v)=\{\rho (v): \rho \in {{\,\mathrm{Aut}\,}}\Gamma \} \end{aligned}$$

and the stabilizer of v is

$$\begin{aligned} {{\,\mathrm{stab}\,}}(v)=\{ \rho \in {{\,\mathrm{Aut}\,}}\Gamma :\rho (v)=v\}; \end{aligned}$$

the Orbit-Stabilizer Theorem states that

$$\begin{aligned} |{{\,\mathrm{Aut}\,}}\Gamma |=|{{\,\mathrm{{\mathcal {O}}}\,}}(v)| \cdot |{{\,\mathrm{stab}\,}}(v)|. \end{aligned}$$

In addition to the orbit of a vertex in ${{\,\mathrm{Aut}\,}}\Gamma$, we also define the orbit of an edge in ${{\,\mathrm{Aut}\,}}\Gamma$. If G is a subgroup of the permutation group $S_{V(\Gamma )}$, then for vertices $u, v \in V(\Gamma )$ the set

$$\begin{aligned} {{\,\mathrm{{\mathcal {O}}}\,}}_G\{u, v\} = \{[\rho (u), \rho (v)]:\rho \in G\} \end{aligned}$$

defines the edge orbit of $[u, v]\in E(\Gamma )$. When the group G is clear from context, we will omit the subscript in ${{\,\mathrm{{\mathcal {O}}}\,}}_G\{u, v\}$ and simply write ${{\,\mathrm{{\mathcal {O}}}\,}}\{u,v\}$. Finally, let $A_v\subseteq V(\Gamma )$ denote the set of all vertices of $\Gamma$ that are adjacent to v. The vertices in $A_v$ are called the neighbors of v. The neighborhood graph of v, denoted N(v), is the subgraph of $\Gamma$ whose vertex set is $A_v$ and whose edge set consists of all edges in $E(\Gamma )$ that have both ends in $A_v$. For intelligible depictions of graphs, our convention is that the neighborhood graph of v does not include v.

This section concludes with a brief overview of the methods we use to establish the value of $\alpha (G)$ in this article. Consider G as a permutation group acting on a set of vertices of a G-graph. The existence of such a graph has implications on the structure of the cycle decomposition of the permutations in G. In particular, the size of the support of a generator in G gives a lower bound on the value of $\alpha (G)$. In the work that follows this lower bound will be sharp; thus, to establish the value of $\alpha (G)$ it suffices to construct a graph $\Gamma$ with $|V(\Gamma )| = \alpha (G)$ and ${{\,\mathrm{Aut}\,}}\Gamma \cong G$. From the construction, the order of $\Gamma$ is easily verified. We will prove that $\Gamma$ is actually a G-graph with the following steps: (1) Establish that G is isomorphic to a subgroup of ${{\,\mathrm{Aut}\,}}\Gamma$, and (2) use the Orbit-Stabilizer Theorem to establish that $|G| = |\!{{\,\mathrm{Aut}\,}}\Gamma |$.

3 The quasi-dihedral group $\hbox {QD}_{2^m}$

The quasi-dihedral group $\hbox {QD}_{2^m}$, where $m \ge 4$ is an integer, admits a GRR by Theorem 2. If $\Gamma$ is a GRR of $\hbox {QD}_{2^m}$, then ${{\,\mathrm{Aut}\,}}\Gamma$ is a regular permutation group that is isomorphic to $\hbox {QD}_{2^m}$ by definition. Consequently, $\alpha (\hbox {QD}_{2^m})\le |\hbox {QD}_{2^m}|=2^m$ and our proof of Theorem 4 will show that equality holds. Since $\Gamma$ is a GRR, it can be thought of as a Cayley graph of $\hbox {QD}_{2^m}$ with no extra automorphisms, and we will continue by constructing such a graph $\Gamma$.

Let G be a group, and suppose that $S \subseteq G\backslash \{1\}$ is closed under inverses; the Cayley graph of G with connection set S, denoted ${{\,\mathrm{Cay}\,}}(G,S)$, is the graph with $V\big (\!{{\,\mathrm{Cay}\,}}(G,S)\big )=G$ and

$$\begin{aligned} E\big (\!{{\,\mathrm{Cay}\,}}(G,S)\big ) = \{ [g,gs]:g \in G \text { and } s \in S\}. \end{aligned}$$

Although it is not required to prove Theorem 4, we write

$$\begin{aligned} \hbox {QD}_{2^m}=\left\langle x,y: x^{2^{m-1}}=1=y^2,\ yxy=x^{2^{m-2}-1}\right\rangle \end{aligned}$$

and construct a $\hbox {QD}_{2^m}$-graph that is also a Cayley graph of $\hbox {QD}_{2^m}$ with connection set

$$\begin{aligned} S=\left\{ x,x^{2^{m-1}-1},y,xy,x^{2^{m-2}+1}y\right\} \subseteq \hbox {QD}_{2^m}. \end{aligned}$$

By definition, ${{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)$ has $2^m$ vertices and $E\big (\!{{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)\big )$ contains the edges in

$$\begin{aligned} E\big (\!{{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)\big ) = \{ [g,gs]:g \in \hbox {QD}_{2^m} \text { and } s \in S\}. \end{aligned}$$

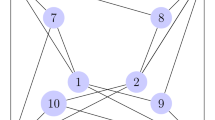
In particular, the edge set of ${{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)$ is comprised of the three edge orbits ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,x\}$, ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,y\}$, and ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,xy\}$ and thus has size $5\cdot 2^{m-1}$. The graph ${{\,\mathrm{Cay}\,}}(\hbox {QD}_{16},S)$ with connection set $S=\{x,x^7,y,xy,x^5y\}$ is depicted in Fig. 1.

Fig. 1

Cayley graph of $\hbox {QD}_{16}=\langle x,y \rangle$ with connection set $\{x,x^7,y,xy,x^5y\}$

Proposition 7

Let $m \ge 4$ be an integer. If $\hbox {QD}_{2^m}=\langle x,y \rangle$, then the Cayley graph ${{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)$ with connection set

$$\begin{aligned} S=\left\{ x,x^{2^{m-1}-1},y,xy,x^{2^{m-2}+1}y\right\} \end{aligned}$$

is a $\hbox {QD}_{2^m}$-graph.

Proof

For each $g \in \hbox {QD}_{2^m}$, define the map $\pi _g:\hbox {QD}_{2^m} \rightarrow \hbox {QD}_{2^m}$ by $\pi _g(h)=gh$, where $h \in \hbox {QD}_{2^m}$. In this case, $\{\pi _g:g \in \hbox {QD}_{2^m}\}$ is a subgroup of ${{\,\mathrm{Aut}\,}}\!\big (\!{{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)\big )$ that is isomorphic to $\hbox {QD}_{2^m}$. To prove these groups $\{\pi _g:g \in \hbox {QD}_{2^m}\}$ and ${{\,\mathrm{Aut}\,}}\!\big (\!{{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)\big )$ are equal (i.e., that ${{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)$ is a $\hbox {QD}_{2^m}$-graph), we will apply the Orbit-Stabilizer Theorem.

Fix $i \in {\mathbb {Z}}$ and consider $x^i\in \hbox {QD}_{2^m}$. Since ${{\,\mathrm{Aut}\,}}\!\big (\!{{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)\big )$ contains all left multiplications by elements in $\hbox {QD}_{2^m}$, it acts transitively on $V\big (\!{{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)\big )=\hbox {QD}_{2^m}$. Therefore, $|{{\,\mathrm{{\mathcal {O}}}\,}}(x^i)|=|\hbox {QD}_{2^m}|=2^m$, and by the Orbit-Stabilizer Theorem,

$$\begin{aligned} \big |{{\,\mathrm{Aut}\,}}\!\big (\!{{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)\big )\big |=|{{\,\mathrm{{\mathcal {O}}}\,}}(x^i)|\cdot |H|=2^m\cdot |H|, \end{aligned}$$

(3)

where $H={{\,\mathrm{stab}\,}}(x^i)$. To find the order of the subgroup H in ${{\,\mathrm{Aut}\,}}\!\big (\!{{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)\big )$, we consider the neighborhood graph of $x^i$, which is denoted by $N(x^i)$ and depicted in Fig. 2a. Since $x^i$ is fixed in H, the subgraph $N(x^i)$ is invariant under any automorphism of H. Moreover, the only neighbor of $x^i$ in $N(x^i)$ with degree 2, namely $x^iy$, is also fixed in H, and thus $\{x^{i+1},x^{i+1}y\}$ and $\{x^{i-1},x^{i+2^{m-2}+1}y\}$ are each H-invariant sets. Additionally, notice that $x^i$ is contained in exactly five 4-cycles in ${{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)$; these 4-cycles are depicted in Fig. 2b. The vertex $x^{i+1}$ is contained in exactly two of these 4-cycles and $x^{i+1}y$ is contained in exactly three of these 4-cycles. Consequently, the H-invariant set $\{x^{i+1},x^{i+1}y\}$ is actually fixed pointwise by every automorphism of H; a similar argument shows that $\{x^{i-1},x^{i+2^{m-2}+1}y\}$ is also fixed pointwise by H.

Fig. 2

Two subgraphs of ${{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)$, which appeared in the proof of Proposition 7

By the argument above, if $x^i$ is fixed, then all of its neighbors in ${{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)$ are fixed by H. Specifically, the vertices $x^{i+1}$, $x^iy$, and $x^{i+1}y$ are fixed by any automorphism of H. Repeating the argument above with $x^i$ replaced by $x^{i+1}$ yields that $x^{i+2}$, $x^{i+1}y$, and $x^{i+2}y$ are fixed by H. Continuing this process by replacing $x^i$ in the argument above with the vertices $x^{i+2}, x^{i+3}, \ldots ,x^{i+2^{m-1}-1}$ proves that every vertex in ${{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)$ is fixed by any automorphism of ${{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)$ that fixes $x^i$. Therefore, H is the identity subgroup and $|H|=1$; because $\hbox {QD}_{2^m}$ is isomorphic to a subgroup of ${{\,\mathrm{Aut}\,}}\!\big (\!{{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)\big )$, the result now follows from Eq. (3). $\square$

Proposition 7 implies that $\alpha (\hbox {QD}_{2^m}) \le 2^m$ because ${{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)$ is a $\hbox {QD}_{2^m}$-graph with $2^m$ vertices. We claim that this graph has minimal order among all $\hbox {QD}_{2^m}$-graphs; we will write $\hbox {QD}_{2^m}$ as a permutation group and consider the cycle decomposition of $\sigma \in \hbox {QD}_{2^m}$ to prove this claim.

Proposition 8

Let $m\ge 4$ be an integer. Assume that $\Gamma$ is $\hbox {QD}_{2^m}$-graph, and consider ${{\,\mathrm{Aut}\,}}\Gamma =\langle \sigma ,\tau \rangle$ as a permutation group where $\sigma ,\tau \in \hbox {QD}_{2^m}$ are as defined in Eq. (1). The cycle decomposition of $\sigma$ contains at least two $2^{m-1}$-cycles.

Proof

The cycle decomposition of the generator $\sigma$ must contain at least one $2^{m-1}$-cycle because the order of $\sigma$ is the prime power $2^{m-1}$. Toward a contradiction, suppose that the cycle decomposition of $\sigma$ contains exactly one $2^{m-1}$-cycle. Without loss of generality, assume that $\sigma =(1,2,3,\ldots ,2^{m-1})\rho$ is the cycle decomposition of $\sigma$, where all of the cycles that appear in the cycle decomposition of $\rho$ have lengths less than $2^{m-1}$ and

$$\begin{aligned} {{\,\mathrm{supp}\,}}(\rho ) \subset {\mathbb {Z}}^+\backslash \{1,2,3, \ldots ,2^{m-1}\}. \end{aligned}$$

In this case, for each $k \in \{1,2, \ldots ,2^{m-1}\}$,

$$\begin{aligned} \{1,2,3, \ldots ,2^{m-1}\} \subseteq {{\,\mathrm{{\mathcal {O}}}\,}}(k) \end{aligned}$$

because $\sigma$ acts transitively on $\{1,2,3, \ldots ,2^{m-1}\}$. Since the cycle decomposition of $\sigma$ contains exactly one $2^{m-1}$-cycle, $\tau$ must transpose k with a symbol in $\{1,2,3, \ldots ,2^{m-1}\}$ by Lemma 6, and thus,

$$\begin{aligned} {{\,\mathrm{{\mathcal {O}}}\,}}(k) \subseteq \{1,2,3, \ldots ,2^{m-1}\}. \end{aligned}$$

Therefore, ${{\,\mathrm{{\mathcal {O}}}\,}}(k)$ has size $2^{m-1}$ and

$$\begin{aligned} 2^m=|{{\,\mathrm{Aut}\,}}\Gamma |=|{{\,\mathrm{{\mathcal {O}}}\,}}(k)|\cdot |{{\,\mathrm{stab}\,}}(k)|=2^{m-1}\cdot |{{\,\mathrm{stab}\,}}(k)|, \end{aligned}$$

(4)

where the second equality holds by the Orbit-Stabilizer Theorem. The remainder of the proof will establish the existence of an integer $n \in \{1,2,3, \ldots ,2^{m-1}\}$ such that $|{{\,\mathrm{stab}\,}}(n)|\ge 3$, which will contradict Eq. (4) with $k=n$.

Since the cycle decomposition of $\sigma$ contains exactly one $2^{m-1}$-cycle, $\tau (1)=\ell$ for some $\ell \in \{1,2, \ldots , 2^{m-1}\}$ by Lemma 6. The relation $\tau \sigma \tau =\sigma ^{2^{m-2}-1}$ implies that for each $k \in \{1,2, \ldots ,2^{m-1}\}$

$$\begin{aligned} \tau (k)\equiv \big ((2^{m-2}-1)(k-1)+\ell \big )\text {mod}~2^{m-1}, \end{aligned}$$

where we identify the integer 0 with $2^{m-1}$. This equation guarantees that $\ell$ is odd; otherwise,

$$\begin{aligned} \tau (\ell ) \equiv \big ((2^{m-2}-1)(\ell -1)+\ell \big )\text {mod}~2^{m-1} \equiv (1-2^{m-2})\text {mod}~2^{m-1}, \end{aligned}$$

which is impossible because $\tau$ has order 2 and $1 \not \equiv (1-2^{m-2})\text {mod}~2^{m-1}$. Moreover, the linear congruence

$$\begin{aligned} n \equiv \big ((2^{m-2}-1)(n-1)+\ell \big )\text {mod}~2^{m-1} \end{aligned}$$

or

$$\begin{aligned} (2-2^{m-2})n \equiv (\ell +1-2^{m-2}) \text {mod}~2^{m-1} \end{aligned}$$

has a solution because $\gcd (2-2^{m-2},2^{m-1})=2$ divides $\ell +1-2^{m-2}$. Without loss of generality, assume that $n \in \{1,2,\ldots , 2^{m-1}\}$ so that $\tau (n)=n$ by the argument above. Therefore, $\tau \in {{\,\mathrm{stab}\,}}(n)$, and we claim that the permutation

$$\begin{aligned} \alpha :={\left\{ \begin{array}{ll} (1,2^{m-2}+1)(3,2^{m-2}+3) \cdots (2^{m-2}-1,2^{m-2}+2^{m-2}-1) &{} \text {if } n \text { is even}\\ (2,2^{m-2}+2)(4,2^{m-2}+4) \cdots (2^{m-2},2^{m-2}+2^{m-2}) &{} \text {if } n \text { is odd}\end{array}\right. } \end{aligned}$$

is also an element of ${{\,\mathrm{stab}\,}}(n)$. To this end, notice that $\alpha$ is either $\sigma ^{2^{m-2}}$ restricted to the even elements in $\{1,2,3, \ldots ,2^{m-1}\}$ or $\sigma ^{2^{m-2}}$ restricted to the odd elements in $\{1,2,3, \ldots ,2^{m-1}\}$. Since $\alpha (n)=n$, to prove that $\alpha \in {{\,\mathrm{stab}\,}}(n)$ it suffices to show that there exists $\beta \in \langle \sigma ,\tau \rangle ={{\,\mathrm{Aut}\,}}\Gamma$ such that $\alpha [u,v]=\beta [u,v]$ for each $[u,v]\in E(\Gamma )$. First, assume that n is odd; the three cases that follow depend on the parity of u and v.

• (a) If u and v are odd, then $\alpha$ and $\beta =1$ both fix the edge [u, v].

• (b) If u and v are both even, then $\alpha [u,v]=\beta [u,v]$ with $\beta =\sigma ^{2^{m-2}}$.

• (c) Now suppose u and v have different parity; without loss of generality, assume that u is even and v is odd. If $u>2^{m-1}$, then $\alpha$ and $\beta =1$ both fix the edge [u, v], while $\alpha [u,v]=\beta [u,v]$ with $\beta =\sigma ^{2^{m-2}}$ provided $u\le 2^{m-1}$ and $v> 2^{m-1}$. Finally, assume that $u,v \le 2^{m-1}$. Recall that 0 is identified with $2^{m-1}$, and notice that

  $$\begin{aligned} \alpha [u,v]=[\alpha (u),\alpha (v)]=[(u+2^{m-2})\text {mod}~2^{m-1},v]. \end{aligned}$$

  Additionally, since u is even,

  $$\begin{aligned} \sigma ^{u+v+2^{m-2}-1-\ell }\tau (u)= & {} \sigma ^{u+v+2^{m-2}-1-\ell }\big (((2^{m-2}-1)(u-1)+\ell )\text {mod}~2^{m-1}\big ) \\= & {} \sigma ^{u+v+2^{m-2}-1-\ell }\big ((-2^{m-2}-u+1+\ell )\text {mod}~2^{m-1}\big ) \\= & {} u+v+2^{m-2}-1-\ell -2^{m-2}-u+1+\ell \\= & {} v \end{aligned}$$

  and

  $$\begin{aligned} \sigma ^{u+v+2^{m-2}-1-\ell }\tau (v)= & {} \sigma ^{u+v+2^{m-2}-1-\ell }\big (((2^{m-2}-1)(v-1)+\ell )\text {mod}~2^{m-1}\big ) \\= & {} \sigma ^{u+v+2^{m-2}-1-\ell }\big ((2^{m-2}v-2^{m-2}-v+1+\ell )\text {mod}~2^{m-1}\big ) \\\equiv & {} (u+2^{m-2}v)\text {mod}~2^{m-1}\\\equiv & {} (u+2^{m-2})\text {mod}~2^{m-1}, \end{aligned}$$

  where the last equality holds because v is odd. Hence,

  $$\begin{aligned} \alpha [u,v]=[(u+2^{m-2})\text {mod}~2^{m-1},v]=\beta [u,v] \end{aligned}$$

  with $\beta =\sigma ^{u+v+2^{m-2}-1-\ell }\tau$.

The three cases above prove that there exists $\beta \in \langle \sigma ,\tau \rangle ={{\,\mathrm{Aut}\,}}\Gamma$ such that $\alpha$ and $\beta$ agree for each edge $[u,v] \in E(\Gamma )$ provided n is odd. When n is even, a similar argument to that above gives the existence of the desired $\beta \in \langle \sigma ,\tau \rangle ={{\,\mathrm{Aut}\,}}\Gamma$. Therefore, $\alpha \in {{\,\mathrm{stab}\,}}(n)\le {{\,\mathrm{Aut}\,}}\Gamma$ and $1,\tau ,\alpha \in {{\,\mathrm{stab}\,}}(n)$, a final contradiction. $\square$

The proof of our first main result follows from Propositions 7 and 8.

Proof of Theorem 4

If $\hbox {QD}_{2^m}=\langle x,y\rangle$, then the Cayley graph ${{\,\mathrm{Cay}\,}}(\hbox {QD}_{2^m},S)$ with connection set

$$\begin{aligned} S=\left\{ x,x^{2^{m-1}-1},y,xy,x^{2^{m-2}+1}y\right\} \end{aligned}$$

is a $\hbox {QD}_{2^m}$-graph by Proposition 7. Hence,

$$\begin{aligned} \alpha (\hbox {QD}_{2^m}) \le |\hbox {QD}_{2^m}|=2^m. \end{aligned}$$

To prove the reverse inequality, suppose that $\Gamma$ is a $\hbox {QD}_{2^m}$-graph and consider ${{\,\mathrm{Aut}\,}}\Gamma =\langle \sigma ,\tau \rangle$ as a permutation group where $\sigma ,\tau \in \hbox {QD}_{2^m}$ are as defined in Eq. (1). The cycle decomposition of $\sigma$ contains at least two $2^{m-1}$-cycles by Proposition 8. Therefore,

$$\begin{aligned} 2^{m-1}+2^{m-1}=2^m \le |{{\,\mathrm{supp}\,}}(\sigma )| \le |V(\Gamma )| \end{aligned}$$

implies that $2^m \le \alpha (\hbox {QD}_{2^m})$ because $\Gamma$ is a $\hbox {QD}_{2^m}$-graph. The result now follows. $\square$

With the value of $\alpha (\hbox {QD}_{2^m})$ established for all integers $m \ge 4$, we now turn our attention to quasi-abelian groups and prove Theorem 5.

4 The quasi-abelian group $\hbox {QA}_{16}$

In this section, we will consider the special case of Theorem 5. In particular, to prove that $\alpha (\hbox {QA}_{16})=18$, we first construct a $\hbox {QA}_{16}$-graph on 18 vertices as follows. Define the permutations $\sigma$ and $\tau$ on $\{1,2,3,\ldots ,18\}$ by

$$\begin{aligned} \sigma =(1,2,3,4,5,6,7,8)(9,10,11,12,13,14,15,16)(17,18) \end{aligned}$$

and

$$\begin{aligned} \tau =(1,9)(2,14)(3,11)(4,16)(5,13)(6,10)(7,15)(8,12)(17,18). \end{aligned}$$

Clearly, $\sigma$ and $\tau$ have orders 8 and 2, respectively; since $\tau \sigma \tau =\sigma ^5$, these permutations satisfy the relations given in Eq. (2) and $\langle \sigma ,\tau \rangle \cong \hbox {QA}_{16}$. Define the graph $\Gamma (4)$ on 18 vertices with $V\big (\Gamma (4)\big ) = \{1,2,3,\ldots ,18\}$ and $E\big (\Gamma (4)\big )$ containing the following four edge orbits:

$$\begin{aligned} {{\,\mathrm{{\mathcal {O}}}\,}}\{1,2\}, \quad {{\,\mathrm{{\mathcal {O}}}\,}}\{1,9\}, \quad {{\,\mathrm{{\mathcal {O}}}\,}}\{1,10\}, \quad \text {and} \quad {{\,\mathrm{{\mathcal {O}}}\,}}\{1,17\}. \end{aligned}$$

The graph $\Gamma (4)$ has 56 edges and is depicted in Fig. 3.

Fig. 3

The $\hbox {QD}_{16}$-graph $\Gamma (4)$ with 18 vertices and 56 edges

A quick computation in GAP [25] proves that $\Gamma (4)$ is a $\hbox {QA}_{16}$-graph. Moreover, a computer search in GAP proves that no graph on less than 18 vertices is a $\hbox {QA}_{16}$-graph. Therefore, $\alpha (\hbox {QA}_{16}) = 18$, and we turn our attention to the value of $\alpha (\hbox {QA}_{2^m})$ with $m \ge 5$ in the next section.

5 The quasi-abelian group $\hbox {QA}_{2^m}$ with $m \ge 5$

The results of Sect. 4 prove that $\alpha (\hbox {QA}_{16})=18$. Thus, to prove Theorem 5, we will assume that $m \ge 5$ is an integer and construct a $\hbox {QA}_{2^m}$-graph, denoted $\Gamma (m)$, with $2^{m-1}+6$ vertices; then, we argue that $\Gamma (m)$ has minimal order among all $\hbox {QA}_{2^m}$-graphs to establish Theorem 5.

Definition 9

Assume that $m \ge 5$ is an integer. Define the graph $\Gamma (m)$ on $2^{m-1}+6$ vertices with $V\big (\Gamma (m)\big ) = \{1,2,\ldots ,2^{m-1}+6\}$ and $E\big (\Gamma (m)\big )$ containing the following $3\cdot 2^m+8$ edges:

$$\begin{aligned} \begin{array}{l} \{u,v\}, \text { where } u,v \in \{1,2,3,\ldots ,2^{m-1}\} \text { and } v-u\equiv k\ \text {mod}~2^{m-1} \text { for }\\ \quad k \in \{1,2,2^{m-2}+1\};\\ \{u,v\}, \text { where } u \in \{1,2,3,\ldots ,2^{m-1}\}, \ v \in \{2^{m-1}+1,\ldots ,2^{m-2}+4\}, \text { and }\\ \quad v-u\equiv k \ \text {mod}~4 \text { for } k \in \{0,1\}; \\ \{u,v\}, \text { where } u,v \in \{2^{m-1}+1,\ldots ,2^{m-2}+4\} \text { and } v-u\equiv 1 \ \text {mod}~4; \text { and }\\ \{u,v\}, \text { where } u \in \{1,2,\ldots ,2^{m-2}+4\},\ v \in \{2^{m-2}+5,2^{m-2}+6\},\\ \quad \text { and } v-u\equiv 0\ \text {mod}~2. \end{array} \end{aligned}$$

Observe that the image of each edge in $\Gamma (m)$ under the permutation

$$\begin{aligned} \sigma =(1,2,3,\ldots ,2^{m-1})(2^{m-1}+1,2^{m-1}+2,2^{m-1}+3,2^{m-1}+4)(2^{m-1}+5,2^{m-1}+6) \end{aligned}$$

(5)

or

$$\begin{aligned} \tau =(2,2^{m-2}+2)(4,2^{m-2}+4)(6,2^{m-2}+6)\cdots (2^{m-2},2^{m-2}+2^{m-2}) \end{aligned}$$

(6)

is also an edge in $\Gamma (m)$ by construction. Consequently, $\langle \sigma ,\tau \rangle$ is a subgroup of ${{\,\mathrm{Aut}\,}}\!\big (\Gamma (m)\big )$ and $E\big (\Gamma (m)\big )$ comprises the following seven edge orbits:

$$\begin{aligned}&{{\,\mathrm{{\mathcal {O}}}\,}}\{1,2\},\quad {{\,\mathrm{{\mathcal {O}}}\,}}\{1,3\}, \quad {{\,\mathrm{{\mathcal {O}}}\,}}\{1,2^{m-1}+1\},\quad {{\,\mathrm{{\mathcal {O}}}\,}}\{1,2^{m-1}+2\},\quad {{\,\mathrm{{\mathcal {O}}}\,}}\{1,2^{m-1}+5\},\\&{{\,\mathrm{{\mathcal {O}}}\,}}\{2^{m-1}+1,2^{m-1}+2\},\quad \text {and}\quad {{\,\mathrm{{\mathcal {O}}}\,}}\{2^{m-1}+1,2^{m-1}+5\}. \end{aligned}$$

The edge orbit ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,2\}$ contains $2^m$ edges of $\Gamma (m)$ and is depicted in Fig. 4a when $m=5$. The edge orbits ${{\,\mathrm{{\mathcal {O}}}\,}}\{2^{m-1}+1,2^{m-1}+2\}$ and ${{\,\mathrm{{\mathcal {O}}}\,}}\{2^{m-1}+1,2^{m-1}+5\}$ each contain four edges. When $m=5$, Fig. 4b gives an illustration of the union of these two edge orbits. The remaining four edge orbits of ${{\,\mathrm{Aut}\,}}\big (\Gamma (m)\big )$ each contain $2^{m-1}$ edges.

Fig. 4

Two subgraphs of the graph $\Gamma (5)$, constructed in Definition 9

Below, we prove that $\Gamma (m)$ is a $\hbox {QA}_{2^m}$-graph.

Proposition 10

If $m \ge 5$ is an integer, then the graph $\Gamma (m)$ given in Definition 9 is a $\hbox {QA}_{2^m}$-graph.

Proof

The permutations $\sigma$ and $\tau$ defined in Eqs. (5) and (6), respectively, satisfy the relations given in Eq. (2). Therefore, $\langle \sigma , \tau \rangle \cong \hbox {QA}_{2^m}$ and $\langle \sigma , \tau \rangle$ is a subgroup of ${{\,\mathrm{Aut}\,}}\!\big (\Gamma (m)\big )$ by construction. To prove that ${{\,\mathrm{Aut}\,}}\!\big (\Gamma (m)\big )=\langle \sigma ,\tau \rangle$, we partition $V\big (\Gamma (m)\big )$ into three subsets, namely

$$\begin{aligned} V_1= & {} \{1,2,3,\ldots ,2^{m-1}\}, \quad V_2 =\{2^{m-1}+1,\ldots ,2^{m-2}+4\}, \quad \text {and} \\ V_3= & {} \{2^{m-1}+5,2^{m-2}+6\}, \end{aligned}$$

and then, apply the Orbit-Stabilizer Theorem twice.

Each vertex in $V_1$, $V_2$, and $V_3$ has degree 9, $2^{m-2}+3$, and $2^{m-2}+2$, respectively. Since these degrees are distinct for each $m \ge 5$, it follows that $V_1$, $V_2$, and $V_3$ are the orbits of ${{\,\mathrm{Aut}\,}}\!\big (\Gamma (m)\big )$ because $\sigma$ acts transitively on each these sets. For $1 \in V\big (\Gamma (m)\big )$, we have that

$$\begin{aligned} \big |{{\,\mathrm{Aut}\,}}\!\big (\Gamma (m)\big )\big |=|{{\,\mathrm{{\mathcal {O}}}\,}}(1)| \cdot |{{\,\mathrm{stab}\,}}(1)|=2^{m-1}\cdot |{{\,\mathrm{stab}\,}}(1)|, \end{aligned}$$

(7)

where the first equality holds by the Orbit-Stabilizer Theorem. To establish the order of ${{\,\mathrm{stab}\,}}(1)$, we consider the neighborhood graph N(1), which is depicted in Fig. 5a.

Fig. 5

Neighborhood graphs N(1) and N(2), which appeared in the proof of Proposition 10

Since 1 is fixed by all automorphisms of ${{\,\mathrm{stab}\,}}(1)$, the neighborhood graph N(1) is invariant under the action of ${{\,\mathrm{stab}\,}}(1)$. Additionally, the only neighbors of 1 that lie in $V_2$, namely $2^{m-1}+1$ and $2^{m-1}+2$, are fixed in ${{\,\mathrm{stab}\,}}(1)$ because they have different degrees in N(1); the vertex $2^{m-1}+5$ is also fixed by every automorphism of ${{\,\mathrm{stab}\,}}(1)$ as the only neighbor of 1 in $V_3$. It follows that 2 and $2^{m-2}+2$ form an orbit of ${{\,\mathrm{stab}\,}}(1)$ in ${{\,\mathrm{Aut}\,}}\!\big (\Gamma (m)\big )$, and thus vertex 3 is fixed by ${{\,\mathrm{stab}\,}}(1)$. Vertices $2^{m-1}$ and $2^{m-2}$ also form an orbit of ${{\,\mathrm{stab}\,}}(1)$ in ${{\,\mathrm{Aut}\,}}\!\big (\Gamma (m)\big )$, and thus, $2^{m-1}-1$ is fixed by ${{\,\mathrm{stab}\,}}(1)$. Moreover, if 1 and now 2 are fixed by some automorphism of $\Gamma (m)$, then the neighborhood graph N(2) is also fixed in ${{\,\mathrm{stab}\,}}(1,2)$ (Fig. 5b). In succession, the neighborhood graphs $N(3),N(4),\ldots ,N(2^{m-1})$ are fixed by every automorphism of $\Gamma (m)$ that fixes 1 and 2. Therefore, $|{{\,\mathrm{stab}\,}}(1,2)|=1$, and by the Orbit-Stabilizer Theorem,

$$\begin{aligned} |{{\,\mathrm{stab}\,}}(1)|=|\{2,2^{m-2}+2\}| \cdot |{{\,\mathrm{stab}\,}}(1,2)|=2\cdot 1=2. \end{aligned}$$

(8)

Equations (7) and (8) imply that $\big |{{\,\mathrm{Aut}\,}}\!\big (\Gamma (m)\big )\big |=2^m$. Since we previously established that $\hbox {QA}_{2^m} \cong \langle \sigma ,\tau \rangle \le {{\,\mathrm{Aut}\,}}\!\big (\Gamma (m)\big )$, the result now follows. $\square$

If $m \ge 5$ is an integer, then the graph $\Gamma (m)$ given in Definition 9 is a $\hbox {QA}_{2^m}$-graph by Proposition 10. Since $V\big (\Gamma (m)\big )=2^{m-1}+6$, we have that $\alpha (\hbox {QA}_{2^m}) \le 2^{m-1}+6$ for all $m \ge 5$. We claim that no graph on fewer than $2^{m-1}+6$ vertices is a $\hbox {QA}_{2^m}$-graph.

Proposition 11

Let $m \ge 5$ be an integer. If $\Gamma$ is a $\hbox {QA}_{2^m}$-graph, then $|V(\Gamma )|\ge 2^{m-1}+6$.

Proof

Assume that $\Gamma$ is a $\hbox {QA}_{2^m}$-graph, and toward a contradiction, suppose that $|V(\Gamma )|< 2^{m-1}+6$. Consider ${{\,\mathrm{Aut}\,}}\Gamma =\hbox {QA}_{2^m}$ as a permutation group, and let $\sigma$ and $\tau$ be the generators of $\hbox {QA}_{2^m}$ as defined in Eq. (2). Since the order of $\sigma$ is $2^{m-1}$, the cycle decomposition of $\sigma$ must contain at least one $2^{m-1}$-cycle. Without loss of generality, assume that $\sigma =(1,2,3,\ldots ,2^{m-1})\rho$ is the cycle decomposition of $\sigma$ with

$$\begin{aligned} {{\,\mathrm{supp}\,}}(\rho ) \subseteq \{2^{m-1}+1,2^{m-1}+2, \ldots ,2^{m-1}+5\}; \end{aligned}$$

this assumption on ${{\,\mathrm{supp}\,}}(\rho )$ is valid because

$$\begin{aligned} |{{\,\mathrm{supp}\,}}(\sigma )|\le |V(\Gamma )|< 2^{m-1}+6 \end{aligned}$$

and this forces the order of $\rho$ to be either 1, 2, or 4.

Since the cycle decomposition of $\sigma$ contains exactly one $2^{m-1}$-cycle, Lemma 6 implies $\tau (1)=\ell$ for some $\ell \in \{1,2, \ldots , 2^{m-1}\}$. Moreover, the relation $\tau \sigma \tau =\sigma ^{2^{m-2}+1}$ defined in Eq. (2) implies that

$$\begin{aligned} \tau (k)\equiv \big ((2^{m-2}+1)(k-1)+\ell \big )\text {mod}~2^{m-1} \end{aligned}$$

for each $k \in \{1,2, \ldots ,2^{m-1}\}$. Because $\tau (\ell )=1$, the equation above implies that $\ell \equiv 1 (\text {mod}~2^{m-2})$. Therefore, $\ell =1$ or $\ell =2^{m-2}+1$ when $\ell \in \{1,2,\ldots ,2^{m-1}\}$, and either

$$\begin{aligned} \tau \big |_{\{1,2,3,\ldots ,2^{m-1}\}}=(2,2^{m-2}+2)(4,2^{m-2}+4) \cdots (2^{m-2},2^{m-2}+2^{m-2}) \end{aligned}$$

or

$$\begin{aligned} \tau \big |_{\{1,2,3,\ldots ,2^{m-1}\}}=(1,2^{m-2}+1)(3,2^{m-2}+3) \cdots (2^{m-2}-1,2^{m-2}+2^{m-2}-1). \end{aligned}$$

As a result, each edge orbit in ${{\,\mathrm{Aut}\,}}\Gamma =\hbox {QA}_{2^m}$ has one of the following three forms:

• (a) ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,a\}$ with $1<a \le 2^{m-1}$;

• (b) ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,a\}$ with $2^{m-1}+1\le a \le 2^{m-1}+5$; or

• (c) ${{\,\mathrm{{\mathcal {O}}}\,}}\{a,b\}$ with $2^{m-1}+1 \le a<b \le 2^{m-1}+5$.

We will conclude this proof by finding an involution $\alpha \in {{\,\mathrm{Aut}\,}}\Gamma \backslash \hbox {QA}_{2^m}$; such an automorphism will contradict the fact that $\Gamma$ is a $\hbox {QA}_{2^m}$-graph and thus conclude our proof. The two cases that follow depend on the order of $\rho$, which appeared in the cycle decomposition of $\sigma$.

First, assume that the order of $\rho$ is 1 or 2. Define the permutation $\alpha$ on $\{1,2,3,\ldots ,2^{m-1}\}$ by

$$\begin{aligned} \alpha =(2,2^{m-1})(3,2^{m-1}-1)\cdots (2^{m-2},2^{m-2}+2)=\prod _{i=1}^{2^{m-2}-1} (1+i,2^{m-1}+1-i). \end{aligned}$$

Since $\alpha$ is an involution and the only involutions of $\hbox {QA}_{2^m}$ are $\tau$, $\sigma ^{2^{m-2}}$, and $\sigma ^{2^{m-2}}\tau$, it follows that $\alpha \not \in \hbox {QA}_{2^m}$. If $1<a \le 2^{m-1}$, then the induced subgraph of $\Gamma$ on $\{1,2,3,\ldots ,2^{m-1}\}$ with edge set ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,a\}$ is a circulant graph. Moreover, the induced bipartite subgraph of $\Gamma$ with partite sets $\{1,2,3,\ldots ,2^{m-1}\}$ and ${{\,\mathrm{supp}\,}}(\rho )$ and edge set ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,a\}$ is either a complete bipartite graph ($K_{1,2^{m-1}}$ or $K_{2,2^{m-1}}$), or $K_{1,2^{m-2}} \oplus K_{1,2^{m-2}}$ for any $a \in \{2^{m-1}+1,\ldots , 2^{m-1}+5\}$. Consequently, $\alpha$ leaves every edge orbit of the form ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,a\}$ with $a \in \{1,2,\ldots ,2^{m-1}+5\}$ invariant. Since $\alpha$ fixes the every edge orbit ${{\,\mathrm{{\mathcal {O}}}\,}}\{a,b\}$ with $2^{m-1}+1 \le a<b \le 2^{m-1}+5$, we have that $\alpha \in {{\,\mathrm{Aut}\,}}\Gamma \backslash \hbox {QA}_{2^m}$, a contradiction.

Now, assume that the order of $\rho$ is 4. After a possible relabeling, suppose that the 4-cycle

$$\begin{aligned} (2^{m-1}+1,2^{m-1}+2,2^{m-1}+3,2^{m-1}+4) \end{aligned}$$

is contained in the cycle decomposition of $\rho$ and that $2^{m-1}+1\le a \le 2^{m-1}+5$. If $E(\Gamma )$ does not contain an edge orbit of the form ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,a\}$ (set $a=2^{m-1}+1$) or contains exactly one edge orbit of the form ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,a\}$, then a similar argument to that above proves that

$$\begin{aligned} \alpha =(\rho (a),\rho ^3(a))\prod _{i=1}^{2^{m-2}-1} (1+i,2^{m-1}+1-i) \in {{\,\mathrm{Aut}\,}}\Gamma \backslash \hbox {QA}_{2^m}, \end{aligned}$$

a contradiction. If there are exactly two edge orbits of the form ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,a\}$ contained in $E(\Gamma )$, say ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,a\}$ and ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,\rho (a)\}$ or ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,a\}$ and ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,\rho ^2(a)\}$, then the involution

$$\begin{aligned} \alpha =(a,\rho (a))(\rho ^2(a),\rho ^3(a))\prod _{i=1}^{2^{m-2}-1} (1+i,2^{m-1}+1-i) \end{aligned}$$

is an element of ${{\,\mathrm{Aut}\,}}\Gamma \backslash \hbox {QA}_{2^m}$ in the first case, whereas

$$\begin{aligned} \alpha =(a,\rho ^2(a))(\rho (a),\rho ^3(a))\prod _{i=1}^{2^{m-2}-1} (1+i,2^{m-1}+1-i) \end{aligned}$$

is an element of ${{\,\mathrm{Aut}\,}}\Gamma \backslash \hbox {QA}_{2^m}$ in the second case. Since the situations when there are three or four edge orbits of the form ${{\,\mathrm{{\mathcal {O}}}\,}}\{1,a\}$ contained in $E(\Gamma )$ are complements of the aforementioned cases, we obtain a final contradiction. Thus, the order of $\Gamma$ is at least $2^{m-1}+6$. $\square$

This article concludes with the proof of our second main result, namely Theorem 5.

Proof of Theorem 5

The results of Sect. 4 prove that $\alpha (\hbox {QA}_{16})=18$. Thus, we assume that $m \ge 5$ is an integer. If $\Gamma$ is a $\hbox {QA}_{2^m}$-graph, then $|V(\Gamma )|\ge 2^{m-1}+6$ by Proposition 11. As a result, $\alpha (\hbox {QA}_{2^m}) \ge 2^{m-1}+6$. Moreover, $\alpha (\hbox {QA}_{2^m}) \le 2^{m-1}+6$ because the graph $\Gamma (m)$ given in Definition 9 with $2^{m-1}+6$ vertices is a $\hbox {QA}_{2^m}$-graph by Proposition 10. Therefore,

$$\begin{aligned} \alpha (\hbox {QA}_{2^m}) = {\left\{ \begin{array}{ll} 18 &{} \text {if } m=4\\ 2^{m-1}+6 &{} \text {if } m \ge 5, \end{array}\right. } \end{aligned}$$

as desired. $\square$