NEMOCED: New Energy Model and Optimal Cluster Estimation Based on Density to Increase Lifetime in Wireless Sensor Networks

Abstract

In recent years, many methods have been presented for clustering in wireless sensor networks (WSNs). Some areas have high density, and the random distribution of the nodes reduces the clustering quality. Moreover, the number of clusters is manually determined before clustering. In this paper, a new clustering algorithm called NEMOCED is presented based on the node distribution. In the NEMOCED, the best cluster head is selected according to the node distribution. Moreover, we propose a new energy model to estimate proper clusters. One of the main features of the energy model is selecting the proper clusters. It is performed based on the number of nodes and the network size. In each round, two cluster heads are selected by using the tree structure. Finally, we introduce five criteria for assessing the quality and accuracy of the proposed algorithm. The NEMOCED can perform the clustering based on the local density of nodes and choose more proper cluster heads in high-density areas. The simulation results demonstrate that the NEMOCED can significantly improve lifetime and energy consumption. Furthermore, the simulation results show that the NEMOCED algorithm has good adaptability and works well under different network lifetime definitions. All the results prove that the NEMOCED algorithm has the advantage of being suitable and efficient for large-scale WSN applications.

1 Introduction

Wireless sensor networks (WSNs) are significant in applications such as traffic control, forest fire control, environment tracking, control of patient status [1,2,3,4,5]. The node distribution in WSNs is random or deterministic [6, 7]. Each node collects data and transmits them to a base station (BS). Finally, the BS processes the collected data. One of the major issues in WSNs is energy consumption and network lifetime [8,9,10,11]. The initial energy of nodes is low and the sensors cannot be recharged [12]. Therefore, the initial energy of nodes is quickly drained during receiving and sending of data. So, they are gradually removed from the network [13, 14].

So far, several clustering algorithms have been proposed to increase lifetime and improve energy consumption in the WSN [15,16,17]. In clustering, several nodes are grouped according to the common properties. In each cluster, a node with better conditions is selected as the cluster head (CH). The CH collects data from cluster members and sends it to the BS. The data collected by CH can be transmitted in a single-hop or multi-hop manner [18,19,20,21,22]. In the single-hop, CHs transfer the collected data to the BS directly. In the multi-hop, the CHs transfer the collected data to the BS by using other CHs [23]. The single-hop manner is proper for regions where nodes' distance is low. Moreover, the multi-hop manner is suitable for large-scale WSNs. Since the node distribution is random, the major problem of the clustering is the node density [20,21,22]. In the other words, the clusters formed in WSN are high-density or low-density. The high-density clusters have more nodes, and the energy of the CHs will quickly drain compared to low-density clusters. Most clustering algorithms do not consider the intra-cluster density that reduces the quality of the cluster. Therefore, these methods are not reliable. In density-based schemes, clusters are high-density regions that have separated from low-density areas. There are criteria such as entropy, intra-cluster, and inter-cluster distances to ensure cluster quality. The separate use of these criteria does not guarantee the quality of the clusters [24,25,26]. For example, in grid-based clustering [27,28,29,30], the nodes are divided into multiple regions called Grid. Then, clustering is performed based on the number of nodes in each grid. The number of nodes in each grid is the only clustering criterion. Therefore, these methods are not efficient because the number of the nodes in each cluster (or grid) may be low but their initial energy is high and vice versa. The number of clusters at the beginning of the clustering process is another. In some methods, such as k-means and c-means, the number of clusters is manually determined before the clustering process [31, 32]. For this reason, these methods are not very secure.

The paper presents a new energy model and by using this model, we determine the number of proper clusters (or proper cluster heads). The clustering is performed using the local density of each node. In addition to the main CH, the successor CH also exists in each cluster. The successor CH is elected to support the main CH. The main advantage of our algorithm is determining the number of clusters based on the number of nodes and the network size. In the NEMOCED, the quality of clustering and its accuracy is ensured by using five criteria. The other advantages are:

• 1. Determining the number of proper clusters using a new energy model, network size, and the number of nodes.

• 2. Performing the clustering process according to the local density of each node.

• 3. Selecting the best node in each cluster as the CH.

• 4. Using a new tree structure to determine the main and the successor CHs

• 5. Determining the high-density and low-density regions and selecting the more proper CH in the high-density regions.

• 6. Presenting the five criteria to ensure the cluster quality and accuracy

The rest of the paper is organized as follows: Sect. 2 briefly reviews related works. Section 3 provides our system model, network model, and radio energy model. The procedure of the NEMOCED algorithm is presented in Sect. 4. Section 5 presents the simulation results and a comparison with the existing algorithms. Finally, Sect. 6 concludes this paper with some discussion of future work.

2 Related Works

The energy consumption issue was addressed very early in the Low Energy Adaptive Clustering Hierarchy protocol (LEACH) [33]. It is a hierarchical, self-organization, and single-hop protocol. In LEACH, the CH selection is randomly performed based on the threshold $T\left(n\right)$. It is defined as follows:

$$T\left(n\right)=\left\{\begin{array}{l}\frac{P}{1-P\left(r\hspace{0.33em}\hspace{0.33em}\mathit{mod}\hspace{1em}\frac{1}{p}\right)}\hspace{1em}if\hspace{0.33em}n\in G\\ 0\hspace{1em}otherwise\end{array}\right.$$

(1)

where P: the percentage of the CH number, r: is the current round number, G: the set of nodes that have not been elected as CH for the past 1/p rounds, n: the number of nodes.

After selecting CHs, they broadcast a message to other nodes. The common nodes are connected to their corresponding CHs based on the lowest power required to connect and the received signal strength indicator (RSSI). The CH role alternates among all of the nodes. So, each node will have a chance to be the CH. Each node selects a random number between 0 and 1. If this random number is less than T(n), then the node is selected as the CH. The CH rotation between the nodes results in load balancing, energy consumption balance, and uniform distribution of the energy. Despite these benefits, LEACH has problems. Firstly, the CH is randomly selected and if a node is the CH in the current round, it cannot be the CH in the next round. Therefore, low-energy nodes also can be CH. This problem is worse in high-density regions. Secondly, the LEACH assumes the communication range of each CH is high and they can directly transfer data to the BS. This is not a realistic assumption because in most cases the BS is not available for all nodes. Third, LEACH uses a single-hop method that is not proper for large-scale networks.

In the next years, different methods were introduced that could improve the LEACH. One of these methods is the ERP algorithm [34]. It is performed in homogeneous WSNs and has a good lifetime and stability. After the formation of clusters, routing is performed in a multi-hop manner. The ERP algorithm produced a 42% lifetime improvement compared with the LEACH protocol. One of the main benefits of the ERP is the new fitness function. It is calculated based on the genetic algorithm. Logambigai et al. presented the EEGBR protocol. It performs multiple clustering based on the grid and fuzzy rules. In the EEGBR, routing is performed through a novel feature called grid coordinator (GC). The results simulations demonstrate that EEGBR can reduce the hops and energy consumption by using the fuzzy rules. The EEGBR has three phases: cluster formation, grid coordinator selection, and grid-based routing. The grid coordinator is determined by using fuzzy rules. The fuzzy inference system uses three parameters: the residual energy of the nodes, the motion model of the nodes, and the distance to sink. In [35], a protocol called OCM-FCM is proposed that uses the fuzzy c-means algorithm for clustering. The OCM-FCM uses a single-hop approach for intra-cluster communication. Furthermore, it uses an inter-cluster manner to transfer data to the BS. In the OCM-FCM, the number of clusters is determined in advance that is not proper. If the node distribution is random, then the OCM-FCM is not a proper method because some areas have a higher density in random distribution. Another problem in the OCM-FCM is the CH selection. It is only performed based on the residual energy of the nodes. Meng et al. [30] have proposed a grid-based protocol called GBRR. It can solve the problem of CH overload by grid-based clustering. This method improves the quality of the node-to-node link between nodes in the WSN. In, authors have proposed a new routing algorithm called ENEFC HRML that has three phases: hierarchical routing using cluster identification (HRCI), hierarchical routing using multi-hop (HRMH), and hierarchical routing using multilevel (HRML). The simulation results show that the HRML phase has high efficiency in energy consumption. The FUZZY-TOPSIS [37] presents a new technique based on fuzzy rules in which CH selection is according to five criteria. By using the five criteria, the common node decides whether to be the CH or not. Then the common nodes are linked to the corresponding CHs based on the maximum RSSI value and the smallest distance. In the MCFL [36] has been proposed a new clustering protocol to reduce energy consumption and increase network lifetime. The MCFL has three rounds that in each round clustering is separately performed. In other words, every three rounds produce different clusters. In [37] has been proposed a hybrid protocol based on density and threshold. The hybrid protocol is based on density and a threshold called C-DTB-CHR and C-DTB-CHR-ADD. It uses the LEACH, T-LEACH, and MT-CHR deficiencies to select the CHs. The main benefit of the C-DTB-CHR is that all of the nodes do not participate in the data transmission. In other words, a density-based approach has been suggested for nodes that will cooperate in the data transmission process. Jinyu Ma et al. [38] introduced a protocol based on an ant colony called ADCAPTEEN. It selects two CHs: the MCH (Master Cluster Head) and VCH (Vice Cluster Head). The MCH and VCH have co-work to collect, aggregate, and send data. The simulation results show that the ADCAPTEEN protocol has better scalability compared with the APTEEN protocol. Therefore, it is proper for large-scale WSNs. The MOFCA protocol [39] is another protocol that uses the residual energy of the nodes, node distance to the BS, and node density. The MOFCA protocol determines the tentative and final CHs via local decision-making. Huamei et al. [40] proposed an energy-efficient and non-uniform clustering protocol based on improved shuffled frog leaping algorithm to increase lifetime in wireless sensor networks. Their method is adopted to divide the sensor nodes into clusters and finds the optimal cluster head. OK-means is another method that improves the position of nodes using the K-means algorithm [41]. The OK-means algorithm uses single step and multi-hop manners for intra-cluster and inter-cluster communications [41].

3 System Model

3.1 Network Model

In the NEMOCED, there are N sensor nodes, and all of the nodes are randomly distributed in a square area measuring n * n. The distribution of sensor nodes is uniform and there is only one BS. In different scenarios is assumed the BS has different positions. The BS position is outside of the nodes’ distribution. Furthermore, the following assumptions are considered:

• 1. Nodes are aware of their position, the position of other nodes, and the BS position. It is performed using the global positioning system (GPS) or positioning algorithms.

• 2. The nodes are stationary in the environment that their initial energy is equal.

• 3. Wireless communication between nodes is symmetrical.

• 4. There is a medium access control (MAC) layer that prevents interference when sending or receiving messages.

• 5. Energy, memory, and computational power of the BS are infinite.

3.2 Radio Energy Model

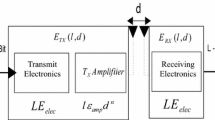
Radio energy consumption is measured based on the distance of the transmitter and receiver. The radio energy model is calculated by using an energy dissipation model [42]. Therefore, to transmit an L-bit message over a distance d, the energy consumption is defined as follows:

$$\left\{\begin{array}{c}{E}_{rcv}\left(L,d\right)=L*\left({E}_{elect}+{\varepsilon }_{fs}*{d}^{2}\right) d<{d}_{c}\\ {E}_{rcv}\left(L,d\right)=L*\left({E}_{elect}+{\varepsilon }_{mp}*{d}^{4}\right) d\ge {d}_{c}\end{array}\right.$$

(2)

where ${d}_{c}$ is the crossover distance. ${\varepsilon }_{fs}$ and ${\varepsilon }_{mp}$ are power consumption of the free space propagation and power consumption of multipath propagation, respectively. They are based on the sensitivity of the sender and noise shape. ${E}_{elect}$ is the energy/bit consumed by the transmitter/receiver electronics. Finally, the energy consumption to receive an L-bit message is:

$${E}_{RX}=L*{E}_{elect}$$

(3)

4 Proposed Method

4.1 Estimation of Proper Number of Clusters

One of the main issues in clustering is to estimate the number of proper clusters before the beginning of the clustering. Therefore, we propose a relation based on the energy consumption model. We compute the number of proper clusters based on this relation. Since the number of clusters indicates the number of cluster heads, we can determine the number of proper cluster heads. Energy consumption in each cluster ${(E}_{cluster})$ includes the energy consumption of common nodes ${(E}_{common-node})$ and the cluster heads $({E}_{CH})$. Energy consumption of common nodes includes both the energy required to receive data ${(E}_{r})$ and the energy needed to send data to CH (${E}_{s}$) over a distance d. The cluster head has three types of energy:

• 1. The energy required to receive data from the common nodes ${(E}_{rcv-CN})$ in each cluster

• 2. Aggregation energy of the collected data (${E}_{agg}$)

• 3. The energy required to transmit the aggregated data from CH to a higher level over the distance d meter (${E}_{send}$). ${E}_{send}$ is based on the type of transmission (single-hop or multi-hop). In the single-hop manner, the CH data are directly transmitted to the BS. In the multi-hop manner, the CH data are transmitted to the BS via higher-level CHs.

Therefore, energy consumption in each cluster is defined as follows:

$${E}_{cluster}={E}_{CH}+{E}_{common-node}={(E}_{rcv-CN}+{E}_{agg}+{E}_{snd})+ {(E}_{r}+{E}_{s})$$

(4)

Assuming that there are k clusters, the total energy consumption of the network is defined as follows:

$${E}_{total}={k*E}_{cluster}=k*({E}_{CH}+{E}_{common-node})={k*((E}_{rcv-CN}+{E}_{agg}+{E}_{snd})+ {(E}_{r}+{E}_{s}))$$

(5)

If ${N}_{\mathrm{Common}}$ is the total number of common nodes in each cluster, then the energy required to receive data is defined as follows:

$${E}_{rcv-CN}=L*{E}_{elect}*{N}_{\mathrm{Common}}$$

(6)

Data aggregation energy is also defined as follows:

$${E}_{agg}=L*{E}_{a}*{N}_{\mathrm{CH}}$$

(7)

where ${N}_{CH}$ and ${E}_{a}$ are the number of clusters and energy needed to aggregate the received data, respectively. In the single-hop method, the energy required to receive data from a cluster head to the BS is defined as follows:

$${E}_{snd}=L*{E}_{elect}+{L*\varepsilon }_{mp}*{d}_{CH2BS}^{4}$$

(8)

where d_CH2BS is the cluster distance to the BS. In the multi-hop method, the distance between the CH and the BS is greater than the CH distance to higher-level CH. Therefore, in Eq. (8), ${d}_{CH2BS}^{2}$ is used instead of ${d}_{CH2BS}^{4}$.

The energy required for receiving and sending data by common nodes are defined as follows:

$${E}_{r}=L*{E}_{elect}$$

(9)

$${E}_{snd}=L*{E}_{elect}+{L*\varepsilon }_{fs}*{d}_{CN2CH}^{2}$$

(10)

where ${d}_{CN2CH}^{2}$ is the common node distance to the CH. We use ${d}_{CN2CH}^{2}$ because the distance between the common node and its cluster is less than the crossover distance. In other words, the relation of the common nodes and their cluster-head is single-hop. Therefore, the total energy consumption is:

$${E}_{total}={k*E}_{cluster}=k*\left[\left(L*{E}_{elect}*{N}_{\mathrm{Common}}\right)+ L*{E}_{a}*{N}_{\mathrm{CH}}\right)+\left(L*{E}_{elect}+{L*\varepsilon }_{mp}*{d}_{CH2BS}^{4}\right)+(L*{E}_{elect}+{L*\varepsilon }_{fs}*{d}_{CN2CH}^{2})]$$

(11)

On the one hand, each cluster has one cluster head. On the other hand, the number of common nodes per cluster is on average equal to N/k−1. Therefore, the total number of cluster heads is k. Finally, the total number of nodes will be k * (N / k−1) or (N−k):

$${E}_{total}=k*\left[L*{E}_{elect}*\left(\frac{N}{k}-1\right)+L*{E}_{a}*\mathrm{k}+L*{E}_{elect}+{L*\varepsilon }_{mp}*{d}_{CH2BS}^{4}+L*{E}_{elect}+L*{E}_{elect}+{L*\varepsilon }_{fs}*{d}_{CN2CH}^{2}\right]=\mathrm{k}*\mathrm{L}[{E}_{elect}*\left(\frac{N}{k}\right)+\mathrm{k}*{E}_{a}+2{E}_{elect}+{\varepsilon }_{mp}*{d}_{CH2BS}^{4}+{\varepsilon }_{fs}*{d}_{CN2CH}^{2}]$$

(12)

The proper value of the cluster (${k}_{opt}$) is obtained by taking the derivative with respect to k in Eq. (12).

In the following, we propose a proper relation for the cluster head distance to the BS (${d}_{CH2BS}$) and the common node distance to the cluster head (${d}_{CN2BS}$). Since our clustering is based on the primary grids, we consider the nodes are distributed in square s * s. In later sections, we will describe an equation to compute the edge of the initial grids.

Lemma 1

The average distance between the nodes in a square with diameter d and side length s is defined as follows:

$$\frac{2+5\mathrm{ln}\left(\sqrt{2}+1\right)+2)\sqrt{2}}{30}*d ,d=s\sqrt{2}$$

(13)

Proof

Let two nodes with coordinates (x₁, y₁) and (x₂, y₂) are in a square to the side length s. The nodes are also independent of the other nodes. The average distance between the nodes is defined as follows:

$${d}_{avg}=\frac{1}{{s}^{4}}{\int }_{0}^{s}{\int }_{0}^{s}{\int }_{0}^{s}{\int }_{0}^{s}\sqrt{{\left({x}_{1}-{x}_{2}\right)}^{2}+{\left({y}_{1}-{y}_{2}\right)}^{2}}d{x}_{2}d{x}_{1}d{y}_{2}d{y}_{1}$$

(14)

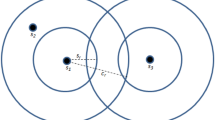
According to Fig. 1 and by reducing integral in Eq. (14), ${d}_{avg}$ in Eq. (15) is define as follows:

Fig. 1

Reducing the integration area from a square to a triangular area

$${d}_{avg}=\frac{4}{{s}^{4}}{\int }_{0}^{s}{\int }_{0}^{{y}_{1}}{\int }_{0}^{s}{\int }_{0}^{{x}_{1}}\sqrt{{\left({x}_{1}-{x}_{2}\right)}^{2}+{\left({y}_{1}-{y}_{2}\right)}^{2}}d{x}_{2}d{x}_{1}d{y}_{2}d{y}_{1}$$

(15)

By defining ${z}_{1}={x}_{1}-{x}_{2}$, ${z}_{2}={x}_{1}+{x}_{2}$, and Jacobian determinant$j=\frac{\partial \left({x}_{1},{x}_{2}\right)}{\partial \left({x}_{1},{x}_{2}\right)}=\frac{1}{2}$:

$${x}_{1}=\frac{{z}_{1}+{z}_{2}}{2}$$

(16)

$${x}_{2}=\frac{{z}_{2}-{z}_{1}}{2}$$

(17)

Figure 2 shows the integral regions with new coordinates.

Fig. 2

Converting variables x₁ and x₂ to z₁ and z₂

According to Fig. 2, ${d}_{avg}$ can be described as follows:

$${d}_{avg}=\frac{2}{{s}^{4}}{\int }_{0}^{s}{\int }_{0}^{{y}_{1}}{\int }_{0}^{s}{\int }_{0}^{{2s-z}_{1}}\sqrt{{{z}_{1}}^{2}+{\left({y}_{1}-{y}_{2}\right)}^{2}}d{z}_{2}d{z}_{1}d{y}_{2}d{y}_{1}=\frac{2}{{s}^{4}}{\int }_{0}^{s}{\int }_{0}^{{y}_{1}}{\int }_{0}^{s}\left(2s-2{z}_{1}\right)\sqrt{{{z}_{1}}^{2}+{\left({y}_{1}-{y}_{2}\right)}^{2}}d{z}_{1}d{y}_{2}d{y}_{1}$$

(18)

We define ${w}_{1}={y}_{1}-{y}_{2}$ and ${w}_{2}={y}_{1}+{y}_{2}$. So:

$${d}_{avg}=\frac{4}{{s}^{4}}{\int }_{0}^{s}{\int }_{0}^{s}\left(s-{z}_{1}\right)\left(s-{w}_{1}\right)\sqrt{{{z}_{1}}^{2}+{{w}_{1}}^{2}}d{z}_{1}d{w}_{1}=\frac{8}{{s}^{4}}{\int }_{0}^{s}{\int }_{0}^{{z}_{1}}\left(s-{z}_{1}\right)\left(s-{w}_{1}\right)\sqrt{{{z}_{1}}^{2}+{{w}_{1}}^{2}}d{z}_{1}d{w}_{1}$$

(19)

Finally, by changing the integration interval to the polar coordinates ${z}_{1}=r\mathrm{cos}\theta$ and ${w}_{1}=r\mathrm{sin}\theta$, the following equation is obtained:

$${d}_{avg}=\frac{8}{{s}^{4}}{\int }_{0}^{\frac{\pi }{4}}{\int }_{0}^{\frac{s}{\mathrm{cos}\theta }}\left(s-r\mathrm{cos}\theta \right)\left(s-r\mathrm{sin}\theta \right){r}^{2}drd\theta $$

(20)

By solving Eq. (20):

$${d}_{avg}=\frac{8}{{s}^{4}}*\frac{2+5\sqrt{2}\mathrm{ln}\left(\sqrt{2}+1\right)+2\sqrt{2}}{120\sqrt{2}}=\frac{2+5\mathrm{ln}\left(\sqrt{2}+1\right)+2)\sqrt{2}}{30}*d$$

(21)

By calculating the Eq. (21), ${d}_{avg}$ will be approximately 0.36869*d. We will use ${d}_{avg}=0.36869*d$ instead of ${d}_{\mathrm{CH}2\mathrm{BS}}$ in the proposed method.

Lemma 2

The distance between two random nodes in a square with side length p is:

$${D}_{avg}=\left( \frac{1}{3}\mathrm{ln}\left(1+\sqrt{2}\right)+\frac{1}{15}\left(2+\sqrt{2}\right)\right)*p$$

(22)

Proof

We first make a proof for the rectangular region with side lengths a and b and then extend it to the square area.

Let two points $\left({x}_{1},{y}_{1}\right)$ and $\left({\mathrm{x}}_{2},{\mathrm{y}}_{2}\right)$ are randomly distributed in the interval (0, a) and (0, b), respectively. The probability distribution function is defined as follows:

$${F}_{a}\left(t\right)=prob({{x}_{1}-{x}_{2})}^{2}\le tp$$

(23)

With respect to the probability distribution function, the corresponding density function is defined as:

$${f}_{\mathrm{a}}\left(\mathrm{t}\right)=\frac{\mathrm{d}{F}_{a}\left(t\right)}{\mathrm{dt}}$$

(24)

We show the density corresponding to $G\left(s\right)=prob(({{x}_{1}-{x}_{2})}^{2}+({{y}_{1}-{y}_{2}))}^{2}\le s$ by g(s), which is obtained by convolving of ${f}_{a}$ and ${f}_{b}$. Finally, the distribution function for the distance is $K\left(v\right)=H\left({v}^{2}\right)\mathrm{ with the density}$ $K\left(v\right)=2vh\left({v}^{2}\right)$.

The probability density for $({{x}_{1}-{x}_{2})}^{2}+({{y}_{1}-{y}_{2})}^{2}\le s$ is equal to the convolution of g from ${f}_{a}$ and ${f}_{b}$:

$$g\left(s\right)=\int {f}_{a}\left(s-t\right){f}_{\mathrm{b}}\left(\mathrm{t}\right)\mathrm{dt}$$

(25)

Due to different domains of ${f}_{a}$ and ${f}_{b}$, there are three main states:

$${g}_{1}\left(s\right)={\int }_{0}^{s}{f}_{a}\left(s-t\right){f}_{\mathrm{b}}\left(\mathrm{t}\right)\mathrm{dt },0<s\le {\mathrm{a}}^{2}$$

(26)

$${g}_{2}\left(s\right)={\int }_{s-{a}^{2}}^{s}{f}_{a}\left(s-t\right){f}_{b}\left(t\right)dt ,{a}^{2}<s\le {b}^{2}$$

(27)

$${g}_{3}\left(s\right)={\int }_{s-{a}^{2}}^{{\mathrm{b}}^{2}}{f}_{a}\left(s-t\right){f}_{\mathrm{b}}\left(\mathrm{t}\right)\mathrm{dt },{\mathrm{b}}^{2}<s\le {{\mathrm{a}}^{2}+\mathrm{b}}^{2}$$

(28)

After calculating the above equations:

$${g}_{3}\left(s\right)={\int }_{s-{a}^{2}}^{{\mathrm{b}}^{2}}{f}_{a}\left(s-t\right){f}_{\mathrm{b}}\left(\mathrm{t}\right)\mathrm{dt },{\mathrm{b}}^{2}<s\le {{\mathrm{a}}^{2}+\mathrm{b}}^{2}$$

(29)

$${g}_{1}\left(s\right)=-2\frac{\sqrt{s}}{{\mathrm{a}}^{2}\mathrm{b}}-2\frac{\sqrt{s}}{{\mathrm{ab}}^{2}}+\frac{\pi }{ab}+\frac{s}{{\mathrm{a}}^{2}{\mathrm{b}}^{2}}-2\frac{\sqrt{s}}{{\mathrm{a}}^{2}\mathrm{b}},0<s\le {\mathrm{a}}^{2} {g}_{2}\left(s\right)=-\frac{1}{{\mathrm{b}}^{2}}+\frac{2}{ab}\mathrm{arcsin}\left(\frac{a}{\sqrt{\mathrm{s}}}\right)+\frac{2}{{a}^{2}b}\sqrt{s-{a}^{2}}-\frac{1}{{\mathrm{b}}^{2}}+\frac{2}{ab}\mathrm{arcsin}\left(\frac{a}{\sqrt{\mathrm{s}}}\right)+\frac{2}{{a}^{2}b}\sqrt{s-{a}^{2}}-\frac{1}{{\mathrm{a}}^{2}}+\frac{2}{ab}\mathrm{arcsin}\left(\frac{b}{\sqrt{\mathrm{s}}}\right)+\frac{2}{a{\mathrm{b}}^{2}}\sqrt{s-{b}^{2}},{\mathrm{a}}^{2}<s\le {\mathrm{b}}^{2}$$

(30)

$${g}_{3}\left(s\right)=-\frac{\pi }{ab}-\frac{s}{{a}^{2}{b}^{2}} , {\mathrm{b}}^{2}<s\le {{\mathrm{a}}^{2}+\mathrm{b}}^{2}$$

(31)

As stated earlier, the above calculations are for a rectangular region. In a square region, a is equal to b. So, ${g}_{2}\left(s\right)$ is omitted. Since s is the square of the distance, so the density of the distance $v=\sqrt{s}$ between two random points in a rectangle with the sides a and b is equal to:

$${g}_{v}\left(v\right)=g\left({v}^{2}\right)\frac{ds}{dv}=2vg\left({v}^{2}\right)$$

(32)

The expectation of the distance or average distance between two random points in a rectangle is defined as follows:

$$E\left[rect\right]={\int }_{0}^{{a}^{2}+{b}^{2}}\sqrt{s}g\left(s\right)ds={\int }_{0}^{\sqrt{{a}^{2}+{b}^{2}}}v{g}_{v}\left(v\right)dv$$

(33)

So:

$$E\left[rect\right]=\frac{{a}^{2}}{6b}\mathrm{ln}\left(\frac{b}{a}+\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}\right)+\frac{{b}^{2}}{6a}\mathrm{ln}\left(\frac{a}{b}+\sqrt{1+\frac{{a}^{2}}{{b}^{2}}}\right)+\frac{1}{15}(\frac{{b}^{3}}{{a}^{2}}+\frac{{a}^{3}}{{b}^{2}})+\left(3-\frac{{a}^{2}}{{b}^{2}}-\frac{{b}^{2}}{{a}^{2}}\right)\sqrt{{a}^{2}+{b}^{2}})$$

(34)

In a square area a = b = p, so:

$${D}_{avg}=E\left[rect\right]=p*\frac{1}{3}\mathrm{ln}\left(1+\sqrt{2}\right)+\frac{1}{15}(2+\sqrt{2})\approx 0.5214p$$

(35)

In the proposed model, we will use ${D}_{avg}$ instead of ${d}_{\mathrm{CN}2\mathrm{CH}}$.

According to lemma 1 and 2, the proposed energy model is defined as follows:

$${E}_{total}=k*L\left[{E}_{elect}*\left(\frac{N}{k}\right)+\mathrm{k}*{E}_{a}+2{E}_{elect}+{\varepsilon }_{mp}*{D}_{avg}^{4}+{\varepsilon }_{fs}*{d}_{avg}^{2}\right]$$

(36)

As mentioned earlier, there is on average N/k node per cluster. So:

$${E}_{total}=k*L\left[{E}_{elect}*\left(\frac{N}{k}\right)+k*{E}_{a}+2{E}_{elect}+{\varepsilon }_{mp}*{D}_{avg}^{4}+{\varepsilon }_{fs}*{\left(\frac{N}{k}*{d}_{avg}\right)}^{2}\right]$$

(37)

By taking the derivative in terms of k in Formula (37), the number of proper clusters (${k}_{opt})$ is obtained.

For example, assume 100 nodes are randomly distributed in a square area of 120 * 120 m². Let the size of the grid length is equal to 40 * 40 m². So:

$${E}_{total}=k*L\left[{E}_{elect}*\left(\frac{100}{k}\right)+\mathrm{k}*{E}_{a}+2{E}_{elect}+{\varepsilon }_{mp}*{\left(0.5214*120\right)}^{4}+{\varepsilon }_{fs}*{\left(\frac{100}{k}*0.36869*40*\sqrt{2}\right)}^{2}\right]$$

With respect to the simulation parameters (see Table 1) and k, ${k}_{opt}$ is equal to 13. Therefore, the initial grid proposes 13 proper clusters. In the next section, we will discuss the clustering process with respect to ${k}_{opt}$ and the selection of cluster centers. The cluster centers are based on the nodes’ density.

Table 1 Simulation parameters

4.2 Clustering Process

4.2.1 Pre-clustering

Assume that N sensor nodes have been distributed randomly, independently, and uniformly in a square area L * L. At first, the network area is divided into cells (or grids) and the side length of the grid is calculated by the following equation:

$${L}_{g}=\alpha \bigg(\prod_{i=1}^{d}{\bigg(\frac{{h}_{i}-{l}_{i}}{n}\bigg)\bigg)}^\frac{1}{d}$$

(38)

where d and n are the dimensions of the area and the number of distributed nodes in the network, respectively. Since the distribution area is two-dimensional, d is equal to 2. ${l}_{i}$ and ${h}_{i}$ are the beginning and the end of the area. For example, if the nodes have been distributed in the square area measuring 0*120, then ${l}_{i}$ and ${h}_{i}$ are 0 and 120, respectively. α is the adjustment parameter of the grid side and is defined as follows:

$$\alpha =\frac{{h}_{i}}{{k}_{opt}}$$

(39)

We consider the density of each cell (or grid) equal to the number of nodes in each grid. Therefore:

$${p}_{g}=Count(n)$$

(40)

Now, with respect to ${k}_{opt}$, we reduce the number of cells to ${k}_{opt}$. This state is called the merge phase. In the merge phase, the total number of cells is reduced to ${k}_{opt}$. In other words, after the merge phase, the number of final cells will be equal to ${k}_{opt}$.

In the merge phase, the cells with the highest ${p}_{g}$ are selected. The number of choices (${p}_{g}$) will be according to ${k}_{opt}$. These cells are called "candidate cells" and the centers of gravity of the nodes in these cells (${\mathrm{X}}_{\mathrm{g}}$, ${\mathrm{Y}}_{\mathrm{g}}$) are calculated according to the following relations:

$${X}_{g}=\frac{\sum_{i=1}^{{n}_{g}}{x}_{i}}{n}$$

(41)

$${Y}_{g}=\frac{\sum_{i=1}^{{n}_{g}}{y}_{i}}{n}$$

(42)

where ${x}_{i}$ and ${y}_{i}$ are node coordinates and ${n}_{g}$ is the number of sensor nodes in each cell. After calculating the centers of gravity, the distance between nodes in adjacent grids to the centers of gravity of candidate grids is calculated. Any node in the adjacent grids which has the smallest distance to the gravity centers of the candidate grids will be a member of the grid. This phase is called pre-clustering. For example, suppose the energy model proposes ${k}_{opt}$ = 5. Therefore, five candidate cells are: 4, 6, 11, 1, and 10. Centers of gravity in five candidate cells are calculated and the nodes of adjacent cells are appropriated to proper candidate cells according to the nearest distance to the centers of gravity of each candidate cell. Note that the output of the pre-clustering phase is to create cells to the number of ${k}_{opt}$. In the following, we discuss the final density-based clustering process.

4.2.2 Density-Based Clustering

In this section, we describe the final density-based clustering process. Let ${x}_{i}$, $\rho$, and ${\delta }_{i}$ are two-dimensional coordinates of each sensor node, local density function, and distance function, respectively. We show the distance between two points ${x}_{i}$ and ${x}_{j}$ with ${d}_{ij}$. The local density function is defined as follows:

$${\rho }_{i}=\sum_{j}\aleph \left(x\right)=\sum_{j}\aleph \left({d}_{ij}-{d}_{c}\right)$$

(43)

where ${d}_{c}$ is crossover distance between two points. In the proposed algorithm, ${d}_{c}$ is the maximum distance between a node with other nodes. If the number of nodes is low, then ${\rho }_{i}$ is defined by the Gaussian kernel function as follows:

$${\rho }_{i}=\sum_{j}{e}^{\bigg(-\frac{{d}_{ij}^{2}}{{d}_{c}^{2}}\bigg)}$$

(44)

The distance function is defined as:

$${\delta }_{i}=\left\{\begin{array}{c}\mathrm{max}\left({d}_{ij}\right): if {\rho }_{i}>{\rho }_{j}\\ \mathrm{min}\left({d}_{ij}\right) otherwise\end{array}\right.$$

(45)

After calculating ${\rho }_{i}$ and ${\delta }_{i}$, any node with the largest value $\Vert {\delta }_{i}-{\rho }_{i}\Vert$ has a better position than local density. So, it is selected as the center of the cluster. Note that ${d}_{ij}$ is based on a matrix called the adjacency matrix.

4.2.3 Cluster Head Selection

In this section, by using a new tree structure and six criteria including the residual energy of the node, node distance to the BS, density (ρ), δ, node distance to the center of gravity in each cluster, and $\Vert {\delta }_{i}-{\rho }_{i}\Vert$ value, the cluster head is selected. The advantage of the new cluster head selection is to elect the original CH and the successor CH in each cluster. Upon completion of the energy of the original CH, the successor CH is substituted. The entropy and information gain are other criteria that play a significant role in our proposed approach. These two criteria increase the accuracy of the CH selection. For each node in the cluster, a table called the decision table is formed. It has six introduced criteria. Then the decision table is normalized and is calculated the entropy of each parameter. Entropy is calculated by using the following equation:

$$Entropy\left(D\right)=-\sum_{i=1}^{c}{p}_{i}*{\mathrm{log}}_{2}{p}_{i}$$

(46)

In Eq. (46), D and C are set of cluster members and the number of clusters, respectively. ${p}_{i}$ is the probability of belonging of nodes to their clusters. Information gain is defined as follows:

$$Information Gain\left(A\right)=Entropy\left(D\right)-{Entropy(D)}_{A}$$

(47)

$${Entropy\left(D\right)}_{A}=\sum_{j=1}^{v}\frac{\left|{D}_{j}\right|}{\left|D\right|}*{Entropy\left(D\right)}_{y}$$

(48)

where v is the member's number of A and ${D}_{j}$ is a part of the initial nodes for which A is equal to ${v}_{\mathrm{j}}$. In the NEMOCED algorithm, the highest amount of information gain will be considered.

There are three phases to calculate the entropy. In the first phase, the decision table is formed according to the six introduced criteria. The computations of the six criteria have been discussed in the previous sections. In the second phase is performed the normalization of the decision table. Normalization uses the simple normalization method (or arithmetic normalization). The equation of simple normalization is defined as follows:

$${p}_{ij=}\frac{{X}_{ij}}{\sum_{i=1}^{m}{X}_{ij}} , j=\mathrm{1,2},\dots ,n$$

(49)

In Eq. (49), ${\mathrm{X}}_{\mathrm{ij}}$ is a parameter that must be normalized. Also, m is the number of nodes in the decision table (or the number of nodes in each cluster).

In the third phase, the entropy of each parameter is calculated by using the following equation:

$${E}_{j}=-k\sum_{i=1}^{m}{p}_{ij}*{\mathrm{log}}_{2}{p}_{ij}, \quad \mathrm{i}=1, 2, \dots ,\mathrm{ n}$$

(50)

where k is the entropy value of each parameter and is defined as follows:

$$k=\frac{1}{{\mathrm{log}}_{2}m} 0\le k\le 1$$

(51)

After performing the three phases, the parameters of the decision table are labeled. This work is performed to the BS and its base table (BT).

$${E}_{Rs}=\left\{ \begin{array}{ll}LOW & \quad {E}_{Rs}\le min \\ MEDIUM & \quad min{<E}_{Rs}\le Avg\\ HIGH & \quad {E}_{Rs}>Avg\end{array}\right.$$

(52)

$${d}_{BS}=\left\{ \begin{array}{ll}NEAR & \quad {d}_{BS}\le min \\ AVERAGE & \quad min{<d}_{BS}\le Avg\\ FAR & \quad {d}_{BS}>Avg\end{array}\right.$$

(53)

$$\rho =\left\{ \begin{array}{ll}LOW & \quad \rho \le min \\ MEDIUM & \quad min<\rho \le Avg\\ HIGH & \quad \rho >Avg\end{array}\right.$$

(54)

$$\delta =\left\{ \begin{array}{ll}GOOD & \quad \delta \le min \\ FAIRLY GOOD & \quad min<\delta \le Avg\\ BAD & \quad \delta >Avg\end{array}\right.$$

(55)

$${d}_{g}=\left\{ \begin{array}{ll}NEAR & \quad {d}_{g}\le min \\ AVERAGE & \quad min<{d}_{g}\le Avg\\ FAR & \quad {d}_{g}>Avg\end{array}\right.$$

(56)

$$\Vert {\delta }_{i}-{\rho }_{i}\Vert =\left\{ \begin{array}{ll}LOW & \quad \Vert {\delta }_{i}-{\rho }_{i}\Vert \le min \\ MEDIUM & \quad min<\Vert {\delta }_{i}-{\rho }_{i}\Vert \le Avg\\ HIGH & \quad \Vert {\delta }_{i}-{\rho }_{i}\Vert >Avg\end{array}\right.$$

(57)

In the above equations, min and max are the smallest amounts and the average value in the decision table, respectively. The main task of the decision table is to identify the successor CHs. The original and successor CHs are determined by the new tree structure. To better understand, we show the details of the CH selection with two examples at Appendix 2.

5 Simulation Results

In this section, we present the results of the proposed method. The proposed NEMOCED algorithm has been evaluated using MATLAB and is compared with other protocols namely LEACH, ENEFC HRML, ADCAPTEEN, MOFCA, MT-CHR, C-DTB-CHR-ADD, EEGBR, ERP, OCM-FCM, and FUZZY-TOPSIS by the same initial values and the scenario with different parameters. Each sensor has initial energy of 0.5 J and is randomly distributed in the square n * n. The simulation parameters are summarized in Table 1.

The efficiency of the proposed algorithm is evaluated in the following cases, and its results are compared with previous works:

• 1. Network lifetime

• 2. The number of cluster heads (or clusters) and selection of them in high-density and low-density regions.

• 3. The Residual energy in each round and each cluster

• 4. Determining the number of clusters using the new energy model, network size, and the number of nodes

• 5. Measuring the quality and accuracy of clustering

5.1 Network Lifetime

One of the NEMOCED goals is reducing energy consumption and increase network lifetime. First Node Die (FND) and Last Node Die (LND) are two main parameters in network lifetime. Figure 3 illustrates the network lifetime compared to similar methods. Figure 4 indicates FND and LND in the NEMOCED and other approaches. From Figs. 3 and 4 it is clear that the NEMOCED protocol has a better lifetime than similar methods.

Fig. 3

Network lifetime in NEMOCED protocol and similar methods

Fig. 4

FND and LND parameters in the NEMOCED protocol and similar methods

5.2 Number of Cluster Head

If the distribution of nodes is random, then more nodes may be located in some areas. Therefore, more cluster heads should be selected so that energy consumption and the loss percentage of nodes in the high-density regions can be well balanced. Figure 5 shows how to choose the original and successor CHs over 160 rounds. From Fig. 5, it is clear that the selection of the original and successor CHs has a proper balance in the environment. Figure 6 indicates the random distribution of 200 nodes, the high-density areas, and selected CHs. As Fig. 6 indicates, in high-density areas more CHs have been selected. The relation given in the preceding sections for calculating the number of clusters (relation 37) is based on the number of nodes and the network size. This is an advantage because, in most of the presented methods, the number of clusters (or cluster heads) is determined only by the number of nodes or network size. Also, in some methods such as k-means and C-means clustering, the number of clusters is predetermined. In the proposed method, if the network size is constant but the number of nodes in the network increases, then the number of proper clusters does not increase significantly and will increase by a small ratio. For example, in a network of (120 × 120) m² with 100 nodes, the proper cluster number is 13. If there are 120 nodes in the same network, then the proper number of clusters will be equal to 15. Similarly, if the number of nodes is 50, then 7 clusters are suggested. In other words, the number of clusters in a network with 50 nodes is approximately equal to half of the proposed clusters with 120 nodes. This means that the proposed algorithm has high accuracy. Table 2 shows the various comparisons between different states. Figure 7 illustrates the effect of increasing the number of nodes and increasing the network size on the proper number of clusters, ${\mathrm{D}}_{\mathrm{avg}}$, and ${\mathrm{d}}_{\mathrm{avg}}$. From Fig. 7, it is clear that with increasing the number of nodes and the size of the network simultaneously, the number of proper clusters has been increased.

Fig. 5

FND and LND parameters in the NEMOCED protocol and similar methods

Fig. 6

a Random distribution of nodes, b-High density regions and c-Cluster heads selection in high density regions

Table 2 ${K}_{opt}$ estimation based on network size, node’s number, ${d}_{avg}$, and ${D}_{avg}$

Fig. 7

The effect of the network size and nodes’ number on ${K}_{opt}$

5.3 Residual Energy

If at the end of each round the amount of the residual energy is high, then the total lifetime will be better. One of the important advantages of the proposed method is that the residual energy level is more uniform than other methods. Figure 8 indicates the amount of residual energy per 1000 rounds of the proposed protocol compared with similar methods. As Fig. 8 shows, the residual energy in the NEMOCED protocol is better. It is due to the presence of successor CHs.

Fig. 8

The residual energy in the NEMOCED and other methods based on the round’s numbers

5.4 The NEMOCED Evaluation

We evaluate the proposed method performance by using the confusion matrix. In general, if the number of clusters is k, the confusion matrix will be k * k. The confusion matrix for n clusters has been defined in Table 3.

Table 3 Confusion matrix

In the confusion matrix, the principal diagonal elements represent the number of nodes that are properly clustered. For example, a₁ and b₂ are the number of nodes the actual clusters of them are A and B respectively and are correctly located in these clusters. The elements on the secondary diagonal elements are the number of nodes that are not properly clustered. For example, b₁ is the number of nodes that its actual cluster is A, but they have been mistakenly located in cluster B.

According to the confusion matrix, the sum of the quantities in the secondary and principal diagonal elements is the number of correct and incorrect cases in the proposed clustering method, respectively. In order to proper clustering method, the matrix elements that are not in the principal diameter should have a value close to zero. We propose five criteria namely accuracy, error rate, sensitivity, specificity, and precision in the proposed method for evaluating the clustering model. All criteria are defined according to the confusion matrix. The accuracy criterion is defined as follows:

$$Accuracy=\frac{sum \, of \, the \, principal \, diagonal \, elements \, of \, confusion \, matrix}{sum \, of \, the \, confusion \, matrix \, elements }=\frac{{a}_{1}+{b}_{2}+\dots +{p}_{k}}{\sum_{{\varvec{i}}=1}^{{\varvec{n}}}{({\varvec{a}}}_{{\varvec{i}}}+{{\varvec{b}}}_{{\varvec{i}}}+\dots +{{\varvec{p}}}_{{\varvec{i}}})}$$

(58)

In fact, the accuracy of the proposed algorithm is equal to the percentage of nodes that are properly clustered. By subtracting this value from 1, the error rate of the model is obtained (Eq. 59).

$$Error Rate\hspace{0.17em}=\hspace{0.17em}\frac{sum \, of \, the \, secondary \, diagonal \, elements \, of \, confusion \, matrix}{sum \, of \, the \, confusion \, matrix \, elements }=\frac{{p}_{1}+\dots +{a}_{k}}{\sum_{{\varvec{i}}=1}^{{\varvec{n}}}{({\varvec{a}}}_{{\varvec{i}}}+{{\varvec{b}}}_{{\varvec{i}}}+\dots +{{\varvec{p}}}_{{\varvec{i}}})}$$

(59)

Other criteria are sensitivity and specificity. A proper trade-off between these two criteria can be helpful. These two criteria are defined as follows:

$$sensitivity=\frac{{a}_{1}}{{a}_{1}+{b}_{1}+\dots +{p}_{1}}$$

(60)

$$specificity=\frac{{p}_{k}}{{a}_{k}+{b}_{k}+\dots +{p}_{k}}$$

(61)

The last criterion is precision. This criterion is defined as follows:

$$precision=\frac{{a}_{1}}{\sum_{i=1}^{n}{a}_{i}}$$

(62)

We have used the five criteria above because any of the above criteria alone cannot guarantee the validity of the proposed algorithm. Therefore, the combination of the above criteria ensures the quality of the NEMOCED protocol. Figure 9 indicates the proposed clustering algorithm. As shown in Fig. 9, some of the nodes are not properly clustered. Table 4 shows the confusion matrix in the proposed method for Fig. 9.

Fig. 9

Clustering in the NEMOCED with 200 nodes. The blank circles represent clustering error. The nodes inside the blank circles are nodes that have been mistakenly located in the other clusters

Table 4 Confusion matrix in Fig. 9

According to Fig. 9 and Table 4, the five proposed criteria are calculated as follows:

$$accuracy=\frac{292}{300}=0.97, \quad error rate=1-0.97=0.03$$

$$sensitivity=\frac{35}{36}=0.972, \quad specificity=\frac{34}{35}=0.9714$$

$$precision=\frac{35}{37}=0.9459$$

As can be seen, the proposed clustering method has high accuracy and low error rate. Figure 10 illustrates the five criteria with different numbers of nodes.

Fig. 10

Five proposed criteria in the NEMOCED protocol with different nodes

6 Conclusion and Future Work

This paper presents a density-based clustering algorithm and a new energy model in wireless sensor networks. The new energy model determines the number of proper clusters based on the network size and the number of nodes. The NEMOCED protocol provides a new tree structure by which two CHs are identified in each cluster. The first type is the main CH, which is responsible for collecting cluster data and sending them to the BS. The second type is the successor CH that is a good successor to the main CH at the time of its energy termination. The CH selection is performed by using residual energy, node distance to the BS, density, δ, node distance to the center of gravity, and $\Vert {\delta }_{i}-{\rho }_{i}\Vert$ criterion. One of the strengths of the NEMOCED is that the choice of the main CH is based on the density of nodes. The clustering process is performed in two steps. In the first phase, environment density is evaluated using grids. In the second phase, clustering is performed based on local density. To validate the performance of the NEMOCED, we made a comprehensive comparison of the NEMOCED with some similar algorithms. The simulation considered different sensor and base station deployments and the various data aggregation ratios. The result shows that the NEMOCED can increase the network lifetime through the proper selection cluster head. To prove the efficiency of our proposed algorithm, we also considered several validation criteria to increase clustering accuracy. An extensive simulation has been performed to test the performance of the NEMOCED under different options. All the conclusions demonstrate that our proposed protocol is suitable and efficient for large-scale WSNs.

In the future, in addition to wireless sensor networks, the proposed protocol can also be used in classification and data mining. In future work, we will reduce base table rules (BS rules) using fuzzy logic to improve the efficiency of the proposed algorithm.

Appendices

Appendix 1: An Example for Calculating the Local Density of a Cluster According to the NEMOCED Algorithm

Assume that five nodes in a cell are in the coordinates a = (10,20), b = (5,7), c = (9,10), d = (15,20), and e = (30,35). The adjacency matrix ${d}_{ij}$, which indicates the Euclidean distance of nodes with each other is defined as follows:

According to the adjacency matrix, the local density for each node is:

$${\rho }_{a}=\sum_{j=1}^{5}{e}^{\left(-\frac{{d}_{1j}^{2}}{{d}_{c}^{2}}\right)}={e}^{\left(-\frac{{0}^{2}}{{25}^{2}}\right)}+{e}^{\left(-\frac{{13.9}^{2}}{{25}^{2}}\right)}+{e}^{\left(-\frac{{10}^{2}}{{25}^{2}}\right)}+{e}^{\left(-\frac{{5}^{2}}{{25}^{2}}\right)}+{e}^{\left(-\frac{{25}^{2}}{{25}^{2}}\right)}=3.9201$$

$${\rho }_{b}=\sum_{j=1}^{5}{e}^{\left(-\frac{{d}_{2j}^{2}}{{d}_{c}^{2}}\right)}=4.0523 {\rho }_{c}=\sum_{j=1}^{5}{e}^{\left(-\frac{{d}_{3j}^{2}}{{d}_{c}^{2}}\right)}=4.1399$$

$${\rho }_{d}=\sum_{j=1}^{5}{e}^{\left(-\frac{{d}_{4j}^{2}}{{d}_{c}^{2}}\right)}=3.6113 {\rho }_{e}=\sum_{j=1}^{5}{e}^{\left(-\frac{{d}_{5j}^{2}}{{d}_{c}^{2}}\right)}=3.2136$$

Since ${\rho }_{a}$ is smaller than ${\rho }_{b}$ and ${\rho }_{c}$, so the maximum value in the row of ${\rho }_{b}$ and ${\rho }_{c}$ is considered as ${\delta }_{a}$ (or ${\delta }_{a}=37.5$). Since ${\rho }_{c}$ is not smaller than any value, so the minimum value in the corresponding row is considered as ${\delta }_{c}$ (or ${\delta }_{c}=5$). The Other values are:

$${\delta }_{b}=32.6, {\delta }_{d}=37.5, {\delta }_{e}=37.5$$

The maximum value of $\Vert {\delta }_{i}-{\rho }_{i}\Vert$ is related to the nodes ${\rho }_{d}$ and ${\delta }_{d}$. Therefore, node d with coordinates (15, 20) is chosen as the center of the cluster. As can be seen, the coordinates of node d are closer to the center of gravity than the other nodes. Therefore, the proposed method has high accuracy in the selection of the cluster centers. After selecting the cluster centers and identifying them, nodes in other candidate grids are allocated to the corresponding cluster. This work is performed based on the proximity of the geographical distance.

Appendix 2

Example 1

Assume that five nodes are in a cluster with coordinates 1 = (5,6), 2 = (10,15), 3 = (9,11), 4 = (20,1) and 5 = (14,8). The nodes have the residual energy of 0.8 J, 0.4 J, 0.9 J, 0.7 J and 0.6 J, respectively. Also, assume that the BS is located at (100,100). As before, with the calculation of ${d}_{ij}$, the parameters $\rho$, δ and $\Vert {\delta }_{i}-{\rho }_{i}\Vert$ are defined as follows:

$${\rho }_{1}=3.5898 \quad {\delta }_{1}=17.2047 \quad \Vert {\delta }_{1}-{\rho }_{1}\Vert =16.6139 $$

$$ {\rho }_{2}=3.8196 \quad {\delta }_{2}=14.8661 \quad \Vert {\delta }_{2}-{\rho }_{2}\Vert =11.0465 $$

$${\rho }_{3}=3.9868 \quad {\delta }_{3}=4.12310 \quad \Vert {\delta }_{3}-{\rho }_{3}\Vert =0.13630 $$

$${\rho }_{4}=3.0308 \quad {\delta }_{4}=17.2047 \quad \Vert {\delta }_{4}-{\rho }_{4}\Vert =14.1739 $$

$${\rho }_{5}=2.8340 \quad {\delta }_{5}=17.2047 \quad \Vert {\delta }_{5}-{\rho }_{5}\Vert =14.3707 $$

Given the coordinates of the nodes, the center of gravity is (11.6, 8.2). Tables 5 and 6 are the decision and normalization tables, respectively.

Table 5 Decision table in Example 1

Table 6 Normalization table in Example 1

According to relations 52–57:

$$k=\frac{1}{{\mathrm{log}}_{2}5}=0.4307$$

$${Entropy\left(D\right)}_{{E}_{RS}}=0.9789$$

Similarly, entropy is calculated for other parameters. The last row in normalization and decision tables represents the average (Avg) and entropy. Also, min is the minimum value of each column. For example, the min value for the residual energy is 0.4. So, the residual energy in the decision table is labeled as follows:

$${E}_{Rs}=\left\{ \begin{array}{ll}LOW & \quad {E}_{Rs}\le 0.4 \\ MEDIUM & \quad 0.4{<E}_{Rs}\le 0.68\\ HIGH & \quad {E}_{Rs}>0.68\end{array}\right.$$

Other parameters are also labeled with the following functions. Table 7 illustrates the labeling of the decision table.

$${d}_{BS}=\left\{ \begin{array}{ll}NEAR & \quad {d}_{BS}\le 123.7942 \\ AVERAGE & \quad 123.7942{<d}_{BS}\le 127.5892\\ FAR & \quad {d}_{BS}>127.5892\end{array}\right.$$

$$\rho =\left\{ \begin{array}{ll}LOW & \quad \rho \le 2.8340 \\ MEDIUM & \quad 2.8340<\rho \le 3.4522\\ HIGH & \quad \rho >3.4522\end{array}\right.$$

$$\delta =\left\{ \begin{array}{ll}GOOD & \quad \delta \le 4.1231 \\ FAIRLY GOOD & \quad 4.1231<\delta \le 14.1207\\ BAD & \quad \delta >14.1207\end{array}\right.$$

$${d}_{g}=\left\{ \begin{array}{ll}NEAR & \quad {d}_{g}\le 2.4083 \\ AVERAGE & \quad 2.4083<{d}_{g}\le 6.2471\\ FAR & \quad {d}_{g}>6.2471\end{array}\right.$$

$$\Vert {\delta }_{i}-{\rho }_{i}\Vert =\left\{ \begin{array}{ll}LOW & \quad \Vert {\delta }_{i}-{\rho }_{i}\Vert \le 0.1363 \\ MEDIUM & \quad 0.1363<\Vert {\delta }_{i}-{\rho }_{i}\Vert \le 10.6685\\ HIGH & \quad \Vert {\delta }_{i}-{\rho }_{i}\Vert >10.6685\end{array}\right.$$

Table 7 Labeling of the decision table

As previously stated, the estimation of the candidate CHs is performed by BS and the base table. From the five nodes, three nodes have a "NO" label. Also, two nodes have a "YES" label. So, the total entropy is:

$$Entropy=-\frac{2}{5}{\mathrm{log}}_{2}\frac{2}{5}-\frac{3}{5}{\mathrm{log}}_{2}\frac{3}{5}=0.9710$$

To calculate the information gain, the entropy corresponding to all the values in the decision table must be calculated. So:

$${Entropy(E}_{RS})=Entropy\left(LOW\right)+Entropy\left(MEDIUM\right)+Entropy\left(HIGH\right)=0.5510$$

$${Entropy(d}_{BS})=Entropy\left(NEAR\right)+Entropy\left(AVERAGE\right)+Entropy\left(FAR\right)=0.5510$$

$$Entropy\left(\rho \right)=Entropy\left(LOW\right)+Entropy\left(MEDIUM\right)+Entropy\left(HIGH\right)=0.5510$$

$$Entropy\left(\delta \right)=Entropy\left(BAD\right)+Entropy\left(GOOD\right)=0.8$$

$${Entropy(d}_{g})=Entropy\left(NEAR\right)+Entropy\left(Medium\right)+Entropy\left(FAR\right)=0.5510$$

$$Entropy(\Vert {\delta }_{i}-{\rho }_{i}\Vert )=Entropy\left(LOW\right)+Entropy\left(HIGH\right)=0.8$$

On one hand, the difference of entropy and information gain in the residual energy, distance to the BS, density, and distance to the center of gravity is the greatest and on the other hand, one case must be selected. Therefore, by referring to the normalization table, ${d}_{g}$ is selected as the root of the tree. Since it has three labels, so the tree has three branches (see Fig. 11).

Fig. 11

Tree structure with three branches in example 1

By repeating the calculations for the right table in Fig. 11, the tree structure is converted into Figs. 12 and 13.

Fig. 12

Tree structure with three branches in example2 and based on Fig. 13

Fig. 13

Tree structure with three branches in example 1 and based on Fig. 12

Therefore, nodes 5 and 1 are selected as the original and successor CHs, respectively. As is clear, these two nodes are better than other nodes. In the process of selecting the cluster head and forming the tree, we may reach a phase that has not any improvement. This mode is when all the parameters of the labeling have the same characteristics and entropy. This mode is called “TRAP”. One of the basic conditions for stopping work is the Trap state. Example 3 illustrates this case.

Example 2

Assume that five nodes with coordinates 1 = (8,7), 2 = (20,10), 3 = (4,15), 4 = (15,1), 5 = (16,15), 6 = (3,20) and 7 = (13,17) with the residual energy of 0,8 J, 0.6 J, 0.5 J, 0.9 J, 0.7 J, 0.2 J and 0.3 J are in a cluster, respectively. Also, assume the BS is located at (100,100). As in Example 1, after forming the decision and normalization tables, the labeling table will be in the form of Table 8.

Table 8 Labeling of the decision table in Example 2

Other parameters are defined as follows:

$$k=\frac{1}{{\mathit{log}}_{2}5}=0.4307,\,\,Entropy\left(D\right)=-\frac{3}{5}{\mathit{log}}_{2}\frac{3}{5}-\frac{4}{5}{\mathit{log}}_{2}\frac{4}{5}=0.9852$$

$$Enropy\left({E}_{RS}\right) = 0.6935 \quad Entropy\left({d}_{BS}\right)=0.5714 \quad Entropy(\rho )=0.6935$$

$$Entropy\left(\delta \right) = 0.6935 \quad {Entropy(d}_{g})=0.7871 \quad Entropy(\Vert {\delta }_{i}-{\rho }_{i}\Vert )=0.6935$$

Figures 14, 15 and 16 illustrate the tree structure in example 2.

Fig. 14

Tree structure with three branches in example 2

Fig. 15

Tree structure with three branches in example 2 based on Fig. 14

Fig. 16

Tree structure with three branches in example 2 based on Fig. 15

As shown in Fig. 16, the TRAP mode has occurred. So, the algorithm does not continue. Therefore, nodes 5 and 3 are selected as main and successor CHs, respectively. Note that there may be more than one successor CH. We assume that the first proper node in the tree structure is selected as the main CH. The rest of the nodes are considered as the successor CH.

This mode happens in high-density clusters. In other words, if the cluster density is higher, then the number of the successor CHs will also be higher. Perhaps at first glance, the reader of this article believes that with the initial look at the labeled table or decision table, it would be possible to find the main and successor CHs. It should be noted that with the initial look at the labeled table in example 2, node 4 should be selected as the original CH because it has the most residual energy. This is a false choice because node 4 just has better residual energy and is worse than nodes 1 or 5 in other parameters such as density or distance to the center of gravity. This is one of the important differences between our proposed method with other proposed methods. Most of the proposed methods choose the CH only based on the residual energy.