1 Introduction

MIMO affords increased channel capacity and data throughput using multiple terminal antennas on both the base station and the subscriber end. MIMO, spatial multiplexing, multicell and massive communications are the eminent research theme for the next generation communication. In the last decade, MIMO received a considerable attention and research, since it can enhance the link reliability without forfeiting the bandwidth efficiency. Recently the concept of multi cell and massive MIMO attracted the interest of many researchers [1,2,3,4,5].

The demands for high data rate influences the deployment of multi cell MIMO and massive communication technology. For such systems, the need for simple decoding and low complexity design is extremely important. This would be achievable through linear decoders. Linear decoders have been well researched in the last decades. Essentially, ZF and MMSE linear precoders are the basic linear detection systems. This types of decoders have been investigated in the literature before. However, the employment of these detectors in the new proposed wireless concept is inevitable. In [4], The performance of a single cell massive MIMO is considered, for multi user massive OFDM MIMO system. The linear precoding complexity issues and reduction issues have been investigated in [6]. In [5], cognitive idea for MIMO systems was considered, and the performance analysis of cooperative networks is also presented.

In most of these linear precoding schemes, one should note that the accuracy of these linear detectors depends heavily on the accuracy of the Channel State Information CSI. For multiuser systems, the base station uses the estimated CSI from the pilot uplink channel and feed them to the linear decoders. These CSI values can be found through interpolation methods. The effects of regression based interpolation of CSI on the linear precoding devices in the downlink channel were addressed in the literature. The performance of a binary input non fading channel has an exact formula for the BER and can be found in [7]. Currently, research is significantly revolving around the SER performance of massive MIMO in different scenarios. In [8], the SER of the ZF and MMSE decoders is carried out. Other performance metrics such as asymptotic properties of the linear precoces are available in [9]. However, the performance was measured under Gaussian noise assumption, and to justify this assumption, the central limit theorem is usually used.

In many physical channels, such as urban, indoor radio channels and underwater acoustic channels, the ambient noise is known to be non-Gaussian, due to impulsive man-made electromagnetic interference. This led to further research on impulsive channels, and the demodulation of these signals [10, 11]. In this paper, we examine the performance of multi cell MIMO systems under non-Gaussian noise assumption. In the literature, the impulsive noise has drawn the attention of many researchers. A research that considers the impact of impulsive noise on wireless systems was conducted in [12,13,14].

The performance of MIMO techniques over fading channels and impulsive noise is a well researched topic in the literature. The degradation of the signal to noise ration (SNR) and Symbol Error Rate (SER) in Orthogonal Frequency Division Multiplexing (OFDM) receivers under impulsive noise is investigated in [15, 16]. The design of optimum receivers over fading channels and impulsive noise has been well studied in the literature. However, the performance of these receivers in a massive MIMO system was not conducted. In this paper, the issue under scrutiny is the topic of non Gaussian channels in multicell MIMO systems. In addition to that, we propose a simple decoder that does not necessitate matrix inversion.

The ZF and MMSE precoders require matrix inversion calculations. This will make the complexity issue substantial. In [17], the computational complicity of a massive MIMO is addressed. The close to optimal and efficient regularized zero forcing precoder is replaced by a truncated polynomial expansion (TPE) precoder, hence, RZF requires fast inversion of large matrices in a coherence period. Obviously this is a very sophisticated implementation. For multiuser MIMO where interference is known at the transmitter, the precoder is utilized to remove these effects. The main drawback of such a coding system is the increased complexity, both at the receiver and transmitter end, see [18]. For cases where users are equipped with single antenna and multi antenna base station system, efficient algorithms based on optimum joint beamforming are proposed, as in [19, 20].

In [18], more general problems were also considered, for example, users could have multiple antenna system. Some methods employ successive interference cancellation for cancelling out the interference term, other methods include beamforming at the receiver. Different algorithms for choosing the downlink transmit vectors using block digonalisation have been also addressed. They are mainly a generalization of the channel matrix inversion and can be applied to throughput maximization or power control problems. In this paper, we study and propose the Newton’s method for solving the Newton’s equation of matrices. More precisely, we use the iterative Newton technique that solves the problem of finding the matrix inversion iteratively. We also investigate the convergence of this method and show that it converges to proper values. We finally replace the matrix inversion step of ZF and MMSE precoders with our proposed iterative solution.

The organization of this paper is as follows: The multicell MIMO signal components are stated in Sect.2, which describes the precoding detection technique in massive MIMO systems, and we clearly explain the system and noise models. Section 3 furnishes the derivation of the probability of error expressions for the ZF and MMSE receivers in non Gaussian noise. Section 4 demonstrates the derivation of the sum rate analysis. In Sect. 5, we explain the proposed simple ZF detector, and work on some derivations to proof the convergence of the system. Section 6 shows the numerical evaluations and simulation results. Conclusions are stated out in the last Section. Before we start the system model, we use the notations below to simplify the reading of this research article.

1.1 Notations

The transpose of a matrix \(\mathbf {A}\) is denoted by \(\mathbf {A}^t\), and the hermitian of the matrix is denoted by \(\mathbf {A}^H\). The bold case represents matrix or vectors. The operator \(\Vert \Vert\) is denoting the norm of the matrix. The \([\mathbf {A}]_k\) stands for the kth row of the matrix \(\mathbf {A}\). \(\mathbf {A}_{i,j}\) is the (i, j)th component of the matrix \(\mathbf {A}\). The operation E[x] is the expectation of the random variable x. \(*\) stands for the complex conjugant.

2 System Model

In Multi cell and massive MIMO systems, the mobile or user equipment terminal is connected to more than one cell at a time. This can be observed by looking at Fig. 1. We consider a system that has L number of cells, the number of users in the system is denoted by K, and it is assumed to be less than the number of the antennas at the base stations (\(K \le M)\). All of the users mobile terminals are single antenna system. The channel model is assumed to split into two parts. The first one stands for the pathloss and shadowing effect, and it is denoted by \(\beta _{ljk}\), where \(\beta _{ljk}\) is the channel gain of the kth user from jth cell to cell l. The second channel gain part is the fading one. By resting on this assumption the model is described as the fading coefficient from the kth user of the jth cell to the mth base station antenna of the lth cell. And denoted by \(h_{kmjl}\). The channel is assumed to change slowly and remains constant over the transmission of one symbol duration. But changes from symbol to symbol. We also assume that the channel is known to all base stations and users. Moreover, the fading gain is assumed to be independent and identically distributed (i.i.d) zero mean unit variance circularly symmetric complex Gaussian random variable (C(N(0, 1))). Considering all of the above assumptions, the transmit receive equation for the lth cell can be given as:

$$\begin{aligned} {\mathbf {y}_l}=\sqrt{\rho _u}\sum _{i=1}^L\mathbf G _{l,i}{\mathbf {x}_i} +{\mathbf {W}_l}, \end{aligned}$$
(1)

where \({\mathbf {y}_l}\) is the received complex vector of dimension M for the lth base station. \(\rho _u\) is the received SNR. \({\mathbf {x}_i}\) is a K dimensional vector, carrying the transmitted signals for the users in cell i. The kth component represent the kth user. \(\mathbf G _{l,i}=(g_{limk})_{M \times K}\), is a matrix that has a size of \(M \times K\) and denotes the channel gains between the lth base station and the K users in the ith cell. \(l,i=1,2,\ldots ,L\). So that the (m, k)th component of \((g_{limk})\) is the channel coefficient between the mth antenna of the lth cell, and the kth user of the ith cell. Finally, we can represent \((g_{limk})\) as follows:

$$\begin{aligned} g_{limk}&\,=\, h_{limk} \sqrt{ \beta _{lik} } , \end{aligned}$$
(2)
$$\begin{aligned} \mathbf {G}_{li}&\,=\, \mathbf {H}_{li} {\mathbf {\beta }}_{li}, \quad l,i=1,2,\ldots ,L, \end{aligned}$$
(3)
$$\begin{aligned} \mathbf {\beta }_{li}&= diag(\sqrt{\beta _{li1}},\sqrt{\beta _{li2}},\ldots , \sqrt{\beta _{liK}}), \end{aligned}$$
(4)

where \(\mathbf H _{l,i}=(h_{limk})_{M \times K}\). Furthermore, we describe the noise model in the system. In this research, we put forward the assumption that the noise term \({\mathbf {W}_l}\) is non Gaussian noise, and follows Middleton’s class-A model distribution and we ignore the relevant interference term hence our main objective is the noise effect on the over all performance of the system. The noise mainly is an infinite expansion of Gaussian density functions with different variances and identical means, [21]. We assume that each noise sample \(w = w_g + w_i\), is the superposition of a background Gaussian component \(w_g\), and impulsive part \(w_i\), with \(X={\mathrm {var}}(w_g)/{\mathrm {var}}(w_i)\), holds their power ratio. The probability density function (PDF)of Middleton’s class-A model complex valued noise can be expressed as:

$$\begin{aligned} p(w_p)=\sum _{m=0}^\infty \frac{\alpha _m}{\pi \sigma _m^2}e^{\left( -\frac{|w_p|^2}{\sigma _m^2}\right) }, \end{aligned}$$
(5)

where \(\alpha _m=\frac{Z^m}{m!}exp(-Z)\), \(\sigma _m^2=\sigma ^2(m/Z+X)/(X+1)\), and \(\sigma ^2={\mathrm {var}}(w_p)\). X represents the power ratio of the background Gaussian noise and the impulsive one. Z is the impulsive index. It results in an impulsive \(w_i\) for small values of Z, and a near-Gaussian when Z is large [22, 23]. As can be observed from its pdf in (5), the noise \(w_p\) is not Gaussian. However, the class-A noise can be viewed as conditionally Gaussian, and called as compound Gaussian. Therefore, \(w_p\) , when conditioned on a Poisson random variable \(Y_p\) with parameter Z, is Gaussian with zero mean and variance given by:

$$\begin{aligned} v_p={\mathrm {var}}(w_p/Y_p)=\sigma ^2\left( \frac{Y_p}{Z(X+1)}+\frac{X}{X+1}\right) , \end{aligned}$$
(6)

The variance of the noise \(w_p\) can be easily found by taking the expectation of (6) with respect to the random variable \(Y_p\) using the fact that \(E(Y_p=Z)\). The random variable \(Y_p\) dominates the impulsive occurrence, if \(Y_p>0\) the impulsive part is present, but if \(Y_p=0\) it is not. Finally, we shall specify the joint distribution of the conditional variances \(v_1,\ldots ,v_{M}\), which find out the joint distribution of \(w_p\). In this case two approaches can be used, one assumes that \(v_p, \quad p=1,2,\ldots , M\) are i.i.d random variables, and the second approach assumes that \(v_1= v_2=\cdots = v_{M}\), and \(v_p\) is related to a single Poisson random variable, This assumption is valuable when the different receive antennas are influenced by the same physical process creating the impulse, thereby making the conditional variance \(v_p\) of each receive antenna the same. This might be an accurate model for a multi-antenna system where the antenna elements spaced close together distance. Mathematically, \(w_1,\ldots ,w_{M}\) will be statistically dependent, but uncorrelated [24]. This model is referred to the spherically invariant noise model and was used in [25]. The joint distribution of the noise samples \(\mathbf w =[w_1,\ldots , w_{M}]\) is:

$$\begin{aligned} p(\mathbf w )=\sum _{m=0}^\infty \frac{\alpha _m}{({\pi \sigma _m^2})^{M}}e^{\left( - \sum _{p=1}^{M}\frac{|w_p|^2}{\sigma _m^2}\right) }, \end{aligned}$$
(7)
Fig. 1
figure 1

Multicell MIMO model

Full size image

Impulsive noise (commonly termed shot or man-made noise) has features quite dissimilar to Gaussian noise, and its corrupting effect on any wireless digital communication system can be substantial due to its volatile characteristics. Furthermore, W-CDMA and wide band signals can be significantly degraded due to the wideband nature of impulsive noise interference. In a W-CDMA system for example, mobile users power is controlled by the base stations while shot noise power is out of control, This indeed one of the real life scenarios for wireless communications. The impulsive scenario in some cases is caused by source of undesired emissions, The effect will depend on the distance between base stations and the sources. The most interesting situation is the urban one because it is categorized by a very high density of users and impulsive noise sources such as cars and motorcycles. In this particular scenario, the impulsive noise level can be several dBs higher than users signal level in the base station receiver. Therefore, BER performance can be dramatically degraded in the presence of shot noise interference.

3 System Performance

By now, we have completed the description of the system and the noise model. In the coming discussion, we study and analyze the ZF and MMSE performance under the aforementioned assumptions. We further assume that the lth base station knows the matrices \(\mathbf {G}_{ll}\) but not \(\mathbf {G}_{li}\) for \(i=1,2,\ldots ,L, i \ne l\). The number of antennas is larger than the number of users. Therefore, the ZF acts as a precoding linear system with matrix multiplication. This precoding matrix can be written as:

$$\begin{aligned} \mathbf {G}_{ll}^{ZF}=\left( \mathbf {G}_{ll}^{H}\mathbf {G}_{ll}\right) ^{-1}\mathbf {G}_{ll}^{H} , \end{aligned}$$
(8)

By using Eq. (8) and multiply it by Eq. (1) we can write the following:

$$\begin{aligned} \mathbf {G}_{ll}^{ZF}*{\mathbf {y}_l}&\,=\, \mathbf {G}_{ll}^{ZF}*[\sqrt{\rho _u}\sum _{i=1}^L \mathbf G _{l,i}{\mathbf {x}_i}+{\mathbf {W}_l}]\nonumber \\&\,=\,\sqrt{\rho }\mathbf {x}_l+\sqrt{\rho }\sum _{i\ne l}^{L}\mathbf {G}_{ll}^{ZF}\mathbf {G}_{li}\mathbf {x}_i+\mathbf {G}_{ll}^{ZF}\mathbf {W}_l, \end{aligned}$$
(9)

we can extract the information of the kth user signal from the total received vector as:

$$\begin{aligned} r_{lk}=\sqrt{\rho }{x}_{lk}+\sqrt{\rho }\sum _{i\ne l}^L\left[ \mathbf {G}_{ll}^{ZF}\right] _k\mathbf {G}_{li}\mathbf {x}_i+\left[ \mathbf {G}_{ll}^{ZF}\right] _k\mathbf {W}_l, \end{aligned}$$
(10)

We can clearly see that the term \([\mathbf {G}_{ll}^{ZF}]_k\mathbf {W}_l\) is projecting some noise enhancement effect on the ZF coding scheme. This indeed, would be mitigated through some precoding technique. For instance, we employ the matrix \(\mathbf {G}_{ll}^{ZF}\) as a precodnig matrix (before we transmit the signal). This will avoid the noise amplification problem. Recalling that the noise term generally follows the distribution as in the foregoing section. For now, let us study the signal in Eq. (10). To do so, we first should detect the data in the signal. Hence, we decode it using maximum likelihood concept, as it is one of the most powerful detection algorithms. First, we rewrite the signal in Eq. (10) with the noise term combined as discussed above, then we find the mean of the signal as:

$$\begin{aligned} r_{lk}&\,=\, \sqrt{\rho }{x}_{lk}+\sqrt{\rho }\sum _{i\ne l}^L\left[ \mathbf {G}_{ll}^{ZF}\right] _k\mathbf {G}_{li}\mathbf {x}_i+{W}_l, \end{aligned}$$
(11)
$$\begin{aligned} E[r_{lk}]&\,=\, E\left[ \sqrt{\rho }{x}_{lk}+\sqrt{\rho }\sum _{i\ne l}^L\left[ \mathbf {G}_{ll}^{ZF}\right] _k\mathbf {G}_{li}\mathbf {x}_i+{W}_l\right] \nonumber \\&\,=\, E\left[ \sqrt{\rho } x_{ik} \right] +\sqrt{\rho }\sum _{i\ne l}^L E\left[ \left[ \mathbf {G}_{ll}^{ZF}\right] _k\mathbf {G}_{li}\mathbf {x}_i \right] +E[W_l] = \sqrt{\rho }x_{ik}, \end{aligned}$$
(12)

The second step is to find the variance. To evaluate the variance of the received signal, we need to find the expression \(E\left[ (r_{lk} -E(r_{lk})(r_{lk} -E(r_{lk}) ^* \right]\). Then we can write the following:

$$\begin{aligned}&E\left[ (r_{lk} -E(r_{lk})(r_{lk} -E(r_{lk}) ^* \right] = E\left[ (r_{lk} -\sqrt{\rho }x_{ik})(r_{lk} -\sqrt{\rho }x_{ik}) ^*\right] \nonumber \\&\quad =\rho E\left[ \sum _{i \ne l} \sum _{j \ne l} \left[ \mathbf {G}_{ll}^{ZF}\right] _k\mathbf {G}_{li}\mathbf {x}_i \mathbf {x}_j^H \mathbf {G}_{lj}^H\left[ \mathbf {G}_{ll}^{ZF}\right] _k^H \right] +E\left[ \left[ \mathbf {G}_{ll}^{ZF}\right] _k \mathbf {W}_l\mathbf {W}_l^H\left[ \mathbf {G}_{ll}^{ZF}\right] _k^H \right] , \end{aligned}$$
(13)

After further manipulations we can make use of the result in [8]. We use the result that was found for Gaussian noise, then we average it with respected to the new distribution of our noise model. This will furnish the lower and upper part bound on the SER performance. So, let us write the error rate probability for 2 code words system. We start by the upper bound as:

$$\begin{aligned} P_e\le \frac{1}{4} \sum _{t=1}^2 \left( 1+\frac{\rho | \varDelta x_{ik}|^2\beta _{llk}}{4(1+\rho u_{l,t})} \right) ^{-(M-K+1)}, \end{aligned}$$
(14)

where \(\varDelta x_{ik}=x_{ik}^2-x_{ik}^1\), and (\(x_{ik}^2, x_{ik}^1\)) are the kth components of (\(\mathbf {x}_{l}^1 , \mathbf {x}_{l}^2\)). \(u_{l,t}= \sum _{i \ne l} \sum _{s=1}^K \beta _{lis} |x_{i,s}^t|^2\). Now, we will average the expression given in Eq. (14) with respect to the noise distribution. Substituting the term SNR \((\sqrt{\rho } =\frac{1}{\sqrt{v_l}})\), where \(v_l\) is the noise variance. This means that we fix the signal power to unity and change the variance amplitude, then the SNR is found accordingly. We assume the worst case scenario. In other words, in a multi antenna system having M antennas, we assume the highest noise variance to occur at all the branches \(v_l=v_{max}. \quad l=1,2,\ldots , M\). Now taking the expectation of both side of Eq. (14) we can write the below:

$$\begin{aligned} E_{v_{max}}(P_e|v_{max})= & {} \sum _{v_{max}} P(v=v_{max})(P_e|v_{max}), \quad {\mathrm {then}} , \end{aligned}$$
(15)
$$\begin{aligned} P_e\le & {} \sum _{v_{max}} \frac{1}{4} \sum _{t=1}^2 \left( 1+\frac{\rho | \varDelta x_{ik}|^2\beta _{llk}}{4(1+\rho u_{l,t})} \right) ^{-(M-K+1)} P(v=v_{max}), \end{aligned}$$
(16)

As we can observe, we need to find an expression for \(P(v=v_{max})\), then the derivation would be completed. Recalling the definition of \(v_{max}\), we assumed it is the worst case scenario, and the maximum noise variance would happen at all antennas. Then it is simply the maximum of i.i.d random variables given in Eq. (11), and can be computed as:

$$\begin{aligned} P\left( \sigma _{m}^2=\sigma _{max}^2\right) =\left( \sum _{k=0}^ne^{-A}\frac{A^k}{k!}\right) ^{M}- \left( \sum _{k=0}^{n-1}e^{-A}\frac{Z^k}{k!}\right) ^{M}, \end{aligned}$$
(17)

Using Eq. (15) and substituting Eqs. (16) and (17) the upper bound equation is derived.

$$\begin{aligned} P_e\le& {}\, \left\{ \sum _{v_{max}} \frac{1}{4} \sum _{t=1}^2 \left( 1+\frac{\rho | \varDelta x_{ik}|^2\beta _{llk}}{4(1+\rho u_{l,t})} \right) ^{-(M-K+1)} \right\} \nonumber \\&\times \left\{ \left( \sum _{k=0}^ne^{-A}\frac{A^k}{k!}\right) ^{M}- \left( \sum _{k=0}^{n-1}e^{-A}\frac{Z^k}{k!}\right) ^{M}\right\} , \end{aligned}$$
(18)

The derived bound is further simplified by sacrificing a little of the bound tightness. To do so, let us use some elementary algebra and rewrite Eq. (16) as below:

$$\begin{aligned} F_v^M(n)- F_v^M(n-1)= \left( F_v(n)- F_v(n-1)\right) \sum _{i=0}^{M-1}F_v^{M-i-1}(n)F_v^{i}(n-1), \end{aligned}$$
(19)

Note that the Cumulative Distribution Function CDF \(F_v(n)\) is always \(\le 1\), then we can replace the sum in Eq. (19) by M, hence it is always \(\le M\). The residual term \(F_v(n)- F_v(n-1)\) is the probability mass function of the random variable v and parameterized \(\alpha _m\). So

$$\begin{aligned} P\left( v_{max}=\sigma _n^2\right) \le M P(v=\sigma _n^2)=M \alpha _m , \end{aligned}$$
(20)

Finally, using the results obtained above, one can write:

$$\begin{aligned} P_e\le \frac{M}{4} \sum _{m=0} ^\infty \sum _{t=1}^2 \left( 1+\frac{\rho | \varDelta x_{ik}|^2\beta _{llk}}{4(1+\rho u_{l,t})} \right) ^{-(M-K+1)} \alpha _m , \end{aligned}$$
(21)

where \(\varDelta x_{ik}=x_{ik}^2-x_{ik}^1\), and (\(x_{ik}^2, x_{ik}^1\)) are the kth components of (\(\mathbf {x}_{l}^1 , \mathbf {x}_{l}^2\)), respectively. In a similar fashion we can derive the lower bound of the error rate of the system. The lower bound in Gaussian model is first written in Eq. (22). Then we follow the averaging trick for the equation, but this time the averaging will be on the conditional non-Gaussian noise variance as we explained. The expectation is shown in Eq. (23).

$$\begin{aligned} P_e\ge & {} \frac{1}{8}\sum _{t=1}^2 \left( 1+\frac{ \frac{1}{v} | \varDelta x_{ik}|^2\beta _{llk}}{\pi (1+\frac{1}{v} u_{l,t})} \right) ^{-(M-K+1)}, \end{aligned}$$
(22)
$$\begin{aligned} E_{v_{max}}\left[ P_e(|v_{max})\right]&\,=\, E_{v_{max}}\left[ \frac{1}{8} \sum _{t=1}^2 \left( 1+\frac{ \frac{1}{v} | \varDelta x_{ik}|^2\beta _{llk}}{\pi (1+\frac{1}{v} u_{l,t})} \right) ^{-(M-K+1)} \right] \nonumber \\\,&\ge \frac{1}{8} \sum _{v_{max}} \sum _{t=1}^2 \left[ P_e(v=v_{max})\right] \left( 1+\frac{ \frac{1}{v} | \varDelta x_{ik}|^2\beta _{llk}}{\pi (1+\frac{1}{v} u_{1,t})} \right) ^{-(M-K+1) } \nonumber \\&\ge \frac{M}{8} \sum _{m=0}^\infty \sum _{t=1}^2 \left( 1+\frac{ \frac{1}{v} | \varDelta x_{ik}|^2\beta _{llk}}{\pi (1+\frac{1}{v} u_{l,t})} \right) ^{-(M-K+1) } \alpha _m, \end{aligned}$$
(23)

For the the lower bound derivation, we would carry on the result in [26] and use the Q-function approximation given in that work. Then we can conclude another bound approximation as:

$$\begin{aligned} Q(x)\approx\,&\, \frac{1}{12}e^{\frac{-x^2}{2}}+ \frac{1}{6}e^{\frac{-2x^2}{3}}, \end{aligned}$$
(24)
$$\begin{aligned} P_e & \approx E_{v_{max}}\left[ \frac{1}{24} \sum _{t=1}^2 \left( 1+\frac{ \frac{1}{v} | \varDelta x_{ik}|^2\beta _{llk}}{4(1+\frac{1}{v} u_{l,t})} \right) ^{-(M-K+1)}\right] \nonumber \\&\quad+\, E_{v_{max}}\left[ \frac{1}{12} \sum _{t=1}^2 \left( 1+\frac{ \frac{1}{v} | \varDelta x_{ik}|^2\beta _{llk}}{3(1+\frac{1}{v} u_{l,t})} \right) ^{-(M-K+1)} \right] \nonumber \\&= M\sum _{m=0}^\infty \alpha _m \times \left( \frac{1}{24} \sum _{t=1}^2 \left( 1+\frac{ \frac{1}{v} | \varDelta x_{ik}|^2\beta _{llk}}{4(1+\frac{1}{v} u_{l,t})} \right) ^{-(M-K+1)} \right) \nonumber \\&\quad +\, M\sum _{m=0}^\infty \alpha _m \times \left( \frac{1}{12} \sum _{t=1}^2 \left( 1+\frac{ \frac{1}{v} | \varDelta x_{ik}|^2\beta _{llk}}{3(1+\frac{1}{v} u_{l,t})} \right) ^{-(M-K+1)} \right) , \end{aligned}$$
(25)

3.1 Extension to MMSE Performance

We carry on the results of Gaussian noise analysis of the MMSE system. Then we average the expression on the conditioned Poisson random variable. Assuming 2 code words then using the result in [8]:

$$\begin{aligned} P_e=Q\left( \sqrt{\frac{{\varrho }_{MMSE,lk}}{{2}}}| \varDelta x_{ik}|\right) , \end{aligned}$$
(26)

where \(\varDelta x_{ik}=x_{ik}^2-x_{ik}^1\), and (\(x_{ik}^2, x_{ik}^1\)) are the kth user components in the lth cell, and \(\varrho _{l}=\frac{\rho }{1+\rho u_{l,t}}\) for \(t=1,2\) (2 codeword system). The performance is found by averaging Eq. (26) with respect to the channel matrix \(H_{ll}\), and the impulsive noise distribution. That is :

$$\begin{aligned} P_e=E_{v_{max} } \left[ Q\left( \sqrt{\frac{{\varrho }_{MMSE,lk}}{{2}}}| \varDelta x_{ik}|\right) \right] , \end{aligned}$$
(27)

for some constants \(c_1, c_2,\widetilde{c}_1,\widetilde{c}_2\) found in [8], the lower bound can be written as:

$$\begin{aligned} P_{e MMSEL}\ge & {} \frac{c_1}{4} E_{v_{max}}\left[ \frac{1}{1+\frac{\beta _{llk}}{4}\varrho _{1} | \varDelta x_{ik}|^2} \right] ^M \varrho _{1}^{K-1} \nonumber \\&+ \frac{\widetilde{c}_1}{4} E_{v_{max}}\left[ \frac{1}{1+\frac{\beta _{llk}}{4}\varrho _{2} | \varDelta x_{ik}|^2} \right] ^M \varrho _{2}^{K-1} \nonumber \\&P_{e MMSE L-Bound} \ge M \sum _{m=0}^\infty \alpha _m P_{e MMSEL}, \end{aligned}$$
(28)

The upper bound expression is also given below:

$$\begin{aligned} P_{e MMSEU}\le & {} \frac{c_2}{8} E_{v_{max}}\left[ \frac{1}{1+\frac{\beta _{llk}}{\pi }\varrho _{1} | \varDelta x_{ik}|^2} \right] ^{M-K+1}\nonumber \\&+ \frac{\widetilde{c}_2}{8} E_{v_{max}}\left[ \frac{1}{1+\frac{\beta _{llk}}{\pi }\varrho _{2} | \varDelta x_{ik}|^2} \right] ^{M -K+1} \nonumber \\&P_{e MMSE U-Bound} \le M \sum _{m=0}^\infty \alpha _m P_{e MMSEU}, \end{aligned}$$
(29)

4 Sum Rate Analysis

In this section we study the sum rate behavior under impulsive noise settings. Bound on Sum Rate (SR) for ZF MIMO systems have been discussed in [27] . In our study we will start by writing the rayleigh fading channel sum rate equation as :

$$\begin{aligned} R_u=N_t\log _2\left[ \frac{1}{N_r-N_t} +\frac{\rho }{N_t}\right] +\frac{N_t}{\ln 2}\varPsi \left[ N_r-N_t+1\right] , \end{aligned}$$
(30)

where \(\varPsi (x)\) is the Euler’s digamma function in [28], \(N_t\) and \(N_r\) stands for the number of transmit and receive antennas respectively. The information in Eq. (46) represents the sum rate of a MIMO system over uncorrelated Rayleigh fading channels, yet, the effect of lognormal shadowing effect is not considered. However, we will carry on the results in [29] and furnish the bounds. First, the SNR and SR are written as:

$$\begin{aligned} \rho _m= & {} \frac{\rho [\beta ]_{mm}}{K[(H^)]}, \end{aligned}$$
(31)
$$\begin{aligned} R= & {} \sum _{i=1}^KE[\log _2(1+\rho _m)], \end{aligned}$$
(32)

The upper bound SR is given as:

$$\begin{aligned} R_{um}&\,= \,K \log _2 \left[ \frac{tr( \beta ^{-1})}{{K(M-K)}} + \frac{\rho }{K^2} \sum _{m=1}^K e^{\frac{U_m}{\eta } + \frac{\sigma _m^2}{2\eta ^2}} D_m^{-v} \right] +\nonumber \\&\quad- \sum _{m=1} ^K \log _2 \left[ \beta ^{-1} \right] _{mm}+\frac{K}{\ln 2}\varPsi \left[ M-K+1\right] , \end{aligned}$$
(33)

Finally, recalling back the trick on averaging over the noise variance then the bound can be approximated as:

$$\begin{aligned} R_u=\sum _{m=0}^ \infty \alpha _mR_{um}, \end{aligned}$$
(34)

The lower bound is also given as

$$\begin{aligned} R_u= & {} \sum _{m=0}^ \infty \alpha _mR_{Lm}, \quad {\mathrm {where}} \end{aligned}$$
(35)
$$\begin{aligned} R_{Lm}= & {} \sum _{m=1}^ K \log _2 \left[ 1+\frac{\rho }{K} e^{\psi (M-K+1)+\frac{u_m}{\eta }-\ln [\beta ^{-1}]_{mm}-v \ln D_m} \right] \end{aligned}$$
(36)

where \(\eta =10/\ln 10\), \(u_m\,and\,\sigma _m\) are the mean and the standard deviation (both in dB) of the natural logarithm variables, more details about these parameters can be found in [30, 31].

5 Simple Iterative ZF Precoder

In ZF massive MIMO system, we clearly observe the matrix inversion required by the ZF coding process. This is an inevitable step in the process. However, we prefer to skip the complex matrix inversion process, and use simple iterative addition for the coding schemes. Thus, in this section we show the derivation for the proposed simple ZF system. We use the below iterative equation to find the inverse of the channel matrix:

$$\begin{aligned} \mathbf {B}_{n+1}=\mathbf {B}_n(2\mathbf {I}-\mathbf {AB}_n) , \end{aligned}$$
(37)

For an arbitrary matrix \(\mathbf {A}\), Eq. (37) iteratively ends up with the inverse (pseudo inverse) of the matrix \(\mathbf {A}\). The below lemma is used for completing this section.

Lemma 1

Suppose that\(\mathbf {A}\)is\(n\times n\)complex matrix with\(\rho (\mathbf {A})\)is the spectral radius, and if\(\rho (\mathbf {A})<1\). Then\(\lim _{n\rightarrow \infty } \mathbf {A}^n=\mathbf {0 }\). This can be easily shown considering the below eigen value-eigen vector equation:

$$\begin{aligned} \mathbf {A}^n \mathbf {S}&\,=\,\lambda ^n \mathbf {S} \nonumber \\ \lim _{n\rightarrow \infty } \mathbf {A}^n \mathbf {S}&\,=\, \lim _{n\rightarrow \infty } \lambda ^n \mathbf {S} =\mathbf {S} \lim _{n\rightarrow \infty } \lambda ^n=\mathbf {0}, \end{aligned}$$
(38)

We denote the eigen values of the \(n\times n\) matrix \(\mathbf {A}\) by \(\lambda _i(\mathbf {A})\) for \(i=1,2,\ldots ,n\). And if \(\mathbf {A}\) is symmetric positive definite matrix \(\mathbf {A}\in R^{n\times n}\), then we can order the relative eigen values (\(\lambda _1(\mathbf {A}) \ge \lambda _2(\mathbf {A})\ge \cdots \ge \lambda _n(\mathbf {A})\ge 0\)). Now, we look deeply on the convergence of Eq. (37). Let us start by the initial matrix \(\mathbf {B}_0=\alpha \mathbf {A}^T\) and \(\alpha\) is a value that is related to the eigen values, say \(\alpha \in (0, \frac{2}{\lambda _1(\mathbf {AA}^T)})\). \(\lim _{n\rightarrow \infty }\mathbf {B}_n=\mathbf {A}^{-1}\). This technique is related to the Newton’s method for solving \(f(\mathbf {B})=0\) for \(f(\mathbf {B})=\mathbf {A}-\mathbf {B}^{-1}\). Now, we work on \(\lim _{n\rightarrow \infty }\mathbf {B}_n=\mathbf {A}^{-1}\) and assure that \(\mathbf {B}_n\) will end in \(\mathbf {A}^{-1}\). First let us assume the following:

$$\begin{aligned} \mathbf {R}_{n}&\,=\, \mathbf {I}_n(2\mathbf {I}-\mathbf {AX}_n) , {\mathrm {then}} \end{aligned}$$
(39)
$$\begin{aligned} \mathbf {B}_{n+1}&\,=\, \mathbf {B}_{n}+\mathbf {B}_n\mathbf {R}_n , \end{aligned}$$
(40)

Recalling that the spectral radius of \(\mathbf {R}_0\) is \(\rho (\mathbf {R}_0)=\rho (\mathbf {I}-\alpha (\mathbf {AA}^T))<1\), then, the eigen values are :

$$\begin{aligned} \lambda _i(\mathbf {R}_0)=1-\alpha \lambda _i(\mathbf {AA}^T), \end{aligned}$$
(41)

We already assumed that \(\alpha <\frac{2}{\lambda _i(\mathbf {AA}^T)}\), then \(|\lambda _i(\mathbf {R}_0)|<1\) and \(\rho (\mathbf {R}_0)<1\) and then:

$$\begin{aligned} \lim _{n \rightarrow \infty } \mathbf {R}_0^n=\mathbf {0}, \end{aligned}$$
(42)

To clarify Eq. (42), we use iterative induction method on Eq. (43) shown below. We can write \(\mathbf {R}_n=\mathbf {R}_0^{2n}\) and then \(\lim _{n \rightarrow \infty } \mathbf {R}_n=\lim _{n \rightarrow \infty } \mathbf {R}_0^{2n}=\mathbf {0}\):

$$\begin{aligned} \mathbf {R}_n=\mathbf {I}-\mathbf {AB}_n&\,=\, \mathbf {I}-\mathbf {A}\left( \mathbf {B}_{n-1}(2\mathbf {I}-\mathbf {AB}_{n-1})\right) \nonumber \\&\,=\, \mathbf {I}-\mathbf {A}\left( \mathbf {B}_{n-1}(\mathbf {I}+\mathbf {I}-\mathbf {AB}_{n-1})\right) \nonumber \\&\,=\, \mathbf {I}-\mathbf {A}\left( \mathbf {B}_{n-1}(\mathbf {I}+\mathbf {R}_{n-1})\right) \nonumber \\&\,=\, \mathbf {I} -\mathbf {AB}_{n-1}-\mathbf {AB}_{n-1}\mathbf {R}_{n-1}\nonumber \\&\,=\, \mathbf {R}_{nn}-\mathbf {AB}_{n-1}-\mathbf {AB}_{n-1}\mathbf {R}_{n-1}= \mathbf {R}_{n-1}(\mathbf {I}-\mathbf {AB}_{n-1})\nonumber \\&\,=\, \mathbf {R}_{n-1}^2 , \end{aligned}$$
(43)

Finally, recalling the definition of \(\mathbf {R}_n\) we observe that \(\mathbf {X}_n=\mathbf {A}^{-1}(\mathbf {I}-\mathbf {R}_n)\), then,

$$\begin{aligned} \lim _{n \rightarrow \infty } \mathbf {X}_0^n=\lim _{n \rightarrow \infty } \mathbf {A}^{-1}(\mathbf {I}-\mathbf {R}_n)= \mathbf {A}^{-1}, \end{aligned}$$
(44)

The final remark we would like to state is about the selection of \(\alpha\), It is clear that one should find the largest eigen value of \(\mathbf AA ^T\). However, we can choose another way. Let \((b_{ij}^n)_{i,j=1}\), denotes the entry of \(\mathbf AA ^T\), then \(\lambda _1(\mathbf AA ^T)\) is bounded by the highest absolute row sum of \(\mathbf AA ^T\). So,

$$\begin{aligned} \lambda _1(\mathbf AA ^T)\le \max _{i\in {1,2,\ldots ,n}} \sum _{j=1}^n|b_{i,j}| \quad {\mathrm {and}} \quad \alpha \in (0,\max _{i\in {1,2,\ldots ,n}}\sum _{j=1}^n|b_{i,j}|), \end{aligned}$$
(45)

5.1 Complexity of the Proposed System

In this section we discuss the complexity of the system and compare it with the conventional detectors (Zf and MMSE). Consider a MIMO channel as the below:

$$\begin{aligned} \mathbf {y}=\mathbf {Hx+n} , \end{aligned}$$
(46)

where \(\mathbf {y}\in C^{M_r}\), \(\mathbf {x}\in X^{M_t}\) and \(\mathbf {H}\in C^{M_r M_t}\). The reciver tries to estimate \(\hat{x}(y)\), The ZF will minimize \(\hat{x}(y)=\arg {{\min }_{x}}{{\left\| \mathbf {y-Hx} \right\| }^{2}}\). The solution is \(\hat{x}(y)={{\mathbf {H}}^{\mathbf {+}}}\mathbf {y}\). Where \({{\mathbf {H}}^{+}}\) is the psuedo inverse (for nonsquare matrices) and given by \({{\mathbf {H}}^{+}}={{({{\mathbf {H}}^{H}}\mathbf {H})}^{-1}}{{\mathbf {H}}^{H}}\) and the complexity of exploiting \({{\mathbf {H}}^{+}}\) from \({{\mathbf {H}}}\) is cubic with respect to the number of transmitters. Inversion of Large size channel matrix is required which means that the high computational complexity is unaccepted If we compute the inversion directly, the resource of hardware would be wasted greatly. Therefore, combining the property of matrices and some mathematic knowledge the proposed system will posses low-complexity precoding scheme to solve this problem. The complexity for the n size Channel matrix ZF is approximted in the order of \({\mathrm O}({{n}^{3}})\), however it is approximted in the order of \({\mathrm O}({a{n}^{2}})\) in our proposed system where a is a constant.

6 Simulation Results

Fig. 2
figure 2

SER versus SNR for \(K=3\) users Massive MIMO system ZF detector, impulsive noise with \(Z=0.0001\,{\mathrm{and}}\,X=0.1, M=5\,{\mathrm{and}}\,10\), Perfect channel knowledge. The curves are for the SER, Lower and upper bounds

Full size image

In this section, in order to validate our study of the system performance, we use Monte Carlo simulations, and examine the performance of the ZF decoder system. We choose two different sets of values of Z and T to represent a channel with near-Gaussian noise, and a channel with highly impulsive noise, which is within the practical range of these parameters. We further assume that the system has two cells with three users, and each BS has variable number of antennas ranging from 5 to 10 antennas. Regarding the path loss and shadow factors \(\beta _{ljk}\), we assume that \(\beta _{1,1,k} = 1 (k = 1, 2, 3)\). Two codewords are designed as \(X1 = [1, 1, 1, 1, 1, 1, 1], X2 = -X1.\) The simulation settings are similar to that in [8]. In the coming figures, we depict the performance of the system BER versus SNR, the lower and upper bounds as well. We then clearly show and comment on the effect of the impulsive noise on the system.

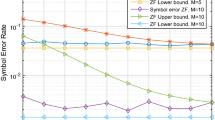
The line graph Fig. 2 illustrates the BER performance of the MIMO system under investigation. The number of antennas under scrutiny is \(M=5\). \(M=10\). The higher number of antennas shows a better SER curve performance as expected. This is due do the higher diversity order generated by \(M=10\). The Simulation is performed for a ZF decoder where the noise parameters are \(Z=0.0001, X=0.1\). In summary, the bounds show a tighter behavior for a smaller number of antennas. The SER curve of the system fluctuates mildly for \(M=10\) and remains unchanged for \(M=5\).

Fig. 3
figure 3

SER versus SNR for \(K=3\) users Massive MIMO system ZF detector, impulsive noise with \(Z=1\,{\mathrm{and}}\,X=0.1, M=5\,{\mathrm{and}}\,10\), Perfect channel knowledge. The curves are for the SER, Lower and upper bounds

Full size image

The line graph Fig. 3 demonstrates the SER performance of \(M=5\). \(M=10\) and different noise parameters. Mainly, \(Z=1, X=0.1\). This is known in the literature as the near gaussian case. The system shows again a closer bounds for a smaller number of antennas, and a BER curve similar to that in the literature for gaussian noise. Furthermore, the BER curve performance drops substantially for \(M=10\). However, the BER curve goes down gradually and slowly for \(M=5\). Finally, the lower bound curves remain steady for both cases.

Fig. 4
figure 4

SER versus SNR for \(K=3\) users Massive MIMO system MMSE ZF detector, impulsive noise with \(Z=0.0001\,{\mathrm{and}}\,X=0.1,\,M=5\,{\mathrm{and}}\,10\), Perfect channel knowledge. The curves are for the SER, Lower and upper bounds

Full size image

Figures 4 and 5 display the error rate performance for MMSE System. The SER performance for \(M=5. M=10\) and different noise parameters as similar to the aforementioned simulations. We can clearly see the error flooring behavior for the MMSE system. The declining shape is not as of the previous ones. Moreover, the near gaussian case and the high impulsive case are very close in their shape. However, there is a slight difference at the low SNR value. For instance, the SER for the high impulsive case at small SNR is closer to \(10^{-2}\) where it is closer \(10^{-3}\) for the same designated SNR at near gaussian case. The bounds are still firm and valid for the MMSE detector. We may conclude that the MMSE has the constant effect behavior on the SER curves.

Fig. 5
figure 5

SER versus SNR for \(K=3\) users Massive MIMO system MMSE ZF detector, impulsive noise with \(Z=1\,{\mathrm{and}}\,X=0.1, M=5\,{\mathrm{and}}\,10\), Perfect channel knowledge. The curves are for the SER, Lower and upper bounds

Full size image

7 Conclusions

In conclusion. In this paper, we show the performance of the impulsive noise on multi cell massive MIMO systems. The derivations were sophisticated but fruitful. The bounds demonstrates reasonable tightness around the simulation curves. The error rate curves were errorflooring for the MMSE more than that in the ZF case. To lessen the sophistication of such detections, we propose an iterative matrix inversion detector and proof the convergence of such schemes. Finally, we studied the sum rate analysis for the system under the impulsive noise model which lies at the heart of this research.