1 Introduction

In recent years, cosmological observations of supernovas and the distribution of galaxies in the universe, as well as detailed maps of the cosmic microwave background, have provided significant data that allow us to follow the evolution of the universe over the past 13.8 billion years and let’s go back to the beginnings of the universe [1,2,3]. A detailed analysis of cosmological observations [4,5,6,7,8,9,10,11,12,13,14,15], supports the idea that the universe has undergone two stages of accelerated expansion during its evolution. The rapid expansion phase in the early period of evolution, known as inflation [16,17,18], which occurred before the dominant radiation period, and the current acceleration phase, known as the late cosmic acceleration [18,19,20,21]. From the perspective of general relativity, the cosmic acceleration occurs when the cosmic fluid is dominated by an unknown source called dark energy, which has a negative value of the equation of state (EoS) parameter [22] and [23].

In the framework of general relativity, scalar fields play an important role in gravitational physics, as they provide theoretical mechanisms to explain observations. Since inflation, which is responsible for the early acceleration phase of the universe, is characterized by a scalar field, the same model can provide dynamical terms in the gravitational field equations with anti-gravitational behavior and can also be used as a model to describe the acceleration of the late universe. The most well-known scalar field model that has been studied in literatures is the quintessence model [24,25,26,27]. Other scalar field models presented in the articles are: phantom fields [28,29,30], quintom models [31,32,33], Chiral models [34,35,36], k-essence scalar fields [37] and [38], and some less and more famous ones [39,40,41,42,43,44,45].

In the quintessence scalar field cosmology [46], the EoS parameter of the scalar field extends to \(\left| \omega _{\phi }\right| \le 1 \) , where \(\omega _{\phi }=1\), corresponds to a stiff fluid in which only the kinetic part of the scalar field dominates, in while the limit \(\omega _{\phi }=-1\), corresponds to the case where only the potential of the scalar field dominates, leading to \(\Lambda \) cosmology. Note that acceleration occurs when \(-1\le \omega <-\frac{1}{3}\). In phantom scalar fields, \(\omega _{\phi }\) can cross the limit \(-1\) and take smaller values, for example, when the kinetic energy is negative [46,47,48,49,50]. Phantom models accept a new type of singularity called Big-Rip singularity [51,52,53,54,55,56], in which when the scale factor a(t), goes to infinity in finite time, the energy density and pressure diverge. This differs from usual singularities in general relativity such as Big-Bang, where the energy density and pressure increase infinitely as the scale factor approaches zero. In general, scalar field models require the choice of a potential \(V(\phi )\) for the scalar field \(\phi \) . The consideration of a specific potential is usually done by a suitable proposal (ansatz).

In the early stages of the universe, quantum effects play an important role in the evolution of the universe. It is believed that the problem of the singularity of the early universe and other types of singularities in general relativity such as black holes should be finally removed by a quantum theory of general relativity. However, in the absence of a full theory of quantum gravity, it would be useful to describe the quantum state of the universe within the context of canonical quantum cosmology based on the Wheeler-Dewitt (WDW) equation. For this reason, quantization of models of scalar fields in cosmology are also of special importance, see [57,58,59,60].

In this paper, using the general form of the action for the usual scalar field, say quintessence and phantom fields, in Section 2, we form the Friedman and Klein-Gordon equations. Then, by writing the Hubble parameter as a function of the scalar field, we establish the required relations for the next sections. In Section 3, we consider the simple case of a exponentially damping potential and some cosmological parameters such as the Hubble parameter, the scale factor, as well as the shape of the potential function and the dynamics of the EoS parameter of the model as a function of the scalar field and time are obtained. In the fourth section, we present two ansatz for the time dependence of the scalar field, which leads to the cosmology of the exponential scalar potential. We extract the dynamics of the Hubble parameter, the scale factor and the EoS parameter of the perfect fluid as functions of the scalar field and time. In Section 5, we deal with the quantum cosmology of the damping exponential scalar potential model extracted in the Section 4 and we form the corresponding WDW equation. By defining some new variables, we rewrite the WDW equation in terms of them and obtain its eigenfunctions using the method of separation of variables. At the end, we determine the probability function with the use of the the wave packet constructed with the Gaussian weight function. Finally, we summarized the main results of the paper in Section 6.

2 Homogeneous and Isotropic Scalar Field Cosmology

The cosmological action of the homogeneous and isotropic scalar field may be written in the form

$$\begin{aligned} \mathcal{S}=\int \,dt\, N\left( -3\frac{a\dot{a}^2}{N^2}\right) +\frac{1}{2}\int \,dt\, N a^3\left[ \epsilon \frac{\dot{\phi }^2}{N^2}-2V(\phi )\right] , \end{aligned}$$
(1)

where \(V(\phi )\) is the potential and \(\epsilon \) indicates the type of scalar field, so that \(\epsilon =1\) indicates the quintessence and \(\epsilon =-1\) corresponds to the phantom. Thus, the Lagrangian may be written as

$$\begin{aligned} \mathcal {L}(N,a,\phi ,\dot{a},\dot{\phi })=\frac{1}{N}\left( -3a\dot{a}^2+\frac{1}{2}a^3\epsilon \dot{\phi }^2\right) -a^3 N V(\phi ). \end{aligned}$$
(2)

The Euler-Lagrange equations with dynamical variables \(\left\{ N,a,\phi \right\} \) with \(N=1\) leads to the equations

$$\begin{aligned} \left\{ \begin{array}{ll} -3a\dot{a}^2+\frac{1}{2}\epsilon a^3\dot{\phi }^2-a^3 V(\phi )=0,\\ \\ -3\dot{a}^2-6a\ddot{a}-\frac{3}{2}\epsilon a^2\dot{\phi }^2+3a^2 V(\phi )=0,\\ \\ 3\epsilon a^2\dot{a} \dot{\phi }+\epsilon a^3\ddot{\phi }+a^3V^\prime (\phi )=0. \end{array} \right. \end{aligned}$$
(3)

In terms of the Hubble parameter \(H=\dfrac{\dot{a}}{a}\), the above equations take the form

$$\begin{aligned} \left\{ \begin{array}{ll} 3H^2=\frac{1}{2}\epsilon \dot{\phi }^2 + V(\phi ),\\ \\ 2\dot{H}+3H^2=-\frac{1}{2}\epsilon \dot{\phi }^2+V(\phi ),\\ \\ \ddot{\phi }+3H\dot{\phi }+\epsilon V^\prime (\phi )=0. \end{array} \right. \end{aligned}$$
(4)

For the given Lagrangian function (2) the momentum conjugate to each variable can be obtained by definition \(p_{i}=\dfrac{\partial \mathcal {L}}{\partial \dot{q}^{i}}\) where \(q^{i} \in \left\{ {a,\phi }\right\} \) and \(p_{i}\in \left\{ {p_{a},p_{\phi }}\right\} \). The results are

$$\begin{aligned} p_{a}=-\frac{6 a \dot{a}}{N}, \hspace{5mm}p_{\phi }=\frac{\epsilon a^3 \dot{\phi }}{N}, \end{aligned}$$
(5)

by means of which we get the Hamiltonian of the model as

$$\begin{aligned} \mathcal {H}=N\left[ -\dfrac{p_{a}^2}{12 a}+\dfrac{p_{\phi }^2}{2\epsilon a^3}+ a^3 V(\phi )\right] . \end{aligned}$$
(6)

In the Hamiltonian formalism, the classical dynamics of each variable is determined by the Hamilton equation \(\dot{q}=\{q,\mathcal {H}\}\), where \(\{.,.\}\) is the Poisson bracket. So, we will have

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{a}=-\dfrac{p_{a}}{6a},\\ \\ \dot{p}_{a}=-\dfrac{p_{a}^2}{12a^2}+\dfrac{3\epsilon }{2}\dfrac{p_{\phi }^2}{a^4}-3a^2 V(\phi ),\\ \\ \dot{\phi }=\dfrac{\epsilon \, p_{\phi }}{a^3},\\ \\ \dot{p}_{\phi }=-a^3 V^\prime (\phi ). \end{array} \right. \end{aligned}$$
(7)

Now, with the use of the above set of equations and the Hamiltonian constraint

$$\begin{aligned} -\dfrac{p_{a}^2}{12 a}+\dfrac{p_{\phi }^2}{2\epsilon a^3}+ a^3 V(\phi )=0, \end{aligned}$$
(8)

we are led to the Friedmann and Klein-Gordon equations

$$\begin{aligned} H^2=\frac{1}{3}\left( \frac{1}{2} \epsilon \dot{\phi }^2 + V(\phi )\right) ,\hspace{5mm}\ddot{\phi }+3H\dot{\phi }+\epsilon V^\prime (\phi )=0. \end{aligned}$$
(9)

For time periods when the scalar field varies uniformly, for example during the period of oscillation between two infinite values, the evolution of the Hubble parameter can be related to the scalar field as \(H(t)=H\left( \phi (t)\right) \), [61] and [62]. In this case we will have \(\dot{H}=H'\dot{\phi }\), where the prime represents the derivative with respect to \(\phi \). Now, the derivation of the Friedmann equation \(2H\dot{H}=\frac{1}{3}(\epsilon \dot{\phi }\ddot{\phi }+\dot{\phi } V^\prime (\phi ))\), and with the help of Klein-Gordon equation we obtain

$$\begin{aligned} \dot{H}=-\frac{1}{2}\epsilon \dot{\phi }^2\Rightarrow H^\prime =-\frac{1}{2}\epsilon \dot{\phi } \end{aligned}$$
(10)

Also, the derivative of (10): \(\ddot{H}=-\epsilon \dot{\phi }\ddot{\phi }\), and combination of (9) results the following set of equations

$$\begin{aligned} 3H^2+\dot{H}=V(\phi ), \end{aligned}$$
(11)
$$\begin{aligned} \ddot{H}+6H\dot{H}=\dot{V}, \end{aligned}$$
(12)
$$\begin{aligned} 3H^2-2\epsilon H^{\prime ^2}=V(\phi ). \end{aligned}$$
(13)

3 Exponentially Damping Scalar Field Model

In this section we consider a scalar field damping exponentially with time as [63]

$$\begin{aligned} \phi (t)=\phi _{0}e^{-\beta t}, \end{aligned}$$
(14)

which tends to zero as \(t\rightarrow \infty \). By putting in (10), after integration we get

$$\begin{aligned} H(\phi )=h+\frac{1}{4}\epsilon \beta \phi ^2, \end{aligned}$$
(15)

where h is an integration constant. The potential function can now be evaluated from (13) as

$$\begin{aligned} V(\phi )=\mu +\frac{m^2}{2}\phi ^2+\frac{\lambda }{4}\phi ^4, \end{aligned}$$
(16)

in which

$$\begin{aligned} \mu =3h^2, \hspace{5mm}m^2=\epsilon \beta (3h-\beta ), \hspace{5mm} \lambda =\frac{3\beta ^2}{4}. \end{aligned}$$
(17)

With the use of (14) and (15) the time evolution of the scale factor is obtained as follows

$$\begin{aligned} a(t)=a_{0}e^{ht+\frac{\epsilon }{8}\dot{\phi }^2(1-e^{-2\beta t})}, \end{aligned}$$
(18)

where in terms of the scalar field takes the form

$$\begin{aligned} a(\phi )=a_{0}\left( \frac{\phi }{\phi _{0}}\right) ^{-\frac{h}{\beta }} e^{\frac{\epsilon }{8}(\phi _{0}^2-\phi ^2)}. \end{aligned}$$
(19)

Now, using the perfect fluid equation of state, \(p=\omega \rho \), we obtain the dynamics of the state parameter \(\omega (t)\):

$$\begin{aligned} \omega (t)=\dfrac{p(t)}{\rho (t)}=\dfrac{\frac{1}{2}\epsilon \dot{\phi }^2-V}{\frac{1}{2}\epsilon \dot{\phi }^2+V}, \end{aligned}$$
(20)

which upon substituting from the (10) and using (14)-(16) one has

$$\begin{aligned} \omega (\phi )=\dfrac{-\mu +\frac{1}{2}(\epsilon \beta ^2 -m^2)\phi ^2-\frac{\lambda }{4}\phi ^4}{\mu +\frac{1}{2}(\epsilon \beta ^2 +m^2)\phi ^2+\frac{\lambda }{4}\phi ^4}, \end{aligned}$$
(21)

and

$$\begin{aligned} \omega (t)=\dfrac{-\mu +\frac{1}{2}(\epsilon \beta ^2 -m^2)\phi _{0}^2 e^{-2\beta t}-\frac{\lambda }{4}\phi _{0}^4 e^{-4\beta t}}{\mu +\frac{1}{2}(\epsilon \beta ^2 +m^2)\phi _{0}^2 e^{-2\beta t}+\frac{\lambda }{4}\phi _{0}^4 e^{-4\beta t}}. \end{aligned}$$
(22)

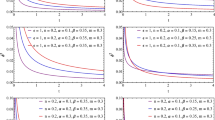
In Figs. 1, 2 and 3, we have shown the behavior of the above functions for for typical values of the parameters. As the Fig. 2 shows the scale factors represent different types of singularities in the cases where the scalar field is of the type of quintessence or phantom. Also, from the Fig. 3, it is clear that the EoS parameter tends to \(-1\) from the values greater (smaller) than \(-1\) when the scalar field is a quintessence (phantom) fluid.

Fig. 1
figure 1

The Hubble parameter (left) and scalar potential (right) for the exponential damping scalar field model. Red and blue curves show the quintessence and phantom scalar field respectively. The figures are plotted for \(h=2\) and \(\beta =10\)

Full size image
Fig. 2
figure 2

Up: the scale factor in terms of time and down: the scale factor versus scalar field for the exponential damping scalar field model. The red and blue curves represent the quintessence and phantom fields respectively. The graphs on the left and right are drawn for \(h=2\) and \(h=-2\). \(\beta =5 \) is considered for all curves

Full size image
Fig. 3
figure 3

EoS parameter of the quintessence (red curve) and phantom (blue curve) field versus time. The figures are plotted for the numerical values \(\beta =2\) and \(h=2\)

Full size image

4 Exponential Scalar Potentials

In this section, in order to achieve the exponential potential function, we present two models for the scalar field as a function of time, and discuss the dynamics of the proposed models. \(\bullet \)The first ansatz:

Fig. 4
figure 4

The red and blue curves show the behavior of the Hubble parameter in terms of the quintessence and phantom scalar fields respectively

Full size image
Fig. 5
figure 5

The scale factor versus time. The figure on the left corresponds to the quintessence, \(\epsilon =+1\), the right one corresponds to the phantom field, \(\epsilon =-1\). For both: \(\lambda =10\)

Full size image

We consider a scalar field of the form

$$\begin{aligned} \phi (t)=A \ln [B(t-t_{0})+C], \end{aligned}$$
(23)

where A, B and C are some non-zero constants. So, from (10) we have

$$\begin{aligned} \dot{H}=-\frac{\epsilon }{2}\frac{A^2B^2}{[B(t-t_{0})+C]^2}, \end{aligned}$$
(24)

where upon integration results the Hubble parameter as

$$\begin{aligned} H(t)=\frac{\epsilon }{2}\dfrac{A^2B}{(t-t_{0})+C}. \end{aligned}$$
(25)

With the use of these relations in (11), we obtain an exponential potential function for the scalar field

$$\begin{aligned} V(\phi )=V_{0} e^{-\lambda \phi }, \end{aligned}$$
(26)

in which \(V_{0}=\frac{1}{4}A^2 B^2(3A^2 -2\epsilon )\) and \(\lambda =\frac{2}{A}\). If in (25) we set \(H(t_0)=H_0\), then \(\frac{B}{C}=\frac{\lambda ^2}{2\epsilon }H_{0}\). In order to establish the limiting conditions of the quintessence and phantom, we set \(C=\epsilon \). By determining the coefficients of B and C, the value of \(V_0\) takes the form \(V_{0}=H_{0}^{2}(3-\frac{1}{2}\epsilon \lambda ^2)\). Now, our ansatz for the scalar field in (23) can be read as

$$\begin{aligned} \phi (t)=\frac{2}{\lambda } \ln \left[ \frac{1}{2}\lambda ^2 H_{0}(t-t_{0})+\epsilon \right] , \end{aligned}$$
(27)

with the Hubble parameter

$$\begin{aligned} H(t)=\frac{\epsilon H_{0}}{\frac{\lambda ^2 H_{0}}{2} (t-t_{0})+\epsilon }, \Rightarrow H(\phi )=\epsilon H_{0} e^{-\frac{\lambda }{2}\phi }, \end{aligned}$$
(28)

where is plotted in Fig. 4.

To obtain the scale factor of the model we may use the definition \(H=\frac{\dot{a}}{a}\) in (28) to get

$$\begin{aligned} a(t)=a_0\left[ \frac{1}{2}\lambda ^2 H_{0}(t-t_{0})+\epsilon \right] ^{\frac{2\epsilon }{\lambda ^2}}. \end{aligned}$$
(29)

In Fig. 5 we have plotted the time behavior of the scale factor. As the figures show the scale factor represents different types of singularity for the quintessence and phantom fields.

Finally, from (9) we can evaluate the energy density \(\rho =3H^2\) as

$$\begin{aligned} \rho (t)=\rho _{0} \left( \frac{a(t)}{a_{0}}\right) ^{-\epsilon \lambda ^2}, \end{aligned}$$
(30)

where \(\rho _{0}=3H_{0}^2\), and from which the EoS parameter will be a constant value as

$$\begin{aligned} \omega =\frac{1}{3}\epsilon \lambda ^2 -1. \end{aligned}$$
(31)

\(\bullet \)The second ansatz:

Let us now consider the a scalar field of the form

$$\begin{aligned} \phi (t)=A\,\ln \left[ \tanh \left( B (t-t_{0})\right) \right] , \end{aligned}$$
(32)

where A and B are non-zero constants. After inserting in (10) and integration we have

$$\begin{aligned} H(\phi )=\epsilon A^2 B \cosh \left( \frac{\phi }{A}\right) +h, \end{aligned}$$
(33)

where h is the integration constant. The potential function can be obtained from (13) as

$$\begin{aligned} V(\phi )=A^2 B^2 \left[ 3A^2 \cosh ^{2}\left( \frac{\phi }{A}\right) -2\epsilon \sinh ^{2}\left( \frac{\phi }{A}\right) \right] +3 h\left[ h+ 2\epsilon A^2 B \cosh \left( \frac{\phi }{A}\right) \right] . \end{aligned}$$
(34)

Now, we examine two cases:

a)We set \(A=\pm \sqrt{\frac{2\epsilon }{3}}\) and \(h=0\), for which we get a positive constant potential \(V=3A^4B^2\), where it can be used to describe models with \(V(\phi )=\Lambda > 0\). Therefore, we have

$$\begin{aligned} \phi (t)=\pm \sqrt{\frac{2\epsilon }{3}} \ln \left[ \tanh \left( \frac{3}{2}H_{0}(t-t_{0})\right) \right] , \end{aligned}$$
(35)

in which we have taken \(B=\frac{3}{2}H_0\). Also,

$$\begin{aligned} H(\phi )=H_{0}\cosh \left( \pm \sqrt{\frac{3\epsilon }{2}}\phi \right) , \hspace{5mm} V(\phi )=3H_{0}^2. \end{aligned}$$
(36)

The EoS parameter in terms of the scalar field in this model may be evaluated from (22) with result

$$\begin{aligned} \omega (\phi )=2 \tanh ^2\left( \sqrt{\frac{3\epsilon }{2}}\,\phi \right) -1. \end{aligned}$$
(37)

Finally, with the relation \(H=\frac{\dot{a}}{a}=\frac{a^\prime }{a}\dot{\phi }\), at hand the scale factor takes the form

$$\begin{aligned} \frac{a^\prime }{a}=\pm \frac{1}{\sqrt{6\epsilon }}\coth \left( \sqrt{\frac{3\epsilon }{2}}\phi \right) \Rightarrow \frac{a(\phi )}{a_{0}} =\left[ \sinh \left( \sqrt{\frac{3\epsilon }{2}}\,\phi \right) \right] ^{\pm \frac{1}{3}}. \end{aligned}$$
(38)

The results of this case are shown in Fig. 6.

Fig. 6
figure 6

The Hubble parameter and the EoS parameter are drawn as a function of the scalar field based on the (36) and (37). The blue and red curves show the quintessence and the phantom fields respectively

Full size image

b)Now, let us consider the situation in which \(A=\pm \sqrt{\frac{-2\epsilon }{3}}\) and \(h=0\), for which we have \(B=-\frac{3}{2}H_{0}\), and the potential function for both phantom and quintessence is equal to

$$\begin{aligned} V(\phi )=V_{0}\cosh \left( \frac{2\phi }{A}\right) \Rightarrow V(\phi )=V_{0}\cosh \left( \pm \sqrt{-6\epsilon }\,\phi \right) , \end{aligned}$$
(39)

where \(V_{0}=3H_{0}^2\). Simple calculations based on the relations obtained previously result the following expressions for the cosmological variables

$$\begin{aligned} \left\{ \begin{array}{ll} \phi (t)=\pm \sqrt{\frac{-2\epsilon }{3}} \ln \left[ \tanh \left( -\frac{3}{2}H_{0}(t-t_{0})\right) \right] ,\\ \\ H(\phi )=H_{0}\cosh \left( \pm \sqrt{\frac{-3\epsilon }{2}}\phi \right) ,\\ \\ \frac{a(\phi )}{a_{0}} =\left[ \sinh \left( \sqrt{\frac{-3\epsilon }{2}}\,\phi \right) \right] ^{\pm \frac{1}{3}},\\ \\ \omega (\phi )=\dfrac{1}{2 \tanh ^2\left( \sqrt{\frac{-3\epsilon }{2}}\,\phi \right) -1}. \end{array} \right. \end{aligned}$$
(40)

Figure 7 shows behavior of the scale factor in terms of the scalar field for \(\epsilon =+1\) and \(\epsilon =-1\).

Fig. 7
figure 7

The scale factor versus the scalar field based on the relations (39) and (40) for \(\epsilon =+1\) (blue curve) and \(\epsilon =-1\) (red curve)

Full size image

Note that the potential (39) may be written as \(V(\phi )=\frac{V_{0}}{2}\left( e^{\frac{2\phi }{A}}+e^{-\frac{2\phi }{A}}\right) \). Since the classical singularities occur for large values of \(\left| \phi \right| \), in regimes when quantum gravity considerations are important, the potential can be approximated as

$$\begin{aligned} V\approx \frac{{ V_{0}}}{{2}} e^{\frac{2\phi }{A}}=\frac{{ V_{0}}}{{2}} e^{\pm \sqrt{-6 \epsilon }\,\phi }. \end{aligned}$$
(41)

At this point it should be noted that finding exact solutions plays a vital role in cosmology. Cosmological models with homogeneous and isotropic scalar field have been widely studied in literature. For instance general solutions for two sets of exponential potentials in a scalar field model for quintessence are discussed in [64], while the scalar field with exponential potentials and transient acceleration is reviewed in [65]. For unified phantom cosmological models see [66] and exponential-like, cosh-like and sinh-like potentials have been studied in [67]. In [68] and [69], the authors have used exact solutions in description of the inflationary, dark matter and dark energy models and also have presented an analysis of an exactly solvable model of an accelerator dominated expanding universe by dark energy in a phantom scalar field model.

What we have done so far in this article is to develop a general approach to the solution of the Einstein-Klein-Gordon equations. Indeed, we investigated the dynamics of the homogeneous and isotropic scalar field cosmological model using potential inverse engineering. In other words, we have shown how to find the scalar potentials that lead to a predetermined scalar field behavior and the associated evolution of the scale factor and dynamics of the EoS parameter. Therefore,in comparison with the other works, by proposing two scalar fields in terms of time, both of which lead to the exponential potential function, we studied the dynamics of the model and extracted cosmological parameters as functions of potential and functions of time. We did this for usual and phantom scalar fields.

5 Quantum Cosmology of the Model

Quantization of the model described above begins with the WDW equation \(H\Psi =0\), where H is the Hamiltonian quantum operator and \(\Psi \) is the wave function of the universe. With the Hamiltonian (6), canonical quantization rule \(p_q\rightarrow -i\frac{\partial }{\partial q}\) and use of the Laplace-Beltrami factor ordering, we arrive at

$$\begin{aligned} \left[ \frac{1}{2}a\dfrac{\partial }{\partial a}a\dfrac{\partial }{\partial a} -\frac{1}{2}\epsilon \dfrac{\partial ^2}{\partial \phi ^2}+ a^6 V(\phi )\right] \Psi (a,\phi )=0. \end{aligned}$$
(42)

Applying the change of variable \(\alpha =\ln a\), and with the potential function (26), the WDW equation takes the form

$$\begin{aligned} \left[ \frac{1}{2}\dfrac{\partial ^2}{\partial \alpha ^2} -\frac{1}{2}\epsilon \dfrac{\partial ^2}{\partial \phi ^2}+ V_{0}e^{6\alpha -\lambda \phi } \right] \Psi (\alpha ,\phi )=0. \end{aligned}$$
(43)

Now, let us introduce two new variables as [70]

$$\begin{aligned} \left\{ \begin{array}{ll} u(\alpha ,\phi )=\sqrt{\frac{2V_{0}}{3}}\,Y\left[ \cosh (X)+\frac{\lambda }{\sqrt{6\epsilon }}\sinh (X)\right] ,\\ \\ v(\alpha ,\phi )=\sqrt{\frac{2V_{0}}{3}}\,Y\left[ \frac{1}{\sqrt{\epsilon }} \sinh (X)+\frac{\epsilon \lambda }{\sqrt{6}}\cosh (X)\right] , \end{array} \right. \end{aligned}$$
(44)

in which

$$\begin{aligned} X=\sqrt{\epsilon }\left( 3\phi -\epsilon \frac{\lambda \sqrt{6}}{2}\alpha \right) ,\hspace{5mm} Y=\frac{e^{3\alpha -\frac{\lambda \sqrt{6}}{2}\phi }}{1-\epsilon (\frac{\lambda }{\sqrt{6}})^2}. \end{aligned}$$
(45)

In terms of these new variables the WDW equation will become

$$\begin{aligned} \left( \dfrac{\partial ^2 }{\partial u^2}-\epsilon \dfrac{\partial ^2 }{\partial v^2}+1\right) \Psi (u,v)=0. \end{aligned}$$
(46)

The solutions of the above equation can be separated into the form \(\Psi (u,v)=U(u)V(v)\), where U(u) and V(v) satisfy the following equations

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{d^2 U}{d u^2 }+k^2 U=0,\\ \\ \frac{d^2 V}{d v^2} +\epsilon (k^2-1)V=0, \end{array} \right. \end{aligned}$$
(47)

with solutions

$$\begin{aligned} \left\{ \begin{array}{ll} U(u)=C_{1}e^{iku}+C_{2}e^{-iku},\\ \\ V(v)=C_{3}e^{i\sqrt{\epsilon (k^2 -1)} v}+C_{4}e^{-i\sqrt{\epsilon (k^2 -1)}v}, \end{array} \right. \end{aligned}$$
(48)

where k is the separation constant and \(C_i\) are integration constants. Therefore, the eigenfunctions of the WDW equation may be written as

$$\begin{aligned} \Psi _{k}^{\pm }(u,v)=D_{1}e^{i(ku\pm \sqrt{\epsilon (k^2 -1)}v)}+D_{2}e^{-i(ku\pm \sqrt{\epsilon (k^2 -1)}v)}, \end{aligned}$$
(49)

where as before \(\epsilon =\pm 1\) stands for the quintessence or phantom fields. The general solutions of the WDW equation should be constructed by a superposition of its eigenfunctions as

$$\begin{aligned} \Psi (u,v)=\int dk A(k) \Psi _{k}(u,v), \end{aligned}$$
(50)

where the weight function A(k) may be chosen as a Gaussian profile \(A(k)=\frac{1}{(\sqrt{\pi }\sigma )^{\frac{1}{2}}}\, e^{-\frac{(k-\bar{k})^2}{2\sigma ^2}}\), to achieve a suitable wave packet. Thus, we will have

$$\begin{aligned} \Psi ^{\pm }(u,v)=\frac{1}{(\sqrt{\pi }\sigma )^{\frac{1}{2}}}\int \,dk\, e^{-\frac{(k-\bar{k})^2}{2\sigma ^2}}\left[ D_{1}e^{i(ku\pm \sqrt{\epsilon (k^2 -1)}v)}+D_{2}e^{-i(ku\pm \sqrt{\epsilon (k^2 -1)}v)}\right] . \end{aligned}$$
(51)

Now, we consider the following cases

\(\bullet \) \(D_1\ne 0\) and \(D_2=0\): In this case the wave packet takes the form

$$\begin{aligned} \Psi ^{\pm }(u,v)\!=\!\frac{-\pi ^\frac{1}{4} \sqrt{\sigma }}{\sqrt{\mp 2+2 \sigma ^2 \sqrt{\epsilon } v}}\,\exp \left( {\dfrac{2 i \bar{k} u \mp 2\sqrt{\epsilon } v\pm \bar{k}^2 \sqrt{\epsilon } v\!-\!\sigma ^2 u^2 +2 \sigma ^2 \epsilon v^2}{2\mp 2\sigma ^2 \sqrt{\epsilon } v}}\right) E^{\pm }(u,v), \end{aligned}$$
(52)

in which the error functions \(E^{\pm }(u,v)\) are

$$\begin{aligned} \left\{ \begin{array}{ll} E^{+}(u,v)= \text{ Erfi }\left[ \dfrac{2 + \bar{k}\ + i \sigma ^2 u -2 \sigma ^2 \sqrt{\epsilon } v }{\sigma \sqrt{-2+2 \sigma ^2 \sqrt{\epsilon } v}}\right] -\text{ Erfi }\left[ \frac{-2 + \bar{k}\ + i \sigma ^2 u +2 \sigma ^2 \sqrt{\epsilon } v}{\sigma \sqrt{-2+2 \sigma ^2 \sqrt{\epsilon } v}}\right] ,\\ \\ E^{-}(u,v)= \text{ Erf }\left[ \dfrac{-2 - \bar{k}\ - i \sigma ^2 u -2 \sigma ^2 \sqrt{\epsilon } v }{\sigma \sqrt{2+2\sigma ^2 \sqrt{\epsilon } v}}\right] -\text{ Erf }\left[ \frac{2 - \bar{k}- i \sigma ^2 u +2 \sigma ^2 \sqrt{\epsilon } v}{\sigma \sqrt{2+2\sigma ^2 \sqrt{\epsilon } v}}\right] . \end{array} \right. \end{aligned}$$
(53)

See the probability function of the wave packet \( \left| \Psi _{\epsilon }^{\pm }(u,v)\right| ^2\) in the Fig. 8.

Fig. 8
figure 8

The figures show the probability function of the wave packet \(\left| \Psi _{\epsilon }^{\pm }(u,v)\right| ^2 \) in the case \( D_{1}\ne 0\) and \( D_{2}=0 \) for the quintessence and phantom scalar fields

Full size image

\(\bullet \) \(D_1=0\) and \(D_2\ne 0\): In this case the wave packet based on the (51) has again an analytical form as

$$\begin{aligned} \Psi _{\epsilon }^{\pm }(u,v)=\frac{-\pi ^\frac{1}{4} \sqrt{\sigma }}{\sqrt{\pm 2+2 \sigma ^2 \sqrt{\epsilon } v}}\,\exp \left( \mp {\dfrac{2 i \bar{k} u + 2\sqrt{\epsilon } v\pm \bar{k}^2 \sqrt{\epsilon } v-\sigma ^2 u^2 \pm 2 \sigma ^2 \epsilon v^2}{\pm 2+2\sigma ^2 \sqrt{\epsilon } v}}\right) E^{\pm }(u,v), \end{aligned}$$
(54)

with the error function

$$\begin{aligned} \left\{ \begin{array}{ll} E^{+}(u,v)= \text{ Erf }\left[ \dfrac{-2-\bar{k}\ + i \sigma ^2 u -2 \sigma ^2 \sqrt{\epsilon } v}{\sigma \sqrt{2+2 \sigma ^2 \sqrt{\epsilon } v}}\right] -\text{ Erf }\left[ \frac{2-\bar{k}\ + i \sigma ^2 u +2 \sigma ^2 \sqrt{\epsilon } v}{\sigma \sqrt{2+2 \sigma ^2 \sqrt{\epsilon } v}}\right] ,\\ \\ E^{-}(u,v)= \text{ Erfi }\left[ \dfrac{2 + \bar{k}\ - i \sigma ^2 u -2 \sigma ^2 \sqrt{\epsilon } v }{\sigma \sqrt{-2+2\sigma ^2 \sqrt{\epsilon } v}}\right] -\text{ Erfi }\left[ \frac{-2 + \bar{k}- i \sigma ^2 u +2 \sigma ^2 \sqrt{\epsilon } v}{\sigma \sqrt{-2+2\sigma ^2 \sqrt{\epsilon } v}}\right] . \end{array} \right. \end{aligned}$$
(55)

The corresponding wave packets are plotted in Fig. 9. We have used the approximation \(\sqrt{(1-k^2)} \cong 1-\frac{1}{2}k^2 \), to evaluate the integrals in the above cases.

Fig. 9
figure 9

The figures show the probability function of the wave packet \(\left| \Psi _{\epsilon }^{\pm }(u,v)\right| ^2 \) in the case \( D_{1}= 0\) and \( D_{2}\ne 0 \) for the quintessence and phantom scalar fields

Full size image

\(\bullet \) \(D_1=D_2\ne 0\) and \(D_1=-D_2\ne 0\): In these cases the wave function is of the form

$$\begin{aligned} \Psi _{\epsilon }^{\pm }(u,v)=\frac{2}{(\sqrt{\pi }\sigma )^{\frac{1}{2}}}\int \,dk\, e^{-\frac{(k-\bar{k})^2}{2\sigma ^2}}\left( \cos (ku\pm \sqrt{\epsilon (k^2 -1)}v) \right) , \end{aligned}$$
(56)

for \(D_1=D_2\), and

$$\begin{aligned} \Psi _{\epsilon }^{\pm }(u,v)=\frac{2 i}{(\sqrt{\pi }\sigma )^{\frac{1}{2}}}\int \,dk\, e^{-\frac{(k-\bar{k})^2}{2\sigma ^2}} \left( \sin (ku\pm \sqrt{\epsilon (k^2 -1)}v)\right) , \end{aligned}$$
(57)

for \(D_1=-D_2\), where their approximate behavior for some typical values of the parameters is shown in Fig. 10.

Fig. 10
figure 10

approximate behavior of the wave packet for the cases \(D_1=D_2\) or \(D_1=-D_2\)

Full size image

It should be noted that our attention here was focused on extracting the damped exponential potential function and the results obtained in this section refer to the quantization of this model. One may find a review of the classical solutions and the semi-classical WKB approximation of the quantum regime for the barotropic FRW model in [71]. Also, the exact solutions of the WDW equation for the exponential scalar potential have been discussed in [72] and [73], and the shape of the wave function has been drawn in terms of the scalar field. However, in the present work, extracting the exponential potential function, the probability function of the wave packets in different states is what we have achieved. We did this for both usual and phantom scalar field models and have made it possible to compare the results by drawing related diagrams.

Fig. 11
figure 11

The time behavior of the scalar field considered in this paper

Full size image

Another point that seems appropriate to mention here is the correlation between these quantum patterns and the classical trajectories. A question in quantum cosmology is the recovery of classical solutions from the corresponding quantum model or, in other words, how the WDW wave packets can predict a classical universe. In quantum cosmology, the coherent wave packets are usually constructed with suitable asymptotic behavior in the minisuperspace, peaking in the vicinity of the classical trajectory. As we have done here, this task is usually done by choosing appropriate weight functions in the integrals that describe the superposition of the eigenfunctions of the WDW equations, see [74,75,76] for more details. In this sense, We expect that the square of the wave functions plotted in Figs. 8, 9, and 10, have their dominant peaks in the vicinity of the classical trajectories obtained in the previous section. However, comparing these, in the presented model may not be straightforward. This is because that the classical solutions are expressed in terms of the variables a and \(\phi \), while the quantum wave functions are finally expressed in terms of the variables u and v, after some change of variables in (44) and (45). Therefore, here we only limited ourselves to a qualitative analysis based on (44) and (45). For example, in the case where \(\epsilon =-1\), from (44), we get \(u\sim Y (\cosh X-i\sinh X)\) and \(v\sim Y(-i\sinh X-\cosh X)\), which may results \(u\sim \pm v\). Now, a glance at the Figs. 8 and 9 shows that these may be interpreted as the locus of peaks of \(|\Psi _{-1}|^2\), in \(u-v\) plane. Other cases can also be checked with a similar analysis, which means that our quantum pattern is in a good agreement with its classical counterpart.

6 Final Remarks

In this article, we presented two proposals for the scalar field. The first one was

$$\begin{aligned} \phi _1(t)=\frac{2}{\lambda } \ln \left[ \frac{1}{2}\lambda ^2 H_{0}(t-t_{0})+\epsilon \right] , \end{aligned}$$

which led to the damping exponential potential \(V(\phi )\sim e^{-\lambda \phi }\). Our second proposal for the scalar field was

$$\begin{aligned} \phi _2(t)=\pm \sqrt{\frac{2\epsilon }{3}} \ln \left[ \tanh \left( \frac{3}{2}H_{0}(t-t_{0})\right) \right] , \end{aligned}$$
$$\begin{aligned} \phi _2(t)=\pm \sqrt{\frac{-2\epsilon }{3}} \ln \left[ \tanh \left( -\frac{3}{2}H_{0}(t-t_{0})\right) \right] , \end{aligned}$$

which gave the potentials \(V(\phi )=3 H_{0}^2\) and \(V(\phi )\sim e^{\pm \sqrt{-6 \epsilon }\phi }\), respectively. These functions for the scalar fields are plotted in Fig. 11.

We also have found the Hubble functions of these models as

$$\begin{aligned} H_{1}(\phi )= H_{0} e^{-\frac{\lambda }{2}\phi }, \end{aligned}$$

for the first proposal and

$$\begin{aligned} H_{2}(\phi )=H_{0}\cosh \left( \pm \sqrt{\frac{3\epsilon }{2}}\phi \right) , \end{aligned}$$
$$\begin{aligned} H_{2}(\phi )=H_{0}\cosh \left( \pm \sqrt{\frac{-3\epsilon }{2}}\phi \right) , \end{aligned}$$

for the second one which have shown in Fig. 12.

Fig. 12
figure 12

The behavior of the Hubble parameter in terms of \(\phi \), considered in this paper

Full size image
Fig. 13
figure 13

The EoS parameter for the models considered in this paper

Full size image

In order to see the application range of the two proposed models for the scalar field, we consider the EoS parameter of these two models. We found that this parameter takes the form

$$\begin{aligned} \omega _{1}=\frac{1}{3}\epsilon \lambda ^2 -1, \end{aligned}$$

for our first proposal which holds for the quintessence and phantom fields for all values of \(\lambda \). For the second model, on the other hand, the EoS parameter is obtained as

$$\begin{aligned} \omega _{2}(\phi )=2 \tanh ^2\left( \sqrt{\frac{3\epsilon }{2}}\,\phi \right) -1, \end{aligned}$$

for the model a, and

$$\begin{aligned} \omega _{2}(\phi )=\dfrac{1}{2 \tanh ^2\left( \sqrt{\frac{-3\epsilon }{2}}\,\phi \right) -1}, \end{aligned}$$

for the model b. According to which we have plotted in Fig. 13, one finds that the scalar potential of the case (a) is useful for describing the quintessence field while (b) is suitable to describe the phantom. Therefore, the cases (a) and (b) of the second proposal can be written in the following form

$$\begin{aligned} \phi _2(t)=\pm \sqrt{\frac{2}{3}} \ln \left[ \tanh \left( \frac{3\epsilon }{2}H_{0}(t-t_{0})\right) \right] . \end{aligned}$$

It should be noted that if the second proposal is examined in the general case \(h\ne 0 \), we will have: \(H_{0}=\epsilon A^2 B+h\), and thus in the case (a) for which \(A=\pm \sqrt{\frac{2\epsilon }{3}}\), the constant B will be \(B=\frac{3}{2} (H_{0}-h)\), and the potential function takes the form

$$\begin{aligned} V(\phi )=\alpha _{1}+\alpha _{2}\cosh (\frac{\phi }{A}), \end{aligned}$$

where \(\alpha _{1}=3(H_{0}-h)^2 +3h^2\), \(\alpha _{2}=6h(H_{0}-h)\) and \(\alpha _{1}+\alpha _{2}=3H_{0}^2=V_{0}\). We also argued that for the purposes of quantum gravity the potential can be written in the following approximate form

$$\begin{aligned} V(\phi )=\alpha _{1}+\frac{\alpha _{2}}{2}\left( e ^{\frac{\phi }{A}}+e ^{-\frac{\phi }{A}}\right) \approx \alpha _{1}+\frac{\alpha _{2}}{2}e ^{\frac{\phi }{A}}, \end{aligned}$$

or

$$\begin{aligned} V(\phi )\approx \alpha _{1}+\frac{\alpha _{2}}{2}e ^{\pm \sqrt{\frac{3\epsilon }{2}}\phi }, \end{aligned}$$

which shows that our second proposal in both cases (a) and (b) results a exponential potential function.

The last part of the article is dedicated to the quantization of the presented model in the framework of the WDW approach of quantum cosmology. We found the eigenfunctions and with the use of them construct the closed form expressions for the wave functions of the universe. The resulting quantum wave packets are then used to draw the probability function of each model. Finally, we would like to emphasize that although some results have been obtained in previous works, as some of them are mentioned, in this paper a comprehensive and detailed study of classical and quantum solutions in a spatially flat FLRW geometry with damped exponential potential function is performed. We extracted the potential function from two proposals for the scalar fields in terms of time.