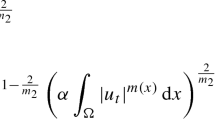1 Introduction

Nonlinear optics studies how light behaves in materials with nonlinear optical properties. It looks at how a one–dimensional wave moves through a nonlinear medium with dispersion [1]. When discussing electromagnetic waves in a waveguide or acoustic waves in a pipe, the phrase “one–dimensional wave” indicates the waves’ restricted capacity to move in more than one dimension [2].

Nonlinear media have optical properties that depend on how strongly the electromagnetic field goes into the material. In other words, the behavior of the wave is no longer proportional to the incoming information, and nonlinear impacts may become significant [3]. Still, dispersion processes explain why the refractive index of a material changes when an electromagnetic wave passes through it. This suggests the wave disperses because its different frequencies move at varying speeds [4].

When modeling how a one–dimensional wave moves through a nonlinear medium with dispersion, it is essential to consider how these two things work together. In particular, nonlinearities can make the wave grow as it moves, leading to soliton propagation when it keeps its original shape and intensity over long distances [5]. Pulse widening happens when the wave’s temporal profile gets longer because of dispersion, which occurs when the wave’s frequency spreads out [6].

These effects may be examined using mathematical models such as the nonlinear Schrödinger equation and GMEW equation, which describes the evolution of the wave envelope during propagation [7]. The behavior of the wave may be anticipated by numerically solving this equation, which accounts for dispersion and nonlinearities. One–dimensional wave propagation in nonlinear media with dispersion processes could be helpful in a number of fields, such as laser physics, photonics, and telecommunications [8]. In order to build devices and systems that exploit nonlinearities and dispersion to achieve specific goals, such as long–distance information transmission or the creation of ultrashort laser pulses, it is necessary to comprehend the interplay between these two phenomena [9].

In this context, this paper studies the GMEW equation that is a flexible and cutting–edge method for evaluating and classifying data [10]. This new method is based on Equal–Width (EW) discretization, often used to prepare data and design features [11]. When discretizing continuous data, the GMEW equation is more flexible and easy to use than the EW method. It was created in part to remedy deficiencies in the EW method. This article is an introduction to the GMEW equation [12]. Its purpose is to teach the reader about its history, key ideas, and possible uses. The GMEW equation is given by [13,14,15]

$$\begin{aligned} -c_{2} \,\frac{\partial ^{3} \,\mathcal {E}}{\partial t\, \partial x\, \partial x}+c_{1} \,\mathcal {E}^{\varrho } \,\frac{\partial \,\mathcal {E}}{\partial x}+\frac{\partial \,\mathcal {E}}{\partial t}=0, \end{aligned}$$
(1)

where \(\mathcal {E}=\mathcal {E}(x,t)\) describes wave propagation in a nonlinear medium with dispersion processes in one dimension. While \(c_{1},\, c_{2},\, \varrho \) are arbitrary constants. There are a variety of computational methods that may be utilized to solve the GMEW equation numerically. Some examples are as follows [16,17,18]:

  • Bulet Finite difference methods are often used to solve partial differential equations quantitatively. Using grid discretization and finite difference approximation, the GMEW equation derivatives are estimated.

  • Bulet Fourier spectral approaches add the sine and cosine functions as a scalar. The GMEW equation is Fourierized with this method. Runge–Kutta and split-step Fourier techniques may be helpful.

  • Bulet Adomian decomposition solves nonlinear differential equations by series extension. The linear differential equations of the GMEW equation are amenable to iterative numerical solutions. The answer is determined using series expansion.

These are some computer–based approaches to solving the GMEW equation [19, 20]. The problem, the available computing power, and how quickly and accurately you need to solve it all influence your chosen strategy [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. Now, we are going to use the extended Khater method to find some novel solitary wave solutions of (1). Employing the next wave transformation \(\mathcal {E}=\mathcal {E}(x,t)=\upsilon (\eta ),\, \eta =\lambda \,t+x\), to Eq. (1), gets

$$\begin{aligned} -c_{2} \,\lambda \,\upsilon ^{(3)}+c_{1} \,\upsilon ' \, \upsilon ^{\varrho }+\lambda \,\upsilon '=0. \end{aligned}$$
(2)

Balancing the nonlinear term and highest order derivative term in (2) along with the extended Khater method’s auxiliary equation \(f''(\eta )= \frac{1}{\log (K)} \left( -\alpha ^{2} \,K^{-2 \,f(\eta )}-\alpha \,\beta \, K^{-f(\eta )}+\right. \) \(\left. \beta \,\gamma \,K^{f(\eta )}+\gamma ^{2} \,K^{2 \,f(\eta )}\right) \), where \(\alpha , \,\beta , \, \gamma \) are arbitrary constants, yields necessary of using another transformation that is given by \(\upsilon =\varphi (\eta )^{2/\varrho }\). The new transformation converts (2) into the following ODE

$$\begin{aligned} \frac{c_{1} \,\varphi ^{4} \varphi '}{\lambda }-c_{2} \,\varphi ^{(3)} \,\varphi ^{2}-\frac{\left( 2 \,c_{2} \,(\varrho -2) \,(\varrho -1)\right) \,\left( \varphi '\right) ^{3}}{\varrho ^{2}}+\frac{\varphi \,\left( 3 \,c_{2} \,(\varrho -2)\right) \, \varphi ' \, \varphi ''}{\varrho }+\varphi ^{2} \,\varphi '=0. \end{aligned}$$
(3)

Using the homogeneous balance principles to (3) and along with the extended Khater method’s headlines, gets the

$$\begin{aligned} \varphi (\eta )=\sum \limits _{i=0}^{n} a_{i} \, \left( K^{f(\eta ) )}\right) ^{i}=a_{1} \,K^{f(\eta )}+a_{0}, \end{aligned}$$
(4)

where \(a_{0},\, a_{1}\) are arbitrary constants.

In our paper, we investigate some new solitary wave solutions of the model under study, and in Sect. 2, we talk about how accurate they are. A graphical representation of the solutions can be found in Sect. 3. The comprehensive study’s conclusion is presented in Sect. 4.

2 Stable Solitary Wave and Approximate Solutions

In this section, we examine the computational solutions of the GMEW equation with the extended Khater method [38, 39] as well as the variational iteration \((\mathcal {VIM})\) method [40, 41].

2.1 Stable Soliton Wave Solution

Employing the extended Khater method to (3) along with Eq. (4), gets the following values of the above–mentioned parameters

Set I

$$\begin{aligned} a_{0}\rightarrow \frac{\sqrt{{a_{1}^{2}} \left( \beta ^{2}-4 \alpha \gamma \right) }+a_{1} \beta }{2 \gamma },c_{1}\rightarrow \frac{3 \gamma ^{2} \lambda }{{a_{1}^{2}} \left( \beta ^{2}-4 \alpha \gamma \right) },c_{2}\rightarrow \frac{4}{\beta ^{2}-4 \alpha \gamma },\varrho \rightarrow -4. \end{aligned}$$

Set II

$$\begin{aligned} a_{0}\rightarrow \frac{a_{1} \beta }{2 \gamma },c_{1}\rightarrow -\frac{6 \gamma ^{2} \lambda }{{a_{1}^{2}} \left( \beta ^{2}-4 \alpha \gamma \right) },c_{2}\rightarrow \frac{1}{8 \alpha \gamma -2 \beta ^{2}},\varrho \rightarrow 1. \end{aligned}$$

Set III

$$\begin{aligned} a_{0}\rightarrow \frac{a_{1} \beta }{2 \gamma },c_{1}\rightarrow -\frac{12 \gamma ^{2} \lambda }{{a_{1}^{2}} \left( \beta ^{2}-4 \alpha \gamma \right) },c_{2}\rightarrow -\frac{2}{\beta ^{2}-4 \alpha \gamma },\varrho \rightarrow 2. \end{aligned}$$

Backing these values into Eq. (4) along with the solution of the extended Khater method’s auxiliary equation’ s solutions, leads to the following solitary wave solutions of the investigated model.

For \(\beta ^{2}-4 \,\alpha \,\gamma <0\), we get

$$\begin{aligned} \mathcal {E}_{\textbf {I},1}(x,t)=\frac{\sqrt{2}}{\sqrt{\frac{\sqrt{{a_{1}^{2}} \left( \beta ^{2}-4 \alpha \gamma \right) }+a_{1} \sqrt{4 \alpha \gamma -\beta ^{2}} \tan \left( \frac{1}{2} \sqrt{4 \alpha \gamma -\beta ^{2}} (\lambda t+x+\mho )\right) }{\gamma }}}, \end{aligned}$$
(5)
$$\begin{aligned} \mathcal {E}_{\textbf {I},2}(x,t)=\frac{\sqrt{2}}{\sqrt{\frac{\sqrt{{a_{1}^{2}} \left( \beta ^{2}-4 \alpha \gamma \right) }+a_{1} \sqrt{4 \alpha \gamma -\beta ^{2}} \cot \left( \frac{1}{2} \sqrt{4 \alpha \gamma -\beta ^{2}} (\lambda t+x+\mho )\right) }{\gamma }}}, \end{aligned}$$
(6)
$$\begin{aligned} \mathcal {E}_{\textbf {II},1}(x,t)=-\frac{{a_{1}^{2}} \left( \beta ^{2}-4 \alpha \gamma \right) \tan ^{2}\left( \frac{1}{2} \sqrt{4 \alpha \gamma -\beta ^{2}} (\lambda t+x+\mho )\right) }{4 \gamma ^{2}}, \end{aligned}$$
(7)
$$\begin{aligned} \mathcal {E}_{\textbf {II},2}(x,t)=-\frac{{a_{1}^{2}} \left( \beta ^{2}-4 \alpha \gamma \right) \cot ^{2}\left( \frac{1}{2} \sqrt{4 \alpha \gamma -\beta ^{2}} (\lambda t+x+\mho )\right) }{4 \gamma ^{2}}, \end{aligned}$$
(8)
$$\begin{aligned} \mathcal {E}_{\textbf {III},1}(x,t)=\frac{a_{1} \sqrt{4 \alpha \gamma -\beta ^{2}} \tan \left( \frac{1}{2} \sqrt{4 \alpha \gamma -\beta ^{2}} (\lambda t+x+\mho )\right) }{2 \gamma }, \end{aligned}$$
(9)
$$\begin{aligned} \mathcal {E}_{\textbf {III},2}(x,t)=\frac{a_{1} \sqrt{4 \alpha \gamma -\beta ^{2}} \cot \left( \frac{1}{2} \sqrt{4 \alpha \gamma -\beta ^{2}} (\lambda t+x+\mho )\right) }{2 \gamma }. \end{aligned}$$
(10)

While, for \(\beta ^{2}-4 \,\alpha \,\gamma >0\), we get

$$\begin{aligned} \mathcal {E}_{\textbf {I},3}(x,t)=\frac{\sqrt{2}}{\sqrt{\frac{\sqrt{{a_{1}^{2}} \left( \beta ^{2}-4 \alpha \gamma \right) }+a_{1} \sqrt{\beta ^{2}-4 \alpha \gamma } \tanh \left( \frac{1}{2} \sqrt{\beta ^{2}-4 \alpha \gamma } (\lambda t+x+\mho )\right) }{\gamma }}}, \end{aligned}$$
(11)
$$\begin{aligned} \mathcal {E}_{\textbf {I},4}(x,t)=\frac{\sqrt{2}}{\sqrt{\frac{\sqrt{{a_{1}^{2}} \left( \beta ^{2}-4 \alpha \gamma \right) }+a_{1} \sqrt{\beta ^{2}-4 \alpha \gamma } \coth \left( \frac{1}{2} \sqrt{\beta ^{2}-4 \alpha \gamma } (\lambda t+x+\mho )\right) }{\gamma }}}, \end{aligned}$$
(12)
$$\begin{aligned} \mathcal {E}_{\textbf {II},3}(x,t)=\frac{{a_{1}^{2}} \left( \beta ^{2}-4 \alpha \gamma \right) \tanh ^{2}\left( \frac{1}{2} \sqrt{\beta ^{2}-4 \alpha \gamma } (\lambda t+x+\mho )\right) }{4 \gamma ^{2}}, \end{aligned}$$
(13)
$$\begin{aligned} \mathcal {E}_{\textbf {II},4}(x,t)=\frac{{a_{1}^{2}} \left( \beta ^{2}-4 \alpha \gamma \right) \coth ^{2}\left( \frac{1}{2} \sqrt{\beta ^{2}-4 \alpha \gamma } (\lambda t+x+\mho )\right) }{4 \gamma ^{2}}, \end{aligned}$$
(14)
$$\begin{aligned} \mathcal {E}_{\textbf {III},3}(x,t)=\frac{a_{1} \sqrt{\beta ^{2}-4 \alpha \gamma } \tanh \left( \frac{1}{2} \sqrt{\beta ^{2}-4 \alpha \gamma } (\lambda t+x+\mho )\right) }{2 \gamma }, \end{aligned}$$
(15)
$$\begin{aligned} \mathcal {E}_{\textbf {III},4}(x,t)=\frac{a_{1} \sqrt{\beta ^{2}-4 \alpha \gamma } \coth \left( \frac{1}{2} \sqrt{\beta ^{2}-4 \alpha \gamma } (\lambda t+x+\mho )\right) }{2 \gamma }. \end{aligned}$$
(16)

2.1.1 Solution’s Stability

Now, we are using the Hamiltonian system’s characterizations to figure out the stability property of the above–constructed solutions [42]. Firstly, we construct the momentum of Eq. (13)

$$\begin{aligned} \begin{aligned} \mathcal {M}&=\frac{1}{2} \int _{-5}^{5} \mathcal {E}^{2} (\eta ) \, d\,\eta \\&=\frac{2 }{3 \lambda }\, \Bigg {(}15 \lambda \Big {(}\tanh ^{-1}\left( \tanh \left( \frac{5 (\lambda +1)}{2}\right) \right) +\tanh ^{-1}\left( \tanh \left( \frac{5}{2}-\frac{5 \lambda }{2}\right) \right) \Big {)}\\&~~+\tanh ^{2}\left( \frac{5 (\lambda +1)}{2}\right) -\tanh ^{2}\left( \frac{1}{2} (5-5 \lambda )\right) +4 \log \left( 1-\tanh ^{2}\left( \frac{5 (\lambda +1)}{2}\right) \right) \\&~~-4 \log \left( 1-\tanh ^{2}\left( \frac{1}{2} (5-5 \lambda )\right) \right) \Bigg {)}. \end{aligned} \end{aligned}$$
(17)

Thus, the stability condition is given by

$$\begin{aligned} \frac{\partial \, \mathcal {M}}{\partial \, \lambda } \bigg {|}_{\lambda =2}=6.52032243>0. \end{aligned}$$
(18)

Consequently, (13) is table solution on the following interval \(x \in [-5,5],\, t \in [-5,5].\) Using same technique, checks the stability property of the other solutions Fig. 1.

Fig. 1
figure 1

Representation for the momentum of (13) in two-dimensional graph

Full size image

2.2 Numerical solutions

Applying the \(\mathcal {VIM}\) to (1) with some specific values for the above–mentioned parameters in (13), yields

$$\begin{aligned} \mathcal {E}_{0}(x,t)=\tanh ^{2}\left( \frac{x}{2}\right) , \end{aligned}$$
(19)
$$\begin{aligned} \mathcal {E}_{1}(x,t)=\tanh ^{2}\left( \frac{x}{2}\right) -48 t \sinh ^{8}\left( \frac{x}{2}\right) \text {csch}^{5}(x), \end{aligned}$$
(20)
$$\begin{aligned} \begin{aligned} \mathcal {E}_{2}(x,t)=&\frac{1}{512} \tanh \left( \frac{x}{2}\right) \text {sech}^{10}\left( \frac{x}{2}\right) \Bigg {(}-504 t^{3}+6 t \cosh (x) \left( 117 t^{2}-6 t \sinh ^{3}(x)+62\right) -3 t \Big {(}4 \left( 18 t^{2}+7\right) \\&\times \cosh (2 x)+\left( 28-6 t^{2}\right) \cosh (3 x)-72 t \sinh ^{3}(x)+\cosh (4 x)\Big {)}+375 t+42 \sinh (x)+48\\&\times \sinh (2 x)+27 \sinh (3 x)+8 \sinh (4 x)+\sinh (5 x)\Bigg {)}. \end{aligned} \end{aligned}$$
(21)

3 Solutions’ Graphical Representation

The GMEW equation is an extension of the conventional EW method that contains a modification factor to produce bins of variable lengths. The distribution of the data may reveal areas with varying densities, which is the typical method for determining this variable. The modification factor modifies the widths of the produced bins to better match the data’s local attributes.

The GMEW equation may be used for several data analysis applications, like:

  • Discreteizing continuous data into more manageable intervals during the preprocessing stage is one way for decreasing computer demands and facilitating subsequent analysis.

  • GMEW equation may be used to generate new features depending on the distribution of the underlying data, hence possibly enhancing the performance of machine learning algorithms.

  • The third use is clustering and classification, where discretized data may be utilized as input for clustering algorithms and classification tasks, enabling the discovery of previously unknown patterns and correlations.

In conclusion, the GMEW equation is a cutting-edge data discretization methodology that gives more flexibility and adaptability than conventional equal–width techniques. By taking into consideration the underlying data distribution and modifying bin widths appropriately, the GMEW equation may improve the efficiency of data analysis and machine learning by providing more accurate and relevant representations of continuous data.

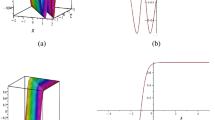
Here, we decompose the discovered computational solutions into their component polar, density, 3-D, and 2-D graphs. We expand on the built-in solutions described before ( (11),  (13),  (15),  (21)) when \( \Bigg {[} \alpha =2,\,a_{1}=-1,\,\beta =3,\,\gamma =1,\,\lambda =4,\,\mho =5\, \& \, \alpha =3,\,a_{1}=-2,\,\beta =5,\,\gamma =2,\,\lambda =10,\,\mho =20\, \& \, \alpha =6,\,a_{1}=3,\,\beta =5,\,\gamma =1,\,\lambda =2,\,\mho =-1 \Bigg {]}\).In these graphs, (11), (13) and (15) show bright–dark soliton waves, and (21) shows periodic waves Figs. 2, 3, and 4. Also, the matching between analytical and numerical solutions are illustrated by Fig. 5 and Table 1. Specifically, we have demonstrated the interaction between the above-analytical and numerical solutions by displaying examples in Figs. 6, and 7  examples concern wave propagation in nonlinear materials with dispersive processes Fig. 8.

Fig. 2
figure 2

Graphically displays of (11) in (a) 3D, (b) 2D, (c) contour and (d) polar plots

Full size image
Fig. 3
figure 3

Graphically displays of (13) in (a) 3D, (b) 2D, (c) contour and (d) polar plots

Full size image
Fig. 4
figure 4

Graphically displays of (15) in (a) 3D, (b) 2D, (c) contour and (d) polar plots

Full size image
Fig. 5
figure 5

Graphically displays of Eq. (21) in (a) 3D, (b) 2D, (c) contour and (d) polar plots

Full size image

   

Table 1 Analytical, semi-analytical, and absolute error values for (13) via \(\mathcal {VIM}\)
Full size table
Fig. 6
figure 6

Constructed solution (11)’s matching with the numerical solutions based of the \(\mathcal {VIM}\) and shown values in Table 1

Full size image
Fig. 7
figure 7

In nonlinear media, these graphs (a,  b,  c,  d,  e,  f,  g,  h,  i) illustrate dispersion mechanisms and wave propagation

Full size image
Fig. 8
figure 8

Dispersion mechanisms and wave propagation are illustrated in these graphs (j,  k,  l,  m,  n,  o) when applied to nonlinear media

Full size image

4 Conclusion

Throughout the course of this study, soliton wave solutions for the GMEW model were generated utilizing a variety of equations. There were rational, hyperbolic, and trigonometric equations among them. These connections give more information about how waves move through nonlinear media. We could ensure success by using the mathematical \(\mathcal {VIM}\) to double-check our calculations. These lessons have been broken down and simplified using various visual aids. We decided if the study was new and vital by comparing its results to those of other studies that had found similar things. Each result was checked in Mathematica 13.1 before being re-implemented in the primary model.