Study of Slowly Rotating Black Hole in Dilatonic Einstein-Gauss-Bonnet Gravity

Abstract

We study some properties of a stationary and axisymmetric slowly black hole in the Einstein-Gauss-Bonnet-dilaton (EGBD) theory. This nontrivial gravity model that is the best motivated alternative to the general relativity (GR) provides quadratic curvature terms in the action. By using pertubative analytical black hole solutions in EGBD theory, we consider the domain of existence and quadrupole moment of slowly spinning BH in the small scaled angular momentum limit. The effects of the Gauss-Bonnet coupling and the spin parameter on the radii of the static limit surface are also investigated.

1 Introduction

The Einstein-Gauss-Bonnet-dilaton (EGBD) theory that is well known as an interesting extension of general relativity (GR) modifies the Einstein-Hilbert action by adding a real scalar feild called as dilaton. In this theory, the dilaton is non-minimally coupled to the Gauss-Bonnet (GB) term [1, 2] that leads to quadratic curvature terms in the action. The EGBD gravity provides a ghost-free theory with second order of equation of motion. Also, the EGBD gravity occurs in the low-energy effective string theory in which case the scalar field can be realized as the string dilaton [3].

Black holes (BHs) that are important objects in the nature introduced as a significant prediction of GR. Due to existence of higher curvature coupling, BH solutions in EGBD gravity are different from those estimated by GR. So, the investigation of BHs in EGBD theory makes new insights on some appearances of quantum gravity and can be used to expand testable predictions of the theory. The first discussion on BH solutions of the EGBD gravity can be found in Refs. [4, 5]. In addition, numerical forms of rapidly spinning BH solutions in EGBD theory have been considered in [6,7,8] within a non-perturbative approach for finite spin and arbitrary values of the angular momentum. While they don’t regard the treatment of EGBD theory as an effective field theory but they found that the EGBD black holes can display some physical differences when compared to the Kerr solution. Their results are also important to study on geodesic properties of BHs and indicates that EGBD black holes can violate the Kerr bound.

Moreover, analytical stationary BH solutions in EGBD gravity were derived for non-spinning BHS [9] and slowly rotating BHS [17] that are spherically symmetric and approximate axisymmetric respectively. Furthermore, by using the perturbative approach, the approximate slowly rotating BH solutions of EGBD theory in the small coupling limit have been found to quadratic order [15] and fifth order in [10] of the BH spin.

We know that Einstein-Gauss-Bonnet-dilaton (EGBD) gravity is a theoretically well-motivated alternative theory of General Relativity (GR) in the strong-gravity. Static and rotating BHs solutions in EGBD gravity that are found numerically can provide deviations from the Kerr black holes of Einstein’s gravity. Thus (EGBD) gravity can be tested with observations of astrophysical black holes. In [22], a preliminary study has been done on the possibility of distinguishing the Kerr black holes in Einstein’s gravity from the black holes in Einstein-dilaton-Gauss-Bonnet gravity with present and future X-ray missions from the analysis of the disk’s reflection spectrum. X-ray reflection spectroscopy that is a promising technique for testing general relativity in the strong field regime may distinguish the black holes in Einstein-dilaton-Gauss-Bonnet gravity from those in Einstein’s gravity in the future. Furthermore, recent gravitational wave observations allow us to test theories of gravity in the strong-gravity regime. For example, the authors of [23] discussed the testing Einstein-dilation Gauss-Bonnet gravity by using two new neutron star black hole binaries (GW200105 and GW200115). They made two independent analyses to find constraints on the Gauss-Bonnet coupling constant of the theory. Constraints on this parameter have also been investigated by the authors of Ref. [24] from a cosmological point of view which is the best constriction up to now using cosmological data at the background level. In addition, results of [28] show that the Gauss-Bonnet coupling should fall in the possible negative range $\frac {\alpha }{M^{2}}\in (-4.5, 0)$ or take very small positive values by using the observation data of M87^∗. More studies related to the (EGBD) gravity can be found in Refs. [25,26,27, 29,30,31,32,33].

In this work, we are interested to study some properties of slowly rotating BHs such as quadrupole moments and domain of existence by utilizing the analytical solutions of Ref. [15] that are quadratic order in the ratio of the spin angular momentum to the BH mass squared. It must be mentioned that previous results on these properties found in [7] are in numerical forms. However their solutions are of limited practical use and are impractical for more studies on geodesic properties of blsck hole. The plan of this study is organized as follows. In Section 2 we review an approximate slowly rotating BH solution in EGBD gravity to quadratic order in the BH spin and coupling parameter. In Section 3, we first study the horizon structure of the BH and then some properties of the EGBD black holes is considered regarding the different values for the EGBD coupling parameters as well as the small spin angular momentum of the BHs. Finally, in Section 4 we present our conclusions.

2 BH Solutions in Einstein-Gauss-Bonnet-dilaton Gravity

In this section, We review the space-time metric and BH solutions in EGBD theory that were obtained by [15] to second order both in the spin and in the coupling parameter. This theory is described by the following action

$$ S\equiv \int d^{4}x \sqrt{-g} \left\lbrace\kappa R+\alpha e^{\vartheta} \left[R^{2}-4R_{ab}R^{ab}+R_{abcd}R^{abcd}\right]-\frac{\beta}{2}\left[\bigtriangledown_{a}\vartheta \bigtriangledown^{a} \vartheta+ 2V(\vartheta)\right]+ \mathcal{L}_{mat}\right\rbrace $$

(1)

where, g denotes to the determination of the metric g_ab and R,R_ab and R_abcd show the Ricci scalar, Ricci tensor and the Riemann tensor respectively. The external matter Lagrangian is represented by ${\mathscr{L}}_{mat}$ and 𝜗 is a scalar field coupled to the Gauss-Bonnet term. The α and β indicate to the coupling constants and $\kappa =\frac {1}{16\pi }$. For simplicity, we take β = 1 in the following discussions. Also, the Latin letters are used for space-time indices and the metric signature is (−,+,+,+). The field equation of EGBD gravity are given by

$$ G_{ab}+\frac{\alpha}{\kappa}\mathcal{D}^{(\vartheta)}_{ab}=\frac{1}{2\kappa}\left( T^{mat}_{ab}+T^{(\vartheta)}_{ab}\right) $$

(2)

where the scalar field stress-energy tensor T^(𝜗) reads as

$$ T^{(\vartheta)}=\beta\left[ \bigtriangledown_{a}\vartheta \bigtriangledown_{b}\vartheta-\frac{1}{2} g_{ab}\left( \bigtriangledown_{c}\vartheta \bigtriangledown^{c}\vartheta-2V(\vartheta)\right)\right], $$

(3)

and

$$ \begin{aligned} \mathcal{D}_{ab}^{(\vartheta)}\equiv &-2R\bigtriangledown_{a}\bigtriangledown_{b}\vartheta+2\left( g_{ab}R-2R_{ab}\right)\bigtriangledown^{c}\bigtriangledown_{c}\vartheta\\ & +8R_{c(a\bigtriangledown^{c}\bigtriangledown_{b})}\vartheta-4g_{ab}R^{cd}\bigtriangledown_{c}\bigtriangledown_{d}\vartheta \\&+4R_{acbd}\bigtriangledown^{c}\bigtriangledown^{d}\vartheta. \end{aligned} $$

(4)

The (2), (3) and (4) are of second differential order and therefore, the EGBD theory is free from the Ostrogradsky instability [11]. It must be noted that, the EGBD theory has a shift symmetry $(\vartheta \rightarrow \vartheta +\text {constant})$ so the theory does not allow mass term in the action (1). Therefore, we can choose V (𝜗) = 0.

2.1 Slowly Rotating BH Solutions

In this section, we study the slowly rotating BH solution in EGBD gravity at quadratic order in spin by using two approximation schemes have been applied in Ref. [12]. We first define a dimensionless parameter ζ as

$$ \zeta=\frac{\alpha^{2}}{\kappa M^{4}} $$

(5)

where M is the typical mass of the system. Theoretical constraint implies an upper bound on α as $\frac {\alpha ^{2}}{M^{2}}\leq 0.691$ for the static BH solution in EGBD gravity [13, 14]. This restriction motivates us to consider slowly BH solution in EGBD theory with small coupling approximation ζ ≪ 1 and χ ≡ a/m ≪ 1 where, m is the mass of the black hole and a = J/m. The parameter J is the magnitude of the spin angular momentum of the BH and then χ is dimensionless.

Let us start with the following Kerr metric by using Boyer-Lindquist-like coordinates (t,r,𝜃,φ)

$$ \begin{aligned} d{s^{2}_{K}}=&-\left( 1-\frac{2mr}{\Sigma}\right)dt^{2}-\frac{4marsin^{2}\theta}{\Sigma}dtd\varphi+\frac{\Sigma}{\Delta}dr^{2}\\ &{\Sigma} d\theta^{2}+\left( r^{2}+a^{2}+\frac{2ma^{2}rsin^{2}\theta}{\Sigma}\right)\sin^{2}\theta d\varphi^{2}. \end{aligned} $$

(6)

with Δ ≡ r² − 2mr + a² and ${\Sigma }\equiv r^{2}+a^{2}\cos \limits ^{2}\theta$.

In the small-coupling and slow-rotation approximation, the full metric can be expanded as [15]

$$ \begin{array}{@{}rcl@{}} g_{ab}&=&g_{ab}^{(0)}+\alpha^{\prime2}g_{ab}^{(2)}+\mathcal{O} \left( \alpha^{\prime4}\right), \end{array} $$

(7)

$$ \begin{array}{@{}rcl@{}} g_{ab}^{(0)}&=&g_{ab}^{(0,0)}+\chi^{\prime}g_{ab}^{(1,0)}+\chi^{\prime2}g_{ab}^{(2,0)}+\mathcal{O} \left( \chi^{\prime3}\right) \end{array} $$

(8)

and

$$ \alpha^{\prime2}g_{ab}^{(2)}=\alpha^{\prime2}g_{ab}^{(0,2)}+\chi^{\prime}\alpha^{\prime2}g_{ab}^{(1,2)}+\chi^{\prime2}\alpha^{\prime2}g_{ab}^{(2,2)}+\mathcal{O}\left( \alpha^{\prime2}\chi^{\prime3}\right), $$

(9)

where $\alpha ^{\prime }$ and $\chi ^{\prime }$ are bookkeeping parameters and show the order of the small-coupling and slow-rotation approximations respectively. It is also mentioned that $g_{ab}^{(0)}$ is the full Kerr metric, while $g_{ab}^{(2)}$ represents a deformation of GR metric. Furthermore, $g_{ab}^{(0,0)}$ is the Schwarzschild metric and the $g_{ab}^{(1,0)}$ and $g_{ab}^{(2,0)}$ are $\chi ^{\prime }$ perturbations.

The scalar field can be expanded as follows

$$ \vartheta=\alpha^{\prime}\left[\vartheta^{(0,1)}+\chi^{\prime}\vartheta^{(1,1)}+\chi^{\prime2}\vartheta^{(2,1)}\right]+\mathcal{O} \left( \alpha^{\prime}\chi^{\prime3}\right), $$

(10)

where

$$ \vartheta^{(0,1)}=\frac{\alpha}{\beta}\frac{2}{mr}\left( 1+\frac{m}{r}+\frac{4}{3}\frac{m^{2}}{r^{2}}\right) $$

(11)

and

$$ \vartheta^{(2,1)}=-\frac{\alpha\chi^{2}}{2\beta mr}\left[1+\frac{m}{r}+\frac{4}{5}\frac{m^{2}}{r^{2}}+\frac{2}{5}\frac{m^{3}}{r^{3}}+\frac{28}{5}\frac{m^{2}\cos^{2}\theta}{r^{2}}\left( 1+\frac{3m}{r}+\frac{48}{7}\frac{m^{2}}{r^{2}}\right)\right]. $$

(12)

Note that due to the Gauss-Bonnet invariant, we get 𝜗^(1,1) = 0 [15].

The authors of Refs. [16] and [17] found that at $\mathcal {O}\left (\alpha ^{\prime 2}\chi ^{\prime 0}\right )$ and $\mathcal {O}\left (\alpha ^{\prime 2}\chi ^{\prime }\right )$ the nonvanishing terms in $g_{ab}^{(0,2)}$ and $g_{ab}^{(1,2)}$ are respectively as follows

$$ \begin{array}{@{}rcl@{}} g_{tt}^{(0,2)}&=&-\frac{\zeta}{3}\frac{m^{3}}{r^{3}}\left[ 1+\frac{26m}{r}+\frac{66}{5}\frac{m^{2}}{r^{2}}+\frac{96}{5}\frac{m^{3}}{r^{3}}-\frac{80m^{4}}{r^{4}}\right], \end{array} $$

(13)

$$ \begin{array}{@{}rcl@{}} g_{rr}^{(0,2)}&=&-\frac{\zeta}{f^{2}}\frac{m^{2}}{r^{2}}\left[ 1+\frac{m}{r}+\frac{52}{3}\frac{m^{2}}{r^{2}}+\frac{2m^{3}}{r^{3}}+\frac{16}{5}\frac{m^{4}}{r^{4}}-\frac{368}{3}\frac{m^{5}}{r^{5}}\right], \end{array} $$

(14)

and

$$ g_{t\varphi}^{(1,2)}=\frac{3}{5}\zeta m\chi\frac{m^{3}\sin^{2}\theta}{r^{3}}\left[ 1+\frac{140}{9}\frac{m}{r}+\frac{10m^{2}}{r^{2}}+\frac{16m^{3}}{r^{3}}-\frac{400}{9}\frac{m^{4}}{r^{4}}\right] $$

(15)

where $f=1-\frac {2m}{r}$. Using the pertubative method, the metric components at $\mathcal {O}(\alpha ^{\prime 2}\chi ^{\prime 2})$ were obtained in Ref. [15] as

$$ \begin{array}{@{}rcl@{}} g_{tt}^{(2,2)}&=&-\zeta\chi^{2}\frac{m^{3}}{r^{3}}\left[\frac{4463}{2625}\left( 1+\frac{m}{r}+\frac{27479}{31241}\frac{m^{2}}{r^{2}}-\frac{2186945}{187446}\frac{m^{3}}{r^{3}}-\frac{448285}{31241}\frac{m^{4}}{r^{4}}-\frac{78975}{4463}\frac{m^{5}}{r^{5}} \right. \right.\\&& \left. \left.+\frac{1229650}{13389}\frac{m^{6}}{r^{6}} +\frac{303800}{13389}\frac{m^{7}}{r^{7}}\right) \times\left( 3\cos^{2}\theta-1\right) -\frac{1}{6}\left( 1+\frac{14m}{r}+\frac{52}{5}\frac{m^{2}}{r^{2}} \right. \right. \\ &&\left. \left. +\frac{1358}{14}\frac{m^{3}}{r^{3}}+\frac{652}{3}\frac{m^{4}}{r^{4}}+\frac{1204}{5}\frac{m^{5}}{r^{5}}-\frac{1792}{3}\frac{m^{6}}{r^{6}}-\frac{1120}{3}\frac{m^{7}}{r^{7}} \right) \right], \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} g_{rr}^{(2,2)}&=&-\zeta\frac{\chi^{2}}{f^{3}}\frac{m^{3}}{r^{3}}\left[ \frac{4463}{2625}\left( 1-\frac{5338}{4663}\frac{m}{r}-\frac{59503}{31241}\frac{m^{2}}{r^{2}}-\frac{7433843}{187446}\frac{m^{3}}{r^{3}}+\frac{13462040}{93723}\frac{m^{4}}{r^{4}}-\frac{7072405}{31241}\frac{m^{5}}{r^{5}} \right. \right. \\&& \left. \left. +\frac{9896300}{13389}\frac{m^{6}}{r^{6}}-\frac{28857700}{13389}\frac{m^{7}}{r^{7}}+\frac{13188000}{4463}\frac{m^{8}}{r^{8}}-\frac{7140000}{4463}\frac{m^{9}}{r^{9}}\right) \times\left( 3\cos^{2}\theta-1\right) \right. \\&& -\frac{r}{2m}\left( 1-\frac{m}{r}+\frac{10m^{2}}{r^{2}}-\frac{12m^{3}}{r^{3}} +\frac{218}{3}\frac{m^{4}}{r^{4}}+\frac{128}{3}\frac{m^{5}}{r^{5}}-\frac{724}{15}\frac{m^{6}}{r^{6}}-\frac{22664}{15}\frac{m^{7}}{r^{7}}\right.\\&&\left.\left.+\frac{25313}{15}\frac{m^{8}}{r^{8}}+\frac{1600}{3}\frac{m^{9}}{r^{9}}\right)\right], \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} g_{\theta\theta}^{(2,2)}&=&-\frac{4463}{2625}\zeta\chi^{2}\frac{m^{3}}{r^{3}}\left( 1+\frac{10370}{4463}\frac{m}{r}+\frac{266911}{62482}\frac{m^{2}}{r^{2}}+\frac{63365}{13389}\frac{m^{3}}{r^{3}}-\frac{309275}{31241}\frac{m^{4}}{r^{4}} \right.\\&& \left. -\frac{81350}{4463}\frac{m^{5}}{r^{5}}-\frac{443800}{13389}\frac{m^{6}}{r^{6}}+\frac{210000}{4463}\frac{m^{7}}{r^{7}}\right) \times r^{2}\left( 3\cos^{2}\theta-1\right), \end{array} $$

(18)

$$ g_{\varphi\varphi}^{(2,2)}= g_{\theta\theta}^{(2,2)}\sin^{2}\theta, $$

(19)

where satisfy the field (2) and all other metric components are zero.

By using the relations derived above, we are able to study some geometrical properties of the slowly spinning black hole in EGBD theory which are presented in the next section.

3 The Geometrical Properties of the Solutions

Now we study the geometrical properties of the analytical slowly BH solutions presented in the previous section. For this purpose, we consider some quantities which characterize the spinning EDGB black hole solution to second order in the spin and the leading order in the coupling parameter.

3.1 Horizon Structure

We first discuss the effects of GB coupling parameter α and spin parameter a on the horizon-like structure of slowly rotating BH in EGBD gravity. Using to metric at $\mathcal {O}(\alpha ^{\prime 2}\chi ^{\prime 2})$ given in (16)–(19) the horizons of rotating EGBD black hole can be obtained as the zero of

$$ g^{\mu\nu}\partial_{\mu}r \partial_{\nu}r=g^{rr}=g_{tt}g_{\varphi\varphi}-g_{t\varphi}^{2}=0. $$

(20)

That is the coordinate singularity of the metric (6). The largest root of equation above gives rise to the event horizon with the following from that is a null surface produced by null geodesic generators [15]

$$ r_{H}=r_{H,K}-\frac{49}{40}\zeta m-\frac{277}{960}\zeta m\chi^{2}, $$

(21)

with

$$ r_{H,K}=m+\left( m^{2}-a^{2}\right)^{\frac{1}{2}} $$

(22)

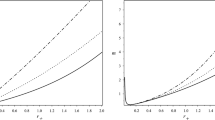
where shows the event horizon for the Kerr results. The behaviour of the event horizon radius with respect to the spin parameter a is plotted in Fig. 1a for fixed values of GB coupling parameter α. As the figure shows, the event horizon radius decreases with increasing a such that slowly rotating BH in EGBD gravity has smaller horizon radius as compared to the Kerr BH. The deviation from the Kerr result increases with increasing α. In Fig. 1b, we also plot the shapes of event horizon radius versus the GB coupling constant for different values of spin parameters a. It can be seen that for a fixed values of a, the radius decreases with increasing α. By this figure, one can find that in the slow rotation limit $\chi \rightarrow 0$, the deviation from the Kerr results is 1% and less for α ≤ 0.1. This deviation increases to 20% when χ ≤ 0.6.

Fig. 1

Variation of event horizon radius versus the spin parameter a (left) and GB coupling parameter α (right) with M = 1

By considering stationary and axisymmetric slowly rotating BH solution in EGBD gravity, the angular velocity Ω_H of the horizon is given by [15]

$$ {\Omega}_{H}=\frac{g_{tt}}{g_{t\varphi}}\vert_{r=r_{H}}={\Omega}_{H,K}\left( 1+\frac{20}{21}\zeta\right), $$

(23)

where the horizon angular velocity of Kerr metric Ω_H,K reads

$$ {\Omega}_{H,K}=\frac{a}{\left( r_{H,K}^{2}+a^{2}\right)}. $$

(24)

From (5) and (23) one can rewrite the parameter ζ as follows

$$ \zeta=\frac{20}{21} \left[ {\Omega}_{H}\frac{a}{\chi^{2}}\left( \chi^{2}+\left( 1-\sqrt{1-\chi^{2}}\right)^{2}-1\right) \right] $$

(25)

that help us to get more information about parameter space of the black hole. Using the obtained relations, the profile of GB coupling parameter α can be displayed versus the spin parameter a which is plotted in Fig. 2 for different values of horizon angular velocity Ω_H. This profile provides us information about the existence condition of the horizons that leads to a bound on the black hole parameters (a,α).

Fig. 2

The parameter space of (a,α) for the existence of the black hole horizon for various vales of Ω_H

The area under each curve shows the region that metric (6) allows different roots corresponding to the black hole horizons. One can see in Fig. 2 that the parameter space (a,α) increases with increasing Ω_H. // Also, the event horizon area of the BH can be found by [15]//

$$ A_{H}=2\pi{\int}^{\pi}_{0}\sqrt{g_{\theta\theta}g_{\varphi\varphi}}\vert_{r=r_{H}}d\theta=A_{H,K}\left[ 1-\frac{49}{40}\zeta\left( 1+\frac{19}{98}\chi^{2}\right) \right], $$

(26)

where the area of the Kerr metric A_H,K is given by

$$ A_{H,K}=4\pi\left( r_{H,K}^{2}+a^{2}\right). $$

(27)

In Fig. 3a and b, the dimensionless horizon area $a_{H}=\frac {A_{H}}{4\pi M^{2}}$ is plotted for different values of spin parameter and GB coupling by using the pertubative solutions. In Fig. 3a, it is clear that for a fixed value of the dimensionless reduced angular momentum J/M², the scaled horizon area a_H decreases with increasing the dimensionless coupling constant α/M². In Ref. [18], it was shown numerically that the EGBD spinning BH can exceed to Kerr bound J/M² ≤ 1 for a particular set of solution near to extremality. In the Fig. 3b, we study this results by using the analytical BHs solutions. We find that the violation from the Kerr bound can not be seen for slowly rotating BH in EGBD gravity by using the perturbative solutions. However, it must be noted that Our results are more valid in small areas of J/M² because of the initial approximations that we have used to obtain the analytical BHs solutions.

Fig. 3

The scaled horizon area $a_{H}=\frac {A_{H}}{M^{2}}$ versus the scaled angular momentum $\frac {J}{M^{2}}$ (right) and the scaled GB coupling $\frac {\alpha }{M^{2}}$ (left)

In addition, it is well known that stationary observes can be outside of the event horizons but, static observers can exist only outside of the static limit surface (SLS) that can be by the worldlines of timelike killing vector $\eta ^{\mu }_{(t)}$ [19]

$$ \eta^{\mu}_{(t)}\eta_{\mu(t)}=g_{tt}=0. $$

(28)

The zeros of (28) give us the radii of SLS which are proportional to the 𝜃 and black hole parameters (a,α) space. These roots are shown in Fig. 4a and b for different values of a,α, and 𝜃. By this curves we find that there are two real positive roots corresponding to the two radii of SLS. As can be seen in Fig. 4e, these radii are more affected by varying the parameter 𝜃 such that the radii of outest SLS increases with decreasing 𝜃 while a and α have fixed values.

Fig. 4

The behavior of SLS versus the GB coupling α and the spin parameter a for a = 0.1M (a), a = 0.5M (b), α = 0.01M² (c), α = 0.1M² (d) with $\theta =\frac {\pi }{6}$ and a = 0.5M,α = 0.1M² (e)

3.2 Quadrupole and Moment of Inertia

The quadrupole moment Q of the BHs that is a measurable parameter can be used to test no-hair theorems [20]. The quadrupole moment as well as the higher-order multipole moments can be achieved by transforming the metric to asymptotically Cartesian and mass-centred (ACMC) coordinates. It must be noted that the quadrupole moment itself is not a directly observable quantity but it does effects on the motion of massive and massless bodies leading to corrections to the gravitational radiation that is indeed observable. The authors of Ref. [6] have computed the quadrupole moment of rapidly spinning EGBD BH numerically. They have found that the scaled quadrupole moment of black holes can deviate by 20% and more from the corresponding Kerr value for a given value of the scaled angular momentum. In the case of stationary and axisymmetric space-time, the quadrupole moment at $\mathcal {O}(\alpha ^{\prime 2}\chi ^{\prime 2})$ is given by [15]

$$ Q=Q_{K}\left( 1+\frac{4463}{2625}\zeta\right), $$

(29)

where Q_K is the Kerr quadrupole moment.

The authors of Ref. [18] could not be able to map out the scaled quadrupole moment for the limit ${J}/{M^{2}}\rightarrow 0$ because the ratios of small numbers were involved in their numerical calculations. In this study, using the perturbative solutions we discuss the quadrupole moment spinning BH in EGBD gravity for $J\rightarrow 0$.

In Fig. 5 the magnitude of the scaled quadrupole moment Q_M/J² is plotted versus the scaled angular momentum J/M² for several values of horizon angular velocity Ω_H in the slow-spin regimes. As the figure shows the deviation from the Kerr value increases with increasing the angular horizon velocity. We find that for J/M² ≤ 0.05 this deviation can exceed the Kerr results by 50% and more.

Fig. 5

The scaled quadrupole moment Q_M/J² versus the scaled angular momentum J/M² for different values of Ω_H

The moment of inertia is described by I = J/Ω_H where Ω_H is the angular velocity given by (23). In this work, the scaled moment of inertia J/(Ω_HM³) can be found as

$$ \frac{J}{{\Omega}_{H}M^{3}}=\left[ j^{2}+\left( 1+\sqrt{1-j^{2}}\right)^{2}\right] \times \left[ 1+\frac{55125}{89260}\frac{1}{\left( \frac{Q}{j}-1\right)}\right]^{-1}, $$

(30)

where j = J/M² is the scaled angular moment and Q denotes to the quadrupole moment of black hole.

Lastly, we plot the scaled moment of inertia versus the scaled quadrupole moment in Fig. 6 for j ≤ 1. One can see for the fixed values of J, the graph has a decreasing trend which is in agreement with the numerical study obtained by [18].

Fig. 6

The scaled moment of inertia $\frac {J}{{\Omega }_{H}M^{2}}$ versus the scaled quadrupole moment Q_M/J² for different values of the scaled angular momentum J/M²

4 Conclusions

In this work, we have reviewed the Einstein-Gauss-Bonnet-dilaton (EGBD) theory that was constructed as a generalization of the Kerr black holes. This theory can exhibit some physical differences when compared to the Kerr solution. For example, the domain of existence of these Einstein-Gauss-Bonnet-dilaton black holes is bounded by the Kerr black holes. Also, their mass is always bounded from below, while their angular momentum can slightly exceed the Kerr bound. An EGBD BH has a higher entropy and temperature than a Kerr black hole for a given mass and angular momentum. By comparing their innermost stable circular orbits (ISCOs) with those of the Kerr black holes, It was shown in [8, 21] that the ISCO is larger for slowly and rapidly rotating EGBd BHs than Kerr BHs. Moreover, the quadrupole moment of the Kerr solution is completely fixed by its global charges while the quadrupole moment of EGBD spinning BHs can take considerably different values from the Kerr case.

Next, we have considered some properties of slowly spinning BHs in EGBD gravity. Previous numerical investigations of Refs. [7, 18] are necessary to study the high-spin regimes but they are impractical for regions where the slow-spin expansion does converge. By using approximate analytical pertubative BH solutions, we have perused the event horizon, domain of existence and quadrupole moment of slowly rotating BHs in EGBD gravity. It was shown that the event horizon radius violates from the Kerr results by 1% and less when $\chi \rightarrow 0$ and α ≤ 0.1. While this deviation increases to 20% when $\chi \rightarrow 0.6$.

We have also studied the parameter space of the black hole (a,α) for different values of the horizon angular velocity and found that the allowed region of parameter space increases with Ω_H. By considering the behavior of the domain of existence of the horizon area, we found that pertubative solutions can not lead to violation from the Kerr bound $\frac {J}{M^{2}}<1$. Furthermore, the radii of the static limit surface have been considered for a wide range of variations of the parameters. It was shown that these radii are more affected by varying the parameter 𝜃.

Finally, by investigation of the quadrupole moment of the slowly rotating BHS in EGBD theory we have obtained that the deviation from the Kerr value increases with angular horizon velocity such that for J/M² ≤ 0.05 this deviation can exceed the Kerr results by 50% and more.