1 Introduction

In practical applications, the research of secure multiparty computation is of great significance, which was first proposed by Yao [1]. The goal of studying secure multiparty computation is to enable numerous participants to collaboratively compute a particular function without disclosing their respective input information. They all receive accurate output information after the calculation. In the current research, to solve various practical problems, many secure multiparty computation protocols are proposed, respectively. For instance, secure multiparty sorting protocols [2, 3], secure multiparty cloud computation protocols [4, 5], and secure multiparty summation protocols [6,7,8,9]. In this paper, we only pay attention to the secure multiparty summation, which is one of the common security problems in current life. Secure multiparty summation protocols allow the existence of multiple participants, and each participant has a private message. Subsequently, these participants jointly compute a summation function under the condition that no personal private message is revealed. Finally, the output information of the summation function is available to each participant.

With the emergence of quantum algorithms [10, 11], quantum secure multiparty computation has attracted much attention [12,13,14,15,16]. At present, the research on quantum secure multiparty summation (QSMS) is still limited. And most of the existing QSMS protocols are (n,n)-threshold protocols. That is to say, in the result output phase, the output information of the summation function can only be obtained when all participants are present. In 2017, Shi et al. [17] designed a special quantum two-party summation protocol, but when one of the two participants is dishonest, the other participant will not get the correct output information. In 2022, Ye et al. [18] proposed a lightweight 2-dimensional three-user secure quantum summation protocol, but if the quantum system is free-space, then the protocol will be less applicable than the protocols of high-dimensional quantum system in some cases. And another consideration in protocols [17, 18] is that the number of participants is limited. Therefore, Liu et al. [19] in 2017, Yang et al. [20] in 2018, Lv et al. [21] in 2019 and Wang et al. [22] in 2021 respectively proposed an (n,n)-threshold QSMS protocol. Compared to previous related protocols, they are more efficient and solve the limitation of the number of participants. However, through analysis, we found that protocols [19,20,21,22] have one thing in common that is not well considered, that is, if any participant provides wrong information in the output result phase, the honest participants cannot get the correct output information and cannot find the specific cheaters. In particular, protocols [19,20,21] still require non-negligible computation cost, as they need to measure more message particles.

In addition, it is also worth noting if one or more participants fail during the result output phase. The applicability of these (n,n)-threshold protocols will be affected. Therefore, to increase the applicability of QSMS protocols. In 2020, Song et al. [23] proposed a (k,n)-threshold quantum secure multiparty computation protocol based on Lagrange unitary operation and Shamir’s threshold secret sharing, which has higher computational efficiency than previous similar protocols. However, in the result output phase, protocol [23] can only identify the existence of the deception and cannot find the specific deceivers. The same year, Sutradhar et al. [24] introduced a quantum multiparty protocol that supports (k,n)-threshold summation and contrasts it with comparable protocols, demonstrating that it is more advantageous in terms of both communication and computation. However, the honest participants in protocol [24] may not obtain the correct output information because there is a possibility that some participants provide invalid measurement results in the result output phase.

In this paper, we present a new verifiable (k,n)-threshold QSMS protocol by using Shamir’s threshold scheme, d-dimensional GHZ (Greenberger-Horne-Zeilinger) state, and hash function. Compared with the existing QSMS protocols, our protocol has the following properties:

  1. (1)

    Based on Shamir’s threshold scheme and d-dimensional GHZ state, we construct a (k,n)-threshold QSMS protocol. Compared with the (n,n)-threshold QSMS protocols, our protocol is more flexible and needs less computation cost when L meets L > 4, where L denotes the length of each participant’s secret.

  2. (2)

    Based on hash function, in the result output phase, this paper can not only achieve verifiability of the deception, but also find the specific cheaters.

  3. (3)

    This paper can resist intercept-resend attack, entangle-measure attack, Trojan horse attack, forgery attack, collusion attack, and malicious attack by the semi-honest third party TP.

The remaining structure of the protocol is as follows: In Section 2, some available basic knowledge are introduced. In Section 3, a verifiable (k,n)-threshold quantum secure multiparty summation protocol is designed. In Section 4, the correctness analysis and the security analysis are given respectively. In Section 5, we present the performance comparison between our protocol and related protocols. Finally, conclusion of this protocol is given.

2 Preliminaries

2.1 Shamir’s Threshold Scheme

In 1979, Shamir [31] proposed a (k,n)-threshold secret sharing scheme based on the Lagrange interpolation formula. The details are as follows:

(1) Preparation phase

Let GF(d) be a finite field (d is a large odd prime number); the shared secret is S; n(< d) participants P1,P2,...,Pn; a secret distributor D; any k(≤ n) of n participants can reconstruct the secret S.

(2) Construction phase

Firstly, D independently chooses k − 1 elements α1,α2,...,αk− 1 ∈ GF(d) and constructs a (k − 1)-th polynomial as

$$ f(x)=S+{{\alpha}_{1}}x+{{\alpha}_{2}}{{x}^{2}}+...+{{\alpha}_{k-1}}{{x}^{k-1}}(\bmod d), $$
(1)

where Eq. 1 satisfies f(0) = S(mod d) and αk− 1≠ 0.

Secondly, D chooses n different non-zero elements x1,x2,...,xn ∈ GF(d), computes yi = f(xi) for i = 1,2,...,n, and takes (xi,yi) as the secret share of the participant Pi.

Finally, D sends (xi,yi) to the corresponding participant Pi for i = 1,2,...,n.

(3) Reconstruction phase

Suppose that there are k participants who want to reconstruct the secret S together, then the following operations are performed:

Firstly, without loss of generality, assuming that the k participants are exactly P1,P2,...,Pk, then the k secret shares (x1,y1),(x2,y2),...,(xk,yk) can be obtained.

Secondly, the polynomial f(x) can be reconstructed by using the Lagrange interpolation formula:

$$ f(x)=\sum\limits_{i=1}^{k}{{{y}_{i}}\prod\limits_{j=1,j\ne i}^{k}{\frac{x-{{x}_{j}}}{x{}_{i}-{{x}_{j}}}}(\bmod d)}. $$
(2)

Finally, the constant term f(0) = S(mod d) of Eq. 2 can be obtained, i.e., the shared secret S is reconstructed.

2.2 d-dimensional GHZ State

In the d-dimensional Hilbert space, the X-basis and Z-basis are defined as follows [25]:

$$ X=\{|J_{j}\rangle,j=0,1,\cdots,d-1\},Z=\{|j\rangle,j=0,1,\cdots,d-1\}, $$
(3)

where \(|J_{j}\rangle =\frac {1}{\sqrt {d}}\displaystyle {\sum }_{j=0}^{d-1}\omega ^{jt}|t\rangle ,\) and \(\omega =e^{\frac {2\pi i}{d}}\). Namely, the d-dimensional GHZ state of n-particles in the Z-basis can be expressed as

$$ {\varPsi}=\frac{1}{\sqrt{d}}\displaystyle\sum\limits_{j=0}^{d-1}|j\rangle^{\bigotimes n}. $$
(4)

If each particle of quantum state Ψ is measured under the X-basis, and we use v1,v2,⋯ ,vn ∈{0,1,⋯ , d − 1} to denote the measurement results |Jj〉(j ∈{0,1,⋯ ,d − 1}) of the n particles, then we can get

$$ v_{1}+v_{2}+\cdots+v_{n}=0 (\bmod d). $$
(5)

2.3 Hash Function

Hash function is a function of many for one, which takes information of different lengths as input and turns it into output of the same length. The process of generating hash value can be expressed as follows:

$$ h=H(m), $$
(6)

where m is a string of different lengths that needs to be changed, H(⋅) denotes the hash function, and h represents a hash value of the fixed length. A secure hash function must have several properties as follows:

  1. 1)

    Rapidity: For any given message m, it is easy to calculate H(m), that is, H(m) is computable in polynomial time.

  2. 2)

    Unidirectionality: For any given hash value h, it is computationally impossible to find the message m satisfying H(m) = h.

  3. 3)

    Collision resistance: It is computationally infeasible to find two different messages m and \(m^{\prime }\) so that \(H(m)=H(m^{\prime })\).

3 Our Scheme

This section consists of three main phases: (1) Preparation phase; (2) Construction phase; (3) Multiparty summation phase, including cheating identification phase and result output phase.

3.1 Preparation Phase

  1. 1)

    n participants: P1,P2,...,Pn.

  2. 2)

    Assume that the unique identity information of the participant Pi is xi ∈{0,1,...,d − 1}, where i = 1,2,...,n.

  3. 3)

    A semi-honest third-party TP is needed. TP will do his best to get the secrets of the participants while implementing the protocol. But he is not allowed to conspire with others [30].

  4. 4)

    Each participant needs to randomly select some decoy particles in the X-basis or Z-basis.

  5. 5)

    TP needs to publish a suitable hash function H(⋅).

  6. 6)

    The symbol “+” indicates the addition operation of modulo d.

3.2 Construction Phase

In this phase, TP and each participant have to do the following operations:

Step 1: Each participant Pi(i = 1,2,...,n) randomly selects a key \(C_{i}=({c_{i}^{1}},{c_{i}^{2}},...,{c_{i}^{n}})\), and keeps \({c_{i}^{i}}\) in his hand, where \({c_{i}^{1}}+{c_{i}^{2}}+...+{c_{i}^{n}}=0\), \({c_{i}^{r}}\in \{0,1,...,d-1\}\), r = 1,2,...,n. Then, the participant Pi sends the correct and valid \({c_{i}^{j}}\) to the participant Pj through a secure quantum channel [26, 27], where j = 1,2,...,i − 1,i + 1,...,n. Finally, the participant Pi has \(({c_{1}^{i}},{c_{2}^{i}},...,{c_{n}^{i}})\), where i = 1,2,...,n.

Step 2: Each participant Pi(i = 1,2,...,n) generates a d-dimensional GHZ state \({{\psi }_{i}}=\frac {1}{\sqrt {d}}\sum \limits _{j=0}^{d-1}{{{\left | j \right \rangle }^{\otimes 3}}}\) of 3-particles in the Z-basis, respectively. When each particle of the quantum state ψi(i = 1,2,...,n) is measured in the X-basis, TP and the participant Pi agree to use \({a_{i}^{1}},{a_{i}^{2}},{a_{i}^{3}}\in \{0,1,...,d-1\}\) denote the measurement results |Jj〉 of the 3 particles, where j ∈{0,1,...,d − 1}.

Step 3: The participant P1 measures a particle of the quantum state ψ1 in the X-basis, and assumes that the measurement result of this particle is \({a_{1}^{3}}\in \{0,1,...,d-1\}\). Subsequently, he sets his secret to be \({{S}_{1}}=(d-{a_{1}^{3}})+{{t}_{1}}\), where t1 ∈{0,1,...,d − 1} is chosen by P1.

Step 4: Similar to Step 2, each participant Pi(i = 2,3,...,n) sets his secret to be \({{S}_{i}}=(d-{a_{i}^{3}})+{{t}_{i}}\), where ti ∈{0,1,...,d − 1} is chosen by Pi.

Step 5: Each participant Pi(i = 1,2,...,n) publishes an integer Ti = ti + Ei, where \(E_{i}={c_{1}^{i}}+{c_{2}^{i}}+...+{c_{n}^{i}}\).

Step 6: Each participant Pi(i = 1,2,...,n) inserts other two particles of the quantum state ψi into the decoy particles prepared in advance, so that two particle sequences \({Q_{i}^{1}}\) and \({Q_{i}^{2}}\) are constructed. At the same time, Pi records the insertion positions and the initial states of the decoy particles in \({Q_{i}^{1}}\) and \({Q_{i}^{2}}\). Subsequently, \({Q_{i}^{1}}\) and \({Q_{i}^{2}}\) are sent to TP, where i = 1,2,...,n.

Step 7: After determining that TP receives \(\{{Q_{i}^{1}},{Q_{i}^{2}}\}\) for i = 1,2,...,n, the participant Pi announces the insertion positions and the measurement basis of the decoy particles. Subsequently, TP uses the announced insertion positions and measurement basis of the decoy particles to judge whether there is an eavesdropping attack during the transmission of the particle sequences \(\{{Q_{i}^{1}},{Q_{i}^{2}}\}\) for i = 1,2,...,n. Assuming there is no eavesdropping attack, TP can obtain other two particles of the quantum state ψi for i ∈{1,2,...,n}; otherwise, TP terminates the protocol immediately and asks the participant Pi(i ∈{1,2,...,n}) to resend the particle sequences \(\{{Q_{i}^{1}},{Q_{i}^{2}}\}\).

Step 8: Assuming that the eavesdropping checks all pass, TP will use the X-basis to measure the particles of the quantum state ψi for i = 1,2,...,n, which in turn yields the corresponding measurement results \({a_{i}^{1}},{a_{i}^{2}}(\in \{0,1,...,d-1\})\) and the pseudo secret \({{S}_{i}}^{*}={a_{i}^{1}}+{a_{i}^{2}}+T_{i}\), where Ti = ti + Ei is a public value, \(E_{i}={c_{1}^{i}}+{c_{2}^{i}}+...+{c_{n}^{i}}\). Then, TP can obtain the summation \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}^{*}(\bmod d)=\sum \limits _{i=1}^{n}{{{S}_{i}}}(\bmod d)\). Finally, TP constructs a (k − 1)-th polynomial based on the obtained S and the chosen b1,b2,...,bk− 1 ∈{0,1,...,d − 1}:

$$ f(x)=S+{{b}_{1}}x+...+{{b}_{k-2}}{{x}^{k-2}}+{{b}_{k-1}}{{x}^{k-1}}, $$
(7)

where the coefficient of the highest order term of Eq. 7 needs to satisfy bk− 1≠ 0.

Step 9: TP generates (xi,yi) by using the unique identity information xi of the participant Pi and Eq. 7, where yi = f(xi), i = 1,2,...,n. Subsequently, (xi,yi) is sent to Pi as his secret share through a secure quantum channel [26, 27]. Meanwhile, TP computes and publishes (xi,H(yi)), where H(yi) denotes the hash value of yi for i = 1,2,...,n.

3.3 Multiparty Summation Phase

3.3.1 Cheating Identification Phase

Step 1: Assuming that k(≤ n) participants want to get the summation of all the secrets together, each participant Pi needs to provide his secret share \(({{x}_{i}},{{y}_{i}}^{\prime })\) to other participant Pj through a secure quantum channel [26, 27], where i,j ∈{1,2,...,n}, and i≠j. If the summation process can be smoothly carried out, the secret share \(({{x}_{i}},{{y}_{i}}^{\prime })\) provided by Pi(i ∈ 1,2,...,n) needs to satisfy the following two conditions:

  • xi and \({{y}_{i}}^{\prime }\) are linearly independent.

  • \(({{x}_{i}},H({{y}_{i}}^{\prime }))=({{x}_{i}},H({{y}_{i}}))\), where \(H({{y}_{i}}^{\prime })\) denotes the hash value of \({{y}_{i}}^{\prime }\) and (xi,H(yi)) is the public information.

Step 2: From Step l above we know that if the participant Pi(∈{1,2,...,n}) is defined as a deceiver, he will be eliminated. Subsequently, the original qualified subsets are updated and the new participant is reselected together to reconstruct the summation \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}^{*}(\bmod d)=\sum \limits _{i=1}^{n}{{{S}_{i}}}(\bmod d)\).

Step 3: Without loss of generality, assuming that the k participants mentioned in the above Step 1 are exactly P1,P2,...,Pk, and they are all verified to be honest participants, the summation S can be obtained by executing Section 3.3.2.

3.3.2 Result Output Phase

Step 4: For participant Pu(u ∈{1,2,...,k}), after receiving the secret shares sent by other honest participants Pi(i = 1,2,...,k;i≠u) (Step 3 has assumed that P1,P2,...,Pk are all honest participants), he can use the k secret shares (xt,yt) owned and the Lagrange interpolation formula to reconstruct the summation \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}^{*}(\bmod d)=\sum \limits _{i=1}^{n}{{{S}_{i}}}(\bmod d)\), where t = 1,2,...,k. The specific output process is shown below:

$$ S=\sum\limits_{i=1}^{n}{{{S}_{i}}}^{*}=\sum\limits_{i=1}^{n}{{{S}_{i}}}=f(0)=\sum\limits_{i=1}^{k}{{{y}_{i}}}\left( \prod\limits_{j=1,j\ne i}^{k}{\frac{-{{x}_{j}}}{{{x}_{i}}-{{x}_{j}}}} \right)(\bmod d). $$
(8)

4 Scheme Analysis

4.1 Correctness Analysis

Theorem 1

If each particle of the Z-basis GHZ state \({{\psi }_{i}}=\frac {1}{\sqrt {d}}\sum \limits _{j=0}^{d-1}{{{\left | j \right \rangle }^{\otimes n}}}\) is measured in the X-basis, and the measurement results |Jj〉(j ∈{0,1,⋯ ,d − 1}) of the n particle denotes the \({a_{i}^{1}},{a_{i}^{2}},...,{a_{i}^{n}}\in \{0,1,...,d-1\}\), then these measurements satisfy \({a_{i}^{1}}+{a_{i}^{2}}+...+{a_{i}^{n}}=0\) for i = 1,2,...,n.

Proof

In Section 2.2, we know that the X-basis and Z-basis are defined as \(X=\{\left | {{J}_{j}} \right \rangle ,j=0,1,...,d-1\}\) and \(Z=\{\left | j \right \rangle ,j=0,1,...,d-1\}\), respectively, where \(|J_{j}\rangle =\frac {1}{\sqrt {d}}\displaystyle {\sum }_{j=0}^{d-1}\omega ^{jt}|t\rangle \), \(\omega =e^{\frac {2\pi i}{d}}\). Therefore, if the quantum state ψi is measured in the X-basis and the measurement results are denoted as \({a_{i}^{1}},{a_{i}^{2}},...,{a_{i}^{n}}\in \{0,1,...,d-1\}\), i = 1,2,...,n, then the quantum state ψi can be expressed by using the following equation:

$$ \begin{aligned} {{\psi }_{i}}=\frac{1}{\sqrt{d}}\sum\limits_{j=0}^{d-1}{{{\left( \frac{1}{\sqrt{d}}\sum\limits_{t=0}^{d-1}{{{\omega }^{jt}}\left| t \right\rangle } \right)}^{\otimes n}}=}\frac{1}{{{(\sqrt{d})}^{n+1}}}\sum\limits_{j=0}^{d-1}{{{\omega }^{j{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}\left| {a_{i}^{1}}{a_{i}^{2}}...{a_{i}^{n}} \right\rangle }. \end{aligned} $$
(9)

From Eq. 9, we can discuss the following two cases:

1) If \({\sum }_{m=1}^{n}{{a_{i}^{m}}}\ne 0\), then we can see

$$ \begin{array}{@{}rcl@{}} \sum\limits_{j=0}^{d-1}{{{\omega }^{j{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}}&=&\sum\limits_{j=0}^{d-1}{{{({{\omega }^{{\sum}_{m=1}^{n}{{a_{i}^{m}}}}})}^{j}}}=1+{{({{\omega }^{{\sum}_{m=1}^{n}{{a_{i}^{m}}}}})}^{1}}+...+{{({{\omega }^{{\sum}_{m=1}^{n}{{a_{i}^{m}}}}})}^{d-1}} \\ &=&\frac{1-{{({{\omega }^{{\sum}_{m=1}^{n}{{a_{i}^{m}}}}})}^{d}}}{1-{{\omega }^{{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}}=\frac{1-{{\omega }^{d{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}}{1-{{\omega }^{{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}}=\frac{1-{{({{e}^{\frac{2\pi i}{d}}})}^{d{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}}{1-{{({{e}^{\frac{2\pi i}{d}}})}^{{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}} \\ &=&\frac{1-{{e}^{2\pi i{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}}{1-{{e}^{\frac{2\pi i}{d}{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}}=\frac{1-{{({{e}^{\pi i}})}^{2{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}}{1-{{e}^{\frac{2\pi i}{d}{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}}=\frac{1-{{(-1)}^{2{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}}{1-{{e}^{\frac{2\pi i}{d}{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}} \\ &=&\frac{1-1}{1-{{e}^{\frac{2\pi i}{d}{\sum}_{m=1}^{n}{{a_{i}^{m}}}}}}=0, \end{array} $$
(10)

where eπi = − 1, and “i” in eπi is imaginary unit.

2) If \({\sum }_{m=1}^{n}{{a_{i}^{m}}}=0\), then we can obtain

$$ \sum\limits_{j=0}^{d-1}{{{\omega }^{j\sum\nolimits_{m=1}^{n}{{a_{i}^{m}}}}}}=\sum\limits_{j=0}^{d-1}{{{\omega }^{0}}}=d $$
(11)

Therefore, according to Eqs. 9–11, in the X-basis, we can know that the quantum state ψi can be represented as:

$$ {{\psi }_{i}}=\frac{1}{{{(\sqrt{d})}^{n-1}}}\sum\limits_{\begin{smallmatrix} {a_{i}^{1}}+{a_{i}^{2}}+...+{a_{i}^{n}}=0, \\ {a_{i}^{1}},{a_{i}^{2}},...,{a_{i}^{n}}\in \{0,1,...,d-1\} \end{smallmatrix}}{\left| {a_{i}^{1}}{a_{i}^{2}}...{a_{i}^{n}} \right\rangle } $$
(12)

To sum up, these measurement results \({a_{i}^{1}},{a_{i}^{2}},...,{a_{i}^{n}}\in \{0,1,...,d-1\}\) can satisfy \({a_{i}^{1}}+{a_{i}^{2}}+...+{a_{i}^{n}}=0\) for i = 1,2,...,n. That is, Theorem 1 is proved.

Remark 1

In our protocol, the GHZ state \({{\psi }_{i}}=\frac {1}{\sqrt {d}}\sum \limits _{j=0}^{d-1}{{{\left | j \right \rangle }^{\otimes 3}}}\) generated by Pi is a special case when it is n = 3. Namely, according to the proof of Theorem 1, the measurement results \({a_{i}^{1}},{a_{i}^{2}},{a_{i}^{3}}\in \{0,1,...,d-1\}\) generated by Pi in this protocol can satisfy \({a_{i}^{1}}+{a_{i}^{2}}+{a_{i}^{3}}=0\) for i = 1,2,...,n.

□

Lemma 1

In our protocol, the summation \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}(\bmod d)=\sum \limits _{i=1}^{n}{{{S}_{i}}}^{*}(\bmod d)\), where \({{S}_{i}}=(d-{a_{i}^{3}})+{{t}_{i}}\), \({{S}_{i}}^{*}={a_{i}^{1}}+{a_{i}^{2}}+T_{i}\), Ti = ti + Ei, \(E_{i}={c_{1}^{i}}+{c_{2}^{i}}+...+{c_{n}^{i}}\), \({c_{i}^{i}}+{c_{i}^{2}}+...+{c_{i}^{n}}=0\), i = 1,2,...,n.

Proof

According to Theorem 1 and Remark 1, we can get

$$ {a_{i}^{1}}+{a_{i}^{2}}+{a_{i}^{3}}=0, $$
(13)

where \({a_{i}^{1}}\) and \({a_{i}^{2}}\) are the measurement results owned by TP, and \({a_{i}^{3}}\) is the measurement result owned by Pi for i = 1,2,...,n.

Subsequently, based on Eq. 13, we can obtain

$$ {a_{i}^{1}}+{a_{i}^{2}}=d-{a_{i}^{3}}. $$
(14)

Furthermore, we can get

$$ \begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{n}{{{S}_{i}}}^{*} &=&\sum\limits_{i=1}^{n}{({a_{i}^{1}}+{a_{i}^{2}}+T_{i})}=\sum\limits_{i=1}^{n}{({a_{i}^{1}}+{a_{i}^{2}}+t_{i}+E_{i})}\\ &=&\sum\limits_{i=1}^{n}{({a_{i}^{1}}+{a_{i}^{2}}+t_{i})}+\sum\limits_{i=1}^{n}{E_{i}} \\ &=&\sum\limits_{i=1}^{n}{[(d-{a_{i}^{3}})+t_{i}]}+\sum\limits_{i=1}^{n}\sum\limits_{r=1}^{n}{{c_{r}^{i}}} \\ &=&\sum\limits_{i=1}^{n}{{S}_{i}}+0=S. \end{array} $$
(15)

Lemma 1 is proved. □

Proposition 1

In the multiparty summation phase, the summation \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}^{*}(\bmod d)=\sum \limits _{i=1}^{n}{{{S}_{i}}}(\bmod d)\) can be reconstructed if there are no less than k honest participants correctly executing this protocol.

Proof

In the multiparty summation phase, firstly, without loss of generality, assuming that the participants P1,P2,...,Pk want to reconstruct the summation \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}^{*}(\bmod d)=\sum \limits _{i=1}^{n}{{{S}_{i}}}(\bmod d)\), then they need to obtain the k secret shares \(\{({{x}_{1}},{{y}_{1}}^{\prime }),({{x}_{2}},{{y}_{2}}^{\prime }),...,({{x}_{k}},{{y}_{k}}^{\prime })\}\) through a secure quantum channel [26, 27]; secondly, for participant Pi(i = 1,2,...,k), he can use the public information (xt,H(yt)) and the hash function H(⋅) to verify the honesty of other participants Pt for t ∈{1,2,...,k}, and i≠t. Assuming that the secret shares provided by P1,P2,...,Pi− 1,Pi+ 1,...,Pk are all verified to be correct and valid (see Section 3.3.1), the participant Pi(i = 1,2,...,k) can obtain the k secret shares {(x1,y1),(x2,y2),...,(xk,yk)}; finally, the participant Pi(i = 1,2,...,k) can use the Lagrange interpolation formula and the secret shares {(x1,y1),(x2,y2),...,(xk,yk)} to reconstruct the summation S:

$$ S=\sum\limits_{i=1}^{n}{{{S}_{i}}}^{*}=\sum\limits_{i=1}^{n}{{{S}_{i}}}=f(0)=\sum\limits_{i=1}^{k}{{{y}_{i}}}\left( \prod\limits_{j=1,j\ne i}^{k}{\frac{-{{x}_{j}}}{{{x}_{i}}-{{x}_{j}}}} \right)(\bmod d). $$
(16)

Proposition 1 is proved. □

4.2 Security Analysis

4.2.1 Intercept-Resend Attack

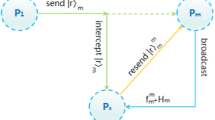
In our protocol, assume that the eavesdropper Eve intercepts the particles sent to TP by the participant Pi(i ∈{1,2,...,n}), and then sends the forged particles to TP so that he can pass the eavesdropping check. This attack is not feasible. Because each participant Pi(i = 1,2,...,n) sends the particle sequences \(\{{Q_{i}^{1}},{Q_{i}^{2}}\}\) to TP, and each particle sequence \({Q_{i}^{r}}(r\in \{1,2\})\) is composed of one particle in ψi and some decoy particles, where each decoy particle is randomly selected in the X-basis or Z-basis. Since the eavesdropper Eve does not know the insertion positions, the initial states, and the measurement basis of the decoy particles, the probability of his attack failing is \(P=1-{{(\frac {1}{2}\times \frac {d-1}{d})}^{q}}\), where q denotes the number of decoy particles. When q is large enough, \(P=1-{{(\frac {d-1}{2d})}^{q}}\) converges to 1. Therefore, Eve’s intercept-resend attack will be detected with a high probability.

4.2.2 Entangle-Measure Attack

In the process of particle transmission, the eavesdropper Eve uses the unitary operation UE to entangle an auxiliary particle, and then steals the privacy information by measuring this auxiliary particle. We assume that this auxiliary particle is |E〉. In order to express entanglement-measurement attack more clearly, we analyze the decoy particles selected under different basis as follows:

1) If the decoy particles are randomly selected from the Z-basis, using the unitary operation UE to act on the decoy particles can obtain:

$${{U_{E}}\left| 0 \right\rangle \left| E \right\rangle = {\beta_{00}}\left| 0 \right\rangle \left| {{e_{00}}} \right\rangle + {\beta_{01}}\left| 1 \right\rangle \left| {{e_{01}}} \right\rangle + {\cdots} + {\beta_{0(d - 1)}}\left| {d - 1} \right\rangle \left| {{e_{0(d - 1)}}} \right\rangle }$$
$${{U_{E}}\left| 1 \right\rangle \left| E \right\rangle = {\beta_{10}}\left| 0 \right\rangle \left| {{e_{10}}} \right\rangle + {\beta_{11}}\left| 1 \right\rangle \left| {{e_{11}}} \right\rangle + {\cdots} + {\beta_{1(d - 1)}}\left| {d - 1} \right\rangle \left| {{e_{1(d - 1)}}} \right\rangle }$$
$$\vdots$$
$${{U_{E}}\left| {d - 1} \right\rangle \left| E \right\rangle = {\beta_{(d - 1)0}}\left| 0 \right\rangle \left| {{e_{(d - 1)0}}} \right\rangle + {\beta_{(d - 1)1}}\left| 1 \right\rangle \left| {{e_{(d - 1)1}}} \right\rangle + \cdots}$$
$$+{{\beta_{(d - 1)(d - 1)}}\left| {d - 1} \right\rangle \left| {{e_{(d - 1)(d - 1)}}} \right\rangle, }$$

where these quantum states |eij〉 (i,j ∈{0,1,⋯ ,d − 1}) are determined by the unitary operation UE, and

$$\begin{array}{c} {\left| {{\beta_{00}}} \right|^{2}} + {\left| {{\beta_{01}}} \right|^{2}} + {\cdots} + {\left| {{\beta_{0(d - 1)}}} \right|^{2}} = 1\\ {\left| {{\beta_{10}}} \right|^{2}} + {\left| {{\beta_{11}}} \right|^{2}} + {\cdots} + {\left| {{\beta_{1(d - 1)}}} \right|^{2}} = 1\\ {\vdots} \\ {\left| {{\beta_{(d - 1)0}}} \right|^{2}} + {\left| {{\beta_{(d - 1)1}}} \right|^{2}} + {\cdots} + {\left| {{\beta_{(d - 1)(d - 1)}}} \right|^{2}} = 1. \end{array}$$

In addition, in order to prevent eavesdropping attacks, the eavesdropper Eve must make the following provisions:

$$\begin{array}{c} {\beta_{01}} = {\beta_{02}} = {\cdots} = {\beta_{0(d - 1)}} = 0 \\ {\beta_{10}} = {\beta_{12}} = {\cdots} = {\beta_{1(d - 1)}} = 0 \\ {\vdots} \\ {\beta_{(d - 1)0}} = {\beta_{(d - 1)1}} = {\cdots} = {\beta_{(d - 1)(d - 2)}} = 0. \end{array} $$

Therefore, we can simplify the above equations as follows:

$$\begin{array}{*{20}{c}} {{U_{E}}\left| 0 \right\rangle \left| E \right\rangle = {\beta_{0}}\left| 0 \right\rangle \left| {{e_{0}}} \right\rangle } \\ {{U_{E}}\left| 1 \right\rangle \left| E \right\rangle = {\beta_{1}}\left| 1 \right\rangle \left| {{e_{1}}} \right\rangle } \\ {\vdots} \\ {{U_{E}}\left| {d - 1} \right\rangle \left| E \right\rangle = {\beta_{d - 1}}\left| {d - 1} \right\rangle \left| {{e_{d - 1}}} \right\rangle }, \end{array}$$

where β0 = β00,β1 = β11,...,βd− 1 = β(d− 1)(d− 1), and e0 = e00,...,ed− 1 = e(d− 1)(d− 1).

2) If these decoy particles are randomly selected from the X-basis, using the unitary operation UE to act on the decoy particles can get:

$$ {{U}_{E}}\left| {{J}_{j}} \right\rangle \left| E \right\rangle = {{U}_{E}}\left( \frac{1}{\sqrt{d}}\sum\limits_{t=0}^{d-1}{{{\omega }^{jt}}\left| t \right\rangle } \right)\left| E \right\rangle = \frac{1}{\sqrt{d}}\sum\limits_{t=0}^{d-1}{{{\omega }^{jt}}{{U}_{E}}\left| t \right\rangle }\left| E \right\rangle =\frac{1}{\sqrt{d}}\sum\limits_{t=0}^{d-1}{{{\omega }^{jt}}{\beta_{t}}\left| t \right\rangle }\left| {{e}_{t}} \right\rangle, $$
(17)

where j ∈{0,1,⋯ ,d − 1}.

Furthermore, due to \(\left | {{J}_{j}} \right \rangle =\frac {1}{\sqrt {d}}\sum \limits _{t=0}^{d-1}{{{\omega }^{jt}}\left | t \right \rangle }\), then we know \(\left | j \right \rangle =\frac {1}{\sqrt {d}}\sum \limits _{t=0}^{d-1}{{{\omega }^{-jt}}\left | {{J}_{t}} \right \rangle }\) and can get

$$ \begin{array}{@{}rcl@{}} {{U}_{E}}\left| {{J}_{j}} \right\rangle \left| E \right\rangle&=&\frac{1}{\sqrt{d}}\sum\limits_{t=0}^{d-1}{{{\omega }^{jt}}{\beta_{t}}}\left| {{e}_{t}} \right\rangle \left( \frac{1}{\sqrt{d}}\sum\limits_{i=0}^{d-1}{{{\omega }^{-it}}}\left| {{J}_{i}} \right\rangle \right) \\ &=&\frac{1}{d}(\left| {{J}_{0}} \right\rangle {\sum}_{t=0}^{d-1}{{{\omega }^{t(j-0)}}{\beta_{t}}\left| {{e}_{t}} \right\rangle +\left| {{J}_{1}} \right\rangle {\sum}_{t=0}^{d-1}{{{\omega }^{t(j-1)}}{\beta_{t}}\left| {{e}_{t}} \right\rangle +...}} \\ &&+\left| {{J}_{d-1}} \right\rangle {\sum}_{t=0}^{d-1}{{{\omega }^{t(j-(d-1))}}{\beta_{t}}\left| {{e}_{t}} \right\rangle }) \end{array} $$
(18)

According to the above analysis, we can know that to avoid eavesdropping inspections, the eavesdropper Eve must set \(\sum \limits _{t = 0}^{d - 1} {{\omega ^{t(j - i)}}} {\beta _{t}}\left | {{e_{t}}} \right \rangle = 0\) for i ∈{0,1,⋯ ,d − 1}, j≠i. There, for ∀j ∈{0,1,2,...,d − 1}, d − 1 equations can be obtained. Then, based on these equations, \({\beta _{0}}\left | {{e_{0}}} \right \rangle = {\beta _{1}}\left | {{e_{1}}} \right \rangle = {\cdots } = {\beta _{d - 1}}\left | {{e_{d - 1}}} \right \rangle \) is easily acquired. In a word, no matter what state the useful particles are in, Eve can only obtain the same information from the auxiliary particles, but cannot obtain the related privacy information. That is, the entanglement-measurement attack stopped.

4.2.3 Trojan Horse Attack

In the case that the particles used in this protocol are photons, two types of Trojan horse attacks [25, 29] as described below may exist: (1) Delayed photon attack; (2) Invisible photon attack. To resist these two attacks, we perform the following analysis:

  • i) To resist the delayed photon attack, participants randomly select a portion of the received photon signal as the sample signal, and separate each sample signal using the PNS (Photon Number Separator) technique. Subsequently, they arbitrarily choose two signals in the X-basis or the Z-basis for measurement, and they can judge whether the particles need to be resent by the multi-photon rate. If the multi-photon rate is too high, the transmission of particles should be stopped and the particles should be resent.

  • ii) To resist the invisible photon attack, participants can add a filter to the device. The filter is added to permit only photons with wavelengths close to the operating particles to enter and to isolate the invisible photons from the attackers.

4.2.4 Participant Attack

Proposition 2

In our protocol, the insider attacks can be stopped.

Proof

In this paper, we consider the following two kinds of insider attacks: Forgery attack and Collusion attack.

  • Forgery attack: In the multiparty summation phase, each participant exchanges the secret share (xi,yi) through a secure quantum channel [26,27], where i ∈{1,2,...,n}. The deception is easily identified if the insider attacker Pt(t ∈{1,2,...,n}) sends \(({{x}_{t}},{{y}_{t}}^{\prime })\) to the honest participant Pi(i ∈{1,2,...,n};i≠t), where \(({{x}_{t}},{{y}_{t}}^{\prime })\) is the forged secret share by Pt. The specific cheating identification is described as follows:

    Step 1: Honest participant Pi hashes the received \({{y}_{t}}^{\prime }\) by using the publicly available hash function H(⋅) to obtain \(H({{y}_{t}}^{\prime })\).

    Step 2: If Equation \(({{x}_{t}},H({{y}_{t}}^{\prime }))=({{x}_{t}},H({{y}_{t}}))\) does not hold, the deception of the participant Pt is identified; otherwise, is honest.

  • Collusion attack: We analyze the following two collusion scenarios:

    I) The secret Si(i = 1,2,...,n) of each participant is safe under the collusion attack of n − 2 secret holders. Without losing generality, we assume that the n − 2 participants happen to be P1,P2,...,Pn− 2. The specific analysis is as follows:

    • 1) On the one hand, the participants P1,P2,...,Pn− 2 have no less than k secret shares through collusion. That is, the summation \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}(\bmod d)\) can be reconstructed by using the Lagrange interpolation formula. On the other hand, the participants P1,P2,...,Pn− 2 conspire to own secrets S1,S2,...,Sn− 2, and then by combining the reconstructed S, they can get Sn− 1 + Sn. That is, they can’t decrypt Sn− 1 and Sn.

    • 2) On the one hand, TP is a semi-honest third party, so he will not conspire with P1,P2,...,Pn− 2 to make them get \({a_{i}^{1}}+{a_{i}^{2}}, i=n-1,n\). That is, Sn− 1 and Sn are safe. On the other hand, according to the analysis in Section 4.2.1, we can know that the intercept-resend attack can be prevented, that is, Sn− 1 and Sn are safe.

    II) For the security of the summation S, we consider the worst case, that is, there are k − 1 insider participants who launch a collusion attack. Without losing generality, we assume that the k − 1 participants happen to be P1,P2,...,Pk− 1. The specific analysis is as follows:

    • 1) The third-party TP needed in this protocol is semi-honest, so he will not reveal \({a_{i}^{1}}+{a_{i}^{2}}\) of each participant voluntarily, where i = 1,2,...,n. That is to say, i) the participants P1,P2,...,Pk− 1 can’t get the secrets Sk,Sk+ 1,...,Si− 1,Si,Si+ 1,...,Sn and the summation \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}(\bmod ~ d)\), where \(S_{i}={a_{i}^{1}}+{a_{i}^{2}}+t_{i}\) for i = k,k + 1,...,n, ti = Ti − Ei, and Ti is a public value; ii) the participants P1,P2,...,Pk− 1 can’t get the pseudo secrets \(S_{k}^{*},S_{k+1}^{*},...,S_{i-1}^{*},S_{i}^{*},S_{i+1}^{*},...,S_{n}^{*}\) and the summation \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}^{*}(\bmod d)=\sum \limits _{i=1}^{n}{{{S}_{i}}}(\bmod d)\), where \(S_{i}^{*}={a_{i}^{1}}+{a_{i}^{2}}+T_{i}\) for i = k,k + 1,...,n.

    • 2) The participants P1,P2,...,Pk− 1 want to get the k-th secret share (xt,yt) by breaking the public information (xt,H(yt)), and then use the secret shares (x1,y1),(x2,y2),...,(xk− 1,yk− 1),(xt,yt) and the Lagrange interpolation formula to reconstruct the summation \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}=f(0)=\sum \limits _{i=1}^{k}{{{y}_{i}}}\left (\prod \limits _{j=1,j\ne i}^{k}{\frac {-{{x}_{j}}}{{{x}_{i}}-{{x}_{j}}}} \right )(\bmod ~ d)\), where t ∈{k,k + 1,...,n}. This is not feasible and the detailed analysis can be found in Section 5 of protocol [28].

    • 3) According to the analysis in Section 4.2.1, we can know that the intercept-resend attack doesn’t work. Therefore, \({a_{i}^{1}}+{a_{i}^{2}}\) of each participant is safe, where i = 1,2,...,n. That is to say, Si, \(S_{i}^{*}\), and \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}^{*}(\bmod d)=\sum \limits _{i=1}^{n}{{{S}_{i}}}(\bmod d)\) cannot be obtained by P1,P2,...,Pk− 1. The specific analysis is similar to that Item “II),1)” of Collusion attack.

Proposition 2 is proved.

Remark 2

This protocol can’t resist the collusion attack from n − 1 secret holders, because they can easily decrypt the last secret from the summation \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}(\bmod d)\).

□

Proposition 3

In our protocol, the external attacks can be resisted.

Proof

If the external attackers want to obtain the secret Si(i = 1,2,...,n) of each participant or the summation \(S=\sum \limits _{i=1}^{n}{{{S}_{i}}}^{*}(\bmod d)=\sum \limits _{i=1}^{n}{{{S}_{i}}}(\bmod d)\), they can only try to get them in the following three ways:

  • 1) The external attackers want to obtain the secret shares (xi,yi) of the participants through the public information (xi,H(yi)) for i = 1,2,...,n. Obviously, this is not feasible. The specific analysis can be found in Section 5 of protocol [28].

  • 2) In the construction phase, the external attackers want to obtain the measurement results \({a_{i}^{1}},{a_{i}^{2}}\) by intercepting the particle sequences \(\{{Q_{i}^{1}},{Q_{i}^{2}}\}\) for i ∈{1,2,...,n}, and then get \({{S}_{i}}^{*}={a_{i}^{1}}+{a_{i}^{2}}+T_{i}\) and \({{S}_{i}}={a_{i}^{1}}+{a_{i}^{2}}+t_{i}\), where ti = Ti − Ei, Ti is a public value, \(E_{i}={c_{1}^{i}}+{c_{2}^{i}}+...+{c_{n}^{i}}\). Obviously, this is not feasible either. The reason can be known in the analysis of Section 4.2.1 and Item “II),1)” of Collusion attack.

  • 3) In the multiparty summation phase, each participant exchanges the secret share though a secure quantum channel [26, 27]. That is, the external attackers cannot intercept the secret share of each participant through this way. Therefore, the summation S will not be stolen.

Proposition 3 is proved. □

Proposition 4

In our protocol, the malicious attack by the semi-honest third party TP can be prevented.

Proof

TP can obtain \({a_{i}^{1}}+{a_{i}^{2}}\) by measuring the received particles, where i = 1,2,...,n. If he wants to get the secret \(S_{i}={a_{i}^{1}}+{a_{i}^{2}}+t_{i}\) of each participant, he also needs to know Ei, where Ti = Ei + ti is a public value. Obviously, this is not feasible because he can’t know Ei.

Proposition 4 is proved. □

5 Performance Analysis

In this paper, a new verifiable (k,n)-threshold quantum secure multiparty summation protocol is proposed. Compared with the existing protocols, the results are as follows:

Under the condition that the quantum environment is a free space, our protocol and protocols [20, 21, 23, 24] are more adaptable in this respect than the 2-dimensional quantum secure multiparty summation [19].

Protocols [17, 19,20,21] respectively construct a (n,n)-threshold quantum secure multiparty summation protocol. That is, if participants of these protocols want to get the output information, they must require all participants to be online. Therefore, compared with protocols [17, 19,20,21], our protocol and protocols [23, 24] are more flexible.

Although protocols [20, 21, 23, 24] considers both external attack and collusion attack, that is, neither external attackers nor internal attackers can obtain the input information of the corresponding participants. However, in the result output phase, if there are malicious internal participants, they may provide wrong information or measurement results to other honest participants, so that they can get correct output information, while other honest participants can’t. In addition, the analysis shows that protocol [23] can determine the existence of cheating behavior by judging whether the relevant equation is true or not, but can’t find out the specific cheaters. Therefore, our protocol has more advantages in this respect.

According to the analysis of Section 4.2.3, we know that if the particles used in protocols are photons, there may be Trojan horse attack. Therefore, our protocol is more secure than protocols [20, 21] which fail to consider Trojan horse attack.

To analyze the efficiency of different protocols, we compare the computation and communication costs between our protocol and protocols [19,20,21, 23, 24]. The computation cost can be considered based on the following six parts: QFT, QFT− 1, measure operation, unitary operation, hash operation, and classical information operation. And the communication cost can be considered based on message particles, decoy particles, and classic information. In protocol [19], nL measure operation + nL unitary operation and nL message particles + q(n − 1) decoy particles are the total computation cost and the total communication cost, respectively. In protocol [20], n QFT + nL measure operation + nL unitary operation and nL message particles + q(n − 1) decoy particles are the total computation cost and the total communication cost, respectively. In protocol [21], nL measure operation + nL unitary operation and L message particles + qn decoy particles are the total computation cost and the total communication cost, respectively. In protocol [23], 1 measure operation + (n + 1) unitary operation + (n + k) classical information operation and 1 message particles + n classical information are the total computation cost and the total communication cost, respectively. In protocol [24], k QFT + k measure operation + k unitary operation + 3n classical information operation and (k − 1) message particles + n(n − 1) classical information are the total computation cost and the total communication cost, respectively. In our protocol, 3n measure operation + n hash operation 4n classical information operation and 3n message particles + 2qn decoy particles + n(n − 1) classical information are the total computation cost and the total communication cost, respectively. In short, on the one hand, compared with the (n,n)-threshold protocols [19,20,21], our protocol requires less computation cost when L satisfies L > 4. But compared with the (k,n)-threshold protocol [23, 24], we need more computation cost. The reason why is that this paper uses more message particles and classic information to achieve secure multiparty summation, and also uses the hash function to achieve verifiability; on the other hand, we can find that there is no advantage in communication cost between our protocol and protocols [19,20,21, 23, 24]. This is because our protocol uses decoy particles to prevent eavesdropping attacks during particle transmission, and also uses classical key information to ensure that the secret of each participant is not known by others.

To understand the performance of related protocols more clearly, we can see Tables 1, 2 and 3.

Table 1 Comparison of basic properties
Full size table
Table 2 Comparison of computation costs
Full size table
Table 3 Comparison of communication costs
Full size table

6 Conclusion

Based on Shamir’s threshold scheme and d-dimensional GHZ state, we proposed a new (k,n)-threshold quantum secure multiparty summation protocol. Based on the one-to-one correspondence of hash values, in the result output phase, the honesty of each participant can be verified, and dishonest participants can be eliminated. In addition, compared with the (n,n)-threshold protocols [19,20,21], our protocol needs less computation cost when L satisfies L > 4, where L is the length of each participant’s secret. Further, the security analysis shows that this paper can resist a series of typical attacks.

This paper put forward a new quantum secure multiparty summation protocol. It has a (k,n)-threshold approach and is verifiable, but it has no clear advantage in computation and communication costs. We hope to propose a more efficient verifiable (k,n)-threshold quantum secure multiparty summation protocol in the future.