A Novel Quantum Protocol for Private Set Intersection

Abstract

Private set intersection(PSI) allows two parties to get all common elements of their private sets without leaking any information about their sets. In this paper, we present a novel PSI protocol which is based on quantum Fourier transform. Correctness analysis shows that our protocol can get the result correctly. And the security of our protocol is also analyzed, it can resist most of outside attacks, such as Trojan horse attack, intercept-resend attack, entanglement-and-measure attack, man-in-the-middle attack and so on. And it also can overcome participant attacks.

1 Introduction

Protocols for private set intersection (PSI) allow two parties to compute the intersection S₁ ∩ S₂ of their respective sets S₁,S₂ without disclosing anything about their sets [1]. PSI is an important problem of secure multi-party computation(SMC) and has many practical applications. It can be used to find the common customers of two companies directly [2] or perform scientific investigation of two hospitals on their private patients data [3]. It can also be used as a sub-protocol to perform privacy preserving data mining [4], to execute search queries of the outsourced data [5] and to test whether two parties are close or not [6].

Because PSI has a wide application, many protocols have been proposed based on classical cryptography. In Ref. [1], Freedman, M.J. et al. presented PSI protocols based on homomorphic encryption and balanced hashing. In Ref. [7], Wu et al. proposed a PSI scheme based on oblivious transfer and universal hash function. In Ref. [8], Hazay, C., Lindell, Y. constructed a PSI protocol based on secure pseudorandom function evaluations. In Ref. [9], Liu, L., Cao, Z. investigated an efficient private matching protocol

which can be used in some scenarios without strong security requirement. In Ref. [10], Kerschbaum, F. presented a novel PSI protocol of malicious adversaries model based on Bloom filter and homomorphic encryption. In Ref. [11], Shao, Z.Y., Yan, B. obtained a novel approach to accomplish PSI, which used the public key encryption with keywords search.

Shor pointed out that SMC tasks can be performed more efficiently by models based on quantum setting than classical setting [12]. Many researchers explored the special SMC problems based on quantum cryptography Ref. [13,14,15,16,17,18,19,20,21]. But there are only few quantum schemes for PSI and its variants. In Ref. [22], Shi, R.H. et al. proposed a novel quantum scheme for PSI, which required O(n) computation and communication complexities. In Ref. [23], Shi, R.H. et al. solved PSI cardinality problem using a quantum approach, which can achieve an exponential reduction in communication complexity. In Ref. [24], Shi, R.H. presented a novel quantum approach to solve PSI cardinality and private set union cardinality problems based on the principle of quantum mechanics, which can resist well-known quantum attacks. In this work, we use quantum Fourier transform approach to perform PSI. Our scheme only needs orbital angular momentum(OAM) basis, so it will be more practical than the schemes using multiple particles.

The structure of our paper is as follows: we introduce some preliminary in Section 2; we propose a PSI protocol based on a coding scheme and quantum Fourier transform in Section 3; and we analyze the correctness and security of our protocol in Section 4. A brief discussion and a concluding summary are given in Section 5.

2 Preliminary

2.1 Quantum Fourier Transform

There are two bases, Z-basis and X-basis. Z-basis can be expressed as $\{ \left | j \right \rangle ,j = - N,$...,0,...,N}, where N is a positive integer. X-basis can be expressed as $\{ QFT\left | j \right \rangle ,j =$ − N,...,0,...,N}

Quantum Fourier transform performed on $\left | j \right \rangle$ in the Z basis can be described as $QFT\left | j \right \rangle = \frac {1}{{\sqrt {2N + 1} }}\sum \limits _{k = - N}^{N} {\omega ^{jk} \left | k \right \rangle }(j={-N,...,0,...,N})$, where $\omega = e^{\frac {{2\pi i}}{{2N + 1}}}$. We have $\omega ^{2N + 1} = e^{2\pi i} = {\cos \limits } (2\pi ) + i{\sin \limits } (2\pi ) = 1$ and $\sum \limits _{k = - N}^{N} {\omega ^{k} } = \frac {{\omega ^{- N} (1 - \omega ^{2N + 1} )}}{{1 - \omega }} = \frac {{\omega ^{- N} (1 - 1)}}{{1 - \omega }} = 0$.

For Z basis, we can get

$$ \begin{array}{l} QFT^{2} (\left| j \right\rangle ) = \frac{1}{{\sqrt {2N + 1} }}\sum\limits_{k = - N}^{N} {\omega^{jk} } \left( \frac{1}{{\sqrt {2N + 1} }}\sum\limits_{l = - N}^{- N} {\omega^{kl} } \left| l \right\rangle\right ) \\ \quad \quad \quad \quad = \frac{1}{{2N + 1}}\sum\limits_{k = - N}^{N} {\omega^{jk} } \left( \sum\limits_{l = - N}^{- N} {\omega^{kl} } \left| l \right\rangle \right) \\ \quad \quad \quad \quad = \frac{1}{{2N + 1}}\sum\limits_{k = - N}^{N} {\sum\limits_{l = - N}^{N} {\omega^{k(j + l)} } } \left| l \right\rangle \\ \quad \quad \quad \quad = \frac{1}{{2N + 1}}\sum\limits_{k = - N}^{N} {\sum\limits_{l = - N}^{N} {\omega^{k(j + l)} } } \left| l \right\rangle \\ \quad \quad \quad \quad = \frac{1}{{2N + 1}}\sum\limits_{k = - N}^{N} {\omega^{k(j - j)} } \left| { - j} \right\rangle + \frac{1}{{2N + 1}}\sum\limits_{k = - N}^{N} {\sum\limits_{l = - N \wedge l \ne - j}^{N} {\omega^{k(j + l)} } } \left| l \right\rangle \\ \quad \quad \quad \quad = \frac{1}{{2N + 1}}\sum\limits_{k = - N}^{N} {1 \times \left| { - j} \right\rangle } + \frac{1}{{2N + 1}}\sum\limits_{l = - N \wedge l \ne j}^{N} {(0 \times \left| l \right\rangle )} \\ \quad \quad \quad \quad =\left| { - j} \right\rangle. \end{array} $$

(1)

Then we can also get $QFT^{4} (\left | j \right \rangle ) = \left | j \right \rangle$ [25].

3 Proposed Protocol

In this section we firstly give an informal definition of PSI and then present a PSI protocol using quantum Fourier transform.

Definition 1

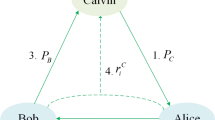
Private Set Intersection(PSI)—-There are two parties, Alice and Bob. Supposed that U = {x₁,x₂,...,x_n} is a complete set. Alice inputs a private set $S_{A} = \left \{ {{s}_{1}^{A}} ,{{s}_{2}^{A}} ,...,{s}_{l_{A} }^{A} \right \}$ and Bob inputs a private set $S_{B} = \left \{ {{s}_{1}^{B}} ,{{s}_{2}^{B}} ,...,{s}_{l_{B} }^{B}\right \}$, where $S_{A} ,S_{B} \subseteq U$. With the help of a semi-honest third party Calvin, Alice and Bob can get the intersection S_A ∩ S_B without leaking any information about their private sets.

Alice and Bob decode their private sets S_A,S_B into two 0 − 1 sequences $C_{A}=\left (c_{1}^{A },c_{2}^{A },...,{c_{n}^{A}} \right ),$ $C_{B}=\left ({c_{1}^{B}},c_{2}^{B }, ...,{c_{n}^{B}} \right )$:

$$ \left\{ {\begin{array}{cc} {{c}_{i}^{A } = 1,\quad if x_{i} \in S_{A}\quad}\\ {{c}_{i}^{A } = 0,\quad if x_{i} \notin S_{A} \quad} \end{array} \left\{ {\begin{array}{*{20}c} {{c}_{i}^{B } = 1,\quad if x_{i} \in S_{B} } \\ {{c}_{i}^{B } = 0,\quad if x_{i} \notin S_{B}} \end{array}} \right.} \right. $$

(2)

The detailed quantum PSI protocol is described as follows:

• (1) Calvin prepares a particles sequence $P_{C}=\left ({{p}_{1}^{C}},{{p}_{2}^{C}},...,{{p}_{n}^{C}}\right )$ and ${{p}_{i}^{C}}(i=1,2,...,n)$ is randomly chosen from $\{ \left | { - N} \right \rangle ,...,\left | { - 1} \right \rangle ,\left | 1 \right \rangle ,...,\left | N \right \rangle \}$. He also inserts l_C particles into P_C for each particle in Z-basis and X-basis. After recording the insert positions Po_C, Calvin sends the sequence $P^{\prime }_{C}$ of (n + l_C) particles to Alice.

• (2) After receiving $P^{\prime }_{C}$, Calvin announces Po_C and measuring basis. Calvin and Alice measure those insert particles and can find the existence of an eavesdropper. If there are cheaters, the scheme will be aborted. Otherwise, Alice discards the insert photons in $P^{\prime }_{C}$ and continues the next step.

• (3) Alice prepares two n-length strings $R_{A}=\left ({r_{1}^{A}},{r_{2}^{A}},...,r_{n+l}^{A}\right )$ and $H_{A}=\left ({h_{1}^{A}},{h_{2}^{A}},...,h_{n+l}^{A}\right )$, where ${r_{i}^{A}}(i=1,...,n)$ is randomly chosen from {0,1} and ${{h}_{i}^{A}}(i=1,...,n)$ is a random positive integer. Then she calculates ${{p}_{i}^{A}} = QFT^{{c_{i}^{A}} \times 2}$ $QFT^{{r_{i}^{A}} \times {h_{i}^{A}} } {p_{i}^{C}}(i=1,2,...,n)$. If ${{r}_{i}^{A}}=0$, ${{r}_{i}^{A}} \times {h_{i}^{A}}=0$, then Alice performs no quantum Fourier transform; If ${{r}_{i}^{A}}=1$, ${{r}_{i}^{A}} \times {{h}_{i}^{A}}={{h}_{i}^{A}}$, then Alice performs ${h_{i}^{A}}$ quantum Fourier transform. The new particles sequence is denoted by $P_{A}=\left ({p}_{1}^{A},{p}_{2}^{A},...,{p}_{n}^{A}\right )$.

  Alice also inserts l_A particles into P_A for each particle in Z-basis and X-basis. After recording the insert positions Po_A, the sequence $P^{\prime }_{A}$ of (n + l_A) particles will be sent to Bob.

• (4) After receiving ${P}_{A}^{\prime }$, Alice announces Po_A and measuring basis. Alice and Bob measure those insert particles to find the existence of an eavesdropper. If there is a cheater, the scheme will be aborted. Otherwise, Bob discards the insert photons in $P^{\prime }_{A}$ and continues the next step.

• (5) Bob prepares two (n)-length strings $R_{B}=\left ({r_{1}^{B}},{r_{2}^{B}},...,{r_{n}^{B}}\right )$ and $H_{B}=\left ({{h}_{1}^{B}},{h_{2}^{B}},...,{h_{n}^{B}}\right )$, where ${r_{i}^{B}}(i=1,...,n)$ is randomly chosen from {0,1} and ${h_{i}^{B}}(i=1,...,n)$ is a random integer. Then he calculates ${p_{i}^{B}} = QFT^{{c_{i}^{B}} \times 2} QFT^{{r_{i}^{B}} \times {h_{i}^{B}} }$ ${p_{i}^{A}}(i=1,2,...,n)$. If ${r_{i}^{B}}=0$, ${r_{i}^{B}} \times {h_{i}^{B}}=0$, then Bob performs no quantum Fourier transform; If ${r_{i}^{B}}=1$, ${r_{i}^{B}} \times {h_{i}^{B}}={h_{i}^{B}}$, then Bob performs ${h_{i}^{B}}$ quantum Fourier transform. The new particles sequence is denoted by $P_{B}=\left ({{p}_{1}^{B}},{{p}_{2}^{B}},...,{{p}_{n}^{B}}\right )$.

  Bob also inserts l_B particles into P_B for each particle in Z-basis and X-basis. After recording the insert positions Po_B, he sends the sequence $P_{B}^{\prime }$ of (n + l_B) particles to Calvin.

• (6) After receiving $P_{B}^{\prime }$, Bob announces Po_B and and measuring basis. Bob and Calvin measure those insert particles to find the existence of an eavesdropper. If there is a cheater, the scheme will be aborted. Otherwise, Calvin discards the insert photons in $P_{B}^{\prime }$ and continues the next step.

• (7) Alice and Bob compute ${{h}_{i}^{C}} = 4 - (\left (\left ({{r}_{i}^{A}} \times {{h}_{i}^{A}} \right )+ \left ({{r}_{i}^{B}} \times {{h}_{i}^{B}} \right )\right ) \bmod 4)(i=1,...,n)$ and send ${{h}_{1}^{C}},...,{{h}_{n}^{C}}$ to Calvin.

  Calvin calculates ${p}_{i}^{C^{\prime }} = QFT^{{h_{i}^{C}} } {p}_{i}^{B}(i=1,2,...,n)$ and measures it using $\{ \left | { - N} \right \rangle ,...,\left | { 0} \right \rangle ,...,$ $\left | N \right \rangle \}$. If the measurement result of $p^{C^{\prime }}_{i}$ is the same as ${p^{C}_{i}}$, Calvin know that ${c}_{i}^{A }={c}_{i}^{B }$; Otherwise, Calvin knows that ${c}_{i}^{A } \ne {c}_{i}^{B }$. Calvin get S_A ∩ S_B.

4 Analysis

4.1 Correctness Analysis

In this section, we verify the correctness of the protocol by taking a concrete example.

In our protocol, Alice performs ${{r}_{i}^{A}} \times {{h}_{i}^{A}}$ quantum Fourier transform on ${{p}_{i}^{C}}$ in step (3); Bob performs ${{r}_{i}^{B}} \times {{h}_{i}^{B}}$ quantum Fourier transform on ${{p}_{i}^{C}}$ in step(3); Calvin performs ${{h}_{i}^{C}}= 4 - ((({{r}_{i}^{A}} \times {{h}_{i}^{A}} ) + ({{r}_{i}^{B}} \times {{h}_{i}^{B}} )) \mod 4)$ quantum Fourier transform on ${p_{i}^{C}}$ in step(7). In Section 2, we know that the particle ${p_{i}^{C}}$ will not change if it has been performed on four quantum Fourier transforms. So Alice, Bob and Calvin have no effects on ${{p}_{i}^{C}}$.

Then the particle $p^{C^{\prime }}_{i}(i=1,2,...,n)$ in step (7) is written as follows:

$$ \begin{array}{@{}rcl@{}} p_{i}^{C^{\prime}} &=& QFT^{{{h}_{i}^{C}} } QFT^{{{c}_{i}^{B}} \times 2} QFT^{{{r}_{i}^{B}} \times {{h}_{i}^{B}} } QFT^{{{c}_{i}^{A}} \times 2} QFT^{{{r}_{i}^{A}} \times {{h}_{i}^{A}} } {{p}_{i}^{C}}\\ &=& QFT^{{{h}_{i}^{C}} + {{r}_{i}^{B}} \times {{h}_{i}^{B}} + {{r}_{i}^{A}} \times {{h}_{i}^{A}} } QFT^{\left( {{c}_{i}^{B}} + {{c}_{i}^{A}} \right) \times 2} {{p}_{i}^{C}}\\ &=& QFT^{4k} QFT^{\left( {{c}_{i}^{B}} + {{c}_{i}^{A}} \right) \times 2} {{p}_{i}^{C}} \\ &=& QFT^{\left( {{c}_{i}^{B}} + {{c}_{i}^{A}} \right) \times 2} {{p}_{i}^{C}} \end{array} $$

(3)

Alice and Bob perform $\left ({{c}_{i}^{A}}+{{c}_{i}^{B}}\right ) \times 2$ quantum Fourier transform on ${{p}_{i}^{C}}$. If ${{c}_{i}^{A}}={c_{i}^{B}}=0$ or ${c_{i}^{A}}={c_{i}^{B}}=1$, Alice and Bob will perform zero or four quantum Fourier transform on ${p_{i}^{C}}$ and the particle ${p_{i}^{C}}$ will not change. If ${c_{i}^{A}}=1, {c_{i}^{B}}=0$ or ${c_{i}^{A}}=0, {c_{i}^{B}}=1$, Alice and Bob will perform two quantum Fourier transform on ${p_{i}^{C}}$ and the particle ${p_{i}^{C}}$ will change. When Calvin measures ${p_{i}^{C}}$, he can know whether ${c_{i}^{A}}, c_{i}^{B }$ are equal or not by comparing the measurement result and the original particle. Alice and Bob discard l results which are used to protect U and determine S_A ∩ S_B.

We give an example throughout the protocol to proof the correctness of our protocol. Supposed that U = {3,4,12} and OAM basis is $\{ \left | { - 2} \right \rangle ,$ $\left | { - 1} \right \rangle ,\left | 0 \right \rangle ,\left | 1 \right \rangle ,\left | 2 \right \rangle \}$. Alice has a private set S_A = {3,12} and Bob has a private set S_B = {4,12}, and their 0-1 codes are (1,0,1) and (0,1,1) respectively. The random strings chosen by Alice are R_A = (1,0,0),H_A = (4,2,2). The random strings chosen by Bob are R_B = (0,1,0),H_B = (2,1,5). Calvin prepares a particles sequence $P_{C}=\left ({p_{1}^{C}},{p_{2}^{C}},{p_{3}^{C}}\right )=(\left | {2 } \right \rangle ,\left | { - 2} \right \rangle ,\left | 2 \right \rangle )$.

According to R_A,H_A and the 0 − 1 code of Alice, Alice performs four quantum Fourier transform on ${p_{1}^{C}}$ firstly, then performs two quantum Fourier transform on ${p_{1}^{C}},{p_{3}^{C}}$. The new particles sequence generated by Alice is $P_{A}=\left ({p_{1}^{A}},{p_{2}^{A}},{p_{3}^{A}}\right )=(QFT^{6}\left | {2 } \right \rangle ,\left | { - 2} \right \rangle ,QFT^{2}\left | 2 \right \rangle )$.

Similarly, according to R_B,H_B and the 0 − 1 code of Bob, Bob performs one quantum Fourier transform on ${{p}_{2}^{A}}$ firstly, then performs two quantum Fourier transform on ${{p}_{2}^{A}},{{p}_{3}^{A}}$. The new particles sequence generated by Bob is $P_{B}=\left ({{p}_{1}^{B}},{{p}_{2}^{B}},{{p}_{3}^{B}}\right )=(QFT^{6}\left | {2 } \right \rangle , QFT^{3}\left | { - 2} \right \rangle ,QFT^{4}\left | 2 \right \rangle )$.

According to H_C = (4,3,0), Calvin performs three quantum Fourier transform on ${{p}_{2}^{B}}$, performs four quantum Fourier transform on ${{p}_{1}^{B}}$, performs no quantum Fourier transform on ${{p}_{3}^{B}}$. The new particles sequence of Calvin is ${P}_{C}^{\prime }=\left ({p}_{1}^{C^{\prime }},{p}_{2}^{C^{\prime }},{p}_{3}^{C^{\prime }}\right )=(QFT^{10}\left | {2 } \right \rangle ,QFT^{6}\left | { - 2} \right \rangle ,QFT^{4}\left | 2 \right \rangle )=(\left | {-2 } \right \rangle ,\left | { 2} \right \rangle ,\left | 2 \right \rangle )$. Calvin compares P_C and $P_{C}^{\prime }$. He can knows that only the 5th particle is equal and others particles are not. Alice and Bob know S_A ∩ S_B = {12}.

4.2 Security Analysis

Firstly, we show that the outside attack is invalid to our protocol. Secondly, we show that Alice and Bob can not get any information about the private information of each other.

4.2.1 Outside Attack

In this protocol, the outside eavesdroppers can attack the quantum channel and get particles sequences of Alice, Bob and Calvin in step (1)(3)(5). In order to resist outside attacks, there are some checking particles inserted by Alice, Bob and Calvin. The intercept-resend attack, the measurement-resend attack, entanglement- measure attack and the denial-of-service (DOS) attack can be detected with nonzero probability during the security checking process in step (2)(4)(6).

Outside eavesdroppers can also adopt some special attacks, such as the delay photon Trojan horse attack, the invisible photon eavesdropping (IPE) Trojan horse attack, the photon-number-splitting (PNS) attack. In order to defeat delay-photon Trojan horse attack, we can use a photon-number splitter. In order to defeat IPE attack, we can insert filters in front of their devices to filter out the photon signal with an illegitimate wavelength. In order to defeat PNS attack, we can use the technology of beam splitters to split the sampling signals and judge whether these received photons are single photons or multiple photons.

In step (7)(8), Alice, Bob and Calvin need to transfer some classical information, which is not relevant to the private sets S_A,S_B. Therefore, outside eavesdropper cannot deduce the private sets S_A,S_B from these classical information..

So we can say the protocol is security under the outside attack.

4.2.2 Participant Attack

The term “participant attack”, which emphasizes that the attacks from dishonest users are generally more powerful and should be paid more attention to, is first proposed by Gao et al. in Ref. [26] and has attracted much attention in the cryptanalysis of quantum cryptography [27,28,29,30,31,32,33]. We analyze the possibility of three parties, Alice, Bob and Calvin, to get information about S_A,S_B in our protocol.

Case 1: Alice wants to learn Bob’s private set $S_{B} = \left \{ {s_{1}^{B}} ,{s_{2}^{B}} ,...,s_{l_{B} }^{B}\right \}$.

In our protocol, Alice only gets a particles sequence $P_{C}=\left ({{p}_{1}^{C}},{{p}_{2}^{C}},...,{{p}_{n}^{C}}\right )$, which is randomly chosen by Calvin. These particles didn’t have any secret information about the Bob’s input S_B. So for Alice, all possible attacks which she can perform with the present technology can not help her to eavesdrop Bob’s secret set.

Case 2: Bob wants to learn Alice’s private set $S_ A = \left \{ {s_{1}^{A}} ,{s_{2}^{A}} ,...,s_{l_{A} }^{A}\right \}$.

In our protocol, Bob’s legal resource in his hand is the sequence $P_{A} = \left ({p_{1}^{A}} ,{p_{2}^{A}} ,...,{p_{n}^{A}}\right )$, where ${p_{i}^{A}} = QFT^{{c_{i}^{A}} \times 2} QFT^{{r_{i}^{A}} \times {h_{i}^{A}} }{p_{i}^{C}}(i=1,2,...,n)$ and ${c_{i}^{A}}$ is related to Alice’s private set. Bob’s eavesdropping is carried out by an unitary operation $\widehat {U_{AB} }$, which acts on ${p_{i}^{A}}=\left | j \right \rangle _{A}$ and an ancillary particle $\left | 0 \right \rangle _{B}$. Using the similar analysis in [34], the effect of Bob’s attack can be described using the following equations:

$$ \widehat{U_{AB} }\left| j \right\rangle_{A} \left| 0 \right\rangle_{B} = \sqrt {\eta_{j} } \left| j \right\rangle_{A} \left| {\phi (j)} \right\rangle_{B} + \sqrt {1 - \eta_{j} } \left| {V(j)} \right\rangle_{AB}. $$

(4)

where $\left | {V(j)} \right \rangle _{AB}$ is a vector orthogonal to $\left | j \right \rangle _{A} \left | {\phi (j)} \right \rangle _{B}$.

In order to pass the eavesdropping checking, it can easily deduce η_j = 1. After perform $\widehat {U_{AB} }$, the particle ${p_{i}^{A}}(i=1,2,...,n+l)$ in P_A should be in the following state:

$$ \begin{array}{l} \widehat{U_{AB} }{p_{i}^{A}} \left| 0 \right\rangle_{B} \\ = \widehat{U_{AB} }QFT^{{c_{i}^{A}} \times 2} QFT^{{r_{i}^{A}} \times {h_{i}^{A}} } \left| j \right\rangle_{A} \left| 0 \right\rangle_{B} \\ = \left\{ {\begin{array}{*{20}c} {\left( \frac{1}{{\sqrt {2N + 1} }}\right)^{2 + {h_{i}^{A}} } \sum\limits_{k_{1} = - N}^{- N} {\sum\limits_{k_{2} = - N}^{- N} {...\sum\limits_{k_{(2+ {h_{i}^{A}} )} = - N}^{- N} {\omega^{jk_{1} + k_{1} k_{2} + ... + k_{1 + {h_{i}^{A}} } k_{2 + {h_{i}^{A}} } } } } } \left| {k_{2 + {h_{i}^{A}} } } \right\rangle_{A} \left| {\phi (j)} \right\rangle_{B} \left( {c_{i}^{A}} = 1,{r_{i}^{A}} = 1\right)} \\ {\left( \frac{1}{{\sqrt {2N + 1} }}\right)^{{{h}_{i}^{A}} } \sum\limits_{k_{1} = - N}^{- N} {\sum\limits_{k_{2} = - N}^{- N} {...\sum\limits_{k_{({h_{i}^{A}} )} = - N}^{- N} {\omega^{jk_{1} + k_{1} k_{2} + ... + k_{{h_{i}^{A}} - 1} k_{{h_{i}^{A}} } } } } } \left| {k_{{h_{i}^{A}} } } \right\rangle_{A} \left| {\phi (j)} \right\rangle_{B} \quad \quad \left( {c_{i}^{A}} = 0,{r_{i}^{A}} = 1\right)} \\ {\left( \frac{1}{{\sqrt {2N + 1} }}\right)^{2} \sum\limits_{k_{1} = - N}^{- N} {\sum\limits_{k_{2} = - N}^{- N} {\omega^{jk_{1} + k_{1} k_{2} } } \left| {k_{2} } \right\rangle_{A} \left| {\phi (j)} \right\rangle_{B} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left( {c_{i}^{A}} = 1,{r_{i}^{A}} = 0\right)} } \\ {\left| j \right\rangle_{A} \left| {\phi (j)} \right\rangle_{B} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left( {c_{i}^{A}} = 0,{r_{i}^{A}} = 0\right)} \end{array}} \right. \end{array} $$

(5)

It implies that Bob cannot get any secret information about Alice’s private set, because he cannot extract out the global phase information from the partial qubits of the entangled quantum systems with the subscripts A and B. In fact, any local unitary operator on the partial qubits cannot fully disentangle the entanglement of the composite system unless it directly measures them.

Case 3: Calvin wants to learn Alice’s and Bob’s private sets $S_ A = \left \{ {s_{1}^{A}} ,{s_{2}^{A}} ,..., s_{l_{A} }^{A}\right \},$ $S_ B = \left \{ {s_{1}^{B}} ,{s_{2}^{B}} ,...,s_{l_{B} }^{B}\right \}$.

In our protocol, Calvin can get $P_{B} = \left ({p_{1}^{B}} ,{p_{2}^{B}} ,...,p_{n + l}^{B}\right )$, where ${p_{i}^{B}} = QFT^{{c_{i}^{B}} \times 2}$ $QFT^{{r_{i}^{B}} \times {h_{i}^{B}}}QFT^{{c_{i}^{A}} \times 2} QFT^{{r_{i}^{A}} \times {h_{i}^{A}} } \left | j \right \rangle _{C} (i=1,2,...,n)$ and ${c_{i}^{B}}, {c_{i}^{A}}$ is related to Alice’s and Bob’s private sets.

Calvin calculates $p^{C^{\prime }}_{i} =QFT^{4 - (\left (\left ({r_{i}^{A}} \times {h_{i}^{A}} \right )+ \left ({r_{i}^{B}} \times {h_{i}^{B}} \right )\right ) \bmod 4)+{r}_{i}^{B} \times {h}_{i}^{B}+{r}_{i}^{A} \times {h_{i}^{A}} }QFT^{{c_{i}^{B}} \times 2}$ $QFT^{{c_{i}^{A}} \times 2}\left | j \right \rangle _{C}(i=1,2,...,n)$.

Calvin measures $p^{C^{\prime }}_{i}$: If the measuring result is $\left | j \right \rangle _{C}$, he cannot determine ${c}_{i}^{A} = {c}_{i}^{B} = 1$ or ${c}_{i}^{A} = {c}_{i}^{B} = 0$; If the measuring result is $\left | -j \right \rangle _{C}$, he cannot determine ${c}_{i}^{A} =1, {c}_{i}^{B} = 0$ or ${c}_{i}^{A} =0, {c}_{i}^{B} = 1$. The maximal probability of correct messages guessed by Calvin is $\left (\frac {1}{2}\right )^{n}$, where n is the length of Alice’s and Bob’s 0 − 1 codes. Alice and Bob can insert some extra codes to obtain higher security.

4.3 Comparison of our Protocol with Previous Studies

In this sub-section, we will take a simple comparison between the a scheme in Ref. [22,23,24] and our scheme, which are used to solve private set intersection problem. With the help of the third party(TP), the comparison result(s) can be known from the following six aspects: the cost of quantum resource, quantum measurement and quantum technology used. The details of differences between our protocol and related studies Ref. [22,23,24] are shown in Table 1.

Table 1 The comparison of Ref. [22,23,24] and our protocol

Obviously, we can very easily find that our scheme has the remarkable advantages of consuming fewer quantum resources. Our protocol is easy to implement and it only needs simple quantum technology QFT.

5 Discussion and Conclusions

In summary, we put forward a novel quantum solution for PSI problem. After performing quantum Fourier transform on particles randomly chosen by Calvin, Alice and Bob privately get all common elements of their respective sets. Our protocol can resist various outside attacks, such as disturbance attack, Trojan horse attack, intercept-resend attack, entanglement-and-measure attack and man-in-the-middle attack. It can also avoid the problem of information leakage with acceptable efficiency.