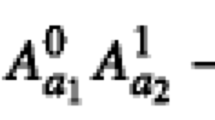Partial Steerability and Nonlocality of Multipartite Quantum States

Abstract

In this paper, we discuss partial steerability and nonlocality of multipartite quantum states. For a state ρ of an n-partite system A₁A₂⋯A_n, we introduce the concepts of the steerability of ρ from i to j and the (i, j)-Bell nonlocality of ρ. By establishing necessary conditions for a state ρ to be unsteerable from i to j (resp. (i, j)-Bell local), we derive sufficient conditions for a state ρ to be steerable from i to j (resp. (i, j)-Bell nonlocal). We prove that if there are some 1 ≤ i < j ≤ n such that ρ is steerable from i to j (resp. (i, j)-Bell nonlocal), then it is steerable from A to B (resp. (A, B)-Bell nonlocal) provided that A = A₁A₂⋯A_k and B = A_k+ 1A_k+ 2⋯A_n with 1 ≤ i ≤ k and k < j ≤ n, leading to new methods for detecting steerability and (A, B)-Bell nonlocal of multipartite states.

1 Introduction

In 1935 the famous EPR paradox was introduced by Einstein, Podolsky and Rosen [1] and developed to quantum steering by Schr$\ddot {\text {o}}$dinger [2]. Quantum steering as a special quantum entanglement is another type of quantum correlations. An experimental about quantum steering was first performed by Ou et al. [3] and then by [4,5,6]. Various steering criteria give yes/no answers to the question of steerability. To study steering, we must understand the standard provided by Reid [7], which developed by Cavalcanti [8], Foster, Reid and Drummond [9], and Walborn et al [10]. Cao and Guo [11] discussed EPR steering of bipartite states, including mathematical definition and characterizations, the convexity as well as the closedness of the set of all EPR unsteerable states. Li et al. in [12] obtained some characterizations of EPR steerability of bipartite states by proving some necessary and sufficient conditions for a state to be unsteerable with a measurement assemblage of Alice. Based on one of the obtained characterizations, they derived an EPR steering inequality, which serves to check EPR steerability of the maximally entangled states. See [13] for more steering inequalities, [14, 15] for the steering of tripartite systems and some applications of the steerable states [16,17,18].

Bell nonlocality [19,20,21,22,23] is usually detected by a violation of some Bell inequalities, such as the CHSH inequality [24]. Dong and Cao obtained a Hardy Paradox-based method for detecting Bell nonlocality [25]. Chen et al [26] showed that Bell nonlocality can be detected through a violation of EPR steering inequality. Cao and Guo [11] discussed mathematical definition and characterizations of Bell locality and proved the convexity as well as the closedness of the sets of all Bell local states.

In this work, we discuss partial steerability and nonlocality of multipartite quantum states. For a state ρ of an n-partite system A₁A₂⋯A_n, we introduce the concepts of the steerability of ρ from i to j and the (i, j)-Bell nonlocality of ρ in Sections 2 and 3, respectively. By establishing necessary conditions for a state ρ to be unsteerable from i to j and (i, j)-Bell local, respectively, we derive sufficient conditions for a state ρ to be steerable from i to j and (i, j)-Bell nonlocal, respectively. We also prove that if there are some 1 ≤ i < j ≤ n such that ρ is steerable from i to j (resp. (i, j)-Bell nonlocal), then it is steerable from A to B (resp. (A, B)-Bell nonlocal) provided that A = A₁A₂⋯A_k and B = A_k+ 1A_k+ 2⋯A_n with 1 ≤ i ≤ k and k < j ≤ n. This suggests new methods for detecting steerability and (A, B)-Bell nonlocal of multipartite states.

2 Steering from i to j

Consider an n-partite system A₁A₂⋯A_n described by Hilbert space ${{\mathscr{H}}}_{1}\otimes {{\mathscr{H}}}_{2}\otimes \cdots \otimes {{\mathscr{H}}}_{n}$. We use I_k to denote the identity operator on H_k and tr_j to denote the partial-trace operation ${\text {tr}}_{A_{j}}$, and use ∥T∥ and ∥T∥₁ to denote the operator-norm and the trace-norm of an operator T. For a nonempty proper subset E of [n] = {1,2,…,n}, we use tr_E to denote the partial-trace operation on subsystem π_i∈EA_i. Thus, ${\hat {E}}:=[n]\setminus E$, ${\text {tr}}_{\hat {E}}$ denotes the partial-trace operation on subsystem ${\varPi }_{i\in \hat {E}}A_{i}={\varPi }_{i\in [n]\setminus {E}}A_{i}$. Specially, when E = {i}, we write tr_E and ${\text {tr}}_{\hat {E}}$ as tr_i and ${\text {tr}}_{\hat {i}}$, respectively.

Let

$$ \mathcal{M}_k=\left\{M^{x_k}=\left\{{M}_{a_k|x_k}^{(k)}\right\}_{a_k=1}^{o_{k}}:x_k=1,2,\ldots,m_k\right\} $$

(2.1)

be a POVM measurement assemblages (a set of POVMs) of system A_k described by a Hilbert space ${{\mathscr{H}}}_{k}$ of dimension d_k for all k = 1,2,…,n. For a state $\rho \equiv \rho ^{A_{1}A_{2}{\cdots } A_{n}}$ of an n-partite system A₁A₂⋯A_n and two subsystems A_i and A_j(i < j), we denote $N_{a_{i}|x_{i}}={\otimes }_{k=1}^{n}T_{ik}$ where $T_{ii}={M}_{a_{i}|x_{i}}^{(i)}$ and T_ik = I_k(k≠i).

Definition 2.1

For a state $\rho \equiv \rho ^{A_{1}A_{2}{\cdots } A_{n}}$ of an n-partite system A₁A₂⋯A_n and two subsystems A_i and A_j(i < j), we say that ρ is unsteerable from i to j (or i can not steer j) with ${\mathscr{M}}_{i}$ if there exists a PD $\{\pi _{\lambda }\}_{\lambda =1}^{d}$ and a set of states $\{\sigma ^{(j)}_{\lambda }\}_{\lambda =1}^{d}$ of A_j such that

$$ {\text{tr}}_{\hat{j}}[N_{a_{i}|x_{i}}\rho]=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} P_{i}({a_{i}|x_{i}},\lambda){\sigma}_{\lambda}^{(j)},\ \ \forall x_{i}\in[m_{i}],a_{i}\in[o_{i}], $$

(2.2)

where $\{P_{i}({a_{i}|x_{i}},\lambda )\}_{a_{i}=1}^{o_{i}}$ is a PD for each (λ, x_i). Equation (2.2) is said to be an LHS model of ρ with respect to ${\mathscr{M}}_{i}$.

A state ρ is said to unsteerable from i to j if it is unsteerable from i to i with any ${\mathscr{M}}_{i}$; A state ρ is said to be steerable from i to j with ${\mathscr{M}}_{i}$ if it is not unsteerable from i to j with ${\mathscr{M}}_{i}$. It is said to be steerable from i to j if it is steerable from i to j with some ${\mathscr{M}}_{i}$. Moreover, a pure state |ψ〉 of A₁A₂⋯A_n is said to be unsteerable (resp. steerable) from i to j with ${\mathscr{M}}_{i}$ if |ψ〉〈ψ| is. Furthermore, we also call the unsteerability and steerability defined here the partial unsteerability and steerability.

Clearly,

$$ {\text{tr}}_{\hat{j}}[N_{a_i|x_i}\rho]= {\text{tr}}_{i}\left[\left( {M}_{a_i|x_i}^{(i)}\otimes I_j\right){\text{tr}}_{\widehat{i,j}}\rho\right]= {\text{tr}}_{i}\left[\left( {M}_{a_i|x_i}^{(i)}\otimes I_j\right)\rho_{ij}\right], $$

(2.3)

where $\rho _{ij}={\text {tr}}_{\widehat {i,j}}\rho$, the reduced state of ρ on the subsystem A_iA_j. Thus, ρ is unsteerable (resp. steerable) from i to j with ${\mathscr{M}}_{i}$ if and only if ρ_ij is unsteerable (resp. steerable) from A_i to A_j with ${\mathscr{M}}_{i}$ in the sense of [11, Definition 3.1].

We use $\mathcal {U}\mathcal {S}(i\rightarrow j,{\mathscr{M}}_{i})$ to denote the set of all states $\rho \equiv \rho ^{A_{1}A_{2}{\cdots } A_{n}}$ of an n-partite system A₁A₂⋯A_n that are unsteerable from i to j with ${\mathscr{M}}_{i}$. Then we see from [11, Corollary 3.1] that $\mathcal {U}\mathcal {S}(i\rightarrow j,{\mathscr{M}}_{i})$ is a compact convex subset of the set $\mathcal {D}(A_{1}A_{2}{\cdots } A_{n})$ of all states of A₁A₂⋯A_n. Therefore, the set $\mathcal {S}(i\rightarrow j,{\mathscr{M}}_{i})$ of all states of A₁A₂⋯A_n that are steerable from i to j with ${\mathscr{M}}_{i}$ becomes an open set. Also, we use $\mathcal {U}\mathcal {S}(i\rightarrow j)$ and $\mathcal {S}(i\rightarrow j)$ to denote the set of all unsteerable and steerable states from i to j of A₁A₂⋯A_n. Thus, we see from Definition 2.1 that

$$ \mathcal{U}\mathcal{S}(i\rightarrow j)=\underset{\mathcal{M}_i}{\bigcap}\mathcal{U}\mathcal{S}(i\rightarrow j,\mathcal{M}_i),\ \mathcal{S}(i\rightarrow j)=\underset{\mathcal{M}_i}\bigcup\mathcal{S}(i\rightarrow j,\mathcal{M}_i). $$

(2.4)

This implies that $\mathcal {U}\mathcal {S}(i\rightarrow j)$ is a compact subset of the set $\mathcal {D}(A_{1}A_{2}{\cdots } A_{n})$ and that $\mathcal {S}(i\rightarrow j)$ is an open subset of $\mathcal {D}(A_{1}A_{2}{\cdots } A_{n})$.

Let us discuss a relationship between the unsteerability (steerability) defined by Definition 2.1 and the unsteerability (steerability) introduced in [11] of an n-partite quantum system A₁A₂⋯A_n as a bipartite system AB where A = A₁A₂⋯A_k, B = A_k+ 1A_k+ 2⋯A_n and 1 ≤ i ≤ k and k < j ≤ n. Suppose that a state ρ of A₁A₂⋯A_n is unsteerable from A to B in the sense of [11, Definition 3.1]. Then for any indices 1 ≤ i ≤ k and k < j ≤ n, and any POVM measurement assemblage

$$ \mathcal{N}_{i}=\left\{M^{(i)}=\left\{{M}_{a_{i}|x_{i}}^{(i)}\right\}_{a_{i}=1}^{o_{i}}: x_{i}\in[m_{i}]\right\} $$

of A_i, we denote $M_{a|x}={\otimes }_{n=1}^{k}T_{in}$ with $T_{ii}={M}_{a|x}^{(i)}$ and T_in = I_n(n≠i) for each a ∈ [o_i] and x ∈ [m_i]. Then we get a measurement assemblage ${\mathscr{M}}_{A}=\{\{M_{a|x}\}_{a=1}^{o_{i}}:x\in [m_{i}]\}$ of system A. From [11, Definition 3.1], there exists a PD $\{\pi _{\lambda }\}_{{\lambda }=1}^{d}$ and a set $\{\sigma _{{\lambda }}\}_{{\lambda }=1}^{d}$ of states of B such that for all x ∈ [m_i],a ∈ [o_i], it holds that

$$ {\text{tr}}_{A}[(M_{a|x}\otimes I_{B})\rho]=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} P_{A}({a|x},\lambda)\sigma_{{\lambda}}, $$

where $\{P_{A}(a|x,\lambda )\}_{a=1}^{o_{i}}$is a PD for each (λ, x). Hence, for all x_i ∈ [m_i],a_i ∈ [o_i], it holds that

$$ {\text{tr}}_{i}\left[\left( {M}_{a_{i}|x_{i}}^{(i)}\otimes I_{j}\right)\rho_{ij}\right]={\text{tr}}_{\hat{j}}\left( {\text{tr}}_{A}[(M_{a|x}\otimes I_{B})\rho]\right)=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} P_{A}({a_{i}|x_{i}},\lambda){\sigma}_{{\lambda}}^{(j)}, $$

where $\hat {j}=\{k+1,k+2,\ldots ,n\}\setminus \{j\}$ and ${\sigma }_{{\lambda }}^{(j)}={\text {tr}}_{\hat {j}}(\sigma _{{\lambda }})$. It follows from (2.3) and Definition 2.1 that ρ is unsteerable from i to j.

Consequently, if there are some 1 ≤ i < j ≤ n such that ρ is steerable from i to j, then it is steerable from from A to B provided that A = A₁A₂⋯A_k and B = A_k+ 1A_k+ 2⋯A_n with 1 ≤ i ≤ k and k < j ≤ n. This leads a method for detecting steerability of multipartite states.

Next, we derive a necessary condition for a state $\rho \equiv \rho ^{A_{1}A_{2}{\cdots } A_{n}}$ ro be unsteerable from i to j. To this, we let $\rho \in \mathcal {U}\mathcal {S}(i\rightarrow j)$. Then the reduced state $\rho _{ij}={\text {tr}}_{\widehat {i,j}}\rho$ is unsteerable from i to j in the sense of [11, Definition 3.1].

Next, we aim to deduce necessary conditions for unsteerability from i to j. To do so, we let X_t,Y_t be observables of A_t(t = i, j) and $F_{t}^{\pm }=X_{t}\pm \i Y_{t}(t=i,j)$. Since X_t and Y_t have the spectral decompositions:

$$ X_t=\sum\limits_{k=1}^{d_t}{x}_k^{(t)} {P}_k^{(t)}, Y_t=\sum\limits_{k=1}^{d_t}{y}_k^{(t)} {Q}_k^{(t)}, t=i,j, $$

(2.5)

we get a decomposition of ${F}_{t}^{s_{t}}$ where s_t = ±≡± 1:

$$ {F}_t^{s_t}=\sum\limits_{k=1}^{d_t}\left( {x}_k^{(t)} {P}_k^{(t)} +\i s_ty^{(t)}_k {Q}_k^{(t)}\right) (t=i,j). $$

(2.6)

Consider the projective POVM measurement assemblages induced by (2.5): ${\mathscr{M}}_{i}=\{P_{i},Q_{i}\}$ where $P_{i}=\left \{P^{(i)}_{k}\right \}_{k=1}^{d_{i}}$ and $Q_{i}=\left \{Q^{(i)}_{k}\right \}_{k=1}^{d_{i}}$. Since ρ is unsteerable from i to j, we see by Definition 2.1 that there exists a PD $\{\pi _{\lambda }\}_{\lambda =1}^{d}$ and a set of states $\left \{\sigma ^{(j)}_{\lambda }\right \}_{\lambda =1}^{d}\subset \mathcal {D}_{A_{j}}$ such that

$$ {\text{tr}}_{i}\left[\left( P^{(i)}_{k}\otimes I_{j}\right)\rho_{ij}\right]=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} P_{i}({k|P_{i}},\lambda){\sigma}_{\lambda}^{(j)},\ \ \forall k=1,2,\ldots,d_{i}, $$

(2.7)

$$ {\text{tr}}_{i}\left[\left( Q^{(i)}_{k}\otimes I_{j}\right)\rho_{ij}\right]=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} P_{i}({k|Q_{i}},\lambda){\sigma}_{\lambda}^{(j)},\ \ \forall k=1,2,\ldots,d_{i}, $$

(2.8)

where $\{P_{i}({k|P_{i}},\lambda )\}_{k=1}^{d_{i}}$ and $\{P_{i}({k|Q_{i}},\lambda )\}_{k=1}^{d_{i}}$ are PDs. Hence,

$$ {\text{tr}}\left[\left( {P}_{k}^{(i)}\otimes {P}_{\ell}^{(j)}\right)\rho_{ij}\right]=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} P_{i}({k|P_{i}},\lambda){\text{tr}}\left( {P}_{\ell}^{(j)}{\sigma}_{\lambda}^{(j)}\right),\ \ \forall k\in[d_{i}],\ell\in[d_{j}], $$

(2.9)

$$ {\text{tr}}\left[\left.\left( {Q}_{k}^{(i)}\otimes {P}_{\ell}^{(j)}\right)\right)\rho_{ij}\right]=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} P_{i}({k|Q_{i}},\lambda){\text{tr}}\left( {P}_{\ell}^{(j)}{\sigma}_{\lambda}^{(j)}\right),\ \ \forall k\in[d_{i}],\ell\in[d_{j}], $$

(2.10)

and so on. With these identities, we compute that

$$ \begin{array}{@{}rcl@{}} \langle X_{i}\otimes X_{j} \rangle_{\rho_{ij}}&=& \underset{k,\ell}{\sum}{x}_{k}^{(i)} {x}_{\ell}^{(j)} \langle {P}_{k}^{(i)}\otimes {P}_{\ell}^{(j)}\rangle_{\rho_{ij}}\\ &=&\underset{k,\ell}{\sum} {x}_{k}^{(i)} {x}_{\ell}^{(j)}\sum\limits_{\lambda=1}^{d}\pi_{\lambda} P_{i}({k|P_{i}},\lambda){\text{tr}}\left( {P}_{\ell}^{(j)} {\sigma}_{\lambda}^{(j)}\right)\\ &=&\sum\limits_{\lambda=1}^{d}\pi_{\lambda}\underset{k}{\sum} {x}_{k}^{(i)} P_{i}({k|P_{i}},\lambda) \underset{\ell}{\sum} {x}_{\ell}^{(j)} {\text{tr}}\left( {P}_{\ell}^{(j)} {\sigma}_{\lambda}^{(j)}\right)\\ &=&\sum\limits_{\lambda=1}^{d}\pi_{\lambda} \langle X_{i} \rangle_{\lambda}\cdot \langle X_{j} \rangle_{\lambda}, \end{array} $$

where

$$ \langle X_{i} \rangle_{\lambda}=\sum\limits_{k=1}^{d_{i}}{x}_{k}^{(i)} P_{i}({k|P_{i}},\lambda), \langle X_{j} \rangle_{\lambda}=\sum\limits_{\ell=1}^{d_{j}} {x}_{\ell}^{(j)} {\text{tr}}\left( {P}_{\ell}^{(j)} {\sigma}_{\lambda}^{(j)}\right). $$

Similarly,

$$ \langle X_{i}\otimes Y_{j} \rangle_{\rho_{ij}}=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} \langle X_{i} \rangle_{\lambda}\cdot \langle Y_{j} \rangle_{\lambda},\ \langle Y_{i}\otimes X_{j} \rangle_{\rho_{ij}}=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} \langle Y_{i} \rangle_{\lambda}\cdot \langle X_{j} \rangle_{\lambda}, \ \langle Y_{i}\otimes Y_{j} \rangle_{\rho_{ij}}=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} \langle Y_{i} \rangle_{\lambda}\cdot \langle Y_{j} \rangle_{\lambda}. $$

Consequently,

$$ \begin{array}{@{}rcl@{}} \langle F^{s_{i}}_{i}\otimes F^{s_{j}}_{j} \rangle_{\rho_{ij}}&=& \langle X_{i}\otimes X_{j} \rangle_{\rho_{ij}}+\i s_{j} \langle X_{i}\otimes Y_{j} \rangle_{\rho_{ij}} +\i s_{i} \langle Y_{i}\otimes X_{j} \rangle_{\rho_{ij}}-s_{i}s_{j} \langle Y_{i}\otimes Y_{j} \rangle_{\rho_{ij}}\\ &=&\sum\limits_{\lambda=1}^{d}\pi_{\lambda}\left[ \langle X_{i} \rangle_{\lambda}\cdot \langle X_{j} \rangle_{\lambda}+\i s_{j} \langle X_{i} \rangle_{\lambda}\cdot \langle Y_{j} \rangle_{\lambda} +\i s_{i} \langle Y_{i} \rangle_{\lambda}\cdot \langle X_{j} \rangle_{\lambda}-s_{i}s_{j} \langle Y_{i} \rangle_{\lambda}\cdot \langle Y_{j} \rangle_{\lambda}\right]\\ &=&\sum\limits_{\lambda=1}^{d}\pi_{\lambda} \langle {F}_{i}^{s_{i}} \rangle_{\lambda}\cdot \langle {F}_{j}^{s_{j}}\rangle_{\lambda}, \end{array} $$

where

$$ \langle {F}_{k}^{s_{k}} \rangle_{\lambda}= \langle X_{k} \rangle_{\lambda}+\i s_{k} \langle Y_{k} \rangle_{\lambda} (k=i,j). $$

Convexity of f(t) = t² implies that

$$ |\langle {F}_i^{s_i}\otimes {F}_j^{s_j}\rangle_{\rho_{ij}}|^2\le \sum\limits_{\lambda=1}^d\pi_{\lambda}|\langle {F}_i^{s_i} \rangle_{\lambda}|^2 | \langle {F}_j^{s_j} \rangle_\lambda|^2. $$

(2.11)

By using convexity of f(t) = t² again, we have

$$ | \langle {F}_i^{s_i} \rangle_\lambda|^2= | \langle X_i \rangle_\lambda+\i s_i \langle Y_i \rangle_\lambda|^2= | \langle X_i \rangle_\lambda|^2+| \langle Y_i \rangle_\lambda|^2 \le \langle {X}_i^2 \rangle_\lambda+ \langle {Y}_i^2 \rangle_\lambda= \langle {X}_i^2+{Y}_i^2 \rangle_\lambda, $$

(2.12)

where

$$ \langle{{X}_{i}^{2}} \rangle_{\lambda}=\sum\limits_{k=1}^{d_{i}}|{x}_{k}^{(i)}|^{2}P_{i}({k|P_{i}},\lambda), \langle{{Y}_{i}^{2}} \rangle_{\lambda}=\sum\limits_{k=1}^{d_{i}}|{y}_{k}^{(i)}|^{2}P_{i}({k|P_{i}},\lambda). $$

By introducing

$$ {\varDelta}_{\lambda}^2T= \langle T^2 \rangle_{\lambda}-(\langle T \rangle_{\lambda})^2= {\text{tr}}(T^2\sigma_{\lambda})-({\text{tr}}(T\sigma_{\lambda}))^2 (T=X_j,Y_j) $$

(2.13)

and letting that

$$ C_j=\underset{\lambda\in[d]}{\min}\left( {\varDelta}_{\lambda}^2X_j+{\varDelta}_{\lambda}^2Y_j \right), $$

(2.14)

we have

$$ | \langle {F}_j^{s_j} \rangle_\lambda|^2= | \langle X_j \rangle_\lambda|^2+| \langle Y_j \rangle_\lambda|^2 = \langle {X}_j^2 \rangle_\lambda+ \langle {Y}_j^2 \rangle_\lambda-\left( {\varDelta}_{\lambda}^2X_j+{\varDelta}_{\lambda}^2Y_j \right) \le \langle {X}_j^2 \rangle_\lambda+ \langle {Y}_j^2 \rangle_\lambda-C_j. $$

(2.15)

Combining (2.11), (2.12) and (2.15), we obtain that

$$ | \langle {F}_i^{s_i} \otimes {F}_j^{s_j} \rangle_{\rho_{ij}}|^2\le \sum\limits_{\lambda=1}^d\pi_\lambda \langle {X}_i^2+{Y}_i^2 \rangle_\lambda \langle {X}_j^2+{Y}_j^2 -C_j \rangle_\lambda. $$

(2.16)

By (2.9) and (2.10), we get

$$ \langle ({{X}_{i}^{2}}+{Y}_{i}^{2})\otimes ({X}_{j}^{2}+{Y}_{j}^{2}-C_{j}) \rangle_{\rho_{ij}}=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} \langle {X_{i}^{2}}+{Y^{2}_{i}} \rangle_{\lambda} \langle {X_{j}^{2}}+{Y^{2}_{j}}-C_{j} \rangle_{\lambda}, $$

and so

$$ | \langle F^{s_i}_i\otimes F^{s_j}_j \rangle_{\rho_{ij}}|^2\le \langle ({X}_i^2+{Y}_i^2)\otimes ({X}_j^2+Y^2_j-C_j) \rangle_{\rho_{ij}}. $$

(2.17)

With the discussion above, we arrive at the following.

Theorem 2.1

Let $\rho \in \mathcal {U}\mathcal {S}(i\rightarrow j)$ and let X_t,Y_t be observables of A_t(t = i, j) and ${F}_{t}^{\pm }=X_{t}\pm \i Y_{t}(t=i,j)$. Then the inequality (2.17) holds for all s_i,s_j = ±. Equivalently, for all s_i,s_j = ± 1, it holds that

$$ | \langle X_i\otimes X_j \rangle_{\rho_{ij}}+\i s_j \langle X_i\otimes Y_j \rangle_{\rho_{ij}} +\i s_i \langle Y_i\otimes X_j \rangle_{\rho_{ij}}-s_is_j \langle Y_i\otimes Y_j \rangle_{\rho_{ij}}|\le \sqrt{ \langle ({X}_i^2+{Y}_i^2)\otimes ({X}_j^2+{Y}_j^2-C_j) \rangle_{\rho_{ij}}}, $$

(2.18)

where C_j is defined by (2.14). In addition, if ${{X}_{t}^{2}}={Y}_{t}^{2}=I_{t}(t=i,j)$, then for all s_i,s_j = ± 1, it holds that

$$ | \langle X_i\otimes X_j \rangle_{\rho_{ij}}+\i s_j \langle X_i\otimes Y_j \rangle_{\rho_{ij}} +\i s_i \langle Y_i\otimes X_j \rangle_{\rho_{ij}}-s_is_j \langle Y_i\otimes Y_j \rangle_{\rho_{ij}}|\le \sqrt{2(2-C_j)}. $$

(2.19)

Recall [27, (5)] that

$$ {\varDelta}_{\lambda}^{2}\sigma^{x}+{\varDelta}_{\lambda}^{2}\sigma^{y}+{\varDelta}_{\lambda}^{2}\sigma^{z}\ge2, 0\le{\varDelta}_{\lambda}^{2}\sigma^{t}\le1(t=x,y,x). $$

Thus,

$$ {\varDelta}_{\lambda}^{2}\sigma^{x}+{\varDelta}_{\lambda}^{2}\sigma^{y}\ge1, {\varDelta}_{\lambda}^{2}\sigma^{x}+{\varDelta}_{\lambda}^{2}\sigma^{z}\ge1, {\varDelta}_{\lambda}^{2}\sigma^{y}+{\varDelta}_{\lambda}^{2}\sigma^{z}\ge1. $$

With these inequalities, we have the following.

Corollary 2.1

Let $H_{i}=H_{j}=\mathbb {C}^{2}$, $\rho \in \mathcal {U}\mathcal {S}(i\rightarrow j)$ and let X_i,Y_i be hermitian unitary operators on H_i, X_j + ıY_j ∈{σ^x ± ıσ^y,σ^x ± ıσ^z,σ^y ± ıσ^z}. Then

$$ | \langle X_i\otimes X_j \rangle_{\rho_{ij}}+\i s_j \langle X_i\otimes Y_j \rangle_{\rho_{ij}} +\i s_i \langle Y_i\otimes X_j \rangle_{\rho_{ij}}-s_is_j \langle Y_i\otimes Y_j \rangle_{\rho_{ij}}|\le\sqrt2,\ \ \forall s_i,s_j=\pm1. $$

(2.20)

Especially,

$$ | \langle X_i\otimes X_j \rangle_{\rho_{ij}}-s_is_j \langle Y_i\otimes Y_j \rangle_{\rho_{ij}}| +|s_i \langle Y_i\otimes X_j \rangle_{\rho_{ij}}+s_j \langle X_i\otimes Y_j \rangle_{\rho_{ij}}|\le 2, $$

(2.21)

$$ | \langle X_i\otimes X_j \rangle_{\rho_{ij}}+s_j \langle X_i\otimes Y_j \rangle_{\rho_{ij}}+s_i \langle Y_i\otimes X_j \rangle_{\rho_{ij}}-s_is_j \langle Y_i\otimes Y_j \rangle_{\rho_{ij}}|\le 2. $$

(2.22)

Clearly, the last inequality is just the famous Bell inequality.

Corollary 2.2

Let $H_{i}=H_{j}=\mathbb {C}^{2}$. If there exist hermitian unitary operators X_i,Y_i on H_i and X_j + ıY_j ∈{σ^x ± ıσ^y,σ^x ± ıσ^z,σ^y ± ıσ^z}, and s_i,s_j = ± such that

$$ | \langle X_i\otimes X_j \rangle_{\rho_{ij}}+\i s_j \langle X_i\otimes Y_j \rangle_{\rho_{ij}} +\i s_i \langle Y_i\otimes X_j \rangle_{\rho_{ij}}-s_is_j \langle Y_i\otimes Y_j \rangle_{\rho_{ij}}|>\sqrt2, $$

(2.23)

then $\rho \in \mathcal {S}(i\rightarrow j)$.

Corollary 2.3

For a state ρ of an n-qubit system, let the reduced state ρ_ij(i < j) of ρ be

$$ \rho_{ij}={\text{tr}}_{\widehat{i,j}}(\rho)= \left[\begin{array}{cccc} a & 0 & 0 & 0 \\ 0& xx^{*} & xy^{*} &0 \\ 0 & x^{*}y & yy^{*} & 0 \\ 0 & 0 & 0 & 0 \end{array}\right] =a|00 \rangle \langle 00|+(1-a)|\varphi \rangle \langle \varphi|, $$

(2.24)

where a = 1 −|x|² −|y|² ≥ 0 and

$$ |\varphi \rangle =\frac{1}{\sqrt{x^{*}x+y^{*}y}}(0,y,x,0)^{T} =\frac{1}{\sqrt{x^{*}x+y^{*}y}}(x|01 \rangle +y|10 \rangle ). $$

If $|xy^{*}|>\frac {\sqrt 2}{4}$, then ρ is steerable from i to j.

Proof

Let σ = (σ^x,σ^y,σ^z) and let r_k = (a_k,b_k,c_k) be unit vectors in $\mathbb {R}^{3}$. Then

$$ X_{1}:=\boldsymbol{r}_{1}\cdot\boldsymbol{\sigma}=a_{1}\sigma^{x}+b_{1}\sigma^{y}+c_{1}\sigma^{z}, Y_{1}:=\boldsymbol{r}_{2}\cdot\boldsymbol{\sigma}=a_{2}\sigma^{x}+b_{2}\sigma^{y}+c_{2}\sigma^{z} $$

are Hermitian unitary operators on $\mathbb {C}^{2}$. Put ${F}_{1}^{s_{1}}=X_{1}+\i s_{1}Y_{1}$ and ${F}_{2}^{s_{2}}=\sigma ^{x}+\i s_{2}\sigma ^{y}$ where s₁,s₂ = ± 1 ≡±, and define

$$ \delta(\rho_{ij})=\max \left\{| \langle {F}_{1}^{s_{1}}\otimes {F}_{2}^{s_{2}} \rangle_{\rho_{ij}}|: \|\boldsymbol{r}_{1}\|_{2}=\|\boldsymbol{r}_{2}\|_{2}=1,s_{1},s_{2}=\pm1\equiv\pm \right\}. $$

We see from Corollary 2.2 that when $\delta (\rho _{ij})>\sqrt 2$, ρ is steerable from i to j. When s₁ = 1 and s₂ = − 1, we have

$$ {F}_{1}^{+}=X_{1}+\i Y_{1}= \left[\begin{array}{cc} c_{1}+\i c_{2} & a_{1}+\i a_{2}-\i b_{1}+b_{2} \\ a_{1}+\i a_{2}+\i b_{1}-b_{2} & -c_{1}-\i c_{2} \end{array}\right], {F}_{2}^{-}= \left[\begin{array}{cc} 0&0\\ 2&0 \end{array}\right], $$

and so

$$ {F}_{1}^{+}\otimes {F}_{2}^{-}= \left[\begin{array}{cccc} 0&0&0&0\\ 2c_{1}+2\i c_{2} &0&2(a_{1}+\i a_{2}-\i b_{1}+b_{2})&0\\ 0&0&0&0 \\ 2(a_{1}+\i a_{2}+\i b_{1}-b_{2}) &0& -2c_{1}-2\i c_{2}&0 \end{array}\right]. $$

Thus,

$$ \langle {F}_{1}^{+}\otimes {F}_{2}^{-} \rangle_{\rho_{ij}}={\text{tr}}\left[\left( {F}_{1}^{+}\otimes {F}_{2}^{-}\right)\rho_{12}\right]=2xy^{*}(a_{1}+\i a_{2}-\i b_{1}+b_{2}). $$

Since ${a}_{k}^{2}+{b}_{k}^{2}\le 1(k=1,2),$ we have

$$ 2|xy^{*}(a_{1}+\i a_{2}-\i b_{1}+b_{2})|\le2|xy^{*}|(|a_{1}-\i b_{1}|+|\i a_{2}+b_{2}|)|\le4|xy^{*}|=2|xy^{*}|f(1,0,0,1), $$

where f(a₁,b₁,a₂,b₂) = |a₁ + ıa₂ − ıb₁ + b₂|≤ 2. Hence, δ(ρ_ij) = 2|xy^∗|f(1,0,0,1) = 4|xy^∗|. We conclude from Corollary 2.2 that ρ is steerable from i to j if $|xy^{*}|>\sqrt {2}/4$. The proof is completed. □

Example 2.1

Consider the four-qubit state ρ(I) = |ψ^(I)〉〈ψ^(I)| where

$$ |\psi^{(I)} \rangle =C_{0001} | 0001 \rangle +C_{0010} | 0010 \rangle +C_{0100} | 0100 \rangle +C_{1000} | 1000 \rangle , $$

(2.25)

with the condition that

$$|C_{0001}|^{2}+|C_{0010}|^{2}+|C_{0100}|^{2}+|C_{1000}|^{2}=1.$$

Case 1

Qubit 1 steers qubit 2, that is, the steerability of ρ^(I) from 1 to 2.

First, we have

$$ \rho_{12}={\text{tr}}_{34}(\rho^{(I)})= \left[\begin{array}{cccc} Q_{0001}+Q_{0010} & 0 & 0 & 0\\ 0& Q_{0100} & C_{0100}C^{*}_{1000} &0 \\ 0 &C^{*}_{0100}C_{1000} & Q_{1000} & 0\\ 0 & 0 & 0 & 0 \end{array}\right], $$

(2.26)

where $Q_{i j k l}={C}_{i j k l}^{*} C_{i j k l}$. Since ρ₁₂ has the form (2.24), Corollary 2.3 implies that |ψ^(I)〉 is steerable from 1 to 2 provided that $|C_{0100}C^{*}_{1000}|>\sqrt 2/4$. For example, when C₀₀₀₁ = C₀₀₁₀ = 0 and $|C_{0100}|=|C_{1000}|=\sqrt 2/2$, we have ρ₁₂ = |β₀₁〉〈β₀₁| where $|\beta _{01} \rangle =\frac {1}{\sqrt 2}(e^{\i \theta _{1}}|01 \rangle +e^{\i \theta _{2}}|10 \rangle )$ with $\theta _{1},\theta _{2}\in {\mathbb {R}}$. Since $|C_{0100}C^{*}_{1000}|=1/2>\sqrt 2/4$, ρ^(I) from 1 to 2.

Case 2

Qubit 2 steers qubit 3, that is, the steerability of ρ^(I) from 2 to 3.

First, we have

$$ \rho_{23}={\text{tr}}_{14}(\rho^{(I)})= \left[\begin{array}{cccc} Q_{0001}+Q_{1000} & 0 & 0 & 0\\ 0& Q_{0010} & C_{0010}C^{*}_{0100} &0 \\ 0 & C^{*}_{0010} C_{0100} & Q_{0100} & 0\\ 0 & 0 & 0 & 0 \end{array}\right], $$

(2.27)

where $Q_{i j k l}={C}_{i j k l}^{*} C_{i j k l}$. Since ρ₂₃ has the form (2.24), Corollary 2.3 implies that |ψ^(I)〉 is steerable from 2 to 3 provided that $|C_{0100} {C}_{0010}^{*}|>\sqrt 2/4$.

Case 3

Qubit 3 steers qubit 4, that is, the steerability of ρ^(I) from 3 to 4.

First, we have

$$ \rho_{34}={\text{tr}}_{12}(\rho^{(I)})= \left[\begin{array}{cccc} Q_{0100}+Q_{1000} & 0 & 0 & 0\\ 0& Q_{0001} & C_{0001}C^{*}_{0010} &0 \\ 0 &C^{*}_{0001}C_{0010} & Q_{0010} & 0\\ 0 & 0 & 0 & 0 \end{array}\right], $$

(2.28)

where $Q_{i j k l}={C}_{i j k l}^{*} C_{i j k l}$. Since ρ₃₄ has the form (2.24), Corollary 2.3 implies that |ψ^(I)〉 is steerable from 3 to 4 provided that $|C_{0001}{C}_{0010}^{*} |>\sqrt 2/4$.

Case 4

Qubit 1 steers qubit 4, that is, the steerability of ρ^(I) from 1 to 4.

First, we have

$$ \rho_{14}={\text{tr}}_{23}(\rho^{(I)})= \left[\begin{array}{cccc} Q_{0010}+Q_{0100} & 0 & 0 & 0\\ 0& Q_{0001} & C_{0001}{C}_{1000}^{*} &0 \\ 0 &{C}_{0001}^{*}C_{1000} & Q_{1000} & 0\\ 0 & 0 & 0 & 0 \end{array}\right], $$

(2.29)

where $Q_{i j k l}={C}_{i j k l}^{*} C_{i j k l}$. Since ρ₁₄ has the form (2.24), Corollary 2.3 implies that |ψ^(I)〉 is steerable from 1 to 4 provided that $|{C}_{1000}^{*} C_{0001}|>\sqrt 2/4$.

Next, let us discuss a relationship between the steerability defined by Definition 2.1 and the steerability of a bipartite system. To this, let us divide an n quantum system A₁A₂⋯A_n as a bipartite system AB where A = A₁A₂⋯A_k and B = A_k+ 1A_k+ 2⋯A_n. Suppose that a state ρ of A₁A₂⋯A_n is unsteerable from A to B as a state of AB in the sense of [11, Definition 3.1]. Then for any indices 1 ≤ i ≤ k and k < j ≤ n, ρ is unsteerable from i to j. Indeed, for any POVM measurement assemblage

$$ \mathcal{M}_{i}=\left\{M^{x_{i}}=\left\{{M}_{a_{i}|x_{i}}^{(i)}\right\}_{a_{i}=1}^{o_{i}}:x_{i}=1,2,\ldots,m_{i}\right\} $$

of A_i, we denote $M_{a_{i}|x_{i}}={\otimes }_{t=1}^{k}T_{it}$ where $T_{ii}={M}_{a_{i}|x_{i}}^{(i)}$ and T_it = I_k(t≠i). Then we get a POVM measurement assemblage

$$ \mathcal{M}_{A}=\left\{\{M_{a_{i}|x_{i}}\}_{a_{i}=1}^{o_{i}}:x_{i}=1,2,\ldots,m_{i}\right\} $$

of system A with $M_{a_{i}|x_{i}}\otimes I_{B}=N_{a_{i}|x_{i}}$. Thus, there exists a PD $\{\pi _{\lambda }\}_{{\lambda }=1}^{d}$ and s set $\{\sigma _{{\lambda }}\}_{{\lambda }}^{d}$ of system B such that

$$ {\text{tr}}_{A}[(M_{a_{i}|x_{i}}\otimes I_{B})\rho]=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} P_{A}({a_{i}|x_{i}},\lambda)\sigma_{\lambda},\ \ \forall x_{i}=1,2,\ldots,m_{i},a_{i}=1,2,\ldots,o_{i}, $$

where $\{P_{i}({a_{i}|x_{i}},\lambda )\}_{a_{i}=1}^{o_{i}}$ is a PD for each (λ, x_i). Hence, for all x_i = 1,2,…,m_i,a_i = 1,2,…,o_i, it holds that

$$ \begin{array}{@{}rcl@{}} {\text{tr}}_{\hat{j}}[N_{a_{i}|x_{i}}\rho]={\text{tr}}_{\hat{j}}{\text{tr}}_{A}[ (M_{a_{i}|x_{i}}\otimes I_{B})\rho]={\sum}_{\lambda=1}^{d}\pi_{\lambda} P_{A}({a_{i}|x_{i}},\lambda)\sigma^{(j)}_{\lambda}, \end{array} $$

where ${\sigma }_{\lambda }^{(j)}={\text {tr}}_{\hat {j}}\sigma _{\lambda }$. It follows from Definition 2.1 that ρ is unsteerable from i to j.

Consequently, if there are some 1 ≤ i < j ≤ n such that ρ is steerable from i to j, then it is steerable from A to B provided that 1 ≤ i ≤ k and k < j ≤ n, where A = A₁A₂⋯A_k and B = A_k+ 1A_k+ 2⋯A_n. This leads a method for detecting steerability a bipartite system AB.

3 (i, j)-Nonlocality

Let 1 ≤ i < j ≤ n. For measurement assemblages ${\mathscr{M}}_{i}$ and ${\mathscr{M}}_{j}$ given by (1), we denote

$$ N_{a_{i}|x_{i}}={\otimes}_{k=1}^{n}T_{ik}, N_{a_{j}|x_{j}}={\otimes}_{k=1}^{n}S_{jk}, $$

where

$$ T_{ii}={M}_{a_{i}|x_{i}}^{(i)}, T_{jj}={M}_{a_{j}|x_{j}}^{(j)},S_{ik}=I_{k}(k\ne i),S_{jk}=I_{k}(k\ne j). $$

Then

$$ M^{(x_{i},x_{j})}=\{N_{a_{i}|x_{i}}N_{a_{j}|x_{j}}:(a_{i},a_{j})\in[o_{i}]\times[o_{j}]\} $$

forms a POVM of A₁A₂⋯A_n for each label (x_i,x_j) in [m_i] × [m_j].

Definition 3.1

Let ρ be a state of an n-partite system A₁A₂⋯A_n and let A_i and A_j(i < j) be given two subsystems.

• (1) ρ is said to be (i, j)-Bell local with respect to $({\mathscr{M}}_{i},{\mathscr{M}}_{j})$ if there exists a PD $\{\pi _{\lambda }\}_{\lambda =1}^{d}$ such that

  $$ {\text{tr}}[N_{a_{i}|x_{i}}N_{a_{j}|x_{j}}\rho] =\sum\limits_{\lambda=1}^{d}\pi_{\lambda} P_{i}({a_{i}|x_{i}},\lambda)P_{j}({a_{j}|x_{j}},\lambda) $$

  (3.30)

  for all x_i ∈ [m_i],a_i ∈ [o_i],x_i ∈ [m_j],a_j ∈ [o_j], where $\{P_{i}({a_{i}|x_{i}},\lambda )\}_{a_{i}=1}^{o_{i}}$ and $\{P_{j}({a_{j}|x_{j}},\lambda )\}_{a_{j}=1}^{o_{j}}$ are probability distributions (PDs). Equation (3.30) is said to be a LHV model of ρ with respect to $({\mathscr{M}}_{i},{\mathscr{M}}_{j})$.

• (2) ρ is said to be (i, j)-Bell local if it is (i, j)- Bell local w.r.t any $({\mathscr{M}}_{i},{\mathscr{M}}_{j})$.

• (3) ρ is said to be (i, j)-Bell nonlocal w.r.t. $({\mathscr{M}}_{i},{\mathscr{M}}_{j})$ if it is not (i, j)-Bell local w.r.t. $({\mathscr{M}}_{i},{\mathscr{M}}_{j})$.

• (4) ρ is said to be (i, j)-Bell nonlocal if it is not (i, j)-Bell local w.r.t. some $({\mathscr{M}}_{i},{\mathscr{M}}_{j})$.

• (5) A pure state |ψ〉 of A₁A₂⋯A_n is said to be (i, j)-Bell local (resp. (i, j)-Bell local) if |ψ〉〈ψ| is (i, j)-Bell local (resp. (i, j)-Bell nonlocal).

Furthermore, we also call the Bell locality and Bell nonlocality defined here the partial Bell locality and Bell nonlocality.

Clearly,

$$ {\text{tr}}[N_{a_i|x_i}N_{a_j|x_j}\rho] ={\text{tr}}\left[{\text{tr}}_{\widehat{ij}} \left( N_{a_i|x_i}N_{a_j|x_j}\rho\right)\right]= {\text{tr}}\left[\left( {M}_{a_i|x_i}^{i}\otimes {M}_{a_j|x_j}^{j}\right)\rho_{ij}\right], $$

(3.31)

where $\rho _{ij}={\text {tr}}_{\widehat {i,j}}\rho$, the reduced state of ρ on the subsystem A_iA_j. Thus, ρ is (i, j)-Bell local if and only if ρ_ij is Bell local in the sense of [11, Definition 2.1].

We use ${\mathscr{B}}{\mathscr{L}}(i,j,{\mathscr{M}}_{i})$ (resp. ${\mathscr{B}}\mathcal {N}{\mathscr{L}}(i,j,{\mathscr{M}}_{i})$) to denote the set of all states $\rho \equiv \rho ^{A_{1}A_{2}{\cdots } A_{n}}$ of an n-partite system A₁A₂⋯A_n that are (i, j)-Bell local (resp. (i, j)-Bell nonlocal) w.r.t ${\mathscr{M}}_{i}$. Then we see from [11, Corollary 3.1] that ${\mathscr{B}}{\mathscr{L}}(i,j,{\mathscr{M}}_{i})$ is a compact convex subset of the set $\mathcal {D}(A_{1}A_{2}{\cdots } A_{n})$ of all states of A₁A₂⋯A_n. Therefore, the set ${\mathscr{B}}\mathcal {N}{\mathscr{L}}(i,j,{\mathscr{M}}_{i})$ becomes an open subset of $\mathcal {D}(A_{1}A_{2}{\cdots } A_{n})$. Also, we use ${\mathscr{B}}{\mathscr{L}}(i,j)$ and ${\mathscr{B}}\mathcal {N}{\mathscr{L}}(i,j)$ to denote the set of all (i, j)-Bell local and (i, j)-Bell nonlocal states of A₁A₂⋯A_n, respectively. Thus, we see from Definition 3.1 that

$$ \mathcal{B}\mathcal{L}(i,j)=\underset{\mathcal{M}_i}{\bigcap}\mathcal{B}\mathcal{L}(i,j,\mathcal{M}_i),\ \mathcal{B}\mathcal{N}\mathcal{L}(i,j)=\underset{\mathcal{M}_i}{\bigcup}\mathcal{B}\mathcal{N}\mathcal{L}(i,j,\mathcal{M}_i). $$

(3.32)

This implies that ${\mathscr{B}}{\mathscr{L}}(i,j)$ is a compact subset of the set $\mathcal {D}(A_{1}A_{2}{\cdots } A_{n})$ and that ${\mathscr{B}}\mathcal {N}{\mathscr{L}}(i,j)$ is an open subset of $\mathcal {D}(A_{1}A_{2}{\cdots } A_{n})$.

When $\rho \in {\mathscr{B}}{\mathscr{L}}(i,j)$, the reduced state $\rho _{ij}={\text {tr}}_{\widehat {i,j}}\rho$ is Bell local in the sense of [11, Definition 2.1]. It follows from [11] that ρ_ij is unsteerable from i to j and so ρ is unsteerable from i to j. Thus,

$$ \mathcal{U}\mathcal{S}(i\rightarrow j)\subset \mathcal{B}\mathcal{L}(i,j), \mathcal{B}\mathcal{N}\mathcal{L}(i,j)\subset\mathcal{S}(i\rightarrow j). $$

(3.33)

Example 3.1

Consider the tripartite pure state

$$ |\psi \rangle =\sum\limits_{i,j=0}^{1}c_{ij}|ij \rangle |ij \rangle |0 \rangle $$

of $\in {\mathbb {C}}^{4}\otimes {\mathbb {C}}^{4}\otimes {\mathbb {C}}^{2}$ with c_ij ≥ 0(i, j = 0,1) and K = 2(c₀₀c₀₁ + c₁₀c₁₁) > 0 and obtain ρ₁₂ := tr₃(|ψ〉〈ψ|) = |φ〉〈φ| where $|\varphi \rangle ={\sum }_{i,j=0}^{1}c_{ij}|ij \rangle |ij \rangle$.

Put

$$ A(\alpha)=(\sin\alpha)\left( \begin{array}{cc} \sigma^{x} & 0 \\ 0 & \sigma^{x} \end{array} \right) +(\cos\alpha)\left( \begin{array}{cc} \sigma^{y} & 0 \\ 0 & \sigma^{y} \end{array} \right), $$

$$ B(\beta)=(\sin\beta)\left( \begin{array}{cc} \sigma^{x} & 0 \\ 0 & \sigma^{x} \end{array} \right) +(\cos\beta)\left( \begin{array}{cc} \sigma^{y} & 0 \\ 0 & \sigma^{y} \end{array} \right), $$

where α, β ∈ [−π, π]. Then A(α) and B(β) are ± 1-valued observables of ${\mathbb {C}}^{4}$. we take s₁ = s₂ = 1 and

$$ X_{1}=A(\alpha), Y_{1}=A(\alpha^{\prime}), X_{2}=B(\beta),Y_{2}=B(\beta^{\prime}), $$

then

$$ \langle X_{1}\otimes X_{2} \rangle_{\varphi}= \langle A(\alpha)\otimes B(\beta) \rangle_{\varphi} =\cos\alpha \cos\beta+K\sin\alpha\sin\beta, $$

$$ \langle X_{1}\otimes Y_{2} \rangle_{\varphi}= \langle A(\alpha)\otimes B(\beta^{\prime}) \rangle_{\varphi} =\cos\alpha \cos\beta^{\prime}+K\sin\alpha\sin\beta^{\prime}, $$

$$ \langle Y_{1}\otimes X_{2} \rangle_{\varphi}= \langle A(\alpha^{\prime})\otimes B(\beta) \rangle_{\varphi} =\cos\alpha^{\prime}\cos\beta+K\sin\alpha^{\prime}\sin\beta, $$

$$ \langle Y_{1}\otimes Y_{2} \rangle_{\varphi}= \langle A(\alpha^{\prime})\otimes B(\beta^{\prime}) \rangle_{\varphi} =\cos\alpha^{\prime} \cos\beta^{\prime}+K\sin\alpha^{\prime}\sin\beta^{\prime}. $$

Especially, letting $\alpha =0,\alpha ^{\prime }=\pi /2,\beta =-\beta ^{\prime }=\arctan (K)$ yields that

$$ \begin{array}{@{}rcl@{}} \langle X_{1}\otimes X_{2} \rangle_{\varphi}+ \langle X_{1}\otimes Y_{2} \rangle_{\varphi} + \langle Y_{1}\otimes X_{2} \rangle_{\varphi}- \langle Y_{1}\otimes Y_{2} \rangle_{\varphi} =2(\cos\beta+K\sin\beta)=2(1+K^{2})^{1/2}>2. \end{array} $$

We conclude from [24, Theorem 3.2] that |ψ〉 is Bell nonlocal and then it is (1,2)-Bell nonlocal.

Let us discuss a relationship between the (i, j)-Bell locality defined by Definition 3.1 and the (A, B)-Bell locality [24] of an n-partite quantum system A₁A₂⋯A_n as a bipartite system AB where A = A₁A₂⋯A_k, B = A_k+ 1A_k+ 2⋯A_n and 1 ≤ i ≤ k and k < j ≤ n. Suppose that a state ρ of A₁A₂⋯A_n is (A, B)-Bell local in the sense of [24], i.e., it is Bell local as a bipartite state of AB in the sense of [11, Definition 2.1]. Then for any indices 1 ≤ i ≤ k and k < j ≤ n, and any POVM measurement assemblages

$$ \mathcal{N}_{t}=\left\{M^{(t)}=\left\{M^{(t)}_{a_{t}|x_{t}}\right\}_{a_{t}=1}^{o_{t}}:x_{t}\in[m_{t}]\right\}(t=i,j) $$

of A_t(t = i, j), we denote $M_{a|x}={\otimes }_{n=1}^{k}T_{in}$ with $T_{ii}={M}_{a|x}^{(i)}$ and T_in = I_n(n≠i) for each a ∈ [o_i] and x ∈ [m_i]; $N_{b|y}={\otimes }_{m=k+1}^{n}S_{jm}$ with $S_{jj}={M}_{b|y}^{(j)}$ and S_jm = I_m(m≠j) for each b ∈ [o_j] and y ∈ [m_j]. Then we get measurement assemblages

$$ \mathcal{M}_{A}=\{\{M_{a|x}\}_{a=1}^{o_{i}}:x\in[m_{i}]\}, \mathcal{N}_{B}=\{\{N_{b|y}\}_{b=1}^{o_{j}}:y\in[m_{j}]\} $$

of systems A and B, respectively. From [11, Definition 2.1], there exists a PD $\{\pi _{\lambda }\}_{{\lambda }=1}^{d}$ such that for all x ∈ [m_i],y ∈ [m_j],a ∈ [o_i],b ∈ [o_j], it holds that

$$ {\text{tr}}[(M_{a|x}\otimes N_{b|y})\rho]=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} P_{A}({a|x},\lambda)P_{B}({b|y},\lambda) $$

where $\{P_{A}(a|x,\lambda )\}_{a=1}^{o_{i}}$ and $\{P_{B}(b|y,\lambda )\}_{b=1}^{o_{j}}$ are PDs for each (λ, x) and each (λ, y), respectively. Hence, for all x_i ∈ [m_i],a_i ∈ [o_i],x_j ∈ [m_j] and a_j ∈ [o_j], it holds that

$$ {\text{tr}}\left[M^{(i)}_{a_{i}|x_{i}}\otimes M^{(j)}_{a_{j}|x_{j}}\rho_{ij}\right] ={\text{tr}}[(M_{a_{i}|x_{i}}\otimes N_{a_{j}|x_{j}})\rho]=\sum\limits_{\lambda=1}^{d}\pi_{\lambda} P_{A}({a_{i}|x_{i}},\lambda)P_{B}({a_{j}|x_{j}},\lambda). $$

It follows from (3.31) and Definition 3.1 that ρ is (i, j)-Bell local.

Consequently, if there are some 1 ≤ i < j ≤ n such that ρ is (i, j)-Bell nonlocal, then it is Bell nonlocal as a state of AB provided that A = A₁A₂⋯A_k and B = A_k+ 1A_k+ 2⋯A_n with 1 ≤ i ≤ k and k < j ≤ n. This leads a method for detecting Bell nonlocality of multipartite states.

It is well-known that Bell inequality is a very useful tool for detecting Bell nonlocality. Next, we deduce a complex Bell inequality for detecting (i, j)-Bell nonlocality. To do this, we let ρ be any state of A₁A₂⋯A_n and X_t,Y_t be hermitian operators on ${{\mathscr{H}}}_{t}(t=i,j)$. Since $| \langle T \rangle _{\rho _{ij}}|^{2}\le \langle |T|^{2} \rangle _{\rho _{ij}}\le \||T|^{2}\|_{1}$, we have for all s_i,s_j = ± 1, it holds that

$$ \begin{array}{@{}rcl@{}} | \langle {F}_{1}^{s_{1}}\otimes {F}_{2}^{s_{2}} \rangle_{\rho_{ij}}|&=&| \langle X_{i}\otimes X_{j} \rangle_{\rho_{ij}}+\i s_{j} \langle X_{i}\otimes Y_{j} \rangle_{\rho_{ij}} +\i s_{i} \langle Y_{i}\otimes X_{j} \rangle_{\rho_{ij}}-s_{i}s_{j} \langle Y_{i}\otimes Y_{j} \rangle_{\rho_{ij}}|\\ &=&| \langle (X_{i}+\i s_{i}Y_{i})\otimes(X_{j}+\i s_{j}Y_{j}) \rangle_{\rho_{ij}}|\\ &\le& \langle |(X_{i}+\i s_{i}Y_{i})\otimes(X_{j}+\i s_{j}Y_{j})|^{2} \rangle_{\rho_{ij}}^{\frac{1}{2}}\\ &=& \langle |(X_{i}+\i s_{i}Y_{i})|^{2}\otimes|(X_{j}+\i s_{j}Y_{j})|^{2} \rangle_{\rho_{ij}}^{\frac{1}{2}}. \end{array} $$

This shows that

$$ | \langle {F}_1^{s_1}\otimes {F}_2^{s_2} \rangle_{\rho_{ij}}|\le \langle |(X_i+\i s_iY_i)|^2\otimes|(X_j+\i s_jY_j)|^2 \rangle_{\rho_{ij}}^{\frac{1}{2}}. $$

(3.34)

Similarly,

$$ \sqrt{ \left\langle \left( {{X}_{i}^{2}}+{{Y}_{i}^{2}}\right)\otimes \left( {{X}_{j}^{2}}+{{Y}_{j}^{2}}\right) \right\rangle_{\rho_{ij}}}\le \langle |(X_{i}+\i s_{i}Y_{i})|^{2}\otimes|(X_{j}+\i s_{j}Y_{j})|^{2} \rangle_{\rho_{ij}}^{\frac{1}{2}}. $$

If in addition, ${{X}_{t}^{2}}={Y}_{t}^{2}=I_{t}(t=i,j)$, then

$$ \begin{array}{@{}rcl@{}} && \langle |(X_{i}+\i s_{i}Y_{i})|^{2}\otimes|(X_{j}+\i s_{j}Y_{j})|^{2} \rangle_{\rho_{ij}}^{\frac{1}{2}}\\ &=& \langle 2I_{i}-\i s_{i}[X_{i},Y_{i}])\otimes(2I_{j}-\i s_{j}[X_{j},Y_{j}]) \rangle_{\rho_{ij}}^{\frac{1}{2}}\\ &=&\left \langle 4I_{i}\otimes I_{j}-2\i s_{i}[X_{i},Y_{i}]\otimes I_{j} -2\i s_{j}I_{i}\otimes [X_{j},Y_{j}]+s_{i}s_{j}[X_{i},Y_{i}]\otimes [X_{j},Y_{j}]\right \rangle_{\rho_{ij}}^{\frac{1}{2}}. \end{array} $$

Since

$$\|s_{i}[X_{i},Y_{i}])\otimes I_{j}\|\le 2, \|s_{j}I_{i}\otimes [X_{j},Y_{j}]\|\le2, \|[X_{i},Y_{i}]\otimes [X_{j},Y_{j}]\|\le4,$$

we have

$$\|4-2\i s_{i}[X_{i},Y_{i}]\otimes I_{j} -2\i s_{j}I_{i}\otimes [X_{j},Y_{j}]+s_{i}s_{j}[X_{i},Y_{i}]\otimes [X_{j},Y_{j}]\|\le 16$$

and therefore,

$$ | \langle {F}_1^{s_1}\otimes {F}_2^{s_2} \rangle_{\rho_{ij}}|\le4. $$

(3.35)

Indeed, the last inequality can be obtained from the fact that

$$\|{F}_{1}^{s_{1}}\otimes {F}_{2}^{s_{2}}\|=\|{F}_{1}^{s_{1}}\|\cdot\|{F}_{2}^{s_{2}}\|\le4$$

when ${X}_{t}^{2}={Y}_{t}^{2}=I_{t}(t=i,j)$. This shows that a quantum upper bound for $| \langle {F}_{1}^{s_{1}}\otimes {F}_{2}^{s_{2}} \rangle _{\rho _{ij}}|$ is 4.

Similar to the derivation of Theorem 2.1, we can obtain the following conclusion, which is a necessary condition for a state ρ to be (i, j)-Bell local.

Theorem 3.1

Let $\rho \in {\mathscr{B}}{\mathscr{L}}(i,j)$ and let X_t,Y_t be hermitian operators on ${{\mathscr{H}}}_{t}(t=i,j)$. Then for all s_i,s_j = ± 1, it holds that

$$ | \langle X_i\otimes X_j \rangle_{\rho_{ij}}+\i s_j \langle X_i\otimes Y_j \rangle_{\rho_{ij}} +\i s_i \langle Y_i\otimes X_j \rangle_{\rho_{ij}}-s_is_j \langle Y_i\otimes Y_j \rangle_{\rho_{ij}}| \le \sqrt{\left \langle \left( {X}_i^2+{Y}_i^2\right)\otimes \left( {X}_j^2+{Y}_j^2\right) \right\rangle_{\rho_{ij}}}. $$

(3.36)

If in addition, ${X}_{t}^{2}={Y}_{t}^{2}=I_{t}(t=i,j)$, then for all s_i,s_j = ± 1, it holds that

$$ | \langle X_i\otimes X_j \rangle_{\rho_{ij}}+\i s_j \langle X_i\otimes Y_j \rangle_{\rho_{ij}} +\i s_i \langle Y_i\otimes X_j \rangle_{\rho_{ij}}-s_is_j \langle Y_i\otimes Y_j \rangle_{\rho_{ij}}|\le 2, $$

(3.37)

and

$$ | \langle X_i\otimes X_j \rangle_{\rho_{ij}}+s_j \langle X_i\otimes Y_j \rangle_{\rho_{ij}}+s_i \langle Y_i\otimes X_j \rangle_{\rho_{ij}}-s_is_j \langle Y_i\otimes Y_j \rangle_{\rho_{ij}}|\le 2. $$

(3.38)

Proof

The proof of (3.36) is similar to the derivation of (2.18), and (3.37) is the special case of (3.36). Inequality (3.38) is essentially given in ref. [24, Theorem 3.1]. The proof is completed.

It is remarkable to note that the famous Tsirelson’s inequality [28, Problem 2.3, pp.118] shows that in the case that ${{\mathscr{H}}}_{i}={{\mathscr{H}}}_{j}={\mathbb {C}}^{2}$, the inequality

$$ | \langle X_i\otimes X_j \rangle_{\rho_{ij}}+s_j \langle X_i\otimes Y_j \rangle_{\rho_{ij}}+s_i \langle Y_i\otimes X_j \rangle_{\rho_{ij}}-s_is_j \langle Y_i\otimes Y_j \rangle_{\rho_{ij}}|\le 2\sqrt2 $$

(3.39)

holds for all two-qubit states ρ_ij. Moreover, the validity of (3.37) is just a necessary condition for a state ρ to be (i, j)-Bell local, but not a sufficient one. For example, when ρ_ij = |ψ〉〈ψ| where $|\psi \rangle =\frac {1}{\sqrt 2}(|00 \rangle +|11 \rangle )$, we take s_i = s_j = 1 and

$$ X_{i}=\sigma^{x},Y_{i}=-\sigma^{z},X_{j}=\frac{1}{\sqrt2}(\sigma^{x}-\sigma^{z}), Y_{j}=\frac{1}{\sqrt2}(\sigma^{x}+\sigma^{z}) $$

and compute that

$$ \langle X_{i}\otimes X_{j} \rangle = \langle X_{i}\otimes Y_{j} \rangle_{\rho_{ij}}= \langle Y_{i}\otimes X_{j} \rangle_{\rho_{ij}}=- \langle Y_{i}\otimes Y_{j} \rangle_{\rho_{ij}}=\frac{\sqrt2}{2}. $$

Thus,

$$ | \langle X_{i}\otimes X_{j} \rangle_{\rho_{ij}}+\i s_{j} \langle X_{i}\otimes Y_{j} \rangle_{\rho_{ij}} +\i s_{i} \langle Y_{i}\otimes X_{j} \rangle_{\rho_{ij}}-s_{i}s_{j} \langle Y_{i}\otimes Y_{j} \rangle_{\rho_{ij}}|=2, $$

and

$$ | \langle X_{i}\otimes X_{j} \rangle_{\rho_{ij}}+s_{j} \langle X_{i}\otimes Y_{j} \rangle_{\rho_{ij}}+s_{i} \langle Y_{i}\otimes X_{j} \rangle_{\rho_{ij}}-s_{i}s_{j} \langle Y_{i}\otimes Y_{j} \rangle_{\rho_{ij}}|=2\sqrt2. $$

Thus, (3.37) holds while ρ_ij is well-known to be Bell nonlocal.

As consequences of Theorem 3.1, we have the following two corollaries, which are sufficient conditions for a state to be (i, j)-Bell nonlocal. □

Corollary 3.1

If there exist hermitian operators on ${{\mathscr{H}}}_{t}(t=i,j)$ and s_i,s_j = ± 1 such that

$$ | \langle X_{i}\otimes X_{j} \rangle_{\rho_{ij}}+\i s_{j} \langle X_{i}\otimes Y_{j} \rangle_{\rho_{ij}} +\i s_{i} \langle Y_{i}\otimes X_{j} \rangle_{\rho_{ij}}-s_{i}s_{j} \langle Y_{i}\otimes Y_{j} \rangle_{\rho_{ij}}|>\sqrt{ \langle ({X_{i}^{2}}+{Y_{i}^{2}})\otimes ({X_{j}^{2}}+{Y_{j}^{2}}) \rangle_{\rho_{ij}}}, $$

then $\rho \in {\mathscr{B}}\mathcal {N}{\mathscr{L}}(i,j)$.

Corollary 3.2

If there exist hermitian unitary operators X_k,Y_k on H_k(k = i, j) and s_i,s_j = ± 1 such that

$$ | \langle X_{i}\otimes X_{j} \rangle_{\rho_{ij}}+\i s_{j} \langle X_{i}\otimes Y_{j} \rangle_{\rho_{ij}} +\i s_{i} \langle Y_{i}\otimes X_{j} \rangle_{\rho_{ij}}-s_{i}s_{j} \langle Y_{i}\otimes Y_{j} \rangle_{\rho_{ij}}|>2, $$

then $\rho \in {\mathscr{B}}\mathcal {N}{\mathscr{L}}(i,j)$.

4 Conclusions

In this paper, we have discussed partial steerability and nonlocality of multipartite quantum states, named steerability from i to j and (i, j)-Bell nonlocality, n-partite states. By establishing necessary conditions for a state ρ to be unsteerable from i to j (resp. (i, j)-Bell local), we derive sufficient conditions for a state ρ to be steerable from i to j (resp. (i, j)-Bell nonlocal). We have proved that if there are some 1 ≤ i < j ≤ n such that ρ is steerable from i to j, then it is steerable from from A to B provided that A = A₁A₂⋯A_k and B = A_k+ 1A_k+ 2⋯A_n with 1 ≤ i ≤ k and k < j ≤ n. This leads a method for detecting steerability of multipartite states. Moreover, we have checked that if there are some 1 ≤ i < j ≤ n such that ρ is (i, j)-Bell nonlocal, then it is Bell nonlocal as a state of AB provided that A = A₁A₂⋯A_k and B = A_k+ 1A_k+ 2⋯A_n with 1 ≤ i ≤ k and k < j ≤ n. This leads a method for detecting Bell nonlocality of multipartite states.