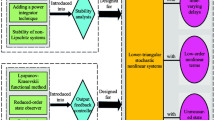
Abstract
This paper considers the design of output tracking and feedback controllers for nonlinear stochastic systems. The system status cannot be measured. The studied system contains nonlinear state functions, noise disturbances and time delays. We use the free weight matrix method to avoid the conservatism caused by the use of model transformation or cross-term bounded techniques. Based on the Lyapunov-Krasovskii functional method, we propose an output tracking and feedback controller design method based on linear matrix inequality (LMI). Numerical examples show the validity of the obtained results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Stochastic system theory is a type of theory that combines stochastic process theory with control theory, and now it become an important branch of mathematics and control theory [1,2,3,4,5,6]. Recently, many scholars have paid attention to the research of robust control for uncertain stochastic time-delay systems, such as the research of robust stabilization and robust \(H_{\infty }\) control for uncertain stochastic time-delay systems, and the research on stochastic time-delay systems with uncertain parameters which satisfy the convex polyhedron structure [7,8,9,10,11]. Most of these studies use Lyapunov function which depends on the parameters and the method combined with the introduction of free matrix variables to obtain sufficient conditions for robust stabilization and robust \(H_{\infty }\) performance of the studied system. On the other hand, the state estimation problem of stochastic systems has always been a relatively important subject in control theory. Since the Luenberger observer [12] was introduced into the research of control systems, there have been many achievements in this area. When the external disturbances do not have accurate statistical characteristics, we can consider utilizing \(H_{\infty }\) filtering and \(L_{2}-L_{\infty }\) filtering [13,14,15] to study the system. For the robust control of the system, there are many research methods currently adopted, such as decomposition of singular values, \(H_{\infty }\) control method, Riccati equation method and so on. The above mentioned methods are mainly based on Lyapunov stability theory for robust analysis of uncertain systems. Among them, the advantage of using the Riccati equation processing method is that the structure of the required controller can be obtained, which is very beneficial to the theoretical analysis of the system. Its disadvantage is that it needs to determine some undetermined parameters , which is more conservatism. Then the inner point method for solving convex optimization problems and THE LMI toolbox introduced by Matlab appeared. When these methods were applied to the robust control problem of stochastic systems, they greatly promoted the progress in stability and robust control of stochastic systems. On the basis of these existing results, in view of the universality and practicability of uncertain stochastic time-delay systems, it is of great significance to study the design and control problem of state estimators for stochastic systems, especially uncertain stochastic systems.
The output analog control has a widespread application in industrial production and life. The main purpose of analog control is reappear the system output, and make the output of the reference model and the original system nearly as much as possible. Output simulation is also widely used in robot control and aircraft control, and output control design problems are generally more complicated and more difficult to implement than stability analysis. In this paper, we study the \(H_{\infty }\) output control problem for nonlinear stochastic time-delay systems. Using Lyapunov stability theory and free weight matrix method, sufficient conditions for time-delay correlation are given to ensure that the output of the stochastic nonlinear system approximates the output of the given reference model in the sense of \(H_{\infty }\). Finally, numerical examples are used to verify the feasibility of the conclusions obtained.
2 Model Description
In this paper, we consider nonlinear stochastic time-delay systems
In the system, assuming that the nonlinear perturbation satisfies the following boundedness conditions
\(\omega (t)\in {{L}_{2}}[0,\infty )\) is a square integrable vector function, its norm is defined as
τ > 0 is a constant time-delay, the reference model is designed as
Where the dimension of zr(t) is the same as the dimension of z(t). \({{x}_{r}}(t)\in {{\mathbb {R}}^{r}}\) is the reference state. D, F are constant matrices of appropriate dimensions, and D is a Hurwitz matrix. The state feedback control rate is
where K and Kr are the control gain matrix. We define that
The state feedback control rate (6) is substituted into the system (1),we can get
Then the following generalized system can be obtained
3 \(H_{\infty }\) Output Tracking of System
Theorem 3.1
Consider the system (8), (9) and the state feedback control rate in the form (6), if there is a matrix P1 > 0, P2 > 0, Q1 > 0, Q2 > 0, R1 > 0, R2 > 0, suitable dimension matrix M, N1, N2, and the constant ε > 0, satisfy the matrix inequality
where
Then the generalized closed-loop system (8), (9) satisfies the \({{H}_{\infty }}\) output tracking performance indicator γ.
Proof
Select Lyapunov-Krasovskii functional as
According to the formula \(It\hat {o}\), we can get the differential operator as
According to the Leibniz-Newton formula
In combination wit
When v(t) = 0,
let
The
Where
and
Using Schur complement lemma, we can find that matrix inequality Σ < 0 is true only if matrix inequality \(\bar {\Sigma }<0\) is true, where
Then multipling simultaneously the left and right sides of the matrix inequality \(\bar {\Sigma }<0\) by the diagonal matrix diag{I,I,I,I,I,I,I,IR1}, we can get
Thus, the system (8), (9) is asymptotically stable.
Next, we continue to prove that the closed-loop system (8), (9) can satisfy the corresponding specified \({{H}_{\infty }}\) output characteristics. Assuming that under zero initial conditions, when the system has a perturbation input v(t) , considering the Lyapunov-Krasovskii functional (11), we can get the random differential as
where
From the S-process, we can see
where
Considering the following indicators
Under zero initial conditions, there are V (0) = 0 and \(V(\infty )\ge 0\), so
However
where
Here
From Schur lemma, the inequality \(\bar {\Pi }<0\) is equivalent to the matrix inequality
Then multipling simultaneously by the diagonal matrix diag{I,I,I,I,I,I,I,R1} on both sides of the inequality, that is easy to obtain the matrix inequality of Theorem 3.1. □
4 Feedback Controller Design
Next, we consider the design problems of \({{H}_{\infty }}\) output tracking controller, and give some conclusions based on Theorem 3.1.
Theorem 4.1
Considering system (8), (9), if there are matrices \({{\bar {P}}_{1}}>0\), \({{\bar {P}}_{\text {2}}}>0\), \({{\bar {Q}}_{1}}>0\), \({{\bar {Q}}_{2}}>0\), R1 > 0, R2 > 0, the appropriate dimension matrix M, N1, N2, and constant ε > 0, makes the matrix inequality
where
Then the generalized closed-loop system (8), (9) satisfies \({{H}_{\infty }}\) output tracking performance γ.
Proof
Let
Then multipling simultaneously both sides of the matrix inequality \(\bar {\Sigma }<0\) by the diagonal matrix \(\text {diag}\left [ {{{\bar {P}}}_{1}} {{{\bar {P}}}_{1}} I {{{\bar {P}}}_{2}} {{{\bar {P}}}_{2}} I I I \right ]\), we can get
where
Let
Then
where
Then under zero initial conditions, we can consider the \({{H}_{\infty }}\) indicator
so
where
Here
Then through the inequality \(\left ( IR \right )\left ( {{R}^{-1}} \right )\left ( IR \right )\ge 0\) is equivalent to − R− 1 ≤ R − 2I, we can prove the Theorem 4.1 . □
5 Numerical Example
In this section, numerical examples are given to illustrate that the proposed theoretical method is feasible.
Example 1
The relevant parameters of the random time-delay system (1), (2) are as follows
Using \(H_{\infty }\) output tracking design method for the stochastic time-delay system proposed in Theorem 3.1, using the LMI control toolbox to solve the matrix inequality (10), the solution matrix can be obtained is
Thus we know that the feasible solution exists, that is, when the time-delay τ ≤ 0.5, the closed-loop system satisfies \({{H}_{\infty }}\) output tracking performance γ in the mean square sense, which shows that our proposed method is very effective.
References
Bucy R.S., Joseph P.D.: Filtering for Stochastic Processes with Applications to Guidance[M]. Interscience, New York (1968)
Gelb A.: Applied Optimal Estimation[M]. Cambridge University Press, Cambridge (1974)
Hsiao, F., Pan, S.: Robust kalman filter synthesis for uncertain multiple time-delay stochastic systems [J]. J. Dynam. Syst. Meas. Control 118, 803–808 (1996)
Hsieh, C., Skelton, R.E.: All covariance vontrollers for linear discrete time systems [J]. IEEE Trans. Autom. Control 35, 908–915 (1990)
Ito, K., Rozovskii, B.: Approximation of the kushner equation for nonlinear filtering [J]. Soc. Indust. Appl. Math. J. Control. Opt. 38, 893–915 (2000)
Jazwinski A.H.: Stochastic Processes and Filtering Theory[M]. Academic Press, New York (1970)
Wang, Z., Burnham, K.J.: Robust filtering for a class of stochastic uncertain nonlinear time-delay systems via exponential state estimation [J]. IEEE Trans. Signal Process. 49, 794–804 (2001)
Shaikhet, L.: Stability of stochastic hereditary systems with markov switching [J]. Theory Stochastic Process. 2, 180–184 (1996)
Willems, J.L., Willems, J.C.: Feedback stabilizability for stochastic systems with state and control dependent noise [J]. Automatica 12, 343–357 (1976)
Basin, M.V., Rodkina, A.E.: On delay-dependent stability for a class of nonlinear stochastic systems with multiple state delays [J]. Nonlinear Anal. Theory Meth. Appl. 68, 2147–2157 (2008)
Huang, L., Deng, F.: Robust exponential stabilization of stochastic largescale delay systems [J]. In: Proceedings of 2007 IEEE international conference on control and automation, pp 107–112 (2007)
Luenberger, D.G.: Observers for multi-variable systems [J]. IEEE Trans. Auto. Con. 11, 190–197 (1996)
He, Y., Wang, Q.G., Lin, C., et al.: Delay-range-dependent stability for systems with timevarying delay [J]. Automatica 43, 371–376 (2007)
Li, H., Chen, B., Zhou, Q., et al.: Delay dependent robust stability for stochastic time-delay systems with polytopic uncertainties [J]. Int. J. Robust Nonlinear Control 18, 1482–1492 (2008)
Li, H., Chen, B., Zhou, Q., et al.: A delay dependent approach to robust\(h_{\infty }\) control for uncertain stochastic systems with state and input delays [J]. Circ. Syst. Signal Process. 28, 169–183 (2009)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Li, Y., Wang, Y. Output Tracking and Feedback Controller Design for Nonlinear Stochastic Time-Delay System. Int J Theor Phys 60, 2499–2510 (2021). https://doi.org/10.1007/s10773-020-04638-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-020-04638-3