Abstract
We explicitly model entanglement in quantum processes by treating entanglement as a kind of parallelism. We introduce a shadow constant quantum operation and a so-called entanglement merge into quantum process algebra qACP. The transition rules of the shadow constant quantum operation and entanglement merge are designed. We also do a sound and complete axiomatization modulo the so-called quantum bisimilarity for the shadow constant quantum operation and entanglement merge. Then, this new type entanglement merge is extended into the full qACP. The new qACP has wide use in verification for quantum protocols, since most quantum protocols have mixtures with classical and quantum information, and also there are many quantum protocols adopting entanglement.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
To unify quantum computing and classical computing under the same process algebra framework [1,2,3,4,5], is attractive and has an important significance, because most quantum communication protocols involve quantum information and classical information, quantum computing and classical computing. There are several so-called quantum process algebra, such as CQP (Communicating Quantum Processes) [8, 9], QPAlg (Quantum Process Algebra) [10,11,12,13], qCCS [7, 14, 15, 17, 18], qACP [19]. These works try to give quantum protocols and quantum computing a process algebra foundation, some are for pure quantum computing, and the other unify quantum computing and classical computing.
There is one core concept called entanglement which is unique in quantum protocols and quantum computing. Unfortunately, this mechanism has not been modeled in quantum process algebra until now, though there are a few theoretical works on entanglement, such as types for quantum computing [20].
In this paper, we give entanglement a process algebra foundation by treating entanglement as a kind of parallelism. Based on our previous work qACP, we introduce a shadow constant quantum operation \(\circledS \) and a new kind of entanglement merge \(\between \) to model entanglement in quantum protocols and quantum computing. We extend the new kind of parallelism into the whole qACP to make that it can verify quantum protocols involving quantum information with entanglement and classical information mixed.
This work uses some results of the previous works, especially qCCS [14] and qACP [20], in the following ways. (1) We still use the concept of a quantum process configuration 〈p, ϱ〉 [7, 7,8,9,10,11, 14, 15, 18, 20], which is usually consisted of a process term p and state information ϱ of all (public) quantum information variables. (2) Like qCCS [14] and qACP [20], quantum operations are chosen to describe transformations of quantum states, and behave as the atomic actions of a pure quantum process. Quantum measurements are treated as quantum operations, so probabilistic bisimilarity are avoided.
This paper is organized as follows. We do not introduce some preliminaries, including quantum mechanics, equational logic, structural operational semantics, please refer to [6] and [7] for details. In Section 2, we introduce quantum process algebra qACP. We model entanglement as a kind of parallelism in Section 3 and extend this new kind of parallelism into the whole qACP in Section 4. In Section 5, we verify a quantum protocol which mixes quantum information (with entanglement) and classical information. Finally, we conclude this paper in Section 6.
2 Preliminaries
For convenience of the reader, we introduce quantum process algebra qACP [20] briefly.
ACP [5] is a kind of process algebra which focuses on the specification and manipulation of process terms by use of a collection of operator symbols. In ACP, there are several kind of operator symbols, such as basic operators to build finite processes (called BPA), communication operators to express concurrency (called PAP), deadlock constants and encapsulation enable us to force actions into communications (called ACP), liner recursion to capture infinite behaviors (called ACP with linear recursion), the special constant silent step and abstraction operator (called ACPτ with guarded linear recursion) allows us to abstract away from internal computations.
Bisimulation or rooted branching bisimulation based structural operational semantics is used to formally provide each process term used the above operators and constants with a process graph. The axiomatization of ACP (according the above classification of ACP, the axiomatizations are \(\mathcal {E}_{\text {BPA}}\), \(\mathcal {E}_{\text {PAP}}\), \(\mathcal {E}_{\text {ACP}}\), \(\mathcal {E}_{\text {ACP}}\) + RDP (Recursive Definition Principle) + RSP (Recursive Specification Principle), \(\mathcal {E}_{\text {ACP}_{\tau }}\) + RDP + RSP + CFAR (Cluster Fair Abstraction Rule) respectively) imposes an equation logic on process terms, so two process terms can be equated if and only if their process graphs are equivalent under the semantic model.
ACP can be used to formally reason about the behaviors, such as processes executed sequentially and concurrently by use of its basic operator, communication mechanism, and recursion, desired external behaviors by its abstraction mechanism, and so on.
ACP is organized by modules and can be extended with fresh operators to express more properties of the specification for system behaviors. These extensions are required both the equational logic and the structural operational semantics to be extended. Then the extension can use the whole outcomes of ACP, such as its concurrency, recursion, abstraction, etc.
qACP [20] is the first axiomatization attempt for quantum processes. A weak bisimilarity (quantum branching bisimulation equivalence) is established for quantum processes. This weak bisimilarity is in a non-probabilistic way that follows [14] and can be used to model silent step and abstract internal actions. qACP still uses the framework of a quantum process configuration 〈p, ϱ〉, but treating it as two relative independent part: the structural part p and the quantum part ϱ, because the establishment of a sound and complete theory is dependent on the structural properties of the structural part p. Let the quantum part ϱ be the outcomes of execution of p to examine and observe the function of the basic theory of quantum mechanics. qACP establishes the relationship between quantum bisimilarity and classical bisimilarity, including strong bisimilarity and weak bisimilarity, which makes an axiomatization of quantum processes possible. qACP establishes a series of axiomatizations of quantum process algebra, including BQPA (Basic Quantum Process Algebra), QPAP (Quantum Process Algebra with Parallelism), AQCP (Algebra of Quantum Communicating Processes), AQCP with guarded linear recursion, and AQCPτ with guarded linear recursion. Though these axiomatizations are based on classical axiomatizations of ACP which is based on the structural analysis the process p, they are not trivial and ordinary, because it is also necessary to examine if the outcomes ϱ of execution of p obey the basic quantum mechanics theory. qACP and classical ACP are unified under the framework of quantum process configuration 〈p, ϱ〉. This unifying means that quantum information and classical information can be mixed in qACP and quantum computing and classical computing are unified in qACP. Thus, qACP can be used widely for verification of quantum communication protocols, which involve not only quantum information, but also classical information.
3 Modeling Entanglement in qACP
In the following, the variables x, x′, y, y′, z, z′ range over the collection of process terms, the variables υ, ω range over the set A of atomic quantum operations, α, β ∈ A, s, s′, t, t′ are closed items, τ is the special constant silent step, δ is the special constant deadlock, and the predicate \(\xrightarrow {\alpha }\surd \) represents successful termination after execution of the quantum operation α, the variables υ, ω range over the set A of atomic quantum operations, and the variable ν, μ range over the set C of atomic communicating actions.
3.1 Entanglement in Quantum Mechanics and Quantum Computing
Quantum information are carried by particles. The simplest non-trivial quantum system is the quantum bit or qubit. A qubit’s state space is the 2-dimensional space which is denoted as Q. The space Q is equipped with a standard basis composed with |0〉 and |1〉. The tensor product of Q is Q ⊗ Q for the space of two qubits and its standard basis composed with the four vectors |00〉, |01〉, |10〉 and |11〉. Another important basis for Q ⊗ Q is called Bell states or EPR states, which contains the four vectors:
The elements of Bell states are entangled states, which represent systems which are correlated with each other. And many quantum protocols and quantum computation can derive extra power of entanglement, since it is unique for quantum computing.
3.2 Modeling Entanglement as a Kind of Parallelism – Entanglement Merge
We consider entanglement as a kind of parallelism, i.e., information formed by entangled particles may be distributed over a long distance, and quantum operations manipulated on one particle not only change the information represented by this particle, but also those represented by other particles entangled with this particular particle dramatically without any interactions among them. This new kind of parallelism does not need any information exchange and any information channel.
So, we extend the Basic Quantum Process Algebra (BQPA) to form a new Algebra of Quantum Communicating Processes (AQCP) which is also called AQCP.
3.2.1 Shadow Constant
Since process algebra, exactly ACP or qACP, is a kind of algebraic manipulation on actions or quantum operations, and information are hidden by actions and quantum operations. Quantum operation manipulated on one particle will change the quantum states of other entangled particles simultaneously, but, the absence of any quantum operation on other entangled particles will disturb the principles of structural operational semantics on which qACP is based. To conquer this problem, we introduce a special constant quantum operation which is called shadow constant \(\circledS \). Now, the set A of all quantum operations is extended to \(A\cup \{\circledS \}\). The shadow constant \(\circledS \) is always depended on some entangled particles, when a quantum operation α is manipulated on one particle, then there will be shadow operations \(\circledS _{\alpha }\) manipulated on the other entangled particles.
Actually, when one quantum operation α is manipulated on one particle, the states of the other entangled particles are changed without any quantum operation. So, the behavior of the shadow operation \(\circledS \) is doing nothing, as the following transition rule says. This is why the shadow constant \(\circledS \) is called a shadow, especially, \(\circledS _{\upsilon }\) is the shadow of υ.
Obviously, we can get the following two conclusions.
Theorem 1
BQPA with shadow constant is a conservative extension of BQPA.
Proof
Since the corresponding TSS of BQPA is source-dependent [20], and the transition rules for the shadow constant \(\circledS \) contain only a fresh constant in their source, so the corresponding TSS of BQPA with shadow constant is a conservative extension of that of BQPA. That means that BQPA with shadow constant is a conservative extension of BQPA. □
Theorem 2
Quantum bisimulation equivalence is a congruence with respect to BQPA with shadow constant.
Proof
The structural part of QTSSs for BQPA with shadow constant and BQPA are all in panth format [20], so bisimulation equivalence that they induce is a congruence. According to the definition of quantum bisimulation, quantum bisimulation equivalence that QTSSs for BQPA with shadow constant induce is also a congruence. □
The axioms for shadow constant is shown in Table 1.
We can easily get the following two theorems.
Theorem 3
\(\mathcal {E}_{\text {BQPA}}\) + SC1 - SC3 is sound for BQPA with shadow constant modulo quantum bisimulation equivalence.
Proof
Since quantum bisimulation is both an equivalence and a congruence for BQPA with shadow constant, only the soundness of the first clause in the definition of the relation = is needed to be checked. That is, if s = t is an axiom in \(\mathcal {E}_{\text {BQPA}}\) + SC1 - SC3 and σ a closed substitution that maps the variable in s and t to basic quantum process terms, then we need to check that \(\langle \sigma (s),\varrho \rangle \underline {\leftrightarrow }\langle \sigma (t),\varsigma \rangle \).
Since axioms in \(\mathcal {E}_{\text {BQPA}}\) + SC1 - SC3 are sound modulo bisimulation equivalence, according to the definition of quantum bisimulation, we only need to check if ϱ′ = ς′ when ϱ = ς, where ϱ evolves into ϱ′ after execution of σ(s) and ς evolves into ς′ after execution of σ(t). We can find that every axiom in Table 1 meets the above condition. □
Theorem 4
\(\mathcal {E}_{\text {BQPA}}\) + SC1 - SC3 is complete for BQPA with shadow constant modulo quantum bisimulation equivalence.
Proof
To prove that \(\mathcal {E}_{\text {BQPA}}\) + SC1 - SC3 is complete for BQPA with shadow constant modulo quantum bisilumation equivalence, it means that \(\langle s, \varrho \rangle \underline {\leftrightarrow } \langle t,\varsigma \rangle \) implies s = t.
It can be easily proved that \(\mathcal {E}_{\text {BQPA}}\) + SC1 - SC3 is complete for BQPA with shadow constant modulo bisimulation equivalence, that is, \(s\underline {\leftrightarrow } t\) implies s = t.
- (1)
The axioms SC1-SC3 are turned into rewriting rules directly from left to right, and added to the three rewriting rules in the proof the completeness of \(\mathcal {E}_{\text {BPA}}\) (see [5]). The resulting TRS is terminating modulo AC (Associativity and Commutativity) of + operator through defining new weight functions on process terms.
$$weight(\circledS)\triangleq 2$$$$weight(\upsilon)\triangleq 2$$$$weight(s+t)\triangleq weight(s) + weight(t)$$$$weight(s\cdot t)\triangleq weight(s)^{2}\cdot weight(t)$$We can get that each application of a rewriting rule strictly decreases the weight of a process term, and that moreover process terms that are equivalent modulo AC of + have the same weight. Hence, the TRS is terminating modulo AC of + .
- (2)
We will show that the normal form n are not of the form \(s+\circledS ,\circledS \cdot s\), \(s\cdot \circledS \). The proof is based on induction with respect to the size of the normal form n.
If n is an atomic action, then it does not contain the shadow constant \(\circledS \).
n cannot be of the form \(s+\circledS \), \(s\cdot \circledS ,\circledS \cdot s\), because in that case, the directed version of SC1, SC2 and SC3 would apply to it, contradicting the fact that n is a normal form.
We proved that normal forms are all basic process terms.
- (3)
We proceed to prove that the axiomatization \(\mathcal {E}_{\text {BQPA}}\) + SC1 - SC3 is complete for BQPA with shadow constant modulo bisimulation equivalence. Let the process terms s and t be bisimilar. The TRS is terminating modulo AC of the + , so it reduces s and t to normal forms n and n′, respectively. Since the rewrite rules and equivalence modulo AC of the + can be derived from \(\mathcal {E}_{\text {BQPA}}\) + SC1 - SC3, s = n and t = n′. Soundness of \(\mathcal {E}_{\text {BQPA}}\) +SC1 - SC3 then yields \(s\underline {\leftrightarrow } n\) and \(t \underline {\leftrightarrow } n^{\prime }\), so \(n\underline {\leftrightarrow } s \underline {\leftrightarrow } t \underline {\leftrightarrow } n^{\prime }\). We shown that the normal forms n and n′ are basic process terms. Then it follows that \(n\underline {\leftrightarrow } n^{\prime }\) implies n =ACn′. Hence, s = n =ACn′ = t.
\(\langle s, \varrho \rangle \underline {\leftrightarrow } \langle t,\varsigma \rangle \) with ϱ = ς means that \(s\underline {\leftrightarrow } t\) with ϱ = ς and ϱ′ = ς′, where ϱ evolves into ϱ′ after execution of s and ς evolves into ς′ after execution of t, according to the definition of quantum bisimulation equivalence. The completeness of \(\mathcal {E}_{\text {BQPA}}\) + SC1 - SC3 for BQPA with shadow constant modulo bisimulation equivalence determines that \(\mathcal {E}_{\text {BQPA}}\) + SC1 - SC3 is complete for BQPA with shadow constant modulo quantum bisimulation equivalence. □
3.2.2 Entanglement Merge
In AQCP, there are two kind of merges: left merge  and communication merge ∣. For parallelism, these two kind of merges remain in the new AQCP. To model entanglement, another new kind of merge called entanglement merge should be added. In this kind of merge, there is not any information exchange via any channel.
and communication merge ∣. For parallelism, these two kind of merges remain in the new AQCP. To model entanglement, another new kind of merge called entanglement merge should be added. In this kind of merge, there is not any information exchange via any channel.
The merge 〈s ∥ t, ϱ〉 can choose to execute an initial transition of process term s or an initial transition of process term t, and change the quantum state, which is captured by the following four transition rules.
And also the merge 〈s ∥ t, ϱ〉 can choose to execute a communication of initial transitions of the process term s and t, and does not change the quantum state, which is expressed by the following four transition rules.
And also the merge 〈s ∥ t, ϱ〉, in which there is entanglement between s and t, can choose to execute an initial transition of process term s or an initial transition of process term t, and change the quantum state, which is expressed by the following eight transition rules.
Since there does not exist a sound and complete finite axiomatization for BPA extended with the merge, modulo bisimulation equivalence, it is can be proved that there does not exist a sound and complete axiomatization for BQPA extended with the merge modulo quantum bisimulation equivalence either. This can be overcome by defining three extra operator that are called left merge  and communication merge ∣, and also entanglement merge \(\between \). We call BQPA extended with the merge operator ∥, the left merge operator
and communication merge ∣, and also entanglement merge \(\between \). We call BQPA extended with the merge operator ∥, the left merge operator  , the communication merge operator ∣ and the entanglement merge \(\between \) as Quantum Process Algebra with Parallelism and entanglement, which is also called QPAP.
, the communication merge operator ∣ and the entanglement merge \(\between \) as Quantum Process Algebra with Parallelism and entanglement, which is also called QPAP.
The left merge  and communication merge ∣ are the same as those in QPAP in qACP. The eight transition rules of entanglement merge \(\between \) are as follows.
and communication merge ∣ are the same as those in QPAP in qACP. The eight transition rules of entanglement merge \(\between \) are as follows.
We can get the following conclusions.
Theorem 5
QPAP is a conservative extension of BQPA with shadow constant.
Proof
Since the corresponding TSS of BQPA with shadow constant is source-dependent [20], and the transition rules for merge operator ∥, left merge operator  , communication merge ∣ and entanglement merge \(\between \) contain only a fresh operator in their source, so the corresponding TSS of QPAP is a conservative extension of that of BQPA with shadow constant. That means that QPAP is a conservative extension of BQPA with shadow constant. □
, communication merge ∣ and entanglement merge \(\between \) contain only a fresh operator in their source, so the corresponding TSS of QPAP is a conservative extension of that of BQPA with shadow constant. That means that QPAP is a conservative extension of BQPA with shadow constant. □
Theorem 6
Quantum bisimulation equivalence is a congruence with respect to QPAP.
Proof
The structural part of QTSSs for QPAP and BQPA with shadow constant are all in panth format [20], so bisimulation equivalence that they induce is a congruence. According to the definition of quantum bisimulation, quantum bisimulation equivalence that QTSSs for QPAP induce is also a congruence. □
We design an axiomatization for QPAP illustrated in Table 2.
Then, we can get the soundness and completeness theorems as follows.
Theorem 7
\(\mathcal {E}_{\text {QPAP}}\) is sound for QPAP modulo quantum bisimulation equivalence.
Proof
Since quantum bisimulation is both an equivalence and a congruence for QPAP [20], only the soundness of the first clause in the definition of the relation = is needed to be checked. That is, if s = t is an axiom in \(\mathcal {E}_{\text {QPAP}}\) and σ a closed substitution that maps the variable in s and t to basic quantum process terms, then we need to check that \(\langle \sigma (s),\varrho \rangle \underline {\leftrightarrow }\langle \sigma (t),\varsigma \rangle \).
Since axioms in \(\mathcal {E}_{\text {QPAP}}\) (same as \(\mathcal {E}_{\text {PAP}}\)) are sound for QPAP modulo bisimulation equivalence, according to the definition of quantum bisimulation, we only need to check if ϱ′ = ς′ when ϱ = ς, where ϱ evolves into ϱ′ after execution of σ(s) and ς evolves into ς′ after execution of σ(t). We can find that every axiom in Table 2 meets the above condition. □
Theorem 8
\(\mathcal {E}_{\text {QPAP}}\) is complete for QPAP modulo quantum bisimulation equivalence.
Proof
To prove that \(\mathcal {E}_{\text {QPAP}}\) is complete for QPAP modulo quantum bisilumation equivalence, it means that \(\langle s, \varrho \rangle \underline {\leftrightarrow } \langle t,\sigma \rangle \) implies s = t.
It can be easily proved that \(\mathcal {E}_{\text {QPAP}}\) (same as \(\mathcal {E}_{\text {PAP}}\)) is complete for PAP modulo bisimulation equivalence, that is, \(s\underline {\leftrightarrow } t\) implies s = t.
- (1)
The axioms QM1, QLM2-QLM4, QCM5-QCM10, QEM11-QEM23 are turned into rewriting rules directly from left to right, and added to the 20 rewriting rules in the proof the completeness of \(\mathcal {E}_{\text {BPA}}\) (see [5]). The resulting TRS is terminating modulo AC (Associativity and Commutativity) of + operator through defining new weight functions on process terms.

We can get that each application of a rewriting rule strictly decreases the weight of a process term, and that moreover process terms that are equivalent modulo AC of + have the same weight. Hence, the TRS is terminating modulo AC of + .
- (2)
We will show that the normal form n are not of the form s ∥ t,
 and \(s\between t\). The proof is based on induction with respect to the size of the normal form n.
and \(s\between t\). The proof is based on induction with respect to the size of the normal form n.
If n is an atomic action, then it does not contain the shadow constant \(\circledS \).
Suppose n =ACs + t or n =ACs ⋅ t. Then by induction, the normal forms s and t do not contain †, so n does not contain any parallel operator.
n cannot be of the form s ∥ t, because in that case, the directed version of QM1 would apply to it, contradicting the fact that n is a normal form.
n cannot be of the form s
 t, because in that case, the directed version of QLM2-QLM4 would apply to it, contradicting the fact that n is a normal form.
t, because in that case, the directed version of QLM2-QLM4 would apply to it, contradicting the fact that n is a normal form.n cannot be of the form s∣t, because in that case, the directed version of QCM5-QCM10 would apply to it, contradicting the fact that n is a normal form.
n cannot be of the form \(s\between t\), because in that case, the directed version of QEM11-QEM20 would apply to it, contradicting the fact that n is a normal form.
We proved that normal forms are all basic process terms.
- (3)
We proceed to prove that the axiomatization \(\mathcal {E}_{\text {QPAP}}\) is complete for QPAP modulo bisimulation equivalence. Let the process terms s and t be bisimilar. The TRS is terminating modulo AC of the + , so it reduces s and t to normal forms n and n′, respectively. Since the rewrite rules and equivalence modulo AC of the + can be derived from \(\mathcal {E}_{\text {QPAP}}\), s = n and t = n′. Soundness of \(\mathcal {E}_{\text {QPAP}}\) then yields \(s\underline {\leftrightarrow } n\) and \(t \underline {\leftrightarrow } n^{\prime }\), so \(n\underline {\leftrightarrow } s \underline {\leftrightarrow } t \underline {\leftrightarrow } n^{\prime }\). We shown that the normal forms n and n′ are basic process terms. Then it follows that \(n\underline {\leftrightarrow } n^{\prime }\) implies n =ACn′. Hence, s = n =ACn′ = t.
\(\langle s, \varrho \rangle \underline {\leftrightarrow } \langle t,\varsigma \rangle \) with ϱ = ς means that \(s\underline {\leftrightarrow } t\) with ϱ = ς and ϱ′ = ς′, where ϱ evolves into ϱ′ after execution of s and ς evolves into ς′ after execution of t, according to the definition of quantum bisimulation equivalence. The completeness of \(\mathcal {E}_{\text {QPAP}}\) for QPAP modulo bisimulation equivalence determines that \(\mathcal {E}_{\text {QPAP}}\) is complete for QPAP modulo quantum bisimulation equivalence.□
For deadlock constant δ and encapsulation operator ∂H, two extra axioms should be added, as Table 3 shows.
We can easily get that the new axiomatization \(\mathcal {E}_{\text {AQCP}}\) is sound for AQCP modulo quantum bisimulation equivalence, and the new \(\mathcal {E}_{\text {AQCP}}\) is complete for AQCP modulo quantum bisimulation equivalence.
4 qACP with Entanglement Merge
Now, we consider the influence of the new AQCP with entanglement to the whole qACP, i.e., AQCP with guarded recursion and AQCPτ with guarded recursion, which are based on AQCP.
Guarded recursion defines infinite computation through guarded recursion specifications. Extension to guarded recursion based on the new AQCP has almost no influence comparing with that in qACP. The axiomatization \(\mathcal {E}_{\text {AQCP}}\) + RDP + RSP is sound and complete for AQCP with linear recursion modulo quantum bisimulation equivalence.
Similarly, the new AQCP does not influence AQCPτ with guarded recursion, i.e., \(\mathcal {E}_{\text {AQCP}_{\tau }}\) + RSP + RDP + CFAR is sound and complete for AQCPτ with guarded linear recursion, modulo quantum rooted branching bisimulation equivalence.
But, entanglement merge \(\between \) makes entanglement explicit in qACP. Based on the framework of quantum process configuration 〈p, ϱ〉, by introducing silent step τ and abstraction operator τI, the definition of ϱ only records the so-called public quantum variables and claim that a τ operation only manipulates on entangled quantum variables which should be included in the so-called private variables. Now, we explicitly define a new entanglement merger to model entanglement in quantum processes and this declaration can be moved away.
Since, shadow constant quantum operation and entanglement merge are defined for quantum operations, i.e., they are only valid for quantum operations. A quantum operation α can only effect with its shadow constant \(\circledS _{\alpha }\), any other mismatch, such as α and β, α and \(\circledS _{\beta }\), a classical action a and a quantum operation α, will all cause a deadlock δ. This leads that qACP with entanglement merge also unify quantum and classical computing in a high level of computational logic, the same as qACP does.
From now on, we call qACP which represents not only the original qACP, but also qACP with entanglement merge.
5 Verification for Quantum Protocols with Entanglement – the E91 Protocol
With support of Entanglement merge \(\between \), now, qACP can be used to verify quantum protocols utilizing entanglement. The E91 protocol [16] is the first quantum protocol which utilizes entanglement and mixes quantum and classical information. In this section, we take an example of verification for the E91 protocol.
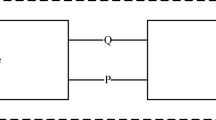
The E91 protocol is used to create a private key between two parities, Alice and Bob. Firstly, we introduce the basic E91 protocol briefly, which is illustrated in Fig. 1.
- 1.
Alice generates a string of EPR pairs q with size n, i.e., 2n particles, and sends a string of qubits qb from each EPR pair with n to Bob through a quantum channel Q, remains the other string of qubits qa from each pair with size n.
- 2.
Alice create two string of bits with size n randomly, denoted as Ba and Ka.
- 3.
Bob receives qb and randomly generates a string of bits Bb with size n.
- 4.
Alice measures each qubit of qa according to a basis by bits of Ba. And the measurement results would be Ka, which is also with size n.
- 5.
Bob measures each qubit of qb according to a basis by bits of Bb. And the measurement results would be Kb, which is also with size n.
- 6.
Bob sends his measurement bases Bb to Alice through a public channel P.
- 7.
Once receiving Bb, Alice sends her bases Ba to Bob through channel P, and Bob receives Ba.
- 8.
Alice and Bob determine that at which position the bit strings Ba and Bb are equal, and they discard the mismatched bits of Ba and Bb. Then the remaining bits of Ka and Kb, denoted as \(K_{a}^{\prime }\) and \(K_{b}^{\prime }\) with \(K_{a,b}=K_{a}^{\prime }=K_{b}^{\prime }\).
We re-introduce the basic E91 protocol in an abstract way with more technical details as Fig. 1 illustrates.
Now, M[qa;Ka] denotes the Alice’s measurement operation of qa, and \(\circledS _{M[q_{a};K_{a}]}\) denotes the responding shadow constant; M[qb;Kb] denotes the Bob’s measurement operation of qb, and \(\circledS _{M[q_{b};K_{b}]}\) denotes the responding shadow constant. Alice sends qb to Bob through the quantum channel Q by quantum communicating action sendQ(qb) and Bob receives qb through Q by quantum communicating action receiveQ(qb). Bob sends Bb to Alice through the public channel P by classical communicating action sendP(Bb) and Alice receives Bb through channel P by classical communicating action receiveP(Bb), and the same as sendP(Ba) and receiveP(Ba). Alice and Bob generate the private key Ka, b by a classical comparison action cmp(Ka, b, Ka, Kb, Ba, Bb). Let Alice and Bob be a system AB and let interactions between Alice and Bob be internal actions. AB receives external input Di through channel A by communicating action receiveA(Di) and sends results Do through channel B by communicating action sendB(Do).
Then the state transition of Alice can be described by qACP as follows.
where Δi is the collection of the input data.
And the state transition of Bob can be described by qACP as follows.
where Δo is the collection of the output data.
The send action and receive action of the same data through the same channel can communicate each other, otherwise, a deadlock δ will be caused. The quantum operation and its shadow constant pair will lead entanglement occur, otherwise, a deadlock δ will occur. We define the following communication functions.
Let A and B in parallel, then the system AB can be represented by the following process term.
where \(H=\{send_{Q}(q_{b}),receive_{Q}(q_{b}),send_{P}(B_{b}),receive_{P}(B_{b}),send_{P}(B_{a}),receive_{P}(B_{a}),\\ M[q_{a};K_{a}], \circledS _{M[q_{a};K_{a}]}, M[q_{b};K_{b}], \circledS _{M[q_{b};K_{b}]}\}\) and I = {cQ(qb), cP(Bb), cP(Ba), M[qa;Ka], M[qb;Kb], cmp(Ka, b, Ka, Kb, Ba, Bb)}.
Then we get the following conclusion.
Theorem 9
The basic E91 protocolτI(∂H(A ∥ B)) exhibits desired external behaviors.
Proof
Let ∂H(A ∥ B) = 〈X1|E〉, where E is the following guarded linear recursion specification:
Then we apply abstraction operator τI into 〈X1|E〉.
We get \(\tau _{I}(\langle X_{1}|E\rangle )={\sum }_{D_{i}\in {\Delta }_{i}}{\sum }_{D_{o}\in {\Delta }_{o}}receive_{A}(D_{i})\cdot send_{B}(D_{o})\cdot \tau _{I}(\langle X_{1}|E\rangle )\), that is, \(\tau _{I}(\partial _{H}(A\parallel B))={\sum }_{D_{i}\in {\Delta }_{i}}{\sum }_{D_{o}\in {\Delta }_{o}}receive_{A}(D_{i})\cdot send_{B}(D_{o})\cdot \tau _{I}(\partial _{H}(A\parallel B))\). So, the basic E91 protocol τI(∂H(A ∥ B)) exhibits desired external behaviors. □
6 Conclusions
We explicitly model entanglement in quantum processes by introducing a shadow constant quantum operation \(\circledS \) and a so-called entanglement merge \(\between \) into quantum process algebra qACP. The new qACP has wide use in verification for quantum protocols, since most quantum protocols have mixtures with classical and quantum information, and also there are many quantum protocols adopting entanglement.
To maintain the principle of structural operational semantics on which qACP is based, the shadow constant quantum operation is really a kind of placeholder, and the entanglement merge \(\between \) actually does a synchronization between two interleaving processes at the point of the quantum operation and its shadows. During verification for quantum protocols, the synchronization point and the shadow constant quantum operations are put in place during the modeling phase.
But, (1) This synchronization and the shadow constant (though it is only a shadow) are not existing actually in quantum protocols and quantum computing; (2) qACP is a kind of high level computational logic, though quantum and classical computing are unified under this high level computational logic, but the hidden quantum information and more technical details can not be observed. In future, more suitable theory should be pursued to satisfy the above two requirements.
References
Baeten, J.C.M.: A brief history of process algebra. Theor. Comput. Sci. Process Algebra 335(2–3), 131–146 (2005)
Milner, R.: Communication and Concurrency. Prentice Hall (1989)
Milner, R., Parrow, J., Walker, D.: A calculus of mobile processes, Parts I and II. Inf. Comput. 1992(100), 1–77 (1992)
Hoare, C.A.R.: Communicating Sequential Processes. http://www.usingcsp.com/ (1985)
Fokkink, W.: Introduction to Process Algebra, 2nd edn. Springer (2007)
Plotkin, G.D.: A structural approach to operational semantics. Aarhus University, Tech Report DAIMIFN-19 (1981)
Feng, Y., Duan, R.Y., Ji, Z.F., Ying, M.S.: Probabilistic bisimulations for quantum processes. Inf. Comput. 2007(205), 1608–1639 (2007)
Gay, S.J., Nagarajan, R.: Communicating quantum processes. In: Proceedings of the 32nd ACM Symposium on Principles of Programming Languages, pp. 145–157. ACM Press, Long Beach (2005)
Gay, S.J., Nagarajan, R.: Typechecking communicating quantum processes. Math. Struct. Comput. Sci. 2006(16), 375–406 (2006)
Jorrand, P., Lalire, M.: Toward a quantum process algebra. In: Proceedings of the 1st ACM Conference on Computing Frontiers, pp. 111–119. ACM Press, Ischia (2005)
Jorrand, P., Lalire, M.: From quantum physics to programming languages: A process algebraic approach. Lect. Notes Comput. Sci 2005(3566), 1–16 (2005)
Lalire, M.: Relations among quantum processes: Bisimilarity and congruence. Math. Struct. Comput. Sci. 2006(16), 407–428 (2006)
Lalire, M., Jorrand, P.: A process algebraic approach to concurrent and distributed quantum computation: Operational semantics. In: Proceedings of the 2nd International Workshop on Quantum Programming Languages, pp. 109–126. TUCS General Publications (2004)
Ying, M., Feng, Y., Duan, R., Ji, Z.: An algebra of quantum processes. ACM Trans. Comput. Logic (TOCL) 10(3), 1–36 (2009)
Feng, Y., Duan, R., Ying, M.: Bisimulations for quantum processes. In: Proceedings of the 38th ACM Symposium on Principles of Programming Languages (POPL 11), pp. 523–534. ACM Press (2011)
Ekert, A.K.: Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67(6), 661–663 (1991)
Deng, Y., Feng, Y.: Open bisimulation for quantum processes. Manuscript, arXiv:1201.0416 (2012)
Feng, Y., Deng, Y., Ying, M.: Symbolic bisimulation for quantum processes. Manuscript, arXiv:1202.3484 (2012)
Wang, Y.: An axiomatization for quantum processes to unifying quantum and classical computing. Manuscript, arXiv:1311.2960 (2013)
Duncan, R.: Types for Quantum Computing. Ph.D. Dessertation, Oxford University (2006)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Wang, Y. Entanglement in Quantum Process Algebra. Int J Theor Phys 58, 3611–3626 (2019). https://doi.org/10.1007/s10773-019-04226-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-019-04226-0


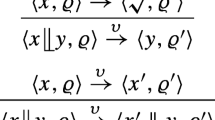


 and
and  t, because in that case, the directed version of QLM2-QLM4 would apply to it, contradicting the fact that n is a normal form.
t, because in that case, the directed version of QLM2-QLM4 would apply to it, contradicting the fact that n is a normal form.