1 Introduction

Digital signature is an essential ingredient of classical cryptography and has been employed in various applications. Unfortunately, most existing classical signature schemes whose security depends on the difficulty of solving some hard mathematical problems were threatened by quantum computation [1]. Therefore, researchers turn to investigate its quantum counterpart with the hope that quantum signature can become an alternative to classical signature and provide unconditional security.

Proxy signature, as an importation cryptographic primitive was firstly introduced in 1996. In a proxy signature scheme, it allows a proxy signer to sign on behalf of an original signer. Since Mambo M et al. proposed a quantum digital signature protocol [2], many efforts have been made on it and lots of schemes have been presented [3,4,5,6,7,8,9,10]. In 2002, Barnum [11] proposed a quantum signature scheme and it was proved to be unconditionally secure. A quantum digital signature scheme based on quantum one-way function was proposed by Gottesman and Chuang [12]. Zeng et al. [13, 14] presented arbitrated quantum signature (AQS) schemes based on a three-qubit Greenberger-Horne-Zeilinger (GHZ) state. Two arbitrated quantum signature schemes with message recovery were proposed by Lee et al. [15]. Recently, Cao et al. presented two quantum proxy signature schemes [16, 17] based on genuine six-qubit entangled state and five-qubit entangled state, respectively.

Chaum [18] first proposed a blind signature scheme. In blind signature schemes, the message anonymity could be guaranteed. When signed, the message is disguised to ensure privacy. In other words, it allows a signatory to sign a message for a user in such a way that she can not learn the content of the message. In 2008, Wen et al. proposed a weak blind signature scheme based on quantum cryptography [19]. Afterwards, a quantum blind signature protocol using GHZ states was proposed by Wang et al. [20].

In this paper, we put forward improvement of a quantum proxy blind signature scheme based on genuine six-qubit entangled state. Our scheme allows a proxy signer Peter to finish the signature on behalf of the original signers Bob and Charlie, which may have applications in e-payment system, e-government, e-business and so on. For instance, elects in the network, a legal person simultaneously was appointed by the two legal representative to replace them to carry on the signature. We use quantum key distribution protocol, quantum one-time pad and other quantum properties to guarantee the unconditional security and signature message anonymity. Compared with the scheme Ref. [16, 21], a trust party Trent is proposed in this paper so as to avoid receiver David’s dishonest behavior. Compared to [22], our scheme adopts the GHZ-state measurement, Bell-state measurement which are easier to implement under current technology and experimental conditions. In addition, the messages may not be forged or modified in any way by the receiver or attacker.

2 Preliminary Theory of Controlled Quantum Teleportation

The quantum proxy blind signature is based on controlled teleportation. In this section, we will introduce the controlled teleportation. A genuine six-qubit entangled state [23] as quantum channel. It is given by

$$ \begin{array}{ll} |\xi \rangle_{123456}= & \frac{1}{4}(|000000\rangle-|000011\rangle+|111100\rangle-|111111\rangle \\ & +|001100\rangle+|001111\rangle+|110000\rangle+|110011\rangle \\ & +|011001\rangle-|011010\rangle+|100101\rangle-|100110\rangle \\ & +|010101\rangle+|010110\rangle+|101001\rangle+|101010\rangle)_{123456}. \end{array} $$
(1)

Alice is a sender, she owns particles (2,5), the controllers Bob and Charlie hold particles (1,3) and particle 6, respectively. The verifier David holds particle 4.

Suppose that the quantum state of particle M carrying message in Alice is given by

$$ |\varphi\rangle_{M}=\frac{1}{\sqrt{2}}(|0\rangle+b|1\rangle)_{M}, $$
(2)

in which b= 1 and b=− 1 is corresponding to \(M(i)\)= 1 and \(M(i)\)= 0, respectively.

The mixed state \(|{\Psi }\rangle _{M123456}\) of the whole system is given by

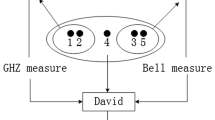
$$ |{\Psi}\rangle_{M123456}=|\varphi\rangle_{M}\otimes|\xi \rangle_{123456} =\frac{1}{\sqrt{2}}(|0\rangle+b|1\rangle)_{M}\otimes|\xi \rangle_{123456}. $$
(3)

The controlled quantum teleportation works in the following process. The frame of teleportation is shown in Fig. 1.

Fig. 1
figure 1

The model of controlled quantum teleportation

Full size image

1) Alice makes a GHZ-state measurement on her particles (M,2,5), and sends her measurement outcomes to Bob, Charlie and David via secure quantum channels. The GHZ-state measurement can collapse the state of particles (1,3,4,6) into one of the following eight states

$$ \begin{array}{ll} \left<Z^{\pm}_{M25}|{\Psi}\right>_{M123456} =& \frac{1}{2\sqrt{2}}(|0000\rangle+|0110\rangle+|1011\rangle +|1101\rangle \\ & \mp b|1111\rangle \pm b|1001\rangle \mp b|0100\rangle \pm b|0010\rangle)_{1346}, \\ \left<H^{\pm}_{M25}|{\Psi}\right>_{M123456} =& \frac{1}{2\sqrt{2}}(-|1111\rangle+|1001\rangle-|0100\rangle +|0010\rangle \\ & \pm b|0000\rangle \pm b|0110\rangle \pm b|1011\rangle \pm b|1101\rangle)_{1346}, \\ \left<S^{\pm}_{M25}|{\Psi}\right>_{M123456} =& \frac{1}{2\sqrt{2}}(-|0001\rangle+|0111\rangle-|1010\rangle +|1100\rangle \\ & \pm b|1110\rangle \pm b|1000\rangle \pm b|0101\rangle \pm b|0011\rangle)_{1346}, \\ \left<T^{\pm}_{M25}|{\Psi}\right>_{M123456} =& \frac{1}{2\sqrt{2}}(|1110\rangle+|1000\rangle+|0101\rangle +|0011\rangle \\ & \mp b|0001\rangle \pm b|0111\rangle \mp b|1010\rangle \pm b|1100\rangle)_{1346}. \end{array} $$
(4)

The eight GHZ states of 3-qubit are

$$ \begin{array}{ll} |Z^{\pm}\rangle= \frac{1}{\sqrt{2}}(|000\rangle\pm|111\rangle), \\ |H^{\pm}\rangle= \frac{1}{\sqrt{2}}(|011\rangle\pm|100\rangle), \\ |S^{\pm}\rangle= \frac{1}{\sqrt{2}}(|001\rangle\pm|110\rangle), \\ |T^{\pm}\rangle= \frac{1}{\sqrt{2}}(|010\rangle\pm|101\rangle). \end{array} $$
(5)

2) If Bob and Charlie agree Alice and David to complete their teleportation, Bob performs a Bell-state measurement on his particles (1,3). Charlie performs single particle measurement on his particle 6 based on \(\{|0\rangle ,|1\rangle \}\). Suppose that Alice’s measurement result is \(|T^{-}\rangle _{M25}\), the Bell-state measurement on Bob’s particles (1,3) will collapse the quantum state of particles (4,6) into one of the following states

$$ \begin{array}{ll} \left<\phi^{\pm}_{13}|T^{-}_{M25}|{\Psi} \right>_{M123456}=\frac{1}{2}(|11\rangle+b|01\rangle\pm|10\rangle \mp b|00\rangle)_{46}, \\ \left<\psi^{\pm}_{13}|T^{-}_{M25}|{\Psi} \right>_{M123456}=\frac{1}{2}(|01\rangle-b|11\rangle\pm|00\rangle \pm b|10\rangle)_{46}. \end{array} $$
(6)

Suppose that Bob’s measurement result is \(|\phi ^{+}\rangle _{13}\), the single particle measurement on Charlie’s particle 6 in the basis \(\{|0\rangle ,|1\rangle \}\) will collapse the particle 4 into one of the following states

$$ \begin{array}{ll} \left<0_{6}|\phi^{+}_{13}|T^{-}_{M25}|{\Psi} \right>_{M123456}=\frac{1}{\sqrt{2}}(|1\rangle-b|0\rangle)_{4}, \\ \left<1_{6}|\phi^{+}_{13}|T^{-}_{M25}|{\Psi} \right>_{M123456}=\frac{1}{\sqrt{2}}(|1\rangle+b|0\rangle)_{4}. \end{array} $$
(7)

The four Bell states of 2-qubit are

$$ |\phi^{\pm}\rangle=\frac{1}{\sqrt{2}}(|00\rangle\pm|11\rangle),|\psi^{\pm}\rangle=\frac{1}{\sqrt{2}}(|01\rangle\pm|10\rangle). $$
(8)

Bob and Charlie send their measurement results to David through secure quantum channels.

3) According to Alice’s, Bob’s and Charlie’s measurement outcomes, David imposes an appropriate unitary operation \(U_{4}\) on particle 4 to successfully reconstruct the original unknown quantum state \(|\varphi \rangle _{M}\). For instance, if Alice’s measurement outcome is \(|T^{-}\rangle _{M25}\), Bob’s and Charlie’s measurement outcomes are \(|\phi ^{+}\rangle _{13}\) and \(|1\rangle _{6}\), respectively, David’s operation on particle 4 is \(\sigma _{x}\). For other cases, the relationship between Alice’s, Bob’s, Charlie’s measurement results and David’s operation are shown in Table 1.

Table 1 The relationship between Alice’s, Bob’s, Charlie’s measurement results and David’s operation
Full size table

Alice successfully transmits the unknown quantum state \(|\varphi \rangle _{M}\) to the receiver David under Bob’s and Charlie’s control.

3 Improvement of Quantum Proxy Blind Signature Scheme

The proposed quantum proxy blind signature scheme includes the following several phases. Alice is the massage owner; Bob and Charlie are the original signers, they delegate a proxy signer Peter to sign message instead of them; David is the verifier; Trent is the trust party.

3.1 Initializing Phase

Step 1 Alice holds a string of n-bit (information bits) which carry the messages to be signed:

$$ M=\{M(1),M(2),\cdots,M(n)\}=\{M(i),i = 1,2,\cdots,n\}. $$
(9)

Step 2 Quantum Key Distribution : Alice shares a secret key \(K_{AD}\) with David, a secret key \(K_{AP}\) with Peter, a secret key \(K_{AT}\) with the trust party Trent, respectively. Bob and Charlie share a secret key \(K_{PBC}\) with Peter. All secret keys are distributed through QKD protocols, which have been proved to be unconditionally secure [24,25,26].

Step 3 Quantum Channel Setup: David produces n six-qubit entangled states as in (1), he gives particles (2,5) to Peter, particles (1,3) to Bob and particle 6 to Charlie, David holds particle 4.

3.2 Blind the Message Phase

Alice blinds the message M and gets \(M^{\prime }=\{M^{\prime }(1),M^{\prime }(2),\cdots ,M^{\prime }(n)\}(M^{\prime }(i)\in \{0,1\}, i = 1,2,\cdots ,n)\). The method of blinding and encoding message are as follows.

(a) The \(M^{\prime }(i)\) is decided by the i th bit of \(K_{AD}\). Alice obtains \(M^{\prime }(i)\) as following

$$ M^{\prime}(i)=K_{AD}^{i}\oplus M(i) ,i = 1,2,\cdots, n. $$
(10)

(b) Alice produces n quantum states: {\(|\varphi _{1}\rangle _{M^{\prime }}\), \(|\varphi _{2}\rangle _{M^{\prime }}\), \(\cdots \), \(|\varphi _{n}\rangle _{M^{\prime }}\)}(\(|\varphi _{i}\rangle _{M^{\prime }}\)= \(\frac {1}{\sqrt {2}}\)(|0〉 + b(i)|1〉),i = 1,2,⋯ ,n). Where \(b(i)\)= 1 and \(b(i)\)=− 1 is corresponding to \(M^{\prime }(i)\)= 1 and \(M^{\prime }(i)\)= 0, respectively. The secret key \(K_{AD}\) is shared by Alice and David, the length of \(K_{AD}\) is large enough. Since \(K_{AD}\) is distributed via QKD protocols [24,25,26] so that it is unknown to other people except Alice and David.

This message blinding and coding rule is only known to Alice and David, and other people do not know it.

3.3 Authorizing and Signing Phase

In our scheme, the quantum one-time pad [27] is adopted to guarantee the transmit secure.Step 1 Alice sends \(E_{K_{AP}}\{|\varphi _{i}\rangle _{M^{\prime }}\}\) to Peter. Peter decrypts \(E_{K_{AP}}\{|\varphi _{i}\rangle _{M^{\prime }}\}\) with the key \({K_{AP}}\) to get \(|\varphi _{i}\rangle _{M^{\prime }}\), then he performs the GHZ-state measurement on particles (M′,2,5) and records his measurement results as \(\alpha _{_{P}}\), where \(\alpha _{_{P}}\) is Peter’s signature of the blind message \(M^{\prime }\). Then he encrypts \(\alpha _{_{P}}\) with key \(K_{PBC}\) to get the message \(E_{K_{PBC}}\{\alpha _{_{P}}\}\) and sends it to Bob and Charlie as his proxy request.Step 2 After Bob and Charlie received the message \(E_{K_{PBC}}\{\alpha _{_{P}}\}\). If they agree to delegate Peter to sign messages instead of them, they will help Peter and David to complete the controlled teleportation. Bob performs the Bell-state measurement on particles (1,3) and records the measuring result as \(\alpha _{_{B}}\). Charlie performs single particle measurement on particle 6 in the basis \(\{|0\rangle ,|1\rangle \}\) and records the measuring results as \(\alpha _{_{C}}\). Then they encrypt \(\alpha _{_{B}}\) and \(\alpha _{_{C}}\) with the key \(K_{PBC}\) to get the message \(E_{K_{PBC}}\{\alpha _{_{B}},\alpha _{_{C}}\}\) and send it to Peter as their proxy authorization. If Bob and Charlie do not agree Peter to sign messages for them, they will not allow Peter and David to perform their teleportation.Step 3 After Peter received the message \(E_{K_{PBC}}\{\alpha _{_{B}},\alpha _{_{C}}\}\), he decrypts it with key \(K_{PBC}\) to get the messages \(\alpha _{_{B}}\) and \(\alpha _{_{C}}\). Then Peter encrypts \(\alpha _{_{B}}\), \(\alpha _{_{C}}\), \(\alpha _{_{P}}\) with key \(K_{AP}\) to get his signature \(E_{K_{AP}}\{\alpha _{_{B}},\alpha _{_{C}},\alpha _{_{P}}\}\) and sends it to Alice.Step 4 Alice decrypts \(E_{K_{AP}}\{\alpha _{_{B}},\alpha _{_{C}},\alpha _{_{P}}\}\) with key \(K_{AP}\) to get the messages \(\alpha _{_{B}}\), \(\alpha _{_{C}}\), \(\alpha _{_{P}}\). She encrypts these messages with key \(K_{AD}\) and \(K_{AT}\) to get \(E_{K_{AD}}\{M^{\prime },\alpha _{_{B}},\alpha _{_{C}},\alpha _{_{P}}\}\) and \(E_{K_{AT}}\{M^{\prime },\alpha _{_{B}},\alpha _{_{C}},\alpha _{_{P}}\}\), then she sends \(E_{K_{AD}}\{M^{\prime },\alpha _{_{B}},\alpha _{_{C}},\alpha _{_{P}}\}\) to David and sends \(E_{K_{AT}}\{M^{\prime },\alpha _{_{B}},\alpha _{_{C}},\alpha _{_{P}}\}\) to Trent, respectively.

3.4 Verifying Phase

Step 1 After David received the message \(E_{K_{AD}}\{M^{\prime },\alpha _{_{B}},\alpha _{_{C}},\alpha _{_{P}}\}\) from Alice, he decrypts it with the key \(K_{AD}\) to get the messages \(M^{\prime }\), \(\alpha _{_{B}}\), \(\alpha _{_{C}}\), \(\alpha _{_{P}}\).

Step 2 Trent decrypts message \(E_{K_{AT}}\{M^{\prime },\alpha _{_{B}},\alpha _{_{C}},\alpha _{_{P}}\}\) with key \(K_{AT}\) to get messages \(M^{*}\) and \(\alpha ^{*}_{_{B}}\), \(\alpha ^{*}_{_{C}}\), \(\alpha ^{*}_{_{P}}\). Then Trent announces his messages \(M^{*}\) and \(\alpha ^{*}_{_{B}}\), \(\alpha ^{*}_{_{C}}\), \(\alpha ^{*}_{_{P}}\). David compares his messages with Trent’s messages, if \(M^{\prime }\) = M∗, \(\alpha _{_{B}}\)=\(\alpha ^{*}_{_{B}}\), \(\alpha _{_{C}}\)=\(\alpha ^{*}_{_{C}}\), \(\alpha _{_{P}}\)=\(\alpha ^{*}_{_{P}}\), he will declare that the process is valid and continue the following verify process. Then David performs appropriate unitary operation on particle 4 to replicate the teleported unknown state \(|\varphi \rangle _{M^{\prime }}\) which carries messages.

Step 3 According to coding rule (b) in 3.2, David obtains \(\{M^{\prime \prime }(1),M^{\prime \prime }(2),\cdots ,M^{\prime \prime }(n)\}\) via measuring {\(|\varphi _{1}\rangle _{M^{\prime }}\), \(|\varphi _{2}\rangle _{M^{\prime }}\), \(\cdots \), \(|\varphi _{n}\rangle _{M^{\prime }}\)} in the basis \(\{|+\rangle ,|-\rangle \}\), where \(|+\rangle =\frac {1}{\sqrt {2}}({|0\rangle +|1\rangle }), |-\rangle =\frac {1}{\sqrt {2}}({|0\rangle -|1\rangle })\). Then he gets message \(M^{\prime \prime }\) and compares it with \(M^{\prime }\). if \(M^{\prime }\) = M″, David accepts the message \(M^{\prime }\) and the signature. Otherwise, David rejects it.Step 4 David unblinds \(M^{\prime }\) with key \(K_{AD}\) according to the rule by (a) in 3.2 to get the message M. The message M has been signed. David confirms the signature (M, \(\alpha _{_{B}}\), \(\alpha _{_{C}}\), \(\alpha _{_{P}}\)).

4 Security Analysis and Discussion

4.1 Impossibility of Disavowal

Firstly, we show that it is impossible for Bob and Charlie to disavow their delegation. According to (3.4.1) in 3.4, David decrypts message \(E_{K_{AD}}\{M^{\prime },\alpha _{_{B}},\alpha _{_{C}},\alpha _{_{P}}\}\) with key \(K_{AD}\) to get Bob’s and Charlie’s proxy authorization \(\alpha _{_{B}}\), \(\alpha _{_{C}}\). The receiver David can verify signature with the help of Trent. All keys are distributed via QKD protocols, which have been proved unconditionally secure and all messages are sent through the secure quantum channel. Hence, Bob and Charlie can not deny their delegation once David accepts the signature.

Secondly, we show that it is impossible for Peter to disavow his signature. From Section 3.4 in Section 3.4, the receiver David can get Peter’s proxy request and verify signature with the help of the trust party Trent. Then Peter can not deny that he indeed has signed the message.

Thirdly, David can not disavow he has received the signature. It is obvious that David knows the secret key \(K_{AD}\) and can obtain the signature by Section 3.4 in Section 3.4. Moreover, the process of the verifying indicates he has received it. Suppose David deny he has received the signature, the sender Alice requests the trust party Trent to resolve the disagreement. The receiver David needs Trent’s help in the process of signature verification so that Trent can confirm that David has received the signature. Hence David can not deny his receipt of the signature.

4.2 Impossibility of Forgery

In our scheme, those who attempt to forge message and signature would definitely be detected.

Firstly, we show that it is impossible for David to forge Peter’s signature. If David wants to forge Peter’s signature, as David needs the trust party Trent’s help in the verifying process and David knows the secret key \(K_{AD}\) shared between Alice and David, so David’s forge attacks will be detected by Trent and Alice. Then, David would not be able to forge the message and signature. David’s cheat will be perceived through Peter, Bob and Charlie measuring their particles, respectively. Similarly, Alice will face the same situation like David. In other words, the trick insider attackers not be able to forge Peter’s signature.

Secondly, suppose that an attacker or eavesdropper Eve forge Peter’s signature. However, he not be able to know the secret key \(K_{AP}\) shared between Alice and Peter, so he can not send message encrypted by \(K_{AP}\), in other words, it is impossible for Eve to forge Peter’s signature. If an attacker Eve intends to forge Peter’s signature, he must get the information about \(K_{AP}\). Assume that Eve guesses \(K_{AP}\) randomly, then he can produce the valid signature with the probability at most \(\frac {1}{2^{n}}\), which vanishes zero if n is large enough. So Eve can forge Peter’s signature with a negligible probability. Therefore, Eve can not forge Peter’s signature.

Thirdly, Refs. [16, 17, 28] has shown that the receiver David can forge a valid signature for his own benefit without being detected. There we will give a thorough analysis and indicates that our scheme be safe from this counterfeit. Suppose that David have obtained \(M^{\prime }\) = M″, he wants to modify them such that \((M^{\prime })^{*}\)=(M″)∗ because \((M^{\prime })^{*}\) is beneficial to him. Then David claims that \(|S\rangle \) is valid signature about the message \((M^{\prime })^{*}\). However, it is impossible, because when Alice knows it, she requires the trust party Trent to solve the controversy by making a comparison between \((M^{\prime })^{*}\) and \(M^{*}\), if \((M^{\prime })^{*}\)\(\neq \)\(M^{*}\), then the behavior of David will be detected.

4.3 Message’s Blindness

In this scheme, the message M has been blinded by the sender Alice into \(M^{\prime }=\{M^{\prime }(1),M^{\prime }(2),\cdots ,M^{\prime }(n)\}(M^{\prime }(i)\in \{0,1\}, i = 1,2,\cdots ,n)\) according to blinding rule (a) in 3.2. The signatory Peter can get \(E_{K_{AP}}\{|\varphi _{i}\rangle _{M^{\prime }}\}\) from Alice, then he decrypts it with key \(K_{AP}\) to get the message \(|\varphi _{i}\rangle _{M^{\prime }}\) and signs the message by measuring his particles, he does not know the content of the message. Firstly, if Peter attempts to determine the message M, the only way is to get the information about \(K_{AD}\). However, it is impossible, because the secret key is distributed via QKD protocols which have been proved unconditionally secure [24,25,26].

Secondly, even if Peter does know the secret key \(K_{AD}\), the message blinding rule in 3.2 is secret to him. If Peter guesses the message blinding rule randomly, then he can determine it with the probability at most \(\frac {1}{2^{n}}\), which will approximate zero if n is large enough. As a result, the proxy signatory Peter can not know the content of the message that he has signed. Hence, this scheme has the property of blindness.

4.4 The Proxy Property

In our scheme, the original signatory Bob and Charlie can give the proxy signatory Peter the proxy authorization by correlation of the controlled teleporation. Meanwhile, Peter can generate the valid signature.

4.5 Impossibility of Some Attacks

In this portion, we show that our scheme can resist some attacks. On the one hand, this scheme can resist the man-in-the-middle attack. Assume that Eve, an attacker, can fabricate Peter send signature to Alice or fabricate Alice send messages to David. However, the message M or signature is encrypted by the secret key. Because of the unconditional security of both quantum key distribution and one-time pad algorithm, it is impossible for Eve to manipulate the message or fabricate Peter’s signature.

On the other hand, this scheme can resist intercept-resend attack. Suppose that Eve, an attacker, know well the signature protocol, and intercept the particles that transmitted from David to Peter, Bob and Charlie, respectively. Suppose Eve manipulate the message M or \(M^{\prime }\) by means of resending his own particles instead of the original particles, however, the behavior will be detected by David because Eve unavoidably destroyed the correlation of particles in the quantum states.

5 Conclusion

In this paper, we present improvement of a quantum proxy blind signature scheme which uses genuine six-qubit entangled state as quantum channel. Compared with previous work Refs. [17], our scheme has the property of blindness. At the same time, the unconditional security is guaranteed by the quantum key distribution [24,25,26], quantum one-time pad and encryption algorithm. Different from the quantum signature proposed in Refs. [16, 17, 21, 29], our scheme introduces a trust party Trent to prevent David from forging a valid signature.

In addition, the message keeps the blind over the whole signature process in this scheme. Compared with the related scheme Refs. [16, 21], the introduction of the trust party Trent makes our scheme achieves a higher security. Moreover, this scheme adopts the GHZ-state measurement, Bell-state measurement and single particle measurement which are feasible to implement with current technologies and experimental conditions. Therefore, our scheme has a more extensive application value.