1 Introduction

The cosmic distance-duality (DD) relation, also well known as Etherington’s reciprocity relation [1], plays a fundamental role in astronomical observation and cosmology, ranging from gravitational lensing studies [2] to analysis of the cosmic microwave black body radiation (CMBR) observations, as well as for galaxy and galaxy clusters observations [3–5]. Even cosmological interpretation of galaxy number counts distribution, as well as the optic theorem that surface brightness of an extended source does not depend on the angular diameter distance between the observer and source, an important result for understanding lensing brightness, are both consequences of this relation [6]. It connects different metric distances via the following identity

$$ \frac{D_{\mathrm{L}}}{D_{\mathrm{A}}}{(1+z)}^{-2}=1, $$
(1)

where D L and D A represent luminosity distance and angular diameter distance (ADD) respectively, with z being the redshift. Given the fundamental hypothesis that, in general relativity, light travels always along null geodesics, and that the sources and observers are connected by null geodesics in a Riemannian spacetime, one can easily prove this equation in the context of Friedmann-Lemaître-Roberson-Walker(FLRW) cosmology [7, 8]. Being independent of Einstein field equations and nature of matter, this equation is generally valid for all cosmological models based on Riemannian geometry.

It is in principle possible to test the validity of the DD relation with astronomical observation data. The basic idea is that the DD relation can be tested directly, if one can obtain both D L and D A at the same redshift from observations. But it is difficult to find objects at the same redshift with both known intrinsic luminosity and sizes. So some model-dependent methods have been employed to perform the tests by using the observed D L or D A. De Bernardis et al. [9] obtained a non violation of the DD relation in the framework of the cosmic concordance ΛCDM model with ADD from galaxy clusters provided by the sample of Ref. [10]. Uzan et al. obtain a test for the DD relation from the observations of Sunyaev- Zeldovich effect (SZE) and X-ray surface brightness of galaxy clusters [11]. With the 18 ADD galaxy clusters from the samples of Ref. [12], they found that there was no significant deviation from the DD relation for a ΛCDM model [13].

Recently, Avgoustidis et al. [14] employed a parametrization d L=d A(1+z)2+𝜖 for the DD relation, in a flat ΛCDM model, to place constraints on the cosmic opacity through combining recent SNe Type Ia data compilation [15] with the latest measurements of the Hubble expansion at redshifts 0<z<2 [16]. They found \(\epsilon =-0.04_{-0.07}^{+0.08}\) at 2σ confidence level (CL). The basic idea of this test is that, while SNe Ia observations are affected by some sources, namely, the Milky Way, the hosting galaxy, the intervening galaxies and the Intergalactic Medium, the current H(z) measurements are obtained from ages estimates of old passively evolving galaxies, which depend only on the detailed shape of the galaxy spectra, not on the galaxy luminosity. Therefore, measurements of the Hubble expansion H(z), which is different from d L measurements of SNe Ia, are not affected by cosmic opacity since this quantity is assumed to be not strongly wavelength dependent in the optical band [14]. In order to obtain distance estimates from the largest Hubble parameter data H(z) which consist of 28 data points [16, 18–23], Holanda et al. solved numerically the comoving distance integral for non-uniformly spaced data using a simple trapezoidal rule [17]. They obtained that a completely transparent universe is in agreement with this largest sample in their analysis. Then with these Hubble parameter data H(z) and the current largest SNe Ia samples (Union2.1) with three cosmological-model-independent methods [24], Liao et al. tested the comic opacity and found that the universe is transparent. More recently, by using luminosity distances of gamma-ray bursts and the latest Hubble data, Holanda et al. [25] placed constraints on the cosmic opacity at high redshifts (z>2) for a flat ΛCDM model, and obtained that both SNe Ia and GRBs samples are compatible with a transparent universe at 1σ CL.

To test the DD relation, one can express it as a function of the redshift z, namely

$$ \frac{D_{\mathrm{L}}}{D_{\mathrm{A}}}{(1+z)}^{-2}=\eta(z). $$
(2)

Firstly, by comparing the elliptical and spherical β model (used to describe the galaxy clusters) in Refs. [10, 26] with the theoretical value \(D_{\mathrm {L}}^{\text {Th}}\) obtained from ΛCDM model [27], Holanda, Lima and Ribeiro used two parameterized forms for η(z) [28]

$$ \eta(z)=1+\eta_{0}z $$
(3)

and

$$ \eta(z)=1+\eta_{0}z/(1+z), $$
(4)

where η 0 is a constant parameter quantifying a possible departure from the validity of the DD relation and when η 0=0, the DD relation holds, to test the possible deviation, and found that the elliptical and spherical β model are consistent with the validity of DD relation at 1σ and 3σ confidence level respectively.

However, the consistency from above quoted literature depends on the assumed cosmology model or some results provided by a chosen set of astrophysical phenomena. Comparing the luminosity distance D L obtained from the current supernovae Ia data with the angular diameter distance D A from FRIIb radio galaxies [55] and ultra compact radio sources [29–32], Bassett and Kunz found that there exists a moderate violation (2σ confidence level) caused by the brightening excess of SNe Ia at z>0.5 [33]. Later on, with the parameterizations in (3, 4), Holanda et al. [34] proposed a model-independent cosmological test for the DD relation by employing two sub-samples of SNe Ia carefully chosen from Constitution data [35] and ADD samples from galaxy clusters obtained through SZE and X-ray measurements with different assumptions concerning the geometry used to describe the clusters: elliptical and spherical β model [10, 26]. For each cluster, they selected one SNe Ia data whose redshift is the closest to the cluster’s with the range Δz=|z−z SNe|<0.005. They found that the elliptical β model is marginally compatible with the validity of the DD relation at 2σ CL, however, the spherical β model indicates a strong deviation from this relation. Then with the selection criterion used in Ref. [34], Li et al., using the Union 2 [36] compilation which contains 557 SNe Ia data and galaxy cluster data [10, 26], performed a model-independent test of the DD relation [37], and finally obtained that DD relation is accommodated at the 1σ CL for the elliptical model, and at 3σ CL for the spherical model. Later on, Fu et al. [38] tested the DD relation by smoothing the noise of the Constitution and Union2 SNe Ia compilations in a model-independent method [39], and found that the elliptical β model with the Constitution compilation is only consistent with the DD relation at 3σ CL, while the spherical β medel is incompatible with the DD relation at 3σ CL. For the Union2 compilation, the elliptical and spherical β are marginally consistent with the DD relation at 1σ and 2σ CL respectively. In order to avoid any bias brought by redshift incoincidence between galaxy clusters and Type Ia Supernave (SNe Ia), Liang et al. [40] obtained the luminosity distance of a certain SNe Ia point at the same redshift of the corresponding galaxy cluster by interpolating from the nearby SNe Ia, and found that DD relation is consistent with the observational data at 2σ CL. Meng et al. [41], aiming at comparing different morphological model of galaxy clusters with four types of parameterizations for η(z), i.e., the first two of which are expressed as the (3, 4), and the last two are shown as follows

$$ \eta(z)=1+\eta_{0}z/(1+z)^{2} $$
(5)

and

$$ \eta(z)=1-\eta_{0}\ln(1+z), $$
(6)

found that DD relation is compatible with the elliptical β model at 1σ CL, but can not be consistent with the spherical β models even at 3σ CL for most of the parameterizations. So they also concluded that the elliptical model is a better geometrical hypothesis describing the structure of the galaxy cluster compared with the spherical β model if the DD relation is valid in cosmological observations. Then, in order to both strengthen the constraints on the DD relation and get rid of the systematics related to the unknown cluster geometry, Cardone et al. [42], with the local regression technique to estimate luminosity distance D L from SNe Ia data, investigated the possibility to use Baryon Acoustic Oscillations (BAO) to infer D A(z) from future BAO surveys.

In this paper, we will perform a cosmological-model-independent test for the DD relation, which is assumed as a function of redshift z, η(z)=D L(1+z)−2/D A, by combining the angular diameter distances D A (or comoving distances D c) with the luminosity distances D L. The function η(z) is parameterized in four general forms, i.e., η(z)=1+η 0 z, η(z)=1+η 0 z/(1+z), η(z)=1+η 0 z/(1+z)2 and η(z)=1−η 0 ln(1+z), where η 0 is a constant parameter quantifying a possible departure from the validity of the DD relation and when η 0=0, the DD relation holds. The D A is given by the spherical β model [9] and elliptical β model [26] of galaxy cluster samples. We get the D c by a usual trapezoidal rule from the Hubble parameter listed in Ref. [24]. In practice, the observational data pairs of the D L and D A(or D c) at the same redshift are obtained with two methods, i.e., method A: binning the SNe Ia data within the range Δz=|z−z SNe|<0.005 to get the D L at the redshift of galaxy cluster or Hubble parameter data, and method B: reconstructing the D L(z) by smoothing the noise of Union2.1 data set over redshift with the Gaussian smoothing function. We also test the validity of the DD relation by comparing the combination of the galaxy cluster data and Hubble parameter data to the SNe Ia data. We find that DD relation is consistent with the present observational data and the results we obtained are not sensitive to the method and parameterization.

2 Samples

In order to test the DD relation with the parameterizations, we employ SZE and X-ray observations of two galaxy cluster samples. The first sample contains 25 galaxy clusters, described by an elliptical β model in the redshift range 0.023≤z≤0.784 [26]. The second sample contains 38 D A of clusters, described by an spherical β model in the redshift range 0.14≤z≤0.89 [10].

Another method proposed by Holanda et al. is to obtain ADD from observational Hubble parameter data [17]. Recently, with the newly released observational Hubble parameter data H(z) and current largest SNe Ia samples (Union2.1), Liao et al. tested the comic opacity and found that the universe is transparent [24]. The Hubble parameter H(z) at z≠0 is obtained by calculating the derivative of cosmic time with respect to redshift [43–47] in the following form

$$ H(z)=-{1\over {1+z}}{dz\over{dt}}. $$
(7)

Using a simple trapezoidal law and 28 data summarized in Table of literature [24], we can obtain the comoving distance (D c ) by the following equation,

$$ D_{\mathrm{c}}=c{{\int}_{0}^{z}} {dz^{\prime}\over H(z^{\prime})}\approx {c\over 2} {\sum}_{i=1}^{n} (z_{i+1}-z_{i})\left[ {1\over H(z_{i+1})}+{1\over H(z_{i})} \right], $$
(8)

and the error associated to the i th bin,

$$ s_{i}={c\over 2}(z_{i+1}-z_{i})\left( {\sigma_{H_{i+1}}^{2}\over H_{i+1}^{4}} + {\sigma_{H_{{i}}}^{2}\over {H_{i}^{4}}}\right)^{1/2}\;, $$
(9)

where \(\sigma _{H_{i}}\) is the error of H(z) data and H 0=73.8±2.4 km/s/Mpc [48]. The relative errors have been studied by Liao et al. [24] and were found to decrease remarkably when the numbers of intervals increase from 12 to 28 compared to the number used in the literature [17].

In order to get D L, we use the Union2.1 compilation [49] which contains 580 data points between the redshift region 0≤z≤1.415 by presenting refinements to the analysis on Union2 compilation [36] and adding 23 SNe Ia data, among which 14 new SNe Ia from the Hubble Space telescope Cluster Survey [49] and 9 low redshift SNe Ia from the Carngie Supernova Project [50].

3 Methods of Dealing with SNe Ia Samples

In principle, given a D A from galaxy cluster data or D c from Hubble parameters at a certain redshift, one should select a D L from SNe Ia data point that shares the same redshift z with the given data to test the DD relation. However, this condition usually can not be met in reality. In this section, we introduce two cosmological-model-independent methods to get the luminosity distance D L of a certain SNe Ia point which has the same redshift of the corresponding galaxy cluster data or Hubble parameters.

3.1 Method A: Binning the SNe Ia Data

In order to test the DD relation with model-independent method, Both Holanda et al. [28] and Li et al. [37] adopted a selection criterion Δz=|z clu−z SNe|<0.005, and choose the nearest SNe Ia data for every galaxy cluster. However, using merely one SNe Ia data point from all those available which meets the selection criterion will lead to larger statistical errors. Instead of using one D L point of Union2.1 SNe Ia, we bin these data available in the range Δz=|z clu/Hub−z SNe|<0.005, where z clu/Hub denotes the redshifts of the galaxy cluster or Hubble parameter data. In this method, we employ an inverse variance weighted anverage of all the selected data. If D Li denotes the ith appropriate SNe Ia luminosity distance data with \(\sigma _{D_{\mathrm {L}i}}\) representing the corresponding observational uncertainty and with the conventional data reduction techniques in Chapter. 4 in [51], we can straightforwardly obtain

$$ \bar{D_{\mathrm{L}}}={\sum(D_{\mathrm{L}i}/\sigma_{D_{\mathrm{L}i}}^{2})\over \sum1/\sigma_{D_{\mathrm{L}i}}^{2}}, $$
(10)
$$ \sigma^{2}_{\bar{D_{\mathrm{L}}}}={1\over \sum1/\sigma_{D_{\mathrm{L}i}}^{2}}, $$
(11)

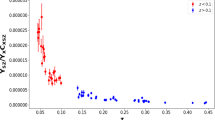
where \(\bar {D_{\mathrm {L}}}\) represents the weighted mean luminosity distance at the corresponding galaxy cluster or Hubble parameter redshift, and \(\sigma ^{2}_{\bar {D_{\mathrm {L}}}}\) is its uncertainty. The selection criteria in this method can be satisfied for all galaxy clusters samples except for the cluster CL J 1226.9+3332 (the nearest one is at Δz=0.005) [10] from spherical model sample, and for most of the Hubble parameter data except for the points at z=0.9,1.037,1.43,1.53 and 1.75. For the sake of completeness of the galaxy cluster, we keep the cluster data point of CL J 1226.9+3332 in our analysis with this method. The distributions of these two angular diameter distance samples and the luminosity distance D L obtained by this method are shown in Fig. 1.

Fig. 1
figure 1

Hubble diagram of the elliptical β model, spherical β model and the corresponding D L from SNe Ia data (Union2.1) with the associated error bars obtained by method A

Full size image

3.2 Method B: Smoothing the SNe Ia Data

In order to avoid any bias brought by redshift incoincidence between galaxy clusters (Hubble data) and Type Ia Supernave (SNe Ia), as well as to ensure the integrity of the galaxy clusters samples, we obtain the luminosity distance of a certain SNe Ia point at the same redshift of the corresponding galaxy cluster (Hubble data) by smoothing the noise of the SNe Ia data directly to obtain the continuous luminosity distance at redshifts z.

Following a procedure in the analysis of large scale structure, Shafieloo et al. [39, 52], with a Gaussian kernel, smoothed the noise of the SNe Ia data directly to reconstruct the expansion history of the universe and property of dark energy. Then Wu and Yu generalized this procedure to eliminate the impact of H 0 and reconstruct the cosmic expansion history [53]. Then, Fu et al. studied the effect of spatial curvature on reconstructing the cosmic expansion history and the property of dark energy by smoothing the noise of the Union2.1 Type Ia Supernovae (SNIa) data with a Gaussian smoothing function [54]. More recently, in order to test the distance-duality relation [38] or examine the cosmic opacity [24], this model-independent method was also used to smooth Constitution, Union2 or Union2.1 SNe Ia compilation to obtain the curves of the luminosity distance. In this paper, in order to obtain the luminosity distance curve D L(z) with Union2.1 compilation, we use lnf(z)= lnD L(z)+ lnh through the following iterative method

$$\begin{array}{@{}rcl@{}} \ln f(z)^{s}_{n}=\ln f(z)^{s}_{n-1}+N(z){\sum}_{i}[\ln f^{\text{obs}}(z_{i})-\ln f(z)^{s}_{n-1}]\exp\bigg[-{\ln^{2}\big({1+z \over 1+z_{i}}\big)\over 2\triangle^{2}}\bigg]\;, \end{array} $$
(12)

with a normalization parameter

$$\begin{array}{@{}rcl@{}} N(z)^{-1}={\sum}_{i} \exp\bigg[-{\ln^{2}\big({1+z \over 1+z_{i}}\big)\over 2\triangle^{2}}\bigg]\;. \end{array} $$
(13)

In (12,13), △ is a quantity needed to be given prior. Since a large value of △ leads to a smooth result but depresses the accuracy of reconstruction, and inversely for a small value of △, it is important to choose a reasonable value of △. Here, following Shafieloo et al. [39, 52] and Wu and Yu [53], we choose △=0.6. Using \(f(z)^{s}_{n}\) in (12), we can get a smoothed luminosity distance at any redshift z after n iteration. When n=1

$$\begin{array}{@{}rcl@{}} \ln f(z)^{s}_{1} &=& \ln f(z)^{\mathrm{s}}_{0}+N(z){\sum}_{i}(\ln f^{\text{obs}}(z_{i})-\ln f(z)^{\mathrm{s}}_{0})\exp\bigg[-{\ln^{2}\big({1+z \over 1+z_{i}}\big)\over 2\triangle^{2}}\bigg]\\ &=&\ln D_{\mathrm{L}}(z)^{\mathrm{s}}_{0}+N(z){\sum}_{i}(\ln f^{\text{obs}}(z_{i})-\ln D_{\mathrm{L}}(z)^{\mathrm{s}}_{0})\exp\bigg[-{\ln^{2}\big({1+z \over 1+z_{i}}\big)\over 2\triangle^{2}}\bigg]\;, \end{array} $$
(14)

where D L(z)0s is the luminosity distance of the suggested background model, and it has been shown that the results are not sensitive to the chosen value of △ and the guessed background model [52]. Here we use a wCDM model with w=−0.9 and Ω m0=0.28 as the guessed background model. lnf obs(z i ) is the observed one from the SNe Ia and can be expressed as:

$$\begin{array}{@{}rcl@{}} \ln f^{\text{obs}}(z_{i})\equiv {\ln 10\over 5} [\mu^{\text{obs}}(z_{i})-42.38]=\ln D_{\mathrm{L}}^{\text{obs}}(z_{i})-\ln h\;. \end{array} $$
(15)

Here h=H 0/100 and μ obs is the observed distance module of SNe Ia. In order to determine whether we obtain a best fit one after some iterations, we calculate, after each iteration, \({\chi _{s}^{2}}\):

$$\begin{array}{@{}rcl@{}} \chi_{\mathrm{s},n}^{2}={\sum}_{i} {(\mu(z_{i})_{n}-\mu^{\text{obs}}(z_{i}))^{2} \over \sigma^{2}_{\mu_{\text{obs},i}}}\;. \end{array} $$
(16)

The best fit result corresponds to the minimum value of \(\chi ^{2}_{\mathrm {s},n}\). For the SNe Ia data from Union2.1, when n=32, the value of \(\chi _{\mathrm {s}}^{2}\) reaches the minimum value, as shown in the left panel of Fig. 2. So, we obtain the best fit smoothed luminosity distance at any redshifts z shown in the right panel of Fig. 2. With this method, we obtain observational data pairs of the D L and D A/D c at the same redshift from the continuous luminosity distance function D L(z), so we consider all available data from galaxy cluster data and Hubble parameters. The distributions of these two angular diameter distance samples and the luminosity distance D L obtained by this method are shown in the right panel of Fig. 2.

Fig. 2
figure 2

Computed \({\chi _{s}^{2}}\) for the reconstructed results at each iteration (left panel), Hubble diagram of the elliptical β model spherical β model and the corresponding D L obtained by method B (right panel) from SNe Ia data (Union2.1)

Full size image

4 Analysis and the Results

Now, with observational data pairs of the D L and D A (or D c) at the same redshift, we will place constraints on the parameter η 0 for the DD relation η(z)=D L(z)(1+z)−2/D A (z) for parameterizations from (3 ∼6). We note that, in general, the SZE + X-ray surface brightness observations technique gives \(D_{A}^{\text {cluster}}(z)=D_{A}(z)\eta ^{2}\), instead of D A (z). In order to test the DD relation in (1) with SZE + X-ray observations, we should replace the angular diameter distance D A(z) by \(D_{\mathrm {A}}^{\text {cluster}}\) in (2), and get \(\eta _{\text {obs}}(z)=D_{\mathrm {A}}^{\text {cluster}}(z)(1+z)^{2}/D_{\mathrm {L}}(z)\). It should be noted that in this paper, we can not obtain D A directly from D c as we have applied the parameterizations for the DD relation. In a flat universe, we explored phenomenologically the expression of \(D_{\mathrm {c}}/[(1+z){\sqrt {\eta (z)}}]\) to determine D A in (2) [17], and get η obs(z)=D L(z)2/[D c(z)(1+z)]2. Thus, using the following equation

$$ {\chi_{D}^{2}} = {\sum}_{z}\frac{{\left[\eta(z)- \eta_{\text{obs}}(z) \right] }^{2}}{\sigma^{2}_{\eta_{\text{obs}}}}\,, $$
(17)

we can obtain the constraints on η 0. Here \({\sigma _{\eta _{\text {obs}}}}\) is the errors of the observation techniques η obs. It, for galaxy cluster data, is given by

$$ \sigma^{2}_{\eta_{\text{obs}}}={\eta_{\text{obs}}^{2}}\left[\left( {\sigma_{D_{\mathrm{A}}^{\text{clu}}(z)}\over{D_{\mathrm{A}}^{\text{clu}}(z)}}\right)^{2}+\left( \sigma_{D_{\mathrm{L}}(z)}\over{D_{\mathrm{L}}(z)}\right)^{2}\right]. $$
(18)

For Hubble parameters, \({\sigma _{\eta _{\text {obs}}}}\) can be expressed as

$$ \sigma^{2}_{\eta_{\text{obs}}}=4{\eta_{\text{obs}}^{2}}\left[\left( {\sigma_{D_{\mathrm{c}}^{\text{Hub}}(z)}\over{D_{\mathrm{c}}^{\text{Hub}}(z)}}\right)^{2}+\left( \sigma_{D_{\mathrm{L}}(z)}\over{D_{\mathrm{L}}(z)}\right)^{2}\right]. $$
(19)

Our results are shown in Figs. 3, 4 and Tables 1, 2.

Fig. 3
figure 3

The likelihood distribution functions from the elliptical β (upper panel), spherical β model (middle panel) and Hubble parameter (bottom panel) respectively. The left and right panels are obtained through method A and B respectively

Full size image
Fig. 4
figure 4

The likelihood distribution functions from combination of the elliptical β model and Hubble parameter (upper panel), spherical β model and Hubble parameter (bottom panel) respectively. The left and right panels are obtained through method A and B respectively

Full size image
Table 1 The summary of maximum likelihood estimation results of η 0 for four parameterizations respectively
Full size table
Table 2 The summary of maximum likelihood estimation results of η 0 for four parameterizations respectively. The η 0 is represented by the best fit value at 1, 2 and 3 σ CL for each data set. The triangle or asterisk represents the case with method A or method B respectively
Full size table

In the upper and middle panels of Fig. 3, with the four forms of parameterizations for η(z) and two methods for D L from SNe Ia data, we find that, for the elliptical β model (the De Filippis et al. sample) [26], the DD relation is consistent with observational data at 1σ CL with both methods. As for the spherical β model (the Bonameta et al. sample [10]), DD relation is marginally consistent at 2σ CL. Compared with the results obtained by Holanda et al. [28], Li et al. [37] and Fu et al. [38], where they obtained that the DD relation is compatible with the observations at 2σ or 1σ CL respectively for the elliptical β model, and almost incompatible at 3σ CL for the spherical β model, our results suggest that the DD relation is more compatible with the observational data of galaxy cluster. Compared to the previous results from the complete ADD sample and the Union2 set (Liang et al. [40]; Meng et al. [41]), our analyses are consistent with their results.

From the bottom panel of this figure, we can conclude that the test between Hubble data and Union2.1 SNe Ia indicates that the DD relation is consistent with the observational data at 1σ CL. Figure 4 shows that the result for the test between the SNe Ia data and the combination of elliptical β model and Hubble data(upper panel) or spherical β model and Hubble data (bottom panel), and it indicates that the DD relation is consistent with the observational data at 1σ and 2σ CL respectively. We can also conclude that the results obtained are not sensitive to the method and parameterization through comparing the results obtained from different parameterizations for η(z) and methods for D L from SNe Ia data.

5 Conclusion

In this paper, we used a cosmological-model-independent method to test the distance-duality (DD) relation η(z)=D L(1+z)−2/D A (when η(z)=1, the DD relation holds), by combining the angular diameter distance D A provided by two galaxy clusters samples compiled by De Filippis et al. (the elliptical β model) [26] and Bonamente et al. (the spherical β model) [10] or comoving distances D c obtained from Hubble parameter data, with the luminosity distance D L from current largest supernovae (SNe) Ia data set (Union2.1). The η(z) is parameterized in four general forms, i.e. η(z)=1+η 0 z, η(z)=1+η 0 z/(1+z), η(z)=1+η 0 z/(1+z)2 and η(z)=1−η 0 ln(1+z), where η 0 is a constant quantifying a possible departure from the validity of the DD relation, and when η 0=0, the DD relation holds. The luminosity distances D L associated with the redshits of the observed D A or D c, is obtained with two methods, i.e., method A: binning the SNe Ia data within the range Δz=|z−z SNe|<0.005, and method B: reconstructing the D L(z) by smoothing the noise of Union2.1 data set over redshift with the Gaussian smoothing function. As for Hubble parameter, we get fistly the comoving distances D c using a usual trapezoidal rule. In a flat universe, we explored phenomenologically the expression of \(D_{\mathrm {c}}/[(1+z){\sqrt {\eta (z)}}]\) to substitute \(D_{\mathrm {c}}/[(1+z){\sqrt {\eta (z)}}]\) for D A, and the parameter η obs(z) can be expressed as η obs(z)=D L(z)2/[D c(z)(1+z)]2. Finally, we test the distance-duality (DD) relation.

Our results show that, for the test of the DD relation between the elliptical β model (the De Filippis et al. sample) [26] and Union2.1 SNe Ia data set, the DD relation is consistent with observational data at 1σ CL with both methods. While for the spherical β model (the Bonameta et al. sample [10]) the DD relation is marginally consistent at 2σ CL. For the test between Hubble data and SNe Ia from Union2.1 data set, we get that the DD relation is consistent with the observational data at 1σ CL. As for the test between the SNe Ia data and the joint of elliptical β model and Hubble data or spherical β model and Hubble data, we find that the DD relation is consistent with the observational data at 1σ or 2σ CL respectively. Compared with the results obtained by Holanda et al. [28], Li et al. [37] and Fu et al. [38], where they obtained that the DD relation is compatible with the observations at 2σ or 1σ CL respectively for the elliptical β model, and almost incompatible at 3σ CL for the spherical β model, our results suggest that the DD relation is more compatible with the present observational data. Our analyses are consistent with the ones obtained by Liang et al. [40]; Meng et al. [41] with the complete galaxy cluster sample and Union2 set. We can also conclude that the results obtained in this paper are not sensitive to the method and parameterization.