Accelerating Detailed Tissue-Scale 3D Cardiac Simulations Using Heterogeneous CPU-Xeon Phi Computing

Abstract

We investigate heterogeneous computing, which involves both multicore CPUs and manycore Xeon Phi coprocessors, as a new strategy for computational cardiology. In particular, 3D tissues of the human cardiac ventricle are studied with a physiologically realistic model that has 10,000 calcium release units per cell and 100 ryanodine receptors per release unit, together with tissue-scale simulations of the electrical activity and calcium handling. In order to attain resource-efficient use of heterogeneous computing systems that consist of both CPUs and Xeon Phis, we first direct the coding effort at ensuring good performance on the two types of compute devices individually. Although SIMD code vectorization is the main theme of performance programming, the actual implementation details differ considerably between CPU and Xeon Phi. Moreover, in addition to combined OpenMP+MPI programming, a suitable division of the cells between the CPUs and Xeon Phis is important for resource-efficient usage of an entire heterogeneous system. Numerical experiments show that good resource utilization is indeed achieved and that such a heterogeneous simulator paves the way for ultimately understanding the mechanisms of arrhythmia. The uncovered good programming practices can be used by computational scientists who want to adopt similar heterogeneous hardware platforms for a wide variety of applications.

1 Introduction

1.1 Challenges in Heterogeneous Computing

Hardware accelerators that incorporate many simple cores per chip have taken a strong hold on high-performance computing (HPC) systems. The two most prominent types of manycore accelerators are graphics processing units (GPUs) and Intel’s Xeon Phi coprocessors. Many of today’s flagship supercomputers [28] are heterogeneous clusters that consist of both multicore CPUs and manycore accelerators.

In particular, the present paper focuses on Intel’s first-generation Xeon Phi coprocessor that adopts the many-integrated-core architecture. Its theoretical peak double-precision floating-point capability is calculated as 16 times the number of cores times the clock frequency. For example, the 1.053 GHz 60-core 5110P coprocessor has $16\times 60\times 1.053=1011$ GFLOPs as its peak capability in double precision [12]. Here, the factor of 16 is due to the 512-bit vector length, which has space for eight double-precision values, together with the fact that two of the four hardware threads per core can work simultaneously on floating-point operations. In other words, the peak performance assumes using all the cores and full vectorization capability.

However, with the tremendous theoretical computing power of the Xeon Phi coprocessors come great programming challenges. In addition to effectively using the large number of hardware threads, the single-instruction-multiple-data (SIMD) vectorization capability of each thread must be utilized as much as possible. The former is typically achieved by careful OpenMP programming, or in combination with of a small number of MPI processes. SIMD vectorization, which can ideally boost the double-precision performance by a factor of 8, is either automatically delivered by the compiler for simple loops of calculation, or manually achieved by painstakingly inserting special intrinsic instructions [14].

Another factor that cannot be ignored in a heterogeneous CPU-Xeon Phi cluster is the computing power of the multicore CPUs. Currently, the number of cores per multicore CPU is relatively small, usually between 8 and 18. However, each CPU core uses a higher clock frequency and can execute operations out-of-order, which makes it much more flexible and capable than a Xeon Phi core. For non-trivial computations where SIMD vectorization is difficult to achieve and/or the performance bottleneck is memory bandwidth, a typical configuration of two 8-core Sandy Bridge CPUs can often produce comparable performance as a manycore Xeon Phi coprocessor. Thus the CPUs and Xeon Phis should ideally join forces to provide the full computing power of a heterogeneous system. With respect to programming, however, heterogeneous computing brings additional tasks, such as using a different AVX instruction set for 256-bit SIMD vectorization on CPU cores, minimizing the impact of CPU-Xeon Phi data transfers, and balancing workload division between the two hardware device types.

1.2 Detailed 3D Tissue-Scale Cardiac Simulations

Parallel computing is now widespread in computational cardiology, as in many other branches of computational science. The demand for computing power is continuously increasing, because computational cardiologists want to adopt more advanced mathematical models to simulate the heart and use higher resolutions in time and space. The arrival of heterogeneous supercomputers is welcome because of their extreme computing power. Some previous work [3, 4] focuses on speeding up the cardiac simulation process.

One of the important subjects in computational cardiology concerns arrhythmias that occur at the tissue and organ scale. Due to limited computing power, however, most of the previous studies have focused on the development of cardiac cell models of electrophysiology and calcium handling that incorporate the discrete nature of subcellular stochastic calcium release processes [11, 18, 24, 32]. These models of calcium handling and action potential are useful for studying causative and preventive mechanisms of arrhythmogenesis, which originates from the local nanoscopic level of channel and dyadic dysfunction, and develops into membrane potential abnormalities at the subcellular and cellular levels. These include delayed afterdepolarizations, early afterdepolarizations [25], and cardiac alternans [19, 20, 24].

However, extrapolating cell-level studies to understand tissue-scale or organ-scale arrhythmias is insufficient. The challenge is rather shifted from the realism of modeling to the scale of computing. A typical human heart has around $2 \times 10^9$ cells [1]. Each cardiac cell has about $10^6$ ryanodine receptors (RyRs) that are distributed over roughly $10^4$ calcium release units, which are also called dyads. Each dyad has a number of L-type channels operating stochastically in response to membrane potentials and local calcium concentrations [5]. Using a preliminary tissue-scale simulator that only makes use of multicore CPUs, we found in [15] that two 8-core Sandy Bridge CPUs need one second of wall-clock time to simulate one time step of 3000 detailed cardiac cells. Since a realistic tissue-scale simulation involves $10^7$–$10^8$ cells and needs $10^4$–$10^5$ time steps, the need for supercomputing is obvious.

2 Mathematical Models and Numerical Methods

This section briefly describes the involved mathematical models and numerical strategy, thereby providing the background knowledge needed in the following sections for discussing the various performance programming techniques on Xeon Phis and multicore CPUs.

2.1 Physiologically Detailed Cell Modeling

We adopt the multiscale model of stochastic calcium handling in a ventricular myocyte from [11]. To mimic the human cardiac ventricular tissue, we replace the electrophysiological current formulation of [11], which models a guinea pig, with the O’Hara-Rudy (ORd) model [22] of a healthy human cardiac ventricular action potential.

Fig. 1

The eight possible transitions between four states of a RyR, where the labels on the arrows indicate the probabilities of the transitions

In each cell, 10,000 calcium release units or dyads are assumed to form an internal $100\times 10\times 10$ grid. Each dyad consists of five calcium compartments: (1) myoplasm, (2) submembrane space, (3) network sarcoplasmic reticulum, (4) junctional sarcoplasmic reticulum, and (5) dyadic space. See [11] for the detailed equations and parameters. The dyadic space, in particular, contains 15 L-type calcium channels and 100 RyRs that operate stochastically. At any given time, each RyR can be in one of four states, denoted as C1, C2, C3, and O1. Figure 1 shows the possible transitions between them, which occur stochastically with probabilities that are related to the local calcium concentrations. The number of open RyRs, i.e. those having state O1, is closely connected to the calcium influx that affects a cell’s interior voltage.

The governing equations that determine the dyadic calcium concentrations can be written as the following ordinary and partial differential equations:

$$\begin{aligned} ca_{\mathrm {ds}}= & {} (J_{\mathrm {rel}} + J_{\mathrm {lca}} + ca_{\mathrm {ss}} / \tau _{\mathrm {efflux}})\times \tau _{\mathrm {efflux}} \end{aligned}$$

(1)

$$\begin{aligned} \frac{d\, ca_{\mathrm {ss}}}{dt}= & {} \overline{B_{\mathrm {ss}}}\left( J_{\mathrm {NCX}} + J_{\mathrm {diff\_myo\_ss}} + J_{\mathrm {diff\_ds\_ss}}\right) \end{aligned}$$

(2)

$$\begin{aligned} \frac{d\,ca_{\mathrm {JSR}}}{dt}= & {} \overline{B_{\mathrm {JSR}}}\left( J_{\mathrm {rel}} + J_{\mathrm {diff\_NSR\_JSR}}\right) \end{aligned}$$

(3)

$$\begin{aligned} \frac{d\,ca_{\mathrm {NSR}}}{dt}= & {} J_{\mathrm {up}} - J_{\mathrm {leak}} - J_{\mathrm {diff\_NSR\_JSR}} \end{aligned}$$

(4)

$$\begin{aligned} \frac{d\,ca_{\mathrm {myo}}}{dt}= & {} \overline{B_{\mathrm {myo}}}\left( J_{\mathrm {cab}} + J_{\mathrm {pca}} + J_{\mathrm {NCX}} - J_{\mathrm {up}} + J_{\mathrm {leak}} - J_{\mathrm {diff\_myo\_ss}}\right) \end{aligned}$$

(5)

$$\begin{aligned} Ca_{\mathrm {ds}}= & {} (J_{\mathrm {rel}} + J_{\mathrm {lca}} + Ca_{\mathrm {ss}} / \tau _{\mathrm {efflux}})\times \tau _{\mathrm {efflux}} \end{aligned}$$

(6)

$$\begin{aligned} \frac{\partial Ca_{\mathrm {ss}}}{\partial t}= & {} \overline{B_{\mathrm {ss}}} \left( J_{\mathrm {NCX}} + J_{\mathrm {diff\_myo\_ss}} + J_{\mathrm {diff\_ds\_ss}} + D_{Ca}\nabla ^2Ca_{\mathrm {ss}}\right) \end{aligned}$$

(7)

$$\begin{aligned} \frac{d\,Ca_{\mathrm {JSR}}}{dt}= & {} \overline{B_{\mathrm {JSR}}}\left( J_{\mathrm {rel}} + J_{\mathrm {diff\_NSR\_JSR}}\right) \end{aligned}$$

(8)

$$\begin{aligned} \frac{\partial Ca_{\mathrm {NSR}}}{\partial t}= & {} J_{\mathrm {up}} - J_{\mathrm {leak}} - J_{\mathrm {diff\_NSR\_JSR}} + D_{\mathrm {SR}}\nabla ^2 Ca_{\mathrm {NSR}} \end{aligned}$$

(9)

$$\begin{aligned} \frac{\partial Ca_{\mathrm {myo}}}{\partial t}= & {} \overline{B_\mathrm {myo}}\left( J_\mathrm {cab} + J_\mathrm {pca} + J_\mathrm {NCX} - J_\mathrm {up} + J_\mathrm {leak} - J_\mathrm {diff\_myo\_ss}\right. \nonumber \\&+ \left. D_{Ca}\nabla ^2Ca_{\mathrm {myo}}\right) \end{aligned}$$

(10)

Here, $J_{\mathrm {rel}}$ is the release flux through RyRs into the dyad, and $J_{\mathrm {lca}}$ is the flux through L-type calcium channels into the dyad. $\tau _{\mathrm {efflux}}$ is the time constant of diffusion between the dyadic space and the submembrane space. $J_{\mathrm {NCX}}$ is the flux through the Na-Ca exchange current into the submembrane space. $J_{\mathrm {diff\_myo\_ss}}$ is the diffusive flux between myoplasm and submembrane space, while $J_{\mathrm {diff\_ds\_ss}}$ is the diffusion flux between the dyadic and the submembrane space. $J_{\mathrm {diff\_NSR\_JSR}}$ is the diffusion flux between NSR and JSR. $J_{\mathrm {up}}$ is the SR uptake into NSR by the SR pump and $J_{\mathrm {leak}}$ is the leak flux from NSR into the myoplasm. $J_{\mathrm {cab}}$ is the flux through the background calcium current. $J_{\mathrm {pca}}$ is the flux through the sarcolemmal Ca pump. The submembrane space is buffered instantaneously by SR and SL buffers. The instantaneous buffering factor is given by $\overline{B_{\mathrm {ss}}}$. $\overline{B_{\mathrm {JSR}}}$ is the buffering factor for JSR by calsequestrin (CSQN) and $\overline{B_{\mathrm {myo}}}$ is the instantaneous buffering factor in myoplasm due to calmodulin (CMDN) and troponin (TRPN). Further details about the various parameters and values can be found in [11].

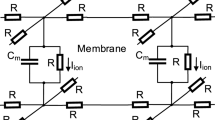
2.2 Tissue Modeling

A slab of cardiac tissue is modeled as a 3D uniform grid of cells. To simulate the tissue-scale electrical activity, we use the following monodomain model:

$$\begin{aligned} \frac{\partial V_{m}}{\partial t}=\frac{-I_\mathrm {ion}}{C_{m}} + D_{\mathrm {vol}}\nabla ^2V_{m}, \end{aligned}$$

(11)

where $V_{m}$ is the membrane potential, $I_\mathrm {ion}$ is the ionic current provided by the underlying multiscale cell model of calcium handling, $C_{m}=1\mu F$cm$^{-2}$ is the membrane capacitance, $D_{\mathrm {vol}}=0.2$ mm$^{2}$/ms is the voltage diffusion coefficient.

2.3 Numerical Strategy

Stochastic methods are used to monitor the number of open L-type calcium channels and RyRs, to be detailed in Sect. 3.3. Explicit time integration is used to solve all the differential equations (2)–(11). The involved diffusion terms are discretized with centered finite differences. For the monodomain equation (11), an operator-splitting approach [23] is used. This means that the diffusion terms are treated separately from the $I_\mathrm {ion}$ term, where the latter is computed by summing up the total ionic currents obtained from solving the ordinary differential equations in the ORd model.

The overall computational procedure is carried out as a time loop, where the work of each time step consists of first looping over all the cells, and then stepping forward the monodomain equation (11). The computational work per cell is in form of another loop that goes through all the dyads one by one, plus the subsequent inter-dyad diffusion computations. This innermost loop in the pseudo code in Fig. 2 contains the most time-consuming computations, due to the large number of dyads per cell. Thus, optimizing these computations is crucial in the development of an efficient implementation.

Fig. 2

Pseudo code of the overall computational procedure

3 Implementation Strategy

The primary aim of our heterogeneous implementation is to incorporate the computational power of Xeon Phis. To this end we extended an existing multi-node CPU implementation [15] significantly with respect to both the parallelization strategy and the SIMD performance.

3.1 Target Hardware

The Intel Xeon Phi coprocessor is a novel hardware accelerator based on the manycore design principle. Unlike traditional multicore CPUs which feature a small number of powerful cores, it is composed of a large number of relatively slow and simple cores with wide vector units. This design makes the device ill-suited for sequential programs, but very powerful for highly parallel workloads.

Our target platform is a multi-node system where each node is equipped with at least one Xeon-Phi coprocessor, in addition to one or more multicore CPUs. The most well-known examples of such a heterogeneous hardware platform are Stampede [26] and TianHe-2. The latter is currently the second fastest system on the TOP 500 list of supercomputers [28]. For our experiments, we have used the Xeon Phi enhanced nodes of Abel [29], a supercomputer operated by the University of Oslo.

To use such systems effectively, we must distribute our computations on four different levels of parallelism: between compute nodes, between CPU and Phi compute devices on the same node, between cores on the same device, and between the SIMD lanes in every core since each core is equipped with SIMD vector units that allow it to perform multiple operations at the same time.

3.2 Heterogeneous Multi-Level Parallelization

Our computational problem allows decompositions at multiple levels. Among these, the top level is the cardiac tissue which is represented as a 3D cartesian grid of cardiac cells. Each compute node is thus assigned a cuboid subdomain containing an equal number of cells. The cell voltage values $V_m$ are exchanged along the faces of the subdomains during every time step using a standard halo exchange approach over MPI [17].

Within each compute node, we further divide its assigned cells between the CPU host and the accelerator(s). However, we do not use a geometric partitioning within the subdomains. This allows for more flexibility in load balancing between CPU and accelerators, independent of the subdomain shape. Thus, each accelerator is assigned a number of cells that is commensurate with its relative computational speed, limited only by the subdomain size. During each time step, the accelerator communicates the computed voltages for all of these cells to the CPU. Doing so is expected to yield the best performance, since load imbalance is expensive due to the computationally heavy nature of the code, while intra-node communication is cheap.

At the cell level, we have two possible parallelization strategies. The first is a straightforward assignment of cells to cores, which means that all computations performed for a cell remain on a single core. Alternatively, we can split computations for the 10,000 calcium release units over the cores of a device. This greatly increases flexibility and can thus lead to better load balancing. However, due to the fact that parts of the cell computations have to be performed sequentially, it can lead to some cores remaining idle during part of the computation. We have performed experiments to quantify this tradeoff, the results of which are discussed in Sect. 7.2.

In both cases, we use the SIMD vector units to process four (CPU) or eight (Xeon Phi) calcium release units in parallel on each core. This vectorization is key to obtaining efficient simulation code. In the following sections, we will give a detailed description of the techniques used for doing so.

3.3 Binomial Distributions

A salient feature of our model is the stochastic simulation of RyR state transitions. As described in Sect. 2.1, the dyadic space contains 100 RyRs, each of which can be in one of four states at any given time. In [15], it was shown that sampling from a number of binomial distributions equal to the number of state transitions is superior to the straightforward alternative, i.e. performing two Bernoulli trials per RyR.

The probability mass function of the binomial distribution B(n, p) which gives the probability of having k successes in n trials with individual probabilities of success p is defined as follows:

$$\begin{aligned} f(k,n,p)=Pr({X}\le {k})=\left( {\begin{array}{c}n\\ k\end{array}}\right) p^k(1-p)^{n-k} \end{aligned}$$

(12)

For each of the four states in Fig. 1, we denote the number of RyRs in state i by $x_i$. We use j and l to denote the two neighbouring states of i, as shown in Fig. 1. Now, for each state i, we sample once from a binomial distribution $B(n,p_{ij})$ where $n = x_i$, and $p_{ij}$ is the transition probability from state i to j computed in the current time step. We thus obtain a number $k_{ij}$ of RyRs that transition to j in the current time step. Then, for each state i we simulate the second transition from i to state l by sampling from $B(n-k_{ij},p_{il}/(1-p_{ij}))$, thus obtaining $k_{il}$. We use $n-k_{ij}$ since only one of the two possible transitions can happen for any RyR, and $p_{il}/(1-p_{ij})$ to obtain an equivalent transition probability relative to $n-k_{ij}$ from $p_{il}$, which is correct in relation to n. Alternatively, one could use sampling from a multinominal distribution, but this would certainly be computationally more expensive since there are only two transitions from each state. The RyRs for which neither transition happened remain in the original state. We add the RyRs that transitioned from neighboring states to obtain the final number of RyRs in each of the four states. Now, the number of RyRs in each state in the next time step $t+1$ is:

$$\begin{aligned} x_i(t+1) = x_i(t) - k_{ij}(t) - k_{il}(t) + k_{ji}(t) + k_{li}(t) \end{aligned}$$

(13)

While the binomial distribution can be approximated using the normal and Poisson distributions, which are e.g. used in [24], we opt against sacrificing accuracy and instead design an optimized implementation, details of which are discussed in Sects. 4 and 5.

4 CPU Code Optimization

Our CPU implementation follows the principles outlined in [15]. Based on that, we performed additional optimizations which apply to both CPU and Xeon Phi.

4.1 Mixed Vectorization

One of the important architectural features of modern processors are wide SIMD vector units. This implies that in order to make full use of their capabilities, all compute-bound parts of the code must be vectorized if possible. Modern compilers are capable of automatically vectorizing simple loops, but fail to do so in more complex cases. On the other hand, if the complexity of the code is very high, manual vectorization of the entire loop, while possible, is prohibitively expensive in terms of coding effort and thus not advisable. In our case, several parts of the innermost dyad-loop (see Fig. 2) contain conditional statements, making the compiler unable to vectorize the loop on its own. A feasible solution is to split the the dyad-loop into sections of two different types. The first type are arithmetic sections which contain expensive computations, but have a trivial control flow (the first, third and fifth statements of each dyad-iteration in Fig. 2). The second type on the other hand is characterized by a complex control flow but relatively inexpensive computations. These sections will be labeled as conditional. Doing so results in multiple smaller loops which perform the same calculation for all dyads, rather than completing computations for one dyad at a time. Figure 3 illustrates this change in control flow.

Fig. 3

Splitting up the original dyad loop from Fig. 2 into five smaller loops, for the purpose of enabling mixed automatic and manual vectorization

The main disadvantage of this technique lies in the reduced data locality when computational loops are split. Instead of performing the entire computation for one element, a partial computation is performed for all elements which implies that intermediate results (such as probabilities for RyR state transitions in our code) must be written to memory and retrieved later, which puts additional pressure on the memory bandwidth. Figure 3 illustrates this change in control flow in our code. It is often beneficial to manually vectorize smaller arithmetic sections and merge them with conditional sections in order to overcome the need for additional memory transfers. We perform a detailed analysis of the benefits of this technique in Sect. 7.

4.2 Binomial Distribution Sampling

Due to the large number of binomial samples used in the computation, using an optimized implementation is crucial for performance. In [15], a basic implementation of the binomial sampling technique was described along with several optimizations that save time when computing the actual distribution can be avoided. Figure 4 shows the pseudocode:

Fig. 4

Core implementation of the binomial distribution sampling function

Since the value of n will be at most 100, we can compute the binomial coefficients prior to the actual simulation and store them in BC_table. In order to further save time, we compute the coefficients pknk and p1p at the start of the function. The distribution function F(k, n, p) is then computed iteratively by applying a sequence of multiplications and subtractions to $F(k-1,n,p)$ and subtracting from randval using the precomputed coefficients. Thus, computation stops when F(k, n, p) effectively exceeds randval and outputs the current iteration number k.

This means that lower results for k take less compute time, which is desirable since most transition probabilities and thus sampling results are low. For very low transition probabilities, we first check whether $k>0$ is possible for the given value of randval by comparing against a precomputed threshold, thereby potentially saving one iteration of the function. In addition, as shown in Fig. 1, transitions from the O1 to the C1 state, and those from the C3 to the C2 state have constant probability, which means that for these cases F(k, n, p) can be precomputed. Doing so further cuts down the number of actual sampling function evaluations.

The AVX vector instructions of the Sandy Bridge CPU lack several crucial instructions to select and compare elements within a vector. Therefore, in the CPU code binomial sampling is not vectorized.

4.3 Use of Precomputed Values

The computation of each dyad in a cell involves a large number of variables, some of which vary from dyad to dyad, whereas others remain constant within each cell. Considering that the number of dyads in our detailed cell model is 10,000, pre-calculating the cell-constant variables outside the innermost for-loop in Fig. 2 yielded substantial performance gains, as discussed in [15]. However, further improvements are possible. A straightforward implementation of the equations in Sect. 2.1 yields a large number of expressions that compute partially the same values. In these cases, solving expressions for cell-constant variables reveals redundant operations. These can be avoided by computing intermediate values that are reused, at the expense of register pressure. Whether doing so is worthwhile depends on the number of times such a value is reused, which is generally between two and four in most parts of the code, and on the type of operations performed. For additions and multiplications, this only pays off if the value is reused many times. However, 64-bit divisions are comparatively expensive on the Sandy Bridge CPU due to their long latency and because AVX vectorization can only double their performance [31]. Therefore, avoiding even a single division in the code in this manner always pays off. While the Xeon Phi does not suffer from this problem, it still takes an order of magnitude more cycles for a division than it does for a multiplication [10]. By the same token, replacing divisions with equivalent multiplications yielded significant performance gains. While these are well known techniques, neither optimization was performed automatically by the compiler in an adequate manner.

5 Xeon Phi Code Optimization

Despite the strong similarities between the x86 CPU and the Xeon Phi, porting high performance code between the two devices is not an easy task. Low sequential performance, long vector units, and higher computational vs. memory performance lead to several challenges that must be addressed when using the device. In addition to the points discussed in the last section, the following issues were addressed in the design of the Xeon Phi code.

5.1 Random Number Generation

We use the standard function vdRngUniform provided by the Intel MKL library [13] to generate all required random numbers at the beginning of every time step. Performance of this function on the Xeon Phi is quite low compared to the CPU, being almost 40 times slower on a single core (see also Fig. 6). In addition, unlike on the CPU, random number generation does not scale perfectly on the Xeon Phi when increasing the number of threads, making it one of the main performance bottlenecks on the accelerator.

Since vdRngUniform is a predefined library function, we can perform no further optimizations on it. However, we mitigate its impact by skipping over all state transitions where the number of channels in the starting state is 0, thereby conserving random numbers. To do so, we keep a count of the random numbers used in the current time step. At the beginning of the subsequent time step, only the random numbers that were actually consumed by state transitions must be replaced. Due to eight possible state transitions for RyR channels and two additional transitions for the L-type channels, up to ten random numbers per dyad can be used in every time step. The above technique cuts the average number approximately in half.

5.2 Automatic Vectorization

Since the Xeon Phi relies heavily on its 512-bit vector length to attain high computational performance, successful vectorization of the arithmetic sections is paramount to rendering the device competitive. Since all relevant variables use double precision, vectorization can provide a fourfold speedup on the CPU and an eightfold speedup on the Xeon Phi. The Intel icc compiler is able to perform this vectorization automatically.

For the intracellular diffusion computations, we found that automatic vectorization is also beneficial since the instructions to be executed are not data-dependent and thus the stencil computation can avoid using conditional statements. However, since these operations are always memory bound, the expected speedup is lower than for the purely arithmetic operations. For the Sandy Bridge processors we attempted to improve performance by using manually vectorized code.

5.3 Manual Vectorization of Binomial Sampling

As discussed in Sect. 4.1, a crucial part in obtaining proper vectorized code is to break up the dyad loop into arithmetic and conditional sections. The conditional sections, which mainly perform sampling from binomial distributions, cannot be vectorized by the compiler. We thus aim to develop a manually vectorized version of the sampling algorithm in order to benefit from the SIMD capabilities of the Xeon Phi. Of course, the irregularity of the computation makes it impossible to obtain the full eightfold speedup, but since the vector units are available on the device, they should be used whenever possible if any speedup can be obtained from doing so.

For the vectorized version which is shown in Fig. 5, we follow the same strategy as described in Sect. 3.3, but process sampling for 8 dyads simultaneously, reducing their input random number by the probability of their current f(k, n, p) value. Vector versions of the coefficients PKNK and P1P are initialized as before. Precomputed binomial coefficients are again stored in BC_table, although it is also possible to compute them on the fly with approximately the same performance. The key to vectorizing the code despite the conditional statements lies in the powerful mask instructions. They allow the SIMD unit to apply vector instructions only on some elements of the vector, which are determined by a bit mask.

Here we use Vector_mask_compare and Vector_mask_add intrinsics to determine for which of the dyads the input random number remains positive, and increase their counter k which determines the output value for the dyad. Once a dyad’s input random number falls to 0 or less, it is removed from consideration via the mask, i.e. the Vector_mask_add will no longer increase its output value, thereby ensuring correct sampling results.

Fig. 5

The vectorized version of the binomial sampling computation. Capital letters denote vector variables. The principal difference to the scalar version lies in the use of MASK to increase the output value for some vector elements, instead of using a while loop

The main problem with this approach is that the computation runs until the last sampling is finished. This means that the speedup depends on the ratio between the sampling results of the 8 dyads within one vector. In case they all happen to be identical, we can obtain a perfect eightfold speedup, but in practice this will rarely be the case. In addition, testing if the MASK value is 0, which means that all sampling operations are complete in order to allow early termination of the loop, is expensive, especially due to lack of branche prediction on the Xeon Phi. We settled for a compromise where we perform this test after every eight iterations of the for loop, and terminate the loop if all eight samplings are finished.

Note that sampling from a binomial distribution is not very amenable to vectorization, and an implementation that stochastically determines the state of every channel individually would vectorize better thanks to the compare intrinsics available on the Xeon Phi. However, the amount of random numbers required for doing so renders this approach prohibitively expensive, as evidenced by the results shown in [15]. This is even more problematic on the Xeon Phi where random number generation is disproportionately more expensive.

6 Experimental Setup and Hardware

The Intel Xeon Phi coprocessor is a novel hardware accelerator based on the manycore design principle. Unlike traditional multicore CPUs which feature a small number of powerful cores, it is composed of a large number of relatively simple cores which are connected to each other and to the device memory via a ring bus. Each core features 64 KB of level 1 cache and 512 KB of level 2 cache. All caches maintain coherency among the cores. We use the 5110P model that is equipped with 60 cores, one of which is used by the operating system and thus not available for our computations. Each core can run up to four hardware threads concurrently, but a given thread is never run in two consecutive clock cycles. This means that effectively 118 threads can run in parallel at half the clock frequency of 1.053 GHz. When using 236 threads, i.e. four per core, each thread effectively runs for half the available processing resource, which has an effect that is similar to hyperthreading. The device is equipped with 8 GB of DDR5 device memory, featuring a theoretical memory bandwidth of 320 GB/s [12]. However, even under ideal circumstances, at most half of that is available for applications [10].

Our test system is Abel [29], a supercomputer operated by the University of Oslo. Abel has four accelerated compute nodes which are equipped with dual Intel Xeon E5-2670 (Sandy Bridge) processors and two Xeon Phis of model 5510P. Each node also has 16 CPU cores running at 2.6 GHz, and each core features 64 KB of level 1 cache and 256 KB of level 2 cache. A core can run two hardware threads using hyperthreading. Unlike the Xeon Phi, each Xeon CPU has 20 MB of L3 cache which is shared among the cores. The interconnect between the nodes is FDR (56 Gbps) Infiniband. We use Intel’s icc compiler 15.1.0 for compilation and Intel MPI 5.0.2 for internode communication.

We spawn only one MPI process per node. This process is controlled by the CPU. To launch Phi computation and to communicate between accelerator and host, we use the low-level COI and SCIF interfaces [8]. While these are not particularly user-friendly or easy to program, doing so gives us full control over the timing of communication and computation. The Xeon Phi accelerators are thus used in an offload strategy, even though we do not employ the directive based offload mode offered by the Intel compiler. Alternatively, it would be possible to use MPI at this level. However, doing so does not allow the same fine-grained control over the workload distribution, which is quite important for attaining high performance since the Xeon Phi is rather sensitive to load balancing problems due to its wide parallelism of at least 118 threads.

It is also possible to parallelize over the dyads, i.e. by using OpenMP to split computations of the 10,000 calcium release units over all cores of a device. While this increases flexibility and thus can lead to better load balancing, the total impact on the performance can be negative due to the fact that parts of the cell computations have to be performed sequentially. Thus, we do not use this method and compute one cell per thread in parallel, except in Sect. 7.2.

On each node we obtain the intra-node cell distribution by performing a 1D decomposition of the subdomain cells according to their local index value, thus ignoring their spatial relations. The key to this decomposition is an input variable PHIspeedFactor, which we set to the relative measured performance of the Phi with respect to the CPU. On our test system, we set PHIspeedFactor to 1 because we obtained performance parity between the devices after extensive optimization on the Xeon Phi of our test system. For other systems, the correct value depends on the Phi model used and on the performance of the installed CPUs. The resulting number of cells to be computed on the Xeon Phi is then rounded to multiples of 236 ¹ to ensure load balance on the Xeon Phi cores. Thus, when using two Phis per node, each Phi and the CPU process roughly one third of the total cells assigned to the node.

As discussed in Sect. 3, this method has the disadvantage that all cell voltage values, not only those of the boundary cells, must be communicated. However, considering that intra-node communication is comparatively fast, and calculating a single time step even for one cell requires significant computational work, this tradeoff clearly favors better load-balancing at the (almost insignificant) cost of a higher intra-node communication volume.

As a consequence, voltage diffusion between the cells is performed by only the CPUs using Jacobi iterations and a standard 7-point stencil. This technique has been studied widely [7, 15], and thus we do not discuss it any further here. While it is possible to overlap communication and computation here, our implementation does not do so due to the extremely limited potential gains.

For all the experiments, a fixed time step size of 0.05 ms is used at both the tissue level and the cell level. For the tissue-scale simulations, we chose a fixed spatial mesh resolution of 0.5 mm to discretize the diffusion terms in (11). In all experiments we run 10,000 time steps which amounts to simulating one cardiac beat of 500 ms. The cells are stimulated at $t=50$ ms. When showing timings for separate sections of the code, we always show the cumulative time the section takes for 10,000 time steps. The number of cells computed varies by experiment, but each cell always has 10,000 dyads.

7 Experimental Results and Analysis

We perform a series of experiments to assess the performance of our heterogeneous code. We begin by studying the performance improvements obtained through our code optimizations. Next, we investigate additional aspects that influence device performance. We conclude this section with the results for scalability of the multi-node system.

7.1 Vectorization

The primary goal of our optimizations is to improve the single-thread performance of the Xeon Phi. The main tool for doing so is the correct use of vectorization. The original CPU code used in [15] cannot benefit from automatic vectorization at all because it mixes arithmetic and conditional sections within the same loop. Separating the code sections as shown in Sect. 4.1 enables the compiler to automatically vectorize the arithmetic sections. We then use manual vectorization on the conditional sections. Figure 6 shows the effect of these optimizations measured on a single cell. The experiment is run on a single core. In addition, we show results for reducing the amount of random numbers generated per time step here.

Fig. 6

Performance improvement of the individual functions in the dyad computations due to three optimization techniques when using a single Xeon Phi thread. The three optimizations are applied cumulatively. Thus, the values for manual vectorization contain the improvements due to automatic vectorization, and the random number reduction method reflects the sum of all three optimizations. Improvement shows the sum of reductions in running time over all code sections due to each optimization. Equivalent CPU performance is the time a CPU core takes for a section, multiplied by the ratio of threads (i.e. 118 to 16). This is done in order to highlight the relative strengths and weaknesses of the compute devices

Clearly, enabling automatic vectorization gives the most effective improvement. For the CPU performance approximately doubled compared to our previous results reported in [15]. Similar can be attained by manually vectorizing the arithmetic sections, but doing so is time-consuming and provided no benefit. Manual coding does allow vectorization of the conditional sections though.

Fig. 7

Compute time for the cell computation and for the entire time step including intercellular diffusion on the CPU and Xeon Phi using dyad-level OMP parallelization. Clearly, this type of parallelization cannot benefit from hyperthreading. Furthermore, the additional effort, which is negligible on the CPU, renders dyad-level parallelization uncompetitive on the Xeon Phi. In contrast, the cell-level parallelization scales better, benefits from hyperthreading, and attains parity between CPU and Phi (Results given only for entire computation)

Overall, the Calcium concentration computation section sped up by a factor of 8, which is the maximum set by the vector length. Even though it is a purely arithmetic section L-type probability calculation attained a factor of only 6. The reason for this lies in the fact that it contains few calculations but sizeable memory transfers, and thus it is most likely memory bound. The intracellular diffusion sped up fivefold. It is quite amenable to vectorization, but the speedup is mostly an artifact of the low performance of a single Xeon Phi core. Because this section is also memory bound, it will not scale perfectly if it is run by many threads at the same time, as discussed in Sect. 7.2. Finally, the speed of the Ryr probability calculation quadrupled. We found that the principal reason inhibiting further speedup is the use of a single exponential function, which takes up the majority of the compute time there and cannot be vectorized perfectly.

For the conditional sections, our expectations are different. Performance is data dependent here because the computation time of a single sampling of a binomial distribution is data dependent, and in the vectorized version the time taken by each group of eight samples is determined by the one that finishes last. Thus, the speedup depends on how homogeneous the values of n, p, and the random numbers in each group of 8 dyads are (see Sect. 3.3 for details). For the L-type channels, we have $n=15$ for every dyad in a cell. Consequently, we observe a large speedup due to vectorization there, about a factor of 5. On the other hand, states of the RyR channels vary widely, and thus we observe a speedup of only $18\,\%$ there. Thus, the improvements due to the manual vectorization are much smaller than those obtained from automatic vectorization on the arithmetic sections. Finally, we see that saving unused random numbers cuts the time taken by random number generation by half.

While the performance of the entire device cannot be inferred from such single-core measurements due to imperfect scaling, it clearly shows which computations are relatively more time consuming on the Phi than on the CPU.

7.2 Dyad Level Parallelization

Due to the large number of dyads per cell, there are two different possibilities of using OpenMP shared memory parallelization. The first method parallelizes over the cells, assigning each cell entirely to a single thread. The second is more fine grained. It distributes the computation of the dyads among the cores. This has the obvious advantage of enabling more fine-grained load balancing. However, in our experiments it turned out to be highly inefficient, being overall $101\,\%$ slower on the CPU and $345\,\%$ slower on the Xeon Phi. We therefore adopt cell based OpenMP parallelization as the standard, but we study the reasons for this discrepancy in performance. Figure 7 shows the total compute time for dyad level parallelization.

Clearly, the additional overhead during every time step which is run sequentially is quite significant on the Xeon Phi, but not on the CPU. More importantly however, placing two threads on each core, i.e. using hyperthreading, is detrimental on the CPU, reducing the performance by $46\,\%$. Going from 118 to 236 threads has no effect on the Xeon Phi performance. On the other hand, when using cell based parallelization, performance due to hyperthreading increased by $25\,\%$ on the CPU and $36\,\%$ on the Xeon Phi. Note that the term hyperthreading is only used for the CPU by the vendor, and implies running two hardware threads per core. However, doing so on the Xeon Phi is not equivalent since using only one thread per core causes the cores to idle in every second clock cycle. Running four threads per core creates an equivalent situation where every thread shares the effectively available compute units with one other thread.

Fig. 8

Distribution of the compute time among the code sections when using dyad-level OMP parallelization on the Xeon Phi. Clearly, the main detriment to scaling performance is the intracellular diffusion

However, the principal detriment to performance in the dyad-level parallelization is the intracellular diffusion. Figures 8 and 9 show the distribution of running time among the different sections of the compute code. The percentage of the diffusion part increases since it is memory bound, and thus cannot be expected to scale with the number of threads. When using cell based parallelization, the same accesses to memory are distributed over a longer stretch of time since the cell computations are not synchronized, thus making more efficient use of the available memory bandwidth.

Fig. 9

Distribution of the compute time among the code sections when using dyad-level OMP parallelization on the CPU

Fig. 10

Performance of weak scaling tests of tissue level simulations

On the other hand, Fig. 9 clearly shows the impact of hyperthreading as the difference between the 16 and 32 thread columns. The conditional sections are significantly accelerated, while diffusion is slowed down in comparison. This shows that partially hiding latency via hyperthreading is crucial in the latency-bound conditional sections of the code.

7.3 Heterogeneous Scaling

We perform a weak scaling experiment for a simulation time of 400 ms, using up to four Phi-accelerated nodes and 10,000 dyads per cell as usual. In this experiment, the PHIspeedFactor parameter was set to 1. We used grids of size $236\times 2\times 3$ per node. Using multiples of 236 for the grid size is the best case for the Xeon Phi, since this matches the number of available threads. The actual grid dimensions have no effect on performance however. While the code can deal with an arbitrary number of Phis per node, the number of cells per Phi is limited to about 2000 due to the limited device memory. Knights Landing, the second generation of Xeon Phi [16], no longer has this limitation.

On our test system, there are two Phis available per node, and we also study ”strong” scaling when varying the number of Phis per node. Figure 10 shows the results. Performance is given in cell computations per second. The total number of cell computations performed is 4000 times the grid size.

Fig. 11

Activation pattern in a 3D human ventricular tissue

Fig. 12

Action potentials, electrophysiological currents and calcium concentration (Ca) values in a 3D tissue-center cell at steady state. a Membrane voltage ($V_m$). b Fast Na current ($I_{Na}$). c L-type Ca current ($I_{CaL}$). d Slow component of delayed rectifier K current ($I_{Ks}$). e Rapid component of delayed rectifier K current ($I_{Kr}$). f Na-Ca exchange current ($I_{NaCa}$). g Ca in the dyadic space ($Ca_{dyad}$). h Intracellular Ca in the myoplasm ($Ca_i$) averaged over 10,000 dyads. i Simulated line-scan image of $Ca_i$ along the long-axis of the myocyte and j Junctional sarcoplasmic reticulum concentration (JSR) averaged over 10,000 dyads

Clearly, the scaling is essentially perfect, which is to be expected due to the heavy computation and light communication. While our test system lacks the number of Phi-accelerated nodes required to perform more extensive weak scaling tests, results in [15] show very good scaling on up to 128 CPU nodes using essentially the same MPI communication code. Thus, it is to be expected that the simulations will scale well even for very large systems.

8 Cardiac Simulations

In this section we present some results of our cardiac simulations under healthy conditions. The aim of this section is twofold. First, we illustrate the scientific goals of the simulation code, and second we verify consistency of the simulations with published results.

Our first experiment simulates the ventricular activation in a 3D tissue of dimensions 32 mm$\times$32 mm$\times$32 mm. Results are shown in Fig. 11. The tissue is stimulated at a plane at t = 0 ms. The excitation wavefront travels in a rectilinear manner and by 70 ms the entire tissue is depolarized. The estimated conduction velocity, 45.7 cm/s (32 mm divided by 70 ms), is consistent with the reported value of 46.4 cm/s in a human ventricular tissue [9].

Figure 12 shows the action potentials (APs), important electrophysiological currents and calcium concentration (Ca) values of the cell at the center of the 3D tissue for three steady-state beats at a cycle length of 500 ms. The AP (Panel A), currents (panel B, C, D, E and F) and Ca values (panel H, J) (averaged over 10,000 dyads) are consistent with the ORd model of the undiseased human ventricular cell [22]. Note that we have used a cell model that includes $\beta$-adrenergic effects adopted from [21]. The corresponding simulated line-scan image of intracellular Ca in the myoplasm ($Ca_i$) along the long-axis of the myocyte (panel I) and Ca in the dyadic space ($Ca_{dyad}$) (panel G) are also shown for clarity.

These results demonstrate the ability of the parallel 3D tissue simulator to predict normal ventricular activation patterns consistent with the reported values. The simulator also predicts cellular APs, Ca values and currents consistent with those reported in published human ventricular cell models.

9 Summary and Conclusions

We have shown how detailed 3D tissue simulations of electrical activity and calcium handling in a human cardiac ventricle can be implemented to run on modern hardware accelerators. The attained performance of one Xeon Phi accelerator is roughly comparable to two Sandy Bridge CPUs with highly optimized code. This is in line with many other studies that outline the difficulties in unlocking the full potential of the accelerator, e.g. [6, 30]. However, the performance attained is valuable for two other reasons. First, the second generation (Knights Landing) of Xeon Phi has shown far better performance than the first generation Knights Corner. Thus, we expect it to accelerate the manycore code beyond the CPU performance, even on the powerful new Broadwell generation of CPUs. The second reason is that some of the fastest current supercomputers such as Stampede [26] and TianHe-2 [27], and many future supercomputers such as those planned in the CORAL initiative [2], are based on Xeon Phi accelerators. Due to the immense computational power required to handle such detailed simulations, it is necessary to run them on the fastest computers available, and make full use of their computational resources.

While performing a large number of smaller code optimizations, we found that in addition to algorithmic improvements such as using binomial distributions and saving random numbers, the largest gains come from judicious use of both manual and automatic vectorization. Furthermore, correct use of nontrivial OpenMP parallelization plays a major role in obtaining high performance for complex manycore codes. These results on effective Xeon Phi performance optimization also apply to many other scientific codes.

Our future work will focus on refining and testing the simulator on large scale systems, and using it on the Knights Landing generation of Xeon Phi. We also intend to use GPUs as accelerators for which preliminary experiments have shown that performance superior to that of the CPU can easily be obtained.