Non-equilibrium Nucleation: Application to Solidification and Molar-Specific Heat Capacity of Pure Metals and Phases

Abstract

A recently derived equation for nucleation is applied for pure aluminum and Al–6 wt% Cu–3 wt% Si alloy under upward solidification conditions to calculate the surface stress, surface energy, nucleus radius, and Gibbs–Thomson Coefficient as a function of the distance from the chill. The microscopic and macroscopic fields are coupled through a Representative Elementary Volume—REV approach. As expected, higher surface energy and lower critical radius values are observed in positions in which high cooling rates occurred. Then, a nucleation model is carried out to simulate the effect of cooling rates for the molar specific heat capacity of pure Al, Fe, and Nb, and for Al₂Cu and Al₃Ni₂ phases. In the case of Nb, a set of experimental data deviates from high temperatures from theoretical predictions, probably due to high O₂ activity as previously observed for the case of pure Fe. A nucleation model for the alloy is proposed as a function of pressure, concentration, and temperature gradients in view to permit the calculation of nucleation radius, surface energy, surface stress, and Gibbs–Thomson Coefficient under non-equilibrium any given cooling rate.

1 Introduction

The coupling of theoretical predictions of thermophysical properties and the laboratory practice is a constant search to improve the quality of experimental data and allow improvements in the experimental setup [1, 2]. Thermophysical properties such as density, heat capacity, and thermal conductivity depend on the thermal history and the applied cooling rate. Considering the case of Differential Thermal Analysis (DTA) and Differential Scanning Calorimetry—DSC [3, 4], different cooling rates used provide entirely different results for molar specific heat capacity, as far as equilibrium curves are dislocated from those of low cooling rate and solute diffusion occurs partially, in a process called finite diffusion. Recently, Ferreira [5] derived for surface energy an equation from Shuttleworth [6,7,8] and Gibbs–Duhem [9, 10] equations and demonstrated the dependence of surface energy and surface stress on the nucleation radius. Several approaches have been proposed in the literature to deal with the temperature and concentration gradients [11,12,13]. By capturing the microscopic fields related to the microstructural evolution, it is possible to solve properly macroscopic transport equations. With this point of view, Ni and Beckermann proposed and applied the Volume-Averaged Method [14] and Voller the Representative Elementary Volume (REV) by solving the density concentration and energy fields in the macroscopic domain, and retrieving the local liquid concentration from the REV, by coupling local solutes concentration and the density fields [15]. Ferreira et al. applied a numerical model to solve thermal and concentration fields based on the REV approach for binary [16, 17] and ternary [18] alloys. Gibbs–Thomson Coefficient, as it relates surface energy and the bulk entropy for an undeformed surface area, can only deal with low thermal gradients close to the equilibrium. As far as the nucleation radius decreases for higher cooling rates, the surface area deformation term promotes the increase in the surface energy, changing the Gibbs–Thomson Coefficient [6, 10] considerably. The normal total thermal gradient, which comprises pressure, concentration, and temperature gradients, changes for spherical shape in the case of anisotropic thermal gradients, for instance, for any anisotropic thermal gradient in the phase-field simulation.

In this paper, a numerical solution for solidification of ternary Al–6 wt% Cu–3 wt% Si plotted against experimental data to obtain the thermal and concentration gradients, and a numerical simulation for the solidification of pure Al to be used as a reference of the behavior of the temperature gradient are carried out to a nucleation model [5] to analyze the influence of the gradients on the nucleation radius, surface stress, surface energy, and the Gibbs–Thomson Coefficient. The nucleation model is applied to the molar specific heat capacity for Al, Fe, Nb pure metals and Al₂Cu and Al₃Ni₂ phases [5, 19,20,21]. Throughout this work, the term equilibrium nucleation signifies that nucleation only occurs due to surface area creation. Meanwhile, non-equilibrium nucleation implies surface area creation and deformation, triggered by the interaction among temperature, chemical species, and pressure gradients, embodied by the expression thermal gradient, indistinctively applied to pure metals, compounds, phases, and alloys.

2 Mathematical Formulation

2.1 Secondary Dendrite Arm Spacing and Nucleation Model Derivations and Observations

Kim and Lee [22] observed the development of nucleation radius and temperature drop by applying the Gibbs–Thomson equation for nanoparticles and more recently by Wu et al. [23] have modified the Gibbs–Thomson equation to improve the melting point depression predictions. Ferreira et al., investigated the effect of transient solidification parameters on secondary dendrite arm spacing evolution predictions [24], modified an existing SDAS model previously derived by Rappaz and Böettinger [13] for equilibrium conditions to encompass the back-diffusion coefficient ${\beta }_{j}$ proposed by Voller [25], which is the Clyne and Kurz correction of the Brody and Flemings finite-diffusion approach, that predicts the finite-diffusion solidification, between Lever Rule and Scheil’s equation, assuming the following form,

$${\lambda }_{2}=5.5 {\left(M\cdot {t}_{SL}\right)}^\frac{1}{3},$$

(1)

and,

$$M=\frac{\Gamma \sum_{j=1}^{n}{w}_{j}{\beta }_{ j}}{\sum_{j=1}^{n}{m}_{j}\left(1-\frac{{k}_{ j}}{{k}_{j}+\left(1-{k}_{j}\right)\mathit{exp}\left(\frac{-\nu {\delta }_{j}}{{D}_{j}}\right)}\right)\left({c}_{f, j}-{c}_{0, j}\right)/{D}_{j}}\mathit{ln}\left[\frac{\sum_{j=1}^{n}{m}_{j}\left(1-\frac{{k}_{ j}}{{k}_{j}+\left(1-{k}_{j}\right)\mathit{exp}\left(\frac{-\nu {\delta }_{j}}{{D}_{j}}\right)}\right){c}_{f, j}/{D}_{j}}{\sum_{j=1}^{n}{m}_{j}\left(1-\frac{{k}_{ j}}{{k}_{j}+\left(1-{k}_{j}\right)\mathit{exp}\left(\frac{-\nu {\delta }_{j}}{{D}_{j}}\right)}\right){c}_{0, j}/{D}_{j}}\right].$$

(2)

Ferreira et al. [24] have compared the secondary dendrite arm spacing predictions in horizontal and upward solidification experiments for aluminum-based ternary alloys and in these experiments the cooling rates varied from 120 to 1560 °C/min. The model agreed well with the experimental scatter, however, something unexpected happened with the surface energy applied to the Gibbs–Thomson Coefficient. The surface energy for five experiments was numerically equal to the surface tension. It just could have a single explanation, due to high cooling rates, the surface energy was increasing, as it also depends on the level of strain in the new created nucleus surface area [6, 8, 10]. Its mean value was found to be very close to the surface tension value for this particular set of high cooling rates in upward and horizontally solidified samples [24].

Bobadilla et al. [11, 13] proposed an equation for SDAS dendrite radius, which is a function of the Gibbs–Thomson Coefficient $\Gamma$, liquid temperature gradient $G$, solute gradients ${G}_{C, j}$, Peclet number function $\zeta \left({Pe}_{j}\right)$, and liquidus slopes ${m}_{j}$ [12],

$$r=2\pi \sqrt{\frac{\Gamma }{\sum_{j=1}^{n} {\left(\frac{\partial T}{\partial C}\right)}_{j}{G}_{C, j} \zeta \left({Pe}_{j}\right)-G}}.$$

(3)

In the case of Bobadilla et al. [11] and Rappaz et al. [12], the function $\zeta \left({Pe}_{j}\right)$ is applied to consider the relationship between convective and diffusive solute transport. Ferreira et al.’s model [24] added the microsegregation transport to Rappaz and Boettinger’s model [13] in which the solute transport is associated with the back-diffusion parameter ${\beta }_{j}$, that influences the liquid fraction, latent heat release and, consequently, the temperature and solute gradients. The Peclet number ${Pe}_{j}$ is only present in the calculation of parameter $M$ in the effective partition coefficient ${k}_{eff, j}$ for each solute $j$.

$$r=2\pi \sqrt{\frac{\Gamma }{\sum_{j=1}^{n} {\left(\frac{\partial T}{\partial C}\right)}_{j}{G}_{C, j} - G}.}$$

(4)

Problems arise when defining the Gibbs–Thomson as considering constant surface energy ${\gamma }_{0}$,

$$\Gamma =\frac{{\gamma }_{0}}{{\nabla \text{S}}_{\forall }},$$

(5)

that contradicts the surface–stress/surface–energy relationship derived from Gibbs–Duhem’s and Shuttleworth’s equations [9, 10, 26], and gives the strain $\varepsilon$ dependence of the surface energy $\gamma \left(\varepsilon \right)$. At a constant temperature $T$ and chemical potential $\mu$, for non-isotropic solid,

$${s}_{\alpha \beta }=\gamma {\delta }_{\alpha \beta }+{\left.\frac{\partial \gamma }{\partial {\varepsilon }_{\alpha \beta }}\right|}_{T,\mu }.$$

(6)

The isotropic form for of the surface stress, considering ${s}_{\alpha \beta }=s {\delta }_{\alpha \beta }$, is given by

$$s=\frac{\gamma \left(\varepsilon \right)A\left(\varepsilon \right)-{\gamma }_{0}{A}_{0}}{\varepsilon { A}_{0}}.$$

(7)

Gurtin and Murdoch [8] stated that whenever a new surface is created it gives rise to strain in the interior of the crystal, confirming the surface area creation and deformation terms in the superficial energy change equation [10]. The authors solved surface stress for a sphere of radius $a$ considering uniform pressure. As the radius decreases by $da$, the surface stress increases by $\frac{d\sigma }{d\varepsilon }$, and so does the strain $d\varepsilon$. By calling Shuttleworth’s equation, an increase in strain will cause an increase in the surface energy by $\frac{d\gamma }{d\varepsilon }$. Therefore, the Gibbs–Thomson Coefficient must consider the increase in the surface energy triggered by both the rise in the stress level and the decrease of the nucleus radius by $da$.

$$\Gamma \left(\varepsilon \right)=\frac{\gamma \left(\varepsilon \right)}{{\Delta \text{S}}_{\forall }}.$$

(8)

Rappaz et al. [12], derived an equation to describe the dependence of nucleus radius on Gibbs–Thomson Coefficient, the temperature and concentration gradients, and a Peclet function to correct solute gradients by the diffusion mean path, which dislocates the solution from the equilibrium (Lever Rule) to a level of finite-diffusion solidification based on the Eq. 3

$$\frac{4{\uppi }^{2}\Gamma }{{r}^{2}}+\frac{2}{\text{r}}\sum_{i=1}^{2}\frac{{Pe}_{i} {m}_{i}{C}_{0,i}\left(1-{k}_{i}\right)\xi \left({Pe}_{i}\right)}{\left[1-\left(1-{k}_{i}\right)\right]Iv\left({Pe}_{i}\right)}+G=0.$$

(9)

The Gibbs–Thomson Coefficient is not constant; it depends on the nucleus radius $r$, the level of strain, and the surface energy. Ferreira et al. observed the dependence on the high cooling rate of the surface energy [24]. In 2021, Ferreira has derived the surface energy as a function of surface stress. The author has found that the surface energy value, for the case of pure Ag, Al, Cu, Fe, Ni, and other metals, is numerically close to the surface tension value for the mean integral surface energy [5]. Consequently, for any upward and horizontally solidified sample, at a high cooling rate, surface stress, surface energy, nucleus radius, and mechanical strength are expected to vary along with the sample.

The expression derived by Ferreira [5] for Gibbs–Thomson Coefficient based on the Gibbs–Duhem [9] and Shuttleworth [6, 8, 26] equations, are able to handle the level of strain in the interior of the nucleus and the surface stress and surface energy occurring during nucleation. In a paper published recently, Ferreira [5], while typing the final Gibbs–Thomson equation following, his paper order number, Eq. 26, which was obtained from the derived surface energy equation, Eq. 18, left an additional entropy term, however, the form Eq. 26 from his paper was not applied in any of his calculation, but Eq. 18 instead, for later combine with Gibbs–Thomson, as shown by the following form,

$$\Gamma \left(\delta \right)=\frac{\gamma \left(\delta \right)}{\Delta {S}_{V}}=\frac{\frac{{\gamma }_{0}}{{\left(1-\frac{\delta }{{r}_{Eq}}\right)}^{2}}-s}{\Delta {S}_{V}},$$

(10)

where $s$ is the surface stress. The relationship among the decrease in radius $\delta$, the equilibrium radius ${r}_{Eq}$ and non-equilibrium radius $r$ is given by

$$\frac{{r}_{Eq}-\delta }{{r}_{Eq}}=\frac{r}{{r}_{Eq}}.$$

(11)

By substituting Eq. 11 into Eq. 10, the Gibbs–Thomson coefficient can be expressed in terms of non-equilibrium radius $r$,

$$\Gamma \left(r\right)=\frac{\gamma \left(\frac{r}{{r}_{Eq}}\right)}{\Delta {S}_{V}}=\frac{\frac{{\gamma }_{0}}{{\left(\frac{r}{{r}_{Eq}}\right)}^{2}}-s}{\Delta {S}_{V}}.$$

(12)

The liquidus isotherm is generally described physically in terms of pressure, for high-pressure applications 50 (GPa) to 300 (GPa) about 1000 (km) to 4700 (km) in Earth’s interior [27], solute content and undercooling/superheating $\Delta \tilde{T }$ related to a cooling/heating kinetic by,

$$T={T}_{F}+{\sum }_{j=1}^{n-1}{\left(\frac{\partial T}{\partial {C}_{L, j}}\right)}_{j}{C}_{L, j}+\frac{\partial T}{\partial P} P-\Delta \tilde{T }.$$

(13)

By calculating the thermal gradient,

$$\frac{dT}{dx}={\sum }_{j=1}^{n-1}{\left(\frac{\partial T}{\partial {C}_{L, j}}\right)}_{j}\frac{\partial {C}_{L, j}}{\partial x}+\frac{\partial T}{\partial P} \frac{\partial P}{\partial x}+\frac{\partial \tilde{T }}{\partial x}.$$

(14)

Rearranging Eq. 7

$$\frac{\partial \tilde{T }}{\partial x}={\sum }_{j=1}^{n-1}{\left(\frac{\partial T}{\partial {C}_{L, j}}\right)}_{j}\frac{\partial {C}_{L, j}}{\partial x}+\frac{\partial T}{\partial P} \frac{\partial P}{\partial x}-\frac{dT}{dx}.$$

(15)

Let $\overrightarrow{h}=x \widehat{i}+ y \widehat{j}+z \widehat{k}$, be the position vector of any point $P\left(x,y,z\right)$ on the surface $S\left(x,y,z\right)=a$. Then, $d\overrightarrow{h}=dx \widehat{i}+ dy \widehat{j}+dz \widehat{k}$, lies on in the tangent plane to the surface $S$ at $P$, what provides $\nabla S\cdot d\overrightarrow{h}=0$, where, $\nabla S=\frac{\partial S}{\partial x}\widehat{i}+\frac{\partial S}{\partial y}\widehat{j}+\frac{\partial S}{\partial z}\widehat{k}$ and $\nabla S\cdot d\overrightarrow{h}=\frac{\partial S}{\partial x}dx+\frac{\partial S}{\partial y}dy+\frac{\partial S}{\partial z}dz=0$. The unit normal vector is obtained as $\widehat{n}=\frac{\nabla S}{\left|\nabla S\right|}$. Now, let’s consider $S\left(r, \theta ,\phi \right)$, $0\le \theta \le 2\pi$ and $0\le \phi \le \pi$, then $\widehat{n}=\frac{\frac{\partial S}{\partial \theta }\left( \theta ,\phi \right)\times \frac{\partial S}{\partial \phi }\left( \theta ,\phi \right)}{\left|\frac{\partial S}{\partial \theta }\left( \theta ,\phi \right)\times \frac{\partial S}{\partial \phi }\left( \theta ,\phi \right)\right|}=-\text{sin}\phi \text{cos}\theta {\widehat{e}}_{r}-\text{sin}\phi \text{sin}\theta {\widehat{e}}_{\theta }-\text{cos}\phi {\widehat{e}}_{\phi }$, pointing toward the origin, and $\widehat{n}=\frac{\frac{\partial S}{\partial \phi }\left( \theta ,\phi \right)\times \frac{\partial S}{\partial \theta }\left( \theta ,\phi \right)}{\left|\frac{\partial S}{\partial \phi }\left( \theta ,\phi \right)\times \frac{\partial S}{\partial \theta }\left( \theta ,\phi \right)\right|}=\text{sin}\phi \text{cos}\theta {\widehat{e}}_{r}+\text{sin}\phi \text{sin}\theta {\widehat{e}}_{\theta }+\text{cos}\phi {\widehat{e}}_{\phi }$, for $\widehat{n}$ pointing toward outside the sphere.

By writing the Gibbs–Thomson Coefficient, as a function of the thermal gradient $\nabla T$ considering the effect of local chemical species, pressure and temperature gradients and nucleus radius vector $\overrightarrow{r}=\left\{\left. \overrightarrow{r}\left(x,y,z\right) \in {R}^{3}\right| \overrightarrow{r} \subset S\right\}$ and the surface $S\left( \overrightarrow{r}\right)$ provides,

$$\Gamma \left(\overrightarrow{r}\right)=\nabla T\cdot \widehat{n} \;S\left(\overrightarrow{r}\right).$$

(16)

By approximating the surface area $S$ for a sphere of radius $r$, unit normal vector $\widehat{n}=\frac{\overrightarrow{r}+d\overrightarrow{r}}{r}$, since $\overrightarrow{r}\times d\overrightarrow{r}=0$, and $\left|\overrightarrow{r}+d\overrightarrow{r}\right|> r$, considering only the radial component,

$$\frac{\gamma \left(\frac{r}{{r}_{Eq}}\right)}{4\uppi { r}^{2}\Delta {S}_{V}}=\frac{\frac{{\gamma }_{0}}{{\left(\frac{r}{{r}_{Eq}}\right)}^{2}}-s}{4\uppi { r}^{2}\Delta {S}_{V}}=\frac{dT}{dr}{\widehat{e}}_{r}\cdot \widehat{n}=\left[{\sum }_{j=1}^{n-1}{\left(\frac{\partial T}{\partial {C}_{L, j}}\right)}_{j}\frac{\partial {C}_{L, j}}{\partial r}{\widehat{e}}_{r}+\frac{\partial T}{\partial P} \frac{\partial P}{\partial r}{\widehat{e}}_{r}+\frac{\partial \tilde{T }}{\partial r}{\widehat{e}}_{r}\right]\cdot \widehat{n.}$$

(17)

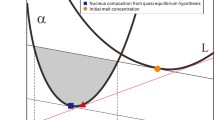
An example of application is the nucleation of Al–3 wt% Cu–9 wt% Si considering isotropic temperature and solute concentration gradients $\nabla T=3827.5 [\text{K}\cdot {\text{m}}^{-1}]$ for $\pi <\theta <2\pi$, and anisotropic $\nabla T=3827.5+862.7\cdot {\text{sin}}^{6}\theta [\text{K}\cdot {\text{m}}^{-1}]$ for $0\le \theta \le \pi$, as shown in Fig. 1.

Fig. 1

Nucleation of $\alpha{\text{-}}phase$ of Al–3 wt% Cu–9 wt% Si alloy for isotropic and anisotropic gradient in (A) Two-dimensional, and (B) Three-dimensional calculations

The analysis of the change of thermophysical properties due to the nucleation in the case of alloys can be derived from the relation between mass fraction and liquid fraction,

$$g=\frac{\rho }{{\rho }_{L }}f.$$

(18)

The volume fraction rate is very important because it is directly correlated to the release of the transformation heat during the change of phase. By deriving Eq. 18 with respect to time, it is possible to determine how the change in the mass fraction and density affect the volume fraction rate.

$$\frac{dg}{dt}=\frac{1}{{\rho }_{L }}\left(\rho \frac{df}{dt}+f\frac{d\rho }{dt}\right).$$

(19)

The change in density can be written in terms of rate of change in solute concentration, the rate of change in pressure, and cooling rate as follows,

$$\frac{d\rho }{dt}={\sum }_{j=1}^{n-1}\frac{\partial \rho }{\partial {c}_{S,j}}\frac{\partial {c}_{L,j}}{\partial t}+\frac{\partial \rho }{\partial P}\frac{\partial P}{\partial t}+\frac{\partial \rho }{\partial T}\frac{\partial T}{\partial t},$$

(20)

and, finally,

$$\frac{dg}{dt}=\left[\frac{\rho }{{\rho }_{L }}\frac{df}{dt}+f\left({\sum }_{j=1}^{n-1}\frac{1}{{\rho }_{L }}\frac{\partial \rho }{\partial {c}_{L,j}}\frac{\partial {c}_{L,j}}{\partial t}+\frac{1}{{\rho }_{L}}\frac{\partial \rho }{\partial P}\frac{\partial P}{\partial t}+\frac{1}{{\rho }_{L }}\frac{\partial \rho }{\partial T}\frac{\partial T}{\partial t}\right)\right],$$

(21)

where $P$ is the pressure. Typically, in metallurgical applications, $P\sim 1 [\text{atm}]$ and $\frac{\partial \rho }{\partial P}\sim 0$.

The importance of this term increases considerably in geophysics, phases transformation under Earth’s crust or any other high-pressure phenomena.

Equation 21, can be expressed in terms of expansivity and compressibility coefficients, that is,

$${\beta }_{P}=-\frac{1}{{\rho }_{L }}{\left(\frac{\partial \rho }{\partial T}\right)}_{P,C},$$

(22)

$${\beta }_{C}=-\frac{1}{{\rho }_{L }}{\left(\frac{\partial \rho }{\partial C}\right)}_{T,P},$$

(23)

$${k}_{T}=\frac{1}{{\rho }_{L}}{\left(\frac{\partial \rho }{\partial P}\right)}_{T,C}.$$

(24)

Whenever a new surface is created, occurs strain in the crystal as a consequence. The surface energy will be a function of the level of strain in the bulk [6, 8]. Surface stress and surface energy are strongly linked by Gibbs–Duhem’s equation, from which Shuttleworth’s equation can be derived [9].

The change in the superficial energy can be expressed in terms of the following contributions: energy, number of particles and surface area [9, 10],

$${\text{dU}}^{surf}=Td{S}^{surf}+{\mu }_{j}{N}_{j}^{surf}+\gamma d{A}^{cre}+{A}_{0}\sum_{\alpha \beta }{s}_{\alpha \beta } d{\varepsilon }_{\alpha \beta },$$

(25)

where the third and the fourth terms in RHS of the Eq. 25 represent the creation and the change in surface area, $U$ is the internal energy,$S$ is the entropy, $\mu$ is the chemical potential, $\gamma$ is the surface energy, ${A}^{cre}$ is the surface area creation, ${A}_{0}$ is the undeformed area, ${s}_{\alpha \beta }$ is the surface stress tensor and $d{\varepsilon }_{\alpha \beta }$ is the bulk strain. The term ${A}_{0}\sum_{\alpha \beta }{s}_{\alpha \beta } d{\varepsilon }_{\alpha \beta }$ is the isothermal work necessary to deform a surface.

By defining internal energy ${\text{U}}^{surf}$ as the surface excess of the bulk internal energy $U$,

$${\text{U}}^{surf}=T{S}^{surf}+{\mu }_{j}{N}_{j}^{surf}+\gamma A.$$

(26)

By comparing the variation of excess of internal energy, Eq. 25, with the differentiated form of Eq. 26 and correlating with the Gibbs–Duhem equation [9],

$$\text{A d}\gamma =-{S}^{surf}dT+{N}_{j}^{surf}{d\mu }_{j}+{A}_{0}\sum_{\alpha \beta }\left({s}_{\alpha \beta }-\gamma {\delta }_{\alpha \beta }\right) d{\varepsilon }_{\alpha \beta }.$$

(27)

The surface stress and surface energy relationship, the so-called Shuttleworth equation [6,7,8,9], can be derived from Eq. 27 by assuming no change in heat and in the number of particles on the surface. For anisotropic solids,

$${s}_{\alpha \beta }=\gamma {\delta }_{\alpha \beta }+\frac{\partial \gamma }{\partial {\varepsilon }_{\alpha \beta }}.$$

(28)

On the other hand, for isotropic surface stress and isothermal volumetric work provides,

$$s {A}_{0} \varepsilon =\gamma \left(\varepsilon \right) A\left(\varepsilon \right)-{\gamma }_{0} {A}_{0},$$

(29)

in the case of equilibrium nucleation, the surface energy is given by ${\gamma }_{0}$ and the surface stress by surface tension ${\sigma }_{0}$. In this case, the fundamental level of strain [5], is the following:

$${\upvarepsilon }_{0}=-\frac{ {\upgamma }_{0}}{{\upsigma }_{0}}.$$

(30)

By integrating Eq. 29 with respect to $r$ [5],

$$\gamma \left(r\right)=\frac{{\gamma }_{0}}{{\left(\frac{r}{{r}_{Eq}}\right)}^{2}}-s.$$

(31)

2.2 Molar Specific Heat Capacity for Pure Elements and Phases

In this work, the nucleation model is applied for the molar specific heat capacity of solid metals and phases to examine the thermal gradients [5, 19,20,21], according to Eqs. 16 and 17.

For pure solid elements,

$${c}_{v}=\left(1.0+D\left(\omega \right)\right) 9 {N}_{a}{k}_{B} {\left(\frac{T}{{\Theta }_{D}}\right)}^{3}\underset{0}{\overset{\frac{T}{{\Theta }_{D}}}{\int }}\frac{{x}^{4} {e}^{x}}{{\left({e}^{x}-1\right)}^{2}}dx \left(1+{c}_{ve}\right)+\left(n+1/2\right)\left[9.0 {c}_{v}^{Rot}+\left(1-\sqrt{\frac{\text{E}\cdot { \rho }_{Dia}}{{E}_{Dia} \cdot \rho } }\right)\frac{R{T}^{3}}{{\Theta }_{D }{T}_{m}^{2}}\right].$$

(32)

In the case of phases and compounds,

$${c}_{v}=\left(1.0+{D}_{Comp}\left({\omega }_{Comp}\right)\right) 9 {N}_{a}{k}_{B} {\left(\frac{T}{{\Theta }_{D,Comp}} \right)}^{3}\underset{0}{\overset{\frac{T}{{\Theta }_{D,Comp}}}{\int }}\frac{{x}^{4} {e}^{x}}{{\left({e}^{x}-1\right)}^{2}}dx \left(1+{c}_{ve}\right)+\left(n+1/2\right)\left[9.0{ c}_{v}^{Rot}+\left(1-\sqrt{\frac{{E}_{i}{ \rho }_{Dia}}{{E}_{Dia}{ \rho }_{i}} }\right)\frac{R{T}^{3}}{{\Theta }_{D,Alloy} {T}_{L}^{2}}\right].$$

(33)

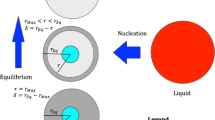
A key part of the solution scheme is to solve the density of state [5, 19,20,21], by considering a sphere of radius ${k}_{D}$ containing $N$ wave vectors, the density of modes $n$, and the volume ${\text{V}}$ containing the total number of modes $N$. The volume ${\text{V}}$ is associated with the nucleation kinetics.

$$\frac{{\left(2\pi \right)}^{3}}{\text{V}}N=\frac{4\pi {k}_{D}^{3}}{3}.$$

(34)

Then, the density of modes $n$ can be given by

$$n = \frac{{k_{D}^{3} }}{{6\pi ^{2} }} = \frac{1}{{6\pi ^{2} }}\left( {\frac{{k_{B} ~\Theta _{{D,Comp}} }}{{\hbar ~\nu }}} \right)^{3}.$$

(35)

In the case of equilibrium, Eq. 12, the radius $r={r}_{Eq}$ gives

$$\Gamma \left({r}_{Eq}\right)=\frac{{\gamma }_{0}}{\Delta {S}_{V}}.$$

(36)

The equilibrium radius ${r}_{Eq}$ can be obtained by the following expression

$${r}_{Eq}=\frac{2 \Gamma \left({r}_{Eq}\right)}{\Delta {T}_{Eq}},$$

(37)

where, $\Delta {T}_{Eq}$ is the equilibrium temperature drop. After calculating the volume of containing the number of Modes $N$ in equilibrium, the density of state of equilibrium can be determined by

$${D}_{Eq}\left(\omega \right)=\frac{{\text{V}}_{Eq} {\omega }^{2}}{2 {\pi }^{2} {\nu }^{3}},$$

(38)

and,

$$\nu =\frac{{k}_{B} {\Theta }_{D,Comp}}{\hslash {k}_{D}}.$$

(39)

Particularly important in the calculation of Debye sound velocity is understanding the Brillouin zone structure to describe waves in solids adequately. According to Simon [28], entirely equivalent to the one-dimensional situation, physical waves in the crystal are unchanged if their wavevector is shifted by a reciprocal lattice vector $k\to k+G$, considering each physical crystal momentum once in the definition of the Brillouin zone. Furthermore, methods to handle the effect of polycrystalline materials on sound velocity can be found in [29]. By defining the Brillouin zone to consider $k=k+G$, velocities $\nu$ calculated for Al and Fe are approximately equal to 5 400 ms⁻¹ and 5 900 ms⁻¹, respectively.

By applying Eqs. 16 and 17,

$$\frac{\frac{{\gamma }_{0}}{{\left(\frac{r}{{r}_{Eq}}\right)}^{2}}-s}{4\uppi { r}^{2}\Delta {S}_{V}}=\left[{\sum }_{j=1}^{m-1}{\left(\frac{\partial T}{\partial {C}_{L, j}}\right)}_{j}\frac{\partial {C}_{L, j}}{\partial r}{\widehat{e}}_{r}+\frac{\partial \tilde{T }}{\partial r}{\widehat{e}}_{r}\right]\cdot \widehat{n}.$$

(40)

As an example of application, Eq. 40 can be applied to the solidification of a metallic alloy. To capture the macroscopic nodal value from the microscopic domain, several approaches are available in the literature such as the Volume Averaged which makes use of interfacial transfers to treat mass, momentum, and species equations [14] as well as the Representative Elementary Volume—REV [15] which is applied to one-dimensional solidification binary [16], two-dimensional binary [17], and one-dimensional ternary [18] alloys.

The density of state $D\left(\omega \right)$ for a nucleus of volume $\text{V},$ is given by

$$D\left(\omega \right)=\frac{\text{V }{\omega }^{2}}{2 {\pi }^{2} {\nu }^{3}}.$$

(41)

The radius $r$ can be obtained hence equilibrium radius ${r}_{Eq}$ was previously calculated.

A numerical simulation of unidirectional solidification of pure Al is considerably important for the present analysis since only the temperature gradient is present,

$$\frac{\frac{{\gamma }_{0}}{{\left(\frac{r}{{r}_{Eq}}\right)}^{2}}-s}{4\uppi { r}^{2}\Delta {S}_{V}}=\frac{\partial \tilde{T }}{\partial r}{\widehat{e}}_{r}\cdot \widehat{n}.$$

(42)

For solidification of pure metals and alloys, at atmospheric pressure $\frac{\partial T}{\partial P}\sim 0$, it is possible to express the temperature gradient $\frac{d\tilde{T }}{dr}$ in respect of ${v}_{f}$,

$$\frac{d\tilde{T }}{dr}{v}_{f}=\dot{T}.$$

(43)

The velocity ${v}_{f}$ could be, for instance, the velocity of solidification front or liquidus isotherm velocity (dendrite tip growth rate). The cooling rate $\dot{T}$ usually is a parameter utilized to control the experimental determination of molar specific heat capacity in the Differential Scanning Calorimetry—DSC devices. The temperature and solute concentration gradients calculated in this paper are determined by applying a multicomponent solidification model [16].

2.3 Numerical Model for Pure Metals and Multicomponent Alloys Solidification

The temperature gradients for pure Al and temperature and solute concentration gradients for Al–6 wt% Cu–3 wt% Si alloy are calculated for an upward transient solidification setup by applying a multicomponent alloy solidification model developed for solving the inverse macrosegregation by considering shrinkage-induced flow and the finite-diffusion solidification conditions associated with the back-diffusion parameter $\beta$. This segregation parameter governs the way in which the local liquid concentration is captured from Representative Elementary Volume—REV to the macroscopic domain, Lever rule ($\beta =1$), finite-diffusion ($0<\beta <1$), and the Scheil’s equation ($\beta =0$). A detailed description of the experimental setup can be found in previously published articles [16, 18].

The solution scheme is based on the implicit–explicit algorithm, implicit for energy, and explicit for momentum and species equations.

The mathematical and physical assumptions considered by the numerical model to solve temperature/solute fields are the following:

• i. the domain is one-dimensional;

• ii. the solid phase is stationary;

• iii. in the Representative Elementary Volume—REV, the liquid concentrations, the temperature, the liquid density, and the velocity are constant [15];

• iv. solutes partition coefficients and liquidus slopes are constant;

• v. the thermophysical properties in the liquid and solid phases are the mean integral inside each phase [30];

• vi. the metal/mold thermal resistance varies with time and it is incorporated through a transient global heat transfer coefficient.

3 Results and Discussion

The importance of the cooling rate in the process of nucleation phases is well-known. It dislocates the equilibrium curve in the phase diagram and allows other metastable phases to be developed due to the atomic diffusion phenomenon be a thermally activated process. Recently, Ferreira [5] has proved that the surface energy depends on the nucleus radius, and the Gibbs–Thomson Coefficient changes accordingly. In the literature, other authors [12, 13] have proposed equations considering the concentration and temperature gradients. However, they have assumed the surface energy independently of nucleus radius, which contradicts Shuttleworth’s and Gibbs–Duhem’s equation [6, 8, 9]. First, numerical simulation of solidification of pure Al is performed considering only the effect of temperature gradient on the surface energy and Gibbs–Thomson Coefficient. Similarly, for the Al–6 wt% Cu–3 wt% Si but concentration gradients are highlighted. Finally, the molar specific heat capacity is expressed for pure Al, Fe, Nb elements and for the Al₂Cu and Al₂Ni₃ phases to permit the cooling rate to be set as observed in the practical application of Differential Scanning Calorimetry—DSC analysis [1, 2].

Figure 2A shows the cooling curve of pure aluminum, for six thermocouple positions, that is, 5, 10, 20, 30, 50 and, 70 mm from metal-mold interface to determine a transient global heat transfer coefficient, ${h}_{g}=4500 {t}^{-0.03}$ [W∙m⁻²∙K⁻¹], by IHCP [16, 18]. It is very close to the global heat transfer coefficient observed for the Al–6 wt% Cu–3 wt% Si alloy. In Fig. 2B the thermal gradient is plotted against the distance. Figure 3A presents the nucleation radius and as can be observed, it decreases considerably for a high cooling rates and gets close to the equilibrium radius, ${r}_{Eq}=3.33\times {10}^{-6} \left[\text{m}\right]$ at the final positions of the solidified sample. In Fig. 3B and C, the surface stress and the surface energy have similar behaviors. It can be seen that both curves are high at positions of high thermal gradients, however, they approximate of equilibrium at the final positions of the casting. In Fig. 4 the equilibrium Gibbs–Thomson Coefficient is ${\Gamma }_{Eq}=1.4 \times {10}^{-7} [\text{K}\cdot \text{m}]$, for the regions close to the chill, the non-equilibrium Gibbs–Thomson is higher than ${\Gamma }_{Non-Eq}=7\times {10}^{-7} [\text{K}\cdot \text{m}]$.

Fig. 2

Upward solidification of pure aluminum, (A) cooling curves, and (B) thermal gradient

Fig. 3

Upward solidification of pure aluminum, equilibrium, and non-equilibrium (A) nucleation radius, (B) surface stress, and (C) surface energy as a function of the distance from the from the metal/mold interface

Fig. 4

Upward solidification of pure aluminum, equilibrium, and non-equilibrium Gibbs–Thomson coefficient

In the case of Al–6 wt% Cu–3 wt% Si alloy, Fig. 5A shows the temperature profile compared with experimental data in which the numerical simulation fits well the experimental scatter. The experimental superheat dependence on height is assumed as parabolic [16]. The transient global heat transfer Coefficient is obtained by IHCP technique and the reckoned time-dependent function is given by ${h}_{g}=4600 {t}^{-0.12}$ [W∙m⁻²∙K⁻¹]. A study of the thermophysical properties, considered their dependence on temperature to obtain the mean integral values to assure they are not influencing the results by setting mean constant values within each phase, however, different between phases [30]. The global heat transfer coefficient remains unchanged concerning the liquidus isothermal velocity predictions, as can be seen in Fig. 5B, where the numerical results for the mean integral and temperature-dependent thermophysical properties agree with the experimental data. In Fig. 5C the thermal gradient is plotted against the ingot height and, similarly, in Fig. 6 in which the liquid solute profiles for Cu and Si are obtained from the numerical simulations. The wave-like oscillations found in the solute profiles are related to the numerical coupling between microscopic solute concentration and macroscopic concentration density fields. As the number of nodes increases, the oscillation decreases for a given space $dz$ and time $dt$ steps. The oscillation levels observed in the liquid concentrations do not compromise the present analysis. By considering the nucleation radius, a decrease can be seen for higher cooling rates (higher thermal gradients) comparably to the case of pure Al. In addition, it crosses the equilibrium radius around the half of the solidified sample in the case of the present solidification kinetic. A probable reason for this behavior is the coupling between the temperature and concentration gradients, which controls the thermal gradients mainly at low-temperature gradient positions. Figure 7 presents nucleation radius (A), surface stress (B), and surface energy (C). It is worth noting that initially, a comparable behavior with pure Al can be observed for higher cooling rates. On the contrary, for regions of low cooling rates nucleation is controlled mainly by concentration gradients. The Gibbs–Thomson Coefficient is higher for higher thermal gradients, i.e., close to the metal/mold interface, as shown in Fig. 8. Therefore, as solute gradients begin to dominate the thermal gradient behavior, as noted in Eq. 40, local Gibbs–Thomson evaluations cross the equilibrium value and stay near it. Typically, a constant Gibbs–Thomson Coefficient can be applied to microstructural evolution models, and a good fit is generally obtained for lower cooling rates. It means that, for lower cooling rates, the nucleation is fully controlled by solute gradients and, consequently, the Gibbs–Thomson Coefficient stays near the equilibrium [13]. On the other hand, temperature gradient dominates the process for higher cooling rates, and both Gibbs–Thomson and surface energy strongly deviate from the equilibrium [13, 24]. Furthermore, by calculating the mean integral of the Gibbs–Thomson Coefficient from Fig. 8, a value higher than the equilibrium is expected, as the surface area creation and deformation terms are both considered in the surface energy prediction, as indicated by Eq. 29, which gives $A=A\left(r\right)<{A}_{0}$ and $\gamma =\gamma\left(r\right) >{\gamma }_{0}$. In contrast, at the equilibrium, no surface area deformation term is computed and, consequently, it provides $A={A}_{0}$ and $\gamma ={\gamma }_{0}$. The change in the surface energy in respect to the nucleation radius, temperature and solute concentration gradients must be considered in the analysis of unsteady-state phase transformation for any local condition, as noticed in Eqs. 11, 12 and 17. In the case of rapid solidification, comparatively to the application of lasers in additive manufacturing, higher cooling rates and thermal gradients of magnitude between 10⁵ $\left[\text{K}\cdot {\text{m}}^{-1}\right]$ and 10⁶ $\left[\text{K}\cdot {\text{m}}^{-1}\right]$ can be easily reached. Therefore, an atypical augment in the surface energy is envisioned. Nucleation of a crystalline phase does not occur indefinitely for any level of temperature, solute concentration, and pressure gradients, and the resulting crystalline or amorphous phase shall depend on the level of gradients interaction. It is mainly because of the impossibility of a stable nucleus to be formed on account of gradients involved in a particular phase-change process. In this case, owing to the degree of internal strain, the surface energy would increase rapidly, and no stable nucleus could be formed from any cluster of atoms acting as substrate in the current phase. Consequently, no long-range order crystalline structure or extended three-dimensional arrangement can occur. In the case of a liquid–solid transformation, a supercooled liquid will arise in the place of long-range crystal three-dimensional arrangements for temperatures below the melting point, as no latent heat, i.e., no ordering state entropy, will be absorbed.

Fig. 5

Upward solidification of Al–6 wt% Cu–3 wt% Si alloy, (A) cooling curves, (B) tip growth rate, and (C) thermal gradient

Fig. 6

Solute gradients during upward solidification of Al–6 wt% Cu–3 wt% Si alloy for Cu and Si

Fig. 7

Upward solidification of Al–6 wt% Cu–3 wt% Si alloy, equilibrium, and non-equilibrium (A) nucleation radius, (B) surface stress, and (C) surface energy as a function of the distance from the metal/mold interface

Fig. 8

Upward solidification of Al–6 wt% Cu–3 wt% Si alloy, equilibrium and non-equilibrium Gibbs–Thomson coefficient

Figure 9A exhibits the molar specific heat capacity for pure Al considering equilibrium and non-equilibrium nucleation. The experimental data are found in Giauque et al. [31] for lower and Brooks et al. [32] for higher temperatures. Theoretical calculation fitted experiments for equilibrium nucleation, where energy is given by ${\gamma }_{0}$ associated with surface area creation only. Thermo-Calc calculations agree well for $r=0.84 {r}_{Eq}$. By comparing with Fig. 3A, nucleation radius $r=0.84 {r}_{Eq}$ is considerably near the equilibrium radius. Similar behavior is noticed concerning the theoretical predictions for pure Fe [33,34,35,36,37], $r=0.94 {r}_{Eq}$. Thermo-Calc simulations conformed well to the experimental data determined by Awbery [33] for cooling rates close to the equilibrium nucleation. In Fig. 9, heat capacity curves for pure Nb agree well with the experimental scatter. In Fig. 10A, the results found by Kirilin [38] and Fig. 10B and Novikov [39,40,41] fit well with the theoretical predictions. According Morohoshi et al. [42] the activity of O₂ changes the surface tension ~ 1 mN∙m⁻¹ to 1.9 mN∙m⁻¹ for a_O2 = − 12. The surface energy and surface tension are correlated by Eqs. 27 and 28 [6, 9]. Another effect of the activity of O₂ is the oxide contribution to the increase in the melting temperature and both effects are considered in Fig. 10B simulations.

Fig. 9

Molar specific heat capacity and nucleation model (A) pure Al and (B) pure Fe

Fig. 10

Molar specific heat capacity and nucleation model (A) pure Nb without activity of O₂ (B) pure Nb with activity of O₂

Figure 11A and B show the application of equilibrium and non-equilibrium Gibbs–Thomson for the molar specific heat capacity of the Al₂Cu and Al₃Ni₂ phases, respectively. The results for the heat capacity of the Al₂Cu phase, calculated by Thermo-Calc using COST507 database for temperatures higher than 550 K deviate from theoretical calculations and of those furnished by TTAL7 and TCMP2 databases.

Fig. 11

Molar specific heat capacity and nucleation model (A) Al₂Cu and (B) Al₃Ni₂ phases

3.1 Considerations on the Sanity Control of Additive Manufacturing Products

Defects due to solidification are common associated with additive manufacturing causing brittle fracture in the part degrading the mechanical properties [43]. For example, in the laser-assisted metal deposition of aluminum-based alloys, the decrease in the cooling rate due to an increasing layer of thermal resistance promotes anisotropic distribution of mechanical strength along length [44]. On the other hand, vaporization of low-vapor pressure of important aluminum-based alloying elements deteriorates the mechanical strength locally. The thermal gradient order of magnitude of laser-assisted metal deposition [45] is about 10⁵–10⁶ $\left(\text{K}\cdot {\text{m}}^{-1}\right)$, and in upward solidification [16] 10³–10⁴ $\left(\text{K}\cdot {\text{m}}^{-1}\right)$. The solution for the vaporization of alloying elements is achieved either by changing alloy composition [46,47,48] or controlling the thermal gradient. It is well stablished that the mechanical strength depends on the local cooling rate. Similarly, for surface energy, nucleation radius, even thermophysical properties, such as density, thermal conductivity, and heat capacity. The thermophysical properties can be engineered by controlling the nucleation radius which is a function the local temperature and chemical species gradients. By combining Eq. 16 with the derivative of Eq. 26 to encompass the change in particle numbers and the change in heat in the superficial energy with the view to consider phase nucleation and growth. The combination of different laser techniques and the proposed set of equations permit a local tuning of the thermal gradient to furnish a designed local thermophysical properties and to assist the automation of the additive manufacturing process.

4 Conclusion

A previously proposed model for the non-equilibrium nucleation to describe the nucleation radius, surface stress, surface energy, and the Gibbs–Thomson Coefficient was successfully extended to deal with the temperature, solute concentration and pressure gradients with the view to permit the potential use in DTA/DSC analysis. By analyzing the solidification of pure Al, it was found that the surface energy and the Gibbs–Thomson Coefficient are hardly influenced by thermal gradient as a function of the sample height. In this sense, the surface energy depends not only on the surface area creation but also on its deformation. A higher thermal gradient causes higher level of deformation in the newly created surface area, which increases the surface energy. For alloys, the concentration gradients play a significant role in lower temperature gradients, which leads the Gibbs–Thomson Coefficient to remain near the equilibrium. Non-equilibrium Gibbs–Thomson Coefficients approximate only the equilibrium value in the transient upward solidified sample for lower local temperature gradients, which occur in the regions of higher thermal resistances associated with the solid phase thickness. The nucleation model was successfully applied to the molar specific heat capacity for pure elements and phases to perform a change in the cooling rate, which dislocates the molar specific heat capacity curves downwards as cooling rate increase. The highest possible heat capacity is obtained for the equilibrium conditions, where no surface area deformation is considered by neglecting any element or phase impurity, such as oxygen. A brief discussion on defects caused by solidification in laser-assisted manufacturing is added to highlight the importance of present formulation in predicting local nucleation and growth and their relevance to the automation of laser-assisted AM processes. Its potential use could help mitigate local defects by combining and controlling different laser sources and process parameters, and by controlling thermal gradients beforehand.