1 Introduction

In recent decades, the technologies in microelectromechanical system and nanoelectromechanical system (MEMS and NEMS) have developed rapidly. Within the past few years, microcantilever-based biosensors have become hot spots and difficult points in the field of sensor due to their ultrahigh sensitivity and low cost. By monitoring the significant changes in its deflection or resonance frequencies, the cantilever-based sensors have widely applied in the field of physical, chemical, biological, medical and environmental monitoring, etc. So study on the response of microcantilevers in dynamic mode and static mode becomes a very important topic. In the study of dynamic mode, usually there are many modes to effectively drive a microcantilever to vibrate at the resonant frequencies with high quality factor (Q factor), including thermal, photothermal, photoacoustic, electrostatic, piezoelectric and magnetic, etc. The behavior and characteristics of microcantilevers under different types of excitation have been studied either experimentally [1,2,3,4,5,6,7] or theoretically [8,9,10,11,12,13], or both. Yan et al. [1] reported a detection of organophosphates using a microcantilever coated with a layer of acetyl cholinesterase. Li et al. [2] presented a remote biosensor platform based on magnetostrictive microcantilever, and their experimental results showed that it works relatively well in either air or liquid. Karnati et al. [3] reported a kind of biosensor, which was manufactured based on organophosphorus hydrolase (OPH) multilayer microcantilever, for detection of organophosphorus compounds. The resonating modes of nanocantilever in liquid were experimentally studied by Ghatkesar et al. [4]. Liu et al. [5] designed and characterized a high resistivity-heated AFM cantilever and found it has higher thermal sensing and better imaging as opposed to the heated cantilevers in the previous works. Lakshmoji et al. [6] experimentally showed the disparity in surface topography on opposite sides of a single-layered microcantilever upon exposure to water molecules, and the study revealed the presence of localized surface feathers on one side led to stress non-uniform. Huber et al. [7] summed up the development of nano-sized biosensors originated from AFM cantilevers for cancer detection. Also, many researchers devoted to investigate the response of microcantilevers theoretically and several different models were proposed. Without considering rotational inertia and shear deformation, Tamayo et al. [8] developed a flexural displacement equation and used it to study the effect of Young’s modulus on the response of microcantilever and nanocantilevers as biological and chemical sensors. Chaterjee and Pohit [9] studied the microcantilever system nonlinearity caused by electric forces, dimension of beam and the inertial effect through a comprehensive model. The Elmer–Dreier model and Sader’s extended viscous model were adopted by Ghatkesar et al. [4] to obtain the nanomechanical cantilevers resonant frequency spectrum in liquid and found the theoretical results had good agreement with the experimental measurements. Tamayo et al. [10] obtained the governing equation using the principle of virtual displacement for a plate, and the results match very well with finite element simulations and experimental measurements for DNA immobilization on microcantilevers. Using microelectromechanical processes, a series of coating microcantilevers, in which a Parylene C film is deposited on a silicon substrate, were fabricated by Peng et al. [11] to measure the residual stresses and found the decrease in substrate thickness decreases the residual stress in the coating layer. The microcantilever dynamics response in tapping mode was investigated by Andreaus et al. [12] via single- and three-mode models, and typical features were addressed. Dufour et al. [13] summarized the three types of vibration modes, i.e., transverse bending, lateral bending and elongation obtained from hydrodynamic force equations and proposed their successful applications in chemical detection in complex fluid environments.

In the last few decades, photothermal (PT) and photoacoustic (PA) methods have gained popularity among many well-established spectroscopic methods. These methods are widely used in MEMS and NEMS due to the advantages of non-contact and nondestructive, especially applicable in toxic, hazardous or extreme condition [14,15,16,17]. These technologies have become as a kind of diagnostic method with high sensitivity. In general, at low frequencies (below 10 kHz), the photoacoustic signal may be quite large. At sufficiently high frequencies, however, the photoacoustic signal is attenuated in comparison with the photothermal signal and can be neglected [18]. So PT methods were a kind of wideband method. PT effect is an effective and important mechanism for driving microstructures, especially for microcantilevers. The photothermal mechanism consists of three stages: conversion of absorbed light into heat energy; changes in sample temperatures; expansion and contraction of sample following the temperature changes. So thermoelastic deformation is the main driven mechanism for microstructures under photothermal excitation. Conventional thermoelastic theory is built according to classical Fourier heat conduction equation and elastic moving equation. The response calculated from conventional thermoelastic theory matches well with those obtained from experimental measurement for millimeter cantilever [19,20,21].

Usually, the microcantilevers thickness in MEMS and NEMS is on micronmeter and sub-micronmeter scale. Experimental research showed that structures exhibit many size-dependent mechanical behaviors when the scale of characteristic size of structure and the internal material length parameter are equivalent [22]. Research results given by Fleck et al. [23], Stolken and Evans [24], Lam et al. [25] and Mcfarland and Colton [26] have shown significant difference in material properties with the decrease in structure dimension. Thus, the classical theory is unable to accurately model the scale effect in microstructures. Utilizing non-classical theories, like micropolar theory, couple stress theory [27,28,29,30] etc., the scale effect of microstructures can be described.

The couple stress elasticity theory was proposed in 1960s. Koiter [27] and Mindlin and Tiersten [28] are pioneers in the study of couple stress theory for isotropic materials. This theory takes into account the effect of couple stress and belongs to higher-order continuum theory. In this theory, four material parameters need to be introduced for homogeneous, isotropic elastic materials. Two of them are material parameters in classical elastic theory (elastic modulus and Poisson’s ratio or two Lame’s constants), and the other two are new additional material internal length parameter which relate to the couple stress and higher-order strain. Consideration of the equilibrium of moment of the representative volume element, Yang et al. [31] reduced the two additional length constants in couple stress theory to one and proposed a new higher-order theory-modified couple stress theory. Due to the convenience to describe scale effect, the modified stress theory has attracted a lot of attention in recent years. Park and Gao [32] presented a new Euler–Bernoulli beam model to analyze its static mechanical properties under this high-order theory and found the predicted scale influence having good agreement with that experimental observation. Kong et al. [33] investigated the dynamic response of Bernoulli–Euler beams analytically under modified couple stress theory. Using modified couple stress theory, the dynamic behavior of fluid-conveying microtubes was studied by Wang [34] and found that natural frequencies and critical flow velocities predicted based on modified couple stress theory are much greater than those predicted from conventional beam theory. Taati and Molaei Najafabadi [35] derived size-dependent thermoelastic governing equations for a Timoshenko microbeam according to coupled non-Fourier heat conduction theory and modified coupled stress theory. Results denoted that the characteristic length and thermal relaxation time are very important parameters, and they have significant effect on the response of microbeam. Based on modified couple stress theory, Kahrobaiyan et al. [36] developed an extensive Timoshenko beam element and observed that the beam response obtained from this kind of beam element coincides well with the experimental measurements. Also, Rahaeifard et al. [37,38,39] studied the scale effect dynamical response of microcantilevers in the case of suddenly applied voltage and electrostatic actuation using modified couple stress theory. Kahrobaiyan et al. [40, 41] gave a new yield criterion to study the effect of scale effect on yielding loads of microstructures.

In this paper, the responses for a microcantilever were investigated on the basis of modified couple stress theory. The governing equation of microcantilever deflection was obtained under uniform laser excitation. Using iterative relaxation method, the deflections of microcantilever were obtained numerically. Comparison was made between experimental measurement and simulation results to validate the correctness of numerical method. Results show that the ratio of microcantilever thickness to material internal parameter has significant effect on the deflection and resonant frequency of microcantilever.

2 Governing Equation for Microcantilever

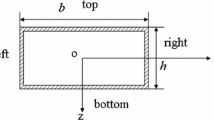
Here, a microcantilever with a rectangular section was considered. The cantilever was stimulated by a uniform periodic modulation excitation laser on front surface and subject to an initial stretching force \( N \) and an external force \( q(x) \). Figure 1 gives the diagrammatic sketch of microcantilever sample. A Cartesian coordinate system (x, y, z) is built on the center of the left end of the cantilever. It is assumed that the length of the cantilever is L (x-direction), width is b (y-direction), and thickness is h (z-direction). It is assumed that the middle plane is located on z = 0. Based on Euler–Bernoulli theory, the governing equations for the microcantilever are established on the basis of modified couple stress theory and now presented.

Fig. 1
figure 1

Schematic figure of a microcantilever

Full size image

2.1 Equilibrium Equation of Microcantilever

The strain energy density based on modified couple stress theory can be written as:

$$ \Omega = \frac{1}{2}\left( {\sigma_{ij} \varepsilon_{ij} + m_{ij} \chi_{ij} } \right),\quad (i,j = 1,2,3) $$
(1)

in which \( \sigma_{ij} ,\varepsilon_{ij} \) are the classical symmetric stress and strain components, \( m_{ij} \) and \( \chi_{ij} \) denote couple stress and curvature components.

For isotropic elastic materials, the governing equation under laser excitation is given below

$$ \sigma_{ij} = \lambda \varepsilon_{mm} \delta_{ij} + 2\mu \varepsilon_{ij} + (3\lambda + 2\mu )\alpha_{t} T $$
(2)
$$ m_{ij} = 2l^{2} \mu \chi_{ij} $$
(3)

in which \( \lambda ,\mu \) and \( \alpha_{t} \) are Lame’s constants and coefficient of thermal expansion of microcantilever. \( T \) is the absolute temperature that above initial temperature \( l \) represents the length scale parameter of material and is given as the square root of the ratio of the curvature modulus to shear modulus. Its influence might become significant as the size of structure is reduced to the same order as the length scale parameter [42].

The geometric equations are

$$ \varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right) $$
(4)
$$ \chi_{ij} = \frac{1}{2}\left( {\theta_{i,j} + \theta_{j,i} } \right) $$
(5)

where \( u_{i} \) and \( \theta_{i} \) are components of displacement vector and rotation vector, and they are related to each other according to

$$ \theta_{i} = \frac{1}{2}curl(u)_{i} $$
(6)

According to Euler–Bernoulli theory, the displacement components for a microcantilever can be given below

$$ u_{1} = u - z\frac{\partial w}{\partial x},\quad u_{2} = 0,\quad u_{3} = w $$
(7)

in which \( u \) and \( w \) denote displacements components of middle plane of microcantilever.

The main components of the strain and the stress under high-order effect are given as

$$ \varepsilon_{11} = \frac{{\partial u_{1} }}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} = \frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} $$
(8)
$$ \begin{aligned} \sigma_{11} & = (\lambda + 2\mu )\left[ {\frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right] + (3\lambda + 2\mu )\alpha_{t} T \\ & \approx E\left[ {\frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right] + (3\lambda + 2\mu )\alpha_{t} T \\ \end{aligned} $$
(9)

in which \( E \) is Young’s modulus. Substituting Eq. 7 into 4–6, the components of rotation, symmetric curvature and couple stress are written as

$$ \theta_{2} = - \frac{\partial w}{\partial x} $$
(10)
$$ \chi_{12} = \chi_{21} = - \frac{1}{2}\frac{{\partial^{2} w}}{{\partial x^{2} }} $$
(11)
$$ m_{12} = m_{21} = - l^{2} \mu \frac{{\partial^{2} w}}{{\partial x^{2} }} $$
(12)

The strain energy U of the microcantilever is given below

$$ \begin{aligned} U & = \iiint\Omega dv = \frac{1}{2}\int\limits_{0}^{L} {\int_{A} {\left[ {\left( {\sigma_{11} + \frac{N}{A}} \right)\varepsilon_{11} + m_{12} \chi_{12} + m_{21} \chi_{21} } \right]} dA} dx \\ & = \frac{1}{2}\int\limits_{0}^{L} {\int_{A} {\left\{ {E\left[ {\frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right]^{2} + \left[ {(3\lambda + 2\mu )\alpha_{t} T} \right.} \right.} } \\ & \quad \left. {\left. { + \frac{N}{A}} \right]\left[ {\frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right] + l^{2} \mu \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} } \right\}dAdx \\ \\ \end{aligned} $$
(13)

Also, the kinetic energy of the cantilever \( \Psi \) is given as

$$ \Psi = \frac{1}{2}\int\limits_{0}^{L} {\int_{A} {\rho \left[ {\left( {\ddot{u} - z\ddot{w}_{,x} } \right)^{2} + \left( {\ddot{w}} \right)^{2} } \right]dAdx} } $$
(14)

Assuming the external force is \( q\left( {x,t} \right) \), the variation of external force work W is as follows:

$$ \delta W = \int\limits_{0}^{L} {q\left( {x,t} \right)\delta w\left( {x,t} \right)dx} $$
(15)

Using Hamilton principle, the moving equation of microcantilever can be given as follows:

$$ \delta \int\limits_{{t_{1} }}^{{t_{2} }} {\left( {U -\Psi - W} \right)dx} = 0 $$
(16)

Substituting Eqs. 13–15 into Eq. 16, we can obtain

$$ \frac{\partial }{\partial x}\left\{ {EA\left[ {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right] + \left( {3\lambda + 2\mu } \right)\alpha_{T} TA + N} \right\} = \rho A\frac{{\partial^{2} u}}{{\partial t^{2} }} - 3I\rho \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}} $$
(17)
$$ \frac{\partial }{\partial x}\left\{ {\left[ {N + \left( {3\lambda + 2\mu } \right)\alpha_{T} TA + EA\left[ {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right]} \right]\frac{\partial w}{\partial x}} \right.\left. { + \left( {EI + \mu l^{2} A} \right)\frac{{\partial^{3} w}}{{\partial x^{3} }}} \right\} = \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} + q\left( {x,t} \right) $$
(18)

where \( A = bh \) and \( I = \frac{{bh^{3} }}{12} \) denote the area and moment of inertia of cantilever. The boundary conditions are given as follows:

$$ \left. {u(x,t)} \right|_{x = 0} = {\kern 1pt} {\kern 1pt} \left. {\frac{\partial u(x,t)}{\partial x}} \right|_{x = 0} = 0, $$
(19)
$$ \left. {w(x,t)} \right|_{x = 0} = {\kern 1pt} {\kern 1pt} \left. {\frac{\partial w(x,t)}{\partial x}} \right|_{x = 0} = 0, $$
(20)
$$ \left. {\left[ {M_{1} (x,t) + X_{12} (x,t)} \right]} \right|_{x = L} = \left. {\frac{{\partial \left[ {M_{1} (x,t) + X_{12} (x,t)} \right]}}{\partial x}} \right|_{x = L} = 0, $$
(21)

in which \( M_{x} \) is the resultant moment, \( X_{xy} \) is the couple stress moment. They are given as

$$ M_{1} = \int\limits_{A} {\sigma_{11} zdA} ,\quad X_{12} = \int\limits_{A} {m_{12} dA} $$
(22)

2.2 Temperature Distribution of Microcantilever

For an isotropic microcantilever, which with constant thermophysical parameters and stimulated by a uniform laser excitation, the following thermal dispersion equation can be used to describe the temperature distribution T in microcantilever:

$$ \rho c_{\text{p}} \frac{{\partial T\left( {{\mathbf{r}},t} \right)}}{\partial t} = k\nabla^{2} T\left( {{\mathbf{r}},t} \right) + \varepsilon_{\text{u}} \rho c_{\text{p}} \vec{\nabla } \cdot \frac{{\partial {\mathbf{u}}\left( {z,t} \right)}}{\partial t} + G ({\mathbf{r}} ,t ) $$
(23)

where \( {\mathbf{u}} = (u,v,w) \) is the displacement vector of microcantilever, \( {\mathbf{r}} = (x,y,z) \) is the spatial coordinate. \( \rho ,k \) and \( c_{p} \) are the density, thermal conductivity and specific heat of a semiconducting sample, respectively. \( G ({\mathbf{r}} ,t ) \) is the thermal sources.\( \varepsilon_{\text{u}} \) is thermoelastic coupling parameter. In the case considered here, the power of excitation laser is about 100 milliwatt. The temperature change in microcantilever is very small; hence, the deformation of microcantilever is very slow. So the thermoelastic coupling can be neglected, and the coupling parameter is taken as zero. This means the temperature distribution is assumed to be completely decoupled from elastic deformation effects.

The temperature distribution in the front and in the rear of cantilever surface is given as

$$ \rho_{i} c_{pi} \frac{{\partial T_{i} \left( {{\mathbf{r}},t} \right)}}{\partial t} = k_{i} \nabla^{2} T_{i} \left( {{\mathbf{r}},t} \right)\quad (i = f,r) , $$
(24)

where \( T_{i} \) denotes the temperature of cantilever surface. \( i = f,r \) represents the front and the rear surface, respectively. \( k_{i} \), \( \rho_{i} \) and \( c_{pi} \) are the thermal conductivity, density and specific heat of the cantilever front and rear surface, respectively. For a single-layer microcantilever in air environment, \( k_{f} = k_{i} = k_{air} \), \( \rho_{f} = \rho_{r} = \rho_{air} \), \( c_{pf} = c_{pi} = c_{pair} \), \( k_{air} \), \( \rho_{air} \) and \( c_{pair} \) denote the thermal conductivity, density and specific heat of air.

For uniform excitation in front surface of microcantilever, the temperature \( T \) and \( T_{i} {\kern 1pt} (i = f,r) \) are only dependent on spatial coordinate T and time t. And the thermalization source term \( G (z ,t ) \) can be given as below:

$$ G(z,t) = \mathop \gamma \nolimits_{\text{G}} \frac{{\alpha F_{ 0} {\text{e}}^{i\omega t} (1 - \mathop R\nolimits_{s} )}}{2} \frac{{\Delta E}}{E} \mathop {\text{e}}\nolimits^{ - \alpha z} , $$
(25)

in which \( R_{\text{s}} \), \( \alpha \) and \( \gamma_{\text{G}} \) are reflectivity, optical absorption coefficient and carrier generation quantum efficiency of microcantilever, respectively. Here, \( \gamma_{\text{G}} \approx 1 \). F0 is excitation laser intensity. In the process of laser excitation, the energy of excitation laser E greatly exceeds band gap \( E_{\text{G}} \). Intrinsic electrons produced by absorption of photons. The excess energy, \( \Delta E = \left( {E - E_{\text{G}} } \right) \), is converted to heat through rapid non-radiation processes. Hence, the temperature distribution in microcantilever can be solved by Eqs. 23 and 24.

Suppose the temperature and heat flow are continuous at the front and rear surfaces, these conditions can be expressed as below:

$$ \left\{ {\begin{array}{*{20}l} {T\left( { - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2},t} \right) = T_{f} \left( {{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2},t} \right),} \hfill \\ {T\left( {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2},t} \right) = T_{r} \left( {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2},t} \right),} \hfill \\ {\left. {k_{f} \frac{{\partial T_{f} \left( {z,t} \right)}}{\partial z}} \right|_{{z = - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} = \left. {k\frac{{\partial T\left( {z,t} \right)}}{\partial z}} \right|_{{z = - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} ,} \hfill \\ {\left. {k_{r} \frac{{\partial T_{r} \left( {z,t} \right)}}{\partial z}} \right|_{{z = {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} = \left. {k\frac{{\partial T\left( {z,t} \right)}}{\partial z}} \right|_{{z = {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} ,} \hfill \\ {\left. {T_{f} \left( {z,t} \right)} \right|_{z \to - \infty } = \left. {T_{r} \left( {z,t} \right)} \right|_{z \to + \infty } = 0} \hfill \\ \end{array} } \right. $$
(26)

The initial conditions are as follows:

$$ T\left( {z,t} \right)\left| {_{t = 0} } \right.{ = 0,}\quad \frac{\partial T}{\partial t}\left| {_{t = 0} } \right.{ = 0} . $$
(27)

2.3 Governing Equation of Deflection for Microcantilever

Usually, the longitudinal inertia \( \rho A{{\partial^{2} u} \mathord{\left/ {\vphantom {{\partial^{2} u} {\partial t^{2} }}} \right. \kern-0pt} {\partial t^{2} }} \) of microcantilever is neglected, and considering axial force N to be constant, also for uniform laser excitation, temperature distribution is also constant along x-axis, using the method given in Ref. [39], we can obtain

$$ \frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} { = }\frac{1}{2L}\int_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} dx} - \frac{3I\rho }{EAL}\int_{0}^{L} {\frac{{\partial^{2} w}}{{\partial t^{2} }}dx} { = } - \frac{1}{2L}\int_{0}^{L} {w\frac{{\partial^{2} w}}{{\partial x^{2} }}dx} - \frac{3I\rho }{EAL}\int_{0}^{L} {\frac{{\partial^{2} w}}{{\partial t^{2} }}dx} $$
(28)

Substituting Eq. 28 into Eq. 18, the governing differential equation for the deflection \( w \) of the microcantilever will be given below:

$$ \begin{aligned} & \frac{\partial }{\partial x}\left\{ {\left[ {N + \left( {3\lambda + 2\mu } \right)\alpha_{T} TA - \frac{EA}{2L}\int_{0}^{L} {w\frac{{\partial^{2} w}}{{\partial x^{2} }}dx} - \frac{3I\rho }{L}\int_{0}^{L} {\frac{{\partial^{2} w}}{{\partial t^{2} }}dx} } \right]\frac{\partial w}{\partial x}} \right.\left. { + \left( {EI + \mu l^{2} A} \right)\frac{{\partial^{3} w}}{{\partial x^{3} }}} \right\} \\ & = \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} + q\left( {x,t} \right) \\ \end{aligned} $$
(29)

Defining the following non-dimensional quantities as

$$ \bar{w} = \frac{w}{L},\quad \bar{x} = \frac{x}{L},\quad \bar{z} = {z \mathord{\left/ {\vphantom {z L}} \right. \kern-0pt} L},\quad \bar{T} = \alpha_{T} T,\quad \bar{t} = t\omega_{1} ,\quad \bar{N} = \frac{{NL^{2} }}{EI},\quad \omega_{1} = \frac{{\rho c_{p} c_{1}^{2} }}{k},\quad c_{1} = \sqrt {\frac{\lambda + 2\mu }{\rho }} , $$
(30)

Here, we considered the spectrum response of microcantilever in frequency domain. Using Fourier transform method (for convenience, the symbols used for field quantities in frequency domain are same as that in time domain), the solution of cantilever temperature is given as

$$ \bar{T} = A_{1} e^{{k_{1} \bar{z}}} + A_{2} e^{{ - k_{1} \bar{z}}} + A_{\alpha } e^{{ - \bar{\alpha }\bar{z}}} $$
(31)

in which

$$ A_{1} = \frac{{A_{\alpha } \left[ {e^{{\frac{{h(k_{1} - \bar{\alpha })}}{2L}}} (\bar{\alpha } - m_{f} \sigma_{f} )(k_{1} + m_{f} \sigma_{f} ) - } \right.\left. {e^{{ - \frac{{h(k_{1} - \bar{\alpha })}}{2L}}} (\bar{\alpha } + m_{f} \sigma_{f} )(k_{1} - m_{f} \sigma_{f} )} \right]}}{{e^{{\frac{{hk_{1} }}{L}}} (k_{1} + m_{f} \sigma_{f} )^{2} - e^{{ - \frac{{hk_{1} }}{L}}} (k_{1} - m_{f} \sigma_{f} )^{2} }} $$
$$ A_{2} = \frac{{A_{\alpha } \left[ {e^{{ - \frac{{h(k_{1} + \bar{\alpha })}}{2L}}} (\bar{\alpha } - m_{f} \sigma_{f} )(k_{1} - m_{f} \sigma_{f} ) - } \right.\left. {e^{{\frac{{h(k_{1} + \bar{\alpha })}}{2L}}} (\bar{\alpha } + m_{f} \sigma_{f} )(k_{1} + m_{f} \sigma_{f} )} \right]}}{{e^{{\frac{{hk_{1} }}{L}}} (k_{1} + m_{f} \sigma_{f} )^{2} - e^{{ - \frac{{hk_{1} }}{L}}} (k_{1} - m_{f} \sigma_{f} )^{2} }} $$
$$ A_{\alpha } = \frac{{G_{T} }}{{\bar{\alpha }^{2} - k_{1}^{2} }},\quad G_{T} = \frac{{\bar{\alpha }L\gamma_{G} (1 - R_{s} )F_{0} \alpha_{T} }}{2k}\frac{\Delta E}{E}, $$
$$ k_{1} = \frac{{i\bar{\omega }}}{{\left( {{{c_{1} } \mathord{\left/ {\vphantom {{c_{1} } {\omega_{1} L}}} \right. \kern-0pt} {\omega_{1} L}}} \right)^{2} }},\quad m_{f} = \frac{{i\bar{\omega }\rho_{air} c_{pair} \omega_{1} L^{2} }}{{k_{f} }},\quad \sigma_{f} = \frac{{k_{f} }}{k},\quad \bar{\alpha } = L\alpha ,\quad \bar{\omega } = \omega \omega_{1} , $$

In frequency domain, the non-dimensional deflection equation for microcantilever is expressed as

$$ \begin{aligned} & \left[ {1 + \frac{12\mu }{E}\left( {\frac{l}{h}} \right)^{2} } \right]\frac{{d^{4} \bar{w}}}{{d\bar{x}^{4} }}{ + }\left[ {\bar{N} + \frac{{12\left( {3\lambda + 2\mu } \right)}}{E}\left( {\frac{L}{h}} \right)^{2} \bar{T} - \frac{{L^{3} }}{2I}\int_{0}^{1} {\bar{w}\frac{{d^{2} \bar{w}}}{{d\bar{x}^{2} }}d\bar{x}} - \frac{{3\rho L^{4} \bar{\omega }^{2} \bar{\omega }_{1}^{2} }}{E}\int_{0}^{1} {\bar{w}dx} } \right]\frac{{d^{2} \bar{w}}}{{d\bar{x}^{2} }} \\ & + \frac{{12\rho L^{4} \bar{\omega }^{2} \bar{\omega }_{1}^{2} }}{{Eh^{2} }}\bar{w} - \bar{q} = 0 \\ \end{aligned} $$
(32)

And the non-dimensional boundary conditions for lateral deflection in frequency domain are

$$ \left\{ {\begin{array}{*{20}l} {\left. {\bar{w}(\bar{x},\bar{\omega })} \right|_{{\bar{x} = 0}} = {\kern 1pt} {\kern 1pt} \left. {\frac{{\partial \bar{w}(\bar{x},\bar{\omega })}}{{\partial \bar{x}}}} \right|_{{\bar{x} = 0}} = 0,} \hfill \\ {\left. {\left[ {\bar{M}_{1} (\bar{x},\bar{\omega }) + \bar{X}_{12} (\bar{x},\bar{\omega })} \right](\bar{x},\bar{\omega })} \right|_{{\bar{x} = 1}} = \left. {\frac{{\partial \left[ {\bar{M}_{1} (\bar{x},\bar{\omega }) + \bar{X}_{12} (\bar{x},\bar{\omega })} \right]}}{{\partial \bar{x}}}} \right|_{{\bar{x} = 1}} = 0, } \hfill \\ \end{array} } \right. $$
(33)

in which

$$ \bar{M}_{1} = - \frac{{Ebh^{3} }}{{12L^{2} }}\frac{{d^{2} \bar{w}}}{{d\bar{x}^{2} }} + (3\lambda + 2\mu )bL\int_{{ - \tfrac{h}{2L}}}^{{\tfrac{h}{2L}}} {\bar{T}\bar{z}d\bar{z}} ,\quad \bar{Y}_{12} = - \frac{{bhl^{2} \mu }}{{L^{2} }}\frac{{d^{2} \bar{w}}}{{d\bar{x}^{2} }}. $$

3 Numerical Methods

In order to get the spectrum response for the cantilever under photothermal excitation, relaxation iterative method is used to solve Eq. 32 numerically. In relaxation method, the governing differential equations are replaced by finite difference discretization algebra equations on the grid points that in the definition domain of the problem. Usually, a general first-order differential equation

$$ \frac{dy}{dx} = g\left( {x,y} \right), $$

will be replaced by an algebraic equation below:

$$ y_{n} - y_{n - 1} { = }(x_{n} - x_{n - 1} )g[\tfrac{1}{2}(x_{n} + x_{n - 1} ),\tfrac{1}{2}(y_{n} + y_{n - 1} )], $$

The relaxation method approaches the solution by starting with an initial guess and iterates to the solution of the problem step by step. Here, the convergence parameter is chosen as \( err = 5 \times 10^{ - 9} \).

4 Results and Discussion

The deflection response of microcantilever is calculated and discussed in this section. The material parameters are considered as follows:

$$ \begin{aligned} & \alpha_{T} = 3 \times 10^{ - 6} \text{K}^{ - 1} ,\;R_{\text{s}} = 0.3,\;E = 2.33\;\text{eV} ,\;E_{G} = 1.11\;\text{eV} ,\\ &\quad \alpha = 5 \times 10\;\text{m}^{ - 1} ,k = 150\;\text{W} \;\text{m}^{ - 1} \;\text{K}^{ - 1} ,E_{Y} = 1.31 \times 10^{11} \;\text{N} \;m^{ - 2} , \\ & \quad \rho = 2.33 \times 10^{3} \;\text{kg} \;\text{m}^{ - 3} ,c_{p} = 695\;\text{J} \;\text{kg}^{ - 1} \;\text{K} .\;k_{air}\\ &\quad = 0.025\;\text{W} \;\text{m}^{ - 1} \;\text{K}^{ - 1} ,\rho = 1.205\;\text{kg} \;{\text{m}}^{ - 3} ,c_{air} = 1013\;\text{J} \;\text{kg}^{ - 1} \;\text{K} . \\ \end{aligned} $$

At first, the responses of cantilever obtained here are compared with our experimental measurements using thermoelastic microscopy [20, 21] to verify the correctness of the solution. Figure 2 gives the amplitude of deflection response versus modulation frequencies for three different dimension cantilevers. Based on couple stress theory, the theoretical calculation is carried out and here \( l \) is set as \( 2\;\upmu{\text{m}} \). Obvious peaks can be observed from the curves of amplitude of the bending. These peaks represent the first resonance of the cantilevers. As shown in Fig. 2, results of theoretical simulation and experimental measurements are in good agreement near resonant frequency.

Fig. 2
figure 2

Theoretical and experimental amplitude versus modulation frequency at the free end of cantilevers (CL1: L = 2505, b = 392, h = 158; CL2: L = 1495, b = 366, h = 64; CL3: L = 2001, b = 392, h = 150; unit: μm)

Full size image

Figure 3 identifies the curves of the dimensionless microcantilever deflection under different values of parameter \( {l \mathord{\left/ {\vphantom {l h}} \right. \kern-0pt} h} \). The dimensions of microcantilever were chosen as: \( L = 200\;\upmu{\text{m}} \), \( b = 20\;\upmu{\text{m}},\;h = 10\;\upmu{\text{m}} \). The result of deflection under classical Euler–Bernoulli theory is obtained for \( {l \mathord{\left/ {\vphantom {l h}} \right. \kern-0pt} h} = 0 \). The figure shows that there are great differences between the deflections obtained by classical and couple stress models. Apparently, the free end deflection of the cantilever decreases with the decrease in the thickness of cantilever. And the microcantilever becomes stiffer with the increase in material length scale parameter \( {l \mathord{\left/ {\vphantom {l h}} \right. \kern-0pt} h} \). This result coincides with that obtained in Ref. [43].

Fig. 3
figure 3

Amplitude of deflection versus length of microcantilever for different height to scale parameter ratio

Full size image

Figure 4 shows the influence of axial force on the microcantilever deflection obtained by couples stress theory for \( {l \mathord{\left/ {\vphantom {l h}} \right. \kern-0pt} h} = 0.2 \). As might be expected, the stiffness of microcantilever increases with the increase in axial force. The variation in dimensionless deflection of cantilever with dimensionless frequency under different heights to scale parameter ratio is plotted in Fig. 5. The first resonance can be clearly seen from the deflection–frequency curves. The figure also indicates that with the increase in \( {l \mathord{\left/ {\vphantom {l h}} \right. \kern-0pt} h} \) the resonant frequencies increase significantly. This fact shows that with the decrease in microcantilever thickness, the influence of scale effect of microcantilever increases. One also can find that the resonant frequency obtained by the modified couple stress theory is obviously larger than that of the traditional classical theory.

Fig. 4
figure 4

Amplitude of deflection versus length of microcantilever for various values of axial force

Full size image
Fig. 5
figure 5

Amplitude of deflection versus dimensionless frequency for different height to scale parameter ratio

Full size image

5 Conclusion

In this paper, the vibrations responses of microcantilever are studied under the coupled stress theory for uniform photothermal excitation. The governing equations for microcantilever are derived considering the scale effect. Using relaxation method, results of response of cantilever are compared with that obtained using thermoelastic microscopy and show good agreement. The influence of the ratio of thickness to scale parameter on the deflection of microcantilever is discussed. The research denotes that when the thickness of the microcantilever is close to the internal material length scale parameter, the resonant frequencies and deflections on the basis of modified coupled stress theory are significantly different from those predicted by the classical theory remarkable. It is shown that the scale effect is remarkable and cannot be neglected for microcantilevers when the thickness of microcantilever decreases. With the thickness of microcantilever close to its length scale parameter, like AFM, the application of non-classical theory is very important for accurately describing its behavior, and also design purpose.