Introduction

Asymptote and asymptotic behaviour are mathematical notions widely explored and used in modern mathematics, from numerical analysis to computational mathematics. They also appear in different mathematical domains and levels of mathematics education—algebra, geometry, and calculus. The relevance of asymptotes is particularly pronounced in the context of the limit of functions in calculus education, since these two notions are mutually entwined, where asymptotes imply limiting behaviour of a function and calculating limits gives the asymptotes. To coherently teach a concept as broad as asymptotes across different educational levels, special attention should be given to the careful integration of different pieces of knowledge—from the first encounter with asymptotes to their feasible formal theoretical grounding and applications. We have conducted comprehensive research on asymptotes and asymptotic behaviour in mathematics education, observing that the literature addresses the secondary or undergraduate student knowledge of particular notions, such as horizontal asymptotes and asymptotes of rational functions, without vertically connecting them through the educational levels. Since the content relating to asymptotes spans through upper secondary and higher education as two consecutive educational levels, we focused on prospective mathematics teachers as a relevant group for our study. On the one hand, they represent university students with recent experience in upper secondary mathematics education. On the other, they are future carriers of the education process and facilitators of mathematical knowledge at that level of education.

The aim of this study was to develop and examine a comprehensive model of the knowledge of asymptotes and asymptotic behaviour of functions in calculus for prospective mathematics teachers. We selected the Anthropological Theory of the Didactic (ATD) as a theoretical framework that provides efficient tools for representing knowledge of particular mathematical notions (Bosch et al., 2020). This enabled us to build the model, examine how future teachers relate to it and, consequently, to refine the model based on the findings. The study results provide good insight into the actual state of mathematics education regarding asymptotes and activities that motivate and enhance the knowledge of function limits and behaviour in calculus, promoting asymptotes as a potentially powerful context for developing knowledge related to the limits and function behaviour. Finally, a transparent and detailed structure and development of the knowledge about asymptotes can serve as a starting point for rethinking and coherently connecting the calculus curricula for upper secondary education and university mathematics teacher education.

Background of the Study

Relationship Between the Knowledge of a Limit and Asymptotes

Asymptotes are mathematical notions closely related to the notion of limits of a function. This was observed in the geometry of the seventeenth century, when French mathematician Girard Desargues named the asymptotes of a hyperbola as its tangent lines, with the tangency point on a branch of a hyperbola at an infinite distance from its centre (Burton, 2011). Today, the asymptotic behaviour of a function is treated dominantly within numerical analysis. For example, two functions are considered asymptotically equivalent if their quotient tends to one as their argument tends to infinity (De Bruijn, 1958). Thus, the formal requirements for a certain asymptotic behaviour of a function are inevitably expressed by a function limit. Following the connection between these notions, the knowledge of asymptotes emerged within the mathematics education research on limits.

Research has shown that university student ideas of limits were reduced to the “image” of a monotonically increasing function bounded from above by the corresponding horizontal asymptote (Conner, 2013; Przenioslo, 2004; Roh, 2008; Szydlik, 2000; Williams, 1991). Students who showed such reduced images were less efficient in problem-solving with limits (Przenioslo, 2004), or had difficulties understanding the definition and finding the limit of a sequence (Roh, 2008). However, knowledge of asymptotes spurred student discourse about the limiting behaviour of functions. Yerushalmy (1997) studied how high school precalculus students related linear and polynomial asymptotes to the quotient of polynomials in a rational function formula by analysing graphical representations using ICT. They justified the procedure informally during classroom discussion, claiming the quotient of the remainder and the denominator in the polynomial division was negligible at infinity. Mok and Johnson (2000) used graphic calculators in secondary school lessons about asymptotes of rational functions with an emphasis on multiple representations of such functions. Following the graphical and numerical representation, students observed that the slant asymptote occurs when the slope of the function graph becomes constant as x → ∞. Swinyard and Larsen (2012) explored college student attempts to “reinvent” the formal definition of the function limit by presenting them examples of functions with a finite limit at infinity. Interpreting the asymptotic behaviour of these functions by focusing on the change of the ordinates of points on their graphs toward the potential limit values helped students to construct the formal definition. Kidron (2011) reported that a high school student who initially described that the graph of a function approaches its horizontal asymptote “in a monotonic way” and does not intersect it, used different tools to explore functions with a finite or infinite number of intersections with their asymptotes. By exploring given examples algebraically and numerically, the student noted that her ideas conflicted with the formal definition of a horizontal asymptote. Nair (2010) found that working in small groups, focused on resolving observed misconceptions regarding limits, asymptotes and continuity of rational functions, helped university calculus students to develop more coherent ideas about these notions.

Studies from different settings and educational systems have shown that an introduction to the notion of asymptotes precedes its formal definition with the limit (Berger & Bowie, 2012; Čižmešija et al., 2017; Elia et al., 2009; Kajander & Lovric, 2009; Kidron, 2011; Mudaly & Mpofu, 2019; Raman, 2002; Yerushalmy, 1997; Zarhouti et al., 2014). Students had their first encounter with asymptotes in a setting with elementary functions with graphs approaching, but not intersecting, their asymptotes (Berger, 2018; Čižmešija et al., 2017; Kidron, 2011; Mpofu & Pournara, 2018; Mudaly & Mpofu, 2019). Though students were required to calculate the limit of various algebraic expressions, they were not required or encouraged to relate the values obtained to the asymptotic behaviour of the corresponding functions (Barbé et al., 2005; Nair, 2010; Zarhouti et al., 2014). Several studies also reported students’ issues with recognizing the limit of a function in the context of vertical asymptotes (Dahl, 2017; Elia et al., 2009; Raman, 2002). Additionally, students related vertical asymptotes of a function only to its domain, such as to the zero of the denominator of an algebraic fraction (Beynon & Zollman, 2015; Dahl, 2017; Kidron, 2011; Nair, 2010), although functions are taught in upper secondary education that are counter-examples to the rule (Elia et al., 2009; Salas et al., 2007; Yerushalmy, 1997). In Croatian upper secondary textbooks, the notion of an asymptote is initially and largely related to the graphing of basic functions and curves. The relationship with limits is realized in the lesson “Application of derivatives in function graphing” by stating and using standard formulas with limits for equations of asymptotic lines, as a part of the procedure of function analysis and graphing (Čižmešija et al.,  2017; Katalenić et al., 2020).

Mathematical Overview of Asymptotes

For convenience, we briefly present the basic mathematical content on asymptotes and asymptotic behaviour of functions. An asymptote of a plane curve is a line such that the distance from a point on the curve to this line tends to zero as the point tends to infinity along an unbounded part of the curve (Janaszak, 2013). The notion of an asymptote extends easily to a real function f of one variable by defining its asymptotes as those of its graph, that is, of the curve y = f(x) in the coordinate plane. Such a function can have vertical, horizontal or slant (oblique) asymptotes, depending on their orientation with respect to the coordinate axes.

Limiting behaviour of functions.

Since asymptotes depict the limiting behaviour of a function at infinity or near a certain point, their formal definition includes function limits. The corresponding representation in the form of a formula depends on the type of asymptote.

  • The line x = a is a vertical asymptote (VA) of the function f if

$$\underset{x\to a}{\lim }f(x)=\infty$$
(1)

Note that the Euclidean distance between the graph of a function and its vertical asymptote is measured along the x-axis and is positive for (almost) all points; that is, the graph and the vertical asymptote can have at most one common point, while they do not intersect if the function is continuous in each point of its domain.

  • The line y = l is a horizontal asymptote (HA) of the function f if

$$\underset{x\to a}{\lim }f(x)=l$$
(2)

This definition includes the case of functions that cross their asymptotes finitely or infinitely many times. The Euclidian distance between points on the function graph and the asymptote is reduced to the vertical distance between ordinates of the corresponding points.

  • The line y = kx + l is a slant asymptote (SA) of the function f if

    $$\underset{x\to \infty }{\lim}\left(f(x)- kx-l\right)=0$$
    (3)

A function and its slant asymptote can intersect finitely or infinitely many times. To deduce explicit formulas for the coefficients k and l, let g(x) = f(x) − kx − l. Then \(\underset{x\to \infty }{\lim }g(x)=0\) and \(\frac{f(x)}{x}-k=\frac{g(x)+l}{x}\) holds, so \(\underset{x\to \infty }{\lim}\left(\frac{f(x)}{x}-k\right)=\underset{x\to \infty }{\lim}\frac{g(x)+l}{x}=0\) follows by the simple application of the algebra of limits (properties of limits). Hence,

$$k=\underset{x\to \infty }{\lim}\frac{f(x)}{x}\ \mathrm{and}\ l=\underset{x\to \infty }{\lim}\left(f(x)- kx\right).$$
(4)

Obviously, if k = 0, the asymptote is horizontal and (4) reduces to (2).

Slant asymptotes are observed geometrically as the lines the function graph approaches at infinity. However, they can also be considered algebraic objects, that is, as functions. Since the slant asymptote y = kx + l is the graph of the linear function h(x) = kx + l, it can, due to (3), be interpreted as a linear approximation of the function f for large (absolute) values of x. Thus, the values f(x) can be approximated with the corresponding values h(x) as x → ∞.

Notice that the formulas above define the two-sided vertical, horizontal and slant asymptotes. If the limit in (1) is one-sided, that is, x → a+ or x → a−, or the limits in  (2) and (3) are taken at +∞ or −∞, then the corresponding asymptotes are respectively regarded as right or left. A function can have zero, finitely or infinitely many one- or two-sided vertical asymptotes, and at most one left and one right one-sided horizontal or slant asymptote. For simplicity, asymptotes shall be referred to as an asymptote, regardless of whether it is one- or two-sided.

Generalizations of asymptotes.

The notion of asymptote can be generalized in many ways, such as by replacing an asymptotic line with an asymptotic curve from a specific class of curves. In terms of functions, instead of a linear approximation of a function as its argument tends to +∞ or −∞, we can look for approximations from another class of functions. Similar to the definition of a linear asymptote, the function g will be a generalized asymptote of a function f if

$$\underset{x\to \infty }{\lim}\left(f(x)-g(x)\right)=0$$
(5)

holds (Janaszak, 2013; Salas et al., 2007; Yerushalmy, 1997). For example, if

$$\underset{x\to \infty }{\lim}\left(f(x)-\left(a{x}^2+ bx+c\right)\right)=0$$
(6)

then the function g(x) = ax2 + bx + c, that is, the curve y = ax2 + bx + c, is the asymptotic parabola (AP) of f. Starting from (6) and by arguments similar to those in the linear case, the following explicit formulas are obtained for the coefficients a, b and c:

$$a=\underset{x\to \infty }{\lim}\frac{f(x)}{x^2},b=\underset{x\to \infty }{\lim}\frac{f(x)-a{x}^2}{x},\mathrm{and}\kern0.5em c=\underset{x\to \infty }{\lim}\left(f(x)-a{x}^2- bx\right).$$
(7)

Such generalizations of asymptotes create a worthy body of knowledge, since a function can be approximated with a simpler one for large values of arguments, that is, with a function whose values are simpler to calculate, such as using Horner’s scheme in the case of a polynomial asymptote. These generalizations provide the opportunity for further study of the asymptotic behaviour of functions. Dobbs (2011) suggested studying asymptotic relations on a well-chosen family D of functions. The functions f, g ∈ D are called asymptotic in the geometric sense if (5) holds, while they are asymptotic in the analytic sense if, for g(x) ≠ 0, \(\underset{x\to \infty }{\lim}\frac{f(x)}{g(x)}=1\). These relations are not equivalent, and one relation does not imply the other. The latter relation is known as the asymptotic equivalence of functions (De Bruijn, 1958).

Anthropological Theory of the Didactic

The study was conducted within the theoretical framework of the Anthropological Theory of the Didactic (ATD). This is a research programme about knowledge and the dissemination of knowledge in institutions (Barbé et al., 2005; Chevallard, 2019), where an institution is considered broadly as any group of individuals who share some knowledge (Winsløw & Grønbæk, 2014), or any created reality of which people can be (permanent or temporary) members (Bosch et al., 2020). ATD postulates that new knowledge is produced in an institution to solve a problem or answer a question. That particular knowledge is then transposed or amended to better fit the context of another institution. Consequently, an individual uses or studies the knowledge under the circumstances of the institution to which they belong. Within ATD, this is formalized as the personal relation of an individual to a body of knowledge in an institution, describing how they know it, under the conditions and constraints of that institution (Chevallard, 2019).

To model knowledge and activities, ATD uses the construct of praxeology. This is one of ATD’s fundamental tools, consisting of two parts: a practical block, praxis, and a discursive block, logos. Praxis refers to knowing how to accomplish something, and logos refers to understanding why that praxis is appropriate, reliable and legitimate. According to García et al. (2006), praxis includes studying problems and how to solve them, while logos includes describing, explaining and justifying praxis and producing new praxes. Praxeological analysis, as a means of structuring and representing knowledge, provides the means to analyse, elaborate and interpret relations to a particular body of knowledge. For example, Barbé et al. (2005) observed that knowledge of limits in the Spanish curriculum for upper secondary education involved two separate and incomplete praxeologies—the praxis of calculating limits of algebraic expressions, stripped of any theoretical considerations, and the logos of stating the formal definition of a function limit without any applications.

ATD considers a body of knowledge as a single praxeology, or a collection of praxeologies, that are recognized by an institution (Chevallard, 2007). In either case, a researcher proposes a reference epistemological model (REM) as a hypothetical, ideal relation to a selected body of knowledge in a selected setting (Chevallard & Bosch, 2014). This REM must be relevant for the observed setting and constructed as a set of connected and coherent praxeologies that are mathematically legitimate. When proposing a REM, the circumstances of the observed institution and the results of mathematics education research must be considered. REM is used for analysis and implementation of didactic problems in educational studies and has to be flexible and open to allow for modifications derived from research results (García et al., 2006; Winsløw et al., 2014).

Reference Epistemological Model for Asymptotes in Calculus

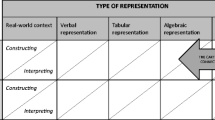
As a starting point for exploring prospective mathematics teachers’ knowledge of asymptotes, we propose a REM to support the body of knowledge about asymptotes and asymptotic behaviour of functions in calculus, denoted as the body of knowledge A. The perspective taken was an extension of the knowledge institutionalized in upper secondary education toward the knowledge institutionalized in the university mathematics education programme in Croatia. Hence, the mathematical content included in this REM originates from two consecutive levels of education. The construction of the REM was based on the literature in mathematics education, our research results, and the formal mathematics related to the body of knowledge A. Our REM consists of four mutually connected praxeologies of increasing complexity. The knowledge about asymptotes develops from introducing and working with asymptotes of familiar elementary functions, through using the function limit to find asymptotes, toward developing formal knowledge of asymptotes. Accordingly, we named the praxeologies: recognition, transformation, calculation and formalization (Fig. 1).

Fig. 1
figure 1

The reference epistemological model (REM) for asymptotes and asymptotic behaviour of functions

Full size image

Recognition and transformation involve precalculus knowledge of function properties, while calculation praxeology is related to calculus and forms a bridge toward the formalization of knowledge of asymptotes in university education. Formalization praxeology is twofold—it provides a reflection on upper secondary work with asymptotes and lays the foundation for further, more advanced and formal mathematical work with them.

Recognition.

We assume the students’ first encounter with the notion of asymptote (logos) is upon exploring the basic classes of elementary functions—exponential, logarithmic, tangent, cotangent and rational—numerically, algebraically and graphically (praxis). We recognize an asymptote as a property of these classes of functions. Thus, the following discourses are appropriate: the function graph approaches the line; the distance between points on the function graph and the line decreases; for argument values of large magnitude, the corresponding function values are approximately equal to the values of a linear function. We observe that prototype functions of the above classes have particular types of asymptotes (Table 1). The knowledge (logos) motivates and supports development of a praxeology for determining asymptotes of these elementary functions.

Table 1 Prototype functions, corresponding types of asymptotes and limit values
Full size table

Transformation.

We transform the formula of an elementary function to determine the equation of its asymptote. The given function formula is algebraically manipulated into an interpretable expression (praxis) with respect to the knowledge of the properties of prototype functions and their asymptotes (logos). If the function is obtained from a prototype function by a certain geometric transformation, then its asymptotes undergo the same transformation. Geometric transformations include vertical and horizontal shift and dilation and reflection of a function graph with respect to the coordinate axes. In the case of a rational function, with polynomials in the numerator and denominator of the corresponding algebraic fraction having no common zeroes, we use polynomial division to break up the formula into the sum of a polynomial and a proper algebraic fraction. Using this algebraic transformation, equations of vertical asymptotes can be obtained from the zeros of the obtained denominator, while the equation of a horizontal or slant asymptote follows from the obtained quotient depending on its degree. The knowledge of limit can be related to and exemplified with the knowledge of asymptotes of elementary functions (Table 1). This motivates and supports the development of knowledge of asymptotes in the domain of calculus (logos).

Calculation.

The formulas (1)–(4) for different types of asymptotes are related to the discourse about the Euclidian distance between points on the graph of a function and its asymptote (logos), introduced earlier. These formulas are introduced informally. We calculate the asymptotes of a function (praxis) from the above formulas (logos) to explore function behaviour at infinity and near certain points.

Formalization.

Further development of the notion of asymptote requires formal mathematics knowledge. This includes proving (justifying, deducing) formulas with limits for asymptotes and producing generalizations of the notion of asymptote, and requires knowledge of limit, including the definition and properties of limit, algebra of limits and knowledge about postulating and proving in formal mathematics (logos).

In view of (5), interpreting non-vertical asymptotes numerically, algebraically and graphically as good and simple approximations of a function for large (absolute) values of argument can elucidate and provide a raison d’être to calculating limits. In particular, this provides meaning (logos) that the functions are asymptotically equivalent in the geometric or analytic sense, to the standard activity (praxis) of calculating the limits of differences and quotients of algebraic expressions, as exemplified in Fig. 2. Considering the above, acquainting prospective mathematics teachers with ideas about generalizations of the notion of asymptote becomes meaningful and reasonable.

Fig. 2
figure 2

Generalizations of asymptotes provide meaning (logos) for evaluating limits of algebraic expressions (praxis)

Full size image

Research Questions

This brief overview of basic mathematical knowledge of asymptotes and asymptotic behaviour of functions, and insights into educational research, indicates the wealth and potential of this research topic. However, the relationship between asymptotic behaviour of functions and the definition, calculation, and interpretation of the function limit is not straightforward to upper secondary and university students. On the other hand, research on asymptotes that explores only students’ or teachers’ comprehension about particular parts of the body of knowledge A, namely, the definition of asymptote or asymptotes of rational functions, fails to address its other aspects.

The aim of this paper was to contribute to the understanding and resolving of these issues by establishing a model of the future mathematics teachers’ relations to body of knowledge A. The study had two objectives. First, we thoroughly explored and built a REM for the body of knowledge A in mathematics teacher education. Second, we investigated and described prospective mathematics teachers’ relations to A in calculus, with respect to the knowledge institutionalized in Croatian upper secondary and university mathematics education, observable through the REM. The following research questions were posed:

  1. 1.

    What praxeologies prospective teachers engage to answer given questions involving asymptotes and asymptotic behaviour of functions? How are these praxeologies related to the institutionalized mathematical knowledge observable through the REM?

  2. 2.

    What discourses about asymptotic behaviour of functions do prospective mathematics teachers give and use in their answers to the given questions? What are the characteristics of their relations to the body of knowledge A?

Methodology

This study was part of a broader research project about asymptotes and asymptotic behaviour in mathematics education in Croatia, conducted under ATD.

Study Participants

In Croatia, initial teacher training for lower and upper secondary mathematics teachers is provided by university mathematics departments. Students enter a 2-year graduate programme in mathematics education after completing a 3-year mathematics or mathematics education undergraduate programme. Participants in this study were the cohort of students—prospective mathematics teachers (age 21 to 23) enrolled in the graduate programme in mathematics education at the Croatian largest mathematics department. They mainly completed the general upper secondary education and graduated with a bachelor’s degree in mathematics education. Their upper secondary education included basic knowledge of elementary functions and calculus (Čižmešija et al., 2017). Undergraduate courses included linear algebra, precalculus, differential and integral calculus and real analysis. The content covered graphs and properties of elementary functions, function investigation and graph sketching using calculus, calculating limits, ε-δ definition of limit and related theorems. Though using ICT is encouraged at all education levels in Croatia, mathematics curriculum still requires students to perform calculations and sketch function graphs manually, without graphing software or using plain scientific calculators only. However, although mentioned, the body of knowledge A was not a subject of particular interest in these courses, nor did the graduate course in the didactic of mathematics cover any content about limits and asymptotic behaviour of functions during our research. We administered three questionnaires to this cohort over 10 months in the didactic of mathematics course. Participation was encouraged, but not mandatory. In total, 37 students were included in this study, where 31 of them completed all three questionnaires and six completed only two.

Selected Questions from the Questionnaires

The administered questionnaires consisted of mathematical tasks and open-ended questions. Students were prompted to work on them without graphing software and explain their work and results. Of the total ten questions, here, we present a qualitative study of students’ answers to six questions which provoked knowledge about asymptotes in calculus (Appendix). The questions omitted here were related to other aspects of asymptotes, such as asymptotes of a hyperbola, and do not contribute to this study. Questions 1.1 and 1.3 regarding graphing elementary functions were selected from the first questionnaire. Although asymptotes were not explicitly mentioned in these questions, they would have occurred in the solutions. Questions 2.2, 2.3 and 2.4 were selected from the second questionnaire, which included four questions addressing different aspects of knowledge about asymptotes: the definition of asymptotes, the relations (1)–(4), finding asymptotes of a rational function, and generalization of the notion of asymptote to higher degree polynomials. We chose Question 3.1 from the third questionnaire, which consisted of three questions regarding the relationship between a function and its asymptote. In Questions 1.1 and 1.3, students had to graph function manually, and in Questions 2.3, 2.4 and 3.1, they were presented with graphs of functions and their asymptotes with different demands. In Table 2, each question was connected to our REM and labelled as routine or non-routine. The question was considered routine if it was a common type of task in the context of upper secondary or university mathematics education; otherwise, it was non-routine. Some questions allowed using different praxeologies from the REM. For example, a slant asymptote of a rational function can be determined by transformation—from polynomial division, or by calculation—from the formulas in (4).

Table 2 Comments on the questions from the questionnaires with respect to REM and routineness
Full size table

Qualitative Analysis of Students’ Answers

The core of our research was a praxeological analysis performed on students’ answers to these questions. All responses were analysed question by question and student by student. First, we determined the praxis in each answer to a particular question as student “know-how”—the way of doing the work (evaluating, calculating, etc.). The corresponding logos was interpreted as the student’s way of thinking according to their written work and explanations. In the second phase, we systematized and described the praxeologies students used in each question, with respect to their peers’ answers and to the proposed REM. Written answers could look differently but still have the same underlying praxeology that describes their work and thinking. An essential step in this phase was to compare the observed student praxeologies with the organisation postulated in the REM. We acknowledged that the observed praxeologies were not necessarily appropriate for the given question.

In addition to the logos of the supporting praxeologies for finding asymptotes, we examined students’ discourses about asymptotes. Descriptions of asymptotic behaviour of functions in Questions 1.1, 1.3 and 3.1 and justification of the characterisation of slant asymptote in Question 2.2.a were expected. Finally, we focused on examining how students used praxeologies in different contexts across questions, in relation to the REM. Their answers can correspond to the expected praxeologies (Table 2 and Table 3) in various ways.

Table 3 Praxeologies from REM in the context of asymptotes of functions from the questionnaires
Full size table

Results

Students’ Praxeologies in Different Questions

The analysis of students’ responses showed they used transformation and calculation from the REM, but with two additional praxeologies: reading-off and asymptotic behaviour. By reading-off, we mean a strategy for determining formula of a function given by its graph. The praxeology works as follows: (1) assume a general form of a formula of a function belonging to a particular class of elementary functions, written with undetermined parameters; (2) read-off coordinates of several points on the function graph in the coordinate plane; (3) evaluate function formula with read-off coordinates and set up a system of equations for function parameters as unknowns; and (4) find the values of parameters by solving the obtained system of equations and write the function formula. By asymptotic behaviour, we refer to examining and evaluating function limiting behaviour, in ways different from evaluating formulas (1)–(4). The numbers of students using certain praxeology varied by question (Table 4). The proportion of students who did not recognize asymptotes was highest for horizontal asymptotes of elementary functions and the slant asymptote of an oscillating function.

Table 4 Frequencies and relative frequencies of using praxeologies across questions
Full size table

Students who used reading-off neglected the context and notion of asymptotes and mostly recognized the equation of the vertical line (x = 0) and the slant line (y = x). In the case of an asymptotic parabola, ten students wrote a formula for a quadratic function and found the parameters by solving a system of linear equations (Fig. 3). Though the coordinate axes were not marked, seven students focused on the coordinates of intersections of the oscillating function and the line. Their logos was based on an unsupported and circular assumption that the intersections have integer abscissas.

Fig. 3
figure 3

A student used reading-off and transformation praxeology to find AP in Question 2.4.c

Full size image

Students mostly used transformation in the case of a vertical asymptote of a rational function and related it to the function domain (Question 2.2b). They rarely used algebraic transformation for the horizontal, slant, or quadratic asymptotes of rational functions (N = 1, N = 1 and N = 6, respectively, Fig. 3). In the case of the oscillating function, five students decomposed the formula into linear and oscillating parts and justified the linear part with respect to the “sinusoidal” shape of the function graph (Fig. 4a).

Fig. 4
figure 4

Students justified the equation of SA in Question 3.1. a Transformation with respect to the function graph. b Preliminary idea about asymptotic equivalence

Full size image

Calculation was used by less than half of students in each question, mostly to obtain the slant (43%) and horizontal asymptotes (35%) of a rational function, or less so (15%) to obtain the slant asymptote of the oscillating function. More students used expressions with a function limit to formalize the definition of vertical asymptote (33%) than using calculation to find vertical asymptotes (0% and 5%). Students wrote different expressions with a function limit for asymptotes. Seven of twelve students wrote \(\underset{x\to a}{\lim }f(x)=a\) or \(\underset{x\to \infty }{\lim }f(x)=a\) instead of (1), while four of eleven wrote the expressions \(b=\underset{x\to \infty }{\lim}\left(f(x)\hbox{--} a{x}^2\right)\) or \(b=\underset{x\to \infty }{\lim}\frac{f(x)}{x}\) for the coefficient b in (7). Three of six students wrote \(k=\underset{x\to \infty }{\lim }f(x)\) for the coefficient k in (4).

As a praxeology, asymptotic behaviour was used by nine students. They started from the concrete equation of a line or a parabola and justified it as a (polynomial) asymptote by evaluating an expression with the function limit (praxis) in the context of the asymptotic behaviour of functions (logos). In one observed logos, students aimed to describe that two functions behave in the same manner at infinity. They wrote the expression \(\underset{x\to \infty }{\lim }f(x)=g(x)\) for an asymptotic function g of the function f. We named this logos a preliminary idea of the asymptotic equivalence of functions, since it is worthy, although the expression with the function limit is awkward. Students used it for the slant asymptotes of rational (N = 2) and oscillating functions (N = 2, Fig. 4b). Another observed logos was characterisation of an asymptotic function g of the function f from (5). Students used it for the slant asymptote (N = 3, Fig. 5) and asymptotic parabola (N = 2) of a rational function. In the case of the oscillating function, two students justified the equation of its asymptote as an approximation.

Fig. 5
figure 5

Student justified equations of both SA and VA by using characterisation (5) in Question 2.3

Full size image

We paid particular attention to students’ praxeologies for justifying the formulas (4). Most of eighteen students who answered Question 2.2b wrote about the slope, y-intercept, or the values of a linear function. Six relevant answers represent the following discourses in calculus: algebra of limits and preliminary ideas about asymptotic behaviour (Fig. 6). Obviously, the students’ supporting logoi for the algebraic manipulation of expressions with limits were incoherent with the formal algebra of limits. Namely, the quotient of limits \(\underset{x\to \infty }{\lim }f(x)\) and \(\underset{x\to \infty }{\lim }x\) cannot be calculated as the limit of the quotient \(\underset{x\to \infty }{\lim}\frac{f(x)}{x}\) as claimed.

Fig. 6
figure 6

Students’ praxeologies for justifying the formulas (4) in Question 2.2.b

Full size image

Further, the informal idea that “the function and asymptote are equal at infinity” cannot be formalized with the equality f(x) = y and operationalized in expressions with a limit. Finally, the relation \(\underset{x\to \infty }{\lim}\left(f(x)-y\right)=0\) does not imply \(\frac{f(x)}{y}\to 1\) as x → ∞ (Dobbs, 2011).

Students’ Discourses in Their Work with Asymptotes

Students gave varied descriptions of asymptotic behaviour. Their phrases were sorted according to the following models of limit: limit as a bound, the dynamic model, and the static model (Table 5). These models emerged in many studies focused on students’ ideas about the notion of limit (Beynon & Zollman, 2015; Bezuidenhout, 2001; Conner, 2013; Cottrill et al., 1996; Fernández-Plaza & Simpson, 2016; Moru, 2009; Przenioslo, 2004; Tall & Vinner, 1981; Williams, 1991). In the dynamic model, the limit of a function is described as a value that function values approach as its argument approaches some given value (including infinity), while in the model of limit as a bound, this (real) value is never reached. The static model is related to the neighbourhood definition of the function limit at a point and at infinity. However, we observed two additional students’ models in our study: the model of limit as a stabilization of values and the model of limit as a tangent line at infinity (Table 5).

Table 5 Students’ descriptions of limiting and asymptotic behaviour in Question 1.3 and 2.2.a, sorted by models of a limit
Full size table

Students mainly used the dynamic model, limit as a bound, or combination of two models. They did not describe asymptotes in other questions, with the exception of one student who combined the static and dynamic model of limit in Questions 1.1 and 3.1:

“For x = 1 the function is not defined, that is, it would be \(\frac{1}{0}=\infty\) so for x close to 1 the function attains very large values [static]. Function values approach 2 as x goes to +∞ or −∞ [dynamic]”,

and

“y = 3x − 1 because sin attains values between −1 and 1, so \(\frac{\mathit{\sin}\left(4\pi x\right)}{x}\) goes to zero as x →  + ∞ [static] and then the function attains values close to values of 3x − 1 [dynamic].”

The stabilization model emerged in students’ descriptions of the limiting behaviour of an exponential function. Their discourses were context driven and unrelated to asymptotes (Milin Šipuš et al., 2019). For example, a student did not recognize the horizontal asymptote of the function, but wrote “as days go by the expected percentage of viewers will stagnate ... around 70%”. The model of a tangent line at infinity emerged in students’ descriptions of (3). They showed no reference to the definition of asymptote as a tangent line of a curve at point at infinity on the curve (Giblin, 1972), although this was introduced in university geometry courses. They wrote “the distance between a point on the graph of the function f and the line is 0 at infinity” or “at infinity, the asymptote and function intersect, that is, f(x) = y, and it follows that, for x →  + ∞, f(x) − y will be = 0”.

Students’ Praxeologies and Their Relation to REM

We observed that students used different praxeologies across and within questions (Table 4). This was most evident in Question 2.4, where 21 students gave a straightforward analogy to equation (3) and wrote (6) to characterize the asymptotic parabola of a function. However, they proceeded with different praxeologies to find the equation of the asymptotic parabola of a given function, namely, calculation (Fig. 7), reading-off (Fig. 3), or transformation (N = 8, N = 5 and N = 2, respectively).

Fig. 7
figure 7

Student used calculation to find the asymptotic parabola in Question 2.4.c

Full size image

We categorized students into six groups (Table 6), based on the praxeologies they applied, and compared with our assumed connections between the questions and REM (Table 2). First, we focused on routine questions with graphs of a rational and exponential function, next on a routine question about asymptotes of a rational function, then a non-routine question about finding the asymptotic parabola and, finally, on a non-routine question about a slant

Table 6 Students’ relations to the body of knowledge A observable through praxeologies applied across questions
Full size table

asymptote of an oscillating function. The remaining questions were excluded from further analysis since students’ responses were too diverse for reasonable categorization. Students’ relations to the body of knowledge A, observable from their praxeologies, were:

  • unsuitable if a student did not recognize asymptotes when graphing elementary functions and used reading-off to determine the equation of a line

  • basic if a student determined asymptotes when graphing elementary functions and used reading-off to determine the equation of a line otherwise

  • routine if a student determined asymptotes in routine questions and used reading-off to determine the equation of a line in non-routine questions

  • explicit if a student determined asymptotes only when explicitly asked to do so, and used praxeologies unrelated to asymptotes otherwise

  • suitable if a student used reading-off to determine the equation of a line when coordinate axes were marked and calculation to determine asymptotes otherwise

  • coherent if a student determined asymptotes of functions in all observed questions.

Students with different relations used different models in their descriptions of asymptotes.

Discussion

Relations of Students’ Praxeologies to the Institutionalized Body of Knowledge A

To describe the body of knowledge A of asymptotes and asymptotic behaviour of functions in calculus, we developed a model (REM) consisting of four connected praxeologies of increasing complexity: recognition, transformation, calculation and formalization, represented at consecutive levels of mathematics education. The results indicated that prospective teachers used different praxeologies. However, many did not recognize, determine or describe asymptotes in the given situations. They relied on reading-off as a universal strategy in situations where they did not recall other effective praxeologies. When reading-off the graph of a line or parabola, students considered them as objects of interest in their own right, focusing on their own properties, separately from the asymptotic behaviour of the corresponding functions. There are several explanations for the use of this praxeology. The first is an emphasis on manipulation with equations of a line and parabola observed in Croatian mathematics education (Čižmešija et al., 2017; Katalenić et al., 2020). The second is an endorsement that students do not manipulate with notions at the object level (Güçler, 2016; Moru, 2009; Nachlieli & Tabach, 2012). In this study, students considered a function and its asymptote as separate objects, rather than interpreting that having an asymptote is a property of a function. The third is that students observed the function and its asymptote from the pointwise perspective—by evaluating the plotted points on the graph of the asymptote, instead from the local one—that the function graph and its asymptote approach at infinity (Katalenić et al., 2020).

Students’ work with asymptotes drew heavily on calculation, that is, on evaluating formulas with a limit to find them. They used calculation in the case of a slant asymptote more often than in other situations. Students mainly used transformation to find vertical asymptotes of rational functions, but rarely to find non-vertical asymptotes by polynomial division. This is in line with the organisation of Croatian upper secondary textbooks (Katalenić, 2020), where obtaining equations of slant asymptotes of rational functions by using (4) is a common activity, while analysing asymptotic behaviour by interpreting function formulas as geometric or algebraic transformations of a familiar prototype function is lacking. The results about vertical asymptotes corroborate the findings of other studies.

On the other hand, student praxeologies varied in the non-routine question on the asymptote of an oscillating function. We interpreted that students were focused on different representations: graphical, numerical or algebraic. Their work in reading-off was based on an algebraic interpretation: using the fact that a slant line is represented by a linear equation, the linear term of the function formula is recognized as a candidate for the equation of the requested line and then justified by evaluating functions pointwise. Students using transformation interpreted the linear and sinusoidal component of the function formula graphically, while those using calculation first graphically interpreted the given line as the slant asymptote of the oscillating function, observing that the function graph approaches it. When using asymptotic behaviour, students numerically interpreted that the sinusoidal term in the given formula is negligible compared to the linear one and discussed the function limiting behaviour at infinity. Students did not recognize that the slant line given in the figure is the asymptote of the given function, so calculation of slant asymptotes was not employed. Although the calculation of slant asymptotes is one of the praxeologies at their disposal, this is not the case with the recognition in the graphical representation of such asymptotes.

The formalization praxeology from the REM had two aspects—proving and generalizing. In both cases, student answers were naive. Although their university education required knowing the neighbourhood definition of limit, properties of limits and infinite limits, most students did not display that knowledge in proving formulas and formally expressing their ideas about generalized asymptotic behaviour. When generalizing to the asymptotic parabola, they made a straightforward analogy between equations (3) and (6) and applied an analogy between the formulas for coefficients k and l in (4) to coefficients a and c in (7). However, deriving the formula for coefficient b from (7) required understanding the asymptotic behaviour rather than giving a direct analogy. Namely, if the asymptotic parabola is observed as an approximation of a rational function for large arguments, then the limiting values of the expressions \(\frac{f(x)}{x^2}\), \(\frac{f(x)-a{x}^2}{x}\) and f(x) − ax2 − bx are directly related to the coefficients of the quadratic quotient in polynomial division. The discourse of approximation serves as a connection between the transformation and calculation praxeologies.

Characteristics of Students’ Discourses and Relations to the Body of Knowledge A

Our insight into students’ discourses relied on the explanations given for their solutions. For example, the supporting discourse in transformation is an asymptote as an algebraic or graphic property of a function, while explaining asymptotic behaviour of a function includes a discourse about approximation. Such discourses were not observed in students’ answers. Students’ discourses related to the asymptote in calculus were algebra of limits and ideas about asymptotic behaviour. The first prevailed in students’ answers since it is part of the upper secondary mathematics education and the essence of formal calculus education in Croatia. Some authors point out, however, that the discourse of algebra of limits is neglected at the expense of evaluating limits of algebraic expressions in upper secondary and university education (Barbé et al., 2005; Bezuidenhout, 2001; Corica & Otero, 2012; Vandebrouck & Leidwanger, 2016). The results of our study support that, since students mainly used calculation in routine questions and showed issues with algebra of limits in non-routine ones. Discourse about asymptotic behaviour appeared sporadically in student answers, and preliminary references about the asymptotic behaviour of functions were related to the generalizations of asymptotes.

Students’ descriptions of asymptotes were related to different models of limit. Their inclination to combine dynamic and bound models of limit was not surprising, since this is the dominant model in the literature. Two additional models of asymptotic behaviour emerged in questions in this study: stabilization and tangent at infinity. A real-life situation described with an exponential-type function induced the model of stabilization that we can relate to the discourse of approximations. The model of tangent at infinity appeared in the discourse about the characterisation of a slant asymptote in (3). The origins of that discourse, and its connection to the limiting behaviour or the geometric definition of an asymptote, remained unclear. Further analysis on this topic is planned.

Our general observation is that students did not easily engage with discourses in mathematics. This is a limitation of our study; hence, deeper insight into student discourses about asymptotes would be beneficial. Additionally, this study is set in the Croatian context, though we believe that the results are generally relevant for mathematics education.

Evaluation of the REM for the Body of Knowledge A in Mathematics Education

The results of this study suggest that our REM described the prospective mathematics teachers’ education about the body of knowledge A suitably but not optimally. We observed that students’ relations to A range from unsuitable to mainly explicit, and their ideas about asymptotic behaviour were informal and intuitive. Students who used transformation in different situations, and asymptotic behaviour in non-routine questions, had coherent relations to A, while most students who used calculation had routine or explicit relations to A. In accordance with the results, we emphasize the following characteristics of the proposed REM as targets for selecting and designing upper secondary and university mathematical tasks and activities that contribute to building comprehensive knowledge of asymptotes and provide support to better understanding function limits:

  • Recognizing an asymptote as a property of various functions, especially in their graphic representation. Using recognition as an essential praxeology, closely related to transformation.

  • Using transformation to determine asymptotes of elementary functions, especially in the context of rational functions. Discussing equations of linear and polynomial asymptotes obtained by polynomial division in the context of approximation of function for arguments of large magnitudes. Making connections between the quotient in polynomial division and formulas with limit at infinity for the coefficients of linear and quadratic asymptotes.

  • Making connections between different representations of asymptotic functions, discourses about asymptotic behaviour and formal expression with a limit.

Observe that implementation of the above characteristics does not require significant interventions in the current precalculus and calculus curricula. On the contrary, they can be taken into account in the usual activities, such as graphing and evaluating functions, calculating limits and finding asymptotes of functions given by a formula, by shifting their focus from praxis (plotting, calculating) to logos (describing, connecting, interpreting). The emphasis is on relating asymptotes of a function to its limiting behaviour and exploring the asymptotic relationship between different functions. Regarding the latter, an interesting direction of further study would be exploration of polynomial asymptotes by prospective mathematics teachers as university students. Polynomial asymptotes provide an analogy to the exploration of slant asymptotes in upper secondary education, formal justifications of upper secondary knowledge of asymptotes, and a generalization of asymptotes that enriches and supplements student knowledge of asymptotes and limits.

The value of the body of knowledge A in mathematics education from the perspective of the designed REM can be discussed. Chevallard (1992) introduced the notions of functional, cultural and epistemological values of a body of knowledge. Asymptotes do not have a cultural or epistemological value comparable to approximation, function or limit, but they are closely related to all these notions. For that reason, asymptotes have functional value since they can provide a context to engage different praxeologies, activities and knowledge, in particular, to motivate and enhance the knowledge of limits.

To elaborate on the functional value of asymptotes and asymptotic behaviour, we used features of the tasks introduced in Gravesen et al. (2017). Linkage potential refers to making connections between different forms of knowledge. As shown above, various interpretations of asymptotic behaviour give meaning to evaluating limits of algebraic expressions, such as the connection between the finite value of a limit of a function at infinity and the equation of its horizontal asymptote (Fig. 2). A task has research potential if it engages students in a scientific-like activity, where they explore objects and relations, observe examples and non-examples, make and investigate hypothesis, prove or disprove it. Our study shows that exploring and formalizing an asymptotic parabola as a generalization of an asymptotic line of a function is a task with research potential in university education. A task with deepening potential provides students with opportunities to elaborate, connect and reflect on their knowledge. Informal ideas about asymptotic behaviour can be formalized to conform with mathematical rigour and algebra of limits.

Conclusions

This study investigated the knowledge of prospective mathematics teachers of asymptotes and the asymptotic behaviour of functions in calculus. We constructed a reference epistemological model for this knowledge with respect to the institutionalized upper secondary and university mathematics education (Fig. 1). To the extent of our knowledge, this is the first educational study to present a comprehensive overview and analysis of the state of knowledge of asymptotes related to the limit of a function.

We discussed that prospective teachers’ discourses were in line with other educational studies and the knowledge institutionalized in Croatian upper secondary education. Most of their work was routine, informal and incoherent. They may have relevant formal knowledge, but did not recall it and associated it with questions about asymptotes. It appeared that the discourse about asymptotes and the tools for working with them were learned in upper secondary education. Bezuidenhout (2001) stated that students entering university education have deficient mathematical knowledge, especially about notions in calculus. Biza and Zachariades (2010) argued in favour of reconstruction of upper secondary mathematical knowledge at the university level. The institution of university mathematics education should question students’ knowledge from upper secondary education, and develop it to be coherent, connected and affirmed with the formal mathematics knowledge.

We explained why the body of knowledge about asymptotes and asymptotic behaviour creates a potentially powerful context to develop students’ knowledge of asymptotes and limits of functions. The potentials of notions and questions discussed here form the basis for designing activities that would engage university students in scientific work and develop their discourses in calculus. By connecting and deepening their mathematical knowledge, we move prospective teachers toward appreciating the comprehensive and coherent knowledge in mathematics and mathematics education.