Introduction

Algebra learning as a preparation for meaningful calculus study requires development of the idea of a function, and particularly functional thinking, defined as a type of “representational thinking that focuses on the relationship between two (or more) varying quantities, specifically the kinds of thinking that lead from specific relationships (individual incidences) to generalizations of that relationship across instances” (Smith 2008, p. 143). Researchers over several decades have highlighted the difficulties students have in advanced algebra and calculus when they have poor conceptual knowledge of functional relationships, which is critical for understanding rate of change concepts and applying calculus in STEM and economics domains (e.g. Bardini and Pierce 2014; Carlson et al. 2002; Oehrtman et al. 2008). Even academically talented undergraduate students have demonstrated conceptual difficulties, suggesting that conventional curriculum content and structure for school algebra have not supported the effective development of students’ understanding of functional relationships (Carlson et al. 2002; Confrey and Smith 1995; Thompson 1994).

In response to calls to prioritise the improvement of algebra teaching in schools (e.g. Carraher and Schliemann 2007; Greenes et al. 2001; Kaput 2008), reform efforts in the USA over the past few decades have drawn attention to the potential of functions-based approaches for algebra learning, even with much younger students. Nevertheless, there are those who continue to advocate the more traditional equations-based approaches (Kieran 2007). In the Australian curriculum context, a hybrid of both traditional and reform approaches to algebra teaching and learning has been adopted (Sutherland 2002). Yet, there are ongoing challenges to ascertain which approach, or a combination of both, might be more effective for helping students develop a comprehensive understanding of functional relationships. Findings from recent research, highlighting the surprising capacity of young students to demonstrate algebraic thinking (e.g. Blanton and Kaput 2004; Brizuela et al. 2015; Swafford and Langrall 2000), continue to challenge long-held beliefs about when and how and in what order algebra concepts ought to be introduced. Nonetheless, researchers have found that students, no matter their age, often exhibit a very limited understanding of even the simplest of functional relationships, linear functions (Van Dooren et al. 2012).

This article discusses findings from a study that investigated Australian secondary school students’ (12 to 18 years old) knowledge of linear functional relationships at different year levels with three different tasks involving four representations—table of values, geometric growing pattern, algebraic equations and graphs. This study is part of a larger international comparative project focusing on relationships among students’ functional thinking development, task design elements, curriculum context and pedagogy (Ayalon et al. 2015, 2016). In our study on linear functions, we intended to explore if, how and when different linear concepts might be understood or develop or connect to each other across the secondary school age range in a particular curriculum context. Our article here reports on the Australian students’ responses to three of the tasks from a survey designed for the larger project. Students from 12 classes in two middle SES (socioeconomic status) government schools (n = 215) attempted a variety of written tasks designed to elicit their knowledge about different functional concepts. The research question for our study was: What evidence of functional thinking do secondary school students demonstrate with linear functions across different contexts and representations?

Given students’ lack of knowledge of linear functions described in the literature, we wanted to consider how students might develop a comprehensive and connected understanding of linear functions and the relationship between variables throughout the secondary years of schooling. We investigated their responses in specific task contexts with chosen representations and also considered how their demonstrated knowledge in one context, such as a real-life scenario represented in a table of values, might relate to their ability to use it in another context, such as pattern generalisation and algebraic rule creation. The following section provides details on theoretical perspectives on knowledge of linear functions and previous research findings that informed the study’s design and analysis.

Related research and context

Two key theoretical perspectives were chosen for exploring secondary students’ knowledge of linear relationships: covariation and correspondence approaches to working with functions, and translating between multiple representations of functions for learning to understand relationships between variables. These are discussed in turn in the following sub-sections along with research findings from the literature. A third sub-section provides information about curriculum content on linear relationships prescribed for Australian secondary students.

Covariation and correspondence views of functions

The development of ideas about change, foundational to the study of functions, begins with quantitative reasoning: “conceptualising an object and an attribute of it so that the attribute has a unit of measure, and the attribute’s measure entails a proportional relationship (linear, bi-linear or multi-linear) with its unit” (Thompson 2011, p. 37). This leads to the idea of variation, in being able to imagine an attribute whose value can vary. Covariational reasoning builds on an awareness of quantification and variation to make sense of the idea of rate of change between two varying quantities in functional relationships (Thompson 1994). Research has highlighted that even young students are able to intuit the basic idea of covariation through observations of change in everyday phenomena (Confrey and Smith 1994).

There are differing meanings for covariation related to how change in varying quantities is perceived. One perspective, built on ratio concepts and related to exponential growth, is that two sequences are generated independently through a pattern of data values and are juxtapositioned (Confrey and Smith 1995). Confrey and Smith (1995) suggested that teaching functions with tables of values can support students in coordinating the two variables in different columns and describing the function covariationally. Carraher and Schliemann (2007) found that even with tables of values, students did not necessarily attend to the invariant relationship between the values in the first and second column but simply relied on term-to-term (recursive) reasoning in each column separately. Another view of covariation based on quantitative reasoning focuses on coordinating two varying quantities (variables) while also attending to the ways in which they change in relation to each other simultaneously (Carlson et al. 2002). Carlson et al. (2002) proposed five levels of covariational reasoning with functions: (1) coordinating the change in one variable with changes in the other variable, (2) coordinating the direction of change, (3) coordinating the amount of change, (4) coordinating the average rate of change of a function and (5) coordinating the instantaneous rate of change of a function.

Thompson et al. (2013) emphasised that students need early experience with the covariation of linear functions that conceptualises a “constant rate of change as two quantities covarying so that changes in one are proportional to changes in the other” (p. 126). Thompson and Carlson (2017) also argued that middle school students building the concept of constant rate of change supports their developing the idea of a function with a non-constant rate of change by thinking of it as “having constant rates of change over small (infinitesimal) intervals of its argument, but different constant rates of change over different infinitesimal intervals of its argument” (p. 452). De Beer et al. (2015) cautioned that the traditional curriculum structure of beginning with only linear functions could make it difficult for students later to understand non-constant rates of change in dynamic situations. In an Australian study of Year 10 secondary students, Herbert and Pierce (2012) examined students’ different ideas about rates of change and found that the students’ highest conception was a numeric relationship between changes in variables in a real-life context, which did not transfer to an abstract context. They suggested that rate of change is complicated for students to understand and troublesome to teach.

A correspondence view of function describes the relationship between two variables with a rule (equation) so that a particular instance of one variable can be used to calculate the matching (corresponding) instance of the other variable, for example y = 3× + 5. Usiskin (1988) considered students learning a correspondence approach to functions an essential aspect of school algebra, and traditional equations-based approaches to algebra have emphasised a correspondence view of functions. Yet, Confrey and Smith (1994) found that students seemed to prefer a covariation approach with tables of values to a correspondence approach with algebraic equations, since tables were “easier and more intuitive” (p. 33).

A development in the past few decades and noticeable in the literature has been an interest in students’ generalisation of growing patterns as a way of developing their functional thinking. There is consensus that generalisation is the foundational cornerstone of mathematical structure (Kruteskii 1976). Moss et al. (2008) argued that patterns “offer a powerful vehicle for understanding the dependent relations among quantities underlying mathematical functions” (p. 156). Although growing pattern generalisation lends itself both to covariation and correspondence approaches, many studies have found that students have been more successful when using a correspondence approach rather than covariation (e.g. Jurdak and Mouhayar 2014; Kaput 2008; Lannin 2005; Radford et al. 2007; Warren and Cooper 2008; Wilkie 2016). Some studies found that students struggled with moving beyond perceiving and describing the patterns recursively (using covariation) to generalising them explicitly and finding the algebraic rule (e.g. Confrey and Smith 1994; English and Warren 1998; Stacey 1989). Hershkowitz et al. (2001) found that after experience with linear growing patterns, lower secondary students could explicitly generalise a more challenging quadratic growing pattern if using a correspondence approach. Jurdak and Mouhayar (2014) studied Lebanese students’ development of linear and quadratic pattern generalisation from grades 4 to 11 and found that despite an increasing level of reasoning across clusters of grades and particularly at grades 10/11, the students tended to struggle to find an explicit generalisation.

Although a correspondence approach has been found to help students create explicit rules for growing patterns, Küchemann (2010) emphasised that the incremental term-to-term (recursive) exploration of functions is nonetheless helpful for students since it is closely allied to the notion of gradient in graphs, necessary for understanding rate of change concepts. He suggested that students learn “to see how term-to-term and position-to-term approaches can complement each other” (p. 242). Thompson et al. (2013) also asserted that a predominant focus on the input-output (correspondence) image of function (e.g. with “function machines”) might not help students learn to understand that variables vary together (covariation). Students are more likely to keep thinking of variables as “letters that stood for constants – but replaceable constants” (p. 129). Despite the recent focus on pattern generalisation in the literature, there is more to understand about how this particular context for developing students’ knowledge of functions might relate to students’ translation of knowledge about functional relationships across other contexts and their ability to understand different representations of functions.

Translating among multiple representations of functions

“A mathematical representation cannot be understood in isolation. The representational systems in mathematics and its learning have structure so that different representations within the system are richly related to one another” (Goldin and Shteingold 2001, p. 2). Schoenfeld (1979) distinguished between learning strategies in isolation and learning to manage a system of specific strategies. Lesh (1981) also emphasised that the ability to use an idea depends on the way it is linked to other ideas and to processes within an appropriate cognitive structure that integrates ideas with a system of processes. These processes are closely related to the representation and organisation of mathematical knowledge. Lesh suggested that mathematical ideas are made meaningful through translations between different representations, such as real-world situations, spoken symbols, written symbols, pictures (static figural models) and manipulative models. Thompson and Carlson (2017) argued that “meaningful learning in calculus relies on students being able to inject meanings they have built in school mathematics into representations of them in calculus while at the same time creating a scheme that unites them symbolically” (p. 453).

One cognitive structure for functions involves conceptualising them operationally as processes or structurally as objects (Sfard 1991) and intersecting these two views with multiple representations of functions (Moschkovich et al. 1993). For example, a graphical representation of a function might encourage an object view since “the infinitely many components of the function are combined into a smooth line” (Sfard 1991, p. 7). An algebraic representation can be interpreted as an operational description of a process (where the equals sign is regarded as a command to execute the right-hand side) or a static relation between two magnitudes (where the equals sign is regarded as a symbol of identity). Historically, an object view suggests a higher-level understanding of functions (Sfard 1991), but Thompson and Carlson (2017) emphasised that when calculus students see functions represented algebraically, they do need to hold a process conception of functions’ rules of assignments to be able to reason covariationally. As with correspondence and covariation views of function, Sfard (1991) highlighted the complementary nature of object and process conceptualisations—their duality rather than dichotomy—so that students learning about functions experience “inseparable, though dramatically different, facets of the same thing” (p. 9).

Romberg et al. (1993) suggested adding the dichotomy of constructing or interpreting a function representation: categories of action that can relate to local or global characteristics of a function (Leinhardt et al. 1990). “Interpretation refers to all actions by which a student makes sense of or acquires a meaning from a specific form of representation. Construction requires an action of generating new parts that are not provided” (Nitsch et al. 2015, p. 664). An integrated framework of these views is presented in Fig. 1.

Fig. 1
figure 1

Conceptualising Moschkovich et al.’s (1993) functions framework with Romberg et al.’s (1993) additional dimensions (source: Wilkie 2016)

Full size image

The “Cartesian connection” is considered a critical translation for students to learn to make—between algebraic equations and their graphs (Moschkovich et al. 1993). It is also foundational for relating the rate of change in a linear equation (described by the co-efficient of x) with the gradient (slope) of its graph. Research has found that this translation is more difficult for students than teachers and curricula assume (Knuth 2000). One study of undergraduate calculus students highlighted their difficulties translating from a graph to an algebraic equation; many of the students had developed isolated pieces of knowledge about functions, which did not transfer across different representations (Knuth 2000). Another study of university students similarly found difficulties in translating between graphs and equations (in both directions) (Van Dooren et al. 2012). It also found that the students were more competent at linking representations to/from concrete pairs of values for variables (tabular representation) than directly translating between a graph and its equation.

The current study was an opportunity to explore Years 7 to 12 students’ use of covariation and correspondence approaches in a variety of tasks involving linear functions represented as a table of values, geometric growing pattern, equation and graph.

Curriculum context of the students in the study

In the Australian curriculum context, a hybrid of both traditional and reform approaches to algebra teaching and learning has been adopted (Sutherland 2002). Content related to linear functions and prescribed for early secondary students includes finding the rule for pattern sequences (reform functional approach), creating and interpreting linear graphs (reform approach), and learning algebraic techniques for manipulating linear expressions and solving linear equations (traditional equations-based approach). The concept of gradient (or slope) appears at a later level in the curriculum and is defined as “a measure of how steeply a line is rising or falling”. Students calculate it using the formula “rise divided by run” with a linear graph or use the co-efficient of x in a linear equation (Australian Curriculum Assessment and Reporting Authority [ACARA] 2014). A rate in “The Australian curriculum: mathematics” is defined as “a particular kind of ratio in which the two quantities are measured in different units” (ACARA 2014), calculated with ratios (unitary method) and with formulae such as for speed. At the middle secondary levels, the curriculum content includes non-linear relationships, such as quadratic, circular and exponential functions.

The following section provides information on the design of the three linear functions tasks completed by the students in the study and how the students’ responses were analysed.

Research design

This study investigated secondary students’ responses to three tasks on linear functions (see Appendices 1 to 3) to look for evidence of students at different year levels being able to use covariation and correspondence views of function across different contexts and with a variety of representations. The tasks were developed by Ayalon et al. (2015, 2016) in collaboration with a group of English and Israeli teachers, and informed by pedagogical experience, knowledge of typical student difficulties and analysis of the different aspects of linear functions knowledge. Leinhardt et al.’s (1990) four constructs for characterising functions tasks were used for designing the tasks (see Table 1) and analysing student responses: the focus of attention within a specific task, the action involved (local or global interpreting or constructing), the task situation (the context of the task and environment of the students) and the variables in the task’s functional relationship.

Table 1 Design of the three tasks using Leinhardt et al.’s (1990) functions constructs
Full size table

In the first task (Appendix 1), the students were asked to interpret a table of values for a linear function in a real-life context. This is likely to be a familiar representation for Australian lower secondary students and encourages both an operational view of function and a covariation approach if paying attention to both of the simultaneously changing variables. It was designed to upset students’ tendency, reported by Stacey (1989) and Orton et al. (1999), to use term-to-term reasoning (which only pays attention to one variable). The task presented independent variable values in the first column that do not increase by one in each row (0, 2, 4, 6, 7). We reasoned that this would encourage students to take the independent variable into account and hence transform a term-to-term approach into a covariational approach. If the students failed to pay attention to both variables, they would be likely to give an incorrect answer to Question 1.1. Question 1.2 prompted the students explicitly to find the rate of change of the function, to elicit subsequent comparison of the two columns and covariational reasoning if it had not occurred in the first question. It is also possible to find the rate of change using a correspondence approach with this task by finding the relationship t = −2n + 14 where n is the floor number and t is the total number of seconds.

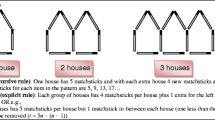
The second task (Appendix 2) was designed to examine the students’ approaches with a geometric growing pattern of chains of hexagons and their construction of a verbal and/or algebraic rule (explicit generalisation). We sought evidence of two aspects of their knowledge: their choice of a correspondence or covariation approach in exploring the relationship between the number of hexagons in a chain and its perimeter, and their ability to generalise the function explicitly and symbolically (task adapted from Wilmot et al. 2011). This type of task encourages a process view of function and a correspondence approach in finding a computational rule where the independent variable (number of hexagons) is operated on to find the matching dependent variable. The students were initially given the perimeters for a chain of 1 hexagon and 3 hexagons, and asked to find the perimeter for some other (non-sequential) chains. A table of values was deliberately excluded from the task, and non-sequential ordered pair examples were also provided to avoid the elicitation of problematic term-to-term (recursive) approaches (Carraher and Schliemann 2007). The students were then asked to explain how they could find the perimeter for 100 hexagons and to construct an algebraic rule for finding the perimeter of any number of hexagons. This was an explicit request for construction of a new representation and no direct support was given, but the prior questions were designed to direct students towards an explicit generalisation. They were then asked to justify their answer to see if they were able to use their reasoning to construct a verbal representation of the functional relationship.

The third task (Appendix 3) was developed to examine the students’ interpretation of a given linear algebraic equation to then select lines parallel to it among four examples, two represented algebraically and two graphically. This abstract context for these two types of representations and the task of finding parallel lines increased the cognitive demand for students in requiring them to draw on and connect their prior knowledge of multiple concepts (parallel lines, algebraic equations, graphs and gradient in different representations). We expected that the task could evoke operational or structural views of function, with a structural view more likely with older students and perhaps related to prior experience with graphical translations. We sought insights into if, how and when the students might connect these concepts in a more abstract linear context by asking them to explain their method.

Data collection and analysis

In matching the data collection for the larger comparative project involving students from Israel and England, this study collected cross-sectional data from 12 classes across two large (middle SES) co-educational government schools in Victoria, Australia—two classes from Years 7, 9 and 11 at one school and two classes from Years 8, 10 and 12 at the other (see Table 2 for numbers of participants at each year level and types of classes). We sought to avoid reporting on individual school effects and overburdening one school and their teaching staff. The two schools adhered to mixed ability classes from Years 7 to 10 and offered a similar range of mathematics subject choices for Years 11 and 12. At each school and in consultation with the Mathematics Leading Teacher and teachers at the requested year levels, two classes of students were invited to complete the functions tasks during a normal time-tabled mathematics lesson (approx. 1-hr duration). All of the students in the classes agreed to participate and submitted a booklet.

Table 2 Number of participants at each year level (n = 215)
Full size table

The students’ responses to Task 1 were analysed for evidence of students’ approaches and ability to find the rate of change using the rubric (0 to 3) presented in Table 3. We did not find any evidence of students using a correspondence approach (developing a rule for the relationship), and so it does not appear in the rubric as a category.

Table 3 Scoring rubric for Task 1 on lift pattern in table of values
Full size table

The students’ responses to Task 2, the hexagon pattern task, were analysed both for evidence of their use of a covariation and/or correspondence approach and their success in finding an explicit generalisation, represented as a verbal description and/or algebraic rule. A rubric for the different approaches was developed and refined collaboratively by the initial research team from the overall project (Ayalon et al. 2015, 2016) and adapted slightly for the Australian responses. For example, an additional Unclear approach category was needed for the Australian data, as there were students who gave a correct algebraic rule but did not explain or show how they found it. The rubric of categories is presented in Table 4 with illustrative samples (note that the numbering of categories is not intended to rank different approaches). The students’ highest level of generalisation of the pattern across their responses to the whole task was also analysed—no generalisation, descriptive generalisation and algebraic generalisation—as the definition for functional thinking focuses on thinking about the relationship between variables in a function for the purpose of generalisation (Smith 2008).

Table 4 Scoring rubric on approaches to Task 2 growing pattern generalisation with Australian illustrative examples
Full size table

In Task 3, we sought evidence of the students’ more formal knowledge of gradient in an abstract context with linear equations and graphs. A scoring rubric (0 to 4) was developed to differentiate between those students who simply responded with incorrect or correct choices and those who explained their responses and gave insight into their method as prompted. To obtain a score of 4, a response needed to include evidence of knowledge about gradient or rate of change that connects equations and graphs. The rubric is presented in Table 5 along with illustrative examples.

Table 5 Scoring rubric for Task 3 on gradient of parallel lines with illustrative examples
Full size table

Cross-tabulations between the students’ responses to the tasks were also analysed for evidence of each students’ ability to translate their linear functions knowledge and understanding of different representations across different problem contexts.

Results

The results of the students’ responses to the three tasks are presented in the first three sub-sections and discussed in terms of their approaches and knowledge demonstrated at different year levels. The results are interpreted in light of their teachers’ expectations and prescribed curriculum content, as well as previous findings from the literature. The subsequent three sub-sections present cross-tabulations to examine the students’ application of knowledge across different contexts.

Task 1 results: Lift pattern in table of values

Figure 2 presents the students’ scored level of their Task 1 response as a percentage within each year level.

Fig. 2
figure 2

Percentages of levels of understanding of rate and covariation within year levels (n = 215)

Full size image

The graph in Table 4 shows some progression across year levels, in the increase of students evidencing covariational reasoning for both parts of the question. The percentage of students in Years 7 and 8, who needed the task prompt to pay attention to both columns in Question 1.2 to calculate the rate of change, decreases in the subsequent year levels. This progression seems to match earlier references in the literature to the benefit of learning about functions with tables of values (Confrey and Smith 1995), since the Australian curriculum content (ACARA 2014) and these students’ textbooks include them for tasks with real-life and abstract functions. Yet, there remain around 20% of students even at higher year levels who, without such a prompt from the task design, would most likely not have detected their faulty term-to-term approach in Question 1.1. All of the teachers, except the Year 7 teachers, expected that their students would be able to complete both questions in the task successfully. The Year 7 teachers expected that only the higher performing students would pay attention to the variables in both columns.

Task 2 results: hexagonal chain pattern task approach and generalisation level

Table 6 presents both the students’ choice of approach for pattern generalisation with their subsequent ability to find an explicit rule for the linear function (no rule or descriptive explicit rule or algebraic rule) at each year level.

Table 6 Approach and levels of pattern generalisation across year levels (n = 215)
Full size table

The data in Table 2 highlight some progression in the ability to create an explicit algebraic rule for the growing pattern, from nearly 20% at Year 7 to 70% at Year 12. There are no noteworthy changes across year levels in the proportion of students choosing a particular approach. As expected, at each year level, a correspondence approach was more popular and more likely to lead to successful explicit generalisation than covariation. Australian students in research studies have been found to be more successful with connecting a correspondence approach conceptually to explicit rules, whether descriptive or algebraic (Stacey 1989; Warren and Cooper 2008; Wilkie 2016). Among those students choosing a covariation approach, there does appear to be a slightly higher likelihood of success in achieving an explicit algebraic generalisation for the upper secondary students, perhaps suggestive of a more connected knowledge of how a linear function’s (constant) rate of change is represented algebraically as the x co-efficient. A surprising number of students did not explain their approach to generalisation but were able to give the correct algebraic rule. Some had actually drawn their own table of values, but it is not clear if they used covariation or correspondence approaches with it. Subsequent individual student interviews (in a later phase of the research and at a different school) have led us to conjecture that some students have learnt a quick procedure for ascertaining the rule from the first difference and starting value in a table or list of ordered pairs (we also found this procedure in lower secondary textbooks).

Overall, the teachers of the Years 7 and 8 students indicated that although they taught these concepts at these year levels, they expected that most students would most likely rely on recursive counting strategies and have difficulty creating an explicit rule. It is interesting that more of the younger students chose a correspondence approach than expected by their teachers, and more students generalised the pattern correctly, but with descriptive rather than algebraic rules. The Years 9 to 12 teachers expected most if not all of their students to be able to generalise the pattern successfully.

Task 3 results: finding parallel lines

Figure 3 presents the students’ knowledge of gradient in the parallel lines task with equations and graphs, as a percentage within each year level.

Fig. 3
figure 3

Percentages of levels of knowledge of gradient within year levels (n = 215)

Full size image

The results in Fig. 3 highlight a noticeable jump in the students’ demonstration of knowledge of gradient at Year 10. The Year 10 teachers, expected most of their students to be able to complete this task successfully, having learnt over several years the meaning of gradient with both algebraic and graphical representations. The Australian Curriculum for Year 10 also explicitly prescribes problem solving with parallel and perpendicular lines (ACARA 2014), which suggests that teachers focus on gradient during that year. It is perhaps surprising that at Year 9, there appears to be very little decrease in the very high proportion of students who evidenced no knowledge of gradient at all with either graphs or algebraic equations since gradient (slope) is taught across Years 7 to 9. The teachers indicated that gradient is taught in the topics “Algebraic equations” (y = mx + c; m is the gradient) and “Straight line graphs” (“rise over run” and later the two points formula) but expected that the parallel lines task context might cause difficulties. In geometry, lower secondary students are introduced to parallel lines, but it seems likely that they were not able to transfer geometric knowledge to an abstract linear functions context. Without a supporting table of values, younger students do not yet easily conceive of gradient, slope or covariation conceptually or transfer them between representations.

A surprisingly large proportion of the Years 11 and 12 students did not demonstrate knowledge of gradient with either the equations or the graphs. Some of the teachers (and the responses of some of the students themselves) suggested that students tend to forget their knowledge of gradient from earlier years of mathematics learning. It seems likely that this type of knowledge develops as an isolated procedure within one context and is therefore difficult to retain or transfer.

In considering the results of the three tasks together across year levels, it can be seen that a higher proportion of the younger students (Years 7–9) evidenced success with finding a rate of change and with explicit pattern generalisation in realistic contexts than expected by their teachers, but an expected (low) proportion evidenced a knowledge of gradient connecting algebraic equations and graphs. Although developmentally, the older cohort of students (Years 9–12) showed an increase in their knowledge across the three tasks, their teachers had expected higher proportions of students to succeed in each task. The following three sub-sections present the results of cross-tabulations of students’ responses across the tasks. In particular, we examined the connection between Tasks 1 and 3 for students who evidenced knowledge of gradient in an abstract context across algebraic and graphical representations, to see if they also successfully found the rate of change in Task 1. We looked for evidence of a connection between successful growing pattern generalisation and creation of an algebraic rule with linear functions knowledge in the other two tasks.

Relating knowledge of gradient and ability to use covariational reasoning with a table of values

Table 7 presents results for the Years 10–12 students, since they were expected to have developed a connected knowledge of gradient as it relates to parallel lines and shows the cross-tabulation of these students’ reasoning in Task 1 with their responses in Task 3.

Table 7 Ability to use covariational reasoning with a table of values and knowledge of gradient Years 10 to 12 (n = 93)
Full size table

The results in Table 7 highlight that nearly half of the Years 10–12 students who evidenced covariational reasoning with the table of values in Task 1 were also able to demonstrate a high level of knowledge of gradient in an abstract context (score of 4 for Task 3). Yet, nearly one third of these students (score of 3 on Task 1) demonstrated no knowledge of gradient at all (22.6% out of 71.0%). There were also small percentages of students who used faulty term-to-term reasoning in Task 1 and either showed no or a high level of gradient knowledge. This result suggests that although many students are able to use covariational reasoning successfully with a table of values to find a rate of change in a real-life context, they do not transfer similar reasoning to the concept of gradient in an abstract context involving algebraic and graphical representations.

Relating successful pattern generalisation by approach and ability to reason with a table of values

The data in Table 8 focus only on those students who were able to generalise the growing pattern in Task 2 (n = 112) and compares their approach with their Task 1 reasoning (table of values).

Table 8 Successful pattern generalisation (n = 112) and ability to use covariational reasoning with a table of values
Full size table

It can be seen that nearly 80% of the students who could generalise the hexagons growing pattern also showed evidence of using covariational reasoning for both questions in Task 1 with the table of values. This suggests that the students who pay attention to the two variables and can apply functional thinking in creating an explicit rule for a growing pattern also pay attention to both variables in the context of interpreting a table of values. Proportionally, more of the students who used a covariation approach for pattern generalisation rather than correspondence evidenced covariational reasoning for both questions in Task 1 (93% rather than 76%), but these amounts are not noteworthy, given the small data sample (n = 112).

Relating successful pattern generalisation by approach with knowledge of gradient

The data in Table 9 focus on only those students who were able to generalise the growing pattern in Task 2 (n = 112) to compare their approach with their knowledge of gradient in Task 3.

Table 9 Successful pattern generalisation by particular approach (n = 112) and knowledge of gradient
Full size table

It can be seen that over half of the students who successfully generalised the growing pattern in Task 2 showed no or an incorrect understanding of gradient in the parallel lines task. This suggests that pattern generalisation tasks as such may not support students’ conceptual understanding of constant rate of change in a different context. This makes sense for students who use a correspondence approach for creating the algebraic rule for the pattern, since they can create the rule without needing to consider the co-efficient of the independent (x or item number) variable as the rate of change of the function. Yet surprisingly, this also appears to be the case even for those students who successfully used a covariation approach for pattern generalisation, since several could not demonstrate a knowledge of gradient with equations in another context.

By far, the most successful approach for pattern generalisation was correspondence (approaches 2 and 5: nearly 70% in total), and these students subsequently evidenced the full range of gradient understanding from no/incorrect knowledge (36.6%) to a connected knowledge across both representations (15.2%). A similar spread of knowledge was found among the much lower percentage of students who had successfully used a covariation approach to generalise (12.5%). A covariation approach to linear pattern generalisation does not seem to correlate with a higher conceptual understanding of gradient or constant rate of change in an abstract context. Proportionally, similar percentages of students choosing either a correspondence or covariation approach demonstrated a high level of gradient knowledge (approx. 25 and 22%, respectively). Nearly 20% of the students successful at pattern generalisation did not explain their approach, and nearly half of these students evidenced no/incorrect gradient knowledge. These results show that for these students, the choice of approach and success with linear pattern generalisation was not noticeably related to their demonstration of gradient or constant rate of change knowledge with abstract linear algebraic equations and graphical representations.

It appears that successfully creating an algebraic rule for a linear growing pattern does not necessarily imply that students can relate the meaning of the parts of a linear equation, such as the co-efficient of the independent variable or the constant, to another abstract linear algebraic equation or graphical representation. And, the reverse also is noticeable, since just over 4% of students could not generalise a growing pattern yet demonstrated a high level of gradient knowledge. This result is at odds with the expectations of their teachers (and the national curriculum) that pattern generalisation occurs at an earlier stage of development than knowledge of constant rate of change and gradient represented algebraically and graphically. It seems that those students who could demonstrate functional thinking in creating an algebraic rule for a pattern generalisation were not more likely to be able to interpret the meaning of the parts of a similar linear equation in another abstract context yet do appear to be more likely to pay attention to both variables when presented with a table of values in a realistic context.

Implications and conclusion

This study investigated Australian secondary students’ functional thinking in three linear contexts with different representations using a cross-sectional survey from Years 7 to 12 (n = 215). The overall intent was to learn more about if, when and how students might develop ideas about relationships between variables using covariation and correspondence views, and connect their knowledge across different task contexts and with different representations of functions. The study contributes to the empirical literature on students’ functional thinking by investigating how students’ approaches to and success with growing pattern generalisation at different year levels might relate to their application of linear functions knowledge in other task contexts used in school algebra teaching.

Developmentally across the range of year levels, there was some increase in the percentage of students demonstrating explicit pattern generalisation ability and an increase in successful algebraic representation at middle secondary school levels and from Years 10/11 to 12. The proportion of students choosing a particular approach (correspondence or covariation) to pattern generalisation also did not vary noticeably at different year levels. Other research studies suggested that the development of functional thinking in this task context might relate more to students’ exposure to and experience with generalisation tasks, than to their maturation over time (Hershkowitz et al. 2001; Jurdak and Mouhayar 2014). In this study, the Year 12 students demonstrated more success with algebraic generalisation (70%) than the Year 7 students (nearly 20%), suggesting that their knowledge of linear functions and equations over time may also have played a role in their success. We wonder if secondary students who have not experienced growing pattern tasks before are nonetheless able to employ a type of representational thinking developed from their exposure to equations-based algebra topics that support successful generalisation. It would be useful in further research to collect data on students’ experience of growing patterns alongside their responses to such tasks and on more challenging non-linear tasks.

The students’ responses evidenced progress with increasing year level in their use of covariational reasoning with tables of values and in their knowledge of gradient across algebraic and graphical representations. Yet, the students did not appear to apply some types of knowledge, for example, the meaning of the parts of a linear equation, used within one task context, to another context. This finding suggests that within a specific task and with a type of representations for learning about functional relationships, these students develop the knowledge for that one context but may not make connections for use in another context, for example, between a linear equation they created from generalising a growing pattern and linear equations in another abstract context. These findings resonate with other studies in the literature highlighting that meaningful learning, particularly for calculus, requires development of connected ways of thinking about function, covariation and rate of change over many years of schooling, rather than the typical memorisation of procedures and rules in many courses (Thompson and Carlson 2017).

This study’s findings indicate that some students experiencing teaching approaches and curriculum content similar to this cohort may not be grasping initially or retaining over time the concepts they have been taught about linear functions. Overall, the older students (Years 9–12) showed an increase in their knowledge within the three tasks, but their teachers had expected higher proportions to succeed at each task. Difficulties with even the foundational ability to find the gradient of a straight line, found in this study, are likely to exacerbate students’ later struggles with rate of change concepts in dynamic situations, an issue highlighted by Carlson et al. (2002).

Overall, a higher proportion of the younger students (Years 7–9) evidenced covariational reasoning for finding an explicit rate of change with a table of values in a realistic context than expected by their teachers. A higher proportion of younger students also demonstrated successful explicit and symbolic pattern generalisation in a familiar geometric context than expected by their teachers, suggesting that professional development highlighting the potential for much earlier teaching with these tasks (Brizuela et al. 2015) would be valuable for upper primary and lower secondary mathematics teachers.

The students across the range of year levels favoured a correspondence approach to explicit generalisation and were more successful with this approach than with covariation. This resonates with other studies of Australian students (Stacey 1989; Warren and Cooper 2008; Wilkie 2016) yet contrasts with a recent study of Israeli students who demonstrated high levels of success with both correspondence and covariation approaches to explicit generalisation. The Israeli students were also more successful than the Australian students with representing their generalisations algebraically and at a younger age (Ayalon and Wilkie under review). Israel’s curriculum content focuses on developing functions concepts more formally at lower year levels (Ayalon et al. 2016), and we suspect that some of the pedagogy described by the Israeli teachers explicitly supports their students making connected meanings for functional relationships at an earlier age.

This study’s findings suggest that these students’ curriculum context of being taught about “rate” as a type of ratio and about “gradient” in abstract contexts with equations and graphs may not highlight to students the system of related ideas about covariation, which is so necessary for understanding non-constant and instantaneous rates of change. Lesh (1981) emphasised that mathematical ideas are made meaningful through translations between different representations. It would have been useful in this study to ask the students specifically about any similar concepts they noticed among the three tasks. Further research would also be worthwhile for developing tasks that require students to use both covariation and correspondence approaches and for examining the effect on students’ development after teaching on comparing and linking several types of representations for the same functional relationship.

There is more to understand about how different representations of functions—tables of values, graphs, algebraic equations, growing patterns and descriptions of functions in real-life contexts—and different task contexts can be used effectively. We suggest that students similar to this cohort, who are experiencing a mixture of equations-based and functions-based approaches to algebra learning, would most likely benefit from earlier and more frequent opportunities to develop stronger connections between covariation and correspondence views of function (Küchemann 2010). For example, with geometric pattern generalisation, there is scope to move beyond simply finding the descriptive and then algebraic rule, to also graphing the pattern and connecting the parts of the algebraic rule not only to the structure of the pattern itself but also to the appearance of the graph and its gradient. Students then have more opportunities to relate the form of a linear algebraic rule they have created themselves, with familiar variables from the pattern, to the function’s behaviour and its constant rate of change. Future research directions include investigating the effect on students’ functional thinking if they learn to generalise the same pattern using both correspondence and covariation approaches, as well as represent the same pattern with multiple representations—verbal, tabular, algebraic and graphical.