Reduction criteria, upper bounds, and a dynamic programming based heuristic for the max–min $k_i$-partitioning problem

Abstract

This paper addresses the max–min $k_i$-partitioning problem that asks for an assignment of n jobs to m parallel machines so that the minimum machine completion time is maximized and the number of jobs on each machine does not exceed a machine-dependent cardinality limit $k_i$ $(i=1,\ldots ,m)$. We propose different preprocessing as well as lifting procedures and derive several upper bound arguments. Furthermore, we introduce suited construction heuristics as well as an effective dynamic programming based improvement procedure. Results of a comprehensive computational study on a large set of randomly generated instances indicate that our algorithm quickly finds (near-)optimal solutions.

1 Introduction

1.1 Problem definition

In this paper we investigate the max–min $k_i$-partitioning problem where we are given a set $\mathcal {M}$ of $m\ge 2$ parallel machines, each having an associated machine-dependent cardinality limit $k_i$ ($i=1,\ldots ,m$) on the maximal number of jobs that can be processed by machine i, and a set $\mathcal {J}$ of n jobs ($m<n\le \sum _{i=1}^mk_i$) with positive integer processing times $p_j\in \mathbb {N}$ ($j=1,\ldots ,n$). Let $C_i$ denote the completion time of machine i ($i=1,\ldots ,m$), which is simply defined as the sum of the processing times of all jobs assigned to i, the objective is to find an assignment (or schedule) that maximizes the minimum machine completion time $C_{{ min}}=\min \left\{ C_1,\ldots ,C_m\right\}$ without exceeding the cardinality limits. Without loss of generality, we assume the jobs and the machines to be labeled so that $p_1\ge p_2\ge \cdots \ge p_n>0$ and $0<k_1\le k_2\le \cdots \le k_m$, respectively.

Introducing binary variables $x_{ij}$ which take the value 1 if job j is assigned to machine i and 0 otherwise, a straightforward formulation of the max–min $k_i$-partitioning problem as an integer linear program consisting of objective function (1) subject to (2)–(5) is provided below.

$$\begin{aligned} \text {Maximize }&C_{{ min}} \end{aligned}$$

(1)

$$\begin{aligned} \text {s.t. }\,&\sum _{j=1}^np_j\cdot x_{ij}\ge C_{{ min}}\qquad i=1,\ldots ,m \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{i=1}^mx_{ij}=1\qquad j=1,\ldots ,n \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{j=1}^nx_{ij}\le k_i\qquad i=1,\ldots ,m \end{aligned}$$

(4)

$$\begin{aligned}&x_{ij}\in \left\{ 0,1\right\} \qquad i=1,\ldots ,m;\,j=1,\ldots ,n \end{aligned}$$

(5)

Objective function (1) maximizes the minimum machine completion time $C_{{ min}}$, which is determined by inequalities (2). Constraints (3) ensure that each job is assigned to exactly one machine and constraints (4) represent the machine-dependent cardinality limits (also referred to as cardinality constraints). Finally, the domains of the binary variables are set by (5).

Obviously, the max–min $k_i$-partitioning problem is a generalization of the classical machine covering problem $P||C_{{ min}}$ which is obtained by dropping constraints (4) or, equivalently, by setting $k_i = n$ for all i (i.e. (4) become redundant). Since problem $P||C_{{ min}}$ is well-known to be $\mathcal {NP}$-hard (cf. Haouari and Jemmali 2008), its generalized version with a limited number of jobs per machine is $\mathcal {NP}$-hard, too.

As mentioned by Dell’Amico et al. (2006), a possible application of $k_i$-partitioning problems arises for instance in the context of Flexible Manufacturing Systems. Here, n is the number of different types of operations, $p_j$ represents the total time required to execute all operations of type j (which have to be assigned to the same cell), m is the number of cells, and $k_i$ represents the capacity of the specific tool magazine of cell i, i.e. $k_i$ restricts the number of types of operations cell i can perform. Another possible application arises in the context of fairly distributing investment projects among different regions (cf. Haouari and Jemmali 2008). Here, the task is to allocate n projects with individual revenues $p_j$ to m regions so that the minimal total revenue of the regions is maximized. If we assume the regions to have individual (staff) capacities to manage and administrate the allocated projects, $k_i$ represents the maximum number of projects that can be handled by region i.

1.2 Literature review

To the best of the authors’ knowledge, specific literature on parallel machine scheduling problems with (machine-dependent) cardinality limits is rather rare. In particular, so far there exists only one contribution to the $k_i$-partitioning problem with the objective of maximizing the minimum completion time. The contribution stems from He et al. (2003) who proposed an approximation algorithm (called HARMONIC2) and studied its worst-case ratio. He et al. (2003) also treated the case where the cardinality limits of the machines are identical, i.e. $k_i = k$ for all $i=1,\ldots ,m$. The corresponding problem is called k-partitioning. Chen et al. (2002) analyzed the worst-case performance of a modified LPT algorithm for 3-partitioning and a variant called Kernel 3-partitioning.

When the objective of maximizing the minimum completion time is altered into the more popular minimization of the maximum completion time (i.e. the makespan), we noticed just three contributions that address machine-dependent cardinality limits $k_i$. The first one is due to Dell’Amico et al. (2006) who provided reduction criteria, lower bounding procedures, and a scatter search algorithm. In the second contribution, Zhang et al. (2009) used an extension of Jain’s Iterative Rounding Method to obtain a polynomial time 3-approximation algorithm. The third contribution stems from Kellerer and Kotov (2011) who presented an elementary 3 / 2-approximation algorithm whose running time is linear in n.

Considering machine-independent cardinality limits, i.e. $k_i=k$ $(i=1,\ldots ,m)$, a few more papers exist. In their extensive study on the $\mathcal {NP}$-hard k-partitioning problem, Babel et al. (1998) derived different lower bound arguments and introduced several approximation algorithms along with their worst-case behaviors. Dell’Amico and Martello (2001) developed further lower bounding procedures and investigated their worst-case performances. In a follow-up paper, Dell’Amico et al. (2004) introduced heuristic and metaheuristic solution procedures such as a scatter search algorithm and they compared their computational performances with a branch-and-bound algorithm. In the special case $k=3$, Kellerer and Woeginger (1993) analyzed the worst-case performance of a modified version of the LPT algorithm and Kellerer and Kotov (1999) introduced a 7 / 6-approximation algorithm. The complexity of Kernel 3-partitioning and the worst-case performance of a modified LPT algorithm have been examined by Chen et al. (1996). Besides, Woeginger (2005) established the existence of a fully polynomial time approximation scheme (FPTAS) for the special case $m=2$.

Regarding the balanced variant of the identical parallel machine scheduling problem with minimum makespan objective, i.e. where each $k_i$ either equals $\lfloor n/m\rfloor$ or $\lceil n/m\rceil$, Tsai (1992) developed a heuristic algorithm for the case $m=2$ and analyzed its asymptotic behavior. Tsai proved that the absolute difference between the optimal makespan and the heuristic makespan is bounded by $\mathcal {O}(\log n/n^2)$, almost surely, when the processing times are independently drawn from a uniform distribution on [0, 1]. Also for $m=2$, Mertens (1999) proposed a complete anytime algorithm. Michiels et al. (2012) investigated the worst-case performance of Karmarkar and Karp’s Differencing Method. They proved that the performance ratio is precisely $2-1/m$ for any fixed $m\ge 2$. When k is given instead of m, they showed that $2-\sum _{i=0}^{k-1} i!/k!$ is a lower bound and $2-1/(k-1)$ is an upper bound on the performance ratio for any fixed k. By means of a novel approach in which the ratios are explicitly calculated using mixed integer linear programming, Michiels et al. also proved that their lower bound is tight for $k\le 7$.

Returning to the objective of maximizing the minimum completion time, we finish our literature review with a selection of substantial contributions to the problem version where no cardinality limits are present, i.e. $P||C_{{ min}}$. Problem $P||C_{{ min}}$ has been first mentioned in Friesen and Deuermeyer (1981) and Deuermeyer et al. (1982) derived a bound on the worst-case performance of the LPT algorithm. Later, Csirik et al. (1992) tightened this bound. Woeginger (1997) presented a polynomial-time approximation scheme (PTAS), and Haouari and Jemmali (2008) provided an exact branch and bound algorithm along with tight upper and lower bounding procedures. Recently, Walter (2013) examined the performance relationship between the LPT algorithm and its restricted version RLPT and Walter et al. (2017) developed improved approaches to the exact solution of $P||C_{{ min}}$ including novel dominance rules and new upper bounding procedures.

1.3 Contribution and paper structure

Motivated by the research gap in the field of upper and lower bounding procedures for the max–min $k_i$-partitioning problem where $C_{{ min}}$ is to be maximized, in this paper we provide new theoretical insights into the problem and propose different approaches towards its efficient solution. Our first major contribution concerns the cardinality limits for which we present procedures to tighten them. Here, we do not only focus on the explicitly given upper limits but also on the derivation of tight (implicit) lower cardinality limits. Secondly, we derive several upper bound arguments and two lifting procedures to tighten the bounds. Eventually, suited solution algorithms—such as fast LPT-based construction heuristics, an exact dynamic programming approach to solve the two-machine case, and a well-performing local search improvement algorithm for multiple machines—constitute the third part of our contribution.

The remainder of the paper is organized as follows. In Sect. 2, we present methods to preprocess a given problem instance. Lifting as well as upper bounding procedures are developed in Sect. 3. Then, Sect. 4 introduces tailor-made construction and improvement heuristics, whose computational performance is tested in a comprehensive computational study (Sect. 5). Finally, Sect. 6 concludes the paper with a brief summary and ideas for future research.

2 Preprocessing

Preprocessing is a proved means to reduce the size of a problem instance, and thus the solution space, often resulting in tighter bounds and an enhanced performance of algorithms in terms of solution quality and/or computation time. In this section, we provide two different approaches to preprocess instances of the max–min $k_i$-partitioning problem. While the first one aims at tightening the cardinality limits of the machines (Sect. 2.1), the second one intends to reduce the dimension of the problem by eliminating machines and jobs in advance (Sect. 2.2).

2.1 Tightening the cardinality limits

As the sum of the cardinality limits $\sum _{i=1}^m k_i$ can be greater than the number of jobs n (cf. Sect. 1), there is basically some potential to tighten the explicitly given upper limits $k_i$ on the maximal number of jobs that can be processed by machine i. At the same time, lower limits $l_i$ on the minimal number of jobs that have to be processed by machine i in any feasible schedule can be derived. Clearly, since we assume that $n>m$, in an optimal solution none of the machines will remain empty, i.e. we are implicitly given lower limits $l_i=1$ $(i=1,\ldots ,m)$. In what follows, we show how to make use of the upper cardinality limits to tighten the lower cardinality limits and vice versa. Later on, in Sects. 3 and 4, the enhanced cardinality limits will not only help us to establish tight upper bounds on the optimal objective value but also to generate high-quality solutions.

To shorten notation, for $1\le i_1\le i_2\le n$ we define

$$\begin{aligned} K_{i_1,i_2}= & {} \min \left\{ \sum _{s=i_1}^{i_2}k_s,\;n-\sum _{s=1}^{i_1-1}l_s-\sum _{s=i_2+1}^{m}l_s\right\} ,\nonumber \\ L_{i_1,i_2}= & {} \max \left\{ \sum _{s=i_1}^{i_2}l_s,\;n-\sum _{s=1}^{i_1-1}k_s-\sum _{s=i_2+1}^{m}k_s\right\} \end{aligned}$$

(6)

and set $K_{i_1,i_2}=L_{i_1,i_2}=0$ in case $i_1>i_2$. It is readily verified that $K_{i_1,i_2}$ represents the maximum number of jobs that can be processed by the machine-subset $\{i_1,\ldots ,i_2\}$: While the first term ($\sum _{s=i_1}^{i_2}k_s$) is due to their individual upper cardinality limits, the second term takes into account that the remaining machines have to process at least $\sum _{s=1}^{i_1-1}l_s+\sum _{s=i_2+1}^{m}l_s$ jobs in order to satisfy their lower limits. Using a similar argument reveals that $L_{i_1,i_2}$ gives the minimum number of jobs that have to be processed on $\{i_1,\ldots ,i_2\}$.

Having in mind that in each feasible solution at most $K_{i,m}$ jobs will be assigned to the last $m-i+1$ machines, there exists at least one machine in $\{i,\ldots ,m\}$ which cannot process more than $\left\lfloor K_{i,m}/(m-i+1)\right\rfloor$ jobs. Moreover, since at most $K_{i,q}$ $(i\le q\le m)$ jobs will be assigned to $q-i+1$ machines $\left\{ i,\ldots ,q\right\}$, there exists at least one machine among them which cannot process more than $\left\lfloor K_{i,q}/(q-i+1)\right\rfloor$ jobs. In conjunction with the initial non-decreasing order of the machines according to their cardinality limits (i.e. $k_1\le k_2\le \cdots \le k_m$), this leads to the following decreased upper cardinality limits

$$\begin{aligned} k_{i}=\min _{q=i,\ldots ,m}\left\{ \left\lfloor \frac{K_{i,q}}{q-i+1}\right\rfloor \right\} ,\quad i=1,\ldots ,m. \end{aligned}$$

(7)

Note that if $K_{i,q} < \sum _{s=i}^{q} k_s$ for at least one $q\in \{i,\ldots ,m\}$, then the upper limit of machine i can be decreased according to (7). In particular, for the first machine we receive $k_1\le \lfloor n/m\rfloor$ which is already quite clear from the fact that not every machine can process more than $\lfloor n/m \rfloor$ jobs.

Analogously, since the $i-q+1$ machines $\left\{ q,\ldots ,i\right\}$ process at least $L_{q,i}$ jobs, there will be at least one machine among them which processes at least $\left\lceil L_{q,i}/(i-q+1)\right\rceil$ jobs. Thus, increased lower cardinality limits are

$$\begin{aligned} l_i=\max _{q=1,\ldots ,i}\left\{ \left\lceil \frac{L_{q,i}}{i-q+1}\right\rceil \right\} ,\quad i=1,\ldots ,m. \end{aligned}$$

(8)

Another option to increase the lower and to decrease the upper cardinality limits, respectively, is described in Walter et al. (2017). Given a valid lower bound LB (see Sect. 4) on the optimal minimum completion time $C_{{ min}}^*$, any improving solution has to process at least $\bar{l}$

$$\begin{aligned} \bar{l}=\mathop {\text {arg min}}\limits _{h=1,\ldots ,n}\left\{ \sum _{j=1}^hp_j> \text {LB}\right\} \end{aligned}$$

(9)

jobs on each machine, i.e $l_i=\max \left\{ l_i,\bar{l}\right\} (i=1,\ldots ,m)$. On the other hand, in an improving solution no machine can process more than

$$\begin{aligned} \bar{k}=\mathop {\text {arg max}}\limits _{h=1,\ldots ,n}\left\{ \sum _{j=n-h+1}^np_j\le \bar{C}\right\} \end{aligned}$$

(10)

jobs, i.e. $k_i=\min \left\{ k_i,\bar{k}\right\} (i=1,\ldots ,m)$, where

$$\begin{aligned} \bar{C}=\mathop {\text {arg max}}\limits _{C\in \mathbb N}\left\{ \left\lfloor \frac{\sum _{j=1}^np_j-C}{m-1}\right\rfloor >\text {LB}\right\} . \end{aligned}$$

Note that if a machine’s completion time exceeds $\bar{C}$, then it is not possible that each of the remaining $m-1$ machines runs longer than LB.

Taking into account that a job will not be processed by more than one machine, an enhanced version of (9) is

$$\begin{aligned} \bar{l}_i=\mathop {\text {arg min}}\limits _{h=1,\ldots ,n-i+1}\left\{ \sum _{j=i}^{h+i-1}p_j> \text {LB}\right\} \end{aligned}$$

(11)

and we obtain $l_i=\max \left\{ l_i,\bar{l}_i\right\}$ $(i=1,\ldots ,m)$. The idea of disregarding the largest $i-1$ jobs when computing enhanced $l_i$-values bases upon the lifting procedure as described in Sect. 3.1 (see proof of Theorem 3.1). Analogously,

$$\begin{aligned} \bar{k}_{m-i+1}=\mathop {\text {arg max}}\limits _{h=1,\ldots ,n-i+1}\left\{ \sum _{j=n-h-i+2}^{n-i+1}p_j\le \bar{C}\right\} \end{aligned}$$

(12)

leads to tightened $k_i$-values by setting $k_{m-i+1}=\min \left\{ k_{m-i+1},\bar{k}_{m-i+1}\right\}$ $(i=1,\ldots ,m)$. Note that if $L_{1,m} > n$ or $K_{1,m} < n$ after application of (9)–(12), then we immediately obtain that LB equals the optimal objective value.

Remark 2.1

Assuming that the machines are sorted according to non-decreasing $k_i$-values and initializing the lower limits with $l_i=1$, application of (7)–(12) will maintain the order of the machines, i.e. we still have $k_1\le \cdots \le k_m$ and $l_1\le \cdots \le l_m$.

2.2 Reduction criteria

Reduction criteria play a crucial role when it comes to reduce a problem’s size (or dimension) and thus the solution space. We start with a straightforward reduction criterion that has already been stated in Dell’Amico et al. (2006).

Criterion 2.2

If $k_1=\cdots =k_{h'}=1<k_{h'+1}$, then there exists an optimal solution in which job 1 is processed by machine 1, job 2 by machine 2,..., and job $h'$ by machine $h'$.

Our other two criteria exploit the lower cardinality limits and require a valid upper bound (denoted by UB) on $C_{{ min}}^*$. Further details on how to compute upper bounds are to be found in Sect. 3.

Criterion 2.3

If the sum of the smallest $l_m$ processing times is greater than or equal to UB, then there exists an optimal solution in which machine m solely processes the jobs $\left\{ n-l_m+1,\ldots ,n\right\}$.

Clearly, if the condition stated in Criterion 2.3 is met, we can reduce the dimension of the problem to $m-1$ machines and $n-l_m$ jobs by fixing the assignment of the shortest $l_m$ jobs to machine m in advance. Afterward, we can check if Criterion 2.3 also applies to the reduced problem. If this is the case, the problem’s dimension reduces further. This process can be iterated until the condition is no longer fulfilled.

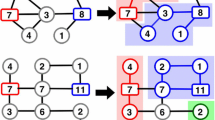
There are two minor drawbacks of the latter approach. First, within each iteration only a single machine is considered and second, the process immediately stops as soon as the condition stated in Criterion 2.3 is not fulfilled any longer. So, if for instance the sum of the smallest $l_m$ processing times is already smaller than UB, then the criterion cannot be applied at all. To overcome these shortcomings, we propose an enhanced iterative reduction procedure as depicted in Fig. 1. In iteration i, we consider the i machines with the largest lower cardinality limits simultaneously. According to their lower limits, these machines have to process at least $L_{m-i+1,m}$ jobs in total. Selecting the shortest $L_{m-i+1,m}$ jobs, we compute a lower bound (e.g. by application of one of our procedures introduced in Sect. 4) on $C_{{ min}}^*$ for the corresponding partial problem (denoted by $PP(\left\{ m-i+1,\ldots ,m\right\} ,\left\{ n-L_{m-i+1,m}+1,\ldots ,n\right\} )$). All in all, the procedure seeks the largest i so that the respective lower bound is at least as large as UB. Then, clearly, we can feasibly reduce the dimension of the problem by removing the machines $m,m-1,\ldots ,m-i+1$ and the shortest $L_{m-i+1,m}$ jobs. A similar reduction procedure for the “dual” $k_i$-partitioning problem with makespan objective is used in Dell’Amico et al. (2006).

Fig. 1

Reduction procedure 1

For problem $P||C_{{ min}}$, Walter et al. (2017) used another trivial reduction criterion which removes a machine and a job if the corresponding processing time is already greater than or equal to UB. Taking the cardinality constraints into account leads us to the following enhanced version of their criterion.

Criterion 2.4

If the sum of the largest processing time $p_1$ and the smallest $l_1-1$ processing times is greater than or equal to UB, then there exists an optimal solution in which the first machine solely processes the jobs $\left\{ 1, n-l_1+2,\ldots ,n\right\}$.

The correctness of Criterion 2.4 is readily verified. As the longest job has to be processed by any machine and all lower cardinality limits are greater than or equal to $l_1$, the machine that processes job 1 has to process at least $l_1-1$ other jobs as well. Thus, its completion time will be at least as large as $p_1+\sum _{i=1}^{l_1-1}p_{n-i+1}$. Clearly, if the completion time is already greater than or equal to UB, then it is not meaningful to assign any other jobs than the shortest $l_1-1$ ones to the machine which processes job 1. As a consequence, the dimension of the problem can be reduced by one machine and $l_1$ jobs.

It is quite obvious, that Criterion 2.4 can also be repeatedly applied in a straightforward manner. However, this raises the same issues as with Criterion 2.3 so that here, too, we propose an enhanced iterative procedure as shown in Fig. 2. This time, in iteration i, we simultaneously consider the first i machines, i.e. the ones with the smallest $l_i$-values, the i largest jobs, and the $L_{1,i}-i$ shortest jobs. For the corresponding partial problem (denoted by $PP\left( \left\{ 1,\ldots ,i\right\} ,\left\{ 1,\ldots ,i,n-L_{1,i}+i+1,\ldots ,n\right\} \right)$) a lower bound on $C_{{ min}}^*$ is determined. The procedure seeks the largest i so that the respective lower bound is greater than or equal to UB and removes the machines $1,\ldots ,i$ and the jobs $1,\ldots ,i,n-L_{1,i}+i+1,\ldots ,n$.

Fig. 2

Reduction procedure 2

3 Bounding the optimal objective value

In this section we are concerned with methods to bound the optimal objective value of the max–min $k_i$-partitioning problem from above. Specifically, we introduce two lifting procedures (Sect. 3.1) and derive several upper bound arguments (Sect. 3.2). The lifting procedures are used to tighten the upper bounds which in turn help us to benchmark our heuristics (see Sect. 4) when optimal solutions are not available.

3.1 Lifting procedures

The basic rationale behind lifting is to identify partial problem instances PP(M, J) of a given instance $(\mathcal {M},\mathcal {J})$ where $M\subseteq \mathcal {M}$, $J\subseteq \mathcal {J}$, and the optimal objective value of PP(M, J) is greater than or equal to the optimal value of the given (initial) instance. Then, by application of upper bounding procedures to PP(M, J) we also obtain upper bounds on the optimal value of the initial instance. Clearly, the more (non-trivial) partial problems we identify, the more likely we obtain a tighter upper bound for the initial instance. For this purpose, we next describe two specific approaches (cf. Corollaries 3.2 and 3.3) to determine a set $\mathcal {P(\mathcal {M},\mathcal {J}})$ of partial problem instances PP(M, J) satisfying the previously mentioned properties.

The first one uses the fact that the i longest jobs ($i\le m-1$) cannot be assigned to more than i machines and the remaining jobs will be assigned to at least $m-i$ machines. For the computation of a feasible upper bound, the remaining jobs can be assumed to be assigned to the $m-i$ machines with the largest upper cardinality limits. Formally, we obtain the following theorem.

Theorem 3.1

For all $i=1,\ldots ,m$, the partial instance $PP(\left\{ i,\ldots ,m\right\} ,\big \{i,\ldots ,i+K_{i,m}-1\big \})$ is an element of $\mathcal {P(\mathcal {M},\mathcal {J}})$.

Proof

Since a job cannot be split among different machines, in any feasible schedule the longest $i-1$ jobs will be assigned to at most $i-1$ machines. Hence, there exist at least $m-i+1$ machines which do not process any of the first $i-1$ jobs. The maximum number of jobs that can be assigned to $m-i+1$ machines is $K_{i,m}$ which is obviously obtained by considering the last $m-i+1$ machines. Thus, the objective value of the optimal assignment of the job-set $\{i,\ldots ,i+K_{i,m}-1\}$ to the machine-set $\{i,i+1,\ldots ,m\}$ constitutes an upper bound for the initial problem, i.e. $PP(\left\{ i,\ldots ,m\right\} ,\left\{ i,\ldots ,i+K_{i,m}-1\right\} )\in \mathcal {P(\mathcal {M},\mathcal {J}})$. $\square$

A generalization of Theorem 3.1 is provided by the next corollary.

Corollary 3.2

For all pairs $(i_1,i_2)$ where $1\le i_1\le i_2\le m$, the partial instance $PP(\{i_1,\ldots ,i_2\},\{i_1,\ldots ,i_1+K_{i_1,i_2}-1\})$ is an element of $\mathcal {P(\mathcal {M},\mathcal {J}})$.

Proof

Clearly, the machine-set $\left\{ i_1,\ldots ,i_2\right\}$ can process at most $K_{i_1,i_2}$ jobs in total. According to Theorem 3.1, there exists an optimal solution in which none of the jobs $1,\ldots ,i_1-1$ is assigned to a machine whose index is greater than $i_1-1$. So, the $K_{i_1,i_2}$ longest remaining jobs that can be processed on $\left\{ i_1,\ldots ,i_2\right\}$ are $\left\{ i_1,\ldots ,i_1+K_{i_1,i_2}-1\right\}$. Optimally assigning this job-set to the machine-set $\left\{ i_1,\ldots ,i_2\right\}$ yields an upper bound on the objective value of the initial instance, i.e. $PP(\left\{ i_1,\ldots ,i_2\right\} ,\left\{ i_1,\ldots ,i_1+K_{i_1,i_2}-1\right\} ) \in \mathcal {P(\mathcal {M},\mathcal {J}})$. $\square$

Our second lifting procedure is based on the following result by Haouari and Jemmali (2008) which proved to be effective in lifting $P||C_{{ min}}$-upper bounds: In any feasible $P||C_{{ min}}$-schedule there exists at least a set of i machines ($i=1,\ldots ,m$) on which in total at most

$$\begin{aligned} \mu _i(n,m)=i\left\lfloor n/m\right\rfloor +\max \left\{ 0,n-m(\left\lfloor n/m\right\rfloor +1)+i\right\} \end{aligned}$$

(13)

jobs are processed. Equation (13) is readily obtained when a “cardinality-balanced” schedule is considered in which the numbers of jobs assigned to the machines are as equal as possible, i.e. each machine processes either $\lfloor n/m\rfloor$ or $\lceil n/m\rceil$ jobs. However, as such a schedule might not be realizable when cardinality limits have to be taken into account, there is some potential to tighten Eq. (13). In that regard, observe that when the first $i-1$ machines process their maximal number of $K_{1,i-1}$ jobs and the upper cardinality limit $k_i$ of the next machine is smaller than or equal to the average number of jobs $\lfloor \frac{n-K_{1,i-1}}{m-(i-1)}\rfloor$ on the remaining machines $i,\ldots ,m$, then the first i machines can process at most $K_{1,i}$ jobs instead of $\mu _i(n,m)$. It is not difficult to see that $K_{1,i}$ is smaller than (or equal to) $\mu _i(n,m)$. We let $\rho$ denote the maximum machine index so that the aforementioned inequality is fulfilled, i.e. 

$$\begin{aligned} \rho =\mathop {\text {arg max}}\limits _{i=1,\ldots ,m}\left\{ k_i\le \left\lfloor \frac{n-K_{1,i-1}}{m-(i-1)}\right\rfloor \right\} . \end{aligned}$$

(14)

Note that $\rho$ is well-defined: For any instance of the max–min $k_i$-partitioning problem we have $\rho \ge 1$ because $k_1\le \lfloor n/m\rfloor$. Then, given $k = (k_1,\ldots ,k_m)$, in any feasible schedule there exists at least a set of i machines ($1\le i\le m$) on which in total at most

$$\begin{aligned} \bar{\mu }_i(n,m,k)={\left\{ \begin{array}{ll} K_{1,i}, &{}\text {if}\,i\le \rho \\ K_{1,\rho }+\mu _{i-\rho }(n-K_{1,\rho },m-\rho ),&{}\text {otherwise} \end{array}\right. } \end{aligned}$$

(15)

jobs are processed. This is a tighter version of Eq. (13), i.e. $\bar{\mu }_i(n,m,k)\le \mu _i(n,m)$ for all n, m, k, and i. Considering the first i machines and the longest $\bar{\mu }_i(n,m,k)$ jobs directly yields the following corollary.

Corollary 3.3

For all $i=1,\ldots ,m$, the partial instance $PP(\{1,\ldots ,i\},\{1,\ldots ,\bar{\mu }_i(n,m,k)\})$ is an element of $\mathcal {P(\mathcal {M},\mathcal {J}})$.

Note that for $i\le q$ the partial instances considered in Corollary 3.3 are identical with the ones in Corollary 3.2 for $i_1=1$ and $i_2=i$.

In sum, we have identified $\mathcal {O}(m^2)$ partial instances (cf. Corollaries 3.2 and 3.3) whose optimal objective values represent upper bounds on the optimal objective value of the given instance. However, as each partial instance itself represents an instance of the max–min $k_i$-partitioning problem we can combine the two lifting procedures, meaning Corollary 3.2 can also be applied to each partial instance obtained from Corollary 3.3 and vice versa. This way, $\mathcal {O}(m^3)$ partial instances are received. Preliminary tests revealed that application of Corollary 3.3 to each partial instance obtained from Corollary 3.2 performs slightly better than the other way around.

Before we proceed to the development of upper bounding procedures we want to emphasize once again that it is not necessary to optimally solve the identified partial instances. Instead, application of upper bounding procedures to the partial instances is sufficient to potentially tighten the upper bound on $C_{{ min}}^*$ of the initial instance.

3.2 Upper bounding procedures

We also derive several upper bound arguments. At first note that any upper bound for $P||C_{{ min}}$ (cf., e.g., Haouari and Jemmali 2008; Walter et al. 2017) is also valid for our max–min $k_i$-partitioning problem. However, as these bounds disregard the cardinality constraints, we will not only consider bounds adapted from $P||C_{{ min}}$ but mainly introduce new upper bounds that explicitly take into account the additional constraints on the minimum as well as maximum number of jobs that can be assigned to each machine. In what follows, we present all of our upper bounds in their most general form, i.e. their computation does not require the application of our preprocessing procedures (see Sect. 2) in advance.

We begin with two simple bounds. The first one is an immediate consequence of Criterion 2.2 (see Sect. 2.2). Recalling that a machine whose upper cardinality limit equals 1 should process the overall longest available job,

$$\begin{aligned} \text {UB}_0=p_{h'} \end{aligned}$$

(16)

where $h' = \mathop {\text {arg max}}\limits _{i=1,\ldots ,m}\{k_i=1\}$ constitutes a trivial upper bound. Note also that $\text {UB}_0$ is the optimal objective if there exists a feasible, but not necessarily optimal, assignment of the remaining jobs to the remaining machines so that each of these machines runs at least as long as $\text {UB}_0$.

Solving the continuous relaxation of $P||C_{{ min}}$ (i.e. (1)–(3) and (5) replaced by $0\le x_{ij}\le 1$ for $i=1,\ldots ,m$ and $j=1,\ldots ,n$) yields the second straightforward upper bound:

$$\begin{aligned} \text {UB}_1 = \left\lfloor \frac{\sum _{j=1}^np_j}{m}\right\rfloor . \end{aligned}$$

(17)

Since $\text {UB}_1$ is easy to compute, application of our two lifting procedures (cf. Sect. 3.1) is to be recommended. If both procedures are combined as described at the end of Sect. 3.1, then the resulting lifted bound is

$$\begin{aligned} \widetilde{\text {UB}}_1=\min _{1\,\le \,i_1\,\le \,i_2\,\le \, m}\left\{ \min _{i=1,\ldots ,i_2-i_1+1}\left\{ \left\lfloor \frac{\sum _{j=i_1}^{i_1+\bar{\mu }_i(K_{i_1,i_2},i_2-i_1+1,k)-1}p_j}{i}\right\rfloor \right\} \right\} . \end{aligned}$$

(18)

Note that $\widetilde{\text {UB}}_1\le \text {UB}_1$ and, if Criterion 2.2 is not applied in advance, we also have that $\widetilde{\text {UB}}_1\le \text {UB}_0$.

At this point, we shall remark that one can also solve the continuous relaxation of the max–min $k_i$-partitioning problem instead of its unconstrained version $P||C_{{ min}}$. However, in order to obtain a (lifted) upper bound from the solution of the continuous relaxation it turned out to be sufficient to consider the unconstrained problem which is not only easier to solve but usually also yields the same bound.

We continue with the development of a more complex upper bound. Let $M\subset \mathcal {M}$ and $J\subset \mathcal {J}$ denote a subset of the machines and jobs, respectively, the next bound bases on the following observation. If the mean completion time of the partial problem PP(M, J) is less than or equal to a valid lower bound LB (cf. Sect. 4) on the optimal objective value $C_{{ min}}^*$, then the mean completion time of the residual problem $PP(\mathcal {M}\setminus M, \mathcal {J}\setminus J)$ is greater than or equal to $C_{{ min}}^*$ and, thus, provides an upper bound UB, i.e.

$$\begin{aligned} \frac{\sum _{j\in J}p_j}{|M|} \le \text {LB}\le C_{{ min}}^*\Rightarrow C_{{ min}}^*\le \frac{\sum _{j\in \mathcal {J}\setminus J}p_j}{m-|M|}= \text {UB}. \end{aligned}$$

(19)

To obtain a tight bound, the determination of M and J is crucial. For this purpose we suggest to solve the following variant of a subset sum problem for each $i\in \{1,\ldots ,m-1\}$:

$$\begin{aligned} \text {Minimize }Z_i=&\sum _{j=1}^n p_j\cdot x_j^i \end{aligned}$$

(20)

$$\begin{aligned} \text {s.t. }\,&\sum _{j=1}^n p_j\cdot x_j^i\ge i\cdot \text {LB} \end{aligned}$$

(21)

$$\begin{aligned}&\sum _{j=1}^n x_j^i\le \bar{\mu }_i(n,m,k) \end{aligned}$$

(22)

$$\begin{aligned}&x^i_j\in \left\{ 0,1\right\} \quad j=1,\ldots ,n. \end{aligned}$$

(23)

By reduction from subset sum, which is well-known to be $\mathcal {NP}$-complete (Garey and Johnson 1979), we obtain that problem (20)–(23) is $\mathcal {NP}$-hard. It seeks for a subset of the jobs whose sum of processing times is minimal (cf. (20)) subject to the constraints that the respective sum is not smaller than i times a given lower bound LB (cf. (21)) and the subset must not contain more than $\bar{\mu }_i(n,m,k)$ jobs (cf. (22)). Then,

$$\begin{aligned} \text {UB}_{2}=\min _{i=1,\ldots ,m-1}\left\{ \left\lfloor \frac{\sum _{j=1}^n p_j-Z_i^*}{m-i}\right\rfloor \right\} \end{aligned}$$

(24)

constitutes an upper bound on $C_{{ min}}^*$ because of the following facts: As LB is a valid lower bound on $C_{{ min}}^*$, in an optimal schedule each machine runs at least as long as LB. In particular, the cumulative completion time of the i machines that process in total at most $\bar{\mu }_i(n,m,k)$ jobs is at least as large as $i\cdot LB$. Recall from Corollary 3.3 that there always exists such a subset of the machines. The optimal objective value $Z_i^*$ of problem (20)–(23) gives the smallest realizable cumulative completion time of the i machines. Hence, the cumulative completion time of the remaining $m-i$ machines is at most $\sum _{j=1}^n p_j - Z_i^*$, i.e. the average completion of these machines is at most $\lfloor (\sum _{j=1}^n p_j - Z_i^*)/(m-i) \rfloor$ so that $\hbox {UB}_2 \ge C_{{ min}}^*$. Clearly, the better the LB the better $\hbox {UB}_2$. We refer to Sect. 4 for the computation of lower bounds.

Since solving each of the $m-1$ problems (20)–(23) requires (at least) pseudo-polynomial time, we abstained from applying our combined lifting approach to $\hbox {UB}_2$. In our experiments (see Sect. 5), we used Gurobi 6.0.3 to solve (20)–(23).

Our next upper bound is a generalization of $\hbox {UB}_0$. Let $r_1\ge 1$ denote the index of the last machine whose upper cardinality limit equals $k_1$, i.e. $r_1 = \mathop {\text {arg max}}\limits _{h=1,\ldots ,m}\left\{ k_h = k_1\right\}$. Then,

$$\begin{aligned} \text {UB}_3 = {\left\{ \begin{array}{ll} \sum _{j = 1}^{k_1-1} p_j + p_{K_{1,r_1}}, &{} \text {if}~K_{1,r_1}=r_1\cdot k_1, \\ \sum _{j = 1}^{k_1-1} p_j, &{}\text {if}~K_{1,r_1}<r_1\cdot k_1 \end{array}\right. } \end{aligned}$$

(25)

constitutes an upper bound. The correctness of $\hbox {UB}_3$ is readily verified. At first recall that $K_{1,r_1}\le r_1\cdot k_1$ (cf. (6)) and $PP(\left\{ 1,\ldots ,r_1\right\} ,\left\{ 1,\ldots ,K_{1,r_1}\right\} ) \in \mathcal {P(\mathcal {M},\mathcal {J}})$ (cf. Corollary 3.2). In case $K_{1,r_1}=r_1\cdot k_1$, the shortest of these jobs, i.e. job $K_{1,r_1}$, must be assigned to one of the first $r_1$ machines. Thus, its assignment to a machine together with the $k_1-1$ longest jobs yields a valid upper bound. In the other case, i.e. $K_{1,r_1}<r_1\cdot k_1$, there exists at least one machine which processes less than $k_1$ jobs.

Since $\hbox {UB}_3$ is easy to compute we suggest to lift this bound according to Corollary 3.2. Let $r_i = \mathop {\text {arg max}}\limits _{h=i,\ldots ,m}\left\{ k_h = k_i\right\}$ for $i=1,\ldots ,m$, then by considering the partial instances $PP(\{i,\ldots ,r_i\},$ $\{i,\ldots ,i+K_{i,r_i}-1\})$ for $i=1,\ldots ,m$ we arrive at the lifted upper bound $\widetilde{\text {UB}}_3=\min _{i=1,\ldots ,m}\left\{ \text {UB}_3(i)\right\}$ where

$$\begin{aligned} \text {UB}_3(i) ={\left\{ \begin{array}{ll} \sum _{j = i}^{i+k_{i}-2} p_j + p_{i+K_{i,r_i}-1}, &{} \text {if}~K_{i,r_i}=(r_{i}-i+1)\cdot k_{i}, \\ \sum _{j = i}^{i+k_{i}-2} p_j, &{}\text {if}~K_{i,r_i}<(r_{i}-i+1)\cdot k_{i}. \end{array}\right. } \end{aligned}$$

(26)

It is readily verified that no other partial instances resulting from application of our lifting procedures (cf. Corollaries 3.2 and 3.3) are able to further improve $\widetilde{\text {UB}}_3$.

Our last upper bound exploits the fact that the well-known LPT algorithm is optimal when $k_i\le 2$ for all $i=1,\ldots ,m$ (cf. also Dell’Amico and Martello 1995). So, let $\underline{r}$ and $\bar{r}$ denote the index of the first and last machine whose upper cardinality limit equals 2, i.e. $\underline{r} = \min \{i\in \{1,\ldots ,m\}:k_i = 2\}$ and $\bar{r} = \max \{i\in \{\underline{r},\ldots ,m\}:k_i = 2\}$, respectively. If $\underline{r}$ exists, then

$$\begin{aligned} \text {UB}_4 = {\left\{ \begin{array}{ll} \min _{j=\underline{r},\ldots ,\bar{r}}\left\{ p_j + p_{2\bar{r}-j+1}\right\} , &{} \text {if}~K_{\underline{r},\bar{r}} = 2(\bar{r}-\underline{r}+1)\\ \min \left\{ \min _{j=\underline{r},\ldots ,2\bar{r}-K_{1,\bar{r}}}\{p_j\}, \min _{j = 2\bar{r}-K_{1,\bar{r}}+1,\ldots ,\bar{r}}\{p_j + p_{2\bar{r}-j+1}\}\right\} , &{} \text {if}~K_{\underline{r},\bar{r}} < 2(\bar{r}-\underline{r}+1) \end{array}\right. }\nonumber \\ \end{aligned}$$

(27)

represents an upper bound which is derived from the (partial) instance $PP(\{\underline{r},\ldots ,\bar{r}\},\{\underline{r},\ldots ,K_{1,\bar{r}}\})$. It is not difficult to see that, this time, the consideration of other partial instances resulting from Sect. 3.1 will not yield a tighter version of $\hbox {UB}_4$.

In case that the best upper bound (denoted by U$^*$) is given by $\widetilde{\text {UB}}_1$ or $\hbox {UB}_2$ there is potential for further improvement. Both $\widetilde{\text {UB}}_1$ and $\hbox {UB}_2$ are grounded on averaged machine completion times, but this does not necessarily mean that a machine can indeed finish exactly at that time. Therefore, we apply the following enhancement procedure (due to Haouari and Jemmali 2008) which computes the largest sum of processing times that is less than or equal to U$^*$ by solving the subset problem (28)–(30):

$$\begin{aligned} \text {Maximize } \text {UB}_5=&\sum _{j=1}^np_j\cdot x_j \end{aligned}$$

(28)

$$\begin{aligned} \text {s.t. }&\sum _{j=1}^np_j\cdot x_j\le \text {U}^* \end{aligned}$$

(29)

$$\begin{aligned}&x_{j}\in \left\{ 0,1\right\} \quad j=1,\ldots ,n. \end{aligned}$$

(30)

Clearly, we have $C_{{ min}}^*\le \text {UB}_5\le \text {U}^*$. In our experiments, problem (28)–(30) is solved via dynamic programming.

We finish this section with an example to illustrate the application of the adjustment procedures (7)–(8) and the lifting procedures (cf. Corollaries 3.2 and 3.3). The effect of combining our two lifting procedures will be clarified as well.

Example 3.4

We consider $n=10$ jobs with processing times $p=(201,102,99,86,82,79,74,73,65,64)$ and $m=5$ machines with upper cardinality limits $k=(3,5,5,5,5)$ and implicit lower limits $l=(1,1,1,1,1)$. An optimal partition of the processing times is $\left\{ \{201\},\{102,74\},\{99,79\},\{86,82\},\{73,65,64\}\right\}$ with $C_{{ min}}^*= 168$.

At first, we apply (7) to tighten the upper limits:

$$\begin{aligned} k_1&=\min \left\{ \left\lfloor \frac{K_{1,5}}{5}\right\rfloor , \left\lfloor \frac{K_{1,4}}{4}\right\rfloor , \left\lfloor \frac{K_{1,3}}{3}\right\rfloor , \left\lfloor \frac{K_{1,2}}{2}\right\rfloor , \left\lfloor \frac{K_{1,1}}{1}\right\rfloor \right\} \nonumber \\&=\min \left\{ \left\lfloor \frac{10}{5}\right\rfloor , \left\lfloor \frac{9}{4}\right\rfloor , \left\lfloor \frac{8}{3}\right\rfloor , \left\lfloor \frac{7}{2}\right\rfloor , \left\lfloor \frac{3}{1}\right\rfloor \right\} =2,\\ k_2&=\min \left\{ \left\lfloor \frac{9}{4}\right\rfloor , \left\lfloor \frac{8}{3}\right\rfloor , \left\lfloor \frac{7}{2}\right\rfloor , \left\lfloor \frac{5}{1}\right\rfloor \right\} =2,\quad k_3=2,\quad k_4=3,\quad k_5=5. \end{aligned}$$

The enhanced upper limits $k=(2,2,2,3,5)$ are now used to improve the lower limits according to (8):

$$\begin{aligned} l_1&=\left\lceil \frac{L_{1,1}}{1}\right\rceil =\left\lceil \frac{1}{1}\right\rceil =1,\quad l_2=\max \left\{ \left\lceil \frac{L_{1,2}}{2}\right\rceil ,\left\lceil \frac{L_{2,2}}{1}\right\rceil \right\} =\max \left\{ \left\lceil \frac{2}{2}\right\rceil ,\left\lceil \frac{1}{1}\right\rceil \right\} =1,\\ l_3&=\max \left\{ \left\lceil \frac{3}{3}\right\rceil ,\left\lceil \frac{2}{2}\right\rceil ,\left\lceil \frac{1}{1}\right\rceil \right\} =1,\quad l_4=\max \left\{ \left\lceil \frac{5}{4}\right\rceil ,\left\lceil \frac{3}{3}\right\rceil ,\left\lceil \frac{2}{2}\right\rceil ,\left\lceil \frac{1}{1}\right\rceil \right\} =2,\\ l_5&=2. \end{aligned}$$

It is readily verified that a repeated application of (7) using the enhanced lower limits $l=(1,1,1,2,2)$ cannot further reduce the upper limits.

Computation of the upper bounds $\text {UB}_1$ and $\text {UB}_3$ yields

$$\begin{aligned} \text {UB}_1 = \left\lfloor \frac{925}{5}\right\rfloor =185\quad \text {and}\quad \text {UB}_3=p_1+p_6=201 + 79 = 280. \end{aligned}$$

Next, we demonstrate the effect of our lifting procedures. With regards to $\hbox {UB}_1$ we first apply Corollaries 3.2 and 3.3 individually. The respective lifted bounds are denoted by $\widetilde{\text {UB}}_1^1 = \min _{1\le i_1\le i_2\le 5} \{\text {UB}_1^1(i_1,i_2)\}$ and $\widetilde{\text {UB}}_1^2 = \min _{i=1,\ldots ,5}\{{ UB}_1^2(i)\}$ where

$$\begin{aligned} \text {UB}_1^1(i_1,i_2)=\left\lfloor \frac{\sum _{j=i_1}^{i_1+K_{i_1,i_2}-1}p_j}{i_2-i_1+1}\right\rfloor ,\quad \text {UB}_{1}^2(i)=\left\lfloor \frac{\sum _{j=1}^{\bar{\mu }_i(n,m,k)}p_j}{i}\right\rfloor . \end{aligned}$$

Now, we briefly present the result of the combined lifting approach (cf. last paragraph of Sect. 3.1). Table 1 provides detailed information on the bounds $\widetilde{\text {UB}}_1^1$, $\widetilde{\text {UB}}_1^2$, and $\widetilde{\text {UB}}_3$. Regarding $\widetilde{\text {UB}}_1^2$, we have $\rho =3$ since $k_4>\left\lfloor 4/2\right\rfloor$ (cf. (14)). As can be seen, we obtain $\widetilde{\text {UB}}_1^1=181$, $\widetilde{\text {UB}}_1^2=185$, and $\widetilde{\text {UB}}_3=184$. Up to this point, $\widetilde{\text {UB}}_1^1$ is the best upper bound. However, when we combine our two lifting procedures as done in (18) we finally receive $\widetilde{\text {UB}}_1 = 174$ which is due to the application of Corollary 3.3 to the partial instance $PP(\{2,\ldots ,5\},\{2,\ldots ,10\})$. Regarding this partial instance, it is readily verified that $\widetilde{\text {UB}}_1^2 = \min \{201,184,174,181\} = 174$.

Table 1 Upper bounds $\hbox {UB}_1^1(i_1,i_2)$, $\hbox {UB}_1^2(i)$, and $\hbox {UB}_3(i)$

4 Algorithms

This section is concerned with the development of lower bounds for the max–min $k_i$-partitioning problem. Specifically, we introduce two LPT-based construction algorithms (Sect. 4.1) and a dynamic programming based improvement heuristic (Sect. 4.2).

4.1 Construction heuristics

To construct initial solutions, we propose two modified LPT algorithms that adequately take the cardinality constraints into account. The two algorithms differ in the way they incorporate the upper and lower limits. While our first variant (called LPT1) primarily concentrates on the upper limits, the second variant (called LPT2) focuses on the lower limits first and observes the upper limits subsequently. Let $n_i$ denote the current number of jobs assigned to machine i, a brief description of our two variants is given below.

LPT1 As long as the number of unassigned jobs, i.e. $n-\sum _{i=1}^m n_i$, is greater than the total number of jobs that are still required to satisfy all lower limits, i.e. $\sum _{i=1}^m\max \{l_i-n_i,0\}$, LPT1 successively assigns the longest remaining job to the machine with the current shortest completion time among all i where $n_i<k_i$. Ties are broken in favor of the machine that has the largest difference $l_i-n_i$. Once $n-\sum _{i=1}^m n_i = \sum _{i=1}^m\max \{l_i-n_i,0\}$, LPT1 successively assigns the longest remaining job to the machine with the current shortest completion time among all i where $n_i<l_i$ until no job remains unassigned. Now, ties are broken in favor of the machine that has the smallest difference $l_i-n_i$.

LPT2 As long as not all lower limits are satisfied, LPT2 successively assigns the longest remaining job to the machine with the current shortest completion time among all i where $n_i<l_i$. This time, ties are broken in favor of the machine that has the smallest lower limit $l_i$. Once $n_i=l_i$ for all i, LPT2 successively assigns the longest remaining job to the machine with the current shortest completion time among all i where $n_i<k_i$ until no job remains unassigned. Now, ties are broken in favor of the machine that has the smallest difference $k_i-n_i$.

4.2 A subset sum based improvement heuristic

To improve on the quality of a given solution we propose an iterative approach whose underlying idea is related to the multi-start local search method used in Haouari and Jemmali (2008) which has proved to be effective for the unconstrained problem version $P||C_{{ min}}$. Assuming the machines to be sorted according to non-decreasing completion times, i.e. $C_1\le \cdots \le C_m$, their method iteratively selects pairs of machines (1, h) for $h=m,\ldots ,2$ and solves the resulting $P2||C_{{ min}}$ instance to optimality. Each $P2||C_{{ min}}$ instance is reformulated as a subset sum problem as follows:

$$\begin{aligned} \text {Maximize }&\sum _{j\in J} p_j\cdot z_j \end{aligned}$$

(31)

$$\begin{aligned} \text {s.t. }\,&\sum _{j\in J} p_j\cdot z_j\le \bigg \lfloor \sum _{j\in J}p_j/2\bigg \rfloor \end{aligned}$$

(32)

$$\begin{aligned}&z_j\in \left\{ 0,1\right\} \quad \forall j\in J \end{aligned}$$

(33)

where $J=J_1\cup J_h$ is the union of jobs that are assigned either to machine 1 or h in the current solution and $z_j$ ($j\in J$) are binary variables that take the value 1 if j is assigned to machine 1 and 0 otherwise. Once a better value for $C_1$ is identified, the machines are resorted and the next iteration begins. If $C_1$ could not be increased after considering all $m-1$ pairs, then the procedure stops. For further details we refer to Haouari and Jemmali (2008).

In the subset sum formulation (31)–(33) for the unconstrained version, one can assume without loss of generality that machine 1 is the one whose completion is not greater than the one of machine h. However, the situation is different when cardinality constraints have to be taken into account. Here, it is not sufficient to simply add the constraint

$$\begin{aligned} \max \{l_1,|J|-k_h\}\le \sum _{j\in J} z_j\le \min \{k_1,|J|-l_h\} \end{aligned}$$

(34)

to (31)–(33) and to solve the model because we can no longer assume the completion time of machine 1 to be smaller than or equal to machine’s h completion time (cf. Example 4.1). Therefore, it is necessary to solve a second model as well where the constraint

$$\begin{aligned} \max \{l_h,|J|-k_1\}\le \sum _{j\in J} z_j\le \min \{k_h,|J|-l_1\} \end{aligned}$$

(35)

is added to (31)–(33) instead of constraint (34) so that this second model, now, forces the completion time of machine h to be not greater than the one of machine 1. In the second model, it is important to note that $z_j$ takes the value 1 if j is assigned to machine h and 0 otherwise.

Example 4.1

Consider $n=5$ jobs with processing times $p=(13,11,7,5,3)$ and $m=2$ machines with upper and lower cardinality limits $k=l=(2,3)$. The corresponding solutions are provided in Tables 2 and 3.

Table 2 Solution w.r.t. (31)–(33) $+$ (34)

Table 3 Solution w.r.t (31)–(33) $+$ (35)

4.2.1 Procedure $k_i$-DP for solving the case $m=2$

To avoid solving two subset sum problems for each pair of machines, we propose the following model (36)–(40) which optimally solves $k_i$-partitioning problems on two parallel machines by minimizing the absolute difference $\Delta$ between the completion time $\sum _{j\in J}p_j\cdot z_j$ of machine 1 and the average completion time $\sum _{j\in J}p_j/2$ of the two machines 1 and h (cf. (36)–(38)) while observing the machine’s cardinality limits (cf. (39)).

$$\begin{aligned} \text {Minimize }&\Delta \end{aligned}$$

(36)

$$\begin{aligned} \text {s.t. }\,&\sum _{j\in J}p_j\cdot z_j\le \sum _{j\in J}p_j/2 + \Delta \end{aligned}$$

(37)

$$\begin{aligned}&\sum _{j\in J}p_j\cdot z_j\ge \sum _{j\in J}p_j/2 - \Delta \end{aligned}$$

(38)

$$\begin{aligned}&\max \left\{ l_{1},|J|-k_{h}\right\} \le \sum _{j\in J}z_j\le \min \left\{ k_{1},|J|-l_{h}\right\} \end{aligned}$$

(39)

$$\begin{aligned}&z_j\in \left\{ 0,1\right\} \quad \forall j\in J \end{aligned}$$

(40)

By reduction from subset sum we obtain that problem (36)–(40) is $\mathcal {NP}$-hard. So, we develop a generic dynamic programming procedure (called $k_i$-DP) to exactly solve $k_i$-partitioning problems on two machines. The input of the procedure is summarized in Table 4. Furthermore, we define a 2-dimensional binary array S of size $(n\,+\,1)\times (C\,+\,1)$ which stores the recursively determined information on the first machine’s realizable completion times—depending on how many of the shortest jobs are considered—without exceeding the maximum allowable number of jobs on that machine (cf. Fig. 3). More precisely, $S[j,c] = 1$ ($0\le j\le n$, $0\le c\le C$) if there exists a subset of the first j jobs (i.e. the shortest ones) so that the subset sum—which represents the completion time of the first machine—equals c and the subset contains at most k elements; otherwise $S[j,c] = 0$. Moreover, associated with each array element [j, c] of S are (i) a binary array $S'_{j,c}$ of length $k+1$ where $S'_{j,c}[k']=1$ ($0\le k'\le k$) if there exists a subset of the first j jobs so that the subset sum equals c and the subset contains exactly $k'$ elements; otherwise $S'_{j,c}[k']=0$, and (ii) an array $P_{j,c}$ of length $k+1$ where $P_{j,c}[k']$ ($0\le k'\le k$) stores the preceding c-value in case that $S'_{j,c}[k']=1$; otherwise $P_{j,c}[k'] = -1$. The arrays $S'_{j,c}$ and $P_{j,c}$ are required to observe the cardinality limits and for backtracking, respectively.

Table 4 Input of $k_i$-DP

Fig. 3

Dynamic programming procedure $k_i$-DP

The initialization of the arrays is as follows:

$$\begin{aligned}&S[0,0] = 1;\quad S[0,c] = 0\;\;(c=1,\ldots ,C)\\&S'_{0,0}[0] = 1;\quad S'_{0,0}[k'] = 0\;\;(k'=1,\ldots ,k);\quad S'_{0,c}[k'] = 0\;\;(k'=0,\ldots ,k)\\&P_{0,c}[k'] = -1\;\;(c=0,\ldots ,C;\,k'=0,\ldots ,k). \end{aligned}$$

Figure 3 provides the pseudo code of $k_i$-DP and the recursion formulas to fill S as well as $S'_{j,c}$ and $P_{j,c}$ for each element [j, c] of S. As can be seen, the respective arrays are filled within three nested loops using conditional statements. The outer loop iterates over the elements p[j] of the array of processing times, the intermediate loop iterates over the allowable completion times c, and the inner loop iterates for each pair (j, c) over the allowable number of jobs $k'$. In case $c<p[j]$ (see 03.–07.), $S[j,c] = S[j-1,c]$ and all entries in the associated $S'_{j,c}$- and $P'_{j,c}$-arrays are copied from the previous row as well. In the other case, i.e. $c\ge p[j]$, it is checked which c-values can be realized—without exceeding the maximum allowable number of addends (or jobs) k—when the integer (or processing time) p[j] becomes available in addition to $p[1],\ldots ,p[j-1]$ (08.–26.). If c can be realized using p[j] (09.–19.), S[j, c] is set to one (11.) and the entries in the associated arrays $S'_{j,c}$ and $P'_{j,c}$ are determined by checking (13.–19.) how many jobs are required to realize c when p[j] is used. Only if c is realized for the first time using exactly $k'$ $(k'=1,\ldots ,k)$ out of the shortest j jobs, $S'_{j,c}[k']$ is set to one and $P'_{j,c}[k']=c-p[j]$ (14.–15.). For all other $k'$, the entries in $S'_{j,c}$ and $P'_{j,c}$ are copied from the previous row (16.–18.). The same is done if c cannot be realized using p[j] (see 20.–25.). After filling the last row of S and the associated arrays $S'_{n,c}$ and $P'_{n,c}$ for all $c=0,\ldots ,C$, the optimal objective value $c^*$ is represented by that column which fulfills $S[n,c^*] = 1$, $S'_{n,c^*}[k'] = 1$ for at least one $k'\in \{l,l\,+\,1,\ldots ,k\}$, and $\left| c^*-\sum _{j=1}^n p[j]/2\right|$ is minimal. The corresponding solution is obtained by backtracking through the $P'$-arrays.

4.2.2 Procedure $k_i$-LS for solving the general case

We use the $k_i$-DP procedure within our iterative local search algorithm (called $k_i$-LS) to generate high-quality solutions for the max–min $k_i$-partitioning problem on an arbitrary (but fixed) number m of machines. Given a feasible solution, each iteration of $k_i$-LS begins with relabeling the machines so that $C_1\le \cdots \le C_m$. Then, we successively consider the machine pair (1, h) for $h=m,\ldots ,2$ and solve the corresponding two machine problem (36)–(40) via $k_i$-DP (where $n=|J|$ $(J=J_1\cup J_h)$, $k=\min \left\{ k_{1},|J|-l_{h}\right\}$, $l=\max \left\{ l_{1},|J|-k_{h}\right\}$, and $C=C_h$). If $C_1< \sum _{j\in J}p_j\cdot z_j < C_h$, then we adopt the new assignment of the jobs in J, i.e. the current solution (to the m-machine problem) is modified by setting $J_1:=\left\{ j\in J: z_j=1\right\}$, $J_h:=J\setminus J_1$, and $C_i:=\sum _{j\in J_i}p_j$ for $i=1,h$. Afterward, the next iteration starts. Otherwise, h is decremented by one. The procedure is stopped if no improvement has been achieved within an iteration, i.e. after sequentially considering all $m-1$ machine pairs (1, h) $(h = m,m-1,\ldots ,2)$.

5 Computational study

This section elaborates on the details of our computational study where we examine the effectiveness of our preprocessing procedures, the tightness of our upper bounding procedures, and the performance of the developed heuristic algorithms. As there is no established test bed available we, first, describe how our test instances have been generated (Sect. 5.1). Then, we specify in which order the developed methods for preprocessing, bounding, and solving a given instance are executed (Sect. 5.2). Finally, we computationally examine the performance of our solution approaches and report on the relevant results in Sect. 5.3.

5.1 Instance generation

In order to generate test instances for our max–min $k_i$-partitioning problem, we adopted the generation scheme used in Dell’Amico et al. (2006) who studied the “dual” problem version, i.e. $k_i$-partitioning with minimum makespan objective. Assuming $n/m\ge 2$, we consider 26 pairs of $n \in \left\{ 10,25,50,100,200\right\}$ and $m \in \left\{ 3,4,5,10,20,40,50\right\}$. For each of these pairs we investigate 81 different combinations of 9 processing time classes (labeled $P_j$) and 9 cardinality classes (labeled $K_i$). For each quadruple ($n,m,P_j,K_i$), 10 independent instances have been randomly generated resulting in a total number of 21,060 ($=26\times 81\times 10$) instances. The full set of instances is available for download from: https://assembly-line-balancing.de/further-data-sets/ki-partitioning.

Table 5 Parameters used for the processing time classes (cf. Dell’Amico and Martello 2001; Dell’Amico et al. 2006)

Regarding the classes $P_j$, the processing times are independently drawn from a discrete uniform distribution on $\{p_{\min },\ldots ,p_{\max }\}$ for classes $P_1$–$P_3$, an exponential distribution with parameter $\lambda$ for classes $P_4$–$P_6$ (disregarding non-positive values), and a normal distribution with mean $\mu$ and standard deviation $\sigma$ for classes $P_7$–$P_9$ (disregarding non-positive values), respectively. Table 5 lists the corresponding parameter values. Turning to the classes $K_i$, the upper cardinality limits are independently drawn from a uniform distribution on $\{k_{\min },\ldots ,k_{\max }\}$ for classes $K_1$–$K_6$ while they are generated according to Fig. 4 for classes $K_7$–$K_9$. The respective parameter values are given in Table 6. Instances where $\sum _{i=1}^m k_i < n$ have been discarded and replaced by new ones. For further information on the cardinality classes we refer to Dell’Amico et al. (2006).

Fig. 4

Cardinality generation method for classes $K_7$–$K_9$ (cf. Dell’Amico et al. 2006)

Table 6 Parameters used for the cardinality classes (cf. Dell’Amico et al. 2006)

Fig. 5

Execution scheme

5.2 Execution scheme

The order in which we executed the developed preprocessing, bounding, and solution methods is provided by Fig. 5. As can be seen, a great deal of effort is put into the preprocessing and bounding step (see Phase 1). With the intention to reduce the problem’s size and to obtain strong upper bounds as well as a good initial solution, we iteratively apply the methods from Sects. 2, 3 and 4.1. Our improvement procedure $k_i$-LS is only applied if the reduced problem contains more than one machine and if there is still a gap between the current best upper and lower bound value U$^*$ and L$^*$ (see Phase 2). After application of $k_i$-LS, we compute the upper bound $\hbox {UB}_2$ (see 26.). The respective subset sum problems (cf. (20)–(23)) are solved with the help of Gurobi (version 6.0.3). Finally, we calculate $\hbox {UB}_5$ in case that the current best upper bound is neither given by $\widetilde{\text {UB}}_3$ nor $\hbox {UB}_4$ (27.–29.; cf. also paragraph on $\hbox {UB}_5$ within Sect. 3.2).

All of our methods have been implemented in C++ using the Visual C++ 2010 compiler and the tests have been carried out on a personal computer with an Intel Core i7-2600 processor (3.4 GHz), 8 GB RAM, and Windows 7 Professional SP1 (64 bit).

5.3 Experimental results

This section reports on the results of our computational tests. Table 7 lists the 12 relevant performance criteria. The first group of criteria (#Ph1, #Red, %$m_{{ elim}}$, %$n_{{ elim}}$) focuses on the performance of the preprocessing and reduction procedures (see Tables 8 and 9). The second group (%GAP, MAX, #OPT, TIME) allows for a general assessment of the overall performance of our bounding and solution methods (see Tables 10 and 11) while the third group (%BESTi, %OPTi, #ImpLift, #$<\widetilde{\text {UB}}_1$) is meant to provide a clear picture on the effectiveness of our bounding and lifting procedures (see Tables 12, 13, 14 and 15).

Table 7 Performance criterion

We start with evaluating the performance of Phase 1 (cf. Fig. 5, steps 01.–22.). The values of the respective performance criteria (cf. first group in Table 7) are provided by Table 8 (broken down by the processing time classes) and Table 9 (broken down by the cardinality classes). The column #Ph1 gives the number of instances that have already been solved within Phase 1 and, thus, allows for an overall assessment of the effectiveness of Phase 1. The column #Red displays the number of instances for which the size could be reduced successfully by application of our reduction criteria (i.e. Criterion 2.2 as well as reduction procedures 1 and 2). In conjunction with the two other criteria %$m_{{ elim}}$ and %$n_{{ elim}}$, #Red allows to judge the performance of the reduction criteria.

Table 8 Performance of the reduction procedures—processing time classes (#instances per class: 2340)

Table 9 Performance of the reduction procedures—cardinality classes (#instances per class: 2340)

Table 10 Overall performance of $\hbox {U}^*$ and $\hbox {L}^*$—processing time classes (#instances per group: 7020)

Table 11 Overall performance of $\hbox {U}^*$ and $\hbox {L}^*$—cardinality classes (#instances per group: 7020)

As can be seen from the #Ph1-column, we are able to optimally solve 3937 out of the 21,060 instances (i.e. almost 19%) already within Phase 1. It is worth noting that for 416 out of the 3937 instances our algorithm has already terminated after step 02. (cf. Fig. 5) because the inequality $\text {UB}_0\ge \text {L}^*$ was fulfilled. Most of these 416 instances belong to the classes $K_2$ and $K_3$ and satisfy $k_i < \lceil n/m\rceil$ for all i.

Phase 1 turned out to be particularly effective when the processing times are drawn from one of the three normal distributions (i.e. $P_7$–$P_9$). Here, 2788 out of the 7020 corresponding instances (i.e. almost 40%) are optimally solved within Phase 1. Regarding the cardinality classes, $K_7$–$K_9$ appear to be the more difficult ones for our reduction procedures as here only 596 (i.e. less than 9%) instances have been solved to optimality at Phase 1.

Table 12 Performance of the upper bounding procedures—processing time classes

Table 13 Performance of the upper bounding procedures—cardinality classes

Table 14 Performance of the lifting procedures and improvement of $\widetilde{\text {UB}_1}$—processing time classes (#instances per class: 2340)

Table 15 Performance of the lifting procedures and improvement of $\widetilde{\text {UB}_1}$—cardinality classes (#instances per class: 2340)

Taking a look at the other three columns, we can state that at least one of our reduction procedures is able to successfully decrease m and/or n for 2443 instances and the overall reduction of m and n is about 3.40 and 3.00% on average, respectively. We shall also remark that $m=2$ holds for 217 of the 2443 reduced instances. Due to the nature of our $k_i$-DP, these instances have later been optimally solved in Phase 2. The largest entries in the columns %$m_{{ elim}}$ and %$n_{{ elim}}$ are to be found in Table 9 (see classes $K_7$–$K_9$). Although the number of instances solved at Phase 1 is rather small for $K_7$–$K_9$, the average numbers of eliminated machines and jobs are ranging between 4.15 and 8.55%. This striking behavior seems to be due to the fact that the cardinality limits are more diverse when they are generated according to $K_7$–$K_9$ (cf. Fig. 4). So, on the one hand, the elimination of machines and/or jobs in advance is fostered but, on the other hand, it is more difficult to optimally solve such instances without application of more elaborate upper and lower bounding procedures as done in Phase 2.

The overall performance of our algorithmic approach and, in particular, Phase 2 is evaluated next. The respective results for each of the 26 parameter settings (n, m) are summarized in the Tables 10 and 11—again broken down by the processing time and cardinality classes, respectively. Analogous to the results reported in Dell’Amico et al. (2006), we noticed that our results are very similar for the related classes $P_1$–$P_3$, $P_4$–$P_6$, $P_7$–$P_9$, $K_1$–$K_3$, $K_4$–$K_6$, and $K_7$–$K_9$, respectively. Therefore, we abstain from providing the results for each individual processing time and cardinality class. Instead, we group the classes accordingly so that each entry in Table 10 and 11 corresponds to 270 ($=3\times 9\times 10$) instances.

Out of the 17,123 instances that remained unsolved after Phase 1, our subset sum based heuristic $k_i$-LS improved the best LPT-solution 15,921 times and $\text {UB}_5$ tightened the best upper bound 696 times so that we were able to solve another 10,743 instances within Phase 2. More precisely, subtracting out the number of instances that have already been solved at Phase 1, we optimally solved 4077 out of the remaining 6438 instances of class $P_1$–$P_3$, 4158 out of 6453 instances of class $P_4$–$P_6$, and 2508 out of 4232 instances of class $P_7$–$P_9$. Regarding the cardinality classes, we optimally solved 3272 out of the remaining 5430 instances of class $K_1$–$K_3$, 2944 out of 5269 instances of class $K_4$–$K_6$, and 4527 out of 6424 instances of class $K_7$–$K_9$. So, the success of Phase 2 in solving an instance is more sensitive to the cardinality limits than the processing times as here the share of solved instances ranges between 55.87 and 70.47% while it ranges only between 59.26 and 64.44% for the processing time classes.

Considering both phases together, we see from the last row in Table 10 that we were able to solve significantly more instances with normally distributed processing times (5296 out of 7020) than with exponentially and uniformly distributed times (4725 and 4659), respectively, and at the same time less computation time was required (0.03 s on average compared to 0.26 and 2.57 s) by $k_i$-LS. On the downside, the overall relative gap between $\hbox {U}^*$ and $\hbox {L}^*$ averages 0.70% for the classes $P_7$–$P_9$ and is therefore greater than the respective average gap (0.61 and 0.39%) for the two other groups of processing time classes. Regarding the cardinality classes, the last row in Table 11 reveals that we identified more optimal solutions (5123 out of 7020 compared to 4862 and 4695) when the cardinality limits were generated according to $K_7$–$K_9$ instead of $K_1$–$K_3$ or $K_4$–$K_6$ although our reduction procedures were not that effective for the classes $K_7$–$K_9$ (cf. Table 9). Altogether, by means of $\hbox {U}^*=\hbox {L}^*$, we were able to identify optimal solutions for 14,680 out of the 21,060 test instances (i.e. almost 70%) and the overall relative gap averaged about 0.57%. While configurations with $n/m>5$ turned out to be rather simple to solve (we found optimal solutions for 9440 out of the corresponding 11,340 instances, i.e. more than 83%), the case $n/m=2.5$ appears to be particularly difficult as we were able to solve only 1154 out of the corresponding 3240 instances (i.e. less than 36%) and the relative gap between $\hbox {U}^*$ and $\hbox {L}^*$ averaged about 2.09%. The greatest relative gaps of up to 27% were also recorded for instances with a small ratio of n to m. The conspicuous behavior of our algorithm on such instances is not that surprising. Haouari and Jemmali (2008) and Walter et al. (2017) also report on similar observations.

Looking at the computational effort of our algorithm, we see that $k_i$-LS requires less time when processing times are small and/or the ratio of n to m is small. These cases typically result in smaller values of C (cf. Sect. 4.2) which itself strongly impacts the time requirement of $k_i$-LS’s sub-routine $k_i$-DP. Clearly, the smaller C, the faster $k_i$-DP determines a solution. Consequently, the computation time of $k_i$-LS is higher for the processing time classes $P_1$–$P_3$ which generate larger processing times on average than the other time classes. Furthermore, the computation time increases when (i) n increases and m is fixed and (ii) n and m increase and n / m is fixed. In both cases, the number of pairs of machines that has to be investigated within the local search part is increasing.

In the last part of our computational study, we carefully evaluate the effectiveness of our upper bound as well as lifting procedures. The respective results are presented in the Tables 12, 13, 14 and 15. The first two tables provide for each of our upper bounds (except $\text {UB}_0$ and $\text {UB}_5$) the relative number of instances for which the respective bound is equal to $\text {U}^*$ and $\text {L}^*$, respectively. The last two tables display the impact of the lifting procedures by counting (i) the number of instances where $\widetilde{\text {UB}}_i<\text {UB}_i$ (for $i\in \{1,3\}$) and (ii) the number of instances where $\text {UB}_i < \widetilde{\text {UB}}_1$ (for $i\in \{2,4\}$) and $\widetilde{\text {UB}}_3 < \widetilde{\text {UB}}_1$.

To allow for a fair comparison of the different upper bounds, we slightly modified the execution scheme in that we did not abort the algorithm as soon as an optimal solution is found but applied each upper bound except for $\text {UB}_0$ and $\text {UB}_5$ since $\text {UB}_0$ can only be calculated in special cases and $\text {UB}_0$ is also dominated by $\widetilde{\text {UB}}_1$. Determining $\text {UB}_5$ is also not meaningful since naturally $\text {U}^*=\text {UB}_5$ holds.

As can be seen from Tables 12 and 13, the rather simple LP-based bound $\text {UB}_1$ and its lifted version $\widetilde{\text {UB}}_1$ are outperforming the other bounds. In terms of numbers, we observed that $\widetilde{\text {UB}}_1 = \text {U}^*$ for 89.04% of the 21,060 problem-instances and $\widetilde{\text {UB}}_1 = \text {L}^*$ for 60.18%. Considering the other, more specialized bounds and their performance with respect to the different cardinality classes it is interesting to note that $\text {UB}_2$ performs quite well for the classes $K_1$–$K_6$ and rather poor for $K_7$–$K_9$ whereas the opposite is the case with the three other bounds. Obviously, the poor quality of $\text {UB}_3$ and $\text {UB}_4$ for $K_1$–$K_6$ is caused by the distribution of the $k_i$-values. Furthermore, Tables 12 and 13 already reveal the significant improvement of $\text {UB}_1$ and $\text {UB}_3$ by application of the combined lifting procedures. From the last two Tables 14 and 15 we see that lifting $\text {UB}_1$ improves the bound for a total of 2790 out of 21,060 instances (i.e. 13.25%) while lifting $\text {UB}_3$ even improves its non-lifted version for a remarkable number of 12,609 instances (i.e. 59.87%) so that application of the lifting procedures is well justified.

Although $\widetilde{\text {UB}}_1$ equals the best upper bound in almost 90%, the last two tables reveal that there exist some instances (about 7%) where $\widetilde{\text {UB}}_3$ and/or $\text {UB}_4$ yield a better upper bound. Most of these instances belong to the class $P_3$ and $K_7$, respectively. So, application of these two bounds is also justified whereas we found that it is not beneficial to also apply $\text {UB}_2$ since it cannot improve on the best upper bound value in about 99.7% although $\text {UB}_2$ equals the best bound in about 45%.

6 Conclusion

The present paper treats the $k_i$-partitioning problem with the objective of maximizing the minimum completion time subject to machine-dependent upper cardinality limits $k_i$ on the maximum number of jobs that can be assigned to machine i. To tackle this problem, we developed powerful preprocessing procedures which proved to be able to reduce the problem’s size by eliminating machines and jobs in advance. One of our preprocessing steps is to exploit the implicitly given lower cardinality limits $l_i$ in order to enhance the upper limits. We also derived several upper bound arguments and proposed effective lifting procedures which often led to even tighter bounds in our experiments. When it comes to generating high-quality solutions to the max–min $k_i$-partitioning problem, we designed a powerful subset sum based improvement procedure $k_i$-LS whose core is built by our exact dynamic programming procedure $k_i$-DP that optimally solves the two-machine case. Computational tests on a large set of randomly generated instances attest to the efficacy of our solution methods: reductions were obtained for about 12% of the instances, the lifting procedures helped to tighten the best upper bound in about 62% of the cases, and the overall relative gap between the best upper and the best lower bound averages 0.57% while we optimally solved at least 70% of the instances within less than one second of computation time on average.

We see the following directions for future research. From a theoretical point of view, analyzing the worst case behavior of our upper bounding procedures as well as the two LPT-based construction heuristics constitutes a challenging task. From an algorithmic point of view, we believe that further improvements in the quality of the generated solutions can be obtained by tailor-made metaheuristics or sophisticated exact algorithms. Moreover, we suggest two ideas that potentially result in even tighter bounds. The first one is to enhance the lifting procedures by explicitly using the information provided by the gaps $k_i-l_i$ between the upper and lower cardinality limits. The second idea is to combine the preprocessing and lifting procedures by applying the reduction criteria not only to the given problem instance but also to the derived partial instances.