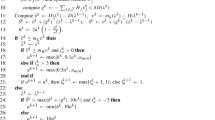On branching heuristics for the bi-objective 0/1 unidimensional knapsack problem

Abstract

This paper focuses on branching strategies that are involved in branch and bound algorithms when solving multi-objective optimization problems. The choice of the branching variable at each node of the search tree constitutes indeed an important component of these algorithms. In this work we focus on multi-objective knapsack problems. In the literature, branching heuristics used for these problems are static, i.e., the order on the variables is determined prior to the execution. This study investigates the benefit of defining more sophisticated branching strategies. We first analyze and compare a representative set of classic branching heuristics and conclude that none can be identified as the best overall heuristic. Using an oracle, we highlight that combining branching heuristics within the same branch and bound algorithm leads to considerably reduced search trees but induces high computational costs. Based on learning adaptive techniques, we propose then dynamic adaptive branching strategies that are able to select the suitable heuristic to apply at each node of the search tree. Experiments are conducted on the bi-objective 0/1 unidimensional knapsack problem.

1 Introduction

1.1 Context

Branch and bound are well-known methods for solving single-objective combinatorial optimization problems, since the beginning of the 1950s. These approaches have been especially studied and used for solving the knapsack problem, which is one of the seminal problems in discrete optimization (see e.g. Kolesar 1967; Thesen 1975; Shih 1979; Gavish and Pirkul 1985 and the books of Martello and Toth 1990 and Kellerer et al. 2004).

In a few words, a branch and bound method is an implicit enumeration principle in which the feasible set (i.e., the set of solutions that satisfy the constraints of the problem) is progressively partitioned, by fixing the value of one or several variables. Generally, considering binary variables, the partitioning procedure consists in fixing a selected variable to 0 or 1. The partitioning of the feasible set can be represented by a search tree whose root node is the initial problem and each node represents a subproblem, in which some variables have been fixed. Therefore, the branching strategy that selects the variable to be assigned at each node of the tree constitutes a key component of a branch and bound method. Branching strategies are the core of this study, in the context of multi-objective combinatorial optimization problems (MOCO), where several criteria have to be optimized simultaneously (see for instance Ehrgott and Gandibleux 2000; Ehrgott 2005 for a detailed presentation).

1.2 pOKP: formulation, efficient solutions and nondominated points

In this work, we focus on the unidimensional 0/1 knapsack problem with multiple objectives, which is often used in order to evaluate solving algorithms in MOCO. In this problem, n items are assigned to profits among p objectives (this profit is denoted by $c^k_j$ for an item $j \in \{1,\ldots ,n\}$ and an objective $k \in \{1,\ldots ,p\}$). The items have also a weight (denoted by $w_j$ for an item $j \in \{1,\ldots ,n\}$). Hence, solving this problem consists in selecting a subset of items that maximizes the profit, while respecting the weight capacity constraint (this capacity is denoted by $\omega$). Therefore, this problem can be formulated as:

$$\begin{aligned} \begin{array}{rll} \max &{} \sum _{j = 1}^{n} c_j^k \, x_j &{} k = 1,\ldots ,p \\ s.t. &{} \sum _{j = 1}^{n} w_{j} \, x_j \le \omega \\ &{} x_j \in \{0,1\} &{} j = 1,\ldots ,n\qquad \qquad \qquad \qquad \qquad ({{\mathrm{{\textit{pOKP}}}}}) \end{array} \end{aligned}$$

This problem is denoted by ${{\mathrm{{\textit{pOKP}}}}}$ with p the number of objective functions, ${{\mathrm{{\textit{KP}}}}}$ stands for the single-objective version. Note that ${{\mathrm{{\textit{pOKP}}}}}$ is $\mathcal {NP}$-hard whatever the value of p. However, the single-objective case is generally considered as practically easy to solve, and can be solved in pseudo-polynomial time. X denotes the set of feasible solutions. $z_k(x) = \sum _{j = 1}^{n} c_j^k \, x_j$ is the objective value of $x \in X$ according to the objective $k \in \{1,\ldots ,p\}$. $z(x)=(z_1(x), \ldots , z_p(x)) \in \mathbb {R}^p$ is the image of $x \in X$ in the objective space. $Y = \{y = z(x), x \in X\}$ is called the outcome set.

In the MOCO context, there does not exist in general a single optimal solution but rather a set $X_E$ of efficient solutions. We assume in the remaining part of the paper that no feasible solution optimizes all objective functions simultaneously.

Let $y^1, y^2 \in \mathbb {R}^p$ be the objective values associated with two feasible solutions $x^1$ and $x^2$. We write $y^1 \geqq y^2$ ($y^1$ weakly dominates $y^2$) if $y^1_k \ge y^2_k$ for all $k \in \{1,\ldots ,p\}$ and $y^1 \ge y^2$ ($y^1$ dominates $y^2$) if $y^1 \geqq y^2$ and $y^1 \ne y^2$. The non-negative orthant is defined by $\mathbb {R}^p_\geqq = \{y \in \mathbb {R}^p:y \geqq 0\}$.

A feasible solution ${x}^*$ is called efficient if there does not exist any other feasible solution x such that $z(x) \ge z({x}^*)$. $z({x}^*)$ is then called a nondominated point. The set of efficient solutions is the efficient set $X_E$ and its image in objective space is the nondominated set $Y_N$. $Y_N$ is alternatively defined by $Y_N = \{y \in Y: \not \exists y' \in Y \hbox { such that } y' \ge y\}$. From this alternative definition, we can define the set of nondominated points relatively to a set $S \subset \mathbb {R}^p$, by $S_N = \{s \in S: \not \exists s' \in S \hbox { such that } s' \ge s\}$. In the MOCO context, we generally make a distinction between supported efficient solutions (that are optimal solutions of a single-objective problem defined by a weighted sum of the objective functions with only positive weights) and the non-supported efficient solution (that are not optimal for any such weighted sum problems). Geometrically, the images of supported efficient solutions (called supported nondominated points) are located on the boundary of ${{\mathrm{\mathrm conv}}}Y - \mathbb {R}^p_\geqq$ and the images of non-supported efficient solutions (called non-supported nondominated points) are located in the interior of ${{\mathrm{\mathrm conv}}}Y - \mathbb {R}^p_\geqq$. A last distinction can be done between extreme supported efficient solutions, which images are vertices of ${{\mathrm{\mathrm conv}}}Y - \mathbb {R}^p_\geqq$, and non-extreme supported efficient solutions, which images are located in the relative interior of a face of ${{\mathrm{\mathrm conv}}}Y - \mathbb {R}^p_\geqq$.

The exact solution of a MOCO problem consists in determining a complete set of efficient solutions, i.e., to determine at least one efficient solution for each nondominated point.

1.3 Review of the relevant literature

As mentioned above, we are interested in the Branch components of branch and bound methods, i.e. branching strategy that selects variables according to a heuristic selection rule. Therefore, we need to recall here (1) the exact solving algorithms based on branch and bound, as well as their classic branching heuristics and (2) other related approaches.

Multi-objective branch and bound and ${{\mathrm{{\textit{pOKP}}}}}$

Several branch and bound methods have been proposed in the literature for multi-objective knapsack problems: Ulungu and Teghem (1997), Visée et al. (1998) for the version 2-objectives, Jorge (2010) for the version 3-objectives, and Florios et al. (2010) for the version 3-objectives and 3-dimensional (i.e. 3 knapsack constraints).

In order to perform an implicit enumeration of all feasible solutions, each subproblem is evaluated. This evaluation aims to prove whether no efficient solutions can be found in the feasible set of this subproblem. In this case, the node is fathomed, i.e. the partitioning stops at this branch and another non-fathomed node is selected to continue the solving process. Otherwise, the partitioning continues from this node. The fathoming of a node can either result from the infeasibility of the corresponding subproblem, or from the comparison of lower and upper bounds computed for this subproblem. Note that, contrary to single-objective optimization, we deal here with lower and upper bound sets (Ehrgott and Gandibleux 2007), instead of single values.

A lower bound set for the nondominated set $Y_N$ is generally composed of the points associated to the feasible points found during the enumeration, filtered by dominance. In other words, it can be considered as an incumbent list, generalizing the notion of incumbent used in a single-objective branch and bound.

An upper bound set U for the nondominated set of a subproblem (defined by a node of the tree) is defined by a set of points (not necessarily feasible) such that there is no point in this set that dominates another one, and such that all feasible points of the subproblem are weakly dominated by points of U. It is generally obtained by the solution of a relaxation of the subproblem. In the following, we will consider the convex relaxation, that is the relaxation defined by extending the feasible set $X'$ of a given problem by ${{\mathrm{\mathrm conv}}}X'$, without modification of the objective functions. Therefore, its nondominated set $({{\mathrm{\mathrm conv}}}Y')_N$ (where $Y' = z(X')$) defines an upper bound set for ${Y'}_N$. Finally, $({{\mathrm{\mathrm conv}}}Y')_N$ is implicitly described by the extremal supported nondominated points of the problem with feasible set $X'$.

This relaxation has in particular been used in Jorge (2010), Delort and Spanjaard (2010).

The node can be fathomed if the upper bound set U is weakly dominated by the lower bound set L, i.e. for all $u \in U$ there is $l \in L$ such that $l \geqq u$. This weak dominance test can be slightly improved under the assumption that objective coefficients and variables are integer (see Sourd and Spanjaard 2008 for details).

The branching strategy and ${{\mathrm{{\textit{pOKP}}}}}$

The efficiency of a branch and bound solving algorithm, or dynamic programming method, is strongly related to the order in which the variables are processed. The variables can be selected randomly but it seems more efficient to consider their potential properties with regards to the instance that is being solved. Therefore, in the general ${{\mathrm{{\textit{pOKP}}}}}$ context, a common variable selection heuristic consists in computing the utility of a variable according to its respective profits and weight. For each item, p utilities can be defined:

$$\begin{aligned} u^k_{j} = \frac{c^k_j}{w_{j}} \text{ for } k \in \{1,\ldots ,p\} \end{aligned}$$

These utilities reflect the benefit of selecting a given item. Obviously, the information emerging from the utilities of the items is easier to exploit for the single-objective case, since a single utility per item can be defined. When the number of objective functions increases, the value of the utilities obtained for a same item can be very different. Hence, several heuristics can be defined, including combinations of different utility measures.

Dynamic programming

A number of dynamic programming methods have been proposed for the ${{\mathrm{{\textit{pOKP}}}}}$: Captivo et al. (2003), Delort and Spanjaard (2010), Figueira et al. (2013) for the ${{\mathrm{2{\textit{OKP}}}}}$, Klamroth and Wiecek (2000) for the ${{\mathrm{{\textit{pOKP}}}}}$ and other variants of knapsack problems, Bazgan et al. (2009b) for the ${{\mathrm{{\textit{pOKP}}}}}$.

The two phase method and ${{\mathrm{{\textit{pOKP}}}}}$

Introduced in Ulungu and Teghem (1995), the two phase method is designed for solving MOCO problems for which there exist efficient algorithms for the single objective variant. The first phase consists in finding the extreme supported efficient solutions. For this, single-objective weighted sum problems are defined, using the classical dichotomic algorithm initially proposed in Aneja and Nair (1979) in the bi-objective case, and one of its extension (Przybylski et al. 2010; Özpeynirci and Köksalan 2010 in the multi-objective case.

The second phase aims to find all the other nondominated points by executing an implicit enumeration method. For this, a search area containing all these points is defined using the points obtained in the first phase. In the bi-objective context, this search area is composed of triangles defined by two adjacent extreme supported nondominated points. Let $y^r$ and $y^l$ be two extreme supported nondominated points with $y^l_1 < y^r_1$ (and thus $y^l_2 > y^r_2$), $y^r$ and $y^l$ are adjacent if there does not exist an extreme supported nondominated point y such that $y_1^l< y_1 < y_1^r$. We define the triangle $\triangle (y^r,y^l)$ composed of the points $y^r, y^l$ and $(y^l_1,y^r_2)$. In most of the proposed algorithms, each triangle is explored individually. Exploitation of the problem structure is a key point of an efficient enumeration. Several strategies have been proposed for this purpose and applied to ${{\mathrm{2{\textit{OKP}}}}}$: branch and bound Visée et al. (1998), dynamic programming in Delort and Spanjaard (2010), ranking strategy Jorge (2010).

Preprocessing and ${{\mathrm{2{\textit{OKP}}}}}$

Preprocessing treatments aim to reduce the size of the instance. Having a reduced set of variables as input of a branching strategy is indeed valuable. Here, we are especially interested of these preprocessing treatments.

The first one has been defined in Visée et al. (1998) and also used in Delort and Spanjaard (2010). It is designed to be applied in a two phase method. It consists first in defining a lower bound set for $Y_N$ using the feasible points obtained in the first phase (and possibly completing it using a local search). Next, before the exploration of each triangle, each variable is considered and fixed individually to a possible value. An upper bound set restricted to the considered triangle is computed for the obtained subproblem (for which $x_j$ is fixed to a value v) and compared to the lower bound set for $Y_N$. If the upper bound set is weakly dominated, the variable $x_j$ is definitively fixed to the value $1-v$, for the exploration of the considered triangle. Note that such a preprocessing could be applied for the whole problem, i.e. without restriction to a given triangle. However, the conflicting nature of objective functions, implies that there are very few common variables for all efficient solutions.

The second preprocessing has been defined in Jorge (2010). Contrary to the first one, it is specific to ${{\mathrm{{\textit{pOKP}}}}}$. This preprocessing is based on a dominance relation between items and the bounds on the cardinality of an efficient solution. The dominance relation between items is defined as follows: an item dominates another if it has greater or equal objective values and lower or equal weight. The bounds on the cardinality of an optimal solution were introduced for ${{\mathrm{{\textit{KP}}}}}$ in Glover (1965) and extended for an efficient solution to the ${{\mathrm{{\textit{pOKP}}}}}$ in Gandibleux and Fréville (2000). The cardinality of an efficient solution is the number of items selected into it. The upper bound $UB(\omega )$ and the lower bound $LB(\omega )$ on this cardinality define a minimum and maximum number of items selected simultaneously. The preprocessing treatment of Jorge (2010) specifies that an item is never selected in an efficient solution if it is dominated by a number of items greater or equal than $UB(\omega )$ or if the capacity constraint does not allow to select this item and all items dominating it. Symmetric properties state when items are always selected in an efficient solutions. The dominance relations can also be exploited in a branch and bound algorithm: when a variable is fixed to 0, all variables dominated by it are also fixed to 0; and symmetrically when a variable is fixed to 1, all variables dominating it are fixed to 1.

1.4 Objectives and contributions

In the literature, only static (i.e. fixed for the whole search process) branching strategies have been considered for solving knapsack problems. Nevertheless, due to the restricted information that is generally taken into account, a fixed branching strategy may reveal inefficient to compute the set $X_E$.

Therefore, it seems interesting to consider alternative branching mechanisms that could be able to adapt to various parameters such as (1) the subset of $Y_N$ currently explored and (2) the current depth of the search tree. To our knowledge, we did not find any such mechanism in the literature. Of course, dynamic mechanisms are used for the choice of the branching variable in the implementation of branch and cut algorithms of MIP solvers, and are therefore implicitly used in $\varepsilon$-constraint methods (see for example Mavrotas and Florios 2013; Zhang and Reimann 2014). However, our purpose is concerns here the branching strategy of multi-objective branch and bound algorithms. Finally, our aim is to better understand the strengths and weaknesses of existing branching strategies and to study if more flexible and adaptive branching strategies could help branch and bound methods to reduce their search effort. A new branching strategy should be

• Adaptive : according to the current state of the search, it should be able to select the most suitable branching variable and thus activate the corresponding branching heuristic,

• Autonomous : information collected during the solving process should be sufficient to control the branching process without external interaction,

• Computationally reasonable : the cost of the dynamic control of the branching process should not drastically increase the overall solving time in order to ensure improved performances with regards to classical solving algorithms.

Starting from a complete panel of known branching heuristics from the literature, the purpose of this study is thus to devise an autonomous branching component that could be able to identify the most suitable heuristics for selecting next variable in the branch and bound method. In this context, several questions arise : does such a technique reduce the size of the search tree that is explored? Does such a technique reduce the overall computational time?

Our contribution can be summarized as follows.

• We provide here a complete study of branching heuristics for branch and bound methods for the 2OKP, which allows us to better understand their behavior and to identify a subset of efficient heuristics. Hence, this study can be useful for devising more efficient algorithms and choose the most suitable branching components.

• We highlight that combining heuristics within the same branch and bound method reduces the search tree. Nevertheless, finding efficient combinations may induce a high computational cost.

• We propose to use learning techniques in order to devise adaptive heuristics selection mechanisms, which are able to dynamically adapt the branching heuristics according to feedback received from the solving process. Our experiments show that these mechanisms can be competitive.

1.5 Organization of the paper

The paper is organized as follows. Branching strategies are fully described in Sect. 2. The experimental evaluation of the branching strategies is then presented in Sect. 2.5, showing that there does not exist a strategy that obtains the best result on all instances. In the second part of this paper, we aim at elaborating an adaptive branching strategy combining several static branching strategies. Section 3 shows that the number of subproblems generated in the solving process can be considerably reduced by such combinations of strategies. The performance obtained by different adaptive methods is then presented in Sect. 4.

2 Branching strategies for the 2OKP

2.1 Variable ordering and branching strategies

Our purpose is to determine the impact of the order in which the variables are set in a branch and bound method. We can remark that a branching strategy can be defined by any order of variables. Thus, we do not present only the strategies introduced for branch and bound methods, but also the orders defined for dynamic programming methods, since they can be adapted to define a branching strategy.

The branching strategies presented below are based on the notion of utility and more precisely on aggregations of the utilities. They use either the numerical value of the utilities or the ranking they induce.

The orders $\mathcal {O}^k$ for each objective function $k=1,\ldots , p$ have been initially introduced in Ulungu and Teghem (1997) for ${{\mathrm{2{\textit{OKP}}}}}$ and extended in Bazgan et al. (2009a) to ${{\mathrm{{\textit{pOKP}}}}}$. In $\mathcal {O}^k$, the variables $j \in \{1,\ldots ,n\}$ are sorted in decreasing order of the utilities $u^k_j$, for $k=1,\ldots ,p$. The rank $r^k_j$ of an item $j \in \{1,\dots ,n\}$ is the position of the item j in the order $\mathcal {O}^k$, $k =1,\ldots , p$. Several orders have been designed based on the notion of rank, using aggregations in order to find a compromise between the ranks.

In Ulungu and Teghem (1997), Bazgan et al. (2009a), Jorge (2010), an order sorts the items in increasing order of the sum of the ranks (i.e. $\textstyle \sum _{k=1}^p r^k_j$).

In Bazgan et al. (2009a), Jorge (2010), Delort (2011), another strategy sorts the items in increasing order of the maximum of the ranks defined for this item. In case of equality, the sum of the ranks is used to break ties. The value associated to each item $j =1,\ldots ,n$, and used to sort the items, is:

$$\begin{aligned} \max \{r^k_j: k=1,\ldots ,p \} + \frac{ \sum _{k=1}^p r^k_j}{p \, n}. \end{aligned}$$

The items are thus sorted according to their worst rank.

Bazgan et al. (2009a), Jorge (2010) also define a strategy symmetric to the previous one. The value associated to each item $j~=~1,\ldots ,n$ is its best rank, i.e.

$$\begin{aligned} \min \left\{ r^k_j: k=1,\ldots ,p \right\} + \frac{ \sum _{k=1}^p r^k_j}{p \, n}. \end{aligned}$$

The items are then sorted in increasing order of their best rank and the equalities are broken by the average rank in $\mathcal {O}^k, k = 1,\dots ,p$.

In Visée et al. (1998), an order to use specifically for the exploration of a triangle in the two phase method, has been defined. When investigating the triangle $\triangle (y^r, y^l)$, the search direction $\lambda = (y^l_2~-~y^r_2, y^r_1 - y^l_1)$ is used to weight the utilities $u^1$ and $u^2$. The items are considered in decreasing order of their weighted average. This order has also been used in Delort (2011).

Finally, we present some orders proposed for multi-dimensional knapsack problems, that can be easily adapted next to the single-dimensional case. The orders presented in Florios et al. (2010) (on the knapsack problem with three constraints and three objective functions) and in Gandibleux and Perederieieva (2011) (on the knapsack problem with two constraints and two objective functions) use directly the numerical value of the utilities. In the context of knapsack problem considering several constraints and several objective functions, a utility is then defined for each pair objective function/dimension.

In Florios et al. (2010), three orders are tested. The first one considers only the maximum of all defined utility and the items are sorted in decreasing order of this value. The second one deals with the average value of the utilities, again the items are sorted in decreasing order of this value. In the last one, the variables are sorted according a lexicographic order of the utilities, in decreasing order.

In Gandibleux and Perederieieva (2011), two branching strategies are used. The first one is the branching strategy based on the average of the utilities presented in Florios et al. (2010). The second one is based on the maximum of the utilities of an item, similarly to the one presented in Florios et al. (2010), except that in case of equality, the average of the utilities is used to break the ties.

The orders considering the value of the utilities can be sensitive to the range of the coefficients. For example, an objective function can have bigger coefficients than another and would then impact the ordering more that another objective function. The orders based on the direction defined by triangles are less sensitive to this phenomenon and the ones based on the notion of rank avoid it.

We can remark that in all the presented orders, the “best” variable (the most promising variable) is selected first. This paradigm aims to increase the chances of obtaining efficient solutions or at least solutions of good quality early in the execution of the algorithm, thus allowing to prune nodes or states earlier in the remaining of the execution.

Each of the previous works compares a restricted number of branching strategies, usually few new branching strategies with one or two branching strategies from the literature assessed as given the best performance. In all the studies, no order leads to a better practical efficiency than the others on all instances, even on a same series of instances, but some are better in average.

2.2 Selection of branching strategies

In this section, we detail a set of 23 branching strategies for ${{\mathrm{2{\textit{OKP}}}}}$ that will be used all along this paper, they are also called branching heuristics. We will consider strategies defined in Sect. 2.1, but also new ones. In particular, we do not consider only the “best variable first” paradigm but also the “worst variable first” paradigm. This second paradigm aims to determine early in the solution method the variables that will never be selected in efficient solutions. The name of a branching strategy will be composed of the criterion used to sort the items, followed by “best” if it follows the “best variable first” paradigm, “worst” otherwise.

The first branching strategy is the (deterministic) random branching strategy Rand, used as a baseline for the comparisons. Since our instances (described in Sect. 2.4) are generated randomly, the random order corresponds to the order of the variables in the instance file.

Table 1 presents the 22 other strategies. The best variable first strategies are presented in the columns (2) to (4) and the worst variable first strategies are in columns (5) and (7). The column (1) indicates the criterion according to which the variables are sorted and columns (4) and (7) the order used for the strategy on this criterion. The identifiers and names of the strategies are given respectively in columns (2) and (5) and in columns (3) and (6).

Table 1 Branching strategies of the study. $\lambda = (y^l_2 - y^r_2, y^r_1 - y^l_1)$ for the investigated triangle $\triangle (y^r, y^l)$

The simplest branching strategies (1–4 of Table 1) order the items only according to their value on the objective functions, without taking into account their weight. On the same idea of considering only one of the two objective functions, four branching strategies (5–8) are defined using either the utility $u^1$ either $u^2$. The utilities $u^1$ and $u^2$ can also be aggregated by a minimum, maximum, average or weighted average function (9–16). The last branching strategies are based on the rank of the variables on $\mathcal {O}^1$ and $\mathcal {O}^2$ (17–22).

We can remark that the strategy presented in Ulungu and Teghem (1997) is SumRank-best. Visée et al. (1998) considers the strategy Triang-best. Bazgan et al. (2009a), Jorge (2010) use strategies SumRank-best, MinRank-best and MaxRank-best. Jorge (2010) also considers strategies equivalent to U1-best and U2-best. Delort (2011) uses Triang-best, MaxRank-best. Florios et al. (2010) uses Avg-best and Max-best and an order which can be associated to U1-best and U2-best. Gandibleux and Perederieieva (2011) compares Avg-best and a modified version of Max-best.

2.3 Algorithm framework designed for conducting the analysis

A two phase method is used here, with a branch and bound method applied to explore each triangle in the second phase. The used lower bound set for $Y_N$ is as usually an incumbent list, and we use the convex relaxation to obtain an upper bound set for the nondominated points of any subproblem. This last bound set requires an intensive use of a single-objective solver. For this, we use the ${{\mathrm{{\textit{KP}}}}}$ solver Combo Martello et al. (1999), available on Pisinger (2002). Finally, the search tree is explored following a depth-first search strategy, that is almost always used in multi-objective branch-and-bound methods (Przybylski and Gandibleux 2017). The branching strategy is the same during all the execution (one of the strategies defined in Sect. 2.2). Each selected variable is fixed to 1 first and next to 0.

The triangles are explored in the lexicographic order, i.e. $\triangle (y^{r1}, y^{l1})$ is investigated before $\triangle (y^{r2}, y^{l2})$ if $y_1^{r1} > y_1^{r2}$ (then $y_1^{r1} < y_1^{r2}$ by definition of the triangles).

We want to study the influence of the preprocessing treatments defined in Jorge (2010) and Delort and Spanjaard (2010) on the performance of the branching strategies. Thus, two versions are considered depending on whether preprocessings are applied or not.

2.4 Dataset used as benchmark

Table 2 Source, size, name, generation of the objective and constraint coefficients and correlations existing between these coefficients for each instance of ${{\mathrm{2{\textit{OKP}}}}}$

We consider 230 instances from the literature. The number of variables in the instance, i.e. the size of the instance, is denoted by n. Table 2 presents the source, the size of the instances, the generation of the objective and constraint coefficient and correlations existing between these coefficients. It is generally claimed that instances with a negative correlation between objectives are more difficult to solve. The notation $a_j \in U[l,u]$ means that the coefficients $a_j, j\in \{1,\ldots ,n\}$ is generated according to a uniform distribution in $\{l,\ldots ,u\}$.

The ratio $\sum _{j =1}^n w_j/\omega$ is of 0.5 for all instances, except 2KP50-11 for which it is 0.11.

The instances F_n_U1, F_n_U2, F_n_W1 and F_n_W2 were initially generated for the knapsack problem with two objectives and two constraints. In this article, we deleted the second constraint to obtain ${{\mathrm{2{\textit{OKP}}}}}$ instances.

For the experiments, we determine four groups of instances $G_1$, $G_2$, $G_3$ and $G_4$ (with $G_1 \subset G_2 \subset G_3 \subset G_4$). $G_1$, $G_2$ and $G_3$ are training benchmarks used during the comparison of the static branching heuristics and the configuration settings of the dynamic methods. $G_4$ is used as a validation benchmark, to evaluate the performance of the dynamic branching strategies leading to the best performance.

$G_1$, $G_2$ and $G_3$ are composed exclusively of instances extracted from Visée et al. (1998), Gandibleux and Fréville (2000), Degoutin and Gandibleux (2002) and Captivo et al. (2003), so that the computational times of the instances are smaller in $G_1$ and larger in $G_3$. These groups are defined based on the size of the instances. However, the instances of the category 4WnW1 being in general more time consuming, they will constitute exceptions in this definition. The composition of the groups of instances is the following:

• $G_1 = \{$ 2KP50-11, 2KP50-50, 2KP100-50 $\} \cup \{$ 2KPn-1A, 2KPn-1B,2KPn-1C,2KPn-1D, $n \in \{50,100,150\}\} \cup \{$ 4WnW1, $n\in \{50,100\}\}$

• $G_2 = G_1 \cup \{$ 2KP200-1A, 2KP200-1B,2KP200-1C,2KP200-1D $\} \cup \{$ 4W150W1 $\}$

• $G_3 = G_2 \cup \{$ 2KPn-1A, 2KPn-1B,2KPn-1C,2KPn-1D, $n \in \{250, 300\}\} \cup \{$ 4WnW1, $n\in \{200,250,300\}\}$

• $G_4$ is the set of all presented instances.

For the experiments presented in this paper, we use a machine equipped with a Intel Core i7 2.60 GHz processor with 15.5 GB of RAM and running under Linux. All algorithms are implemented in C++.

2.5 Comparison of the branching heuristics

In this section, the performance of the branching heuristics presented in Sect. 2.2 are assessed on the benchmark $G_3$ of instances presented above.

Obviously, the preprocessing treatments of Jorge (2010) and Delort and Spanjaard (2010) reduce the number of variables and thus the size of the search tree (i.e. the number of sub-problem generated) and the execution time of the algorithm. While the version of the algorithm using the preprocessing treatment can handle all instances of the benchmark group $G_3$, the version without the preprocessing treatments cannot solve four of them in less than an hour: 2KP300-1A, 2KP300-1C, 4W250W1 and 4W300W1. The comparisons of the heuristics when no preprocessing treatment is used do not take these four instances into account.

The time required to compute the order of the variables is negligible in the algorithm and is more or less the same for all the branching heuristics. The computational time is thus essentially proportional to the size of the search tree obtained during the algorithm. Therefore, the size of the resulting search tree is the only criteria used to assess the branching heuristics, it is a reliable measure. Two criteria are considered in order to evaluate the average performance of a branching heuristic:

• For the first criterion, an order of the branching heuristic is defined for every instance. The branching heuristics are sorted by increasing order of the size of the search tree obtained. A score is associated to each branching strategy for each instance and is inversely proportional to the rank of the heuristic in the order defined according to the instance. The score equals 22 if the heuristic leads to the smallest search tree, 21 if it leads to the second smallest, etc. Figure 1 shows for each branching heuristic the sum of the scores obtained on all the instances. A high sum of scores corresponds to a branching heuristic having good average performance.

• The second evaluation criterion measures for each instance the relative difference between the size of the search tree obtained when using the branching heuristics and the size of the smallest search tree obtained. This measure will be called the improvement ratio of the size of the search tree (${{\mathrm{\mathcal {IRS}}}}$). For a given instance, we note $s^t$ the size of the search tree obtained by the tested heuristic and $s^r$ the size of the smallest search tree obtained (used as a reference), we define ${{\mathrm{\mathcal {IRS}}}}= \frac{s^r - s^t}{s^r}$. A high value of ${{\mathrm{\mathcal {IRS}}}}$ indicates a good performance of the branching heuristic. On the contrary, a negative value indicates a degradation of the size of the search tree. If ${{\mathrm{\mathcal {IRS}}}}$ is equal to $-2$, then the size of the search tree is twice the size of the search tree obtained for the reference. The comparison is done with the smallest search tree for all instances, so it is no possible to have a positive value of ${{\mathrm{\mathcal {IRS}}}}$ here. Figure 2 shows for each branching heuristic the average and standard deviation of ${{\mathrm{\mathcal {IRS}}}}$ over all instances.

Fig. 1

Sum of the scores obtained on the instances, for each branching heuristic. a Without preprocessing treatments. b With preprocessing treatments

Fig. 2

Average and standard deviation of ${{\mathrm{\mathcal {IRS}}}}$ for each branching heuristic. a Without preprocessing treatments. b With preprocessing treatments

When no preprocessing is used (Figs. 1 and 2a), we observe a significant difference between the performance of the branching heuristics. The branching heuristic Triang-worst has a significantly higher score and ${{\mathrm{\mathcal {IRS}}}}$ than other strategies.

When using the preprocessing treatments (Figs. 1 and 2b), the difference of performance between the branching heuristics is less important.

Figures 1 and 2 also show that no branching heuristic is the best for all instances. Table 3 provides the ordering of the branching strategies according to these two evaluation criteria.

Table 3 Branching heuristics ordered according to the evaluation criteria

For a given version of the algorithm, the orders defined by the two evaluation criteria are similar. However, the orders on the heuristics (Table 3) are very different depending on whether preprocessing is applied or not. In particular, Min-worst is ranked 1 or 2 when the preprocessing treatments are activated but a rank 5 or 10 when they are inactive.

Usually, branching strategies use “best variable first” paradigm. However, this paradigm is not necessarily better than the opposite paradigm. For example, Min-worst show better performance than Min-best. According to Table 3, the “best variable first” paradigm is better than the “worst variable first” paradigm in only half of the cases.

The branching heuristic Rand has poor performance, which varies from an execution to another, thus it will not be considered in the remaining of this study.

3 Combinations of heuristics

Section 2 highlighted that no branching heuristic outperforms all heuristics on all instances, even if some heuristics provide good average performance. The efficiency of branching heuristics may indeed depend on problem instances, whose characteristics may vary, even during the search process within a branch and bound method. Unfortunately, no clear relationships between instances and the most suitable branching strategies for these instances has been found, with regards to their size, correlation of objectives, etc.

A remaining possibility to improve the performance of the branch and bound method is to use different branching heuristics within the same search tree (at different nodes). Within this scope, an ideal method would be able to always select the best combination of heuristics for any instance. However, according to the number of possible heuristics and the size of the search trees, an exhaustive exploration of the possible combinations is not tractable.

Hence, we propose to evaluate possible combination of heuristics by means of an oracle method. This oracle is simply a branch and bound method that applies a heuristics selection rule at each node of the search tree. At each separation procedure, the 22 branching heuristics presented in Sect. 2 are evaluated and the current best (according to a criterion to define) is selected. This oracle can be thus considered as a myopic oracle, i.e., one step forward. In order to select the best branching heuristic, the quality of the resulting nodes should be carefully evaluated. The purpose of this oracle is definitely not to provide an efficient solving algorithm, since the computational cost induced by the heuristics selection process is prohibitive, but rather to assess that combining heuristics can be beneficial.

In Sect. 3.1, we define three criteria to evaluate a separation. The performances of these criteria are then evaluated within the previously described oracle approach.

3.1 Selection of branching heuristics

Concerning selection criteria, the quality of a separation can be assessed by several characteristics of the two child nodes, based on the variation of the upper bound set or lower bound set.

3.1.1 Selection criteria

Since the coefficients of the objective functions and the variables are non-negative in a ${{\mathrm{2{\textit{OKP}}}}}$, the feasible solutions are in $\mathbb {R}^2_\geqq$. Next, upper and lower bound sets can be used to define areas, from which their variation will be measured. We will in particular use the following notation: ${{\mathrm{\mathcal {A}}}}(V)$ is the area of the polyhedron $V \cap \mathbb {R}^2_\geqq$, with $V \subset \mathbb {R}^2$.

• Upper Bound (UB) : given an upper bound set U, feasible solutions are located in $(U - \mathbb {R}^2_\geqq ) \cap \mathbb {R}^2_\geqq$, called the feasibility zone. Remark that the feasibility zones of child nodes are included in the parent node’s zone. The reduction the feasibility zones by a branching heuristic is expected to have an impact on the size of the search tree.

Definition 1 Let us consider $U^0$ the upper bound set of the parent node and $U^1$, $U^2$ the corresponding sets for the two children nodes. The relative reduction of the feasible zone of the child node $l \in \{1,2\}$ compared to the parent node is defined as :

$$\begin{aligned} \frac{{{\mathrm{\mathcal {A}}}}\left( U^0-\mathbb {R}^2_\geqq \right) -{{\mathrm{\mathcal {A}}}}\left( U^l-\mathbb {R}^2_\geqq \right) }{{{\mathrm{\mathcal {A}}}}\left( U^0-\mathbb {R}^2_\geqq \right) } \end{aligned}$$

This criterion measure the quality of a separation by considering the average of $U^1$ and $U^2$. The higher the value, the better is the quality of a branching.

• Lower Bound (LB) : a common lower bound set is computed for the entire search tree, and is potentially updated with the computation of any upper bound set. Note that the area ${{\mathrm{\mathcal {A}}}}({L-\mathbb {R}^2_\geqq })$ may increase if new potentially efficient solutions are found (i.e. solutions which are not dominated by solutions of the lower bound set). The probability of fathoming a node by dominance increases with the quality of the lower bound set. Thus a large variation of ${{\mathrm{\mathcal {A}}}}({L-\mathbb {R}^2_\geqq })$ indicates a good choice of the branching variable.

• Other : when computing an upper bound set, potentially efficient solutions, located in another triangle than the one currently investigated, can be found. These solutions do not have any impact on currently investigated triangle, but they are likely to speed-up the overall solving process. Indeed, at the beginning of the investigation of the triangle where they are located, introducing these solutions in the lower bound set might lead to earlier pruning in the considered triangle. Hence, the size of the search tree is likely to be reduced.

3.1.2 Comparison of selection rules

Roughly speaking, a selection rule is efficient if the corresponding oracle leads to smaller search trees. Therefore, the comparisons of the different oracles will be achieved using the ${{\mathrm{\mathcal {IRS}}}}$ measure presented in Sect. 2.5.

The reference $s^r$ is the same as in Fig. 2, i.e. the smallest search tree obtained for each instance. In the following, we call this reference Best-heur, since it corresponds to a method applying the best branching heuristic for each instance. Note that compared to the oracle, this method applies only one heuristic for a given instance. Best-heur is not realistic since it requires to know a priori which of the 22 branching heuristics would lead the smallest search tree.

Several selection rules based on the three criteria have been evaluated. Due to the difference of scale and measurement unit, a weighted sum on the criteria is not easy to define and might be dependent on the range of the coefficients in the considered instance. Thus, we consider the criteria in lexicographic ordering (when necessary ties are broken randomly). For instance, UB-Other orders the branching heuristics according to the criterion UB, the equalities on this criteria are broken thanks to the criterion Other. For this measure, the criterion LB is not considered.

Figure 3 shows the average and standard deviation of ${{\mathrm{\mathcal {IRS}}}}$ for oracle methods corresponding to the different selection rules. “With preprocessing” (resp. “Without preprocessing”) corresponds to the results obtained for the version of the branch and bound method using (resp. not using) the preprocessing treatments (see Sect. 1.3). Since the oracle considers 22 branching heuristics at each separation, the method is time consuming. Thus the biggest instances presented in Sect. 2.4 are not considered here. For the version using the preprocessing treatments, the benchmark used is $G_1$. The set of benchmark is even more restricted when no preprocessing treatment is used: the 28 instances of 50 variables or less, 2KP100-1B and 2KP100-1D composed this benchmark.

Fig. 3

Average and standard deviation of ${{\mathrm{\mathcal {IRS}}}}$ obtained for the oracle methods using the different selection rules

Using or not preprocessing treatments does not impact the evaluation of the criteria, even if the difference is larger when no preprocessing treatment is used. Figure 3 highlights that the criterion UB is essential in the selection process. Indeed, if not used, the performance degrades. The best performance is obtained when UB is the first criterion in the lexicographic order. No significant difference exists between the average ${{\mathrm{\mathcal {IRS}}}}$ of these measures when we use preprocessing treatments (they differ from less than 0.02). However, when no preprocessing treatment is applied, the measure presenting the best performance in average is obtained by UB-Other-LB, which will be used for the oracle in the following.

3.2 Evaluation of the Oracle

In this section, the oracle is more deeply investigated, taking into consideration not only the size of the search tree, but also the computational time.

The measure relative to the computational time is based on the same idea as ${{\mathrm{\mathcal {IRS}}}}$. Let $t^m$ be the computational time spent by the evaluated method on a given instance and $t^r$ the computational time spent by the reference method on the same instance. ${{\mathrm{\mathcal {IRT}}}}~=~\frac{t^r-t^m}{t^r}$ is called the improvement ratio on the computational time. Similarly to ${{\mathrm{\mathcal {IRS}}}}$, a positive value of ${{\mathrm{\mathcal {IRT}}}}$ indicates that the evaluated method leads to a smaller computational time than the reference method, thus the evaluated method is better regarding the computational time.

Figure 4 aims to highlight the impact of the size of the instances on the oracle method. The reference method taken is Best-heur. The set of benchmark instances used is $G_3$ when the preprocessing treatments are applied and $G_2$ otherwise.

Fig. 4

Comparison of the oracle method and Best-heur, with respect to the size of the instances. a According to the size of the search tree. b According to the computational time

On Fig. 4, we observe that the behavior of the oracle method varies according to the size of the instances. This variation is observed whether the preprocessing treatments are used or not.

Figure 4a shows that the average ${{\mathrm{\mathcal {IRS}}}}$ increases with the size of the instance (between 50 and 200 variables). ${{\mathrm{\mathcal {IRS}}}}$ seems to stagnate when the size of the instances is between 200 and 300, for the version of the algorithm using the preprocessing treatments. When the preprocessing treatments are used, the average ${{\mathrm{\mathcal {IRS}}}}$ is between 30 and 43% for all size of instances.

The size of the instances has an opposite effect on the computational time (Fig. 4b). ${{\mathrm{\mathcal {IRT}}}}$ seems to decrease when the size of the instances increases (between 50 and 200) and then stagnates. As expected, the computational time is largely more important for the oracle method than for Best-heur (at each separation the oracle method tries 22 branching heuristics, compute the upper and lower bound sets for the two child nodes, before choosing only the best heuristic).

However, the reference method is not a realistic method since it supposes to know which of the branching heuristics is the best for every instance. Figure 5 shows the performances obtained by the oracle method compared to Best-heur and the two branching heuristics presenting the best performance in Table 3, i.e. Min-worst and Triang-best. The three reference methods apply the same branching heuristic all along the execution.

Fig. 5

Comparison of the oracle method and the use of one heuristic. a According to the size of the search tree. b According to the computational time

Figure 5a presents the average and standard deviation of the measure ${{\mathrm{\mathcal {IRS}}}}$. It shows that the size of the search tree is reduced on average by 34% compared to Best-heur and by 44% compared the branching heuristics Min-worst and Triang-best, when preprocessing treatments are used. Thus there exist combinations of branching heuristics leading to smaller search tree than when the same branching heuristic is applied all along the branch and bound method.

Figure 5b shows that the computational time for the oracle method is 14–16 times larger than for the references, when the preprocessing treatments are applied. The difference of computational time is even larger when no preprocessing treatment is used.

Even if the oracle allows to reduce significantly the size of the search tree compared to the use of one single branching heuristic, the computational time largely exceeds the one obtained by the use of one branching heuristics. Because of the computational cost, the oracle method cannot be used in practice to solve a ${{\mathrm{2{\textit{OKP}}}}}$.

3.3 Selection of a subset of branching heuristics

In this section, we aim to find a reduced subset of branching heuristics in order to decrease the computational time, without compromising the quality of the separations. This subset will serve as basis for our adaptive branch and bound method.

The subset must thus be composed of the branching heuristics that often provide good performances. In order to determine this subset, we apply an incremental method, on each instance.

Let us denote H the set of the branching heuristics (the 22 used in the oracle method presented above), $H'$ the target subset of branching heuristics. S is the set of all branchings performed by the oracle method on a given instance. The incremental method assigns $\mathcal {B}_{h,s}$ to 1 if h has the best quality measure during the branching s, 0 otherwise, for $h \in H$ and $s \in S$. Note that it is possible to have $\mathcal {B}_{h,s} = 1$ for several $h \in H$ for a given branching $s \in S$, since several branching heuristics can lead to the same branching variable.

Then the method incrementally builds the set $H'$ by executing the following steps:

• 1. Let $h'$ be the branching heuristic with the maximum value for $\sum _{s \in S} \mathcal {B}_{h,s}$ then $h'$ is included in $H'$.

• 2. All branchings for which $h'$ had the best measures are deleted from S and $h'$ is no longer considered in the remaining of the execution.

• 3. If $S \ne \emptyset$, go to Step 1.

The aim of this approach is to find a small subset of heuristics $H'$ containing at least one of the heuristics with best quality measure for each branching.

By definition of the incremental method, the first branching heuristic added in $H'$ is more interesting for the oracle method, on the given instance, than the last one. In order to reflect this relative importance of the branching heuristics, a score is assigned to each branching heuristic for each instance. The score is 22 for the first branching heuristic added in $H'$, 21 for the second, etc. If a branching heuristic is not added in $H'$, its score is 0.

During Step 1, several branching heuristics may have the same $\textstyle \sum _{s \in S} \mathcal {B}_{h,s}$. Thus $h'$ may be chosen among several branching heuristics. In order to be fair, when this situation occurs one set is created for every possible choice of $h'$ and the method continues independently on each one of these sets. At the end of the method, the score assigned to each branching heuristic is the average of the score obtained for each set built.

When this method is executed on each instance of a set of benchmarks, the branching heuristics can be sorted according to the decreasing average score. The branching heuristics are sorted for both versions of the oracle method presented in Sect. 3.2 (using or not preprocessing treatments). The orders obtained are presented in Table 4. Using or not the preprocessing treatments leads to very similar orders.

Table 4 Orders obtained by analyzing the performance of the branching heuristics during the oracle method, for the two versions of the method

We now define a reduced oracle method using the order given in column (2) of Table 4 to select a subset of the c best evaluated heuristics.

The number of considered heuristics c is a parameter of the method.¹ In case of equalities regarding the quality measure, the reduced oracle method favors the branching heuristics with a better rank in the order presented in Table 4.

Figure 6 presents the performances of the reduced oracle method for different values of c, for the two versions of the algorithm. The reduced oracle methods are evaluated according to two aspects: the size of the search tree (measured by ${{\mathrm{\mathcal {IRS}}}}$) and the computational time (measured by ${{\mathrm{\mathcal {IRT}}}}$). The reference method used in the measures ${{\mathrm{\mathcal {IRS}}}}$ and ${{\mathrm{\mathcal {IRT}}}}$ is Best-heur.

Fig. 6

Impact of the number of branching heuristics used in the reduced oracle method. a According to the size of the search tree. b According to the computational time

The evolution of the reduced oracle method regarding the number of considered branching heuristics is similar whether preprocessing treatments are used or not. ${{\mathrm{\mathcal {IRS}}}}$ increases following a logarithmic curve when the number of branching heuristics used increases. The growth of ${{\mathrm{\mathcal {IRS}}}}$ seems to stagnate when more than 5 branching heuristics are used. When the preprocessing treatments are used, the reduced oracle using 5 branching heuristics has an average ${{\mathrm{\mathcal {IRS}}}}$ only 0.05 less than for the reduced oracle method using the 22 branching heuristics. When no preprocessing treatment is used, the difference on the average ${{\mathrm{\mathcal {IRS}}}}$ of the reduced oracle method compared to the oracle method using the 22 branching heuristics is 0.13 when 5 branching heuristics are used and 0.05 when 9 branching heuristics are used.

${{\mathrm{\mathcal {IRT}}}}$ decreases linearly when the number of heuristics considered in the reduced oracle method increases. This evolution was expected since the number of upper bound sets computed (which is the most expensive component) is linear in the number of branching heuristics considered by the reduced oracle method.

The combination of the 5 first heuristics in the order given in Table 4 (with preprocessing treatments) allows to reduce the average size of the search tree compared to a method using the same branching heuristic all along the execution. Moreover this improvement is relatively close from the one obtained by the oracle method (using 22 branching heuristics). However, the computational time required to execute this reduced oracle method is 3 times more important than when using only one branching heuristic when preprocessing treatments are used and 11 times more important when no preprocessing treatments are considered.

These results concerning the reduced oracle method allow us to conclude that using the 5 branching heuristics Z1-best, Z2-best, Triang-worst, U1-worst and U1-best can reduce significantly the size of the search tree (with an ${{\mathrm{\mathcal {IRS}}}}$ of 0.26 compared to Best-heur when using preprocessing treatments). However, the oracle method is not suitable since the computational time is still significantly more important.

The analysis of the oracle method did not allow to determine any correlation between features of the instances and combination of branching heuristics with good performance. Thus we did not succeed to elaborate static combinations of branching heuristics with satisfying performance. The following section aims to elaborate a dynamic branching strategy, based on adaptive methods, for ${{\mathrm{2{\textit{OKP}}}}}$.

4 Adaptive combinations of branching heuristics

In Sect. 3, we have investigated that combining several branching heuristics within a same algorithm may lead to reduced search trees. Nevertheless, the selection of the branching heuristics at each node in the tree may be highly time-consuming.

This heuristic selection problem is indeed fully related to the adaptive selection of operators (or parameters values) in search algorithms. This problem has been widely studied in the context of evolutionary algorithms (Da Costa et al. 2008a; Maturana et al. 2012). More recently, such techniques have been applied to search tree based constraint solvers (Loth et al. 2013; Balafrej et al. 2015).

These approaches use reinforcement learning techniques in order to choose the most suitable next solving step (in our case the choice of a separation heuristic) with regards to the current observed state of the search. Since the performances of the heuristics are likely to vary during the search, adaptive methods aim to use previously collected information in order to empirically evaluate expected performances at a given search state.

4.1 Adaptive methods for heuristics selection

Adaptive methods aim to evaluate the quality of the applied heuristics. A reward is assigned to the heuristic and the quality of a heuristic is thus assessed by an aggregation of its successive rewards (for instance, its average reward).

In Sect. 3, the quality of the branching heuristics was computed by a lexicographic ordering on three different criteria. Nevertheless, these criteria do not use similar ranges of values and their aggregation may be complex. Based on Fig. 3, the most important evaluation criterion is the upper bound set UB. Moreover, the oracle method using only this criterion provides performances close to the best one (the difference on ${{\mathrm{\mathcal {IRS}}}}$ is less than 0.03 when no preprocessing treatment is applied and less than 0.005 when the preprocessing treatments are applied). Therefore, in the following we use only UB to compute the rewards of the heuristics.

We consider different adaptive methods for branching heuristics selection in both versions of the branch and bound method (with and without preprocessing treatments).

4.1.1 Uniform wheel

As baseline for comparing selection mechanism, we use a uniform wheel that assigns to each branching heuristic the same probability to be selected at each node.

4.1.2 Probability matching

Probability matching Goldberg (1990) is a wheel-like process. Let us consider $H = \{1,\ldots ,k\}$ a set of k branching heuristics. The probability $P_h(t)$ of a heuristic $h \in H$ to be chosen at iteration $t \in \mathbb {N}$ is proportional to its previous performances, evaluated by means of rewards. $R_h(t)$ is the reward obtained by strategy h at iteration t if it has been applied (the reward is 0 otherwise). The reward $R_h(t)$ is computed using UB (see Section 3). Let us denote $Q_h(t)$ the estimated quality of h up to the iteration t, computed as $Q_h(t) = \frac{\sum _{l=1}^t R_h(l)}{n_h(t)}$, where $n_h(t)$ is the number of times the heuristic h has been applied up to iteration t.

At the beginning of the algorithm, the probability is $\frac{1}{h}$ for each h. At each iteration, a heuristic is randomly chosen according to the probabilities $P_h(t), h \in H$. At a given iteration $t+1, t \in \mathbb {N}$, the probability of the strategy h is updated by the formula:

$$\begin{aligned} P_h(t+1)=P_{min} +(1 + k \, P_{min} ) \frac{Q_h(t)}{ \sum _{h'=1}^{k} Q_{h'}(t) } \end{aligned}$$

The minimum probability $P_{min}$ ensures that no strategy can have a probability lower than $P_{min}$. Note that $P_{min}$ is the only parameter of this method.

4.1.3 Upper confidence bound

The selection of the next heuristic can also be considered as a multi-armed bandit problem (see Cesa-Bianchi and Lugosi (2006) for instance), where a player has to find an optimal sequence of actions in order to maximize its gain. The upper confidence bound [UCB, Auer et al. (2002)] allows to achieve an optimal regret for this problem. In an UCB based algorithm, at each iteration, the heuristic h with the highest value for the following formula (using the notations presented in Sect. 4.1.2) is selected:

$$\begin{aligned} Q_h(t) + \alpha \sqrt{ \frac{2 \, \log \sum _{h'=1}^k n_{h'}(t)}{n_h(t)}} \end{aligned}$$

Note that, in this formula a tradeoff between exploration and exploitation of heuristics is ensured by the two terms of the sum. The first term tends to favor the best strategy, while the second term ensures that each strategy is taken infinitely many times as t increases. $\alpha \in \mathbb {R}$ is the scaling factor balancing exploration and exploitation.

UCB has many variants (see DaCosta et al. (2008b) for further details). The dynamic multi-armed bandit (DMAB) method has been introduced to take into account the dynamicity of the performance of the heuristics during the search. A Page-Hinkley test Page (1954) is used in the DMAB method to detect changes in the reward. The Page-Hinkley test measures the difference between the reward obtained at an iteration with the average reward obtained for the same strategy in the previous executions. If this difference exceeds a given threshold $\gamma$ then the method interprets it as a change in the quality obtained by the strategies and the UCB method is restarted from scratch. This restart makes it possible to find quickly the new best strategy. When the value of $\gamma$ is small then the method is really sensitive to changes and might restart very frequently. On the contrary when the value of $\gamma$ is high, the method does not restart frequently. The DMAB considers thus two parameters: the threshold $\gamma$ and the scaling factor $\alpha$.

Another variant of UCB consists in considering a sliding time window. The numbers of iterations, on which the empirical quality is computed, takes only into account the last iterations. The size of the considered window is a parameter of this method. In the experiments, the size of the window depends on the number of variables in the considered instances.

4.2 Selection by vote

As already mentioned, different branching heuristics may select the same variable. We may thus assume that a variable selected by several branching heuristics constitutes a good choice. Based on this assumption, we propose a vote method, where the branching variable is selected when it has been chosen by the majority of heuristics (ties are broken randomly). Note that this method does not have any parameter.

A drawback of this vote method is that there are frequently ties and the selection of heuristics is thus a random choice between these winning variables. We propose a hybrid method mixing vote method and a reduced oracle method (see Sect. 3). At each separation, if there exist only one heuristic winning the vote then this heuristic is chosen for the branching, otherwise the oracle method is used to break equalities. Again no parameter is required.

At last, we define a weighted vote method. The selection of the variable is similar to the previous hybrid vote, except that the votes are weighted. At the beginning of the execution all the heuristics have the same weight. When the reduced oracle method is executed (when they are equalities), the weight of branching heuristics selected by the reduced oracle method increases (by one). The underlying idea is to give more importance to the branching heuristics that have been chosen by the oracle part.

4.3 Evaluation of the adaptive selection methods

4.3.1 Experimental setup

The evaluation of the performances of the previously described selection methods will be assessed according to (1) the size of the search tree evaluated by ${{\mathrm{\mathcal {IRS}}}}$ and (2) the computational time evaluated by ${{\mathrm{\mathcal {IRT}}}}$ (see Sect. 3).

As baseline, we consider three reference methods that apply the same heuristics during the search: Min-worst, Triang-best and Best-heur.

We consider the benchmark $G_1$ (the smallest instances) to highlight the best value of the parameters for each method and the method leading to the best performance. Since some methods include stochastic choices, all the results presented here are mean values using 10 executions of the algorithm.

Concerning the set of heuristics, we may consider the full set of 22 branching heuristics or a restricted set (as in the reduced oracle method). In particular, we have observed that the set of five branching heuristics Z1-best, Z2-best, Triang-worst, U1-worst and U1-best leads to good performances in the reduced oracle method, when considering the size of the search trees.

4.3.2 Parameters setting

Uniform wheel The suffix 22-heur stands for the uniform wheel using the set of 22 branching heuristics and 5-heur for the one composed of five branching heuristics.

According to experimental results, we consider only the reduced set of five branching heuristics for the following selection methods.

Probability matching We set $P_{min} = 0.05$, which corresponds to the best setting (obtained by experimentally testing different value $P_{min}$).

UCB For UCB and DMAB we have $\alpha = 0.2$ and $\gamma = 0.8$. Sliding is UCB using a sliding window for reward computation.

Vote Vote denotes the first simple vote method, Hybrid-vote-oracle is the hybrid method mixing the vote method and the reduced oracle method and weighted vote is the last proposed method (see Sect. 4.1).

4.4 Experimental results

Figures 7 and 8 summarize the performances obtained by all the adaptive methods presented in this section, for the instances of the group $G_2$.

Fig. 7

Performance of the adaptive methods as branching strategies when no preprocessing treatment is applied. a According to the size of the search tree. b According to the computational time

Fig. 8

Performance of the adaptive methods as branching strategies when the preprocessing treatments are applied. a According to the size of the search tree. b According to the computational time

4.4.1 Detailed comments

Uniform Wheel In Fig. 8, we can observe that the performances of the versions using the restricted set of branching heuristics offer better performances than the one using the set of 22 branching heuristics. The observation concerning the reduced oracle method seems to be confirmed here: the set of branching heuristics Z1-best, Z2-best, Triang-worst, U1-worst and U1-best are enough to bring diversity and using the 22 branching heuristics is not necessary.

Probability matching Probability matching does not allow to improve the results obtained for Best-heur, neither regarding the computational time nor the size of the search tree, for both versions of the algorithm (using or not preprocessing treatments). However, this method presents smaller search tree and computational time in average than Min-worst and Triang-best.

UCB We can observe that UCB allows to reduce in average the size of the search tree and the computational time, compared to Min-worst and Triang-best. The performances obtained for DMAB and sliding UCB are worse than for the classical UCB. In this case, it appears that these additional mechanisms (i.e., dynamic restart of the learning mechanism and time window for computing rewards) are not necessary.

Vote The hybrid vote allows to reduce significantly the size of the search tree. However the computational time is much more important (in average four time more important). Indeed this method applies the reduced oracle method when the vote does not allow to select one branching heuristic. The performances obtained for the hybrid method are actually similar to those obtained for the reduced oracle method (important reduction of the search tree and increase of the computational time).

Thanks to the dynamic adaptation of the weights in the weighted vote method, less iterations of the reduced oracle method are performed. This method presents better results than both the hybrid method and the vote method, in terms of computational time and size of the search tree.

Table 5 Percentage of instances for which the adaptive methods UCB and weighted vote give a smaller computational time than the reference methods Min-worst and Triang-best, regarding the class of the instances

Table 6 Percentage of instances for which the adaptive methods UCB and weighted vote give a smaller computational time than the reference methods Min-worst and Triang-best, regarding the size of the instances

4.4.2 Overview of the best adaptive methods

We can notice that the use of adaptive methods makes it possible to reduce the computational time more significantly when the preprocessing treatments are used. Two methods are distinctly worse than the others: the uniform wheel based on the 22 branching heuristics and the hybrid method. However, only three adaptive methods have a positive ${{\mathrm{\mathcal {IRT}}}}$ with respect to one of the reference method (Min-worst): the probability matching, the UCB and the weighted vote methods.

When the preprocessing treatments are used, the difference on ${{\mathrm{\mathcal {IRS}}}}$ are more important. Except for the uniform wheel with 22 heuristics and the hybrid method, the adaptive methods allow to obtain a positive value of ${{\mathrm{\mathcal {IRT}}}}$ regarding at least one reference. The adaptive method leading to the best performance in terms of computational time, over the three reference methods, is the method UCB. Since the computational time is lower when the preprocessing treatments are executed, in this paragraph, we only consider the version of the algorithm using these treatments.

In Tables 5 and 6, the performance of the UCB method and of the weighted vote is compared to Min-worst, Triang-best. Since Best-heur is not a realistic method, we do not consider it. The methods are compared on the set $G_4$ of instances (i.e. all presented instances). Tables 5 and 6 present the percentage of instances for which the adaptive methods give smaller computational time or smaller search tree, according to, respectively, the class and the size of the instances. Values are in bold if the computational time is reduced more than half of the instances.

The tables show that the UCB method is significantly better than the weighted vote. The UCB method leads to a reduction of the search tree for 86.5% of the instances when compared to Min-worst and 90.43% when compared to Triang-best.

Table 5 shows that the performance of UCB method depends on the class of instances. It can be noted that the UCB method performs particularly well on the class D_n_s. Moreover the UCB method allows to solve 5 instances that the two reference methods could not solve in less than 30 min.

In Table 6, we can see that for large instances, even if the search-tree is reduced in most of the cases, the computational time is reduced only in less than half of them. This can mean either than the subproblems obtained for the UCB method are more expensive to bound (the computation of the upper bound set is the most expensive phase of the algorithm), or that the adaptive mechanism (computation of scores, selection of the branching strategy) is expensive.

5 Conclusion and perspectives

The first purpose of our work was to better understand the behavior of branching heuristics and to compare their respective performances. We have evaluated a sufficiently large set of possible heuristics for the ${{\mathrm{2{\textit{OKP}}}}}$ and we have highlighted that, depending on the instances of the problem, there does not exist a dominant heuristic. Moreover, the performance of the heuristics may depend on preprocessing treatments that are often used to simplify the instances and that change their structures.

From this first observation, we have tried to combine different heuristics within the same search process. An oracle, which selects at each node the most promising heuristic according to a quality measure, allows us to highlight that, given an instance, some combinations of heuristics may perform better than the best single heuristic. Unfortunately, this oracle requires a huge amount of computational time in order to estimate the best heuristic at each node. Hence, from this observation, our purpose is to provide a less costly mechanism for this heuristics selection problem.

Inspired by works that have been conducted in the context of adaptive search algorithms Hamadi et al. (2012), we have proposed different adaptive selection techniques, which aim at selecting heuristics according to their previously observed performances, using machine learning techniques. We also propose a simplified oracle that uses weighted votes. Using an initial set of heuristics, these adaptive methods provide interesting results by reducing the size of search trees.

We have conducted many experiments in order to highlight our different observations as well as to evaluate our proposals. Even if we have not been able to devise an adaptive branching mechanism that improve branch and bound methods on all instances (which could be deceptive), the proposed approaches are able to reduce the sizes of the search trees but their cost is sometimes still too expensive.

Nevertheless, as previously mentioned, our main purpose is not to enter a solving competition but rather to better understand how solving algorithms work and to precisely study their components. In particular, we have observed that only a few branching heuristics were really useful for solving the proposed problem and we have highlighted the importance of the pre-treatment process in branch and bound algorithms. From these conclusions, adaptive mechanisms can still be improved, one way could be to use more information collected during the search.