Analysis of the Final Ranking Decisions Made by Experts After a Consensus has Been Reached in Group Decision Making

Abstract

Traditional approaches to group decision making (GDM) problems for ranking a finite set of alternatives terminate when the experts involved in the GDM process reach a consensus. This paper proposes ways for analyzing the final results after a consensus has been reached in GDM. Results derived from this last step can be used to further enhance the understanding of possible hidden dynamics of the problem under consideration. The proposed approach for post-consensus analysis is in part based on a novel idea, known as preference maps (PMs) introduced recently in the literature on how rankings should be described when ties in the rankings are allowed. An original contribution of this paper is how to define the difference between two PMs. This is achieved by using a metric known as the Marczewski–Steinhaus distance. Approaches for analyzing the final results of a GDM process after consensus has been reached may reveal hidden but crucial insights in the way the experts reached the consensus and also new insights related to the alternatives. These approaches rely on the concept of differences in the rankings, defined by traditional means or as the difference between two PMs as defined in this paper. This is the second group of original contributions made in this paper. The various issues are illustrated with numerical examples and an application inspired from a real-world problem described in the literature. The new contributions described in this study offer an exciting potential to enrich the group decision making process considerably.

1 Introduction

Most research on group decision making (GDM) focuses on approaches that can guide a group of decision makers (also known as decision experts or just experts) to reach a consensus when ranking a finite set of alternatives (Tindale et al. 2003; Saaty and Peniwati 2008; Ureña et al. 2019; Pérez et al. 2014). However, no work has been done on what happens after a consensus has been reached. The argument can be made that by studying the decision makers’ individual rankings of the alternatives and the consensus reached, one might be able to discover some interesting issues related to key aspects of the group’s decision making process. In this way one may gain deeper insights of the alternatives and also on the decision makers themselves. More knowledge on the various dynamics of the particular decision problem under consideration may ultimately lead to a better understanding of the problem and thus of its final conclusions. Thus, doing research on this important subject may offer a new, and so far unutilized, opportunity to benefit the GDM process in ways not imagined before.

The structure of the decision problem considered in this paper is best described as follows. Available is a finite set of the alternatives which have been considered in a GDM process. This set of alternatives is denoted as {A₁, A₂, …, A_n} where n is a positive integer number. These alternatives have been evaluated and ranked by some experts denoted as E₁, E₂, …, E_m, where m is a positive integer number. The experts have evaluated these alternatives by considering some evaluative criteria and using a multi-criteria decision making (MCDM) process such as the ones described by Triantaphyllou (2000). Next a GDM approach [such as the ones described by Hou and Triantaphyllou (2019), Davis (2014), Dong et al. (2015), or Herrera et al. (1996)] was followed and a consensus has been reached on the way these alternatives should be ranked. Is this the end of the group decision making process or is there something more that could be done to gain more useful insights? This paper describes how more analysis can be performed at this stage to potentially derive some very useful and unexpected results.

This paper is organized as follows. Section 2 describes some relevant developments from the literature. These are various approaches for determining the difference between rankings. Special emphasis is given to a recently developed method which can be used when rankings involve ties. That is, when multiple ranks are assigned to the same alternative. This method is based on developments first introduced by Hou (2015a, b, 2016) and later refined in Hou and Triantaphyllou (2019). They constitute what is referred to preference maps (PMs). Sections 3 and 4 present two novel definitions and some theoretical results related to PMs. In particular, how to analyze the information described in a PM and how to express the difference of two PMs. This is achieved by defining the concepts of “expansion of a PM” and then use it to define the “difference between two PMs.” These two definitions and the three relevant theorems in Sects. 3 and 4 are some of the original contributions of this paper. These concepts, along with the traditional ways for defining the difference between two rankings, can be used in Sect. 5 to demonstrate how the final results of a GDM process can be analyzed after a consensus has been reached. Some illustrative examples are used for this purpose. The proposed approaches for analyzing the final results after a consensus has been reached is the second group of original contributions made in this study. An example, inspired from a real-life application described in the literature, is analyzed in Sect. 6 to further demonstrate the applicability of the new concepts and approaches. Finally, the paper ends with Sect. 7 which summarizes the main contributions and highlights some areas for possible future research.

2 Some Relevant Developments from the Literature

This section presents some relevant developments from the literature that describe how differences in rankings can be quantified. It considers two general settings. In the first setting each alternative is assigned to a unique rank. The second setting is more general. Now an alternative may be assigned to multiple ranks, which must be represented by consecutive positive integers. These two settings are elaborated in the following two subsections, respectively.

2.1 When Each Alternative is Assigned to a Unique Rank

This is the most common scenario. There are multiple ways of how one may define the difference between two such rankings. Ray and Triantaphyllou (1999) describe five different methods for determining the difference of two rankings (with no ties). For illustrative purposes, consider the two rankings R₁ = (1, 2, 3) and R₂ = (2, 3, 1). Then these five methods are as follows:

(1) Number of disagreements	Difference between R1 and R2 = 3
(2) Weighted number of disagreements	Difference between R1 and R2 = 7
(3) Sum-of-squares of differences in rank	Difference between R1 and R2 = 6
(4) Normalized sum-of-squares of differences in rank	Difference between R1 and R2 = 0.75
(5) Sum of the absolute values of differences in rank	Difference between R1 and R2 = 4

For the second method mentioned above the three weights were assumed to be as follows: W₁ = 3.0, W₂ = 2.0, and W₃ = 1.0. For the forth method one first computes the value as in the third method and then that value is divided by the largest possible value when one considers two ranking vectors of size 3 (as is the case in the previous example). That value is equal to 8, and hence the corresponding result is equal to 0.75 (= 6/8). Another relevant study is the results reported in Ray and Triantaphyllou (1998) which describes the evaluation of rankings by considering the possible number of agreements and conflicts. One may easily define even more such methods and many more methods exist as this is an open problem and cannot be answered exhaustively.

2.2 When an Alternative May be Assigned to Multiple Ranks

Now it is assumed that the experts’ preferences can be expressed as ties-permitted ordinal rankings. Such rankings can be expressed in terms of the so-called preference sequence vectors (or PSVs) (Hou 2015a, b, 2016). The term preference sequence vector was later changed by Hou and Triantaphyllou (2019) to be called the preference map (PM). The notion of the preference map is described next along with some key definitions and related concepts from the literature.

Let us denote as [S_i]_n×1 a column vector of size n × 1 (i.e., with n entries), each entry of which is denoted as S_i, for i = 1, 2, 3, …, n. This notation is used to formally define the concept of a preference sequence vector (PSV) as it was first introduced by Hou (2015a, b, 2016). Please note that in the following definitions the term PM is used instead of the initial PSV one.

Definition 1

(Hou 2015b) A vector $\left[ {S_{i} } \right]_{n \times 1}$ is called a preference map (PM) of a ties-permitted ordinal ranking on the alternative set $X = \{ A_{1} ,A_{2} , \ldots ,A_{n} \}$ with respect to a weak order relation ${ \preccurlyeq }$ such that

$$ S_{i} = \{ |P_{i} | + 1,|P_{i} | + 2, \ldots ,|P_{i} | + |T_{i} |\} , $$

(1)

where $P_{i} = \{ A_{j} |A_{j} \in X,A_{j} \succ A_{i} \}$ is the set containing the alternatives that predominate $A_{i}$, and T_i = {A_r | A_r$\in$X, A_i ~ A_r} is the set containing the alternatives that are indifferent to $A_{i}$, for i = 1, 2, 3, …, n.

We illustrate the PM idea by means of a simple example. Suppose that we have the following ties-permitted ordinal ranking: A₁ ~ A₂$\succ$A₃. This ranking implies such preferences on the alternative set {A₁, A₂, A₃}. In particular, it indicates that alternatives A₁ and A₂ are in a tie and should occupy positions 1 and 2; meanwhile, alternative $A_{3}$ is dominated by A₁ and A₂ hence it is ranked at position 3. We represent these preferences in the following PM:

$$ \left[ {S_{i} } \right]_{3 \times 1} = \left[ {\begin{array}{c} {\{ 1,2\} } \\ {\{ 1,2\} } \\ {\{ 3\} } \\ \end{array} } \right], $$

whose entries indicate the alternatives’ possible ranking positions. These positions are deduced by using formula (1). For instance, according to the preferences contained in the ranking, the predominating sets of A₁ and $A_{3}$ are:

$$ P_{1} = \emptyset \;{\text{and}}\;P_{3} = \{ A_{1} ,A_{2} \} , $$

respectively. Meanwhile, their indifference sets are:

$$ T_{1} = \{ A_{1} ,A_{2} \} \;{\text{and}}\;T_{3} = \{ A_{3} \} , $$

respectively. Therefore, by formula (1) we obtain their corresponding entries in the PM as $\{ 1,2\}$ and $\{ 3\}$, which are, in fact, their possible ranking positions which correspond to the ordinal ranking of A₁ ~ A₂$\succ$A₃.

Currently, the term ‘preference map’ is also used in a different context to graphically communicate, based on some statistical analysis, the relationships between product characteristics and the consumer preferences in some application areas [see e.g. Gere et al. (2014) and Yenket et al. (2011)]. In comparison the term ‘preference map’ used in this paper, as defined by Definition 1, is a sequence whose entries are sets containing alternatives’ possible ranking positions. We use the term “preference map” to represent an ordered partition of an alternative set, and vice versa.

The introduction of the PM concept brings a much needed convenience and flexibility for describing ranking preferences that are constructed based on weak order relations. Moreover, a powerful mathematical definition of consensus can now be constructed too as it is shown in the following definition taken from the literature.

Definition 2

(Hou 2015b) Let $\left[ {S_{i}^{(1)} } \right]_{n \times 1}$, $\left[ {S_{i}^{(2)} } \right]_{n \times 1}$, …, $\left[ {S_{i}^{(m)} } \right]_{n \times 1}$ be PMs. These PMs are said to be in consensus if and only if $\forall i\left( {\bigcap\nolimits_{k = 1}^{m} {S_{i}^{(k)} } \ne \emptyset } \right)$, or equivalently, $\forall i,j,k\left( {S_{i}^{(j)} \cap S_{i}^{(k)} \ne \emptyset } \right)$. Moreover, the consensus PM is defined by $\left[ {S_{i}^{(c)} } \right]_{n \times 1} = \left[ {\bigcap\nolimits_{k = 1}^{m} {S_{i}^{(k)} } } \right]_{n \times 1}$.

The above mathematical definition of consensus based on PMs, is intuitively appealing because it reflects two fundamental observations in GDM (Hou and Triantaphyllou 2019): (1) Two experts’ preferences may not be identical but they may still exhibit a type of consensus; and (2) Consensus may not be transitive among experts. For example, as it has been demonstrated in Hou (2015a, b) and Hou and Triantaphyllou (2019), suppose that there are three persons, say Rudy, Scott and Tracy, and two drinking alternatives, say coffee and tea. We assume that these persons’ preferences are as follows: Rudy prefers coffee to tea, Scott prefers both coffee and tea, while Tracy prefers tea to coffee. Evidently, Rudy’s and Scott’s preferences exhibit a type of consensus. Meanwhile, Scott’s and Tracy’s preferences also exhibit some consensus, while Rudy’s and Tracy’s preferences do not exhibit any consensus. This simple example describes some key observations on consensus in GDM defined as in Definition 2.

Consider the following three PMs assumed to be the judgments of three experts when they have reached a consensus (as defined in Definition 2) in a GDM process:

$$ V_{1} = \left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 3,4\} \hfill \\ \{ 5\} \hfill \\ \{ 3,4\} \hfill \\ \end{array} \right],\quad V_{2} = \left[ \begin{array}{l} \{ 1,2,3\} \hfill \\ \{ 1,2,3\} \hfill \\ \{ 1,2,3\} \hfill \\ \{ 4,5\} \hfill \\ \{ 4,5\} \hfill \\ \end{array} \right],\quad V_{3} = \left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 3\} \hfill \\ \{ 4,5\} \hfill \\ \{ 4,5\} \hfill \\ \end{array} \right]. $$

These three PMs imply that the consensus PM of the three experts is the PM termed as V₄ depicted below:

$$ V_{4} = \left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 3\} \hfill \\ \{ 5\} \hfill \\ \{ 4\} \hfill \\ \end{array} \right]. $$

The above PM termed as V₄ can be derived as the intersection of the previous three PMs which express the judgments of the three experts. For instance, the third entry of V₄ is the element {3} which is derived as follows:

$$ \{ 3,4\} \cap \{ 1,2,3\} \cap \{ 3\} = \{ 3\} . $$

A similar interpretation holds for the rest of the entries of V₄.

The problem examined in this paper is described next. Given are the individual final ranking decisions produced by a group of experts after they have reached a consensus (defined as in Definition 2 or otherwise). The individual ranking decisions and the consensus are described by PMs. They can be rankings where ties are permitted (in which case the concept of PM as described above needs to be used) or they can be of the traditional type with no ties. Furthermore, the consensus PM may or may not be the result of performing the intersection operation on the PMs that described the experts’ final ranking decisions. Given the above PMs the main question examined in this paper is described as follows: What more can be inferred about the experts involved and the alternatives at the end of the formal GDM process that could potentially lead to a better understanding of the GDM process and the derived consensus? Before this question is addressed, the concept of PM is analyzed to facilitate a better understanding of how the difference between two PMs can be quantified.

3 Analyzing a Preference Map (PM)

Sections 3 and 4 introduce a number of original concepts related to group decision making and especially when conducting a post-consensus analysis by using PMs. To help fix ideas, consider the previous PM termed as V₁ (i.e., the final ranking as proposed by expert E₁) which is repeated here for convenience:

$$ V_{1} = \left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 3,4\} \hfill \\ \{ 5\} \hfill \\ \{ 3,4\} \hfill \\ \end{array} \right]. $$

The above PM implies that the following nine rankings (also PMs) are in consensus with V₁ (this includes V₁ itself). These nine PMs are derived by expanding the entries of V₁ and then considering all possible combinations. As V₁ has two entries equal to {1, 2} and {3, 4} (each appearing twice in V₁), it follows that this expansion has the nine members which are exhaustively enumerated next.

$$ V_{1} = \left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 3,4\} \hfill \\ \{ 5\} \hfill \\ \{ 3,4\} \hfill \\ \end{array} \right] \to \left[ \begin{array}{l} \{ 1\} \hfill \\ \{ 2\} \hfill \\ \{ 3\} \hfill \\ \{ 5\} \hfill \\ \{ 4\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 2\} \hfill \\ \{ 1\} \hfill \\ \{ 3\} \hfill \\ \{ 5\} \hfill \\ \{ 4\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 1\} \hfill \\ \{ 2\} \hfill \\ \{ 4\} \hfill \\ \{ 5\} \hfill \\ \{ 3\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 2\} \hfill \\ \{ 1\} \hfill \\ \{ 4\} \hfill \\ \{ 5\} \hfill \\ \{ 3\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 3\} \hfill \\ \{ 5\} \hfill \\ \{ 4\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 4\} \hfill \\ \{ 5\} \hfill \\ \{ 3\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 1\} \hfill \\ \{ 2\} \hfill \\ \{ 3,4\} \hfill \\ \{ 5\} \hfill \\ \{ 3,4\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 2\} \hfill \\ \{ 1\} \hfill \\ \{ 3,4\} \hfill \\ \{ 5\} \hfill \\ \{ 3,4\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 3,4\} \hfill \\ \{ 5\} \hfill \\ \{ 3,4\} \hfill \\ \end{array} \right]. $$

We will call this set of nine members (i.e., the PMs following the arrow after V₁) the expansion of PM V₁. Obviously, the expansion of the PM termed as V₄ in Sect. 2.2, is the intersection of the expansions of the PMs termed as V₁, V₂, and V₃ in Sect. 2.2. Formally, we define the notion of PM expansion as follows:

Definition 3

Let vector V be a PM. Then its expansion, denoted as EXPANSION (V), is the following set of all PM vectors V_i, where V_i denotes a ranking which is not in conflict with the rankings implied by V. That is, the following is true:

$$ {\text{EXPANSION}}\;(V) = \{ V_{i} \} ,\;\;\;{\text{where}}\;V_{i} \;{\text{is}}\;{\text{a}}\;{\text{PM}}\;{\text{and}}\;{\text{the}}\;{\text{ranking}}\;{\text{implied}}\;{\text{by}}\;V_{i} \;{\text{is}}\;{\text{not}}\;{\text{in}}\;{\text{conflict}}\;{\text{with}}\;{\text{the}}\;{\text{ranking}}\;{\text{implied}}\;{\text{by}}\;V. $$

The set of PMs defined as the expansion of a PM V has some interesting properties. Suppose that the vector V can be defined as the intersection of m PMs denoted as V_j, for j = 1, 2, 3, …, m. Then the following theorem follows directly from the previous definition:

Theorem 1

Let$V = \bigcap\nolimits_{j = 1}^{j = m} {V_{j} }$. Then the following relation is true: EXPANSION (V) = $\bigcap\nolimits_{j = 1}^{j = m} {}$ EXPANSION (V_j).

Let V be a PM. Next define as UNIQUE (V) the ordered list of all the unique members of V. For instance, UNIQUE (V₁) = (U₁, U₂, U₃) = ({1, 2}, {3, 4}, {5}). That is, U₁ = {1, 2}, U₂ = {3, 4}, and U₃ = {5}. This definition can be used next to compute the size (cardinality) of the EXPANSION (V) set of the PM termed as V. The following theorem is based on a result reported in Maassen and Bezembinder (2002). According to that result if we have a finite set of m alternatives, then the total number of weak orders on m alternatives is as follows:

$$ W_{m} = \mathop \sum \limits_{k = 1}^{m} k!S\left( {m,k} \right) = \mathop \sum \limits_{k = 1}^{m} \mathop \sum \limits_{i = 0}^{k} \left( { - 1} \right)^{i} \left( {\begin{array}{*{20}c} k \\ i \\ \end{array} } \right)\left( {k - i} \right)^{m} , $$

where $S\left( {m,k} \right)$, a Stirling number of the second kind, indicates the number of partitions of a set of $m$ elements into $k$ nonempty subsets. When this result is used in conjunction with the previous definition of the UNIQUE (V) ordered list, then the following theorem follows:

Theorem 2

Let V be a PM and the members of the corresponding UNIQUE (V) set be U₁, U₂, U₃, …, U_t. Then the size of the set EXPANSION (V) is equal to$\mathop \prod \nolimits_{j = 1}^{t} \left[ {\mathop \sum \nolimits_{k = 1}^{{\left| {U_{j} } \right|}} k!S\left( {\left| {U_{j} } \right|,k} \right)} \right]$, where |U_j|, for j = 1, 2, 3, …, t, are the sizes of the members of the set UNIQUE (V), and $S\left( {m,k} \right)$is a Stirling number of the second kind.

When this theorem is applied to the vector V₁ it turns out that the set EXPANSION (V₁) has nine members.

4 Assessing the Difference Between Two PMs

Suppose that given are two PMs. For instance, let us consider V₁ and V₃ as defined in Sect. 2.2. How can one best describe their difference? In other words, how similar or dissimilar are the two experts who submitted the rankings implied by these two PMs? These two experts are in consensus but still their final decisions are described by two distinct PMs. The answer to this question will be determined by using the notion of the corresponding EXPANSION (V) sets. If these two sets are identical, then we can say that the two PMs are identical too in the way they ranked the alternatives. Therefore, it is reasonable to express the difference of the two PMs in terms of how different the corresponding EXPANSION sets are. This is achieved by introducing the following definition.

Definition 4

Let X and Y be two PMs. Then their relative difference, denoted as DIFFERENCE (X, Y), is defined as follows:

$$ {\text{DIFFERENCE }}\left( {X, Y} \right) = 1 - \frac{{\left| {{\text{EXPANSION }}\left( X \right) \cap {\text{EXPANSION }}\left( Y \right)} \right|}}{{\left| {{\text{EXPANSION }}\left( X \right) \cup {\text{EXPANSION }}\left( Y \right)} \right|}} $$

To appreciate the intuition of the previous definition, consider the following issues. If the previous quantity DIFFERENCE (X, Y) is equal to 0, the implication is that the two PMs X and Y are identical. This follows from the fact that the set of the numerator and the set of the dominator of the fraction involved in the previous formula will be of equal size. On the other hand, if the two PMs do not have any elements in common, then their intersection will be equal to the empty set and thus the quantity DIFFERENCE (X, Y) will be equal to 1. In other words, the values the quantity DIFFERENCE (X, Y) takes have as range the interval [0, 1] (i.e., including 0 and 1). Obviously, if the two PMs correspond to a situation where the experts have reached a consensus as described in Definition 2, then the value of the difference will never be equal to 1 (as the intersection of the corresponding EXPANSION sets will never be equal to the empty set). Since the denominator of the previous ratio will never be the empty set, the previous ratio can always be defined.

As an illustrative example, let us consider the case of the PMs V₁ and V₃ defined in Sect. 2. That is, we need to compute the value of DIFFERENCE (V₁, V₃). The set EXPANSION (V₁) was given in Sect. 3. The case of EXPANSION (V₃) is described next.

$$ V_{3} = \left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 3\} \hfill \\ \{ 4,5\} \hfill \\ \{ 4,5\} \hfill \\ \end{array} \right] \to \left[ \begin{array}{l} \{ 1\} \hfill \\ \{ 2\} \hfill \\ \{ 3\} \hfill \\ \{ 5\} \hfill \\ \{ 4\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 2\} \hfill \\ \{ 1\} \hfill \\ \{ 3\} \hfill \\ \{ 5\} \hfill \\ \{ 4\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 1\} \hfill \\ \{ 2\} \hfill \\ \{ 3\} \hfill \\ \{ 4\} \hfill \\ \{ 5\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 2\} \hfill \\ \{ 1\} \hfill \\ \{ 3\} \hfill \\ \{ 4\} \hfill \\ \{ 5\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 3\} \hfill \\ \{ 5\} \hfill \\ \{ 4\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 3\} \hfill \\ \{ 4\} \hfill \\ \{ 5\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 1\} \hfill \\ \{ 2\} \hfill \\ \{ 3\} \hfill \\ \{ 4,5\} \hfill \\ \{ 4,5\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 2\} \hfill \\ \{ 1\} \hfill \\ \{ 3\} \hfill \\ \{ 4,5\} \hfill \\ \{ 4,5\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 3\} \hfill \\ \{ 4,5\} \hfill \\ \{ 4,5\} \hfill \\ \end{array} \right]. $$

Given the above analysis, it turns out that the intersection of the two sets EXPANSION (V₁) and EXPANSION (V₃) is equal to the set S₁:

$$ S_{1} = \left\{ {\left[ \begin{array}{l} \{ 1\} \hfill \\ \{ 2\} \hfill \\ \{ 3\} \hfill \\ \{ 5\} \hfill \\ \{ 4\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 2\} \hfill \\ \{ 1\} \hfill \\ \{ 3\} \hfill \\ \{ 5\} \hfill \\ \{ 4\} \hfill \\ \end{array} \right],\;\left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \{ 3\} \hfill \\ \{ 5\} \hfill \\ \{ 4\} \hfill \\ \end{array} \right]} \right\}. $$

Therefore, its size is equal to 3 and this is the value of the numerator of the expression in Definition 4. Working similarly, it can be easily verified that the size of the union of these two EXPANSION sets is equal to 15. This is the value of the dominator of the expression in Definition 4. Hence, the value of DIFFERENCE (V₁, V₃) is equal to: 1 − (3/15) = 12/15 = 0.800.

More specifically, suppose that X, Y and Z are any three PMs. Then the following properties follow easily from Definition 4:

(1) DIFFERENCE (X, Y) ≥ 0	(non-negativity property)
(2) DIFFERENCE (X, Y) = 0, if and only if X = Y	(non-degeneracy property)
(3) DIFFERENCE (X, Y) = DIFFERENCE (Y, X)	(symmetry property)
(4) DIFFERENCE (X, Y) + DIFFERENCE (Y, Z) ≥ DIFFERENCE	(triangle property)

The above relationships are true because the concept of DIFFERENCE (X, Y), as defined in Definition 4, is consistent with the well-known Marczewski–Steinhaus distance (Marczewski and Steinhaus 1958). Therefore, DIFFERENCE (X, Y) is a metric measurement. The Marczewski–Steinhaus distance has received considerable attention in the literature [see, for instance, the work by Karoński and Palka (1977), and Heine (1973)]. Applications of this distance include areas in the fields of biology (Dunn 2000), transportation (Kubiak 2007), ecology (Safford and Harrison 2001), computer vision and pattern recognition (Gardner et al. 2014), and microbiology (Engel et al. 2012), among many other areas. More recent references to this important distance measure can be found in (Ricotta and Podani 2017; Yao and Deng 2014).

The following Theorem 3 states a useful property when one PM is a subset of another PM. Its proof follows directly from Definition 4. It is based on the fact that if a set Y is a subset of another set X (i.e., Y$\subseteq$X), then Y ∩ X = Y and Y ∪ X = X. This theorem is useful if one wishes to compute the quantity DIFFERENCE (X, Y) when EXPANSION (Y) $\subseteq$ EXPANSION (X), as is the case when Y is a consensus ranking according to Definition 2 and X is a ranking proposed by any of the GDM experts.

Theorem 3

Let X, Y be two PMs defined on the same alternatives space and EXPANSION (Y) $\subseteq$ EXPANSION (X). Then the following relation is always true:

$$ \begin{aligned} {\text{DIFFERENCE (}}X,Y )& = 1 - \frac{{\left| {{\text{EXPANSION (}}X ) \cap {\text{EXPANSION }}(Y)} \right|}}{{\left| {{\text{EXPANSION (}}X ) \cup {\text{EXPANSION }}(Y)} \right|}} \\ & = 1 - \frac{{\left| {{\text{EXPANSION }}(Y)} \right|}}{{\left| {{\text{EXPANSION (}}X )} \right|}} = \frac{{\left| {{\text{EXPANSION (}}X )} \right| - \left| {{\text{EXPANSION }}(Y)} \right|}}{{\left| {{\text{EXPANSION (}}X )} \right|}} \\ \end{aligned} $$

5 Some Applications of the Proposed Difference Measurement

The difference measure DIFFERENCE (X, Y) (regardless of which way was used to define it) offers some novel and highly exciting opportunities for gaining a deep understanding of key issues involved in a GDM process, after consensus has been reached and when ties in the rankings of alternatives are permitted.

If the rankings do not have ties, then any of the methods described in Sect. 2.1 may be applicable or any other method from the literature that expresses the difference of two rankings may be applicable. The following three applications illustrate the kind of analyses one may seek to perform after a consensus ranking has somehow been reached as part of the GDM process.

5.1 Application #1: Grouping the Experts Based on Their Final Recommendations When All the Alternatives are Considered

Suppose that m experts have been involved in ranking a set of n alternatives and a consensus has been reached by using the concept of PM vectors for expressing individual expert judgments. Next, it is proposed that one compares in a pairwise manner the final recommendations made by these m experts and also the consensus ranking. That is, one computes all possible DIFFERENCE (V_i, V_j) quantities by using Definition 4, where V_i and V_j are the final recommendations of Experts E_i and E_j, respectively, and also the consensus ranking. As one has m + 1 entities to compare, there are ((m + 1) × m)/2 comparisons to be considered. If ties in the ranks are not permitted, then the function DIFFERENCE (V_i, V_j) can be replaced by any other function that expresses the difference between two rankings (such as the ones mentioned in Sect. 2.1).

These values can be used to explore any potential clusters that may be identifiable based on these difference measures. Such clusters can be identified by applying some of the well-known clustering methods such as the ones described by Tan et al. (2013), Larose and Larose (2014), and Witten et al. (2016). The general idea when identifying clusters, is that members within the same cluster to be similar to each other in some way, while members across different clusters to be dissimilar. A key issue here is the number of clusters. Usually, this is explored in an ad-hoc manner. Clustering is by nature an open-ended issue and thus there are multiple clustering approaches. In this application we used a simple approach as it is explained next.

Once clusters are determined an immediate result is to identify subsets of experts that provably ranked the n alternatives in a highly similar manner. Such clustering knowledge may offer new opportunities on the way the alternatives are ranked by next identifying reasons why the experts within clusters assessed them the way they did.

The above concepts are applied to all possible pairs when the final recommendations of the three experts in the illustrative example described in Sect. 2.2 are used along with the consensus ranking. The case of DIFFERENCE (V₁, V₃) was calculated in the previous section. Table 1 presents the numerical results of all possible pairwise comparisons when the three experts are considered. The same table also considers the consensus decision as described in Sect. 2.2 (i.e., the one described by the PM termed V₄).

Table 1 All possible pairwise comparisons among all the experts and the consensus decision when all the alternatives are considered simultaneously

If we consider the case of having two clusters, then Experts E₂ and E₃ are (relatively speaking) the closest ones with each other as their DIFFERENCE (V₂, V₃) value is the smallest one (equal to 0.769) among all the non-diagonal values in Table 1. Expert E₁ is rather distinct than either E₂ or E₃. Thus, one cluster is comprised of Experts E₂ and E₃, while the second cluster of Expert E₁. Another scenario is to have three clusters (with one expert on each) or a single cluster (with all the experts together). The derived consensus decision is also quite distinct than the final ranking recommendations made by each one of the three experts of this illustrative example. This indicates that each expert had to compromise quite a bit in order for a consensus to be reached. In summary, this kind of results can only be derived if one follows an analytical approach based on the concept of difference between two rankings as demonstrated in this application.

5.2 Application #2: Grouping the Experts Based on their Final Recommendations When a Single or a Subset of the Alternatives are Considered

This application is similar to the previous one, but now the interest is narrower as it focuses on a single alternative or a non-empty subset of the set of the alternatives. For illustrative purposes consider only alternative A₄ and again the two experts E₁ and E₃ whose EXPANSION sets were determined earlier. The only difference now is the way the intersection and union operations are defined in a modified version of Definition 4. In this illustrative example alternative A₄ has been ranked by Expert E₁ as {5} (i.e., as having rank value equal to 5) and by Expert E₃ as {4, 5} (see also the two corresponding PMs in Sect. 2.2). Thus, the intersection returns only the set {{5}} while the union operation returns the set {{4}, {5}, {4, 5}}. Hence, a modified version of Definition 4 would result in the following calculations for the adjusted quantity (where “(V₁, V₃)/A₄” indicates the pair of experts E₁ and E₃ when it is examined in terms of the way they ranked alternative A₄): DIFFERENCE ((V₁, V₃)/A₄) = 1 – (1/3) = 0.667.

Next, all ((m + 1) × m)/2 pairwise comparisons can be calculated similarly to the previous illustrative example and again the m experts can be clustered as in the first application. However, now the focus is limited to a single alternative (i.e., to alternative A₄) or a non-empty subset of the alternatives. This approach may reveal hidden aspects of the way the m experts pursued the rankings of single alternatives or subgroups of them. As was the case with the previous application, if ties in the rankings are not permitted, then the difference function described in Definition 4 can be replaced by other definitions of ranking difference (such as the ones mentioned in Sect. 2.1).

5.3 Application #3: Analysis of Individual Alternatives by Using the Final Recommendations of the Experts

This type of analysis focuses directly on the alternatives, one at a time. It expands on the previous ideas regarding ways for assessing the differences between pairs of experts. Given an alternative, say A₁ of the illustrative example presented in Sect. 2.2, a ratio is formed as follows. The numerator is the size of the set formed as the modified intersection of the rankings made by all the experts (when represented as PMs) and then expanding it. For this case the intersection is the set {1, 2} and thus it expands into the set {{1}, {2}, {1, 2}}. Since this set has three members the numerator of the ratio is the number 3. The dominator is determined by first forming the modified union of the sets that correspond to all the ranking decisions made by the experts (expressed as PMs). This is the set {{1, 2}, {1, 2, 3}} which expands to the following set {{1}, {2}, {3}, {1, 2}, {2, 3}, {1, 2, 3}}. This set has six members (please note that the entry {1,3} is ignored as it cannot be in a PM due to the fact the integers 1 and 3 are not consecutive). Therefore, the dominator of the ratio is the number 6. As result of the previous analysis, the value for this ratio for alternative A₁ is equal to 3/6 = 0.500.

When a similar analysis is performed with regard to alternatives A₂, A₃, A₄, and A₅, the corresponding ratios are equal to 3/6 = 0.500, 1/8 = 0.125, 1/3 = 0.333, and 1/5 = 0.200, respectively. Obviously, the value of the above ratios is at most equal to 1 (when all the experts agree with each other) and it is strictly greater than 0 (because we have a consensus reached (according to Definition 2), and thus the intersection set is never empty). The above results for the illustrative example are summarized in Table 2. If we do not use the approach based on PMs (i.e., when ties in the ranks are allowed), then the same approach can still be applied, but it is possible for some ratios to be equal to 0 (if not all the experts agree with the ranking of an alternative).

Table 2 Calculation results for the five alternatives for the illustrative example

The results (final ratio values) can be clustered by using the methods described in the previous application. For this particular illustrative application, from the last column (entitled “Final Value”) of the results in Table 2 one may observe that alternatives A₁, A₂, and perhaps A₄ can be viewed as belonging to the same group (cluster), while the remaining two alternatives (e.g., alternatives A₃ and A₅) seem to belong to a different group. The high values (e.g., 0.500, 0.500, and 0.333, respectively) for alternatives A₁, A₂, and A₄, relatively speaking, are closer to the maximum value of 1. This indicates that the group of the three experts ranked these three alternatives with higher consistency with each other when compared to the way they ranked the other two alternatives (i.e., A₃ and A₅). Perhaps the latter two alternatives are more complex in nature than the former three ones. This suggests that some additional evaluative criteria on the way to evaluate the alternatives and more deliberations might shed more light into the nature of the GDM process of this illustrative example.

In an ideal situation all five alternatives should result in values which would be very close to the maximum possible value of 1. On the contrary, if the values are very close to the minimum possible value of 0, the opposite is true. That is, now the implication is that the experts involved may have reached a consensus on how the alternatives should be ranked, but the way they reached their individual final ranking decisions is significantly different from each other.

The results of the previous analysis can be very sensitive to the ranking decision of a single expert. This happens because a single ranking decision may impact the composition of the union set (which is used to compute the value of the dominator) in a significant manner. A similar situation may also occur for the intersection set. This is more likely to occur with large groups of experts. Thus, a complementary approach to the previous idea is to follow a more traditional method based on some simple statistical concepts.

To help fix ideas let us consider again alternative A₁. There are three ranking decisions regarding this alternative (see also Sect. 2). They are as follows: {1, 2}, {1, 2, 3}, and {1, 2}, as made by expert E₁, E₂, and E₃, respectively. Each ranking decision has a starting (smallest) rank and an ending (largest) rank (in general, these two ranks may be identical or different). The starting rank by each expert is equal to {1}, {1} and {1} (i.e., they are the same). The ending rank is equal to {2}, {3}, and {2}, respectively. The average of the starting rank is equal to 1.000, with a standard deviation equal to 0.000 (as all three numbers are identical). For the ending rank the average is equal to 2.333 with standard deviation equal to 0.222. We define as “length” the difference between the ending rank from the starting rank for each expert when a particular alternative is considered. Thus, the three lengths are equal to 1, 2, and 1, for expert E₁, E₂, and E₃, respectively for alternative A₁. The average of these values is equal to 1.333 while their standard deviation is equal to 0.222. Table 3 presents these results along with the results for all the alternatives which have been computed in a similar manner. Regarding Table 3, of interest is the observation that the average length of the ranking decisions (i.e., the 5-th column) is equal to 1 for alternatives A₃ and A₅, while it is significantly different than 1 for the rest. That is, the spread of the rankings for these two alternatives was smaller when compared to that for the other three alternatives.

Table 3 A statistical analysis of the ranking decisions for the five alternatives for the illustrative example

A comparison between the results in Tables 2 and 3 shows that both tables seem to suggest that alternatives A₁, A₂, and A₄ can be grouped together while alternatives A₃ and A₅ form a second group as it was explained earlier. However, the results in Table 3 are more compact and easier to interpret. It is suggested that, in general, these two analytical approaches should be followed together in a complementary manner.

6 An Illustrative Example Based on a Real-World GDM Application

This section examines an illustrative example taken from the literature (Boroushaki and Malczewski 2010). The real-world problem was to select the best location for a new major parking facility for the city of Canmore, Alberta, Canada. The actual application used a computer software package (ParticipatoryGIS.com) which was created for that purpose to collect input from the public and then analyze it. Those authors do not provide the raw data for the actual problem as the size of that data set is huge (58 decision makers were used for that purpose), but instead they describe a small scale version but still similar in nature problem for illustrative purposes. Thus, in this section we will use the same small version data set to demonstrate some of the previous concepts and approaches.

The small version data set is summarized in Table 4. The integer numbers in this table represent ranks. This table corresponds to Table 1 of the original publication (Boroushaki and Malczewski 2010). These data describe how a sample of five candidate locations (indicated as alternative A₁, A₂, …, A₅) were ranked by six experts (indicated as expert E₁, E₂, …, E₆). Some criteria relevant to this location problem were used by these experts. Somehow a consensus solution was reached and it is presented in the last column of Table 4.

Table 4 Data used for the illustrative example

The implied rankings by the six experts and that of the consensus solution are depicted next. One may observe that ties are allowed in the original data. Table 5 is derived from Table 4 and presents the PMs of the rankings made by the six experts plus the PM of the consensus ranking.

Table 5 The preference maps (PMs) that correspond to the rankings depicted in Table 4

The Rankings by the Six Experts and the Consensus Solution are as follows:

• Expert E₁: $A_{4} \succ A_{1} \succ A_{3} \succ A_{2} \succ A_{5}$

• Expert E₂: $A_{5} \succ A_{1} \succ A_{2} \succ A_{4} \succ A_{3}$

• Expert E₃: $A_{1} \succ A_{4} \sim A_{5} \succ A_{2} \succ A_{3}$

• Expert E₄: $A_{1} \sim A_{5} \succ A_{2} \sim A_{3} \sim A_{4}$

• Expert E₅: $A_{1} \succ A_{5} \succ A_{4} \succ A_{2} \succ A_{3}$

• Expert E₆: $A_{1} \succ A_{5} \succ A_{4} \succ A_{2} \succ A_{3}$

• Consensus: $A_{1} \succ A_{5} \succ A_{2} \succ A_{4} \succ A_{3}$

The intersection between almost any pair of the PMs depicted in Table 5 is the empty set. For instance, the intersection of the PMs derived from the rankings by experts E₁ and E₃ is the empty set. Therefore, the distance between most of the pairs of experts will be equal to the maximum value (i.e., 1.00) and thus would be meaningless. However, this particular application possesses a special characteristic: it aims at finding the best location for a parking facility. In other words, one is interested to identify the alternative with the top (i.e., #1) rank. Thus, it makes sense to focus the analysis on the alternative(s) which have received many top ranks. For the current application, this is the subset of alternatives A₁ and A₅ (see also Table 5). When the rankings (PMs) of the six experts and the consensus solution are considered in terms of only these two alternatives (i.e., A₁ and A₅) some interesting observations can be derived.

For instance, let us consider the pair of experts E₃ and E₄. The PMs of experts E₃ and E₄ in terms of only these two alternatives, denoted as PM₃ and PM₄, respectively, are as follows (see also Table 5):

$$ {\text{PM}}_{3} = \left[ \begin{array}{l} \{ 1\} \hfill \\ \{ 2,3\} \hfill \\ \end{array} \right],\;\;\;\;{\text{PM}}_{4} = \left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \end{array} \right], $$

However, it can be observed now that the previous entity denoted as “PM₃” does not strictly satisfy Definition 1 because {2, 3} cannot be a legitimate ranking set as now we have just two alternatives. Thus, we call such entities “partial preference maps” (PPMs). The previous operations on union and intersection can be performed as usually.

Therefore, the previous two entities will be called PPM₃ and PPM₄, respectively. When the function DIFFERENCE is applied on this pair of PPMs the following result is derived:

$$ {\text{DIFFERENCE}}\;\left( {{\text{PPM}}_{3} ,{\text{ PPM}}_{4} } \right) = 0.800. $$

In a similar manner, any pair of PPMs can be analyzed.

In Boroushaki and Malczewski (2010) the authors computed the proximity (distance) of two rankings based on a method originally proposed in Herrera-Viedma et al. (2002). That approach is based on the absolute value of the difference of the ranks of the alternatives, taken one at a time. That is, a method similar (but not identical) to method 5 presented in Sect. 2.1. Such approach, however, fails to compute the essence of PMs when ties are present. That is, the proposed approach based on Definition 4 (in Sect. 4) is more appropriate.

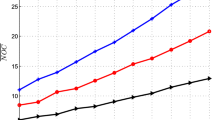
Table 6 presents all the pairwise differences derived when one considers the PMs shown in Table 5 but only in terms of the two alternatives A₁ and A₅ (i.e., to consider the PPMs as defined above). As this table (matrix) is a symmetric one, only the entries in the upper-right half of it are shown for simplicity of the presentation. The data in Table 6 are next used to explore any relationships that may exist among the experts involved in this GDM process. These relationships can be explored by following a clustering approach as follows (see also Fig. 1). The same results are also presented in tabular form in Table 7.

Table 6 All pairwise differences between the PMs depicted in Table 5 (only the upper triangular entries are shown for simplicity)

Fig. 1

Clusters defined among the experts and the consensus solution (each denoted by the small solid rectangle symbol) which are derived by analyzing the data in Table 6

Table 7 Clustering schemes forming as the difference threshold value changes

The data in Table 6 suggest that the two experts E₅ and E₆, along with the consensus solution are identical (their pairwise differences are equal to 0) when one focuses on the rankings of the two best alternatives (i.e., A₁ and A₅). This is why the experts E₅ and E₆ and the consensus ranking (denoted as E₀ in Fig. 1 and Table 7) are the only members of the inner most cluster in Fig. 1 (see also Table 7).

Next we can observe that if one expands the notion of belonging to the same cluster (i.e., the distance threshold increases from 0 to 0.667), then experts E₂ and E₄ form a single cluster. At the same time, expert E₃ can form a cluster with E₅, E₆ and E₀, and another cluster is formed by E₄ and E₅, E₆ and E₀. However, experts E₃ and E₄ cannot be placed yet inside the same cluster. For this to happen, one needs to further relax the notion of belonging to the same cluster by considering difference values less than or equal to the threshold value 0.800 (see also Table 6). Now, E₃, E₄, E₅, E₆, and E₀ are all members of the same cluster. However, expert E₁ is still considered very different than the rest to be placed within the same cluster, while expert E₂ forms a cluster only with expert E₄. In order for one to also include experts E₁ and E₂ in the same cluster, then the threshold distance needs to be expanded to the highest value (i.e., to become equal to 1). In this way everybody would be included in a single cluster (see also Fig. 1 and Table 7). However, such scenario might be practically meaningless.

In summary, the previous clustering analysis reveals that experts E₅ and E₆ are practically of the same ranking preferences in terms of the top two alternatives which coincides with the consensus ranking. The next closest way experts can be considered as similar is when one considers experts E₃ and E₄ as indicated in Fig. 1 (or Table 7) and so on.

The previous results cannot be attained unless one follows the analytical procedures described in this study. Depending on the nature of the application at hand, the definition of difference between two rankings may change. However, one would still have to compute all possible pairwise differences and then examine how clusters among the experts may form. These clusters have the potential to uncover actionable new knowledge pertinent to the group decision making process and the current application. The proposed methods are very versatile and can be adapted to different problem settings. Current GDM methods do not offer this kind of post-consensus exploration.

7 Concluding Remarks

Smart decision making always requires to have a feedback mechanism at each stage of the decision making process. This is true in group decision making too. When a consensus has been reached after (possibly) a laborious decision making process, this should not be treated as the end of the process. A feedback step that further analyzes the final results may offer the last opportunity to uncover some hidden but nevertheless critical dynamics of the problem under consideration or even of the experts themselves.

The proposed methodology analyzes differences among pairs of experts when all the alternatives are considered simultaneously and also when a single alternative or subsets of alternatives are considered. A way to analyze the decisions made regarding each alternative is presented as well. The results of such analyses, after a consensus has been reached, may shed light to aspects of the problem or the experts that cannot be explored unless a consensus has first been reached and comprehensive analyses like the ones proposed in this paper are undertaken.

In summary, this paper made original contributions in two fronts. First, it contributed on how to define the concept of difference when rankings are allowed to include ties. That is, when one alternative can be assigned to multiple (but consecutive) ranks. This type of rankings can capture more realistically the way decision makers express ranking preferences. This issue has not been explored adequately so far and this study offers some exciting new developments. The second group of original contributions is on ways for analyzing the final results of a GDM process after a consensus has been reached. It provides the means to infer potentially useful new knowledge regarding the group of experts and the alternatives that were evaluated during the GDM process.

These analyses are proposed to be done post-consensus. The original GDM problem may need to be re-examined if new insights uncover important reasons to do so, especially if certain patterns seem to hold true over time when multiple GDM sessions with the same group of experts are considered. For instance, if it is discovered that very often the same subgroup of experts make decisions in an identical or semi-identical manner with each other. Such finding may be considered as an actionable insight. The proposed methodology can be executed automatically and be presented to the experts and/or to any other relevant stakeholder in an intuitive manner. This is a novel aspect of this study and has not been explored in other studies to have results to compare with.

Future research may focus on how to explore other ways for defining the difference between two rankings, especially when ties are permitted. For instance, consider the following three PPMs:

$$ {\text{PPM}}_{1} = \left[ \begin{array}{l} \{ 2\} \hfill \\ \{ 3\} \hfill \\ \end{array} \right],\quad {\text{PPM}}_{2} = \left[ \begin{array}{l} \{ 4\} \hfill \\ \{ 5\} \hfill \\ \end{array} \right],\quad {\text{PPM}}_{0} = \left[ \begin{array}{l} \{ 1,2\} \hfill \\ \{ 1,2\} \hfill \\ \end{array} \right], $$

According to Definition 4 in Sect. 4, the difference between PPM₁ and PPM₀ is equal to 1, and the same is true for the difference between PPM₂ and PPM₀. However, one may argue that PPM₁ is closer to PPM₀ than PPM₂ is to PPM₀. This is not captured by this definition. Thus, in the future the concept of PM (or PPM) difference may need to be enhanced to be able to capture such issues.

Another possible extension for the future might be to consider the various stages the GDM process may have to go through during a single session. Usually, consensus is not reached in a single stage and the process may have to go through a sequence of iterations (stages) for this to happen. Information gathered during each stage and also across different GDM sessions (with the same or similar groups of experts) may be analyzed in a similar manner. Such data, however, may offer more ways for exploring the dynamics of the GDM processes and the experts involved with them. As a final note we state that the results of this study have been used in Triantaphyllou et al. (2020) as the foundation for a post-consensus analysis that considers multiple GDM sessions, each session having a number of stages. That study considers some graph theoretic formulations and then it employs an association rules mining approach to derive potentially important relations in the way experts make decisions during GDM processes.