1 Introduction

The existence of gravitational waves (GWs), which was confirmed when LIGO detected GW150914 (stellar-mass binary black holes) in September 2015 (and announced in February 2016) heralded new era of physics and astronomy [1]. In this context, QNMs [2, 3] of a black hole are related with the ringdown phase of GWs. Namely, a perturbed black hole settles down through the characteristic damped oscillations i.e., by the QNMs [4,5,6,7,8]. Since the discovery of GWs, studies on the QNMs have gained more attention [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Moreover, in the gauge/gravity dualities theories, there is a relation between the QNMs and the poles of a propagator in the dual field theory so that physicists use it as a tool to work on strong coupled gauge theories (or holography) [29,30,31,32,33,34,35]. The frequencies of QNMs are obtained by applying perturbation to the spacetime of the black hole with appropriate boundary conditions. One of the most difficulties in studying QNMs is that they admit an eigenvalue problem, which is not self-adjoint: the system is non-conservative and therefore energy is lost both at spatial infinity and at the black hole horizon. Thus, unlike the ordinary normal modes, QNMs are not a basis (see [36] and references therein). Moreover, QNMs can be also used for testing the no-hair theorem, which states that BHs have only mass, angular momentum and charge (neutral to quantum effects) and black hole quantization [18, 37]. Namely, studying the QNMs can give us new hints about physics beyond the Einstein’s theory of general relativity [38].

On the other hand, the complete theory of quantum gravity is still an open problem. However, black holes can be used as a test arena for the quantum gravity. From this point of view, Hawking [39,40,41,42,43,44,45,46,47,48,49] made a pioneering work by showing how the strong gravitational field around a black hole can affect the production of virtual particles (pairs of particles and anti-particles: existing all the time in apparently vacuum according to quantum field theory). According to the theory of Hawking, virtual particles are likely to be created outside the event horizon of a black hole. Thus, it is possible that the positive energy (mass) member of the pair can escape from the black hole—observed as thermal radiation—while the negative particle (with its negative energy or mass) can fall into the black hole, which gives rise the black hole to lose its mass. This phenomenon is known as the Hawking radiation and it was perhaps one of the first ever examples of the quantum gravity theory. Since then, there is a continuously growing interest to the thermodynamics of black holes, Hawking radiation and QNMs [50,51,52,53,54,55,56,57,58].

Born and Infeld proposed the non-linear electromagnetic field theory to solve the problem of divergences in the Maxwell theory [59]. After the studies on the superstring theory, which admits the D-branes that are derived from the Born–Infeld action, various researches are done by using the Einsten-dilaton–Born–Infeld theory to obtain non-singular charged black hole solutions. From the high energy levels to the the low energy limit, the string theory reduces to the Einstein gravity non-minimally coupled scalar dilaton field [60,61,62,63,64]. The main motivation for studying the BIDBHs is that they are a promising candidate for the quantum gravity. In the light of all mentioned above, in this paper, we shall use the black hole solution in the Born–Infeld-dilaton with a Liouville-type potential. This kind of Liouville-type potential appears when one applies a conformal transformation to the low-energy limit of the string tree level effective action for the massless boson sector and in sequel write the action in the Einstein frame [61,62,63,64]. Furthermore, if the dilaton filed is removed from the action, the action of Einstein–Born–Infeld with \(\Lambda \) is obtained. Use of the dilaton field causes the changes on the asymptotic behavior of the spacetime and also leads to curvature singularities at finite radii. Therefore, such black holes can be used in the studies on AdS/CFT correspondence, where the holography is occurred near the horizon [29].

Cosmic strings are one dimensional topological defects extensively studied in the past [65,66,67,68,69,70]. It is widely believed that such topological defects may have formed during a symmetry breaking process which is usually associated with the phase transition in the early universe. There are, unfortunately, no experimental measurements supporting their existence until today. However the possible detection of these exotic objects in the future will have a great impact in current understanding on the physics of the early universe. Our main aim in this paper is to explore an analytical solution of the QNMs and Hawking radiation in spacetime of BIDBHs [62] including the effect of the cosmic string.

The remainder of this paper is arranged as follows. In Sect. 2, we briefly review the BIDBH spacetime and its thermodynamics. In Sect. 3, we study the Klein–Gordon equation (KGE) of the massive scalar particles propagating in the geometry of BIDBH. Section 4 is devoted to the exact solution of the radial equation. We also derive the QNMs of BIDBH. In Sect. 5, we introduce a thin cosmic string in the BIDBH spacetime and solve the KGE for a massive scalar field for that geometry. Then, we obtain the effect of the cosmic strings on the QNMs of BIDBH spacetime. In Sect. 6, we calculate the effective temperature and reveal the effects of the cosmic strings on the quantization of the BIDBH spacetime. In Sect. 7, we summarize our results.

2 Spacetime of BIDBH

In this section, we shall review and give the insights of the BIDBH spacetime [62]. The action of the Einstein-dilaton–Born–Infeld theory, which comprises the dilaton field \(\phi \) and the Born–Infeld parameter \({\widehat{\gamma }}\) coupled to the Maxwell field is given by

$$\begin{aligned} S=\int d^{4}x\sqrt{-g}\left[ {\mathcal {R}}-2(\nabla \phi )^{2}-V(\phi )\ +4 {\widehat{\gamma }}e^{-2\tau \phi }\left( 1-\sqrt{1+\frac{F_{\mu \nu }F^{\mu \nu }}{2{\widehat{\gamma }}}}\right) \right] \end{aligned}$$
(1)

where \(V(\phi )\) denotes potential, \(\tau \) is the dilaton coupling constant, \({\mathcal {R}}\) stands for the Ricci scalar, and \(F_{\mu \nu }\) is the Maxwell tensor. Dilaton has the following solution [62]

$$\begin{aligned} \phi (r)=\frac{\tau }{1+\tau ^{2}}\ln (b_{1}r-b_{2}) \end{aligned}$$
(2)

where \(b_{1}\) and \(b_{2}\) are integration constants. Throughout the paper, we set, without loss of generality, \(b_{1}=1\) and \(b_{2}=0\). The dilaton potential can be considered either as \(V(\phi )=0\) or as a Liouville-type potential \(V(\phi )=2\Lambda e^{-2\tau \phi }\) [\(\Lambda \) is the mass scale of \(V(\phi )\)]. For both potentials, the metric function h(r) is found to be linear in r [63, 64]. In other words, h(r) is irrespective of the dilaton potential and it admits the following solution:

$$\begin{aligned} h(r)=\frac{r}{L}-b_{0}, \end{aligned}$$
(3)

where \(b_{0}\) is a constant. Length scale L is given by

$$\begin{aligned} L^{-1}=2(1-2\rho -\Lambda ), \end{aligned}$$
(4)

where the constant \(\rho \) is given by

$$\begin{aligned} \rho =-{\widehat{\gamma }}+\sqrt{{\widehat{\gamma }}(Q^{2}+{\widehat{\gamma }})}, \end{aligned}$$
(5)

by which Q is the background charge:

$$\begin{aligned} Q^{2}=\frac{1+\sqrt{1+16{\widehat{\gamma }}^{2}}}{8{\widehat{\gamma }}}. \end{aligned}$$
(6)

Finally, as it can be seen from [62,63,64], the line-element of the BIDBH spacetime takes the following form

$$\begin{aligned} ds^{2}=-h(r)dt^{2}+h(r)^{-1}dr^{2}+rd\Omega ^{2}. \end{aligned}$$
(7)

Setting \(r_{H}=Lb_{0},\) metric function 3 recasts in

$$\begin{aligned} h(r)=\frac{r-r_{H}}{L}. \end{aligned}$$
(8)

Thus, one can easily interpret \(r_{H}\) as the event horizon of the BIDBH. On the other hand, due to the non-asymptotically flat character of the metric 7, one can employ the Brown–York formalism [71] to compute the quasi-local mass, \(M_{QL}\) (the interested reader is referred to [72, 73] and references therein for \(M_{QL}\)) of the black hole, which results in:

$$\begin{aligned} r_{H}=4LM_{QL}. \end{aligned}$$
(9)

2.1 Thermodynamics of BIDBH

Considering the following 4-velocity

$$\begin{aligned} {\varvec{u}}=u^{t}\partial _{t}, \end{aligned}$$
(10)

one can easily verify that the normalization condition is satisfied by

$$\begin{aligned} 1=u^{\mu }u_{\mu }, \end{aligned}$$
(11)

with

$$\begin{aligned} u^{t}=\frac{1}{\sqrt{g_{tt}}}. \end{aligned}$$
(12)

Since the metric components are functions of r and \(\theta \), particle acceleration \(a_{p}^{\mu }\) is obtained from [74]

$$\begin{aligned} a^{\mu }=-g^{\mu \upsilon }\partial _{\upsilon }\ln u^{t}. \end{aligned}$$
(13)

Surface gravity (\(\kappa \)) is defined by [74] as follows

$$\begin{aligned} \kappa =\lim _{r\rightarrow r_{h}}\frac{\sqrt{a^{\mu }a_{\mu }}}{u^{t}}, \end{aligned}$$
(14)

which yields

$$\begin{aligned} \kappa =\frac{1}{2}\left. \frac{dh\left( r\right) }{dr}\right| _{r=r_{h}}=\frac{1}{2L}. \end{aligned}$$
(15)

Thus, we obtain the Hawking temperature as

$$\begin{aligned} T_{H}=\frac{\kappa }{2\pi }=\frac{1}{4\pi L}. \end{aligned}$$
(16)

It can be deduced from the above result that Hawking radiation of BIDBH is nothing but a isothermal process. Surface area of the BIDBH can be computed as

$$\begin{aligned} A_{BH}=\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }\sqrt{-g}\ d\theta =4\pi r_{h}. \end{aligned}$$
(17)

by which \(\sqrt{-g}\) is considered for the hypersurface of BIDBH. Hence, the entropy of BIDBH becomes [37, 75, 76]

$$\begin{aligned} S_{BH}=\frac{A_{BH}}{4 }=\pi r_{h}. \end{aligned}$$
(18)

The physical quantities given in Eqs. (9), (17), and (18) satisfy the first law of thermodynamics:

$$\begin{aligned} dM_{QL}=T_{H}dS_{BH}. \end{aligned}$$
(19)

3 QNMs of BIDBH spacetime

In this section, we shall study the wave equation of the massive scalar particles propagating in the geometry of BIDBH. To this end, we first consider the KGE for a massive scalar particle [77]

$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _{\alpha }\left( \sqrt{-g}g^{\alpha \nu }\partial _{\nu }\Psi \right) -m_{b}^{2}\Psi =0, \end{aligned}$$
(20)

where \(m_{b}\) is the mass of the boson having scalar field \(\Psi \). Owing to the spherical symmetry and time independence of the spacetime, the scalar field can be written as

$$\begin{aligned} \Psi =\Psi ({\varvec{r}},t)=P(r)A(\theta )\text{ e }^{im\varphi }\text{ e } ^{-i\omega t}\ , \end{aligned}$$
(21)

where \(\omega \) is the frequency and m denotes the azimuthal quantum number. Thus, KGE (20) takes the following form in the BIDBH geometry

$$\begin{aligned}&-\,{\frac{{\omega }^{2}r}{h\left( r\right) }}-\frac{{\cot }\left( \theta \right) }{A\left( \theta \right) }\frac{dA\left( \theta \right) }{d\theta }- \frac{1}{A\left( \theta \right) }\frac{d^{2}A\left( \theta \right) }{d{ \theta }^{2}}+{\frac{{m}^{2}}{\sin ^{2}\left( \theta \right) }}+m_{b}^{2}r \nonumber \\&\quad -\,{\frac{h\left( r\right) \left[ \frac{dP\left( r\right) }{dr}+r\frac{ d^{2}P\left( r\right) }{d{r}^{2}}\right] +r\left( {\frac{dh\left( r\right) }{ dr}}\right) {\frac{dP\left( r\right) }{dr}}}{P\left( r\right) }=0.} \end{aligned}$$
(22)

Thus, if one uses an eigenvalue \(\lambda ,\) we can separate Eq. (22) and get an angular equation:

$$\begin{aligned} -\,\frac{1}{A\left( \theta \right) }\frac{d^{2}A\left( \theta \right) }{d{ \theta }^{2}}-\frac{{\cot }\left( \theta \right) }{A\left( \theta \right) } \frac{dA\left( \theta \right) }{d\theta }+{\frac{{m}^{2}}{\sin ^{2}\left( \theta \right) }+\lambda }=0, \end{aligned}$$
(23)

and a radial equation:

$$\begin{aligned} m_{b}^{2}r-{\frac{{\omega }^{2}r}{h\left( r\right) }-\frac{h\left( r\right) \left[ \frac{dP\left( r\right) }{dr}+r\frac{d^{2}P\left( r\right) }{d{r}^{2}} \right] +r\left( {\frac{dh\left( r\right) }{dr}}\right) {\frac{dP\left( r\right) }{dr}}}{P\left( r\right) }-\lambda =0.} \end{aligned}$$
(24)

As it is well-known, we obtain Legendre polynomials [78, 79] for the angular equation (23) with \({\lambda =-l}\left( l+1\right) \) in which l denotes orbital or azimuthal quantum number.

3.1 Exact solution of the radial equation and QNMs

Changing the independent variable from r to y

$$\begin{aligned} r=r_{h}\left( 1-y\right) , \end{aligned}$$
(25)

we transform Eq. (24) into

$$\begin{aligned}&y\left( 1-{y}\right) {\frac{d^{2}P\left( y\right) }{d{y}^{2}}}+\left( 1-2\,y\right) {\frac{dP\left( y\right) }{dy}} \nonumber \\&\quad +\,\left[ {L}^{2}{\omega }^{2}\left( -1+\frac{1}{y}\right) +m_{b}^{2}Lr_{h}\left( 1-y\right) +{l}\left( l+1\right) L\right] P\left( y\right) =0. \end{aligned}$$
(26)

We also introduce a new function U(y):

$$\begin{aligned} P\left( y\right) ={y}^{i\omega \,L}U\left( y\right) , \end{aligned}$$
(27)

and thus Eq. (26) becomes

$$\begin{aligned}&y\left( 1-{y}\right) {\frac{d^{2}U\left( y\right) }{d{y}^{2}}}+\left[ 1-2\,y+2\,i\omega \,L\left( 1-y\right) \right] {\frac{dU\left( y\right) }{dy} } \nonumber \\&\quad +\,\left[ -i\omega \,L+m_{b}^{2}Lr_{h}\left( 1-y\right) +{l}\left( l+1\right) L \right] U\left( y\right) =0, \end{aligned}$$
(28)

which is the confluent Heun equation [80, 81] (and see for example [82,83,84,85,86,87,88] for its applications). Its generic form is given by

$$\begin{aligned} {\frac{d^{2}U\left( y\right) }{d{y}^{2}}}+\left( {\widetilde{a}}+\frac{1+ {\widetilde{b}}}{y}-\frac{1+{\widetilde{c}}}{1-y}\right) {\frac{dU\left( y\right) }{dy}}+\left( \frac{{\widetilde{m}}}{y}-\frac{{\widetilde{n}}}{1-y} \right) U\left( y\right) =0. \end{aligned}$$
(29)

Comparing Eq. (28) with Eq. (29), we get

$$\begin{aligned} {\widetilde{a}}= & {} {\widetilde{c}}=0,\ \ {\widetilde{b}}=2i\omega \,L, \end{aligned}$$
(30)
$$\begin{aligned} {\widetilde{m}}= & {} \frac{1}{2}({\widetilde{a}}-{\widetilde{b}}-{\widetilde{c}}+ {\widetilde{a}}{\widetilde{b}}-{\widetilde{b}}{\widetilde{c}})-{\widetilde{e}}=L\left[ {l}\left( l+1\right) +m_{b}^{2}r_{h}\right] -i\omega \,L, \end{aligned}$$
(31)
$$\begin{aligned} {\widetilde{n}}= & {} \frac{1}{2}({\widetilde{a}}+{\widetilde{b}}+{\widetilde{c}}+ {\widetilde{a}}{\widetilde{c}}+{\widetilde{b}}{\widetilde{c}})+{\widetilde{d}}+ {\widetilde{e}}=L\left[ i\omega -{l}\left( l+1\right) \right] . \end{aligned}$$
(32)

Thus, we have

$$\begin{aligned} {\widetilde{e}}=-L\left[ {l}\left( l+1\right) +m_{b}^{2}r_{h}\right] ,\ \ {\widetilde{d}}=m_{b}^{2}Lr_{h}, \end{aligned}$$
(33)

The solution of Eq. (29) is given by [80, 81]

$$\begin{aligned} U\left( y\right) =A_{1}\text{ HeunC }({\widetilde{a}},{\widetilde{b}},{\widetilde{c}} ,{\widetilde{d}},{\widetilde{e}};y)+A_{2}y^{-{\widetilde{b}}}\text{ HeunC }( {\widetilde{a}},-{\widetilde{b}},{\widetilde{c}},{\widetilde{d}},{\widetilde{e}};y), \end{aligned}$$
(34)

where \(A_{1},A_{2}\) are the constants. Thus, the general exact solution of the radial equation (26), in the entire range \(-\infty <y\le 0,\) is given by

$$\begin{aligned} P(y)=A_{1}{y}^{i\omega \,L}\text{ HeunC }({\widetilde{a}},{\widetilde{b}}, {\widetilde{c}},{\widetilde{d}},{\widetilde{e}};y)+A_{2}{y}^{-i\omega \,L} \text{ HeunC }({\widetilde{a}},-{\widetilde{b}},{\widetilde{c}},{\widetilde{d}}, {\widetilde{e}};y). \nonumber \\ \end{aligned}$$
(35)

For matching the near horizon and asymptotic regions, we are interested in the large r behavior (\(y\rightarrow -\,\infty \)) of the solution (35). For this purpose, one needs such a connection formula:

$$\begin{aligned} \text{ HeunC }\left( {\widetilde{a}},{\widetilde{b}},{\widetilde{c}},{\widetilde{d}}, {\widetilde{e}};y\right) \rightarrow \text {Gamma function multiplier}\times \text{ HeunC }({\overline{a}},{\overline{b}},{\overline{c}},{\overline{d}},{\overline{e}} ;y^{-1}), \nonumber \\ \end{aligned}$$
(36)

thus the normalization condition [80]: \(\text{ HeunC }( {\widetilde{a}},{\widetilde{b}},{\widetilde{c}},{\widetilde{d}},{\widetilde{e}} ;y^{-1}=0)=1\) is going to be satisfied while \(y\rightarrow \infty \). The parameters \({\overline{a}},{\overline{b}},{\overline{c}},{\overline{d}},{\overline{e}}\) and the parameters of “Gamma function multiplier” seen in the above equation have to be related with \({\widetilde{a}},{\widetilde{b}},{\widetilde{c}}, {\widetilde{d}},{\widetilde{e}}\) according to the transformation rules of the special functions [78]. Thus, the asymptotic solution of the radial equation (35) would be obtained. In sequel, we should impose the second boundary condition (pure outgoing QNMs survive at spatial infinity) and compute the QNMs, analytically. Unfortunately, the absence of Eq. (36) like transformation in the literature does not allow us to find analytical forms of the ingoing and outgoing waves at spatial infinity. Namely, the connection formula (36) of the confluent Heun functions remained intact [80, 81].

From Eq. (A12), the confluent Heun functions can be reduced to the Gauss hypergeometric functions:

$$\begin{aligned} \text{ HeunC }(0,\pm \, {\widetilde{b}},0,{\widetilde{d}},{\widetilde{e}};y)=\left( 1-y\right) ^{-X_{\pm }}{F\Bigg (X_{\pm },X_{\pm };\,1\pm \widetilde{{b}};\,{ \frac{y}{y-1}}}\Bigg ), \end{aligned}$$
(37)

if \({\widetilde{d}}=0\text { and }1\pm {\widetilde{b}}\ne 0\text { for }y\ne 1.\) In Eq. (37), \({X_{\pm }}\) are given by

$$\begin{aligned} X_{\pm }= & {} \frac{1\pm {\widetilde{b}}+\sqrt{\widetilde{{b}}^{2}-4{\widetilde{e}} +1}}{2}, \nonumber \\= & {} \pm i\omega \,L+{\widehat{p}}, \end{aligned}$$
(38)

in which

$$\begin{aligned} {\widehat{p}}=\frac{1}{2}+i{\omega \Omega }, \end{aligned}$$
(39)

where

$$\begin{aligned} {\Omega }=\sqrt{{L}^{2}-\frac{l\left( l+1\right) L+\frac{1}{4}}{{\omega }^{{2 }}}}. \end{aligned}$$
(40)

The condition of \({\widetilde{d}}=0\) corresponds to the case of massless bosons (\(m_{b}=0\)). Therefore, the radial solution (35) for the massless scalar fields in the BIDBH geometry becomes

$$\begin{aligned} P(y)= & {} A_{1}{y}^{i\omega \,L}\left( 1-y\right) ^{-{X_{+}}}{F\Bigg ( X_{+},X_{+};1+}\widetilde{{b}}{;\,{\frac{y}{y-1}}}\Bigg ) \nonumber \\&+\,A_{2}{y}^{-i\omega \,L}\left( 1-y\right) ^{-{X_{-}}}{F\Bigg (X_{-},X_{-};1- }\widetilde{{b}}{;\,{\frac{y}{y-1}}}\Bigg ), \end{aligned}$$
(41)

Furthermore, if we change the independent variable from y to a new variable z via the following transformation

$$\begin{aligned} z={{\frac{y}{y-1}=}}\frac{r-r_{h}}{r}, \end{aligned}$$
(42)

the generic massless radial solution to Eq. (26) reads

$$\begin{aligned} P(z)=\left( 1-z\right) ^{{\widehat{p}}}\Big [ A_{1}z^{i\omega \,L}(1-z)^{ {\widehat{p}}}F({X_{+},X_{+};1+}\widetilde{{b}};z)+A_{2}z^{-i\omega \,L}F({ X_{-},X_{-};1-}\widetilde{{b}};z)\Big ]. \nonumber \\ \end{aligned}$$
(43)

Tortoise coordinate of the BIDBH is given by

$$\begin{aligned} r_{*}= & {} \int \frac{dr}{h\left( r\right) }=L\ln \left( r-r_{h}\right) \nonumber \\= & {} L\int \frac{dy}{y}=L\ln \left( y\right) , \end{aligned}$$
(44)

It is worth noting that the range \(r_{h}<r<\infty \) corresponds to \(-\infty<r_{*}<\infty \), since \(r_{*}\rightarrow -\infty \) as \(r\rightarrow r_{h}\). For this reason, \(r_{*}\) is known as a tortoise coordinate: as we approach the horizon, r changes more and more slowly with \(r_{*}\) since \(\frac{dr}{ dr_{*}}\rightarrow 0.\) On the other hand, from Eq. (44) we have

$$\begin{aligned} y=e^{\frac{r_{*}}{L}}\, \,\rightarrow \, \, z=\frac{e^{\frac{ r_{*}}{L}}}{e^{\frac{r_{*}}{L}}-1}. \end{aligned}$$
(45)

Near the event horizon [\(r\rightarrow r_{h}\); \(r_{*}\rightarrow -\infty \); \(y\cong z\rightarrow 0\)], the hypergeometric functions approximate to one. Therefore, the radial solution reduces to

$$\begin{aligned} P_{NH}(z)\sim A_{1}z^{i\omega \,L}+A_{2}z^{-i\omega \,L} \end{aligned}$$
(46)

and thus we have the near horizon form of the scalar field \(\varphi \) as follows

$$\begin{aligned} \Psi \sim A_{1}e^{-i\omega (t-r_{*})}+A_{2}e^{-i\omega (t+r_{*})}. \end{aligned}$$
(47)

It is obvious from Eq. (47) that first term \(\left( A_{1}e^{-i\omega (t-r_{*})}\right) \) represents the outgoing wave, the second term \(\left( A_{2}e^{-i\omega (t+r_{*})}\right) \) corresponds to the ingoing wave. For having the QNMs, we impose one of the boundary conditions that only ingoing waves survive at the event horizon. To satisfy this condition, we simply set \(A_{1}\) \(=0\). Namely, the radial solution admitting the QNM is given by

$$\begin{aligned} P(z)=A_{2}z^{-i\omega \,L}\left( 1-z\right) ^{{\widehat{p}}}F(\overset{ {\widehat{a}}}{\overbrace{{X_{-}}}}{,}\overset{{\widehat{b}}}{\overbrace{{X_{-}}} }{;}\overset{{\widehat{c}}}{\overbrace{{1-}\widetilde{{b}}}};z). \end{aligned}$$
(48)

Performing the connection formula for \(z\rightarrow 1-z\) of the hypergeometric functions [78]:

$$\begin{aligned} P\left( z\right)&=A_{2}z^{-i\omega \,L}(1-z)^{^{{\widehat{p}}}}\frac{\Gamma ( {\widehat{c}})\Gamma ({\widehat{c}}-{\widehat{a}}-{\widehat{b}})}{\Gamma ({\widehat{c}} -{\widehat{a}})\Gamma ({\widehat{c}}-{\widehat{b}})}F({\widehat{a}},{\widehat{b}};1+ {\widehat{a}}+{\widehat{b}}-{\widehat{c}};1-z) \nonumber \\&\quad +\,A_{2}z^{-i\omega \,L}(1-z)^{{\widehat{p}}-{\widehat{a}}-{\widehat{b}}+\widehat{c }}\frac{\Gamma ({\widehat{c}})\Gamma ({\widehat{a}}+{\widehat{b}}-{\widehat{c}})}{ \Gamma ({\widehat{a}})\Gamma ({\widehat{b}})}F(c-{\widehat{a}},{\widehat{c}}- {\widehat{b}};1\nonumber \\&\quad +\,{\widehat{c}}-{\widehat{a}}-{\widehat{b}};1-z). \end{aligned}$$
(49)

in which

$$\begin{aligned} {\widehat{p}}-{\widehat{a}}-{\widehat{b}}+{\widehat{c}}=1-{\widehat{p}}=\frac{1}{2}-i{ \omega \Omega }. \end{aligned}$$
(50)

Therefore, the asymptotic form (\(r\rightarrow \infty \); \(r_{*}\rightarrow \infty \); \(z\rightarrow 1\)) of the radial solution (49 ) is given by

$$\begin{aligned} P\left( z\right) \sim A_{2}\sqrt{1-z}\left[ (1-z)^{i{\omega \Omega }}\frac{ \Gamma ({\widehat{c}})\Gamma ({\widehat{c}}-{\widehat{a}}-{\widehat{b}})}{\Gamma ( {\widehat{c}}-{\widehat{a}})\Gamma ({\widehat{c}}-{\widehat{b}})}+(1-z)^{-i{\omega \Omega }}\frac{\Gamma ({\widehat{c}})\Gamma ({\widehat{a}}+{\widehat{b}}-\widehat{c })}{\Gamma ({\widehat{a}})\Gamma ({\widehat{b}})}\right] . \nonumber \\ \end{aligned}$$
(51)

Correspondingly, the near spatial infinity form of the scalar field becomes

$$\begin{aligned} \Psi \sim A_{2}\sqrt{1-z}\left[ \underset{\text {Ingoing Wave }}{\underbrace{ e^{-i\omega \left( t-{\Omega }\right) }\frac{\Gamma ({\widehat{c}})\Gamma ( {\widehat{c}}-{\widehat{a}}-{\widehat{b}})}{\Gamma ({\widehat{c}}-{\widehat{a}})\Gamma ({\widehat{c}}-{\widehat{b}})}}}+\underset{\text {Outgoing Wave}}{e\underbrace{ ^{-i\omega \left( t+{\Omega }\right) }\frac{\Gamma ({\widehat{c}})\Gamma ( {\widehat{a}}+{\widehat{b}}-{\widehat{c}})}{\Gamma ({\widehat{a}})\Gamma ({\widehat{b}} )}}}\right] . \nonumber \\ \end{aligned}$$
(52)

It is worth noting that in order the waves to be ingoing and outgoing as shown above, we impose a condition, which is named as the wave type identifier condition by [89,90,91]

$$\begin{aligned} {\Omega } = \sqrt{{L}^{2}-\frac{l\left( l+1\right) L+\frac{1}{4}}{{\omega }^{{2 }}}}{\in {\mathbb {R}} >0}. \end{aligned}$$
(53)

Namely, Eq. (53) helps us to distinguish the advanced and retarded times and thus the ingoing and outgoing waves. Spatial infinity boundary condition of QNMs is conditional on the vanishing ingoing waves at spatial infinity. In other words, only the outgoing waves are allowed to propagate at the spatial infinity. To this end, one should terminate the first term (i.e., the ingoing wave). To this end, we use the poles of the gamma functions stand in the denominator of the ingoing wave term [\(\Gamma ({\widehat{c}}-{\widehat{a}})\) or \(\Gamma ({\widehat{c}}- {\widehat{b}})\)] of Eq. (52). It is a well-known fact that the gamma functions \(\Gamma (q)\) have poles when \(q=-n\) with \(n=0,1,2,\ldots \). Thus, QNMs of the massless scalar waves of the BIDBH are found out as follows:

$$\begin{aligned} {\widehat{c}}-{\widehat{a}}={\widehat{c}}-{\widehat{b}}=-n, \quad ( n=0,1,2,\ldots \text {)} \end{aligned}$$
(54)

From above, we find out the following QNMs:

$$\begin{aligned} \omega _{QNM}= & {} -{\frac{i\left[ n\left( n+1\right) -Ll\left( l+1\right) \right] }{L\left( 1+2\,n\right) },} \nonumber \\= & {} -i2\pi T_{H}\frac{\left[ n\left( n+1\right) -Ll\left( l+1\right) \right] }{\left( n+\frac{1}{2}\right) }. \end{aligned}$$
(55)

Stable QNMs should have \( Im (\omega _{QNM}<0)\). Therefore, one can immediately observe from Eq. (55) that the stable QNMs are conditional on

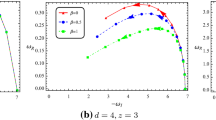
$$\begin{aligned} n\left( n+1\right) \ge Ll\left( l+1\right) . \end{aligned}$$
(56)

One can immediately ask the existence of unstable modes depending on the values of n,  L,  and l; see Fig. 1. However, we want to take the attention of the reader to Eq. (53), which helps us to decide the wave-type: ingoing or outgoing. When \(\omega _{QNM}\) is used in Eq. (53), one gets

$$\begin{aligned} \left. {\Omega }\right| _{\omega =\omega _{QNM}}={\frac{\frac{1}{2} +n\left( n+1\right) +Ll\left( l+1\right) }{n\left( n+1\right) -Ll\left( l+1\right) }>0}, \end{aligned}$$
(57)

which is possible only with the condition of Eq. (56). It is clear from Eqs. (53) and (57) that only stable \( \omega _{QNM}\) allows us to distinguish ingoing and outgoing waves at spatial infinity. Namely, the analytical method that we applied comprises a basis for the stable QNMs.

It is important to remark that while we are about to complete the present study, we have realized that the problem of QNMs of BIDBH has very recently studied in [94]. However, we have differences not only in the ways to be followed, but in the obtained results as well. We have used the massive KGE, obtained its radial equation solution in terms of the confluent Heun functions, and shown how it yields the QNMs of BIDBH in the massless case. They instead started with massless KGE (relatively simpler scalar wave equation) and in sequel they directly obtained the hypergeometric function solution to the radial equation, which made QNMs easily to be found. At the end, QNM result of [94] is given by

$$\begin{aligned} \omega _{n}= & {} -i\left( \frac{1}{4L\left( 2n+1\right) }+\frac{l(l+1)}{2n+1}- \frac{n+\frac{1}{2}}{2L}\right) , \nonumber \\= & {} {\frac{i\left[ n\left( n+1\right) -Ll\left( l+1\right) \right] }{L\left( 1+2\,n\right) },} \nonumber \\= & {} {i2\pi T_{H}\frac{\left[ n\left( n+1\right) -Ll\left( l+1\right) \right] }{\left( n+\frac{1}{2}\right) },} \end{aligned}$$
(58)

which can be easily seen that there is a minus sign difference between Eqs. (55) and (58). In fact, both results are true and they are complementary to each other. Our result (55), which likes the results of [22, 92, 95,96,97] admits unstable modes when \(n=0\) but their result (58) does not. On the other hand, Eq. (58) does not admit stability for the s-wave (\(l=0\)) case [98]; QNMs (58) lead to exponentially growing modes i.e., unstable modes. However, our result (55) is stable for the s-waves, which have strong impact on the testing of the stability since their motion is perpendicular to the direction of wave propagation.

Fig. 1
figure 1

Im(\(\omega _{QNM}\)) versus L graph. The plots are governed by Eq. (55). For various n and l values, the behaviors of \(\omega _{QNM}\) are depicted. It is clear that once condition (56) does not hold, the perturbation becomes unstable [92, 93]) since Im(\(\omega _{QNM})>0\) shows exponential increase instead of decay: recall the wave function (21)

Full size image

4 Spacetime of BIDBH with cosmic string

Let us now introduce a thin cosmic string within the BIDBH spacetime. To this end, letting \(\varphi \rightarrow \alpha \varphi \) (\(\alpha \in (0,1]\)) for metric (7), we get

$$\begin{aligned} ds^{2}=-h(r)dt^{2}+h(r)^{-1}dr^{2}+rd\theta ^{2}+r\alpha ^{2}\sin ^{2}\theta d\varphi ^{2}, \end{aligned}$$
(59)

with \(\alpha =1-4\mu \), in which \(\mu \ge 0\) is the mass density of the cosmic string [99]. We may remark here that although the cosmic strings are usually expressed in the cylindrical coordinates for describing the conical topology of the spacetime, for some cases, in particular for the problems in a black hole geometry plus a cosmic string like, it is better to use the spherical coordinates. Namely, the choice of spherical coordinates enables us to make easier computations. After all, no physics changes using different coordinates. In fact, numerous studies in which cosmic strings are expressed in the spherical coordinates are available in the literature (see for instance [100,101,102] and references therein). On the other hand, very recent study of Blanco-Pillado et al. [69] shows that the gravitational wave background to be expected from cosmic strings with the latest pulsar timing array limits puts an upper bound on the energy scale of the possible cosmic string network: \(\mu <1.5\times 10^{-11}\) (in dimensionless units; at \(95\%\) confidence level). The surface area and entropy of the BIDBH now modifies to

$$\begin{aligned} A_{BH,\alpha }= & {} \int _{0}^{2\pi }d\varphi \int _{0}^{\pi }\sqrt{-g}\ d\theta =4\pi \alpha r_{h}, \end{aligned}$$
(60)
$$\begin{aligned} S_{BH,\alpha }= & {} \frac{A_{BH}}{4\hslash }=\frac{\pi \alpha r_{h}}{\hslash }. \end{aligned}$$
(61)

Furthermore, since global topology changes, one has to take into account that the mass (energy) of the system changes this is simply due the volume change (deficit angle) of the spacetime. To see this, one can calculate the quasi-local mass [71] for the spacetime (59) as follows

$$\begin{aligned} M_{QL,\alpha }=\frac{\alpha }{2}\sqrt{h}\left( \sqrt{h}_{0}-\sqrt{h}\right) , \end{aligned}$$
(62)

where

$$\begin{aligned} h=\frac{r}{L}-4M_{QL},\,\,\,h_{0}=\frac{r}{L}. \end{aligned}$$
(63)

Using the above equations, in the large radial limit, one can find that

$$\begin{aligned} M_{QL,\alpha }=\alpha \,M_{QL}. \end{aligned}$$
(64)

Thus, the first law of thermodynamics is can be written as

$$\begin{aligned} dM_{QL,\alpha }=T_{H}\,dS_{BH,\alpha }, \end{aligned}$$
(65)

in which the Hawking temperature Eq. (16) is not affected by the cosmic string.

5 Exact solutions and QNMs of BIDBH with cosmic string

One can show that, with ansatz Eq. (21), the radial equation of the massive KGE on the geometry of Eq. (59) remains intact, however the angular equation takes the following form

$$\begin{aligned} -\frac{1}{A\left( \theta \right) }\frac{d^{2}A\left( \theta \right) }{d{ \theta }^{2}}-\frac{{\cot }\left( \theta \right) }{A\left( \theta \right) } \frac{dA\left( \theta \right) }{d\theta }+{\frac{{m}^{2}}{\alpha ^{2}\,\sin ^{2}\left( \theta \right) }+\lambda }=0, \end{aligned}$$
(66)

From Eq. (66), one can naturally set

$$\begin{aligned} m_{(\alpha )}=\frac{m}{\alpha }, \end{aligned}$$
(67)

In the case of \(\alpha \ne 1\), the quantum number \(m_{(\alpha )}\) is no longer integer. Thus, Eq. (66) can be recast in the following form

$$\begin{aligned} \frac{1}{\sin \theta }\frac{d}{d\theta }\left( \sin \theta \frac{dA}{d\theta }\right) +\left( \lambda -\frac{m_{(\alpha )}^{2}}{\sin ^{2}\theta }\right) A=0. \end{aligned}$$
(68)

This type of differential equation was exactly solved by [99, 103] in the following way. First, one needs to introduce a new coordinate \(w=\cos ^{2}\theta \), which transforms Eq. (66) to

$$\begin{aligned}&\frac{d^{2}A}{dw^{2}}+\left( \frac{1/2}{w}+\frac{1}{w-1}\right) \frac{dA}{dw} \nonumber \\&\quad +\,\left[ \frac{\lambda -m_{(\alpha )}^{2}}{4}\frac{1}{w}+\frac{m_{(\alpha )}^{2}-\lambda }{4}\frac{1}{w-1}-\left( \frac{m_{(\alpha )}^{2}}{2}\right) ^{2}\frac{1}{(w-1)^{2}}\right] A=0. \end{aligned}$$
(69)

Then, if we let \(A(w)=(w-1)^{m_{(\alpha )}/2}V(w)\), the above equation reduces to the confluent Heun equation:

$$\begin{aligned} \frac{d^{2}V}{dw^{2}}+\left( \underline{{\tilde{a}}}+\frac{\underline{{\tilde{b}} }+1}{w}+\frac{{\tilde{c}}+1}{w-1}\right) \frac{dV}{dw}+\left( \frac{{\tilde{m}}}{ w}+\frac{{\tilde{n}}}{w-1}\right) V=0, \end{aligned}$$
(70)

where the parameters of HeunC\(({\tilde{a}},{\tilde{b}},{\tilde{c}},{\tilde{d}}, {\tilde{e}};w)\) now are given by

$$\begin{aligned} {\tilde{a}}=0,\quad \,{\tilde{b}}=-\frac{1}{2},\quad \,{\tilde{c}}=m_{(\alpha )},\quad \,{\tilde{d}} =0,\quad \,{\tilde{e}}=\frac{1+m_{(\alpha )}^{2}-\lambda }{4}. \end{aligned}$$
(71)

The general solution to Eq. (69) thus becomes

$$\begin{aligned} A(w)=(w-1)^{m_{(\alpha )}/2}\Big (C_{1}\text {HeunC}({\tilde{a}},{\tilde{b}}, {\tilde{c}},{\tilde{d}},{\tilde{e}};w)+C_{2}w^{-{\tilde{b}}}\text {HeunC}({\tilde{a}},- {\tilde{b}},{\tilde{c}},{\tilde{d}},{\tilde{e}};w)\Big ),\nonumber \\ \end{aligned}$$
(72)

in which \(C_{1}\) and \(C_{2}\) are two integration constants. Hence, we remark that the general behavior of the scalar wave function (21) of the BIDBH is influenced by the presence of the cosmic string \(\alpha \).

It is interesting to note that the radial solution is quite similar to the case covered in the previous section, thus we are going to skip the solution procedure. However, there is a crucial point that must be considered. In the existence of the cosmic string, the energy of the particles measured at spatial infinity changes since the volume of the spacetime has a deficit angle. That is to say, when a wave packed (particle) is emitted from the black hole, its energy is shifted by a factor of \(\alpha \). For this reason, we have

$$\begin{aligned} \omega \rightarrow \omega _{\alpha }=\omega \alpha . \end{aligned}$$
(73)

So, the general wave solution of the BIDBH with cosmic string is given by [recall Eq. (52)]

$$\begin{aligned} \Psi \sim A_{2}\sqrt{1-z}\left[ \underset{\text {Ingoing Wave }}{\underbrace{ e^{-i\omega _\alpha \left( t-{\Omega _\alpha }\right) }\frac{\Gamma ({\widehat{c}})\Gamma ( {\widehat{c}}-{\widehat{a}}-{\widehat{b}})}{\Gamma ({\widehat{c}}-{\widehat{a}})\Gamma ({\widehat{c}}-{\widehat{b}})}}}+\underset{\text {Outgoing Wave}}{e\underbrace{ ^{-i\omega _\alpha \left( t+{\Omega _\alpha }\right) }\frac{\Gamma ({\widehat{c}})\Gamma ( {\widehat{a}}+{\widehat{b}}-{\widehat{c}})}{\Gamma ({\widehat{a}})\Gamma ({\widehat{b}} )}}}\right] ,\nonumber \\ \end{aligned}$$
(74)

in which

$$\begin{aligned} {\Omega _{\alpha }}=\sqrt{{L}^{2}-\frac{l\left( l+1\right) L+\frac{1}{4}}{{ \omega _{\alpha }}^{{2}}}}{\in {\mathbb {R}} >0}. \end{aligned}$$
(75)

In the presence of the cosmic string, Eq. (73) thus modifies the QNMs (55) of the BIDBH as

$$\begin{aligned} \omega _{QNM,\alpha }=\omega _{QNM}\,\alpha =-{\frac{i\alpha \,\left[ n\left( n+1\right) -Ll\left( l+1\right) \right] }{L\left( 1+2\,n\right) }}. \end{aligned}$$
(76)

We remark that the general scalar wave solution is modified when the cosmic string is introduced and thus the QNMs are shifted by a parameter \(\alpha \). In this way, QNMs might provide a new method to detect topological defects like cosmic strings by the virtue of GWs.

6 Effective temperature and quantization of BIDBH

Hawking radiation [74] is a quantum process associated with the quantum fields near the event horizon. During the Hawking radiation one expects not only photons, but also gravitons to be emitted from the black hole, which, in a classical level, can be viewed as the GW [104]. Since a black hole is an open system (it continuously interacts with the quantum fields), this implies a loss in the energy via Hawking radiation. Thus, it is natural to expect a possible link between the QNMs and black hole thermodynamics, but there is no satisfactory answer yet. In fact, Hod [105] first argued that the damping rate of the fundamental (\(n=0\)) QNMs of any black hole is constrained by its Hawking temperature via

$$\begin{aligned} |\text {Im}\omega |\le \pi \,T_{H}. \end{aligned}$$
(77)

One can check the validity of Hod’s conjecture by using the fundamental modes of the s-waves. In this case, Eq. (55) admits the following imaginary part

$$\begin{aligned} |\text {Im}\omega |=4\pi \,T_{H}>\pi \,T_{H}. \end{aligned}$$
(78)

The result obtained in Eq. (78) is against to the Hod’s conjecture. However, considering the fact that metric (59) is non-asymptotically flat, such a result should not be seen as very surprising. Besides, the violation of Hod’s conjecture has been recently reported in the context of Gauss–Bonnet de Sitter black hole [106].

We now consider the asymptotic highly damped (\(n\rightarrow \infty \)) QNMs (55), which has the imaginary part related to the Hawking temperature in a very simple way:

$$\begin{aligned} \omega _{n}\simeq -2\,\pi \,i\,T_{H}\,\left( n+\frac{1}{2}\right) =-i\kappa _{H}\left( n+\frac{1}{2}\right) . \end{aligned}$$
(79)

We recall that the Parikh–Wilczek’s quantum tunneling method [43], which includes the back reaction effects in the spacetime i.e., a change of the black hole horizon when a Hawking quanta is emitted, this implies a deviation from the thermal nature of the Hawking spectrum. Corda [107,108,109], inspiring from the Bohr correspondence principle and the quantum tunneling method, argued that QNMs can be re-interpreted by introducing the effective temperature \(T_{H}\rightarrow T_{E}\), which incorporates the back reaction effects in the black hole horizon. Along this line of thinking, Eq. (79) should take the following form

$$\begin{aligned} \omega _{n}\simeq -2\,\pi \,i\,T_{E}\,\left( n+\frac{1}{2}\right) . \end{aligned}$$
(80)

As a result of the quantum tunneling near the event horizon, we can interpret the imaginary part, seen in the above equation, as a loss of the black hole energy via QNMs. In other words, as it was suggested by Maggiore [18], a black hole behaves pretty much like a quantum harmonic oscillator. Namely, it constantly interacts with the quantum fields and hence never stops to oscillate. This argument is also supported by a recent paper [110], which argues that highly damped modes always exist and are related to the presence of the horizon.

The probability of emission is given by [43]

$$\begin{aligned} \Gamma _{BH}=\exp \left[ -\frac{\omega _{QL}}{T_{H}}\left( 1-\omega _{QL}\right) \right] . \end{aligned}$$
(81)

For this reason, if one wants to take into account the dynamical geometry of the BH during the emission of the particle, the effective temperature [107,108,109] should be considered:

$$\begin{aligned} T_{E}\equiv \frac{T_{H}}{1-\omega _{QL}}=\frac{1}{4\pi L\left( 1-\omega _{QL}\right) }. \end{aligned}$$
(82)

Thus, Eq. (80) becomes

$$\begin{aligned} \omega _{n}\simeq -\frac{\,i}{2L(1-|\omega _{n}|)}\,\left( n+\frac{1}{2} \right) , \end{aligned}$$
(83)

where \(|\omega _{n}|=E_{n}=\omega _{QL,n}\) is the total energy emitted at level n. We impose a condition that a black hole cannot emit more energy than their total mass, i.e., \(|\omega _{n}|\le M\). From Eq. (83) it follows that

$$\begin{aligned} |\omega _{n}|=\frac{1}{2}+\frac{\sqrt{L-1-2n}}{2\sqrt{L}}, \end{aligned}$$
(84)

which yields the following condition

$$\begin{aligned} n\le n_{max}=\frac{L-1}{2}. \end{aligned}$$
(85)

Now, if we consider an emission from the ground state (i.e., a BH which is not excited) to a state with \(n=n_{1}\), we can write down

$$\begin{aligned} M_{n_{1}}=M-|E_{n_{1}}|=M-\frac{1}{2}-\frac{\sqrt{L-1-2n_{1}}}{2\sqrt{L}}, \end{aligned}$$
(86)

and similarly to a state with \(n=n_{2}\),

$$\begin{aligned} M_{n_{2}}=M-|E_{n_{2}}|=M-\frac{1}{2}-\frac{\sqrt{L-1-2n_{2}}}{2\sqrt{L}}. \end{aligned}$$
(87)

Taking the difference of these two energy states, one gets

$$\begin{aligned} \Delta E_{n_{1}\rightarrow n_{2}}= & {} M_{n_{2}}-M_{n_{1}}, \nonumber \\= & {} -\frac{\sqrt{L-1-2n_{2}}}{2\sqrt{L}}+\frac{\sqrt{L-1-2n_{1}}}{2\sqrt{L}}. \end{aligned}$$
(88)

Now setting \(n_{1}=n-1\) and \(n_{2}=n\), we find out

$$\begin{aligned} \Delta E_{n_{1}\rightarrow n_{2}}=\frac{\sqrt{L-2n+1}}{2\sqrt{L}}-\frac{ \sqrt{L-2n-1}}{2\sqrt{L}}. \end{aligned}$$

It can be assumed that the length scale is the same for emission and absorption. Let us define the effective length scale \(L_{E(n,n-1)}\) as [109]

$$\begin{aligned} L_{E(n,n-1)}=\frac{L_{n-1}+L_{n}}{2}=\frac{\sqrt{L-2n-1}}{2\sqrt{L}}+\frac{ \sqrt{L-2n+1}}{2\sqrt{L}}. \end{aligned}$$
(89)

Since \(A_{BH}=16\pi LM\), the change in area can be defined as

$$\begin{aligned} \Delta A_{BH}=16\pi L_{E(n,n-1)}\Delta E_{n_{1}\rightarrow n_{2}}, \end{aligned}$$
(90)

in which

$$\begin{aligned} L_{E(n,n-1)}\Delta E_{n_{1}\rightarrow n_{2}}=\frac{1}{2L}, \end{aligned}$$

and thus we have

$$\begin{aligned} \Delta A_{BH}=8\pi . \end{aligned}$$
(91)

Equation (91) is nothing but the original result of Bekenstein [37]. Note that this relation seems to be universal and not affected when the Hawking radiation spectrum is non-thermal [107, 108]. We also remark that the Hod’s conjecture is not only violated, but also affected by the conical topology, when we replace \(T_{H}\rightarrow T_{E}\); because the imaginary part of the fundamental modes reads

$$\begin{aligned} |\text {Im}\omega _{\alpha }|=4\,\pi \,T_{E}(1-4\mu )>\pi T_{E}. \end{aligned}$$
(92)

On the other hand, one can also show the validity of the Bekenstein’s result [37] by employing the method of Maggiore [18]. For the highly damping modes (\(n\rightarrow \infty \)), the transition frequency can be obtained from Eq. (79) as follows

$$\begin{aligned} \Delta \omega \approx \text {Im}\left( \omega _{n-1}-\omega _{n}\right) =\kappa _{H}=\frac{1}{2L}. \end{aligned}$$
(93)

With the help of the adiabatic invariance formula:

$$\begin{aligned} I_{adb}=\int \frac{T_{H}\Delta S_{BH}}{\Delta \omega }, \end{aligned}$$
(94)

which basically suggests the Bohr–Sommerfeld quantization condition: \( I_{adb,n\rightarrow \infty }=n\hbar \), we find out that entropy is quantized as follows

$$\begin{aligned} S_{BH,n}=2\pi n. \end{aligned}$$
(95)

Thus, the area spectrum can be easily found as

$$\begin{aligned} A_{BH,n}=4\hbar S_{BH,n}=8\pi \hbar n. \end{aligned}$$
(96)

One can observe that this reveals the Bekenstein’s conjecture \( [A_{n}=\epsilon n\hbar ]\), with the minimum change to the area of the horizon i.e., \(\Delta A_{min}=A_{n}-A_{n-1}=8\pi \hbar \), or \(\Delta A_{min}=8\pi \) within the geometric unit sytem: \(\hbar =1\) [37].

When considering the cosmic string, the adiabatic invariance formula would be modified to

$$\begin{aligned} I_{adb}=\int \frac{T_{H}\Delta S_{BH,\alpha }}{\Delta \omega _{\alpha }}, \end{aligned}$$
(97)

in which

$$\begin{aligned} \Delta \omega _{\alpha }=\alpha \Delta \omega =\alpha \kappa _{H}, \end{aligned}$$
(98)

we get the entropy change as \(S_{BH,n\alpha }=2\pi \alpha n\). Hence, \( A_{BH,n\alpha }=4S_{BH,n\alpha }=8\pi \alpha n\), and the change in area results in \(\Delta A_{min,\alpha }=8\pi \alpha \). In other words, the minimal change in entropy/area spectrum is affected by the cosmic string parameter.

7 Conclusions

We have studied the analytical solution to the KGE for a massive scalar field in the BIDBH spacetime. Radial exact solution is given in terms of the confluent Heun functions [80, 81], and it covers the whole range of the observable space \(0\le z<1\).

The obtained radial solution could not be extended to the asymptotic region because of the lack of the inverse connection formula (36) which would help us to get the exact asymptotic form of the radial solution. This gap has enforced us to consider the massless scalar fields. Using the particular transformation (A12), we have managed to express the confluent Heun functions in terms of the hypergeometric functions. By this was, we have transferred the radial solution from the near horizon region to asymptotic region [78, 79]. Afterward, we have computed QNMs of the massless scalar waves propagating in the BIDBH. In particular, Eqs. (56) and (57) have shown us that our analytical QNM results are possible with stable waves. We have also compared Eq. (55) with the QNM results of [94]. We have remarked that both results are complementary with each other. It is important to note that our solution (55) violates the Hod’s conjecture [22] such as being discussed in [106].

In the presence of a cosmic string, QNMs are found to be shifted by a parameter \(\alpha \) when a cosmic string is introduced:

$$\begin{aligned} \omega _{QNM,\alpha }=-{\frac{i\,\left[ n\left( n+1\right) -Ll\left( l+1\right) \right] }{L\left( 1+2\,n\right) }}\alpha , \end{aligned}$$
(99)

which obeys the same condition of Eq. (56) to possess the stable QNMs. In short, our QNM analysis might provide an information to identify the topological defects (i.e., cosmic strings) in the fingerprints of the GWs. We have also shown that the minimum change in the area of the black hole is shifted by the cosmic string parameter \(\alpha \), which means a deviation from the Bekenstein’s result [37]: \(\Delta A_{min}=8\pi \alpha \).

The results of the present study motivate us for doing further works in this direction. In the near future, we plan to extend our analytical analysis to the other fields (Dirac fields, vector fields, gravitons etc.) and explore the effects of spin and cosmic string on the QNMs and quantization of the black hole.