1 Introduction

The no-hair theorems assert that the asymptotically flat spacetime can not admit any hairy black hole solutions [1, 2], since the scalar field was divergent on the horizon and stability analysis showed that they were unstable [3]. Nevertheless, when a negative cosmological constant is considered, the no-hair theorems can usually be circumvented, and then there exists a broad literature of black hole solutions with a (non)minimal scalar field in the four or higher dimensional Einstein’s gravity, including static [4,5,6,7,8,9,10,11,12,13], and rotating [14,15,16] extensions with a complex, massive scalar field and in higher order derivative gravity [17,18,19,20].

Inspiring by the pioneering work of Banados, Teitelboim and Zanelli (BTZ) [21], \((2+1)\)-dimensional spacetimes admitting black hole solutions have attracted much attention. Besides sourced by a mass and a negative cosmological constant, pure BTZ black holes can be also to added new sources such as electric/magnetic fields from Maxwell’s theory [22,23,24], Maxwell-dilaton [25], rotation [26], perfect fluid [27, 28] and others [29, 30]. However, there exist the so-called electromagnetic singularities due to point charges that occur in the linear Maxwell theory. It is interesting to note that the nonlinear electrodynamics (NED) is useful to overcome this obstacle, and the nonlinear electrodynamics are a good laboratories to construct black hole solutions [31,32,33]. Black hole solutions with nonlinear electrodynamics sources have interesting asymptotic behaviors and exhibit interesting thermodynamics properties [34,35,36,37]. For example, they satisfy the zeroth and first laws of black-hole mechanics [38]. After considering the cosmological constant as a dynamical pressure, the Smarr relation works as well and there are rich phase structure which have the first order phase transitions and the reentrant phase transitions [39, 40].

With a negative cosmological constant in the action, the \((2+1)\)-dimensional black holes with the minimal [41,42,43] or nonminimal [44, 45] scalar fields have been constructed in the Einstein’s gravity. Furthermore, the charged [46, 47], rotating [48,49,50], charged rotating [51] and Einstein–Born–Infeld [52] black holes with nonminimally scalar hair, and rotating black hole [53, 54] dressed with minimal scalar field hair in the \((2+1)\) dimensional Einstein’s gravity. Beyond the linear Maxwell electromagnetism in theory with scalar fields, in this paper, we study the charged black hole solution in the \((2+1)\)-dimensional EPM theory with nonminimally coupled scalar field. Actually, asymptotically AdS black holes with nonlinear electrodynamics sources endowed with extra scalar field have been related to superconductors by means of the gravity/gauge duality [55,56,57,58,59]. Especially, the larger power parameter k of the power Maxwell field makes it harder for the scalar hair to be condensate [55]. This makes it more interesting to study the black hole solutions in this paper. Considering the different values of k in \((2+1)\)-dimensional EPM theory, we will obtain two different branches of charged hairy black hole solutions, which correspond to the cases of \(k=1\) and \(k\ne 1\) respectively. The power parameter k is a rational number, which satisfies \(k>\frac{1}{2}\) because of the weak energy conditions (WEC) and strong energy conditions (SEC). In addition, we will present the null geodesics in detail, in order to have a further understanding of the properties of this solution.

This paper is organized as follows. In Sect. 2, we present the charged black hole solution in the EPM gravity with nonminimally coupled scalar field, and then discuss the properties of the scalar potential. Moreover, the basic geometric properties and horizon structures of the metric are also outlined. In Sect. 3 the geodesics motions are given for the photon. The Sect. 4 is devoted to the closing remarks.

2 Charged black hole in the EPM theory with nonminimally coupled scalar field

2.1 Charged hairy black hole solution

The \((2+1)\)-dimensional action in the EPM theory with nonminimally coupled scalar field is written as

$$\begin{aligned} I=\int \mathrm {d}^{3}x\sqrt{-g}\left[ \frac{1}{2\pi }\bigg ( R- \nabla _{\mu } \phi \nabla ^{\mu } \phi -\frac{1}{8} R\phi ^2-2V(\phi )\bigg )+L(\mathcal {F})\right] , \end{aligned}$$
(1)

in which R is Ricci scalar, \(\phi \) is scalar field, \(V(\phi )\) is self-coupling potential of scalar field, and \(L(\mathcal {F})=\mathcal {|F|}^k\) is the power Maxwell Lagrangian with Maxwell invariant \(\mathcal {F}=F_{\mu \nu }F^{\mu \nu }\). k is power parameter and should be a rational number, which satisfies \(k>\frac{1}{2}\) because of the weak energy conditions (WEC) and strong energy conditions (SEC).Footnote 1

Considering the variation of the action, we can obtain the field equations

$$\begin{aligned} G^{\mu }{}_{\nu }-\pi \,T_{[A]}^{\mu }{}_{\nu }-T_{[\phi ]}^{\mu }{}_{\nu } +V(\phi )\delta ^{\mu }{}_{\nu }&=0, \end{aligned}$$
(2)
$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _{\nu }(\sqrt{-g}F^{\mu \nu }\mathcal {|F|}^{k-1})&=0, \end{aligned}$$
(3)
$$\begin{aligned} \nabla _{\mu }\nabla ^{\mu }\phi -\frac{1}{8}R\phi -\partial _{\phi }V(\phi )&=0, \end{aligned}$$
(4)

where the energy-momentum tensor of the power Maxwell field and scalar field are given by

$$\begin{aligned} T_{[A]}^{\mu }{}_{\nu }&=-\mathcal {|F|}^{k}\left( \frac{4k(F_{\nu \sigma } F^{\mu \sigma })}{\mathcal {F}}-\delta ^{\mu }{}_{\nu }\right) , \end{aligned}$$
(5)
$$\begin{aligned} T_{[\phi ]}^{\mu }{}_{\nu }&=\partial ^{\mu }\phi \partial _{\nu }\phi -\frac{1}{2}\delta ^{\mu }{}_{\nu }\nabla ^{\rho }\phi \nabla _{\rho }\phi +\frac{1}{8}\big (\delta ^{\mu }{}_{\nu }\square -\nabla ^{\mu }\nabla _{\nu }+G^{\mu }{}_{\nu } \big )\phi ^2. \end{aligned}$$
(6)

The metric ansatz is chosen as

$$\begin{aligned} \mathrm {d}s^2=-f(r)\mathrm {d}t^2+\frac{1}{f(r)}\mathrm {d}r^2+r^2\mathrm {d}\theta ^2 \end{aligned}$$
(7)

with the coordinate range \(-\infty<t<+\infty , r>0\) and \(0<\theta <2\pi \). Substituting the metric (7) into the nonlinear Maxwell equation (3), the nonvanishing component of vector potential \(\mathbf {A}\) is given by [24]

$$\begin{aligned} \mathbf {A}=A(r)dt, \quad A(r)= \left\{ \begin{array}{ll} \frac{(2k-1)}{2(k-1)}Q r^{\frac{2(k-1)}{(2k-1)}}, \qquad k\ne 1, \\ Q\ln \left( \frac{r}{r_0}\right) , \qquad \qquad k=1. \end{array} \right. \end{aligned}$$

Here Q and \(r_0\) are integration constants. Q corresponds to the electric charge, and \(r_0>0\) corresponds to the radial position of the zero electric potential surface, which can be set equal to \(+\infty \). Evidently, the vector potential \(\mathbf {A}\) takes the different forms in case of \(k=1\) and \(k\ne 1\). Viewed from this perspective, the respective discussions for the charged hairy black holes in two branches (\(k=1\) and \(k\ne 1\)) are very necessary.

From the other field equations (2) and (4), we can obtain the simplified form of scalar field [46, 48]

$$\begin{aligned} \phi (r)=\pm \sqrt{\frac{8B}{r+B}}, \end{aligned}$$
(8)

black hole solution

$$\begin{aligned} f(r)= \left\{ \begin{array}{ll} &{}\frac{r^2}{\ell ^2}+\frac{\alpha B^2(2B+3r)}{48r}+\frac{2^{k}(2k-1)^2\pi \left( qB^{\frac{1}{(2k -1)}}\right) ^{2k}}{2(k-1)}\frac{\left( r+\frac{2kB}{(4k-1)}\right) }{r^{\frac{1}{(2k-1)}}}, \quad k\ne 1, \\ &{}\frac{{r}^{2}}{\ell ^2}+\left( 3\mu +\frac{{q}^{2}}{4}\,\right) B^2 + \left( 2\mu +\frac{q^2}{9}\right) \frac{B^3}{r} +q^2B^2\left( \frac{1}{2}+\frac{B}{3r} \right) \ln \left( \frac{r}{B}\right) , \quad k=1 \end{array} \right. \end{aligned}$$
(9)

and the scalar potential

$$\begin{aligned} V(\phi )= \left\{ \begin{array}{ll} &{}-\frac{1}{\ell ^2}+\frac{1}{512}\left( \frac{1}{\ell ^2}+\frac{\alpha }{48}\right) \phi ^6 +\frac{2^{k}(2k-1)\pi \,q^{2k}}{1024(k-1)(4k-1)}\left( \frac{\phi ^2}{8-\phi ^2}\right) ^{\frac{2k}{(2k-1)}}\\ &{}\times \bigg (64k\phi ^2-16k(2k-1)\phi ^4+(2k-1)^2\phi ^6\bigg ), \qquad \qquad k\ne 1, \\ &{}-\frac{1}{\ell ^2}+\frac{1}{512}\left( \frac{1}{\ell ^2} +\mu \right) \phi ^6 + \frac{1}{18432}\, q^2\left( 192\,{\phi }^{2}+ 48{\phi }^{4}+5\,{\phi }^{6} \right) \\ &{}-\frac{1}{3}q^2\left[ \frac{2\phi ^2}{ \left( 8-{\phi }^{2} \right) ^2} -\frac{1}{1024}{\phi }^{6}\ln \left( {\frac{8-{\phi }^{2}}{{\phi }^{2}}} \right) \right] ,\qquad \qquad \qquad \qquad k=1. \end{array} \right. \end{aligned}$$
(10)

Here q, \(\alpha \), \(\mu \) are parameters in the action, and the parameter q is related with the charge Q of black hole through

$$\begin{aligned} q= \left\{ \begin{array}{ll} \frac{2\left( 2\pi \right) ^{\frac{1}{2}}Q}{B}, \quad k=1, \\ \frac{2^{\frac{1}{2k}}Q}{B^{\frac{1}{2k-1}}}, \qquad k\ne 1. \end{array} \right. \end{aligned}$$
(11)

In addition, \(V(0)=\Lambda =-\frac{1}{\ell ^2}\) is the constant term emerging naturally in the potential which plays the role of cosmological constant. The parameter l denotes the AdS radius.

Notice that the branch \(k=1\) of these charged hairy black hole solutions (10) has been discussed in [46]. Consequently, we mainly focus on the case of \(k\ne 1\). Especially, for the power parameter \(k=\frac{3}{4}\), the potential (10) is not longer just proportional to \(\phi ^6\), so that the full matter sector in the action is not conformal invariant. As a result, our solution reduces to the charged hairy black hole solution, which is different from the one in [47].

For the scalar potential \(V(\phi )\) with \(k\ne 1\), the negative cosmological constant \(\Lambda =V(0)=-\frac{1}{\ell ^2}\) is necessary for obtaining black hole solutions because of the No-Go theorem in three dimensions [60]. The parameter \(\alpha \) is related to the mass of black hole as shown later. Moreover, the potential \(V(\phi )\) always keeps regular when \(\phi ^2<8\).

2.2 Physical properties

For this charged hairy black hole, the mass can be calculated simply by adopting the Brown–York method [61]. The quasilocal mass m(r) at a r takes the following form [61,62,63]

$$\begin{aligned} m(r)=2\sqrt{f(r)}(\sqrt{f_0(r)}-\sqrt{f(r)}). \end{aligned}$$
(12)

Here \(f_0(r)\) is a background metric function which determines the zero of the energy. One natural choice for these solutions are the one for the massless BTZ black hole, i.e. \(f_0(r)=\frac{{r}^{2}}{\ell ^2}\).Footnote 2 Note the mass of black hole in the regular Einstein–Maxwell theory (i.e. the case with \(k=1\)) is present in [46]; as we have corrected the scalar potential (10) for \(k=1\) to get the invariant action, the mass is modified slightly as \(M=\left( \frac{q^2}{2}\ln {B}-\frac{{q}^{2}}{4}-3\mu \right) B^2\). With regard to \(k\ne 1\), the corresponding mass is obtained as

$$\begin{aligned} M\equiv \lim _{r\rightarrow \infty }m(r)=-\frac{\alpha B^2}{16}. \end{aligned}$$
(13)

Consequently, Eq. (9) in the branch of \(k\ne 1\) can be rewritten as

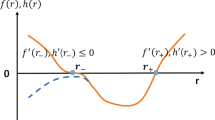
$$\begin{aligned} f(r)=\frac{r^2}{\ell ^2}-M\left( 1+\frac{2B}{3r}\right) -\frac{X(2k-1)\left( r+\frac{2Bk}{(4k-1)}\right) }{r^{\frac{1}{(2k-1)}}} \end{aligned}$$
(14)

with \(X=-\frac{(2k-1){Q}^{2k}}{2^{k+1}(k-1)}\). Consider the leading term contributed to f(0) and \(f(+\infty )\) and the first order derivative, it is easy to find that f(r) increases monotonically from \(-\infty \) to \(+\infty \) for solutions with \(k>\frac{1}{2}, M>0\), hence contains exactly one zero, which corresponds to the event horizon of a charged AdS black hole with a scalar hair. In order to avoid the appearance of a naked singularity, a horizon in the spacetime is needed at least. In this sense, we see that the physically acceptable region for mass M is \(M>0\) for any values of parameter k. In Fig. 1, we plot the horizon function f(r) with \(Q=0.5,B=0.1,\ell =1,M=1.5\) and different values of parameters k, in order to have a more clear understanding of the above horizon structure.

Fig. 1
figure 1

The horizon structure with \(Q=0.5,B=0.1,\ell =1,M=1.5\)

Full size image

In order to have a further understanding of the solutions, we calculate some geometric quantities. Firstly, the Ricci scalar reads as

$$\begin{aligned} R=-\frac{6}{\ell ^2}+\frac{2(k-1)X}{(2k-1)}\left( (4k-3)-\frac{2Bk}{(4k-1)r}\right) r^{\frac{-2k}{(2k-1)}}, \end{aligned}$$
(15)

which shows that the solution has an essential singularity at \(r=0\) whenever \(Q\ne 0\). Higher order curvature invariants such as \(R_{\mu \nu }R^{\mu \nu }\) and \(R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }\) both have much complicated expressions. One can also find the further behavior as \(O(\frac{M}{r})\), hence the solution is also singular at \(r=0\) whenever \(M\ne 0\). As we are interested in the black holes, the solutions need to contain a event horizon to surround the singularity. On the other hand, in order to indicate that the metric is nonconformally flat, we can find some non-vanishing components of the Cotton tensor, e.g.

$$\begin{aligned} C_{\theta \theta \,r}=\frac{MB}{r^2}+\frac{k \bigg ((1-k)+\frac{Bk}{r}\bigg )X}{(2k-1)^2r^{\frac{1}{(2k-1)}}}, \end{aligned}$$
(16)

which does not vanishes whenever \(B\ne 0\), \(M\ne 0\) or \(Q\ne 0\).

3 Null geodesics

Let us consider the geodesic equations for uncharged test particles around the solution with scalar hair in the EPM Theory. Since this spacetime has two Killing vectors \(\partial _t\) and \(\partial _\theta \), there are two constants of motions, i.e.

$$\begin{aligned} E=f(r)\frac{\mathrm {d} t}{\mathrm {d} \lambda },\quad L=r^2\frac{\mathrm {d} \theta }{\mathrm {d} \lambda }, \end{aligned}$$
(17)

where \(\lambda \) is the affine parameter along the geodesics.

The geodesic equation can be derived from the Lagrangian for a test particle

$$\begin{aligned} f(r)\left( \frac{\mathrm {d} t}{\mathrm {d} \lambda }\right) ^2-\frac{1}{f(r)}\left( \frac{\mathrm {d} r}{\mathrm {d} \lambda }\right) ^2-r^2\left( \frac{\mathrm {d} \theta }{\mathrm {d} \lambda }\right) =-m^2, \end{aligned}$$
(18)

where \(m=0\) corresponding to null geodesics and \(m=1\) corresponding to time-like geodesics (without loss of generality). Inserting Eq. (17) into the above equation, one can obtain

$$\begin{aligned} \frac{1}{2}\left( \frac{\mathrm {d} r}{\mathrm {d} \lambda }\right) ^2+V_{eff}(r)=0, \end{aligned}$$
(19)

where \(V_{eff}(r)\) is the effective potential and takes the form as

$$\begin{aligned} V_{eff}(r)=\frac{1}{2}\bigg [f(r)\left( \frac{L^2}{r^2}+m^2\right) -E^2\bigg ]. \end{aligned}$$
(20)

Then Eqs. (17) and (19) lead to the orbit equation

$$\begin{aligned} \left( \frac{\mathrm {d} r}{\mathrm {d} \theta }\right) ^2=-\frac{2r^4}{L^2}V_{eff}(r). \end{aligned}$$
(21)

Now we consider the null geodesics, i.e. the geodesics for a photon. The effective potential (20) reduces to

$$\begin{aligned} V_{eff}(r)=\frac{1}{2}\bigg [f(r)\left( \frac{L^2}{r^2}\right) -E^2\bigg ]. \end{aligned}$$
(22)

In the following subsections, we focus on the orbit equation (21) and effective potential (22) to classify all possible geodesic motions.

3.1 Radial geodesics where \(L=0\)

Firstly we examine the radial geodesics where \(L=0\). The corresponding effective potential (22) further reduces to

$$\begin{aligned} V_{eff}(r)=-\frac{E^2}{2}. \end{aligned}$$

Obviously, the behavior of these geodesics do not depend on the electric charge Q and mass M of the black hole. As E is a constant, this resembles the geodesic motion of a free photon.

Combining Eqs. (17) and (19), we can get

$$\begin{aligned} \frac{\mathrm {d} t}{\mathrm {d} r}=\pm \frac{1}{f(r)}. \end{aligned}$$
(23)

Here we are only interested in the geodesics of the black holes. The metric function can be rewritten as

$$\begin{aligned} f(r)=(r-r_{E})(r-r_{C})F(r) \end{aligned}$$
(24)

with \(r_{E}\) being the Event horizon and \(r_{C}\) being the Cauchy horizon of the black holes, respectively. However, it is difficult to find the form of F(r), but we still know that F(r) can have either no real roots or negative roots. For non-extreme charged black hole with two horizons, \(r_{E}\) and \(r_{C}\) are both positive. For extreme charged black hole, \(r_{E}=r_{C}\) is positive. For our solutions, i.e. the charged black hole with single horizon, only \(r_{E}\) is real and positive.

Rewriting the right side of Eq. (23), it is equal to

$$\begin{aligned} \frac{1}{f(r)}&=\frac{1}{(r_{E}-r_{C})}\bigg [\frac{1}{F(r_{E})}\bigg (\frac{1}{(r-r_{E})} -\frac{G(r,r_{E})}{F(r)} \bigg )\nonumber \\&\quad -\frac{1}{F(r_{C})}\bigg (\frac{1}{(r-r_{C})}-\frac{G(r,r_{C})}{F(r)} \bigg )\bigg ], \end{aligned}$$
(25)

where \(G(r,r_{i})=\frac{F(r)-F(r_i)}{(r-r_i)}\) with i being (E, C). Note \(G(r_{i},r_{i})=F'(r_{i})\) is finite. After integrating Eq. (23), we find

$$\begin{aligned} t&=\pm \frac{1}{(r_{E}-r_{C})}\bigg [\frac{1}{F(r_{E})}\bigg (\ln (r-r_{E})-\int \frac{G(r,r_{E})}{F(r)}\mathrm {d}r \bigg )\nonumber \\&\quad -\frac{1}{F(r_{C})}\bigg (\ln (r-r_{C})-\int \frac{G(r,r_{C})}{F(r)}\mathrm {d}r \bigg )\bigg ], \end{aligned}$$
(26)

where the sign “\(+\)” denotes the out going null rays and the sign “−” denotes the ingoing null ray. Consider the ingoing null rays, when \(r\rightarrow \,r_{E}\), the coordinate time \(t\rightarrow +\infty \) for the black holes.

On the other hand, the geodesic equation (19) can be integrated to give

$$\begin{aligned} r(\lambda )=\pm \,E \lambda . \end{aligned}$$
(27)

When \(r\rightarrow \,r_{E}\) (in-going case), \(\lambda \) has a finite value \(\frac{r_{E}}{E}\). Hence one can see that a photon without angular momentum arrives the horizons in its own finite proper time, while it is an infinite coordinate time.

3.2 Radial geodesics where \(L\ne 0\)

We consider the radial geodesics with \(L\ne 0\). From Eq. (22), the effective potential can be obtained as

$$\begin{aligned} V_{eff}(r)=\frac{L^2}{2r^2}\bigg [\left( \frac{1}{\ell ^2}-\Xi ^2\right) r^2 -\left( 1+\frac{2B}{3r}\right) M-\frac{X(2k-1)\left( r+\frac{2Bk}{(4k-1)}\right) }{r^{\frac{1}{(2k-1)}}}\bigg ], \end{aligned}$$
(28)

where \(\Xi =\frac{E}{L}\).

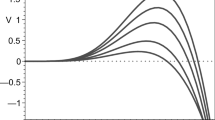
Consider the behavior of geodesics, one can turn to the behavior of the effective potential. Similarly as the metric function f(r), \(V_{eff}(r)\) increases monotonically from \(-\infty \) to \((+\infty )\times (\frac{1}{\ell ^2}-\Xi ^2)\), for solutions with \(k>\frac{1}{2}, M>0\), hence contains exactly one or no vanishing point. One can find no photon stay at the circular motion. We give an example presented in Fig. 2. When the constant of motions \(\Xi \) changes, the geodesic motions of a photon are all the unbounded spiral motions. For subcases with \(0\le \Xi <\frac{1}{\ell }\) and \(\Xi \ge \frac{1}{\ell }\), there is still one difference: the latter one has no perihelion, thus the photon for the latter one will fall into the black holes. Follow the similar discussion with the radial geodesics of un-rotating photon in the previous subsection, one can find that the photon with \(\Xi \ge \frac{1}{\ell }\) also arrive the black hole horizon in an infinite coordinate time.

Fig. 2
figure 2

The effective potential V(r) with \(k=5,Q=0.5,B=0.1,\ell =1\). On the plot, the constant of motions \(\Xi \) decreases from top to bottom

Full size image

4 Closing remarks

In this paper, we have presented black hole solutions to Einstein–Power–Maxwell theory with nonminimally coupled scalar field in \((2+1)\) dimensional AdS spacetimes. The rational number k satisfies \(k>\frac{1}{2}\) because of the weak energy conditions (WEC) and strong energy conditions (SEC). There exist charged hairy black hole solutions with two branch of \(k=1\) or \(k\ne 1\). For \(k\ne 1\), we found that the solution contains a curvature singularity at the origin and is non-conformally flat. The solution with positive mass \(M>0\) always corresponds to black holes with single horizon. In addition, the geodesic motions for a photon in this spacetime have been discussed in detail. It is also interesting to consider the geodesics of this spacetime further, including the time-like one for a photon and the one for charged particle.