The Slope-Attribute-Regularized High-Resolution Prestack Seismic Inversion

Abstract

Prestack seismic inversion can be regarded as an optimization problem, which minimizes the error between the observed and synthetic data under the premise of certain geological/geophysical a priori information constraints. It has been proved to be a powerful approach for reconstructing the subsurface properties and building the elastic parameter models (e.g., P- and S-wave velocity, and density). With respect to the specific expressions of a priori information, the starting model and regularization are expected to be the most widely used and indispensable constraints to reconstruct structural features and subsurface properties. The conventional prestack inversion (trace-by-trace) methods perform well when the geological structure of the target area is not too complex. However, due to the lack of lateral constraint, such trace-independent methods are inevitably limited by their capability of characterization (including accuracy, resolution, and robustness) in the case of geologically complex structures, such as tilted stratum and steep faults. The geological structure-guided constraint, herein referred to as the seismic slope attribute, can be exploited as a lateral constraint integrated into the prestack inversion algorithm. In this work, the seismic slope attribute is introduced to the amplitude variation with offset/angle inversion from two aspects, i.e., starting model building and regularization penalty. Firstly, using the seismic slope attribute, instead of the traditional manual interpreted geological horizons, as a constraint, the well-log data are interpolated to build the initial model. The interpolation algorithm is formulated as solving the inverse problem by using the shaping regularization method rather than the kriging-based algorithm. Secondly, by rotating the coordinate system according to the seismic slope attribute, the directional total variation regularization is used as a constraint to improve the resolution (in both vertical and horizontal directions) and lateral continuity of the inversion results. Finally, the proposed methods are applied to synthetic and real seismic data. Synthetic tests and field data applications demonstrate that the proposed method is capable of revealing complex structural features and achieving stabilized inversion of multi-parameters with less uncertainty.

FormalPara Article Highlights

• First, we review a structure-oriented starting model method by interpolating well-log data, and the interpolation algorithm is formulated as solving the inverse problem by using the shaping regularization method rather than the Kriging-based algorithm.

• Second, we review a structure-guided directional total variation (DTV) regularization, which is exploited as a constraint to improve the resolution (in both vertical and horizontal directions) and lateral continuity of the inversion results.

• Finally, to maximize the generalization performance, the proposed methods are applied to several complex synthetic and real seismic datasets.

1 Introduction

Prestack AVO/AVA inversion has been proved to be one of the most important technologies for exploration geophysics. It can quantitatively extract multiple elastic parameters regarding the subsurface properties from the observed seismic data (Karimpouli and Malehmir 2015; Li et al. 2017; Liu et al. 2018; Cheng et al. 2019; Pan et al. 2020; Luo et al. 2020). Sustained efforts have been devoted to both theoretical and engineering applications of prestack inversion. At present, it has established itself as one of the most effective approaches for reservoir characterization and fluid identification (Huang et al. 2017; Guo et al. 2018a; Huang et al. 2018a; Guo et al. 2018b, 2019; Luo et al. 2019). However, due to various reasons, such as noise, a band-limited intrinsic property of seismic data, and inappropriate forward operators, ill-posedness is still one of the most common and intractable issues that arise when solving the inverse problem. Aiming to mitigate the ill-posedness, regularization has been achieved high-quality (including accuracy, resolution, and robustness) inversion results by incorporating prior information into seismic inversion. Thus, the prior information is important to improve the quality of inversion results.

With respect to the specific expressions of the prior information, it can be well-log data, the probability distribution of desired parameters, geological information, etc. (Chen and Zhang 2017; Pan et al. 2018a, b; Pan and Zhang 2018; Chen 2020). The statistical-based inversion methods are developed under a Bayesian linearized inversion and geostatistical framework. They make full use of the probability distribution information as constraints for the inversion (Grana and Rossa 2010; Grana et al. 2017; Azevedo et al. 2018, 2019; Pereira et al. 2020). However, such methods are a kind of statistical inversion or random inversion, and the inversion results are highly uncertain. This paper mainly focuses on the work of deterministic inversion. For the deterministic inversion, a priori constraints are essential for the accuracy and resolution of the final inversion results. In particular, among variants of prior constraints, the starting model of the inversion and Tikhonov-type regularization are expected to be the most widely used constraints to reconstruct structural features and subsurface parameters. However, conventional prestack inversion algorithms are always conducted trace by trace; therefore, almost no lateral constraints are used during the inversion process. In the horizontal direction, the association to the parameters almost depends on the initial model, which provides the background trend of the subsurface properties. However, structural features of the desired model are always presumed or hypothesized as low geological complexity. In terms of the complex geological structures, it is difficult to yield an ideal result by the conventional method unless some geological structure-guided information can be involved in the model building algorithm.

The seismic data itself contain some geological structural information, but the utilization of seismic data is still not enough, especially for the long-wavelength component of seismic data. The travel time information in seismic data corresponds to the long-wavelength component (Zelt and Barton 1998; Korenaga et al. 2000; Osypov 2000; Noble et al. 2010; Li 2013; Chen et al. 2013; Huang et al. 2020), which is often closely related to tectonic information, while the amplitude and waveform information usually corresponds to the mid-to-short-wavelength component, which is often related to lithological information (Sen and Roy 2003; Zong et al. 2015; Wang et al. 2020). Generally, the present prestack AVA inversion methods mainly focus on amplitude information, and the long-wavelength components related to structural information have not caught enough attention. Therefore, introducing long-wavelength information hidden in seismic data into the inversion algorithm can well resolve the complex geological structures (Ba et al. 2017; Guo et al. 2020). Here, we briefly review the widely used prior information from the two perspectives, i.e., the initial model building and regularization constraints, and then attempt to introduce the geological structure factor to this prior information.

It is widely known that seismic data are band-limited, i.e., lacking low-frequency information in the seismic amplitude (Oezsen 2004; Jiao et al. 2008). Such missing information is closely related to the geological structure, thereby leading to the lack of accurate structural information in the seismic inversion results (Wang et al. 2008; Zhang and Castagna 2011). Thus, seismic inversion methods are generally model-based and the initial model should first be built before the inversion. Then the model can be updated according to the specific inversion approach. Based on artificial interpretation results, traditional initial model building methods extend the well-log data along with the horizontal direction by using interpolation algorithms, such as inverse distance power and kriging-based interpolation (Deutsch and Journel 1994; Piatanesi et al. 2001). The geological prior information can be horizons, faults, lithologies, and lithofacies. Lateral interpolation of well-log data with geological information as a constraint makes the initial model contain structural information (Greenberg and Castagna 1992; Li et al. 2016; Hamid et al. 2018; Chen et al. 2019b). Although the existing starting model building approaches have achieved effective results in solving the prestack seismic inversion problems, there remain two limitations that ought to be addressed, i.e., manual interpretation errors and labor costs. Reservoirs that have the characteristics of large structural undulations, complex internal structures, and strong lateral heterogeneity are difficult to build an accurate initial model for inversion. It is also one of the reasons for limiting the accuracy of modeling in oil and gas recovery. Due to the close relationship between a highly accurate initial model and final inversion results, the initial model has a prominent impact on reservoir characterization with a high geological structure complexity. If the conventional modeling method is still used for the complex structural medium, it will not only introduce unpredictable artificial errors but also consume a lot of manual interpretation costs. Instead of interpreting each layer, the horizon picking operation can be conducted to some specific horizons of the target area, which makes the initial model usually have the same structural fluctuation characteristics that are inconsistent with the real case. Thus, the conventional initial model building relies too much on the manually interpreted geological information, which is prone to errors and labor costs. Here, we introduce a geological structure-guided initial model building approach (Chen et al. 2016, 2019a), which interpolates the well-log data with the seismic slope attribute as a lateral constraint.

In addition to the low-frequency components, the mid- and high-frequency components of the seismic data are also very important for reservoir characterization. The mid- and high-frequency components are related to the detailed information for lithological interpretation. Generally, the prestack AVA inversion performs on the angle gathers trace by trace, and there are few horizontal constraints introduced for regularization (Tarantola 2005; Velis 2005; Buland and Omre 2003; Erik Rabben et al. 2008; Pérez et al. 2017; Li and Zhang 2017). Due to the lack of constraints in the lateral direction, it sometimes causes poor lateral resolution and continuity. It is mainly reflected in the insufficient ability to describe faults, titled strata with a large slope, and some special rock bodies. Especially when the nonlinear forward operator, such as the exact Zoeppritz equation (Zhi et al. 2016; Huang et al. 2018b), is exploited as a forward operator to directly invert ${\textit{v}}_{p}$, ${\textit{v}}_{s}$, and ${\rho }$, the Gaussian distribution (corresponding to the $\ell _{2}$ norm) is usually exploited as a priori distribution. Such constraints will greatly decrease the resolution of the inverted parameters, resulting in the defects of blurred reflection interfaces and insufficient ability to describe special geological structures (Castagna and Smith 1994; Zhang et al. 2015).

Therefore, with respect to the incorporation of a priori information into seismic inversion, both the stability of the inversion algorithm and the resolution of the inverted results (in both horizontal and vertical directions) should be taken into account (Geman and Geman 1984; Terzopoulos 1986; Geman and Reynolds 1992; Geman and Yang 1995; Charbonnier et al. 1997; Bhatt and Joshi 2016). Some researchers have been introducing several AVA inversion methods based on a global approach. These methods use geostatistics as model perturbation technique and update. However, most prestack deterministic inversion algorithms are based on a single prestack angle gather at present. These gather-based algorithms do not take into account adjacent data, and the inversion process of each trace is conducted independently. The total variation (TV) regularization (or Markov random field (MRF)) is generally exploited as a constraint to a deblurring image by deconvolution methods, which is an effective spatial texture modeling tool (Zhang et al. 2007; Qu and Verschuur 2016; Guo et al. 2017; Liang et al. 2017; Zhang et al. 2018). However, different from the digital images, the subsurface properties always change according to some specific geologic structures, such as the tilted layers, faults, and edges of some special geological bodies. Regardless of the geologic direction of the subsurface medium, the TV regularization only tends to reduce the horizontal and vertical gradients of each grid point in the model. Therefore, TV is not suitable for the stratum where the local structure has a dominant direction (Bayram and Kamasak 2012a, b). Here, we can also introduce the seismic slope attribute to the TV regularization algorithm so that the method can be used effectively.

In summary, the key to the two problems mentioned above lies in the extraction of seismic slope attributes, which can be extracted by using the plane wave destruction (PWD) technique (Claerbout 1992; Fomel 2002; Fomel et al. 2003; Fomel 2005). Indeed, the seismic local slope attribute is a useful lateral constraint condition, which has been widely used in the data regularization (Chen et al. 2017, 2018) and full-waveform inversion (Qu et al. 2017, 2019) by using shaping regularization constraints. In this paper, the seismic slope attribute is introduced to two perspectives, i.e., the starting model building and the TV regularization, as the lateral constraint to help achieve a high-accuracy and high-resolution prestack inversion results.

To handle the problem mentioned above, firstly, we abandon the traditional artificial horizon interpretation results and use seismic slope attributes as lateral interpolation constraints. Besides, instead of using the kriging-based interpolation method, the interpolation is formulated as an inverse problem by the sampling operator. The shaping regularization is used here to solve the inverse problem and then yield the initial models of multi-parameter simultaneous inversion of prestack inversion. Note that it is a part of our preliminary work Huang et al. (2020), where we introduce the geological structure-guided initial model building method for the AVA inversion and validated via it field data. Furthermore, the seismic slope attribute is introduced to the total variation (TV) regularization to extend the total variation prior constraints from the Cartesian coordinates to geological structure-oriented coordinates, so as to enhance the stability and lateral resolution of the inversion results. Besides, it is the first time that the DTV regularization is utilized in the AVA/AVO inversion and validated via two sets of field data.

In this work, we first briefly review the seismic slope estimation, which is also an essential theoretical basis of this work. Then, we introduce the starting model building method based on the seismic slope attribute and directional total variation regularized seismic inversion. Finally, both slope attribute-based methods are demonstrated by the synthetic data and further validated by the real seismic data.

2 Theory

2.1 Seismic Local Slope Attribute Extraction

Seismic local slope attribute is one of the seismic kinematic attributes, which describe the distribution of seismic wave events in the space-time domain. It can also indirectly characterize the spatial structure of underground media, which has been widely used in exploration geophysics, including wave-field separation, denoising, seislet transform, predictive painting, etc. The seismic slope attribute can be extracted using the plane-wave destruction (PWD) algorithm (Fomel 2002). According to Claerbout (1992), plane waves can be expressed by the first-order differential equation as follows:

$$\begin{aligned} \frac{\partial P (x, t)}{\partial x}+\sigma (x, t)\frac{\partial P(x, t)}{\partial t}=0, \end{aligned}$$

(1)

where P(x, t) denotes the wave field of plane waves and $\sigma (x, t)$ corresponds to the local slope of the seismic event. In the discrete domain, the slope between the adjacent points (spatial interval $\Delta x$) can be expressed by the time interval $\Delta t$ and $\sigma (x, t)$:

$$\begin{aligned} p=\sigma (x, t)\Delta x/\Delta t. \end{aligned}$$

(2)

P(x, t) can be calculated by its neighbor point via

$$\begin{aligned} P (x, t)= P (x+\Delta x, t+p\Delta t). \end{aligned}$$

(3)

By using Z-transform, the above equation can be transformed from $X-T$ domain to the $Z_{x}-Z_{t}$ domain as:

$$\begin{aligned} (1-Z_{x}Z_{t}^{p})P(Z_{x},Z_{t})=0, \end{aligned}$$

(4)

where $Z_{x}$ and $Z_{t}$ are the unit of spatial- and time-shift operators. Here we refer $C(p)=(1-Z_{x}Z_{t}^{p})$ as a plane-wave destructor. By using Thiran’s fractional delay filter $\small {\frac{1/B(Z_{t})}{B(Z_{t})}}$ to approximate the time-shift operator $e^{i\omega \sigma }$, the plane-wave destructor can be formulated as (Thiran 1971):

$$\begin{aligned} C(p,Z_{t}, Z_{x})=B(Z_{t})-Z_{x}B(\frac{1}{Z_{t}}),\quad B(Z_{t})=\sum _{n=-N}^{N}b_{k}Z^{-k}_{t}. \end{aligned}$$

(5)

The coefficient of filter $B(Z_{t})$ can be derived by fitting the filter frequency response at low frequencies to the response of the phase-shift operator. Besides, P is dependent on the local slope $\sigma$; thus, we can determine the slope by minimizing the following least-squares goal by using an iterative method, such as conjugate gradient method,

$$\begin{aligned} C(\sigma ,Z_{x},Z_{t})P(Z_{x},Z_{t})\approx 0. \end{aligned}$$

(6)

2.2 A Data-Driven Initial Model Building

Assume that several well logs are randomly and sparsely are distributed in a 2-D or 3-D work area, which can be regarded as a sparse spatial sampling of subsurface properties. The well-log data acquisition can be expressed as a process of spatial sampling (Chen et al. 2016; Gan et al. 2016; Liu et al. 2016):

$$\begin{aligned} \mathbf{S }\mathbf{m }=\mathbf{d }_{\text {log}}, \end{aligned}$$

(7)

where S denotes the sampling or mask operator, m denotes the subsurface properties, which is a spatial varying parameter, and $\mathbf{d }_{\text {log}}$ denotes the well-log data. Due to the high condition number of the sampling operator S, solving Eqn. 7 is an ill-posed problem. The regularization approach, which introduces some additional prior knowledge related to the target parameters, has been proved to be effective to mitigate the ill-posedness of the inverse problems. The Tikhonov-type regularization is one of the most widely used methods, which can be expressed as:

$$\begin{aligned} {\hat{\mathbf{m }}}=\text {arg}\min ||\mathbf{S }\mathbf{m }- \mathbf{d }_{\text {log}}||^{2}_{2}+\lambda ^{2}||\mathbf{m }||^{2}_{2}, \end{aligned}$$

(8)

where $\lambda$ is the regularization weight, and ${\hat{\mathbf{m }}}$ corresponds to the interpolated model. The interpolation without horizontal constraints is not meaningful for the seismic inversion. Then, we introduce the information related to the geological structures into equation 8, to better constrain the well-log interpolation problem. Here, the shaping regularization is used to solve the inverse problem.

Shaping regularization introduces a shaping operator P and a backward operator B (Chen et al. 2015; Xue et al. 2016; Hestenes and Stiefel 1952; Diaz 2012).

$$\begin{aligned} {\mathbf{m }}_{n+1}=\mathbf{P }\begin{bmatrix} {\mathbf{m }}_{n}+\lambda \mathbf{B }(\mathbf{d }_{log}-\mathbf{S } {\mathbf{m }_{n}}) \end{bmatrix}. \end{aligned}$$

(9)

When the operators S and B are both linear operators, and the iteration converges at ${\hat{\mathbf{m }}}$:

$$\begin{aligned} {\hat{\mathbf{m }}}=\mathbf{P }\begin{bmatrix} {\hat{\mathbf{m }}}+\lambda \mathbf{B }(\mathbf{d }_{log}-\mathbf{S } {\hat{\mathbf{m }}}) \end{bmatrix}. \end{aligned}$$

(10)

Then we can obtain the ${\hat{\mathbf{m }}}$ as:

$$\begin{aligned} {\hat{\mathbf{m }}}=\begin{bmatrix} \mathbf{I }-\mathbf{P }+\lambda \mathbf{PBS} ^{-1} \end{bmatrix}\lambda \mathbf{P }\mathbf{B }\mathbf{d }_{log}. \end{aligned}$$

(11)

Since this operator is usually related to construction information, it is also called structural smoothing operator. It applies the role of horizontal constraint for the model interpolation. The operator is generally obtained according to the prior information, such as sparsity, coherency, and smoothness. Here, define the shaping operator P as:

$$\begin{aligned} \mathbf{P }=\mathbf{L }\mathbf{T }\mathbf{T }^{*}\mathbf{L }^{*}, \end{aligned}$$

(12)

where $()^{*}$ denotes adjoint operator and T stands for a triangle smoothing operator (Xue et al. 2016). L is a summation operator along with the local slope attribute retrieved from the above subsection. Here, define the backforward operator $\mathbf{B }=\mathbf{S }^{*}$, then

$$\begin{aligned} {\hat{\mathbf{m }}}=[\mathbf{I }-\mathbf{LTT }^{*}\mathbf{L }+\lambda ^{2} \mathbf{LTT }^{*}\mathbf{L }^{*}\mathbf{L }]^{-1} \lambda ^{2}\mathbf{LTT }^{*}\mathbf{L }^{*}\mathbf{Sd }_{log}, \end{aligned}$$

(13)

and it can also be expressed as:

$$\begin{aligned} {\hat{\mathbf{m }}}=\mathbf{LT} [\mathbf{I }+\mathbf{T }^{*}\mathbf{L }^{*} (\lambda ^{2}\mathbf{S }^{*}\mathbf{S }-\mathbf{I })\mathbf{LT} ]^{-1} \mathbf{T }^{*}\mathbf{L }^{*}\mathbf{S }\mathbf{d }_{\text {log}}. \end{aligned}$$

(14)

Since the sampling operator S is a block diagonal matrix, i.e., $\mathbf{S }^{*}=\mathbf{S }$, the equation can be rewritten as:

$$\begin{aligned} {\hat{\mathbf{m }}}=\mathbf{LT} [\mathbf{I }+\mathbf{T }^{*}\mathbf{L }^{*} (\lambda ^{2}\mathbf{S }\mathbf{S }-\mathbf{I })\mathbf{LT} ]^{-1} \mathbf{T }^{*}\mathbf{L }^{*}\mathbf{S }\mathbf{d }_{\text {log}}. \end{aligned}$$

(15)

Then the equation can be solved via conjugate gradient algorithm.

2.3 Automatic Directional Total Variation Constraint

The proposed initial model building algorithm uses the kinematic attribute of seismic data as constraints, i.e., travel time information, to interpolate the well-log data. In addition to the low-frequency component of structural information, the exploration and development process requires more detailed information in the reservoir, especially the fluid. Thus, we attempt to introduce kinematic attributes (seismic slope attribute) into the seismic prestack inversion algorithm to improve the accuracy and resolution of dynamic attributes (the amplitude-related attributes). Here, the dynamic properties refer to elastic parameters, such as $v_{p}/v_{s}$, Poisson’s ratio $\sigma$, and bulk density $\rho$, which are related to the physical characteristics of the reservoir. In this paper, in order to improve the simulation accuracy of mid- and far-angle seismic data, the exact Zoeppritz equation is adopted as a forward operator, whose expression and derivative are shown in Appendix A. Thus, the forward problem can be defined as:

$$\begin{aligned} \text {F}(\mathbf{d },\mathbf{m })=\mathbf{d }-\text {G}(\mathbf{m })=\mathbf{n }, \end{aligned}$$

(16)

where m corresponds to the elastic properties of the subsurface rock $[v_{p}, v_{s}, \rho ]^{T}$, d denotes measured data, $\text {G}(\cdot )$ is the forward operator as a nonlinear function of m, and the misfit n denotes the noise.

However, solving the inverse problem corresponding to Eqn. 16 is usually ill-posed. In particular, Tikhonov-type regularization is usually exploited to ameliorate the ill-posedness. By introducing prior constraints into the inversion algorithm can not only enhance the uniqueness of the solution, but also helps to improve the accuracy of parameter inversion. According to the Tikhonov regularization theory, the objective function can be expressed as:

$$\begin{aligned} \text {J}(\mathbf{m })=||\mathbf{d }-\text {G}(\mathbf{m })||^{2}_{2}+\lambda ^{2} \text {Rc}(\mathbf{m }), \end{aligned}$$

(17)

where $\lambda$ denotes the regularization weight or trade-off factor, which balances the noise and the prior information. $||\mathbf{d }-\text {G}(\mathbf{m })||$ denotes the misfit function, and Rc(m) represents the prior regularization, also known as a penalty norm. The prior distribution can impose the distribution of the target parameters, and correlate the target multi-parameters and stabilize the results. The structural features of the desired model are always presumed or hypothesized to be smooth ($\ell _{2}$ regularization), blocky (TV regularization), sparse ($\ell _{1}$ regularization), etc.

Generally, the elastic parameters $[v_{p}, v_{s}, \rho ]^{T}$ are assumed to conform to the Gaussian distribution. However, such an assumption would lead to over-smooth results. Such inversion results have a poor ability to describe the internal and boundary details of the reservoirs.

Thus, in addition to the accuracy of the results, edge preservation is important in seismic inversion as well. TV regularization can be adopted as the regularization method, because it can smooth the model and preserve blocky features by enhancing the sparsity of the spatial gradient of the velocity difference. Furthermore, we restrict ourselves to the 2D case, although an extension to the full 3D situation is straightforward.

The augmented misfit function with TV regularization can be expressed as:

$$\begin{aligned} \text {J}_{tv}(\mathbf{m })=\text {J}(\mathbf{m })+\alpha (||\nabla _{x} \mathbf{m }||_{1}+||\nabla _{z}\mathbf{m }||_{1}), \end{aligned}$$

(18)

where $\nabla _{x}$ and $\nabla _{z}$ correspond to the horizontal and vertical gradient operators in a Cartesian coordinate, which takes the forms of:

$$\begin{aligned} \nabla _{x}\mathbf{m }(i,j)=\mathbf{m }_{i+1,j}-\mathbf{m }_{i,j}, \nabla _{z}\mathbf{m }(i,j)=\mathbf{m }_{i,j+1}-\mathbf{m }_{i,j}. \end{aligned}$$

(19)

The horizontal and vertical gradient is the spatial finite difference of the model, which is also called a Markov random field (MRF). More points can be introduced to the difference operations to avoid the continuity becoming worse due to the abnormality of individual points. According to the number of points ($2k+1$) involved in the difference calculation, it is also called a kth-order Markov random field. Thus, Eqn. 19 corresponds to the first-order Markov random field.

However, conventional TV regularization can only regularize the model in the horizontal (x) and vertical (y) direction regardless of the geological structure information. Thus, the target parameters with severe lateral tectonic fluctuations, such as tilted layers, faults, and salt body, cannot be completely represented by using the conventional TV regularization. However, the x and y directions can be decomposed along and perpendicular to the seismic local slope. The seismic local slope attribute can be retrieved from subsection 1.

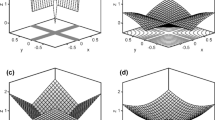
Figure 1 shows a stratum with steep fault, and we use the Models 1, 2, 3, and 4 correspond to different geological conditions. The points in the red boxes denote the data involved in the first-order difference operation. Model 1 represents the point within an isotropic stratum, which can get satisfactory results by using traditional inversion algorithms. The others indicate the points associated with the geological edge. Model 2 denotes the point located at the horizontal interface. In order to clearly depict the lateral boundary/edge, using sparse spike inversion or the traditional TV regularization can yield encouraging results. Model 3 denotes the point at the tilted fault (emphasized in this work), which can hardly depict the fault interface well and even introduce undesired bias to the results when using the conventional TV regularization. The same situation will appear in Model 4, corresponding to the point of the stratum extinction zone.

Fig. 1

Schematic illustration of geological structure with the models (spatial points) for the first-order difference TV regularization (within the red lines). Note that: Model 1 corresponds to the points located at the isotropic media; Models 2 denotes the points located at the horizontal interface; Model 3 stands for the points located at the tilted boundary; and Model 4 represents the points located at the vanishing point of special geological body

By introducing the seismic slope attribute, the directional TV (DTV) regularization project the data from the Cartesian coordinate system to the directions along and perpendicular to the seismic slope, and then implements the differential operation. An illustration of the transform from the conventional TV regularization (corresponding to the black solid arrows) to the DTV regularization (corresponding to the dashed blue arrows) is shown in Fig. 1. Thus, according to the idea of the DTV regularization, the objective function (equation 19) can be rewritten as:

$$\begin{aligned} \text {J}_{dtv}(\mathbf{m })=\text {J}(\mathbf{m })+\alpha (||\nabla _{x'} \mathbf{m }||_{1}+||\nabla _{y'}\mathbf{m }||_{1}), \end{aligned}$$

(20)

where $\nabla _{x'}$ and $\nabla _{y'}$ represent the gradient operators along and perpendicular to the dominant direction of the seismic slope. With the seismic slope, the regularization can be easily projected from the Cartesian coordinates to the appropriate coordinates for the local area as:

$$\begin{aligned} \left( \begin{aligned} \nabla _{x'}\mathbf{m }(i,j) \\ \nabla _{y'}\mathbf{m }(i,j)\\ \end{aligned} \right) =\Lambda \mathbf{R } \left( \begin{aligned} \nabla _{x}\mathbf{m }(i,j) \\ \nabla _{y}\mathbf{m }(i,j)\\ \end{aligned} \right) , \end{aligned}$$

(21)

where the scaling matrix $\Lambda$ and rotation matrix $\mathbf{R }$ can be expressed as:

$$\begin{aligned} \Lambda = \begin{pmatrix} \alpha _{1}&{}0\\ 0&{}\alpha _{2} \end{pmatrix}, \mathbf{R }= \begin{pmatrix} \cos \theta &{}-\sin \theta \\ \sin \theta &{}\cos \theta \end{pmatrix}, \end{aligned}$$

(22)

and $\alpha _{1}$ and $\alpha _{2}$ represent the scale on the gradient parallel and perpendicular to the seismic local slope $\theta$.

The objective function like equation 17 can be solved by the alternating direction method of multipliers (ADMM) algorithm (see Algorithm 2) as follows:

$$\begin{aligned} \begin{aligned} \mathbf{m }^{k+1}=\text {arg}\min \begin{Bmatrix} [\mathbf{d }-\mathbf{G }(\mathbf{m }^{k})]^{T}[\mathbf{d }-\mathbf{G }(\mathbf{m }^{k})]+\mathbf (m ^{k})^{T}\mathbf{C }_{m}(\mathbf{m }^{k}) \end{Bmatrix},\\ \qquad \mathbf{m }^{k+1}= \mathbf{m }^{k+1}-\lambda (\nabla _{1}^{T}(\mathbf{a }_{1}^{k} -\nabla _{1}\mathbf{m }^{k}-\mathbf{b }_{1}^{k})+\nabla _{2}^{T}(\mathbf{a }_{2}^{k} -\nabla _{2}\mathbf{m }^{k}-\mathbf{b }_{2}^{k}),\\ \qquad \mathbf{a }_{1}^{k+1}=\text {shrink}\left( \nabla _{1}\mathbf{m }^{k+1} +\mathbf{b }_{1}^{k},\frac{1}{\lambda }\right) , \mathbf{b }_{1}^{k+1}=\mathbf{b }_{1}^{k}+(\nabla _{1}\mathbf{m }^{k+1} -\mathbf{a }_{1}^{k+1}),\\ \qquad \mathbf{a }_{2}^{k+1}=\text {shrink}\left( \nabla _{2}\mathbf{m }^{k+1} +\mathbf{b }_{2}^{k},\frac{1}{\lambda }\right) , \mathbf{b }_{2}^{k+1}=\mathbf{b }_{2}^{k}+(\nabla _{2}\mathbf{m }^{k+1} -\mathbf{a }_{2}^{k+1}),\\ \end{aligned} \end{aligned}$$

(23)

where a and b are the temporary variables during iterations, and shrink represents the soft thresholding operator, which can be expressed as:

$$\begin{aligned} \text {shrink}(m,\rho )=\frac{m}{|m|}*\max (|m|-\rho , 0). \end{aligned}$$

(24)

3 Analysis

3.1 Impact on Initial Model

As shown in step 6 of Algorithm 2, the ADMM algorithm decomposes the original optimization problem into two (or more) subproblems. Firstly, we use a conventional gradient-based method to minimize the objective function J(m). Then, the algorithm highlights the sparsity of the first-order spatial difference by using soft thresholding. Finally, both two subproblems can be optimized through multiple iterations.

Algorithm 1 Geological structure-oriented starting model for prestack inversion
Input: well-log data, post-stack seismic data
Output: high-accuracy starting model
1.	Executing seismic migration process to obtain the post-stack or seismic images.
2.	Extracting seismic slope from post-stack data with PWD algorithm
3.	Establish objective function of the inversion-based interpolation
	${\hat{\mathbf{m }}}=\text {arg}\min ||\mathbf{S }\mathbf{m }-\mathbf{d }_{\text {log}}||^{2}_{2}+\lambda ||\mathbf{m }||^{2}_{2}$
4.	Minimizing the shaping regularized function to obtain the interpolated model with conjugate gradient
	method ${\hat{\mathbf{m }}}=\mathbf{LT} [\mathbf{I }+\mathbf{T }^{*}\mathbf{L }^{*}(\lambda ^{2}\mathbf{S }^{*}\mathbf{S }-\mathbf{I })\mathbf{LT} ]^{-1}\mathbf{T }^{*}\mathbf{L }^{*}\mathbf{S }\mathbf{d }_{\text {log}}.$
5.	Output the interpolated model with geological structure constraint.

Algorithm 2 The seismic slope regularized high-resolution prestack inversion
Input: well-log data, seismic data or image
Output: high-resolution inversion results, starting model
1.	Executing seismic migration process to obtain the post-stack or seismic images.
2.	Extracting seismic slope from seismic data or images of Step 2 with PWD algorithm
3.	Establish objective function of the inversion-based interpolation
	${\hat{\mathbf{m }}}=\text {arg}\min ||\mathbf{S }\mathbf{m }-\mathbf{d }_{\text {log}}||^{2}_{2}+\lambda ||\mathbf{m }||^{2}_{2}$
4.	Minimizing the shaping regularized function to obtain the interpolated model with conjugate gradient
	method ${\hat{\mathbf{m }}}=\mathbf{LT} [\mathbf{I }+\mathbf{T }^{*}\mathbf{L }^{*}(\lambda ^{2}\mathbf{S }^{*}\mathbf{S }-\mathbf{I })\mathbf{LT} ]^{-1}\mathbf{T }^{*}\mathbf{L }^{*}\mathbf{S }\mathbf{d }_{\text {log}}.$
5.	Initializing: $\mathbf{m} ^{0}$= ${\hat{\mathbf{m }}}$, and a$_{1}^{0}$ = a$_{2}^{0}$ = b$_{1}^{0}$ = b$_{2}^{0}$ = 0.
6.	do while(iter$\le$Maxiter or misfit$\le \epsilon$)
	$\mathbf{m }^{k+1}=\text {arg}\min \begin{Bmatrix} [\mathbf{d }-\mathbf{G }(\mathbf{m }^{k})]^{T}[\mathbf{d }-\mathbf{G }(\mathbf{m }^{k})]+\mathbf (m ^{k})^{T}\mathbf{C }_{m}(\mathbf{m }^{k}) \end{Bmatrix}$
	m$^{k+1}$= m$^{k+1}-\lambda$($\nabla _{1}^{T}$(a$_{1}^{k}-\nabla _{1}$ m$^{k}-\mathbf{b }_{1}^{k}$)+$\nabla _{2}^{T}$(a$_{2}^{k}-\nabla _{2}$ m$^{k}-\mathbf{b }_{2}^{k})$
	a$_{1}^{k+1}$=shrink($\nabla _{1}\mathbf{m }^{k+1}+\mathbf{b }_{1}^{k},\frac{1}{\lambda })$, b$_{1}^{k+1}$=b$_{1}^{k}$+($\nabla _{1}\mathbf{m }^{k+1}-\mathbf{a }_{1}^{k+1})$
	a$_{2}^{k+1}$=shrink($\nabla _{2}\mathbf{m }^{k+1}+\mathbf{b }_{2}^{k},\frac{1}{\lambda })$, b$_{2}^{k+1}$=b$_{2}^{k}$+($\nabla _{2}\mathbf{m }^{k+1}-\mathbf{a }_{2}^{k+1})$
	end
7.	Output the inversion result m$_{k+1}$ and starting model ${\hat{\mathbf{m }}}$

With respect to the objective function like Eqn. 14, the gradient-based methods can be used to achieve optimization. The m-update can be obtained by the following equation:

$$\begin{aligned} \mathbf {m} ^{k+1}=\mathbf {m} ^{k}-{\mathbf {H}} (\mathbf {m} ^{k})^{-1}\varvec{\gamma }(\mathbf {m} ^{k}), \end{aligned}$$

(25)

where k is the iteration times, $\varvec{\gamma }$ is the gradient of the objective function, and $\mathbf{H }$ is the Hessian matrix. The specific expression of the exact Zoeppritz equation and its gradient is given in Appendix.

Thus, the final inversion results are closely related to the initial model m$^{0}$. Moreover, m-update $\Delta \mathbf{m }^{k}=-{\mathbf {H}}(\mathbf {m} ^{k})^{-1} \varvec{\gamma }(\mathbf {m} ^{k})$ is a model-dependent variable as well. In other words, the initial model $\mathbf{m }^{0}$ can not only provide a low-frequency model basis for the inversion, but also have a significant impact on the m-update. The m-update is closely related to the misfit between the observed and synthetic data $\Delta \mathbf{d }$.

Here a two-layer model is exploited to demonstrate the importance of the initial model to the m-update. The two-layer model is shown in Fig. 2a. By adjusting the lower-layer parameters, we can obtain the physical realization by using the exact Zoeppritz equation. The variations of the seismic response relative to match pre- and post-perturbation are shown in Fig. 2b (blue solid line).

Gradient-based optimization step along with the first- or second-order gradient of the objective function to get the optimal solutions. Thus, when dealing with a nonlinear optimization problem, the optimization itself is actually an approximation. The red dashed line in Fig. 2b shows the approximated seismic response physical realization of the model perturbations. Due to the inaccuracy of the model, we can find that the nonlinear forward operator itself will also be biased. Besides, a severe deviation of the errors will occur as the model increases bias, as shown in Fig. 2c.

Fig. 2

a Two-layer model with ${\textit{v}}_{p}$, ${\textit{v}}_{s}$, and ${\rho }$, and b the comparison of the variations of real seismic response perturbation (blue line) and the approximated perturbation (red line) simulated by the linearized operator with different initial models, and c the relative difference of the perturbation with different initial models

Therefore, the accuracy of the initial model $\mathbf{m }^{0}$ can not only provide low-frequency components to avoid being trapped into more local extrema, but also directly affect the accuracy of the forward operator. In terms of gradient-based optimization, a good initial model building algorithm lays a fundamental basis for the solution of subsequent inverse problems.

3.2 Impact on Regularization

As mentioned above, obtaining the optimal solution when minimizing J(m) is the first step of the proposed method. To describe the boundaries/edges of strata or faults, conventional regularizations are not enough. The TV regularization can highlight the spatial sparsity of the first-order difference, that is, to make use of the characteristics of discontinuous interface information to highlight anomalies. However, some problems will occur when using conventional TV regularization to characterize tilted strata. Here, a set of two-layer models with $0^{\circ }$, $30^{\circ }$, $60^{\circ }$, $90^{\circ }$ tilted layers are exploited to verify the superiority of the DTV regularization. The models are shown in Fig. 3a–d.

Fig. 3

Two-layer models with a)$0^{\circ }$, b $30^{\circ }$, c $60^{\circ }$, and d)$90^{\circ }$ faults, and the corresponding edge-blurred models (e-h). The deblurring results using the conventional TV regularization and the DTV regularization

Figure 3e–h corresponds to the smooth-constraint regularized results. We can see that the smooth constraint results cannot accurately locate interfaces, but present a data transition zone. In the case of complex strata, such results cannot be used to distinguish the stratum, not to mention the internal details of the reservoir.

Further, conventional TV and DTV regularizations are implemented to these models to demonstrate their difference, and the results are shown in Fig. 3. Figure 3i–l indicates the deblurred results by using TV regularization, and Fig. 3m–p denotes the corresponding results of the DTV regularization.

When strata are horizontal or vertical in the Cartesian coordinate system, corresponding to the models shown in Fig. 3a, d, both the conventional and the proposed DTV regularizations can well characterize the boundaries/edge of the geological bodies. However, when the reflecting interface is inclined, results yielded by the conventional TV regularization present some characterization defects. In this case, the difference in the traditional Cartesian coordinate system is likely to cause anomalies due to the drastic lateral change of parameters. Some artifacts can be found in the results shown in Fig. 3j and k. However, the DTV regularization solves this problem well, as shown in Fig. 3n and o.

To further verify the effects of the DTV regularization, we zoomed in some parts of the result corresponding to the red boxes in Fig. 3. The highlighted results are shown in Fig. 4. By comparison, we can find that the DTV regularization is obviously advantageous in describing information of the tilted strata.

Fig. 4

Zoomed parts of the deluring results with $0^{\circ }$ (a, b, c) and $45^{\circ }$ (d, e, f) faults by using the $\ell _{2}$-norm(a, d), the TV(b, e), and the DTV (c, f) regularizations

By the theoretical and numerical analysis above, we can find that the initial model and regularization are the key factors affecting the final inversion results. Both factors provide prior information for prestack inversion. Therefore, providing accurate prior information is essential for improving inversion accuracy and resolution. Besides, structure-oriented information is important for the inversion, especially for the cases with geological structural complexity or limited prior information.

4 Numerical Examples

In order to demonstrate the proposed method, the SEAM model is exploited for seismic inversion. Several tests of inversion using different regularization methods are performed for comparison.

The elastic parameters ${\textit{v}}_{p}$, ${\textit{v}}_{s}$, and ${\rho }$ of partial SEAM model in the time domain are shown in Fig. 5. The prestack seismic inversion tests are conducted to verify the effectiveness and superiority of the proposed strategy. As shown in Fig. 5, the geological structure of the model is relatively complex, including many tilted formations, faults, and other complex-textured geological structures. Obviously, the initial model of such a geologically complex structure cannot be well prepared using the traditional artificial interpretation and kriging-based well-log interpolation method. Here the traditional artificial interpretation refers to manually picking up seismic horizon information. The geological structure of the model is complex, including many special geological bodies. Thus, manual interpretation cannot only introduce artificial errors, but also consumes a lot of labor. The effect of the kriging-based method will largely depend on the number of wells versus the spatial continuity model imposed.

Fig. 5

Elastic parameter a ${\textit{v}_{p}}$, b ${\textit{v}_{s}}$, and c $\rho$ of the SEAM model

The essential factor in the proposed strategy is the seismic slope attribute, which can be extracted from the migrated images or post-stack seismic profiles. The slope attribute can be in the time domain (for prestack inversion) and depth domain (full-waveform inversion) according to the requirement. Here we use a synthetic seismic post-stack profile for extracting this attribute. With the elastic parameters shown in Fig. 5, the reflection coefficient can be obtained. Then, the model reflectivities are convolved with a 30 Hz Ricker wavelet, and we obtain a zero-offset synthetic profile, as shown in Fig. 6a. By using the PWD algorithm, the seismic slope attribute of the seismic data can be extracted as shown in Fig. 6b. The estimated slope provides us with the key to the lateral constraint of well-log data interpolation and essential factors to rotate the coordinate system when using the proposed DTV regularization.

Fig. 6

a Zero-offset synthetic data profile and b estimated seismic slope using PWD algorithm

4.1 Starting Model Building

Here, we extract elastic parameters of several CDPs as well-log data, and the well-log distribution is shown in Fig. 7a. By using the proposed initial model building method, we obtain the interpolated P-wave velocity, as shown in Fig. 7b. Comparing Figs. 5a and 7b, we can find that the interpolation result is very similar to the real model.

Fig. 7

a Well-log data extracted from the SEAM model, where the yellow lines indicate the well-log locations, and b the interpolated initial P-wave velocity model

To further verify the superiority of the proposed method, we highlight the most complex part of the model (corresponding to the data in the black dashed rectangle). We compare the interpolated result with the ray-tracing-based tomography result, as shown in Fig. 8. Figure 8a shows the initial model using tomography, and Fig. 8b plots the zoomed interpolated results. One can find that the slope attribute-guided well-log data interpolation can obtain an initial model with a higher resolution and higher accuracy than the conventional one, which lays a good foundation for later seismic inversion. Similarly, we can obtain the S-wave velocity ${\textit{v}}s$ and bulk density ${\rho }$ of the SEAM model, as shown in Figure 9.

Fig. 8

a Initial model from seismic tomography, and b zoomed interpolated initial model

Fig. 9

Interpolated a S-wave velocity ${\textit{v}_{s}}$ and b bulk density ${\rho }$ initial models using the slope-attribute-regularized inversion

From the above experiments, we can find that the key to the interpolation lies in the estimation of seismic slope and the quantity of well-log data. Firstly, as mentioned above, to build a high-fidelity initial model for seismic inversion, a highly accurate seismic slope should be extracted from the seismic data, which closely depends on the quality of the seismic data. Secondly, the locations and quantity of well-log data are of importance as well.

Thus, seismic data with several noise levels and different well-log numbers are implemented for inversion. By calculating the correlation between the interpolated results and the real model, we can find the impact of these two elements on model building (see Table 1). The S/N metric is defined as (Chen et al. 2019a):

$$\begin{aligned} \text {S/N}=10\text {log}_{10}\frac{||{\mathbf{d }}_{\text {ref}}||_{2}^{2}}{||{\mathbf{d }}_{\text {ref}}-{\mathbf{d }}||^{2}_{2}}, \end{aligned}$$

(26)

where ${\mathbf{d }_{\text {ref}}}$ and ${\mathbf{d }}$ denote the reference data with and without noise, respectively.

By comparison, one can find that the interpolation effect is less sensitive to the noise, while the well-log data shows a greater impact on the interpolation. The random noise corrupted seismic section ($\hbox {S/N}=3$) is shown in Fig. 10. Figure 11 shows the starting models built under $\hbox {SNR}=3$ with ten well logs as the constraint.

The initial model generally selects the low-frequency model for inversion. The inaccurate mid- and high-frequency components of the initial model are likely to induce local extrema in subsequent inversion algorithms. Therefore, the interpolated starting models ought to be smoothed before the seismic inversion.

4.1.1 DTV Regularized Prestack AVA Inversion

Next, we conduct the parameter inversion with the smoothed interpolated results. To demonstrate the importance of structure-oriented factors prestack inversion in geologically complex media, several methods are implemented for the inversion test. Here we apply the conventional $\ell _{2}$-norm regularized method, TV regularized method, and the DTV regularized method for the prestack seismic inversion, where the forward operator is the exact Zoeppritz equation. Figures 12a, 13a, and 14a correspond to the initial model by smoothing the interpolated well-log data ${\textit{v}}_{p}$, ${\textit{v}}_{s}$ and ${\rho }$ in the above section. The prestack AVA inversion results using these methods are shown in Figs. 12, 13, 14, respectively.

Table 1 Correlation between the real model and the initial model using different numbers of wells and under different signal-to-noise ratio (S/N) conditions

Fig. 10

Random noise corrupted post-stack seismic data

Fig. 11

Interpolated a P-wave velocity ${\textit{v}}_{p}$, b S-wave velocity ${\textit{v}}_{s}$ , and c bulk density ${\rho }$ models from ten wells with $\hbox {SNR}=5$ dB

Fig. 12

a Smoothed initial model and inverted results of the P-wave velocity ${\textit{v}}_{p}$ by using b the $\ell _{2}$-norm regularized method, c the conventional TV regularization, and d the DTV regularization

Fig. 13

a Smoothed initial model and inverted results of the S-wave velocity ${\textit{v}}_{s}$ by using b the $\ell _{2}$-norm regularized method, c the conventional TV regularization, and d the DTV regularization

Fig. 14

a Smoothed initial model and inverted results of the density ${\rho }$ by using b the $\ell _{2}$-norm regularized method, c the conventional TV regularization, and d the DTV regularization

Figures 12b–d corresponds to the inverted ${\textit{v}}_{p}$ parameters by using (b) $\ell _{2}$-norm regularization, (c) conventional TV regularization, and (d) the proposed DTV regularization, respectively. The smooth constraint ($\ell _{2}$-norm regularization) yields spatial blurred results, which are difficult to describe the boundary/edge. Even though such spatial blurred results can restore some structures of the subsurface medium, it cannot be reliable enough for the interpretation, especially for the tilted stratum, steep faults, etc.

Different from the smoothed constraint, i.e., the $\ell _{2}$-norm regularization, the TV regularization presents a stronger for reservoir characterization, as shown in Figs. 12c and d. Besides, the TV regularization better resolves some defects of the conventional single-trace method, i.e., being able to describe the lateral perturbation. In particular, both the vertical and horizontal resolutions of the inversion results have been improved where the seismic slope is small. However, the conventional TV method causes a discontinuity in the horizontal direction when the seismic slope becomes large, e.g., for tilted stratum and steep faults. Thus, some vertical artifacts can be found where there are severe lateral variations in the inversion results. The reason for these artifacts is that the difference in the Cartesian coordinate system is likely to cause anomalies due to the drastic lateral change of parameters. TV regularization describes the spatial variation boundary of data by highlighting the sparsity of the first-order difference. However, when the data do not vary abruptly along the spatial grid direction, the TV regularization is prone to a staircase effect.

By introducing the seismic slope attribute to the TV regularization, the spatial variation boundaries have been fully described, as shown in Fig. 12d. Structure-oriented information enhances the sparsity of the first-order difference. The inverted results using the proposed method improves the inverted results by avoiding the artifacts in the inverted results. Hence, the interface, tilted strata, and steep faults have been characterized well. Besides, the details have been preserved due to the essence of the TV regularization. When dealing with the tilted interface, the DTV regularization can rotate the coordinate system according to the slope to highlight this abnormality to the greatest extent. It is obvious that introducing the structure-guided information to the inversion algorithm is an effective strategy to make the tilted interface better preserved. Through the comparison, we can observe similar phenomena from the inversion results of S-wave velocity and density, as shown in Figs. 13 and 14.

To further highlight the superiority of the detailed characterization, we magnified the most violent part of the strata, which corresponds to the black dotted rectangle in Figs. 12b–d. The highlighted results of the P-wave velocities are shown in Fig. 15. The tilted interface information is sufficiently described, and the details of the reservoir are clearly characterized. The results are consistent with the previous conclusions but are much clearer. However, compared with ${\textit{v}}_{p}$ and ${\rho }$, the results of ${\textit{v}}_{s}$ are slightly worse due to the insensitivity of the P–P-wave seismic data to the ${{\varvec{v}}}_{s}$ property.

Fig. 15

Partially zoomed inverted ${\textit{v}}_{p}$ using a the $\ell _{2}$-norm regularized method, b the conventional TV regularized method, c the proposed DTV regularized method, and d the reference truth

Fig. 16

Boundary characterization by using DTV regularization of the final results shown in Fig. 12d

Figure 16 corresponds to the DTV regularization interfaces of the final results. From the figure, we can see that the DTV constraint well describes the interface information. We extracted the first trace of these inverted results. Figure 17a shows the comparison of the extracted ${\textit{v}}_{p}$ from the inverted results by using the $\ell _{2}$-norm regularization (blue line), the conventional TV regularization (green line), and the proposed TV regularization (red line). By comparison, we can find that the proposed method can indeed obtain a better inversion result than the other two.

Fig. 17

a Single-trace inversion results extracted from Fig. 12 using the conventional method and the DTV method (red), and b the convergence diagrams of prestack AVA inversion with the conventional TV regularization method (black) and the DTV method (red)

Figure 17b shows the normalized data misfit between the observed and synthetic data for the conventional TV regularization and the DTV regularization. We can conclude that the DTV regularization converges faster than the TV regularization.

5 Real Data Application

The proposed inversion method is tested via two field datasets. Both datasets come from an oilfield locating in the southern part of the central Congo. The oil/gas mainly accumulates in the Lower Congo Basin and the Kwanza Basin. The total sedimental system includes both subsalt and post-salt source rocks and Oligocene to Miocene turbidite reservoirs. The research area is distributed along the South Atlantic Ocean Coast and lies primarily in the deep water. Thus, the quality of the acquired seismic data is low. However, due to the geological structural complexity, the inversion results obtained by the traditional methods in this area are unsatisfactory.

5.1 Field Data I

The post-stack profile of the first field data is shown in Fig. 18a. We can find that the geological structure of this area is relatively complex, including obvious faults and fluctuate strata. As shown in Fig. 18a, we can see an obvious dominant fault, corresponding to the red dashed line. Based on the PWD algorithm, we can extract the slope attribute from the post-stack seismic data, as shown in Fig. 18b.

Fig. 18

a Post-stack seismic profile of the real seismic data and the seismic slope attribute of the real seismic data estimated by PWD algorithm. The red dashed line is the dominate fault of the field data, and black dashed line indicates the well-log location

Although it is an anticline structure, the seismic slope of the upper and lower strata is different. Thus, in order to ensure the accuracy of the initial model, it is necessary to pick the geological horizon information as much as possible. But obviously, this will not only introduce a lot of artifact errors but also cost-intensive labor.

Instead of using the artificially picked horizons as a constraint, the seismic slope attribute is exploited to interpolate the well-log data. Figure 19 shows the initial models for the multi-parameter prestack seismic inversion using the well-log interpolation using the conventional method (a, c, e) and the proposed method (b, d, f).

Fig. 19

Interpolated starting models based on the conventional method (a, c, e) and the proposed method (b, d, f)

The comparison demonstrates that the proposed method can yield a set of initial models that are more consistent with the seismic data structure than the conventional methods. Moreover, the proposed method can characterize some geological details, especially fault structures. As mentioned in the previous analysis, the accuracy of the low-frequency models is essential for the seismic inversion. Therefore, such models lay a good foundation for the subsequent inversion.

Fig. 20

Inverted P-wave velocity ${\textit{v}}_{p}$ properties using the conventional smooth constraint (a, b) and the proposed DTV regularization (c, d) with the initial models built by the conventional and proposed methods

Fig. 21

Inverted S-wave velocity ${\textit{v}}_{s}$ properties using conventional smooth constraint (a, b) and the proposed DTV regularization (c, d) with the initial models built by the conventional and proposed methods

Fig. 22

Inverted density ${\rho }$ properties using conventional smooth constraint (a, b) and the proposed DTV regularization (c, d) with the initial models built by the conventional and proposed methods

Fig. 23

Geological faults interpretation and Poisson’s ratio with the inversion result of the proposed method

Fig. 24

Inverted a porosity $\phi$ and b water saturation Sw by using Hertz–Mindlin model

Fig. 25

Post-stack seismic profile of the real seismic data and its estimated seismic slope of the seismic data using the PWD algorithm

In addition to the seismic data and initial model, seismic wavelets are another significant factor for the seismic inversion. We extract the seismic wavelets from the prestack seismic data. Then, we exploit the exact Zoeppritz equation as the forward operator for inversion. Then, we use the conventional and the proposed method to build the initial model, and adopt the $\ell _{2}$ norm and the proposed DTV norm as the penalty norm for the prestack inversion. Figures 20-22 show the inversion results. After comparing these results, the following phenomena can be observed:

• (1) Figures 20a, 21a, and 22a show the inverted ${\textit{v}}_{p}$, ${\textit{v}}_{s}$, and ${\rho }$ properties by using the smoothness constrained regularization with the initial models shown in Fig. 19. The standard Tikhonov regularization reveals detailed structural information with blurred boundaries and edges. Besides, the faults within this area are difficult to be identified by such results.

• (2) Figures 20b, 21b, and 22b correspond to the inverted properties by using the Tikhonov regularization with the well-log interpolated initial model. Comparing the results with the former one, we can clearly find that the low-frequency components of the final inversion results are dominated by the initial model. Based on these low-frequency components, which are closely related to the structure, the inversion can describe some details of the subsurface. The blue boxes in Figs. 20a and 20b highlight the difference between the two sets of results. The structural information at the bottom of the stratigraphic uplift can be well characterized. However, the defects of the smoothness constraint can not be overcome by only improving the accuracy of the initial model.

• (3) Figures 20c, 21c, and 22c show the results of the proposed DTV regularization algorithm but using the traditional initial model building method. Comparing with Figs. 20a, 21a, and 22a, these results can describe more details of the subsurface properties, especially for the boundaries of the geological bodies and edges of the faults. As shown in Figs. 20c, 21c, and 22c, we can see some obvious fault structures. However, it is difficult to judge which is better when comparing the second set of results with this one.

• (4) Combining the initial model building method based on well-log interpolation and the DTV regularization method, we obtained the inverted properties as shown in Figs. 20d, 21d, and 22d. Compared with the former three, we can find that the resolution has been improved a lot in both vertical and horizontal directions. We can clearly see the distribution of fault layers and the interface information of strata. We can pick the faults with such results, as shown in Fig. 23a. However, it is difficult to get such good results using the traditional method. It can not only accurately represent the low-frequency structure information by using the geological structure-guided model building method, but also describe the detailed information by applying the directional total variation regularization. The real data application demonstrates that the effectiveness of the seismic slope-attribute-regularized seismic inversion.

For oil/gas exploration and development, it is not intuitive with the elastic parameters. In contrast, reservoir parameters have a better fluid indication, like the Poisson’s ratio. The reservoir fluid will mainly have an impact on the P-wave velocity ${\textit{v}}_{p}$, but will not greatly change the S-wave velocity ${\textit{v}}_{s}$. Therefore, when encountering a fluid, Poisson’s ratio usually decreases. Figure 23b shows the converted Poisson’s ratio by using the inverted results of the proposed method. The high-resolution results perform well on the characterization of the deepwater reservoir.

Likewise, by using the petrophysical model as a bridge, we can invert some reservoir parameters, such as porosity $\phi$ and water saturation Sw. Thus, we apply the Hertz–Mindlin (H–M) model to simulate the elastic behavior of a turbidite sandstone by establishing a link between reservoir parameters and elastic parameters. The details about the model are given in Appendix B. Fig. 24a and b correspond to the inverted porosity $\phi$ and water saturation Sw.

5.2 Field Data II

Then, we applied the conventional and the proposed methods to another field dataset with a more complex geological structure. Figure 25a shows the post-stack seismic profile. It can be found that the structure of the subsurface medium is complex and the seismic S/N is low. The undulations of the strata in this area are more obvious, and there are even many dithering strata. The faults are commonly distributed in this complex geological structural area. Therefore, it is very difficult to carry out horizon picking and fault interpretation of this dataset. In order to compare with the traditional method, we spent a lot of time to pick the geological horizons and faults. Then, the seismic slope attribute is extracted from the post-stack seismic data by using the PWD algorithm for the proposed method, as shown in Fig. 25b. Then we use the results of geological horizon interpretation and the seismic slope attribute as constraints to build the initial model, respectively.

Fig. 26

Interpolated starting model of a ${\textit{v}}_{p}$, b ${\textit{v}}_{s}$, and c ${\rho }$ regularized by the conventional method with less picked horizons

For the conventional initial model building method, geological horizon piking is essential. Figure 26 shows the initial model with a small number of horizons. We can find that the obtained initial model generally maintains the same structural characteristics when there are fewer layers. Obviously, such initial models are inappropriate but have been widely used in the industry, since we cannot pick all the layers, especially the 3D work area.

Fig. 27

Interpolated starting model of a ${\textit{v}}_{p}$, b ${\textit{v}}_{s}$, and c ${\rho }$ regularized by the conventional method with enough picked horizons

To improve the accuracy of the initial model, we pick as many geological horizons and faults as possible, which is shown in Fig. 27. With these interpreted results, we obtained the interpolated initial models by using the inverse distance power algorithm. Figure 27 shows that the results of geological horizon constraints are much affected by the interpretation of horizons. Comparing the models shown in Figs. 26 and 27, we can find that increasing number of horizons can yield an initial model close to the facies of the seismic data. However, once the horizon interpretation includes errors, it will affect the quality of the inversion results. Because the seismic data itself lacks low-frequency information, it is problematic if inaccurate low-frequency information is provided for the inversion.

Fig. 28

Interpolated starting model of a ${\textit{v}}_{p}$, b ${\textit{v}}_{s}$, and c ${\rho }$ regularized by the proposed method

Figure 28 corresponds to the starting models of the multi-parameter inversion by using the seismic slope-attributes-regularized modeling method. Note that there is no need to manually interpret any horizons or faults throughout the modeling process. Besides, the morphology of the models and the seismic data maintain a high consistency. By comparing the models in Figs. 26, 27, 28, we can find that when the geological horizons are not enough or there are obvious errors in the interpretation results of geological horizons, the initial model is not reliable. If the results shown in Fig. 26 are used for subsequent inversion, it will significantly affect the accuracy of the final inversion results.

Then, we adopt the starting model shown in Figs. 27 and 28 to prestack AVA inversion. Then, we exploit the exact Zoeppritz equation as a forward operator for the inversion. The $\ell _{2}$ norm, conventional TV norm, and the proposed directional TV norm are used as the penalty norm for the prestack inversion.

Fig. 29

Inverted results of a ${\textit{v}}_{p}$, b ${\textit{v}}_{s}$, and c ${\rho }$ parameters by using the $\ell _{2}$ regularization with the initial models shown in Figs. 27

Figure 29 corresponds to the inverted ${\textit{v}}_{p}$, ${\textit{v}}_{s}$, and ${\rho }$ results using the $\ell _{2}$ norm as a penalty. It can be seen that the result is too smooth, the formation interface is blurred, and it is almost impossible to distinguish the position of the formation interface. Besides, due to the low SNR of seismic data, the inversion results have a poor horizontal continuity.

Fig. 30

Inverted results of a ${\textit{v}}_{p}$, b ${\textit{v}}_{s}$, and c ${\rho }$ parameters by using the conventional TV regularization with the initial models shown in Figs. 27

Figure 30 shows the inversion results using the conventional TV regularization with the initial models shown in Fig. 27. Compared with the former, the quality of these results have been improved, and the vertical resolution has been enhanced. However, due to the inclination of the stratum, the conventional TV regularization method still causes poor vertical and horizontal resolutions, and also the lateral discontinuity.

Fig. 31

Inverted results of a ${\textit{v}}_{p}$, b ${\textit{v}}_{s}$, and c ${\rho }$ parameters using the proposed DTV regularization with the initial models shown in Fig. 28

Figure 31 shows the inverted ${\textit{v}}_{p}$, ${\textit{v}}_{s}$, and ${\rho }$ parameters using the proposed method. Compared with the previous two, we can find that the quality of the inversion results has been significantly improved. The position highlighted by the black arrows in the figure corresponds to the locations of the faults. The location and direction of these faults can be clearly described by the inversion results by using the proposed method. Besides, through the inversion results, we can also clearly see the formation interface, and the position of the reflection interface of the formation, the occurrence of the inclined formation. The good lateral continuity demonstrates strong robustness of the proposed method.

6 Discussion

Seismic local slope-attribute-regularized prestack seismic inversion has proved to be an effective method to accurately describe the subsurface properties with complex geological structures. Different from traditional algorithms, the seismic slope attribute plays a crucial role here. It is equivalent to an important geological structure-guided constraint, which is unprecedented in traditional algorithms. In practical applications, the seismic slope attribute can be extracted from post-stack seismic profiles, images, and inversion results. Here, the slope attribute is introduced to the inversion in two aspects, i.e., initial model building and regularization. These two aspects correspond to the low-frequency, mid-frequency, and high-frequency components of the seismic data. Both of them are vital components in the seismic inversion.

The initial model building determines the background trend of properties in the inversion results. Due to the lack of low-frequency information, such a trend can not be adjusted in subsequent inversion processing. Therefore, the establishment of an accurate low-frequency model is a difficult problem in the inversion of complex geological structure conditions. The proposed model building algorithm with the seismic slope attribute as a constraint perfectly solves this problem. However, we can find that both the number of wells and the quality of seismic data are the key factors affecting the accuracy of constructed geological models that are too complex.

With respect to the regularization, the proposed DTV regularization method overcomes the defects of the traditional single-trace method. The data association is established through geological structure guidance. By considering the local structural directions of the spatial gradient and their weights according to the local slope attribute, the DTV regularization achieves a better result compared to the $\ell _{2}$-norm regularization and the conventional TV regularization.

7 Conclusions

Here we review the application of the seismic slope attribute in two specific aspects of the prestack inversion algorithm. On the one hand, the seismic slope attribute can be exploited as a lateral constraint when building the starting model. The initial model is constructed by interpolating the well logs based on the shaping regularization framework. In the well-log interpolation method, there is no need to manually interpret any horizons or faults throughout the modeling process, which not only avoids manual interpretation errors, but also reduces labor workload. On the other hand, the seismic slope attribute can be introduced into the AVA inversion objective function, through a DTV regularization penalty to improve the resolution and lateral continuity of the inversion results. The inversion results of the synthetic and real seismic data demonstrate the superiority of the new prestack inversion framework. Taking advantage of the data-driven starting model building approach and DTV regularization algorithm, the resulted hybrid inversion framework inverts the subsurface properties with higher resolution (in both horizontal and vertical directions) and more robust performance in geologically complex structures.

Appendices

Appendix A: The Exact Zoeppritz Equation

Without loss of generality, the forward problem of seismic wave propagation can be expressed as a nonlinear equation as follows:

$$\begin{aligned} \mathbf{d }=\mathbf{G }(\mathbf{m }). \end{aligned}$$

(A.1)

According to the convolution theory, the seismic data can be considered as the convolution between the stationary wavelet and reflectivity: Then, the P–P seismic data can be simulated by convolving the P–P reflectivity coefficient with the stationary wavelet as:

$$\begin{aligned} \mathbf{d }=\mathbf{W }\mathbf{R }(\mathbf{m }). \end{aligned}$$

(A.2)

With respect to the prestack seismic inversion, the reflectivity coefficients can be obtained by the Zoeppritz’s equation. When a plane-wave propagates onto a surface, according to the Zoeppritz’s equation, the reflection and transmission coefficients can be expressed as:

$$\begin{aligned} \mathbf{AR} =\mathbf{B }, \end{aligned}$$

(A.3)

where

$$\begin{aligned} \mathbf{A }= & {} \begin{bmatrix} \sin \theta _{1} &{} \cos \phi _{1} &{} -\sin \theta _{2} &{} \cos \phi _{2}\\ \cos \theta _{1} &{} -\sin \phi _{1} &{} \cos \theta _{2} &{} \sin \phi _{2}\\ \sin 2\phi _{1} &{} -\frac{V_{s1}}{V_{p1}}\sin 2\phi _{1} &{} -\frac{\rho _{2}V_{p2}}{\rho _{1}V_{p1}}\cos 2\phi _{2} &{} -\frac{\rho _{2}V_{p2}}{\rho _{1}V_{p1}}\sin 2\phi _{2}\\ \sin 2\theta {1} &{} \frac{V_{p1}}{V_{s1}}\sin \phi _{1} &{} \frac{\rho _{2}V_{s2}^{2}V_{p2}}{\rho _{1}V_{s2}^{2}V_{p1}}\cos 2\phi _{2} &{} -\frac{\rho _{2}V_{s2}V_{p1}}{\rho _{1}V_{s1}^{2}}\sin 2\phi _{2}\\ \end{bmatrix},\quad \mathbf{R }= \begin{bmatrix} R_{pp}\\ R_{ps} \\ T_{pp} \\ T_{ps} \end{bmatrix},\nonumber \\ \mathbf{B }= & {} \begin{bmatrix} -\sin 2\theta \\ \cos 2\theta \\ -\cos 2\phi \\ \sin 2\phi \end{bmatrix} \end{aligned}$$

(A.4)

where ${\textit{v}_{p1}}$, ${\textit{v}_{s1}}$, and ${\rho _{1}}$ denote the elastic parameters of the upper layers, and ${\textit{v}_{p1}}$, ${\textit{v}_{s1}}$, and ${\rho _{2}}$ correspond to the counterpart of the lower layers, $\theta _{1}$ and $\phi _{1}$ are the angles of the P- and S-wave reflections, and $\theta _{1}$ and $\phi _{1}$ stand for the angles of P- and S-wave transmissions.

The partial derivative with respect to the parameter m can be expressed as:

$$\begin{aligned}&\frac{\partial \mathbf{R }}{\partial \mathbf{m }}=\mathbf{A }^{-1}\left( \frac{\partial \mathbf{B }}{\partial \mathbf{m }}-\frac{\partial \mathbf{A }}{\partial \mathbf{m }}\mathbf{R }\right) , \end{aligned}$$

(A.5)

$$\begin{aligned}&\begin{aligned} \frac{\partial \mathbf{A }}{\partial \textit{V}_{p1}}&=\frac{1}{V_{p1}}\cdot \\&\begin{bmatrix} 0&{}\tan \phi \sin \phi _{1} &{}\sin \theta _{2} &{}\tan \phi _{2}\sin \phi _{2}\\ 0&{}\sin \phi _{1} &{}\sin \theta _{2}\tan \theta _{2}&{}-\sin \phi _{2}\\ 2(1-\cos 2\phi _{1})&{}(2-\tan ^{2}\phi _{1})\frac{V_{s1}}{V_{p1}}\sin 2\phi _{1} &{}\frac{\rho _{2}}{\rho _{1}}\frac{V_{p2}}{V_{p1}}(3\cos 2\phi _{2}-2) &{}(2-\tan ^{2}\phi _{2})\frac{\rho _{2}}{\rho _{1}}\frac{V_{s2}}{V_{p1}\sin 2\phi _{2}}\\ 0&{}\frac{V_{p1}}{V_{s1}}(2-\cos 2\phi _{1})&{} \frac{\rho _{2}}{\rho _{1}}\frac{V^{2}_{s2}}{V^{2}_{s1}}\frac{V_{p1}}{V_{p2}} \sin 2\theta _{2}\tan ^{2}\theta _{2}&{}\frac{\rho _{2}V_{p1}V_{s2}}{\rho _{1} V^{2}_{s1}}(\cos 2\phi _{2}-2) \end{bmatrix}, \end{aligned}\nonumber \\ \end{aligned}$$

(A.6)

$$\begin{aligned}&\frac{\partial \mathbf{A }}{\partial \textit{V}_{s1}}=\frac{1}{V_{s1}} \begin{bmatrix} 0&{}-\tan \phi _{1}\sin \phi _{1}&{}0&{}0\\ 0&{}-\sin \phi _{1}&{}0&{}0\\ 4\sin ^{2}\phi _{1}&{}(\tan ^{2}\phi _{1}-2)\frac{V_{s1}}{V_{p1}}\sin 2\phi _{1}&{}0&{}0\\ 0&{}\frac{V_{p1}}{V_{s1}}(\cos 2\phi _{1}-2)&{}-2\frac{\rho _{2}V^{2}_{s2} V_{p1}}{\rho _{1}V^{2}_{s1}V_{p2}}\sin 2\theta _{2}&{}2\frac{\rho _{2}}{\rho _{1}} \frac{V_{s2}V_{p1}}{V^{2}_{s1}}\cos 2\phi _{2} \end{bmatrix} \end{aligned}$$

(A.7)

$$\begin{aligned}&\frac{\partial \mathbf{A }}{\partial {\rho }_{1}}=\frac{1}{\rho _{1}} \begin{bmatrix} 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}\frac{\rho _{2}}{\rho _{1}}\frac{V_{p2}}{V_{p1}}\cos 2\phi _{2}&{} \frac{\rho _{2}}{\rho _{1}}\frac{V_{s2}}{V_{p1}}\sin 2\phi _{2}\\ 0&{}0&{}-\frac{\rho _{2}}{\rho _{1}}\frac{V^{2}_{s2}}{V^{2}_{s1}} \frac{V_{p2}}{V_{p1}}\sin 2\theta _{2}&{}\frac{\rho _{2}}{\rho _{1}} \frac{V_{s2}V_{p1}}{V^{2}_{s1}}\cos 2\phi _{2}\\ \end{bmatrix}, \end{aligned}$$

(A.8)

$$\begin{aligned}&\frac{\partial \mathbf{A }}{\partial \textit{V}_{p2}}=\frac{1}{V_{p2}} \begin{bmatrix} 0&{}0&{}-\sin \theta _{2}&{}0\\ 0&{}0&{}-\sin \theta _{2}\tan \theta _{2}&{}0\\ 0&{}0&{}-\frac{\rho _{2}}{\rho _{1}}\frac{V_{p2}}{V_{p1}}\cos 2\phi _{2}&{}0\\ 0&{}0&{}-\frac{\rho _{2}}{\rho _{1}}\frac{V^{2}_{s2}}{V^{2}_{s1}} \frac{V_{p1}}{V_{p2}}\sin 2\theta _{2}\tan ^{2}\theta _{2}&{}0\\ \end{bmatrix}, \end{aligned}$$

(A.9)

$$\begin{aligned}&\frac{\partial \mathbf{A }}{\partial \textit{V}_{s2}}=\frac{1}{V_{s2}} \begin{bmatrix} 0&{}0&{}0&{}-\tan \phi _{2}\sin \phi _{2}\\ 0&{}0&{}0&{}\sin \phi _{2}\\ 0&{}0&{}2\frac{\rho _{2}}{\rho _{1}}\frac{V_{p2}}{V_{p1}}(1-cos2\phi _{2}) &{}\frac{\rho _{2}}{\rho _{1}}\frac{V_{s2}}{V_{p1}}\sin 2\phi _{2}(2\tan ^{2}\phi _{2}-2)\\ 0&{}0&{}\frac{\rho _{2}}{\rho _{1}}\frac{V^{2}_{s2}}{V^{2}_{s1}}\frac{V_{p1}}{V_{p2}} \sin 2\theta _{2}&{}-\frac{\rho _{2}}{\rho _{1}}\frac{V_{p1}V_{s2}}{V^{2}_{s1}}(2+3\cos \phi _{2}) \end{bmatrix}, \end{aligned}$$

(A.10)

$$\begin{aligned}&\frac{\partial \mathbf{A }}{\partial {\rho }_{1}}=\frac{1}{\rho _{2}} \begin{bmatrix} 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}-\frac{\rho _{2}}{\rho _{1}}\frac{V_{p2}}{V_{p1}}\cos 2\phi _{2} &{}-\frac{\rho _{2}}{\rho _{1}}\frac{V_{s2}}{V_{p1}}\sin 2\phi _{2}\\ 0&{}0&{}\frac{\rho _{2}}{\rho _{1}}\frac{V^{2}_{s2}}{V^{2}_{s1}}\frac{V_{p2}}{V_{p1}} \sin 2\theta _{2}&{}-\frac{\rho _{2}}{\rho _{1}}\frac{V_{s2}V_{p1}}{V^{2}_{s1}}\cos 2\phi _{2}\\ \end{bmatrix}, \end{aligned}$$

(A.11)

$$\begin{aligned}&\frac{\partial \mathbf{B }}{\partial \textit{V}_{p1}}=\frac{1}{V_{p1}} \begin{bmatrix} 0&0&-4sin^{2}\phi _{1}&0 \end{bmatrix}^{T},\qquad \frac{\partial \mathbf{B }}{\partial \textit{V}_{p2}}=\frac{\partial \mathbf{B }}{\partial \textit{V}_{s1}}=\frac{\partial \mathbf{B }}{\partial \textit{V}_{s2}}=\frac{\partial \mathbf{B }}{\partial \rho _{1}}=\frac{\partial \mathbf{B }}{\partial {\rho }_{2}}=\begin{bmatrix} 0&0&0&0 \end{bmatrix}^{T}, \end{aligned}$$

(A.12)

Appendix B: The Hertz–Mindlin Model

The Hertz–Mindlin contact model (Mindlin 1949) calculates the bulk and shear modulus of two spherical grains in contact. It appears to be the most commonly used contact model to describe seismic parameter changes caused by the pressure changes (Dadashpour et al. 2007). Although the Hertz–Mindlin contact model is proved to be only applicable to perfect elastic contacts of spherical bodies, it works fairly well for sandstones (Avseth et al. 2005). According to he Hertz–Mindlin theory, the effective bulk modulus and shear modulus of a dry random identical sphere packing can be expressed as

$$\begin{aligned}&\textit{K}_{H\text {-}M}=\left[ \frac{c^2(1-\phi _{c})^2G^2P_{\text {eff}}}{18\pi ^2(1-\nu )^2}\right] ^{\frac{1}{n}}, \end{aligned}$$

(B.1)

$$\begin{aligned}&\textit{G}_{H\hbox {-}M}=\frac{5-4\nu }{5(2-\nu )} \left[ \frac{3c^2(1-\phi _{c})^2G^2P_{\text {eff}}}{2\pi ^2(1-\nu )^2}\right] ^{\frac{1}{n}}, \end{aligned}$$

(B.2)

where $\textit{K}_{H\text {-}M}$ and $\textit{G}_{H\text {-}M}$ indicate the bulk and shear modulus calculated by the Hertz–Mindlin model, $\phi _{c}$ denotes critical porosity, $\textit{P}_{\text {eff}}$ represents the effective pressure, and $\textit{G}$ and $\nu$ are the shear modulus and Poisson’s ratio of the solid grains, respectively. n is the coordination number and c denotes the average number of contacts per sphere. In the original Hertz–Mindlin theory, n is equal to 3, which indicates that the variation in velocity is proportional to the 1/6 power of $\textit{P}_{\text {eff}}$.

Some laboratory measurements of samples gave a larger number for n. Vidal et al. (2000) found $\textit{n}=5.6$ for P-wave and $\textit{n}=3.8$ for S-wave for gas-saturated sands, while Landro et al. (2001) used $\textit{n}=5$ for oil-saturated sands.