Scoring and Testing Procedures Devoted to Probabilistic Seismic Hazard Assessment

Abstract

This review addresses long-term (tens of years) seismic ground-motion forecasting (seismic hazard assessment) in the presence of alternative computational models (the so-called epistemic uncertainty affecting hazard estimates). We review the different approaches that have been proposed to manage epistemic uncertainty in the context of probabilistic seismic hazard assessment (PSHA). Ex-ante procedures (based on the combination of expert judgments about inherent characteristics of the PSHA model) and ex-post approaches (based on empirical comparison of model outcomes and observations) should not be considered as mutually exclusive alternatives but can be combined in a coherent Bayesian view. Therefore, we propose a procedure that allows a better exploitation of available PSHA models to obtain comprehensive estimates, which account for both epistemic and aleatory uncertainty. We also discuss the respective roles of empirical ex-post scoring and testing of alternative models concurring in the development of comprehensive hazard maps. In order to show how the proposed procedure may work, we also present a tentative application to the Italian area. In particular, four PSHA models are evaluated ex-post against macroseismic effects actually observed in a large set of Italian municipalities during the time span 1957–2006. This analysis shows that, when the whole Italian area is considered, all the models provide estimates that do not agree with the observations. However, two of them provide results that are compatible with observations, when a subregion of Italy (Apulia Region) is considered. By focusing on this area, we computed a comprehensive hazard curve for a single locality in order to show the feasibility of the proposed procedure.

1 Introduction

The forecast of accelerations expected at a site during a future time span (the exposure time) of the order of tens of years (long-term seismic hazard assessment) plays a basic role in the definition of effective strategies for seismic risk reduction. Since available knowledge about the seismogenic process is presently inadequate to predict future seismic occurrences, several situations are considered as possible from the physical point of view. The major task of seismologists in this context is the assessment of the likelihood to be associated with each possible level of the seismic ground motion (the seismic scenario), i.e. to provide a probabilistic seismic hazard assessment (PSHA). This outcome is generally formalized in terms of probability distributions that associate with a scenario an exceedance probability during a given exposure time. For engineering purposes, these distributions are finally represented by a single value of ground shaking (such as reference values for the horizontal peak ground acceleration PGA _α ) that corresponds to a specific exceedance probability level α fixed as a function of the degree of conservativism considered as acceptable (Reiter 1990). This representation tends to mask the inherent probabilistic character of outcomes provided by PSHA computational models: actually, each of them can be seen as a ‘probability generator’ as defined by Lind (1996) and, consequently, its outcomes can be considered as ‘forecasts’ and not as ‘predictions’ by following De Finetti’s terminology (De Finetti 1974).

Since methodological improvements are much faster than data set upgrades, a number of different computational models devoted to PSHA have been proposed that are based on different assumptions and views of the seismogenic process. In general, PSHA can be performed by considering different pieces of information concerning both deterministic aspects (seismic sources location and geometry, geodetic strain field, etc.) and statistical evidence (past seismic history, magnitude-frequency distribution, etc.). Available models (e.g., Cornell 1968; McGuire 1978; Frankel 1995; Woo 1996; Pace et al. 2006; Bozkurt et al. 2007; D’Amico and Albarello 2008) mainly differ for the balance between deterministic and statistical evidence used in each case to evaluate the likelihood of the possible future seismic scenarios: in this view, no dichotomy exists between probabilistic and deterministic models (Bommer 2002). Anyway, several alternative PSHA computational models (in terms of basic assumptions, considered information, etc.) coexist, each ex-ante plausible and internally consistent, but resulting in quite different hazard estimates (see, e.g., Pace et al. 2011). Beside this multiplicity of alternative models, for some of them one must also consider the high sensitivity to empirical information that, in its turn, is characterized by high or poorly defined uncertainty (e.g., geometry of seismogenic sources and empirical attenuation relationships for the ground motion). This implies that, even adopting the same computational scheme, important differences in the final assessment can be induced by different choices concerning basic empirical information. In the following, we will consider each PSHA model as a whole, including computational aspects and data used to feed computations.

In general, uncertainty relative to the choice among alternative PSHA models and basic pieces of information is defined as epistemic to distinguish it from the one (aleatory) related to the inherent variability of the physical processes responsible for ground motion (Budnitz et al. 1997). In principle (De Finetti 1974), all sources of uncertainty are inherently epistemic in that they belong to the lack of knowledge of the observer and can be coherently expressed in terms of probability (see, e.g., O’Hagan and Oakley 2004). Thus, distinction between epistemic and aleatory uncertainty only has a heuristic value: while the second one is accounted within each PSHA model by introducing a suitable modelling of relevant aleatory processes, accounting for epistemic uncertainty requires a sort of meta-analysis with respect to each single model. This meta-analysis is mandatory since the presence of different PSHAs for the same area poses a number of problems to stakeholders responsible for political decisions and risk reduction strategies, who must choose among several apparently equivalent hazard evaluations.

Since probabilistic hazard models are of concern here, each resulting in a probability distribution associated with a ground-motion parameter (hazard curve), comparing them can also be seen as a typical probability scoring problem developed and applied in other contexts (e.g., Lind 1996). In the following, we will use the term scoring to indicate procedures devoted to evaluating epistemic uncertainty of competing PSHA models.

One can achieve scoring in two ways. The first one is ex-ante, that is by considering inherent properties of the PSHA model, i.e. its internal coherency and capability to take into account current knowledge about underlying physical process evaluated by panels of scientists. The second way is ex-post, that is by comparing outcomes of each PSHA model (‘forecasts’) with observations; it is incorrect to use the term validation for this kind of meta-analysis (Oreskes et al. 1994); the term empirical scoring will be preferred here. The problem of judging heuristic value of competing models (probabilistic or not) is quite general and has been also addressed by Lipton (2005). A major conclusion is that, despite the fact that ex-post tests based on the comparisons of forecasts and observations cannot be judged as inherently better, they can be considered as more robust against fudging.

Scoring is inherently different from empirical testing. Here, we will use this last term to indicate a procedure devoted to evaluate the absolute feasibility of an approach and results into a dichotomic outcome: the considered estimates are or are not compatible with observations to a confidence threshold. In principle, testing aims at identifying wrong PSHA models while scoring aims at comparing models each considered plausible.

In the following, we propose an attempt to go beyond the contraposition of ex-post/ex-ante and scoring/testing procedures and their essential complementary character will be enlightened. In Sects. 2 and 3, we will propose a unitary formalization to provide a comprehensive PSHA combining epistemic and aleatory uncertainty. Then, in Sects. 4 and 5, scoring and testing procedures proposed in the literature will be reviewed and discussed to enlighten relative advantages and drawbacks in the general frame outlined here. Lastly, we will describe an exemplary application of the proposed integrated approach to Italy.

2 A Generalized Frame for PSHA

We denote by H _i a generic ith PSHA model (including the computational scheme and the relevant pieces of information considered for the assessment). We assume that M of such models actually exist and that this set includes all the possible methodologies considered as plausible. Each hazard estimate relative to a ground-shaking parameter g (e.g., PGA, response spectrum ordinate and macroseismic intensity) deduced by using the i th model can be considered as a conditional probability in the form P(g|H _i ). Here, P is the probability that the threshold g will be reached or exceeded during a future earthquake occurred during the exposure time of interest. This conditional probability parameterizes aleatory uncertainty managed by the ith PSHA model. In this context, the unconditional hazard estimate P(g) can be given in the form

$$P\left( g \right) = \sum\limits_{i = 1}^{M} {Q\left( {H_{i} } \right)P\left( {g\left| {H_{i} } \right.} \right)}$$

(1)

where the probability Q(H _i) is the degree of belief associated with the procedure H _i . In this form, Q(H _i ) represents epistemic uncertainty.This formalization is defined ensemble forecasting by Marzocchi et al. (2012) and represents a rational merging procedure allowing one to include different aspects of the seismogenic process (differently accounted by the considered models) in a single forecasting.

Strictly speaking, Eq. (1) only holds in the case that one considers the M procedures as mutually exclusive and collectively exhaustive (the MECE criterion by following Bommer and Scherbaum 2008). Furthermore, this position implicitly assumes that one of the considered models may be the ‘true’ model, i.e. at least one model exists that is able to describe exhaustively what it is supposed to model (see, e.g., Burnham and Anderson 2002). However, one can note that the MECE condition can hardly be considered to hold. As concerns exhaustiveness, one should be aware that further PSHA models can exist in the grey literature not accessible to most researchers: not considering these PSHA models implies that Q(H _i ) = 0 is implicitly associated with each of them. More important is the lack of exclusiveness. In fact, most models share a number of features (e.g., seismotectonic zoning and seismic catalogue) and, thus, they are not mutually exclusive. A possibility accounting for correlation among forecasts provided by the considered models is proposed by Marzocchi et al. (2012). In general, one should be aware that in the presence of mutual dependence among the M models, P(g) defined in Eq. (1) anyway represents an upper bound for the unconditional probability (e.g., Gnedenko 1976). This implies that ensemble estimates provided by Eq. (1) include a certain degree of conservativism.

For engineering purposes, hazard relative to an exposure time of interest is generally expressed in terms of the ground shaking g _α (here addressed as a reference ground-motion threshold) associated with a fixed exceedance probability α such that

$$\alpha = P\left( {g_{\alpha } } \right)$$

(2)

In other terms, g _α is the reference ground motion representing a percentile of the ensemble probability distribution P(g) accounting for both aleatory and epistemic uncertainty associated with a set of PSHA models.

It is worth noting that the above formulation resulting in a single ensemble hazard curve allows some potential conceptual difficulties described by Bommer and Scherbaum (2008) to be overcome. These are inherent to the formulations currently adopted to manage epistemic and aleatory uncertainty. Commonly, a suite of hazard curves $P\left( {g\left| {H_{i} } \right.} \right)$ from a number of PSHA models is available, and this implies that a number of $g_{\alpha }^{i}$ values exist for a fixed value of α (or equivalently for a fixed average return time by following Bommer and Scherbaum 2008).

There are two ways to select a value accounting for the relevant epistemic uncertainty. The first is the one proposed above [Eq. (2)] by considering the percentile of the ensemble hazard curve P(g) from Eq. (1). The second one is based on the definition of a new discrete probability distribution $G\left( {g_{\alpha }^{i} } \right)$ over the domain of the M possible ground-shaking values $g_{\alpha }^{i}$, each representing the α percentile of the hazard function relative to a single ith PSHA model.

In this view, selecting a representative ground-shaking threshold implies the definition of a new percentile $g_{\alpha \beta }$ associated with a probability β such that $\beta = G\left( {g_{{\alpha \beta }} } \right)$.

It is worth noting that, in general, the reference ground-shaking value obtained in this way differs from the one obtained from Eq. (2). In fact, g _α and $g_{\alpha \beta }$ are the percentiles of two different distribution functions: g _α for P(g) (i.e. the unconditional hazard function) and $g_{\alpha \beta }$ for the discrete distribution $G\left( {g_{\alpha }^{i} } \right)$ relative to the percentiles associated with the set of conditional hazard functions P(g|H _i ) and with a fixed exceedance probability α.

This way of combining epistemic (Q) and aleatory (P) uncertainty, however, makes a correct interpretation of the outcome difficult. What is the exceedance probability associated with this value: α, β or a combination of these values? This ambiguity is inherent to the splitting of aleatory and epistemic uncertainties into two levels of ontologically different probabilities and to the lack of a clear and formally coherent combination of probability distributions relative to both kinds of uncertainty. The formulation here proposed avoids this drawback, since epistemic uncertainty is fully included in the estimate of g _α via Eqs. (1) and (2). In Fig. 1, one can see a theoretical example showing relationships among P(g), P(g|H _i ), g _α and $g_{\alpha \beta }$.

Fig. 1

Comparison between the unconditional hazard curve P(g) computed by Eq. (1) and hazard curves obtained from different models (H1, H2, H3, H4). In this theoretical example, the Q values of 0.1, 0.3, 0.2 and 0.4 have been assumed for epistemic uncertainty associated with the models H1, H2, H3 and H4, respectively. The quantiles relative to an exceedance probability α = 0.1 have also been indicated by following the two possible approaches described by Bommer and Scherbaum (2008): the one (g _α ) deduced from the approach proposed here [Eqs. (1), (2)] and the one (g _αβ ) determined by the alternative approach with β = 0.5 (see text for details)

3 Scoring and Testing PSHA Outcomes

By considering the definition of the ensemble hazard estimate in Eq. (1) and the fact that each term P(g|H _i ) is entirely defined in the frame of the single ith computational scheme H _i , the final PSHA outcome P(g) relies on the estimation of the values attributed to the likelihoods Q(H _i ). Scoring PSHA procedures aims at assessing Q(H _i ) values, and this can be achieved by considering expert judgement or numerical modelling (the ex-ante approach) or from the comparison of PSHA outcomes with observations (the ex-post approach). These two approaches, however, should not be considered as alternative, and their complementary character can be made evident in the frame of a Bayesian view considered by Marzocchi et al. (2012) and others (see also Humbert and Viallet 2008; Viallet et al. 2008; Selva and Sandri 2013).

In this view, the reliability of each PSHA procedure Q(H _i ) after the set of S seismic occurrences e _S is known (the ‘evidence’ E) can be expressed in terms of a conditional probability Q(H _i |E). In this condition, the Bayes theorem holds by stating that

$$Q\left( {H_{i} } \right) = Q\left( {H_{i} \left| E \right.} \right) = \frac{1}{K}\,Q^{*} \left( {H_{i} } \right)\,Q\left( {E\left| {H_{i} } \right.} \right)$$

(3)

In this formalization, Q(H _i |E) is the ex-post reliability evaluation of the PSHA model H _i and Q ^*(H _i ) is the prior degree of belief associated with H _i and corresponds to the ex-ante evaluation. The term Q(E|H _i ) represents the likelihood of the evidence E in the case that the H _i model is applied. This term actually represents the probability that the model H _i explains the evidence E: in other words, it is the forecast of the model about that specific observed scenario. The factor K is a normalization factor that is constant for the whole set of considered possible PSHA models.

The above formalization enlightens the fundamental and complementary role played by both ex-post evaluations of performances of the models H _i [through the likelihood Q(E|H _i )]) and ex-ante evaluations [through the term Q ^*(H _i )] to provide an hazard estimate able to capture both aleatory and epistemic uncertainty and also taking advantage by including a set of PSHA models. By including Eq. (3) into Eq. (1), one has

$$P\left( g \right) = \frac{1}{K}\sum\limits_{i = 1}^{M} {Q^{*} \left( {H_{i} } \right)Q\left( {E\left| {H_{i} } \right.} \right)P\left( {g\left| {H_{i} } \right.} \right)}$$

(4)

The hazard estimate P(g) from Eq. (4) is here defined a comprehensive hazard estimate. If M mutually exclusive competing PSHA models exist and that this set is complete, one has

$$K = \sum\limits_{i = 1}^{M} {Q^{*} \left( {H_{i} } \right)Q\left( {E\left| {H_{i} } \right.} \right)}$$

(5)

Generally, this factor could be difficult to know (e.g., Gelman et al. 1995) but, as suggested by Marzocchi et al. (2012), the tentative normalization in Eq. (5) can also be adopted if one interprets Q(H _i |E) as the ex-post probability that the H _i model is the best among as a set of candidate models.

In the case that the relative effectiveness of the considered hazard models is of concern only, a ‘Bayes factor’ can be defined as

$$B_{ij} = \frac{{Q\left( {H_{i} \left| E \right.} \right)}}{{Q\left( {H_{j} \left| E \right.} \right)}} = \;\frac{{Q^{*} \left( {H_{i} } \right)\;Q\left( {E\left| {H_{i} } \right.} \right)}}{{Q^{*} \left( {H_{j} } \right)\;Q\left( {E\left| {H_{j} } \right.} \right)}}$$

(6)

(Kass and Raftery 1995) that is independent of K and allows the evaluation on an empirical basis and ex-ante evaluations of the relative effectiveness of one ith computational model against the jth other (the ‘skill’ in the terminology proposed by Marzocchi et al. 2012). Bayes factors in Eq. (6) can be useful to evaluate the relative role of each PSHA model contributing to the comprehensive hazard estimate in Eq. (4).

Whatever the definition of K is, a basic problem of the Bayes formulation is that it provides a comprehensive estimate P(g) also in the case that none of the PSHA models considered provide realistic results. Thus, one can evaluate (test) in advance the reliability of each single model, before applying Eq. (5). Such testing can be performed ex-post by comparing forecasts provided by each PSHA model with a set of observations (e.g., Schorlemmer et al. (2007)).

Testing presents a number of specific problems discussed by Marzocchi et al. (2012). One among the others concerns the definition of a specific (and conventional) significance threshold for considering a PSHA model not compatible with observations. By following Box and Draper (1987): ‘how wrong any model has to be not to be useful?’. In the view presented here, the importance of testing should not be emphasized too much. Actually, the basic aim of testing is only the preliminary evaluation if at least one of the considered PSHA models is compatible with observations, i.e. it is not explicitly rejected (at a significance level) when compared with observations. In this frame, committing type-II error (i.e. accepting the null hypothesis when it is wrong) is less important than committing type-I error (rejecting the null hypothesis when it is correct), which corresponds to wrogly exclude from the comprehensive hazard estimate a model actually able to capture correctly specific features of the seismogenic process. Thus, relatively low-power tests are acceptable for the empirical testing of PSHA models. On the other hand, when considered in the weighting structure of Eq. (4), one can expect that relative importance of an empirically weak model is downsized by the respective Q(H _i |E) value.

Despite the fact that some similarity exists between scoring and testing procedures, we will review them separately to clarify respective specificities and similarities.

4 Ex-ante Scoring

4.1 Logic Tree

In the seismological practice, the ex-ante approach has led to the formulation of the logic tree, that is the most widely used tool to elicit epistemic uncertainty (see, e.g., Kulkarni et al. 1984; Coppersmith and Youngs 1986; Reiter 1990; Budnitz et al. 1997).

The concept of the logic tree is very simple: for each input element, branches are set up for different aspects of the considered PSHA models (e.g., probability distribution for earthquake inter-event times, magnitude-frequency distribution and ground-motion predictive equation). Weights are thus assigned to each branch by considering expert judgements to reflect the relative confidence that the analyst has in each model being the best representation of that component of the hazard input. The weights on branches originating from a single node of the logic tree are assigned to sum to unity because they are subsequently used as probabilities (likelihoods) associated with a specific realization (branch) of the considered PSHA procedure.

This approach is in principle appealing and apparently ‘democratic’ since it allows the combination of different opinions by a panel of experts. However, it leaves completely unresolved the issue of assessing each of these opinions, that is completely ex-ante with respect to the final outcome of the PSHA model, and only depends on the degree of belief attributed to the opinions of each expert in the panel (and ultimately to the expert himself).

The whole procedure has been often applied without a thorough discussion of the underlying principles and interpretations (Bommer and Scherbaum 2008). On the other hand, a coherent interpretation is mandatory for its correct application. In fact, ‘Although this seems to be a philosophical issue at first glance, its consequences are not, since the issue is intimately linked to the question of which hazard curve should be used’ (Scherbaum et al. 2005; Abrahamson and Bommer 2005). Bommer and Scherbaum (2008) have examined the most important methodological fallacies attributable to a wrong use of logic trees.

An important problem for the logic-tree approach can be the cost-benefit ratio. In order to allow a coherent interpretation of the logic tree in the frame of probability theory, MECE conditions must hold (Bommer and Scherbaum 2008): one has to consider all possibilities and these must be mutually exclusive. To reduce efforts (and expenses), one can consider incomplete relatively small trees that only account for a limited number of alternatives. This situation requires the agreement of all experts in excluding an alternative considered ex-ante totally unreliable, and this can be the source of endless discussions in the relevant scientific community that potentially weaken outcomes of this logic-tree analysis. Otherwise, one can involve large panels of experts and construct enormous logic trees made of thousands of branches (e.g., Abrahamson et al. 2002). This, however, may provide unmanageable outcomes, by requiring some form of Monte Carlo exploration for eliciting relevant epistemic uncertainty (e.g., Musson 2000; Bradley et al. 2012); this also enhances the problem of the mutual dependency of the considered models. Preliminary sensitivity analyses focusing on outcomes instead of single elements of the procedures may help to reduce a dangerous proliferation of branches (Bommer and Scherbaum 2008).

In any case, the logic tree remains a controversial tool producing harsh disputes that involved a number of researchers (see Krinitzky 1993; 1995; Klügel 2005; Musson et al. 2005; Page and Carlson 2006).

Possibly, most of the difficulties disappear if one considers the logic tree not as a coherent formal approach to elicit epistemic uncertainty but just a tool aiming at facilitating panel discussion and the quantitative expression of expert judgements in a probabilistic language. Actually, the logic-tree procedure does not quantify the variability on the physical parameter itself but the variability on expert opinion (Viallet et al. 2008).

This last view should not be considered as reductive with respect to the actual importance of expert discussions and evaluations. When the internal coherency of the logic-tree outcome, i.e. the condition

$$\sum\limits_{i = 1}^{M} {Q^{*} \left( {H_{i} } \right)} = 1$$

(7)

is fulfilled, the logic tree may effectively provide prior probabilities to be used as a first step for the prior scoring of PSHA models (see Eq. (3)).

4.2 Numerical Simulations

A different ex-ante approach has been proposed (Grandori 1993; Grandori et al. 1998; 2004; 2006), which is based on the analysis of the outcomes provided by each PSHA model when fed by synthetic seismic catalogues assumed representative of the ‘true’ seismicity. The major outcome of this approach is the comparative evaluation of robustness of PSHA models against deviations from the relevant input reference model. In practice, as each procedure is based on a specific seismicity model, one aims at evaluating the performances of each procedure when data used for its parameterization do not fit the input model. In the applications proposed so far, this approach only resulted in generic considerations about the adequacy of a model and no explicit evaluation of the relevant Q ^*(H _i ) values was provided.

5 Ex-post Scoring and Testing

The ex-post perspective leads to the development of classes of procedures that in the literature are known as scoring rules (see, e.g., Winkler 1996; Johnstone 2007). An outstanding example of scoring procedures in the field of Earth Sciences was the early one proposed by Brier (1950) to evaluate weather forecasts (see also, Sanders, 1967). Beauval (2011) has provided a first review of ex-post testing in the field of PSHA.

In general, ex-post procedures are based on the direct comparison of probabilistic outcomes of the relevant PSHA model with empirical observations concerning what actually occurred during a control time period. In the case of time-independent PSHA estimates, one can choose on purpose any control period. This is not the case for time-dependent hazard estimates, which require as a control period the specific time interval involved in the considered forecast. The relationship between the learning data set (i.e. the sample of data considered to parameterize the PSHA model) and the control data set used for scoring or testing is a critical aspect in that their mutual independency should be warranted. However, in most cases, the parameterization of PSHA models cannot ignore most recent information. An example in this sense is the definition of seismogenic sources considered in the PSHA Cornell–McGuire computational scheme (Cornell 1968; McGuire 1978) that can be considered as ‘standard’ in the common PSHA practice. This problem reduces in some way the feasibility of such forward comparison. An alternative possibility is to perform backward evaluations, by comparing forecasts with past observations, i.e. by using as the control data set information in some way included in the model. This could bias results in favour of the PSHA model. When one considers for testing backward comparison, the statistical significance of discrepancy eventually revealed between forecasts and observations is an upper bound of the actual significance. If, even in this case, the discrepancies reveal to be significant (e.g., with respect to a fixed significance threshold), the eventual rejection of the model under study could be considered as safe.

The further problematic aspect concerns the choice of observables one uses for testing and scoring. Although non-seismometric observables might be considered (see, e.g., Brune 1996; Anooshehpoor et al. 2004), past seismicity (in terms of observed earthquake rates, maximum ground-shaking levels, etc.) represents the most important benchmark for testing hazard estimates.

The most straightforward approach to score PSHA models is obviously the direct comparison with observations relative to the ground-shaking parameters considered in the probabilistic forecast. These parameters are generally those of engineering interest and are mainly instrumental (e.g., PGA). At least for Italy, reliable accelerometric data are available for about 40 years at a number of sites (Luzi et al. 2008; Pacor et al. 2011). On the other hand, PSHA models aim at forecasting potentially damaging earthquakes, i.e. those characterized by larger magnitudes. In low seismicity areas, these events have very low probabilities of occurrence for exposure times of the order of tens of years. This makes empirical testing quite problematic when single sites are considered (Beauval et al. 2008; Iervolino 2013). Mak et al. (2014) report a discussion concerning the power of such tests in most common situations.

To overcome this problem, two approaches have been proposed. The first one is performing an area-based test (Ward 1995). In this case, a number of sites are examined for the same exposure time. The basic idea is that such sample can be considered as a multiple realization of the same process. Depending on the characteristics of the model of concern, ergodicity can be assumed or not to evaluate relevant statistics. The second possibility is using macroseismic information. This kind of data is largely available in many countries (Italy, at first), by covering the whole territory for hundreds of years (e.g., Usami 2003; Locati et al. 2011; Mezcua et al. 2013a). This database, eventually integrated by instrumental data suitably rescaled (e.g., Mezcua et al. 2013b), could thus represent an important benchmark for a PSHA model due to its wide space/time coverage. In both cases, one must consider specific statistics for scoring and testing.

5.1 Scoring

In the general frame here proposed, the most natural approach to scoring is using likelihood. Given the PSHA model H _i and the set of S sites where ground shaking has been monitored during the control interval Δt ^*, the model’s likelihood can be estimated from the control sample E _{Δt *} (the evidence) of seismic occurrences e _s at each of the S sites. Such occurrences concern probabilistic forecasts provided by the PSHA model (e.g., overcoming of a PGA threshold during the control interval). In general, one has

$$Q\left( {E\left| {H_{i} } \right.} \right) = c_{i} L_{i}$$

(8)

where L _i is the probability that the PSHA model attributes to the single configuration of observed seismic occurrences and the coefficient c accounts for number of possible equivalent combinations of occurrences in the model considered.

If the expected seismic occurrences e _s are mutually independent (in the ith PSHA model of concern) and if, over the duration of the control period, at N _i out of S sites the forecast was fulfilled, then we have

$$L_{i} = \left\{ {\prod\limits_{s = 1}^{{N_{i} }} {P\left( {e_{s} \left| {H_{i} } \right.} \right)} } \right\}\left\{ {\prod\limits_{{s = N_{i} + 1}}^{S} {\left[ {1 - P\left( {e_{s} \left| {H_{i} } \right.} \right)} \right]} } \right\}$$

(9)

where P(e _s |H _i ) is the probability that the ith model associates with the occurrence e _s at the sth site. When all occurrences have the same probability in the ith model, one has

$$c_{i} = \frac{{N_{i} !}}{{\left( {N_{i} - S} \right)!S!}}$$

(10)

It is worth noting that the reliability of the hypothesis of mutual independence of the considered occurrences e _s has to be evaluated in the frame of the considered PSHA model: Q(E|H _i ) is a feature of the model H _i and not of the seismogenic process to be modelled.

As an example, in the case that the ground-motion parameter considered for hazard assessment is PGA, S could be the number of accelerometric stations permanently active during Δt ^*. One can keep as fixed the probability of exceedance α within an exposure time of duration Δt = Δt ^* for all the sites (e.g., 0.1), and the corresponding values of ground shaking g _si are determined at each sth site from the ith PSHA model. Then, the number N of stations where at least one event with ground shaking exceeding g _si has occurred during Δt ^* is computed and, finally, the value of L _i can be derived from Eq. (9).

5.2 Testing by the Likelihood Approach

Likelihood has been recently applied for testing short-term (e.g., Schorlemmer and Gerstenberger 2007; Schorlemmer et al. 2007; Zechar et al. 2010) and long-term (Albarello and D’Amico 2008) earthquake forecasting. The basis of this testing procedure is the definition of the support l _i to the ith PSHA procedure that is defined in form

$$l_{i} = \log (L_{i} )$$

(11)

and L _i is the same as in Eq. (8). One can consider this statistics as a minimal sufficient statistics for the ith model and the relevant evidence (Edwards 1972). If the conditions of Eq. (9) hold, one has

$$l_{i} = \sum\limits_{s = 1}^{{N_{i} }} {\log \left[ {P\left( {e_{s} \left| {H_{i} } \right.} \right)} \right]} + \sum\limits_{{s = N_{i} + 1}}^{S} {\log \left[ {1 - P\left( {e_{s} \left| {H_{i} } \right.} \right)} \right]}$$

(12)

That reduces to

$$l_{i} = N_{i} \log \left( \alpha \right) + \left( {S - N_{i} } \right)\log \left( {1 - \alpha } \right)$$

(13)

when P(e _s |H _i ) = α are equal. The larger the support, the larger is the probability that what has been observed during the control period is the result of a stochastic process whose features are captured by the computational model H _i . If l _i is the support value relative to the observed control set and the ith PSHA model, then the random quantity

$$Z_{i} = \frac{{l_{i} - \mu_{i} \left( l \right)}}{{\sigma_{i} \left( l \right)}}$$

(14)

is asymptotically distributed as the standard Gauss distribution (Kagan and Jackson 1994). In the case that P(e _s |H _i ) = α and occurrences are mutually independent, expectation of the random variable l _i only depends on N _i that is Bernoullian variable with expectation Sα and variance Sα (1−α). In this situation, one has

$$\mu \left( l \right) = S\left[ {\alpha \,\log \left( \alpha \right) + \left( {1 - \alpha } \right)\log \left( {1 - \alpha } \right)} \right]$$

(15)

and

$$\sigma \left( l \right) = \left[ {\log \left( \alpha \right) - \log \left( {1 - \alpha } \right)} \right]\sqrt {S\alpha \left( {1 - \alpha } \right)}$$

(16)

Dependance of μ(l) and σ(l) on α is shown in Fig. 2. When Eqs. (15) and (16) hold, one has

$$Z_{i} = \frac{{N_{i} - S\alpha }}{{\sqrt {S\alpha \left( {1 - \alpha } \right)} }}$$

(17)

Fig. 2

Expected value and standard deviation of the support l _i [Eqs. (15) and (16)] as a function of the exceedance probability α when S = 100

In general, negative Z values indicate that ith model overestimated the hazard since the actual number of exceedances is lower than the observed one. The reverse is true for positive Z values. One could consider the outcomes of the ith model not supported by observation when $\left| {Z_{i} } \right| > 2$.

Rhoades et al. (2011) proposed a similar approach to test seismicity rates (T test).

5.3 Testing by the Counting Approach

In general, this method is based on the comparison of the expected and the observed frequency of occurrences relative to any seismic observable (Albarello and D’Amico 2005; Rhoades et al. 2008; Fujiwara et al. 2009). A number of authors applied this approach for testing seismic hazard estimates (Ordaz and Reyes 1999; Dowrick and Cousins 2003; Stirling and Petersen 2006; Stirling and Gerstenberger 2010; Gerstenberger and Stirling 2011; Mezcua et al. 2013b). To this purpose, they analysed at a number of sites the statistics

$$Z_{\text{si}} = \frac{{N_{s} \left( {g_{0} } \right) - F_{\text{si}} \left( {g_{0} } \right)}}{{\sqrt {F_{\text{si}} \left( {g_{0} } \right)} }}$$

(18)

where N _s (g ₀) is the observed number of times that a ground-motion threshold g ₀ is overcome at the sth site during the control interval Δt ^* and F _si (g ₀) ≈ Δt ^* λ _si (g ₀), with λ _si (g ₀) representing the exceedance rate of g ₀ deduced from the considered ith PSHA model at the sth site. Values in Eq. (18) that are much lower than −1 or much larger than 1, respectively, indicate that the PSHA model tends to overestimate or underestimate the actual hazard level of the site under study. A similar approach, based on different observables (i.e. inter-event times), was used by Mucciarelli et al. (2000; 2006).

In order to obtain a more comprehensive evaluation of a hazard map as a whole, Humbert and Viallet (2008) consider the overall number of times that a ground-motion threshold g ₀ is exceeded at all the S sites where an accelerometric station is available for the time period considered for testing. In this case, Eq. (18) can be used by substituting F _i (g ₀) with

$$\overline{F}_{i} \left( {g_{0} } \right) = \sum\limits_{s = 1}^{S} {F_{si} \left( {g_{0} } \right)}$$

(19)

where F _si is the number of occurrences at the sth station expected on the basis of the ith PSHA model. In the same way, N(g ₀) becomes the overall number of times that g ₀ was exceeded during the control period. To take into account possible mutual dependence of occurrences at the considered sites, Humbert and Viallet (2008) also suggest increasing the SD of the relevant distribution of occurrences by a factor that they estimated by Monte Carlo simulations.

A slightly different statistical procedure was adopted by McGuire (1979), McGuire and Barnhard (1981) and Albarello and D’Amico (2008). One can formalize this last approach as follows.

A binary variable e _s (g ₀) is defined which assumes the value of 1 in case that during the control interval Δt ^* (which has the same extension of the hazard exposure time Δt) at least one earthquake occurred producing a ground motion in excess of g ₀ at the sth site; otherwise, e _s (g ₀) = 0. The control sample E _Δt* is defined as the set of realizations of the variable e _s (g ₀) at S sites. The ith considered PSHA model H _i provides a probability P(e _s |H _i ) = P _si for the case e _s (g ₀) = 1.

The number N of sites that are expected to experience at least one earthquake during Δt ^* with ground shaking >g ₀ when the ith PSHA model holds is

$$\mu_{i} \left( N \right) = \sum\limits_{s = 1}^{S} {P_{\rm si} }$$

(20)

In the hypothesis that the realizations of the binary variable e _s (g ₀) are mutually independent (in the PSHA model of concern), one has

$$\sigma_{i} \left( N \right) = \sqrt {\sum\limits_{s = 1}^{S} {P_{\text{si}} \left( {1 - P_{\text{si}} } \right)} }$$

(21)

When S is relatively large, the Lyapunov variant of the central limit theorem (e.g., Gnedenko 1976) implies that

$$Z_{i} = \frac{{N - \mu_{i} \left( N \right)}}{{\sigma_{i} \left( N \right)}}$$

(22)

follows the standard Gauss distribution: negative Z values indicate that the ith model overestimated hazard, since the actual number of exceedances is lower than the observed one. The reverse is true for positive Z values.

Equation (22) allows us to evaluate whether a potential disagreement between the experimental value N and the forecast μ _i (N) is statistically significant (e.g., $\left| {Z_{i} } \right| > 2$), thus rendering the H _i PSHA model not supported by the set of S observations.

One can apply the same approach to test hazard estimates expressed in terms of g _s , which is the ground-motion values that correspond to a fixed exceedance probability α, assessed through the considered PSHA computational procedure for an exposure time equal to Δt. In this case, we have e _s  = 1 if the ground shaking at the site during the control period Δt ^* (of duration Δt) exceeded g _s at the sth site; otherwise, e _s  = 0. By definition, P(e _s  = 1) = α. In this case, one has

$$\mu_{i} \left( N \right) = S\alpha$$

(23)

and

$$\sigma_{i} \left( N \right) = \sqrt {S\alpha \left( {1 - \alpha } \right)}$$

(24)

Thus, if N _i exceedances have been obtained for the ith model, Eq. (22) becomes identical to Eq. (17) making the counting and likelihood tests entirely equivalent (in these conditions).

5.4 Testing by Comparing Hazard Estimates with Intensity Data

Historical macroseismic data represent an important benchmark for testing long-term hazard estimates. However, such a comparison requires specific cautions and may provide controversial results when maximum intensity observations are considered only (Miyazawa and Mori 2009, 2010; Beauval et al. 2010).

Another possibility has been explored by Mucciarelli et al. (2006, 2008) that is based on the comparison of outcomes of the standard PSHA (in terms of PGA _α values) with hazard estimates provided by the direct analysis of local seismic histories, i.e. from the list of effects of past earthquakes documented at the site. Unlike previous approaches, in this case, the comparison is not between forecasts and observations but between two kinds of forecasts. In particular, forecasts provided by the standard Cornell–McGuire approach have been compared with those deduced by a PSHA procedure specifically devoted to the full exploitation of macroseismic information (Magri et al. 1994; Albarello and Mucciarelli 2002), that has been recently implemented in the computer program SASHA (D’Amico and Albarello 2008). This approach (hereafter ‘site approach’) has been applied to the PSHA in Italy and elsewhere (Guidoboni and Ferrari 1995; Mucciarelli et al. 1996, 2000, 2008; Azzaro et al. 1999, 2008; Albarello et al. 2002; D’Amico and Albarello 2003, 2008; Galea 2007; Bindi et al. 2012) and shares with the Cornell–McGuire approach the hypothesis that the seismogenic process is stationary. However, it is strongly different from the latter, in that it does not consider seismotectonic constraints, and is mainly based on local macroseismic information that is not taken into account in standard PSHA procedures.

The basic idea of Mucciarelli et al. (2006, 2008) is that PSHA provided by the analysis of macroseismic observations at the site could provide a more direct image of the local hazard than that provided by standard approaches. In fact, these last ones are based on a number of assumptions (seismogenic sources, ground-motion attenuation relationships, etc.), that in many cases can be considered as debatable.

Of course, such comparison requires some cautions. In fact, PSHA estimates provided by the analysis of local seismic histories are expressed in terms of macroseismic intensity. This implies that to compare such results with standard outcomes (e.g., in terms of PGA _α ) requires some form of conversion. To tackle this problem, two possibilities exist. The first possibility is comparing standard PSHA outcomes (expressed as PGA, PSA, etc.) with macroseismic hazard estimates relying on the availability of conversion relationships between macroseismic and instrumental parameters (e.g., for Italy, Faccioli and Cauzzi 2006; Faenza and Michelini 2010; 2011). However, these relationships are empirical in nature and the relevant large uncertainties are expressed in the form of a suitable probability distribution. When the comparison of standard PSHA outcomes and macroseismic estimates is performed, one must take into account this additional source of uncertainty. It is worth noting that converting the ground-motion value g ₀ deduced by a PSHA model (PGA to say) into another observable (macroseismic intensity) just using the average estimates, without taking into account relevant variance, could severely bias the comparison. A correct procedure requires the convolution of the relevant probability distributions (hazard curves and probabilistic conversion relationship) inside the PSHA model (e.g., D’Amico and Albarello 2008). Selva and Sandri (2013) adopted a different approach, by considering uncertainty associated with conversion relationships in the selection of observables.

The second possibility relies on the use of rank comparisons. Actually, this implies that the comparison will only concern the relative ranking that each PSHA model attributes to the investigated localities in the respective domains of the shaking parameters considered (see Mucciarelli et al. 2008 for details). The geographical distribution of rank differences could allow us to individuate possible biases introduced by seismotectonic zoning in the standard hazard estimates. In fact, in the case that these differences show a regional pattern, possible distortions induced by incorrect seismotectonic characterization can be detected. In the case that rank differences show local-scale variations, these can be attributed to local amplification effects that are discarded by standard procedures but taken into account in the analysis of site seismic history.

5.5 Testing by Monte Carlo Procedures

The Monte Carlo approach proposed and applied by Musson (2004, 2012) offers a possible further alternative to the scoring procedures. The author proceeded from the consideration that the hazard estimate is a combination of probability distributions relative to different aspects of the seismic process (e.g., location and size of future earthquakes or attenuation of seismic energy from the source to the site). These probability distributions are then used to build up a number of synthetic catalogues (relative to source activations or ground shaking at the site) randomly generated on the assumption that the probability distributions considered in the computational model are representative for the actual seismogenic process. From these virtual catalogues, a number of statistics are derived and compared with those obtained from observed catalogues. The major drawback of this kind of approach is that it is extremely time-consuming when applied to a large number of sites. Furthermore, in the proposed applications, no likelihood estimate for the tested PSHA models has been actually supplied.

6 An Application to Italy

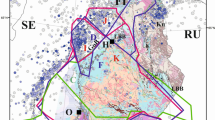
In order to show a possible application of the approaches proposed above, we consider four seismic hazard maps of Italy in terms of macroseismic intensity (Fig. 3). In these maps, the highest Mercalli–Cancani–Sieberg (MCS) intensity degree with probability of exceedance not less than 10 % in 50 years (hereafter indicated as the reference intensity I _ref) is shown for all the Italian municipalities (each estimate refers to the relevant main town) in the mainland and Sicily (7,722 sites). In one case (Fig. 3a), the hazard map (Gómez Capera et al. 2010) was obtained by following the standard Cornell–McGuire approach implemented in the Seisrisk III computer program (Bender and Perkins 1987) modified to account for the use of intensity attenuation relationships. Actually, the outcome here considered is the result of a logic-tree procedure where epistemic uncertainty relative to some aspects of the model was accounted for (see, for details, Gómez Capera et al. 2010). In the other cases (Fig. 3b, c, d), the maps were obtained on purpose in the present study by using the site approach implemented in the SASHA code (D’Amico and Albarello 2008), which is based on the statistical analysis of local seismic history (see Sect. 5.4). We consider three possible implementations of this approach. The first one is based on virtual local seismic histories, i.e. time series of intensity values deduced at each site from epicentral data through attenuation relationships (Fig. 3b). The second one only uses intensity data actually observed at each site (Fig. 3c). The third implementation considers integrated local seismic histories built by combining observed intensities with virtual intensities for known earthquakes whose effects were not documented at the relevant site (Fig. 3d). In general, since larger uncertainty affect virtual intensities, one can expect that hazard estimates in Fig. 3b may tend to overestimate hazard. On the other hand, hazard estimates based on observed intensities only (Fig. 3c) may generally provide underestimate of the hazard due to incompleteness of local seismic histories. In principle, one can expect that the best estimates will correspond to the combination of both pieces of information (virtual and observed intensities) as reported in Fig. 3d.

Fig. 3

Hazard maps of Italy in terms of the highest intensity degree with probability of exceedance not less than 10 % in 50 years (I _ref). Dots correspond to municipalities of Italy (except Sardinia), and the hazard estimates refer to the relevant main towns. The maps were obtained using: (a) the standard Cornell–McGuire approach (Gómez Capera et al. 2010); (b) the site approach (D’Amico and Albarello 2008) by considering virtual intensities only; (c) the site approach by considering observed intensities only; and (d) the site approach by considering a combination of virtual and observed intensities (see text for details). To allow visual comparison, the real-valued I _ref estimates in a were truncated to the lowest integer intensity class. The boundaries of the Apulia Region are also shown (southeast of the Italian mainland)

In order to illustrate how the procedures in Sects. 2, 3, 4 and 5 work, to each of the above PSHA models an ex-ante degree of belief Q ^* has been tentatively attributed. In particular, based on expert judgement, we, respectively, assessed the values of 0.4, 0.1, 0.2 and 0.3 for the standard Cornell McGuire model, for the site approach models based on virtual intensities only, observed intensities only and for combined observed and virtual intensities. These choices could be motivated as follows. The highest Q* value is attributed to the Cornell–McGuire model since it includes seismotectonic information, and this, in principle, makes this PSHA model more complete than the other ones. Since no information at the site is actually considered, we attributed the smallest Q* value to the PSHA model based on virtual intensities. We attributed a slightly higher Q* value to the PSHA model based on the analysis of documented intensities only since it is expected that large incompleteness may affect most of localities. Finally, we attributed a higher Q* value to the PSHA model based on the analysis of combined observed and virtual intensities that in principle is able to take full advantage from available information about the seismic history.

It is worth noting that, in the case of the standard approach, conventional real-valued I _ref intensities are obtained which correspond to the exceedance value of 10 %, while, in the case of the site approach, integer intensity values are considered and, thus, I _ref is the highest intensity degree with exceedance probability not less than 0.1.

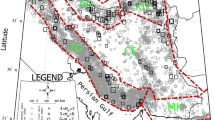
We compared the outcomes of the four models with maximum MCS intensities observed during the control period 1957–2006 at the same sites considered for the hazard assessment (Fig. 4). We deduced intensity data from the Italian macroseismic database DBMI11 (Locati et al. 2011). It is worth noting that these data are the result of a revision and extension of the previous database (DBMI04: Stucchi et al. 2007) used to feed the hazard maps in Fig. 4. In the case of the standard estimates, we considered all information available at the time of publication (2010) about past seismicity (up to 2002) to feed the computational model. In the case of the site approach models, instead, we took into account only information up to 1956. This implies that, in principle, the first model is favoured with respect to the other ones, and the test is actually prospective only in the case of the site approach models.

Fig. 4

Maximum observed MCS intensities at the main towns of the Italian municipalities in the period 1957–2006 reported in the DBMI11 database (Locati et al. 2011)

We did not decluster the data set considered for scoring for two reasons. The first one is that intensity databases cannot be declustered since intensity values mainly reflect cumulative damage induced by a seismic sequence. In fact, after a damaging event, the seismic effects relative to subsequent earthquakes on the same settlement are biased by the conditions of buildings affected by the previous events. The second reason is that PSHA in terms of macroseismic intensity aims at fixing a reasonable upper bound for seismic effects expected to be not exceeded at a fixed probability during the exposure time, irrespective of the fact that these effects result from a mainshock, an aftershock or a seismic swarm. The fact that some PSHA models (e.g., the one based on the Cornell–McGuire approach) assume seismicity as a stationary Poisson process (and only independent events are considered for the model parameterization) is a possible limitation of these models. They fail when they underestimate seismic occurrences with respect to observations and changing observations to fit model requests may bias the correct evaluation of performances of those models.

At first, all the hazard maps in Fig. 3 were tested by computing respective Z _i values for a fixed value of α = 0.1 by Eq. (17). In this situation, one can expect that 772 sites [see Eq. (23)] would have experienced at least one earthquake with local effects (intensity) larger than the values in Fig. 3 and the expected SD [Eq. (24)] is 26. Actually, the number of observed exceedances is 92, 174, 5382 and 165, respectively, in the case of the Cornell–McGuire model (Fig. 3a) and the site approach models based on virtual intensities only (Fig. 3b), observed intensities only (Fig. 3c) and combined observed and virtual intensities (Fig. 3d). These outcomes clearly indicate that hazard appears largely overestimated, except in the case of the model in Fig. 3c, that dramatically underestimates the hazard. Respective Z values are −26, −23, 175 and −23, and they indicate that all the models provide outcomes that are not supported by observations. In particular, except the model in Fig. 3c, all the PSHA models tend to overestimate largely the observed seismicity. On the contrary, the model in Fig. 3c strongly underestimates observed occurrences.

Possibly the site approach performs a little bit better than the standard one (despite the fact that only for the former the test is actually prospective), but the mismatch with observations is anyway significant. This result suggests that observations do not support any of the maps in Fig. 3, and this makes possibly unreliable a comprehensive estimate based on these PSHA models.

However, the above conclusions generally hold when one considers the area under study as whole. This does not imply that the PSHA models considered do not perform when parts of the whole area are of concern. An example of this is the hazard estimate in the Apulia Region whose boundaries are indicated in the maps in Fig. 3. By considering this area only, we considered for testing 258 localities. In this case, the expected number of exceedances is 26 with an expected SD of 4.8. Observed number of exceedances for the considered models is 0, 28.5, 187 and 19, respectively, for hazard models in Figs. 3a, b, c, d. Respective Z values are −5.4, 0.6, 33.3 and −1.5. In this case, observations do not support two out of the set of considered models: the Cornell–McGuire model (providing significant hazard overestimation) and the site approach model based on observed intensities only (providing significant hazard underestimation). In terms of Z values, best performing PSHA model is the one relative to the PSHA model in Fig. 3b (site approach by considering virtual intensity values only). The value of L relative to this model is 0.072. By considering this model as reference, Bayes factors relative to the other models can be computed (Eq. 6) and result in 0.95 for the PSHA model in Fig. 3d relative to the site approach by considering the integration of observed and virtual intensities and ≪10⁻⁵ for both the remaining models. As one can see that, due to the very low likelihood values that characterize these last models, these cannot play any role in the definition of the comprehensive estimate by Eq. 4. It therefore does not matter if these two models are excluded from the analysis. We report in Fig. 5 an example of the comprehensive hazard estimate obtained through Eq. (4) at a site of Apulia (Acquaviva delle Fonti).

Fig. 5

Hazard curve for the site of Acquaviva delle Fonti in Apulia. For each MCS intensity threshold, the probability is reported that at least one earthquake with intensity at the site equal or larger than the threshold will occur during a time span of 50 years. The two PSHA models actually contributing to the comprehensive estimate (continuous line) deduced from Eq. (4) are shown: the one deduced by the site approach considering site intensity data from epicentral data only (dashed line) and the one deduced by the same approach from a combination of virtual and observed data (dotted line)

7 Discussion and Conclusions

In the frame of a formally coherent Bayesian approach, the problem of providing seismic hazard estimates in the presence of alternative computational models has been analysed. The basic idea is that several PSHA models can be combined and weighted as a function of the degree of belief in their actual reliability (scoring). This approach is in line with the one proposed by Marzocchi et al. (2012) with a basic difference concerning the complementary role here assigned role to ex-ante (logic-tree approach and expert judgements) and ex-post evaluations (by matching hazard outcomes with observations) of the considered PSHA models. This overcomes the drawbacks implicit in both approaches. As concerns ex-ante scoring procedures, we suggest the logic-tree approach as a tool to allow a panel of experts to better elicit in a quantitative form their opinions and can be considered useful for supplying prior probabilities for the Bayesian analysis. This requires, of course, that all plausible PSHA models are actually considered and the eventual selection only discards incoherent or clearly wrong models. The fact that these ex-ante evaluations are only used to supply prior information in the frame of a Bayesian analysis reduces the possible impact of drawbacks related to the lack of a perfect formal coherency of the logic-tree procedure and to the inherent subjectivity of expert judgements. This ex-ante scoring is then combined by an ex-post empirical scoring based on the comparison of outcomes provided by each PSHA model with sets of observables. Due to the presence of prior evaluations, possible drawbacks of ex-post scoring (e.g., the limited amount of empirical observations or the short duration of their time coverage) can be mitigated.

In this way, comprehensive hazard estimates can be provided which account for both epistemic and aleatory uncertainty within a unique frame. In line with Bommer and Scherbaum (2008), the scoring techniques here considered concern each procedure as a whole by focusing on final outcomes. In fact, evaluating single parts of a PSHA methodology (e.g., seismicity rates of seismogenic sources and ground-motion attenuation relationship) and attributing the relevant results to the whole procedure can lead to misleading conclusions. Rabinowitz and Steinberg (1991) and Stirling and Petersen (2006) convincingly demonstrated that a significant interplay exists among single elements contributing to the final hazard estimate. Thus, the overall reliability of the procedure is more than just a simple combination of single reliabilities relative to individual components. Scoring should therefore consider each PSHA methodology as a whole, as well as the results each methodology provides (Grandori et al. 2006).

We described and discussed several procedures devoted to scoring and testing PSHA models. Approaches based on likelihood computations seem to be more effective and coherent with the strategy here proposed to provide comprehensive hazard estimates.

In the perspective here presented, we consider empirical testing as inherently different from scoring since it only aims at identifying PSHA models not supported by observations. In other words, it provides a dichotomic outcome that is a function of a conventional significance threshold testing. A relatively marginal role here is assigned to empirical testing, which is used to prevent pathological situations where none of the PSHA models considered is supported by observations. We reviewed several testing procedures and showed that, under specific conditions, at least two of them (likelihood and counting test) are equivalent.

In order to show the feasibility of the proposed approach, four hazard maps available for Italy deduced from different approaches and expressed in terms of macroseismic intensity as ground-shaking parameter have been considered as an example. It is worth noting that these maps were not converted from analogous maps expressed in terms of instrumental parameters (PGA), but they were specifically determined by considering intensity data as input. In particular, intensity values characterized by an exceedance probability of 10 % in 50 years have been considered as representative of seismic hazard at each site. The scoring/testing analysis considered as evidence the maximum MCS intensities observed at the Italian municipalities during the 50-year time span from 1957 to 2006. This analysis is intrinsically different from the previous ones. Mucciarelli et al. (2008), in fact, only compared hazard maps developed on different bases and providing different outcomes (I _α vs. PGA _α ) without an explicit likelihood analysis. Selva and Sandri (2013) compared converted PGA _α values with macroseismic observations, while Albarello and D’Amico (2008) compared hazard maps in terms of PGA _α with accelerometric observations. The present analysis, instead, compares outcomes of PSHA model entirely developed estimating intensities against macroseismic observations. The test indicated that none of the PSHA models taken into account provides results that are supported by observations at least when the Italian area is considered as a whole. The fact that all the models here considered fail in reproducing observations could possibly mean that the stationarity assumption (shared by all the four models) is unrealistic. As an alternative, one can hypothesize that the data set is biased (e.g., due to the fact that macroseismic observations of past earthquakes are not actually comparable with the ones relative to most recent events) and/or that the adopted attenuation relationships tend to overestimate predicted intensities. Anyway, discussing the failure of the hazard maps here considered is well beyond the aims of the present paper and will deserve further studies.

An important aspect of the above analysis deserves a specific discussion. In the applications of the scoring and testing procedures outlined above, we assumed the mutual independence among seismic occurrences to compute relevant statistics [Eqs. (9), (12), (17)]. It is worth noting that this assumption does not concern the actual seismogenic process but the PSHA model of concern. All the PSHA models considered in the example only provide forecasts about the possible exceedance of an intensity value at each site (during the exposure time) without any reference about eventual synchronous occurrence at sites nearby. On the other hand, however, when a counting testing procedure is considered [e.g., Eq. (17)], in computing the variance of the expected number of exceedances during a fixed exposure time, one should account for the mutual correlation of hazard estimates at the considered sites induced, e.g., by the use of attenuation relationships in the relevant PSHA model (e.g., Rhoades and McVerry 2001). This effect may bias the relevant Z value in that it may result in an overestimate. This increases the probability of a Type-I error when one uses Z for testing PSHA models. One can consider numerical simulations to evaluate and correct this possible bias (e.g., Humbert and Viallet 2008).

An aspect should be underlined and concerns future development of seismometric databases to be used for testing and scoring. In general, ground-motion parameters of engineering interest (e.g., PGA, PSA) are of main concern in seismic hazard estimates. Thus, data provided by accelerometric stations are of primary importance, and operational continuity of these networks becomes an important requisite for testing: a small amount of control sites renders the results strongly sensitive to minor variations in the observational data set. In many cases, this makes testing ineffective, though scoring is possible anyway. In our opinion, major efforts in the development of reliable strategies for scoring and testing PSHA procedures should be devoted more to the collection of extended and well-documented ground-motion data sets rather than to the development of new testing procedures. A key aspect in this sense is the availability of accelerometric observations at the reference soil conditions considered for hazard estimates. This aspect seems to be obvious, but it is in many cases overlooked: very rough soil characterization is generally available at most accelerometric sites and this prevents an effective comparison between forecasts provided by the single PSHA procedure and observations.