Primary singularities of vector fields on surfaces

Abstract

Unless another thing is stated one works in the $C^\infty$ category and manifolds have empty boundary. Let X and Y be vector fields on a manifold M. We say that Y tracks X if $[Y,X]=fX$ for some continuous function $f:M\rightarrow \mathbb {R}$. A subset K of the zero set ${\mathsf {Z}} (X)$ is an essential block for X if it is non-empty, compact, open in ${\mathsf {Z}}(X)$ and its Poincaré-Hopf index does not vanishes. One says that X is non-flat at p if its $\infty$-jet at p is non-trivial. A point p of ${\mathsf {Z}}(X)$ is called a primary singularity of X if any vector field defined about p and tracking X vanishes at p. This is our main result: consider an essential block K of a vector field X defined on a surface M. Assume that X is non-flat at every point of K. Then K contains a primary singularity of X. As a consequence, if M is a compact surface with non-zero characteristic and X is nowhere flat, then there exists a primary singularity of X.

1 Introduction

Whether a family of vector fields has a common singularity is a classical issue in dynamical systems. For instance, on a compact surface with non-vanishing Euler characteristic there always exists a common zero provided that the vector fields commute (Lima [10]) or if they span a finite-dimensional nilpotent Lie algebra (Plante [11]). On the existence of a common singularity for a family of commuting vector fields in dimension $\ge 3$ several interesting results are due to Bonatti [2] (analitic in dimension 3 and 4) and Bonatti and De Santiago [3] (dimension 3). For a complementary discussion on the existence of a common zero the reader is referred to the introduction of [6].

In this paper one shows that on surfaces every essential block of a nowhere flat vector field X includes a point at which all vector fields tracking X vanish (see Theorem 1.1 below).

Throughout this work manifolds (without boundary) and their associated objects are real $C^\infty$ unless another thing is stated. Consider a tensor $\mathcal {T}$ on a manifold P. Given $p\in P$ the principal part of $\mathcal {T}$ at p means $j_p^n \mathcal {T}$ if $j_p^{n-1} \mathcal {T}=0$ but $j_p^n \mathcal {T}\ne 0$, or zero if $j_p^\infty \mathcal {T}=0$. The order of $\mathcal {T}$ at p is n in the first case and $\infty$ in the second one. One will say that $\mathcal {T}$ is flat atp if its order at this point equals $\infty$, and non-flat otherwise.

In coordinates about p the principal part is identified to the first significant term of the Taylor expansion of $\mathcal {T}$ at p. Given a function f such that $f(p)\ne 0$, the principal part of $f\mathcal {T}$ at p equals that of $\mathcal {T}$ multiplied by f(p).

$\mathsf {Z}(\mathcal {T})$ denotes the set of zeros of $\mathcal {T}$ and $\mathsf {Z}_n (\mathcal {T})$, where $n\in \mathbb {N}'$ and $\mathbb {N}':=\mathbb {N}\cup \{\infty \}$, the set of zeros of order n. (Here $\mathbb {N}$ is the set of positive integers.) Notice that $\mathsf {Z}(\mathcal {T})=\bigcup _{k\in \mathbb {N}'} \mathsf {Z}_n (\mathcal {T})$ where the union is disjoint.

Consider a vector field Y on P. Ytracks$\mathcal {T}$ provided $L_Y \mathcal {T}=f\mathcal {T}$ for some continuous function $f:P\rightarrow \mathbb {R}$, referred to as the tracking function. (When $\mathcal {T}$ is also a vector field this means $[Y,\mathcal {T}]=f\mathcal {T}$.) A set $\mathcal {A}$ of vector fields on P tracks $\mathcal {T}$ provided each element of $\mathcal {A}$ tracks X.

A point $p\in \mathsf {Z}(\mathcal {T})$ is a primary singularity of $\mathcal {T}$ if every vector field defined about p that tracks $\mathcal {T}$ vanishes at p. Obviously isolated singularities are primary. The notion of primary singularity is the fundamental new concept of this work.

Let X be a vector field on P. Consider an open set U of P with compact closure $\overline{U}$ such that $\mathsf {Z}(X)\cap (\overline{U}{\setminus }U)=\emptyset$. The index of X on U, denoted by ${\mathsf {i}}(X,U) \in \mathbb {Z}$, is defined as the Poincaré-Hopf index of any sufficiently close approximation $X'$ to $X|\overline{U}$ (in the compact open topology) such that $\mathsf {Z}(X')$ is finite. Equivalently: ${\mathsf {i}}(X, U)$ is the intersection number of X|U with the zero section of the tangent bundle (Bonatti [2]). This number is independent of the approximation, and is stable under perturbation of X and replacement of U by smaller open sets containing ${\mathsf {Z}}(X)\cap U$.

A compact set $K\subset \mathsf {Z}(X)$ is a block of zeros for X (or an X-block) provided K is non-empty and relatively open in $\mathsf {Z}(X)$, that is to say provided K is non-empty and $\mathsf {Z}(X){\setminus }K$ is closed in P. Observe that a non-empty compact $K\subset \mathsf {Z}(X)$ is a X-block if and only if it has a precompact open neighborhood $U\subset P$, called isolating for (X, K), such that $\mathsf {Z}(X)\cap \overline{U}=K$ (manifolds are normal spaces). This implies $\mathsf {i}(X,U)$ is determined by X and K, and does not depend on the choice of U. The index ofXatK is $\mathsf {i}_K (X):=\mathsf {i}(X,U)$. The X-block K is essential provided $\mathsf {i}_K (X)\ne 0$, which implies $K\ne \varnothing$, and inessential otherwise.

If P is compact, it is isolating for every vector field on P and its set of zeros. Therefore, in this case, ${\mathsf {i}}_{\mathsf {Z}(X)}(X)=\mathsf {i}(X, P) =\chi (P)$.

This is our main result, which will be proved in the Sect. 2.1.

Theorem 1.1

Consider an essential block K of a vector field X defined on a surface M. Assume that X is non-flat at every point of K. Then K contains a primary singularity of X.

As a straightforward consequence:

Corollary 1.2

On a compact connected surface M with $\chi (M)\ne 0$ consider a vector field X. Assume that X is nowhere flat. Then there exists a primary singularity of X.

Moreover, four examples illustrating these results are given in Sect. 3.

Remark 1.3

• (a) The hypothesis on the non-flatness of Theorem 1.1 and Corollary 1.2 cannot be omitted as the following example shows. On $S^2 \subset \mathbb {R}^3$ consider the vector field $X=\varphi (x_3) (-x_2 \partial /\partial x_1 +x_1 \partial /\partial x_2 )$ where $\varphi (0)=1$ and $\varphi (\mathbb {R}{\setminus }(-1/2,1/2))=0$. Then the vector fields $Y=-x_2 \partial /\partial x_1 +x_1 \partial /\partial x_2$ and $V=\psi (x_3 )(-x_3 \partial /\partial x_1 +x_1 \partial /\partial x_3 )$ where $\psi (1)=\psi (-1)=1$ and $\psi ([-3/4,3/4])=0$ track X and $\mathsf {Z}(Y)\cap \mathsf {Z}(V)=\emptyset$. Therefore X has no primary singularity.

• (b) Two particular cases of Theorem 1.1 were already known, namely: if X and K are as in the foregoing theorem and $\mathcal {G}$ is a finite-dimensional Lie algebra of vector fields on M that tracks X, then the the elements of $\mathcal {G}$ have a common singularity in K provided that $\mathcal {G}$ is supersolvable (Theorem 1.4 of [5]) or $\mathcal {G}$ and X are analytic (real case of Theorem 1.1 of [6]). Thus these two results are generalized here.

For general questions on Differential Geometry readers are referred to [9], and for those on Differential Topology to [4].

2 Other results

One will need:

Lemma 2.1

On a manifold P of dimension $m\ge 1$ consider a vector field X of finite order $n\ge 1$ at a point p. Then for almost every $v\in T_p P$ there exists a vector field U defined around p such that $U(p)=v$ and the n-times iterated bracket $[U,[U,\dots [U,X]\dots ]]$ does not vanish at p.

Proof

It suffices to prove the result for $0\in \mathbb {R}^m$ and a non-vanishing n-homogeneous polynomial vector field $X=\sum _{\ell =1}^m Q_\ell \partial /\partial x_\ell$. Up to a change of the order of the coordinates, we may suppose $Q_1 \ne 0$.

Given $a=(a_1 ,\dots ,a_m )\in \mathbb {R}^m$ set $U_a :=\sum _{\ell =1}^m a_\ell \partial /\partial x_\ell$. It suffices to show that for almost any $a\in \mathbb {R}^m -\{0\}$ one has $(U_a \cdot \cdot \cdot U_a \cdot Q_1 )(0)\ne 0$, which is equivalent to show that the restriction of $Q_1$ to the vector line spanned by a does not vanish identically. But this last assertion is obvious. $\square$

Given a vector field V on a manifold P, a set $S\subset P$ is V-invariant if it contains the orbits under V of its points.

Proposition 2.2

Consider two vector fields X, Y on a surface M. Assume that Y tracks X with tracking function f. Then each set $\mathsf {Z}_n (X)$, $n\in \mathbb {N}'$, is Y-invariant.

Moreover f is differentiable on the open set

$$\begin{aligned} {[}M{\setminus }\mathsf {Z}(X)]\cup [(\mathsf {Z}(X){\setminus }\mathsf {Z}_\infty (X))\cap (M{\setminus }\mathsf {Z}(Y))]. \end{aligned}$$

This result is a consequence of the following two lemmas.

Lemma 2.3

Under the hypotheses of Proposition 2.2 consider $p\in \mathsf {Z}_n (X)$, $n<\infty$, such that $Y(p)\ne 0$. One has:

• (a) f is differentiable around p.

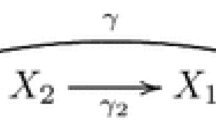
• (b) Let $\gamma :(a,b)\rightarrow M$ be an integral curve of Y with $\gamma (t_0 )=p$ for some $t_0 \in (a,b)$. Then there exists $\varepsilon >0$ such that $\gamma (t_0 -\varepsilon ,t_0 +\varepsilon )\subset \mathsf {Z}_n (X)$.

Proof

Around p consider a vector field U as in Lemma 2.1 such that U(p), Y(p) are linearly independent. Then there are coordinates $(x_1 ,x_2 )$ about $p\equiv 0$, whose domain D can be identified to a product of two open intervals $J_1 \times J_2$, such that $Y=\partial /\partial x_1$ and $U=\partial /\partial x_2 +x_1 V$.

Let $X=g_1 \partial /\partial x_1 +g_2 \partial /\partial x_2$. Then

$$\begin{aligned} {\frac{\partial g_k }{\partial x_1}}=fg_k ,\, k=1,2. \end{aligned}$$

Since f is continuous the general solution to the equation above is:

$$\begin{aligned} g_k (x)=h_k (x_2 )e^\varphi ,\, k=1,2, \end{aligned}$$

where $\partial \varphi /\partial x_1 =f$ and $\varphi (\{0\}\times J_2 )=0$.

From the Taylor expansion at p of X and U it follows that

$$\begin{aligned} {[}U,[U,\dots [U,X]\dots ]](0)=\left[ {\frac{\partial }{\partial x_2} }, \left[ {\frac{\partial }{\partial x_2} },\dots \left[ {\frac{\partial }{\partial x_2} },X \right] \dots \right] \right] (0) \end{aligned}$$

for the n-times iterated bracket.

Note that

$$\begin{aligned} \left[ {\frac{\partial }{\partial x_2} }, \left[ {\frac{\partial }{\partial x_2}},\dots \left[ {\frac{\partial }{\partial x_2} },X \right] \dots \right] \right] (0) ={\frac{\partial ^n g_1}{\partial x_2^n}}(0){\frac{\partial }{\partial x_1}} +{\frac{\partial ^n g_2}{\partial x_2^n}}(0){\frac{\partial }{\partial x_2}}. \end{aligned}$$

Since on $\{0\}\times J_2$ each $g_k =h_k$ finally one has

$$\begin{aligned} {\frac{\partial ^n h_1}{\partial x_2^n}}(0){\frac{\partial }{\partial x_1}} +{\frac{\partial ^n h_2}{\partial x_2^n}}(0){\frac{\partial }{\partial x_2}} =[U,[U,\dots [U,X]\dots ]](0)\ne 0, \end{aligned}$$

which implies the existence of two diferentiable functions $\tilde{h}_1 (x_2)$ and $\tilde{h}_2 (x_2)$ such that $h_k =x_2^n \tilde{h}_k (x_2)$, $k=1,2$, and $\tilde{h}_1^2 (0)+\tilde{h}_2^2 (0)>0$.

Therefore by shrinking D if necessary, we may suppose that at least one of these function, say $\tilde{h}_\ell$, does not have any zero. Observe that f will be differentiable if $\tilde{h}_\ell e^\varphi$ is differentiable because $\tilde{h}_\ell$ is differentiable without zeros and $\partial \varphi /\partial x_1 =f$.

As $g_\ell =x_2^n \cdot (\tilde{h}_\ell e^\varphi )$, it follows that $g_\ell$ is divisible by $1,x_2 ,\dots ,x_2^n$ and the respective quotient functions are at least continuous. Moreover $g_\ell /x^r$, $r=1,\dots ,n-1$, vanish if $x_2 =0$, that is to say on $J_1 \times \{0\}$.

The Taylor expansion of $g_\ell$ transversely to $J_1 \times \{0\}$ leads

$$\begin{aligned} g_\ell =\sum _{r=0}^{n-1}x_2^r \mu _r (x_1 ) +x_2^n \mu _n (x_1 ,x_2 ) \end{aligned}$$

where each $\mu _k$, $k=1,\dots ,n$ is differentiable.

Now since $g_\ell (J_1 \times \{0\})=0$ one has $\mu _0 =0$.

In turn as $g_\ell /x_2$ equals zero on $J_1 \times \{0\}$ it follows $\mu _1 =0$, and so one. Hence $\mu _0 =\dots =\mu _{n-1}=0$, which implies $g_\ell =x_2^n \mu _n (x_1 ,x_2 )$. Therefore $\tilde{h}_\ell e^\varphi =\mu _n$ is differentiable, which proves (a).

On the other hand, as $e^\varphi$ is differentiable and positive, X and

$$\begin{aligned} X':=e^{-\varphi }X=x_2^n \left( \tilde{h}_1 {\frac{\partial }{\partial x_1}} +\tilde{h}_2 {\frac{\partial }{\partial x_2}}\right) \end{aligned}$$

have the same order everywhere. Thus X has order n at every point of $J_1 \times \{0\}$ and (b) becomes obvious. $\square$

Lemma 2.4

Under the hypotheses of Proposition 2.2 consider $p\in \mathsf {Z}_\infty (X)$ with $Y(p)\ne 0$. Let $\gamma :(a,b)\rightarrow M$ be an integral curve of Y passing through p for some $t_0 \in (a,b)$. Then there exists $\varepsilon >0$ such that $\gamma (t_0 -\varepsilon ,t_0 +\varepsilon )\subset \mathsf {Z}_\infty (X)$.

Proof

Around $p\equiv 0$ consider coordinates $(y_1 ,y_2 )$, whose domain E can be identified to a product of two open intervals $K_1 \times K_2$, such that $Y=\partial /\partial y_1$ and $X=a_1 (y_2 )e^\rho \partial /\partial y_1 +a_2 (y_2 )e^\rho \partial /\partial y_2$ where $\partial \rho /\partial y_1 =f$ and $\rho (\{0\}\times K_2 )=0$. These coordinates exist by the same reason as in the proof of Lemma 2.3.

Assume the existence of a $q\in K_1 \times \{0\}$ of finite order n.

Since $p\in \mathsf {Z}_\infty$ and $e^\rho$ equals 1 on $\{0\}\times K_2$, it follows that $j_0^\infty a_1 =j_0^\infty a_2 =0$. Therefore $a_k (y_2 )=y_2^{n+1}b_k (y_2 )$, $k=1,2$, where each $b_k$ is differentiable. Hence there exists a continuous vector field $X_n$ such that $X=y_2^{n+1}X_n$; that is to say X is continuously divisible by $y_2^{n+1}$.

In turn one can find coordinates $(x_1 ,x_2 )$ around $q\equiv 0$ whose domain D can be identify to $J_1 \times J_2$ as in the proof of Lemma 2.3, which implies that

$$\begin{aligned} X=x_2^n e^\varphi \left( \tilde{h}_1 (x_2 ){\frac{\partial }{\partial x_1}} +\tilde{h}_2 (x_2 ){\frac{\partial }{\partial x_2}}\right) \end{aligned}$$

where $\tilde{h}_1 \partial /\partial x_1 +\tilde{h}_2 \partial /\partial x_2$ has no zero on D.

By shrinking D if necessary, we may suppose $D\subset E$. Then, regarded both sets in M, $J_1 \times \{0\}$ is a subset of $K_1 \times \{0\}$ since they are traces of integral curves of Y with q as common point.

On the other hand as $y_2$ vanishes on $K_1 \times \{0\}$ but its derivative never does, on D one has $y_2 =x_2 c(x_1 ,x_2 )$ where c has no zero. This fact implies that X on D is continuously divisible by $x_2^{n+1}$ because it was continuously divisible by $y_2^{n+1}$.

But clearly from the expression of X in coordinates $(x_1 ,x_2 )$ it follows the non-divisibility by $x_2^{n+1}$, contradiction. In short the order of X at each point of $K_1 \times \{0\}$ is infinite. $\square$

Remark 2.5

Under the hypotheses of Proposition 2.2 the tracking function f can be not differentiable around a flat point. For instance, on $\mathbb {R}^2$ set $Y=x_1^4 \partial /x_1 +\partial /\partial x_2$ and $X=g(x_1 )\partial /x_1$, where $g(x_1 )=e^{-1/x_1}$ if $x_1 >0$, $g(x_1) =e^{-1/x_1^2}$ if $x_1 <0$ and $g(0)=0$. Then $f(x)=x_1^2 -4x_1^3$ if $x_1 >0$, $f(x)=2x_1 -4x_1^3$ if $x_1 <0$ and $f(\{0\}\times \mathbb {R})=0$, which is not differentiable on $\{0\}\times \mathbb {R}$.

Proof of Proposition 2.2

Let us proves the first assertion. Consider a non-constant integral curve of Y (the constant case is clear) $\gamma :(a,b)\rightarrow M$. By Lemmas 2.3 and 2.4, $\gamma ^{-1}(\mathsf {Z}(X))$ is open in (a, b). As this set is closed too one has $\gamma ^{-1}(\mathsf {Z}(X))=\emptyset$ or $\gamma ^{-1}(\mathsf {Z}(X))=(a,b)$. The first case is obvious; in the second one $(a,b)=\bigcup _{n\in \mathbb {N}'}\gamma ^{-1}(\mathsf {Z}_n (X))$ where each term of this union is open. Therefore a single term of this disjoint union is non-empty since (a, b) is connected.

For the second assertion apply (a) of Lemma 2.3 taking into account that f is always differentiable on $M{\setminus }\mathsf {Z}(X)$ because, on this set, the quotient [Y, X] / X has a meaning. $\square$

Proposition 2.6

On a surface M consider a vector field X such that $\mathsf {Z}(X)\ne \emptyset$ but $\mathsf {Z}_\infty (X)=\emptyset$. Then at least one of the following assertions holds:

• (1) $\mathsf {Z}(X)$ is a regular (embedded) 1-submanifold.

• (2) There exists a primary singularity of X.

Proof

Assume the non-existence of primary singularities.

Consider any $p\in \mathsf {Z}(X)$ and a vector field Y defined around p with $Y(p)\ne 0$ that tracks X. Let U be a second vector field about p as in Lemma 2.1 such that U(p), Y(p) are linearly independent. Then there exist coordinates $(x_1 ,x_2 )$, about $p\equiv 0$, whose domain D can be identified to a product of two open intervals $J_1 \times J_2$ such that $Y=\partial /\partial x_1$ and $U=\partial /\partial x_2 +x_1 V$.

The same reasoning as in the proof of Lemma 2.3 allows to suppose that

$$\begin{aligned} X=x_2^n e^\varphi \left( \tilde{h}_1 {\frac{\partial }{\partial x_1}} +\tilde{h}_2 {\frac{\partial }{\partial x_2}}\right) \end{aligned}$$

with $\tilde{h}_1^2+\tilde{h}_2^2 >0$ everywhere.

Therefore $\mathsf {Z}(X)\cap D$ is given by the equation $x_2 =0$, which implies that $\mathsf {Z}(X)$ is a regular 1-submanifold. $\square$

Theorem 2.7

Consider a vector field X on a surface M. Assume that:

• (1) $\mathsf {Z}_\infty (X)=\emptyset$.

• (2) There is a connected component of $\mathsf {Z}(X)$ that is not included in a single $\mathsf {Z}_n (X)$.

Then there exists a primary singularity of X.

Proof

Assume there is no primary singularity. By Proposition 2.6, $\mathsf {Z}(X)$ is a regular 1-submanifold of M. By hypothesis there are a connected component C of $\mathsf {Z}(X)$ and two different natural numbers m and n such that C meets $\mathsf {Z}_m (X)$ and $\mathsf {Z}_n (X)$.

As C is a regular 1-submanifold, Proposition 2.2 and Lemma 2.3 imply that each $C\cap \mathsf {Z}_r (X)$, $r\in \mathbb {N}$, is open in C. Therefore C is a disjoint union of a family of non-empty open sets with two or more elements hence not connected, contradiction. $\square$

2.1 Proof of of Theorem 1.1

It consists of three steps.

1. Assume that there is no primary singularity in K. From Proposition 2.6 applied to an isolating open set it follows that K is a compact 1-submanifold. Notice that at least one of its connected component is an essential block. Therefore one may suppose that K is diffeomorphic to $S^1$ and, by shrinking M, that $\mathsf {Z}(X)=K$.

Consider a Riemannian metric g on M. Given $p\in K$ by reasoning as before one can find coordinates $(x_1 ,x_2 )$ such that $p\equiv 0$ and

$$\begin{aligned} X=x_2^n e^\varphi \left( \tilde{h}_1 {\frac{\partial }{\partial x_1}} +\tilde{h}_2 {\frac{\partial }{\partial x_2}}\right) \end{aligned}$$

where $\tilde{h}_1 \partial /\partial x_1 +\tilde{h}_2 \partial /\partial x_2$ has no zero. Therefore around p there exists an 1-dimensional vector subbundle $\mathcal {E}$ of the tangent bundle that is orthogonal to X. Such a vector subbundle is unique because clearly it exists and is unique outside K. Thus, gluing together the local constructions gives rise to an 1-dimensional vector subbundle $\mathcal {E}$ of TM that is orthogonal to X.

2. If $\mathcal {E}$ is trivial there exists a nowhere singular vector field V such that $g(V,X)=0$. Let $\varphi :M\rightarrow \mathbb {R}$ be a function with a sufficiently narrow compact support such that $\varphi (K)=1$. Set $X_\delta :=X+\delta \varphi V$, $\delta >0$. Then $X_\delta$ approaches X as much as desired and $\mathsf {Z}(X_\delta )=\emptyset$, so K is an inessential block.

3. Now assume that $\mathcal {E}$ is not trivial. There always exists a twofold covering space $\pi :M'\rightarrow M$ such that the pull-back $\mathcal {E}'\subset TM'$ of the vector subbundle $\mathcal {E}$ is trivial.

Consider the vector field $X'$ on $M'$ defined by $\pi _* (X')=X$. Then $\mathsf {Z}(X')=\pi ^{-1}(K)$ and $X'$ is nowhere flat. Moreover $\mathcal {E}'$ is orthogonal to $X'$ with respect to the pull-back of g. Now the same reasoning as in the foregoing step shows that $\mathsf {i}_{\mathsf {Z}(X')}(X')=0$. But clearly $\mathsf {i}_{\mathsf {Z}(X')}(X')=2\mathsf {i}_K (X)$ and hence K is inessential.

3 Examples

Example 3.1

In this example one shows two facts. First, primary singularities can exist even if the index of X is not definable. Second, being nowhere flat is a weaker hypothesis than being analytic.

Consider a proper closed subset C of $\mathbb {R}$ and a function $\varphi :\mathbb {R}\rightarrow \mathbb {R}$ such that $\varphi ^{-1}(0)=C$. Set $X:=x^2_1 \partial /\partial x_1 +x_1 \varphi (x_2 )\partial /\partial x_2$. Then $\mathsf {Z}(X)=\{0\}\times \mathbb {R}$, $\mathsf {Z}_1 (X)=\{0\}\times (\mathbb {R}{\setminus } C)$, $\mathsf {Z}_2 (X)=\{0\}\times C$ and $\mathsf {Z}_n (X)=\emptyset$ for $n\ne 1,2$, so X is nowhere flat. By Theorem 2.7 the vector field X has primary singularities.

More exactly the set $S_a$ of primary singularities of X equals $\{0\}\times (C{\setminus } {\buildrel {\circ }\over {C}})$. Indeed:

• (1) $\varphi (x_2 )\partial /\partial x_2$ tracks X and does not vanish on $\{0\}\times (\mathbb {R}{\setminus } C)$.

• (2) $\partial /\partial x_2$ tracks X on $\mathbb {R}\times {\buildrel {\circ }\over {C}}$.

Therefore $S_a \subset \{0\}\times (C{\setminus }{\buildrel {\circ }\over {C}})$.

Take $p=(0,c)\in \{0\}\times (C{\setminus }{\buildrel {\circ }\over {C}})$. Assume the existence around this point of a vector field Y with $Y(p)\ne 0$ that tracks X. Them from Proposition 2.2 and Lemma 2.3 it follows the existence of $\varepsilon >0$ such that the order of X at every point of $\{0\}\times (c-\varepsilon ,c+\varepsilon )$ is constant and hence c belongs to the interior of $\mathbb {R}{\setminus } C$ or to that of C. Therefore $c\not \in C{\setminus }{\buildrel {\circ }\over {C}}$ contradiction.

In short, each element of $\{0\}\times (C{\setminus }{\buildrel {\circ }\over {C}})$ is a primary singularity and $S_a =\{0\}\times (C{\setminus }{\buildrel {\circ }\over {C}})$.

Finally observe that if C is a Cantor set, then X is not analytic for any analytic structure on $\mathbb {R}^2$ since $\mathsf {Z}_2 (X)=\{0\}\times C$ is never an analytic set.

Example 3.2

In this example one gives a vector field on $S^2$, which is analytic so with no flat points, whose zero set is a circle just with two primary singularities.

The sphere $S^2$ can be regarded as the leaves space of the 1-dimensional foliation on $\mathbb {R}^3{\setminus }\{0\}$ associated to the vector field $V=\sum _{k=1}^3 x_k \partial /\partial x_k$, while the canonical projection $\pi :\mathbb {R}^3 {\setminus }\{0\}\rightarrow S^2$ is given by $\pi (x)=x/\parallel x\parallel$.

Every linear vector field $U'$ commutes with V and can be projected by $\pi$ on a vector field U on $S^2$. Moreover $U(a)=0$, where $a=(a_1 ,a_2 ,a_3 )\in S^2$, if and only if a is an eigenvector of $U'$ regarded as an endomorphism of $\mathbb {R}^3$, that is to say if and only if

$$\begin{aligned} \left[ \sum _{k=1}^3 a_k {\frac{\partial }{\partial x_k }},U'\right] =\lambda \sum _{k=1}^3 a_k {\frac{\partial }{\partial x_k }} \end{aligned}$$

for some scalar $\lambda$.

Set $X:=\pi _* (x_1 \partial /\partial x_2 )$. Then $\mathsf {Z}(X)=\{x\in S^2 :x_1 =0\}$ is an essential block of index two since $\chi (S^2)=2$. By Corollary 1.2 the set $S_a$ of primary singularities of X is not empty.

For determining it consider the vector field $Y:=\pi _* (x_3 \partial /\partial x_2 )$. Then $[X,Y]=0$ because $[x_1 \partial /\partial x_2 ,x_3 \partial /\partial x_2]=0$. Moreover $\mathsf {Z}(Y)=\{x\in S^2 :x_3 =0\}$.

As Y tracks X, the vector field Y is tangent to $\mathsf {Z}(X)$. On the other hand $\mathsf {Z}(X)\cap \mathsf {Z}(Y)=\{(0,1,0),(0,-1,0)\}$, so $S_a\subset \{(0,1,0),(0,-1,0)\}$. Since $F_* X=X$, where F is the antipodal map, one has $F(S_a )=S_a$ and hence $S_a=\{(0,1,0),(0,-1,0)\}$.

Example 3.3

Let M be a connected compact surface of non-vanishing Euler characteristic. As it is well known, on M there always exist two vector fields X, Y with no common zero such that $[Y,X]=X$ (Lima [10], Plante [11]; see [1, 13] as well). Therefore there is no primary singularity of X, but there always exists a periodic regular trajectory ofYincluded in$\mathsf {Z}_\infty (X)$.

Indeed, by Corollary 1.2 and Proposition 2.2 the set $\mathsf {Z}_\infty (X)$ is non-empty and Y-invariant. Since $\mathsf {Z}_\infty (X)$ is compact, there always exists a minimal set $S\subset \mathsf {Z}_\infty (X)$ of (the action of) Y.

As $\mathsf {Z}(X)\cap \mathsf {Z}(Y)=\emptyset$, a generalization of the Poincaré–Bendixson theorem [12] implies that S is homeomorphic to a circle. In other words, there exists a non-trivial periodic trajectory of Y consisting of flat points of X.

More generally, given a vector field $\widehat{X}$ on M let $\mathcal {A}$ be the real vector space of those vector fields on M that track $\widehat{X}$. Assume that $\mathsf {Z}(\widehat{X})\ne M$ and $\mathsf {Z}(\widehat{X})\cap (\bigcap _{V\in \mathcal {A}}\mathsf {Z}(V))=\emptyset$. Then by Corollary 1.2 the compact set $\mathsf {Z}_\infty (\widehat{X})$ is not empty and contains a minimal set $\widehat{S}$ of $\mathcal {A}$ (more exactly of the group of diffeomorphisms of M spanned by the flows of the elements of $\mathcal {A}$).

Clearly $\widehat{S}$ is not a point. A second generalization of the Poincaré–Bendixson theorem [8] shows that $\widehat{S}$ is homeomorphic to a circle.

Even more, in our case $\widehat{S}$ is a regular 1-submanifold and hence diffeomorphic to a circle. Let us see it. Take $p\in \widehat{S}$; then there is $V\in \mathcal {A}$ with $V(p)\ne 0$. Consider coordinates $(x_1 ,x_2 )$ around $p\equiv 0$ whose domain D is identified in the natural way to a product $(-\varepsilon ,\varepsilon )\times (-\varepsilon ,\varepsilon )$ such that $V=\partial /\partial x_1$.

Let $\gamma :(-\delta ,\delta )\rightarrow M$ be an integral curve of V with initial condition $\gamma (0)=p$. Then $\gamma (-\delta ,\delta )\subset \widehat{S}$. Moreover, if $\delta$ is sufficiently small $\gamma (-\delta ,\delta )$ is a relatively open subset of $\widehat{S}$. Indeed, $\gamma :(-\delta ,\delta )\rightarrow \widehat{S}$ will be injective so open because $\widehat{S}$ is a 1-dimensional topological manifold (actually $S^1$). Now by shrinking D and $(-\delta ,\delta )$ if necessary, we may suppose that $\gamma (-\delta ,\delta )\subset D$, $\delta =\varepsilon$ and $\gamma (t)=(t,0)$. Thus $(-\varepsilon ,\varepsilon )\times \{0\}=\gamma (-\delta ,\delta )$ is relatively open in $\widehat{S}$ and there exists an open set E of M such that $E\cap \widehat{S}=(-\varepsilon ,\varepsilon )\times \{0\}$. Hence $\widehat{S} \cap (D\cap E)$ is defined by the equation $x_2 =0$ in the system of coordinates $(D\cap E,(x_1 ,x_2 ) )$.

3.1 An example from the blowup process

In this subsection one constructs a homogeneous polynomial vector field on $\mathbb {R}^2$ whose trajectories but a finite number, let us call them exceptional, have the origin both as $\alpha$ and $\beta$-limit. Then by blowing up the origin one obtains a new vector field on a Moebius band whose number of primary singularities equals half that of exceptional trajectories of the first vector field.

Thus a global property on the trajectories of a vector field becomes a semi-local property on the primary singularities of another vector field.

First some technical facts. Denote by $\widetilde{\mathbb {R}}^2$ the surface obtained by blowing up the origin of $\mathbb {R}^2$ and by $\tilde{p}:\widetilde{\mathbb {R}}^2\rightarrow \mathbb {R}^2$ the canonical projection. Recall that $\widetilde{\mathbb {R}}^2$ is a Moebius band. If X is a vector field on $\mathbb {R}^2$ that vanishes at the origin, the blowup process gives rise to a vector field $\widetilde{X}$ on $\widetilde{\mathbb {R}}^2$ such that $\tilde{p}_* \widetilde{X}=X$. When the origin is an isolated singularity of index k and the order of X at this point is $\ge 2$, then $\tilde{p}^{-1}(0)$ is a $\widetilde{X}$-block of index $k-1$.

Now identify $\mathbb {C}$ to $\mathbb {R}^2$ by setting $z=x_1 +ix_2$. Then each complex vector field $z^n \partial /\partial z$, $n\ge 2$, can be considered as a vector field $X_n =P_n \partial /\partial x_1 +Q_n \partial /\partial x_2$ on $\mathbb {R}^2$ where $z^n =(x_1 +ix_2 )^n =P_n (x_1 ,x_2 )+iQ_n (x_1 ,x_2 )$. Our purpose will be to show that $\mathsf {Z}(\widetilde{X}_n )=\tilde{p}^{-1}(0)$ contains $n-1$ primary singularities of $\widetilde{X}_n$. (Recall that the origin is a singularity of $X_n$ of index n and hence $\tilde{p}^{-1}(0)$ is a $\widetilde{X}_n$-block of index $n-1$.)

3.1.1 $\tilde{\mathbb {R}}^2$ from another point of view

Consider the map $\varphi :\mathbb {R}\times S^1\rightarrow \mathbb {R}^2$ given by $\varphi (r,\theta )=(rcos\theta ,rsin\theta )$. Then $\varphi :\mathbb {R}_+ \times S^1\rightarrow \mathbb {R}^2 {\setminus }\{0\}$ and $\varphi :\mathbb {R}_- \times S^1\rightarrow \mathbb {R}^2 {\setminus }\{0\}$ are diffeomorphisms, and $\varphi (r,\theta )=\varphi (r',\theta ')$ with $(r,\theta ),(r',\theta ')\in (\mathbb {R}{\setminus }\{0\})\times S^1$ if and only if $(r,\theta )=(r',\theta ')$ or $(r',\theta ')=(-r,\theta +\pi )$.

Let $\sim$ be the equivalence relation on $\mathbb {R}\times S^1$ defined by $(r,\theta )\sim (r',\theta ')$ if and only if $(r,\theta )=(r',\theta ')$ or $(r',\theta ')=(-r,\theta +\pi )$. Then the quotient space $M_s:=(\mathbb {R}\times S^1 )/\sim$ is a Moebius strip and the canonical projection $p:\mathbb {R}\times S^1 \rightarrow M_s$ is a (differentiable) covering space with two folds. Moreover the map $\bar{\varphi }:M_s \rightarrow \mathbb {R}^2$ given by $\bar{\varphi }(p(r,\theta ))=\varphi (r,\theta )$ is well defined and differentiable.

Recall that $\tilde{p}^{-1}(0)=\mathbb {R}P^1$ is the space of vector lines in $\mathbb {R}^2$ and $\tilde{p}:\widetilde{\mathbb {R}}^2{\setminus }\tilde{p}^{-1} (0) \rightarrow \mathbb {R}^2{\setminus }\{0\}$ a diffeomorphism. Now one defines $\Psi :M_s \rightarrow \widetilde{\mathbb {R}}^2$ as follows:

• (a) $\Psi (p(r,\theta ))=\tilde{p}^{-1}(\varphi (r,\theta ))$ if $r\ne 0$,

• (b) $\Psi (p(r,\theta ))$ equals the vector line of $\mathbb {R}^2$ spanned by $(cos\theta ,sin\theta )$ if $r=0$.

It is easily checked that $\Psi :M_s \rightarrow \widetilde{\mathbb {R}}^2$ is a diffeomorphism and $\tilde{p}\circ \Psi =\bar{\varphi }$. Therefore $\tilde{p}:\widetilde{\mathbb {R}}^2\rightarrow \mathbb {R}^2$ and $\bar{\varphi }:M_s \rightarrow \mathbb {R}^2$ can be identified in this way. For sake of simplicity in what follows $\tilde{p}:\widetilde{\mathbb {R}}^2\rightarrow \mathbb {R}^2$ will replaced by $\bar{\varphi }:M_s \rightarrow \mathbb {R}^2$ in our computations. Thus if X is a vector field on $\mathbb {R}^2$ that vanishes at the origin, then $\widetilde{X}$ will be the single vector field on $M_s$ such that $\bar{\varphi }_* \widetilde{X}=X$.

On the other hand $X'$ will denote the pull-back by p of $\widetilde{X}$. Clearly $\varphi _* X'=X$. Moreover with respect to $X'$ the index of $\{0\}\times S^1$ and the number of primary singularities included in it are twice those of $\bar{\varphi }^{-1}(0)$ relative to $\widetilde{X}$.

As a consequence, in the case of $X_n$ it will suffice to show that $\mathsf {Z}(X'_n )=\{0\}\times S^1$ contains $2n-2$ singularities of $X'_n$.

3.1.2 Computation of the primary singularities of $X'_n$

As $\varphi :(\mathbb {R}{\setminus }\{0\})\times S^1 \rightarrow \mathbb {R}^2 {\setminus }\{0\}$ is a covering space any vector field on $\mathbb {R}^2 {\setminus }\{0\}$ can be lifted up. Denote by $\partial '/\partial x_k$, $k=1,2$, the lifted vector field of $\partial /\partial x_k$. Then

$$\begin{aligned} {\frac{\partial '}{\partial x_1}}=cos\theta {\frac{\partial }{\partial r}} -r^{-1}sin\theta {\frac{\partial }{\partial \theta }} \qquad \text {and}\qquad {\frac{\partial '}{\partial x_2}} =sin\theta {\frac{\partial }{\partial r}} +r^{-1}cos\theta {\frac{\partial }{\partial \theta }}. \end{aligned}$$

Since $(rcos\theta +irsin\theta )^n =r^n cos(n\theta )+ir^n sin(n\theta )$ one has $P_n \circ \varphi =r^n cos(n\theta )$ and $Q_n \circ \varphi =r^n sin(n\theta )$. Observe that on $(\mathbb {R}{\setminus }\{0\})\times S^1$ the vector field $X'_n$ is the lifted one of $X_n$, so $X'_n =r^n cos(n\theta )\partial '/\partial x_1 +r^n sin(n\theta )\partial '/\partial x_2$. Finally, developing the foregoing expression of $X'_n$ and extending it by continuity to $\mathbb {R}\times S^1$ yields:

$$\begin{aligned} X'_n=r^{n-1}\left( rcos((n-1)\theta ){\frac{\partial }{\partial r}} +sin((n-1)\theta ){\frac{\partial }{\partial \theta }}\right) \end{aligned}$$

The vector field $Y=rcos((n-1)\theta )\partial /\partial r+sin((n-1)\theta )\partial /\partial \theta$ tracks $X'_n$ with tracking function $(n-1)cos((n-1)\theta )$. Therefore the set $S_a$ of primary singularities of $X'_n$ is included in $\{0\}\times T_n$ where $T_n :=\{\theta \in S^1 :sin((n-1)\theta )=0\}$.

On the other hand, the order of $X'_n$ at the points of $\{0\}\times (S^1{\setminus } T_n)$ is $n-1$ and strictly greater than $n-1$ at the points of $\{0\}\times T_n$. As $T_n$ is finite, more exactly it has $2n-2$ elements, Proposition 2.2 and Lemma 2.3 imply that all the points of $\{0\}\times T_n$ are primary singularities. In short $S_a=\{0\}\times T_n$ and hence $\mathsf {Z}(\widetilde{X}_n )=\tilde{p}^{-1}(0)$ contains $n-1$ primary singularities.

3.1.3 The geometric meaning of the primary singularities of $\tilde{X}_n$

When $n\ge 2$ the complex flow of $z^n \partial /\partial z$ is

$$\begin{aligned} \Phi (z,t)=z\left[ (1-n)tz^{n-1}+1\right] ^{\frac{1}{1-n}} \end{aligned}$$

with initial condition $\Phi (z,0)=z$.

(Fixed $z\ne 0$ consider as domain of the variable t the open set $D_z :=\mathbb {C}{\setminus } R_z$ where $R_z :=\{s(n-1)^{-1}z^{1-n} :s\in [1,\infty )\}$. Note that $D_z$ is star shaped with respect to the origin. Since $D_z$ is simply connected, the initial condition $\Phi (z,0)=z$ defines a single continuous and hence holomorphic map $\Phi (z,\quad ):D_z \rightarrow \mathbb {C}$. Thus the apparent ambiguity introduced by the root of order $n-1$ is eliminated.)

On the other hand considering, in the foregoing expression of $\Phi$, real values of t only and identifying z with $(x_1 ,x_2 )$ yield the real flow of $X_n$. Therefore given $(x_1 ,x_2 )\in \mathbb {R}^2 {\setminus }\{0\}$ if $z^{n-1}=(x_1 +ix_2 )^{n-1}$ is not a real number, its $X_n$-trajectory is defined for any $t\in \mathbb {R}$ and has the origin both as $\alpha$ and $\omega$-limit.

On the contrary when $z^{n-1}=(x_1 +ix_2 )^{n-1}$ is a real number, the $X_n$-trajectory of $(x_1 ,x_2 )$, as set of points, equals the open half-line spanned by the vector $(x_1 ,x_2 )$ and hence one of its limits is the origin and the other one the infinity.

It is easily checked that the set of $(x_1 ,x_2 )\in \mathbb {R}^2$ such that $(x_1 +ix_2 )^{n-1}\in \mathbb {R}$ consists of $n-1$ vector lines each of them including two exceptional trajectories. These lines regarded as elements of $\mathbb {R}P^1 =\tilde{p}^{-1}(0)$ are the primary singularities of $\widetilde{X}_n$.